Article Highlights

  • A review is presented of the main improvements in the precise orbit determination of altimetry satellites made in the last thirty years

  • Altimetry satellite orbit accuracy in the radial direction improved from a few decimeter to 1 cm level in this time

  • Major improvements are due to using new reference frames, Earth time-variable gravity field models, GPS and DORIS data

1 Introduction

Satellite radar altimetry is one of the main methods to investigate the changes of the global, regional, and coastal sea levels and their trends since 1992 (Stammer and Cazenave 2017; Legeais et al. 2018; International Altimetry Team 2021). According to the recent study by Cazenave et al. (2019) based on using radar altimetry observations from January 1993 to February 2019, the mean sea level rises globally with a rate of 3.15 ± 0.3 mm/year and an acceleration of 0.10 ± 0.04 mm/year\(^2\). The current uncertainty of the global mean sea level (GMSL) trend is estimated to be 0.3–0.4 mm/year (Ablain et al. 2019). The regional mean sea level (MSL) trend reaches 10 mm/year, i.e., about three times as large as the GMSL trend, in the western and southern parts of the Pacific, the central part of the Indian ocean, the southern part of the Atlantic ocean and some other regions (Legeais et al. 2021). Precise knowledge on the mean sea level observed during the altimetry era is important also for its extrapolation for the next decades for practical reasons and climate change studies (Nerem et al. 2022). The satellites TOPEX/Poseidon, Jason-1/-2/-3, and Sentinel-6A covering in total the time span from 1992 until now are the reference missions for sea level investigation (Quartly et al. 2017). Precise orbits of altimetry satellites are a prerequisite for the investigation of global, regional, and coastal sea levels together with their changes, since accurate orbit information is required for the reliable determination of the water surface height. Since the radar distance is measured from the altimetry satellite to the ocean, lake or river surface, satellite positions should be known precisely (at sub-centimeter level) to get precise information on the water level (Couhert et al. 2015).

Errors in the wet tropospheric correction and link between successive altimetry missions remain the major contributions to the GMSL uncertainty (Cazenave et al. 2019). Additional errors come from a reference frame realization in which the orbits are computed, orbit modeling and corrections applied to observations. Since orbit differences (errors) in the radial direction will map into the sea level, their investigation allows studying and minimizing orbit-related (non-geophysical) sea level errors. Ablain et al. (2019) provide current estimates of the uncertainties of the global and regional sea level trends due to various errors in radiometer, sea-state-bias, wet tropospheric correction, altimeter noise, altimeter instabilities (for TOPEX/Poseidon) and other sources. According to their study, orbit errors are still a significant source of uncertainties of the global and regional sea level trends.

Substantial advance in the improvement of altimetry satellite orbit quality has been made in the last 30 years. In this paper, we review the main improvements in precise orbit determination (POD) obtained for altimetry satellites in the recent decades (see Sect. 2). Additionally, we evaluate the accuracy of contemporary orbits of 11 altimetry satellites (Cryosat-2, Envisat, ERS-1, ERS-2, Jason-1, Jason-2, Jason-3, SARAL, Sentinel-3A, Sentinel-3B, and TOPEX/Poseidon) derived by six various institutions (Sect. 3). This is done by orbit inter-comparison (Sect. 4) and multi-mission crossover analysis (Sect. 5) of historical and contemporary orbit solutions. The latter were derived in the state-of-the-art reference frames using up-to-date background models for POD by using various observation types. We present the results of our analysis of satellite orbit differences in the radial direction, single-satellite crossover differences, radial and geographically correlated errors of various orbit solutions. Conclusions are made in Sect. 6.

2 The Main Improvements in the Altimetry Satellite Precise Orbit Determination in the Last Thirty Years

Orbits of altimetry satellites are nowadays usually computed using DORIS (Doppler Orbitography and Radiopositioning Integrated by Satellite), SLR (Satellite Laser Ranging) and, for some satellites, GPS (Global Positioning System) observations of the global network of tracking stations (e.g., Couhert et al. 2015; Soudarin et al. 2016; Zelensky et al. 2017). The SLR, DORIS, and GPS systems have been improved in the last three decades. Thus, from 2001–2002 onward altimetry satellites were equipped with the second generation DORIS receivers (Tavernier et al. 2003). Since 2008, the satellites are equipped with the third-generation (DGXX) DORIS receivers (Auriol and Tourain (2010)). These innovations together with DORIS Immediate Orbit Determination (DIODE) real-time on-board software upgrade contributed to the improvement of the measurement accuracy and led to 2.7–3.3 cm root mean square (RMS) real-time radial orbit accuracy (Jayles et al. 2016). Improvements in DORIS antenna modeling also enhanced the orbit quality (Lemoine et al. 2016). GPS has been further enhanced in the recent decades by ending selective availability, adding new civil signals, using new control segments, launching GPS satellites of new generation, and by using modern technologies (https://gssc.esa.int/navipedia/index.php/GPS_Future_and_Evolutions). The SLR system has been also improved in the recent decades by using high repetition rate and ultra-short pulsed lasers, micro-channel plate detectors, single-photon avalanche diodes, GPS receivers as frequency standards, and by performing frequent calibrations to terrestrial targets (Rodriguez and Appleby 2021). SLR range and time biases caused by unaccounted electronic delays and technical problems in station equipment may degrade the orbit quality if not modeled or estimated (Exertier et al. 2017 and Luceri et al. 2019). Therefore, the estimation of range biases of SLR measurements mitigates radial errors in altimetry satellite Precise Orbit Determination (POD) (Soudarin et al. 2016). The determination of orbits of altimetry satellites from the combination of measurements of different space geodetic techniques, such as DORIS, SLR, and GPS, allows to investigate and determine technique-specific deficiencies, such as SLR range and time biases, DORIS time bias, deficiencies in the information on location of phase centers of measuring devices of various tracking techniques on the satellite, and thus improve consistency and accuracy of the orbits (e.g., Perosanz et al. 1997; Luthcke et al. 2003; Willis et al. 2003).

The DORIS network consisted of 30–60 beacons over the past 30 years (Saunier 2016). This network is more homogeneous than the network of SLR stations, but not so dense as the GPS network. DORIS measurements are disturbed by the troposphere. Various tropospheric correction models have been developed for space-based microwave observations. Most widely used is Vienna Mapping Function (VMF)1 (Boehm et al. 2006b). To absorb remaining mismodeling, a troposphere correction scale factor is usually estimated per each satellite pass over a beacon. Additionally, for each beacon, a frequency bias between the frequencies of the beacon and satellite sender is estimated. The satellite clock is realized by using ultra-stable oscillator onboard the DORIS satellite. These oscillators are, unfortunately, affected by the South Atlantic Anomaly (SAA). To mitigate its influence on DORIS Doppler measurements, a corrective model was developed for Jason-1 (Capdeville et al. 2016). The application of this model reduces the radial orbit error by 16% for this satellite. Ultra-stable oscillators of the satellites Jason-2 (Willis et al. 2016) and Sentinel-3A (Jalabert et al. 2018) are also affected by the SAA, but to a lesser extent. The effect is, however, mainly on station positions derived from DORIS observations rather than on satellite orbits.

Three different approaches are used to determine orbits of altimetry satellites: dynamic, reduced-dynamic and kinematic. Dynamic orbits are derived by applying precise models of forces acting on a satellite (see, e.g., Perosanz et al. 1997). Reduced-dynamic orbits are determined by estimating many empirical parameters to fit space geodetic, mainly GPS or DORIS, observations (see, e.g., Yunck et al. 1994). Kinematic orbits are computed without using any a-priori dynamic modeling information (see, e.g., Suesser-Rechberger et al. 2022). The accuracy of reduced-dynamic orbits improved in general from about 3 cm in 1994 (Yunck et al. 1994) to 0.5–0.7 cm nowadays (Bertiger et al. 2020).

Orbits of altimetry satellites are usually derived in an inertial celestial reference frame using observations performed from a global network of tracking stations. Therefore, accurate information on the positions of tracking stations in a terrestrial reference frame realization and their changes with time as well as on the transformation between these reference frame realizations is very important to derive satellite orbits of high accuracy. Historically, realizations of the International Terrestrial Reference Frame (ITRF, e.g., ITRF2005 (Altamimi et al. 2007), ITRF2008 (Altamimi et al. 2011), ITRF2014 (Altamimi et al. 2016)) were used as a basis for orbit determination. Morel and Willis (2005) obtained an uncertainty of 0.3 cm in the mean sea level and 0.37 mm/year in the mean sea level trend when using the ITRF97 realization for DORIS data-derived TOPEX/Poseidon orbits. Regional mean sea level trends are significantly more affected by the errors of terrestrial reference frame realizations. Thus, the regional sea level trends computed using ITRF2005 showed significant north/south hemispherical differences of ±1.5 mm/year, as compared to the trends obtained using ITRF97 (Beckley et al. 2007). The accuracy of the TRF realizations improved in the recent decades. However, for the change from the ITRF2008 to the ITRF2014 reference frame, the respective changes in the regional sea level trend up to 0.4 mm/year in the time span from April 1993 to July 2008 and up to 1.0 mm/year in the time span from July 2008 to April 2015 were found by Rudenko et al. (2019).

The motion of an altimetry satellite is affected by gravitational and non-gravitational forces acting on it. Table 1 shows average accelerations acting on altimetry satellites at the altitude of about 800 km (Envisat) and about 1350 km (Jason-1) above the Earth due to various perturbing forces.

Table 1 Average accelerations (m/s\(^2\)) of Envisat and Jason-1 due to various perturbing forces
Full size table

Gravitational forces are the major forces acting on the Earth’s altimetry satellites. The orbit accuracy in the radial direction at the beginning of the satellite altimetry era amounted to 48 cm for Seasat altimetry crossover RMS values (Schutz et al. 1985). A significant reduction of geographically correlated and radial errors of altimetry satellite orbits was obtained in the last three decades due to improvements in modeling the Earth’s gravity field. Thus, development of the Joint Gravity Models (JGM) 1 and 2 resulted in a reduction of the radial orbit errors down to about 2 cm (Nerem et al. 1994). Further significant improvement of the orbit quality was obtained due to the development of static and, in particular, time-variable Earth’s gravity field models from the Gravity Recovery And Climate Experiment (GRACE, Tapley et al. 2004). Thus, the application of the first static geopotential model from the GRACE mission (GGM01S) revealed ±1.0 cm mean geographically correlated errors in the Jason-1 orbits derived using the JGM-3 geopotential model (Haines et al. 2004). Ignoring secular (drift) terms in the Earth’s geopotential models leads to ±3 mm/year errors in the regional mean sea level trends (Rudenko et al. 2014). Therefore, time-variable geopotential models containing secular and periodic terms should be used to get the best orbit quality. A series of static and time-variable gravity field models of the Earth has been derived from the analysis of measurements to GRACE, GRACE-Follow-On, GOCE (Gravity field and steady-state Ocean Circulation Explorer), and other satellites (Flechtner et al. 2021). One of the latest models used in POD of altimetry satellites is EIGEN-GRGS.RL04.MEAN-FIELD (Lemoine et al. 2018). It is complete to degree and order (d/o) 300 and additionally contains time-variable gravity coefficients for degrees 1 to 90.

Solar radiation pressure, Earth’s albedo and infrared radiation, thermospheric drag, and thermal dissipation are the non-gravitational forces acting on altimetry satellites at the altitude of 800-1350 km. Satellite acceleration due to non-gravitational forces is proportional to the satellite area to mass ratio that is the largest (about 2 \(\times\) 10\(^{-2}\) m\(^2\)/kg) for Jason-1, -2, -3 among all altimetry satellites.

Altimetry satellites are non-spherical satellites of a complex form usually modeled as a main body equipped with one or a few solar arrays. Since different surfaces of the satellite have different sizes and various optical properties, precise knowledge on the orientation of the satellite in space is important, on the one hand, for precise modeling of non-gravitational perturbations acting on the satellite, on the other hand, for precise computation of modeled observations measured by the tracking instruments located on the different parts of the satellite main body. Mismatched orientation of the satellite and its solar panels causes errors in non-gravitational perturbations. Therefore, precise modeling of non-gravitational perturbations requires a precise knowledge on spacecraft form, size and orientation. Moreover, the attitude directly impacts the vector from the satellite center-of-mass towards the phase center of the altimeter. This correction is also used during the post-processing of altimetry observations. For all altimetry satellites, nominal attitude models provide satellite orientation in space. Nominal yaw-steering mode for attitude modeling is still widely used for altimetry satellite POD. However, for some altimetry satellites, measured attitude (quaternions of the spacecraft body orientation and rotation angles of the solar arrays, if applicable) is available. Bloßfeld et al. (2020) showed that using the measured (observation-based) attitude of altimetry satellites instead of nominal attitude laws improves the orbit quality.

Orbits of altimetry satellites, especially at altitudes of up to 1000 km like those of European Remote Sensing satellites ERS-1, ERS-2, Envisat, Cryosat-2, SARAL, Sentinel-3A, and Sentinel-3B are sensitive to the changes of thermospheric neutral total density causing a decrease of the satellite altitude and requiring more orbit maneuvers (Doornbos and Klinkrad 2006). However, altimetry satellites at higher altitudes of about 1350 km like the Jason satellites are also sensitive to thermospheric density changes, in particular, caused by severe geomagnetic events. Willis et al. (2005) suggested a new approach to frequently estimate the drag parameter coefficients. This approach reduces mismodeling errors, fits of SLR and DORIS observations, as well as radial orbit overlaps. Applying this approach improves also the accuracy of DORIS station coordinates and benefits the DORIS contribution to the ITRF realization (Gobinddass et al. 2010). A recent study by Zeitler et al. (2021) shows that scale factors of modeled thermospheric densities estimated from SLR and accelerometer measurements agree rather well (with a correlation coefficient of 0.7–0.8 depending on the height) and give a possibility to rescale the modeled thermospheric density.

Additional factors contributed to the improvement of the orbit quality of altimetry satellites are improvements in solar radiation pressure and thermal re-radiation modeling. Satellite acceleration due to solar radiation pressure at the Jason satellite altitude is comparable to the acceleration due to Earth tides (Table 1). Together with the improvements in DORIS and GPS processing they resulted in 0.6–0.7 cm average RMS of the radial difference between reduced-dynamic Jason-2 orbits derived using different tracking techniques and different modeling approaches (Cerri et al. 2010).

So, various factors impact the quality of altimetry satellite orbits. They include:

  • type of observations used for orbit determination or their combination (SLR-only, DORIS-only, GPS-only, DORIS+SLR, DORIS+GPS),

  • observation quality (unmodeled time biases, range biases, frequency biases, frequency drifts, etc.) as well as the distribution of observations in time and space,

  • proper corrections of measurements (tropospheric refraction, center-of-mass, ionospheric refraction, satellite phase center corrections, etc.),

  • proper modeling of satellite shape, size, optical properties of its surfaces (macro-model), mass and its orientation in space,

  • accurate modeling of gravitational and non-gravitational forces acting on a satellite,

  • accurate terrestrial and celestial reference frame realizations and the transformation between them,

  • proper modeling of geophysically caused displacements of tracking stations,

  • a proper parameter adjustment algorithm, observation weighting,

  • other factors.

The original requirement of the orbit accuracy in the radial direction for the first reference (TOPEX/Poseidon) mission was set to 13 cm consisting of 10 cm RMS error due to Earth’s gravity field mismodeling, 3 cm due to the errors in solid Earth and ocean tides, 6 cm due to radiative force mismodeling, and 3 cm due to atmospheric drag (Nerem et al. 1993). Remarkable steps forward in the improvement of the altimetry satellite orbit quality have been made in the last three decades (International Altimetry Team 2021). This became possible due to the improvements in all factors influencing the orbit quality mentioned above. Already at the beginning of the TOPEX/Poseidon mission in 1994, a reduction of the error to 3–5 cm in the radial direction was reported (Tapley et al. 1994; Nouel et al. 1994). This became possible due to increased accuracy of the Earth’s gravity field and surface force models, as well as due to improved performance of the laser and Doppler tracking systems. The invention of the box-wing satellite macromodels (e.g., Marshall and Luthcke 1994) and their further enhancement (Kubitschek and Born 2001) allowed reduction of the mismodeling of the non-conservative forces acting on satellites. The accuracy of GPS data-based orbits in the radial direction improved from about 3 cm for TOPEX/Poseidon in 1995 (Kang et al. 1995) to 0.6–1.0 cm nowadays for Jason-2 (Bertiger et al. 2020).

The application of IERS (International Earth Rotation and Reference Systems Service) 2003 standards for ocean and Earth tides, updates to the ITRF2005 reference frame for SLR and DORIS stations, GRACE-derived models for modeling of the static and time-variable gravity, the University College London (UCL) radiation pressure model for Jason-1, improved troposphere modeling for the DORIS data and the GOT4.7 ocean tide model (Ray 2013) for dynamical ocean tide modeling and for ocean loading (Lemoine et al. 2010) led to a radial orbit accuracy of 1.5–2.0 cm for TOPEX/Poseidon and 1.2 cm for Jason-2 based on the values of SLR observation RMS of fit and the orbit differences with different sets of orbits.

Besides tidal loading, non-tidal loading (NTL) consisting of atmospheric pressure loading, oceanic loading and hydrological loading should be taken into account. For a consistent correction for NTL, one should correct station coordinates for NTL loading displacements (geometric effect) and satellite velocity for NTL gravitational acceleration (dynamic effect). Further improvement in the orbit quality of altimetry satellites became possible due to the application of the Atmospheric and Oceanic De-aliasing Level-1B (AOD1B) products (Rudenko et al. 2016) and non-tidal atmospheric and oceanic loading (König et al. 2021).

Satellite acceleration due to thermal emission is generally not modeled for altimetry satellites, since it requires knowledge on satellite surface temperature and needs to take into account self-shadowing. Some information on the thermal emissivity of Jason-1 is given in https://ilrs.cddis.eosdis.nasa.gov/docs/Jason-1_specs.pdf and used, e.g., by Bloßfeld et al. (2020). Knowledge on the thermal emission of other altimetry satellites would benefit the orbit quality.

Relativistic corrections are usually modeled according to IERS Conventions (2010).

Orbits of altimetry satellites have been derived in the last 30 years using different sets of background models. More widely known and used models are called Geophysical Data Records (GDR) standards. These standards are a set of corrections to altimetry observations and background models used for POD. These standards were elaborated from the original version GDR-A to the latest version GDR-F. To distinguish the orbit standards from the altimetry data ones, GDR orbit standards starting from version F are called POE-F (Precise Orbit Ephemeris). The main models used in the various versions of the GDR orbit standards from GDR-C to POE-F are listed in Table 2 compiled using information available at https://ids-doris.org/documents/BC/data/POD_configuration_GDRD.pdf and https://ids-doris.org/documents/BC/data/POD_configuration_POEF.pdf. In these standards, various versions of the IERS Conventions (IERS Conventions 2003 and IERS Conventions 2010), Earth’s gravity field and other models are used. At the same time, all these standards include the same models. For example, third-body gravitational attraction from the Sun, Moon, Venus, Mars, and Jupiter is modeled. Additionally, post-launch values of the satellite mass and positions of the center of gravity with variations generated by the control center were used in all standards. A South Atlantic Anomaly model (Capdeville et al. 2016) was applied for Jason-1 DORIS data. The major improvements in these standards are related to using new ITRF realizations, new time-variable models of the Earth’s gravity field, ocean tide models, improved atmospheric density models and improved modeling of propagation delays. Additional improvements in the orbit quality are due to inter-comparison of the positions of phase centers of measuring devices due to the combination of a few tracking techniques for the same satellite.

Table 2 The main models of the GDR POD standards. Abbreviation: PR—pressure fields
Full size table

Geocenter motion represents the position of the center-of-mass of the total Earth system including atmosphere, oceans and continental water with respect to the center-of-figure of the solid Earth surface (Wu et al. 2012). Many studies were devoted to the determination of geocenter motion from various observations, such as SLR, GNSS, DORIS and GRACE. Generally, the amplitude of the annual oscillation of the geocenter motion derived by these techniques is of the order of 2 mm for the X coordinate, 2.4–3.6 mm for the Y coordinate and 2.8–5.6 mm for the Z coordinate, and the amplitude of the semi-annual oscillation is variable and about two times smaller than the annual one (Kosek et al. 2020). In GDR orbit standards prior to the version GDR-E, no geocenter motion was modeled. In the GDR-E orbit standards, a seasonal model derived from SLR data (Cheng et al. 2013) was used. In the POE-F orbit standards, non-tidal model including semi-annual, annual, and inter-annual variations derived from DORIS and Jason-2 data was applied (Jason-3 Products Handbook 2021). For both latest versions of the GDR orbit standards, tidal geocenter variations were modeled using ocean loading and S1-S2 atmospheric pressure loading. For ITRF2014, an annual geocenter motion model (Altamimi et al. 2016) is provided.

The radial orbit accuracy for Envisat improved from 2–3 cm in terms of SLR RMS fits using the EIGEN-GRACE02S Earth gravity filed model (Doornbos and Scharroo 2005) to 1.3 cm using the EIGEN-6S4 geopotential model (Rudenko et al. 2017). The ERS-1 and ERS-2 orbit quality was improved from 5.0 to 2.1 cm within the REAPER project (Brockley et al. 2017). Nowadays, the radial orbit accuracy estimated by various authors reaches 0.8–1.0 cm RMS for Jason-2 DORIS-only orbits, as estimated from high elevation (>80\(^{\circ }\)) SLR measurements (Belli et al. 2021), and 1.0 cm for Jason-2 DORIS-only orbits relative to GPS JPL RLSE18 orbits (Bertiger et al. 2020).

3 Orbit Solutions Used in this Study

To investigate radial orbit errors of contemporary altimetry satellite orbits, we use in this study seven orbit solutions of 11 altimetry satellites from six institutions (Centre National d’Etudes Spatiales (CNES), Copernicus POD Service (CPOD), Deutsches Geodätisches Forschungsinstitut, Technische Universität München (DGFI-TUM), GFZ German Research Centre for Geosciences (GFZ), Goddard Space Flight Center (GSFC), and Jet Propulsion Laboratory (JPL)) available to us and listed in Table 3. For each orbit solution, type of observations used for POD for a specific satellite for the given orbit solution is provided. Most orbit solutions are derived using two types of observations, namely, DORIS and SLR or DORIS and GPS. Some orbit solutions are derived using just one type of observations (DORIS, GPS, or SLR). For ERS-1, SLR and altimeter crossover data (XO) were used, while the ERS-2 orbit was derived using additionally Precise Range And Range-rate Equipment (PRARE) measurements. All contemporary orbit solutions selected for this study and listed in Table 3 are in the extended ITRF2014 realization (Altamimi et al. 2016) of the International Terrestrial Reference System (ITRS) meaning that the information on stations not present in the ITRF2014 is taken from SLRF2014 (SLRF2014 station coordinates 2017) for SLR stations and DPOD2014 (Moreaux et al. 2019) for DORIS stations. ITRF2014 is the latest ITRS realization in which orbits of altimetry satellites were available by April 2022 from various institutions. Additionally, using the same ITRS realization minimizes orbit differences caused by using different ITRS realizations. As a result, the number of the orbit solutions in the extended ITRF2014 available to us for various satellites varies significantly from just one orbit solution for such satellites as Cryosat-2, ERS-1, ERS-2, and SARAL to six orbit solutions for Jason-2. Three orbit solutions are available for Envisat and Jason-1, four orbit solutions are available for Sentinel-3A, Sentinel-3B and TOPEX/Poseidon and five orbit solutions are used for Jason-3. Additionally, CNES orbit solutions of Jason-2 derived using the GDR-C, GDR-D, GDR-E and POE-F orbit standards are used to investigate improvements in the orbit quality over recent decades. The main background models used to derive each orbit solution are described in the references given in Table 3. Additionally, the main models used for the CNES solutions are described in Table 2. More information on the CPOD orbits and their evaluation can be found at https://sentinels.copernicus.eu/web/sentinel/technical-guides/sentinel-3-altimetry/pod/documentation.

Table 3 Type of observations of the orbit solutions in the extended ITRF2014 reference frame used in this study. Abbreviation: TOPEX—TOPEX/Poseidon, PSO—Precise Science Orbit
Full size table

To investigate the quality of the orbit solutions derived using up-to-date background models, but using only SLR observations, we have computed DGFI-TUM DSO1 orbits of Jason-1, Jason-2, Jason-3, and TOPEX/Poseidon using just SLR observations (Rudenko et al. 2023). These orbits are called in this paper DGFI SLR or simply DGFI orbits for shortness. These orbits are computed using the DGFI-TUM Orbit and Geodetic parameter estimation Software (DOGS) and the background models that coincide with those given in Bloßfeld et al. (2020) (Tables A1–A4) with the following exceptions. We use the EIGEN-GRGS.RL04.MEAN-FIELD Earth gravity field model (Lemoine et al. 2018) up to d/o 120 in the static part and d/o 90 in the time variable part, the lunar gravity field model up to d/o 50, and the secular mean pole model (updated IERS 2010 Conventions; https://iers-conventions.obspm.fr/content/chapter7/icc7.pdf). Additionally, we estimate more parameters, namely, SLR range biases once per station per arc and coefficients of a linear polygon of empirical accelerations are estimated additionally in the transverse and normal directions with a step of 12 hours. For TOPEX/Poseidon, station-dependent satellite laser ranging measurement corrections (Zeitlhöfler et al. 2022) are applied.

4 Radial Orbit Differences of Contemporary Altimetry Satellite Orbits

To investigate internal consistency of the orbits, the impact of different processing methods and observation types used, orbit differences in the radial, transverse, and normal directions between various orbit solutions have been computed. The orbit solutions shown in Table 3 are provided in various orbit formats (SP1, SP3c, and SP3d) with different time steps. These are 10 s for the CPOD orbits, 30 s for the GFZ and DGFI orbits and 60 s for the CNES and JPL orbits. Additionally, the time instants of the orbits are given in different time systems. These are GPS time for the CPOD, JPL, and GFZ orbits, TAI (International Atomic Time) for the CNES orbits, and UTC (Coordinated Universal Time) for the DGFI orbits. This requires a transformation of time instants between different time systems and an interpolation of satellite coordinates. Orbit differences are computed at the time instants being in the middle of the time instants of the respective orbit solutions to minimize interpolation errors. For each entry of an SP1/SP3 file, orbit differences in the Cartesian coordinates are computed and transformed in the radial, transverse, and normal directions of the orbit reference system. Since any error in the radial direction transfers into the sea height, the following discusses orbit differences in the radial directions only. The interpolation errors of the spline interpolation method used are below 0.047 cm for standard deviation and 0.0005 cm for absolute mean of the radial orbit differences. For each SP1/SP3 file, mean values of the orbit differences with respective file(s) of another orbit solutions are computed.

Figures 1, 2, 3, 4, 5, 6, 7 show the RMS and mean differences of satellite coordinates in the radial direction of the orbit solutions given in Table 3. In these computations, time spans of 4 minutes before and after orbit maneuvers, before and after orbit gaps, as well as after the arc start and before the arc end were excluded, since we are interested in the average level of orbit differences and to avoid some outliers in the orbit differences caused by data gaps and lack of observations at these periods. A few outliers with the RMS values of radial orbit differences larger than 10 cm were excluded from the computation of these values and are not shown in the figures.

One can see that the RMS values of the radial orbit differences for three TOPEX/Poseidon orbit solutions are of 1.61–2.18 cm (Fig. 1). The mean values of the radial orbit differences of these solutions are from \({-}\)0.094 to 0.089 cm. The outliers in the orbit differences are due to the gaps in SLR observations for the orbit based on SLR-only data. One can see a stable level of both the RMS and mean values of radial orbit differences during the complete 12-year time span. This can be an indication that the models used for POD of this satellite, in particular an ITRS realization, provide consistent level of orbit accuracy during the complete mission. The GFZ PSO v02 orbit solution of TOPEX/Poseidon is available only until 31 October 2004 (the date for which DORIS data are available for this satellite), while the GFZ VER13 and DGFI SLR orbit solutions are available until 8 October 2005 and were derived from SLR data only for the last year of the mission. One can see slightly increased scatter in the mean values of the radial orbit differences between the DGFI SLR and GFZ VER13 orbit solutions after 31 October 2004, as compared to the period before this date, since both orbits are based on SLR data only beyond 31 October 2004.

Fig. 1
figure 1

The RMS (a) and mean (b) values of the radial orbit differences of TOPEX/Poseidon orbits

Full size image

The GFZ VER13 and PSO v02 orbits of Envisat are based on using DORIS and SLR observations. The CNES POE-F orbits of this satellite were derived using DORIS-only observations. Figure 2 shows that the RMS values of the radial orbit differences of all three orbit solutions are of 0.72–0.87 cm and the mean values of the radial orbit differences are from 0.015 to 0.046 cm. Larger RMS values of orbit differences at the beginning and the end of the mission can be explained by higher solar and geomagnetic activities in 2002–2003 and 2011–2012 to which Envisat is more sensitive through atmospheric drag due to its lower orbit altitude (about 800 km), as compared to, e.g., Jason satellites (orbit altitude of about 1350 km). Annual variations with an amplitude of about 0.2–0.3 cm are present in the RMS values of the radial orbit differences and annual variations with an amplitude of about 0.03 cm are visible in the mean values of the radial orbit differences (Fig. 2) of all three orbit solutions and can be caused by the differences in modeling of non-tidal loading effects being a part of geocenter motion.

Fig. 2
figure 2

The RMS (a) and mean (b) values of the radial orbit differences of Envisat orbits

Full size image

For Jason-1, we compare two orbit solutions both derived using DORIS and SLR observations (these are GFZ VER13 and GFZ PSO v02 solutions) and an SLR-only solution from DGFI. The solutions derived using both DORIS and SLR observations agree at 1.06 cm in the RMS values with the mean value of \({-}\)0.093 cm of the radial orbit differences (Fig. 3). The SLR-only solution indicates the RMS values of the orbit differences of 1.56–1.76 cm with the mean values of \({-}\)0.016 to 0.077 cm with respect to two other orbit solutions. As for TOPEX/Poseidon, some outliers in the orbit differences for Jason-1 are due to gaps in SLR data of the SLR-only solution. This shows importance of using continuous DORIS and GPS observations to derive consistent, high-quality orbit solutions. Increased variations in the mean values of the radial orbit differences for the time interval from May 2012 (geodetic phase) are, most probably, caused by different modeling of Jason-1 attitude in the GFZ VER13 orbit solution, as compared to two other solutions.

Fig. 3
figure 3

The RMS (a) and mean (b) values of the radial orbit differences of Jason-1 orbits

Full size image

For Jason-2, we have the maximum number (six) of orbit solutions available among the missions used in this study. Orbits of this satellite derived using DORIS+SLR or DORIS+GPS or GPS observations agree with each other with the RMS values of the radial orbit differences of 0.47–0.82 cm with the mean values of the radial orbit differences from \({-}\)0.143 to 0.111 cm (Fig. 4). The SLR-only orbits indicate a bit larger differences to the orbits derived using the types given above with the RMS values of 1.20–1.30 cm and the mean values from \({-}\)0.088 to 0.050 cm.

Fig. 4
figure 4

The RMS (a) and mean (b) values of the radial orbit differences of Jason-2 orbits

Full size image

The Jason-3 orbits derived using DORIS+SLR, DORIS+GPS, and GPS observations agree with each other in the radial direction with the RMS values of 0.48–1.09 cm and the mean values from \({-}\)0.140 to 0.054 cm (Fig. 5). The SLR-only orbits agree with the orbits derived using the observation types given above with the RMS values of 1.12–1.49 cm and the mean values from \({-}\)0.091 to 0.036 cm.

Fig. 5
figure 5

The RMS (a) and mean (b) values of the radial orbit differences of Jason-3 orbits

Full size image

The Sentinel-3A orbits derived using DORIS+SLR, DORIS+GPS, and GPS observations agree with each other in the radial direction with the RMS values of 0.37–0.78 cm and the mean values from \({-}\)0.153 to 0.235 cm (Fig. 6). The JPL orbit of Sentinel-3A seems to be shifted in the radial direction with respect to the GFZ PSO, CPOD and CNES POE-F orbits by about 0.15–0.24 cm.

Fig. 6
figure 6

The RMS (a) and mean (b) values of the radial orbit differences of Sentinel-3A orbits

Full size image

As for the Sentinel-3A orbits, the Sentinel-3B orbits derived using DORIS+SLR, DORIS+GPS, and GPS observations agree with each other in the radial direction with the RMS values of 0.40–0.83 cm and the mean values from \({-}\)0.156 to 0.169 cm (Fig. 7). The JPL orbits of Sentinel-3B seem to be shifted in the radial direction by 0.15–0.16 cm with respect to the GFZ PSO, CPOD and CNES POE-F orbits.

Fig. 7
figure 7

The RMS (a) and mean (b) values of the radial orbit differences of Sentinel-3B orbits

Full size image

The JPL and CNES POE-F orbits show very good agreement from the point of the RMS values of the radial orbit differences that are of 0.473–0.477 cm for Jason-2 and Jason-3 and 0.370–0.395 cm for Sentinel-3A and Sentinel-3B. This can be explained by using GPS observations for orbits of both institutions, though DORIS observations are additionally used by CNES. At the same time, JPL orbits indicate the following mean radial orbit differences with respect to CNES POE-F orbits: \({-}\)0.131 cm for Jason-2, \({-}\)0.140 cm for Jason-3, \({-}\)0.153 cm for Sentinel-3A, and \({-}\)0.156 cm for Sentinel-3B. The CPOD solutions are the operational solutions. That is why no common orbit standards were used for the entire time span. This explains jumps in the orbit differences of the CPOD solutions of Sentinel-3A and Sentinel-3B with respect to other orbit solutions.

Table 4 provides the range of the RMS and mean values of the radial orbit differences obtained for the orbit solutions shown in Figs. 1, 2, 3, 4, 5, 6, 7 . One can see that the RMS values of the radial orbit differences vary from 0.4 to 1.8 cm for 7 satellites for the orbit solutions derived using DORIS or GPS observations and from 1.1 to 2.2 cm, when comparing to the SLR data only solution. The mean values of the radial orbit differences vary from \({-}\)0.16 to 0.24 cm for the orbit solution based on using DORIS or GPS observations and from \({-}\)0.09 to 0.08 cm for the SLR data only solution.

Table 4 A summary on the RMS and mean values of radial orbit differences of orbit solutions derived by various institutions using various observation types: D—DORIS, G—GPS, S—SLR
Full size table

5 Multi-mission Crossover Analysis and Its Results

In order to investigate the orbit quality of altimetry satellites, the sea surface measurements themselves can be used, namely the consistency of measurements of crossing tracks, so-called crossover differences. Based on the assumption that these collocated measurements should show identical sea surface heights (SSH), if taken close in time, any systematic differences can be analyzed and accounted to errors originating from range measurements, geophysical corrections, or satellites orbits. Even if a separation of these effects is challenging, the comparison of results based on different orbit solutions (with all other parameters unchanged) contain valuable information to describe the orbit quality and especially the differences.

In this study a multi-mission crossover analysis (MMXO) is used. The approach applied to estimate time series of radial errors from the crossover differences between multiple missions was first described by Bosch et al. (2014). As input, sea surface height observations of all available radar altimetry missions listed in Table 3 are used. Sea surface height differences at all possible track crossings are computed as long as they have been observed within two days and are located in open ocean. This comprises single-satellite crossovers (SXO) as well as dual-satellite crossovers. Coastal areas as well as areas covered by sea ice are excluded and differences larger than 100 cm or with uncertainties larger than 10 cm are handled as outliers. All valid SSH crossover differences are used to estimate time series of radial errors (RE) for all missions included in the analysis. These radial errors are further processed to geographically correlated errors (GCE), i.e., the mean component of the radial errors following the theory of Rosborough (1986). For that purpose, the radial errors of ascending and descending satellite tracks are averaged independently in small grid cells (per mission). The mean of ascending and descending radial errors per grid cell is then averaged again to derive gridded GCE. More details on this method are published in Bosch et al. (2014).

Within this paper, the MMXO is applied for three different studies. First, in order to investigate the evolution of orbit quality over the last decades, four different Jason-2 orbit solutions derived by the same institution (CNES) using different orbit standards from GDR-C to POE-F are compared by processing four different MMXO, for which only the Jason-2 orbit differs (Sect. 5.1). Then, the same exercise is performed with six different Jason-2 orbit solutions, all based on the latest standards and on the extended ITRF2014 reference frame, but derived by different institutions and with slightly different standards and parameters (Sect. 5.2). Lastly, MMXO results from one run are presented for all missions involved to provide an overview over the accuracy that is currently achieved for 11 different altimetry satellites (Sect. 5.3).

5.1 Improvements in the Radial Orbit Quality from GDR-C to POE-F Orbit Standards

To illustrate the improvements in POD for satellite altimetry applications, four different Jason-2 orbit solutions from CNES are analyzed (GDR-C, GDR-D, GDR-E, POE-F). Detailed information on the different solutions is summarized in Table 3 and the description of the POD standards used to derive these orbits is summarized in Table 2. Since the GDR-C solution is only publicly available for cycles 67 to 145 (April 2010 to June 2012), only these two years are used for the comparisons.

Figure 8a shows the global statistics for single-mission crossover differences (SXO) with a maximum time limit of two days and restricted to ±55\(^{\circ }\) latitude. Clearly visible are the improvements of about 0.2 cm (from 4.5 to 4.3 cm) due to the advanced orbit determination, which however become smaller from version to version. The same applies to the standard deviation of the estimated radial errors (Fig. 8b), which decreases from 1.14 cm (for GDR-C orbits) to 0.98 cm (for POE-F orbits). Looking at the geographically correlated errors (Fig. 8c), the largest difference is seen when switching from the GDR-C to the GDR-D orbit standards. This is due to the switch from the EIGEN-GL04S-ANNUAL to the EIGEN-GRGS.RL02bis.MEAN-FIELD Earth’s gravity field model based on longer time span of GRACE and LAGEOS data, namely, 8 instead of 2 years, and due to the switch from the ITRF2005 to ITRF2008 reference frame realization. There is no clear improvement and the patterns remain at similar levels, even if they change slightly, after the switch to GDR-D (Fig. 9).

Fig. 8
figure 8

Quality comparison of different Jason-2 CNES orbit solutions for altimetry applications: a standard deviation of single-satellite crossover differences, b standard deviation of radial errors, c standard deviation of geographically correlated errors; all derived from a multi-mission crossover analysis

Full size image
Fig. 9
figure 9

Geographically correlated errors for four Jason-2 CNES orbit solutions (cycles 67–145)

Full size image

5.2 Comparison of Different Orbit Solutions for One Satellite

Here, orbit solutions from different institutions all based on the extended ITRF2014 are inter-compared. This is done exemplarily for one mission, namely Jason-2, because for this satellite, the highest number of independent solutions exists. In detail, six different solutions, from CNES, GSFC, JPL, GFZ (VER13 and PSO v02), and DGFI are analyzed regarding their single-satellite crossover differences, as well as for radial errors and geographically correlated mean errors.

The standard deviation of the single-satellite crossover differences varies between 4.34 cm for the JPL solution and 4.58 cm for the DGFI solution, as visible in Fig. 10a. Using of just SLR data in the DGFI solution leads to 0.24 cm larger value than in the GPS data based JPL solution. This difference accounts for about 5% of the total effect. The differences in performance can also be seen in the standard deviations of the estimated radial errors. While the estimated mean range bias for Jason-2 is hardly influenced by the orbit solution and only shows a maximum difference of 0.013 cm (not shown), the scatter of the radial errors varies between 0.99 cm for the JPL solution and 1.24 cm for the DGFI solution (see Fig. 10b). When looking at the geographical distribution of errors, two solutions can be identified which show higher GCE standard deviations than expected from the temporal mean: GSFC with 0.176 cm and GFZ VER13. The latter shows slightly higher GCE than GFZ PSO, even if SXO and RE performs better (Fig. 10c).

Fig. 10
figure 10

Quality comparison of ITRF2014 Jason-2 orbit solutions from different institutions: a standard deviation of single-satellite crossover differences, b standard deviation of radial errors, c standard deviation of geographically correlated errors; all derived from a multi-mission crossover analysis

Full size image

For all solutions, the GCE patterns are well below 1 cm as visible from Fig. 11. The highest values are reached for the DGFI SLR-only data orbit. For all solutions, positive errors are visible in the Western Pacific and in the South Atlantic Ocean, while the GCE are negative west of South America, in the northern Atlantic and south of Africa. Differences with respect to CNES solutions are shown in Fig. 12. While JPL and GFZ VER13 are very similar to CNES, GSFC and DGFI solutions show discrepancies up to about 0.5 cm.

Fig. 11
figure 11

Geographically correlated errors (GCE) for six different orbit solutions for the Jason-2 mission

Full size image
Fig. 12
figure 12

Relative GCE for six different orbit solutions for the Jason-2 mission, all with respect to the CNES POE-F orbit solution (top left plot)

Full size image

5.3 Comparison of Optimal Orbit Solutions for Different Satellites

For the altimetry missions listed in Table 3, results from one multi-mission crossover analysis are presented in the following. For seven missions, CNES POE-F orbit solutions are used, whereas for four missions (ERS-1/2, TOPEX, Jason-1), for which no CNES solutions are available, GFZ VER13 solution is used, as this solution performs very good in the inter-solution test for Jason-2 (see Sect. 5.2) and is available for many satellites.

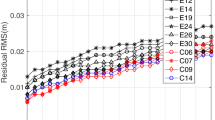
For all 11 missions, single-satellite crossover differences are analyzed, as well as radial errors and geographically correlated errors. Figure 13 shows the standard deviation of SXO and its temporal variation for all missions: Jason-1 (J1), Jason-2 (J2), Jason-3 (J3), Envisat (ENV), ERS-1 (E1), ERS-2 (E2), Cryosat-2 (CS2), TOPEX (TP), Sentinel-3A (S3A), Sentinel-3B (S3B) and SARAL (SRL). One can clearly see, how the quality evolves with time and how it depends on the solar cycle (which leads to enlarged values around the year 2000). This shows that most of the SXO differences are due to measurement uncertainty, geophysical correction (as the ionospheric correction), and sea level variability. Only a small part is due to orbit errors. The same holds to the radial errors, for which the standard deviations vary from 0.97 cm (Sentinel-3B) to 1.66 cm (ERS-2) and have the same ratios as the SXO (not shown).

Fig. 13
figure 13

Single-satellite crossover statistics for 11 missions, all based on ITRF2014 orbits (CNES POE-F and GFZ VER13)

Full size image

GCE instead are meant to represent mostly orbit errors, since most of the other error sources are not stationary. The estimated GCE are plotted in Fig. 14; their statistics in Fig. 15. In order to make the numbers more consistent, only areas up to 55\(^{\circ }\) North and South have been used for computing the mean and standard deviation values. When generating the GCE, radial offsets are subtracted per cycle and mission, so that only the variations around zero are included in the data that are shown. This results in mean GCE caused by rounding only, i.e., well below 0.1 cm. All missions show mean GCE smaller than 0.1 cm; mostly even below 0.04 cm. The largest variations of about 0.25 cm standard deviation are visible in the ERS GCE, whereas the Jason satellites show the smallest pattern.

Fig. 14
figure 14

GCE for 11 altimetry missions based on newest orbit standards (CNES POE-F and GFZ VER13)

Full size image
Fig. 15
figure 15

Mean (left) and standard deviation (right) of GCE for 11 altimetry missions; limited to 55\(^{\circ }\) N and S

Full size image

6 Conclusions

In this paper, we have provided a review of the main improvements in the determination of precise orbits of altimetry satellites in the recent 30 years from the beginning of the TOPEX/Poseidon mission in 1992 until now (2022). The major improvements in the orbit quality of altimetry satellites are due to significant enhancements in the modeling of the Earth’s time variable gravity, elaboration of International Terrestrial Reference System realizations, modeling periodic effects in the system Earth, and using GPS observations in addition to DORIS and SLR observations. Comparisons of contemporary orbit solutions of altimetry satellites derived in the extended ITRF2014 reference frame indicate that satellite positions of the orbits derived using DORIS and GPS observations agree in the radial direction at 0.4–1.0 cm RMS values for the Jason and Sentinel-3 missions and of 1.9 cm for TOPEX/Poseidon. Orbit solutions derived using only SLR observations show larger differences in the radial direction compared to the orbits derived using DORIS and GPS observations with the RMS values of 1.2–1.8 cm for the Jason missions and of 1.6–2.2 cm for TOPEX/Poseidon. Our study shows that the RMS values of orbit differences in the radial direction can be considered as an estimate of the radial orbit errors.

The multi-mission crossover analysis of two year (April 2010 to June 2012) CNES orbits of Jason-2 derived using four versions of the GDR standards for orbit computations (GDR-C, GDR-D, GDR-E, and POE-F) shows a clear reduction (improvement) of the standard deviation of single-satellite crossover differences by about 0.18 cm (4.0%) from 4.52 to 4.34 cm from GDR-C to POE-F standards-based orbits. The standard deviation of radial errors decreased (improved) from 1.14 (for GDR-C) to 0.98 cm (for the POE-F standards-based orbits). The largest difference of the standard deviation of geographically correlated errors was found for the switch from GDR-C to GDR-D standards. For later versions of the GDR standards, no clear improvements in the standard deviation of geographically correlated errors were found, even if they change slightly.

The multi-mission crossover analysis of six Jason-2 orbit solutions derived in the extended ITRF2014 reference frame using the POE-F-consistent POD standards derived at five institutions using various observation techniques shows that the standard deviation of single-satellite crossover differences are of 4.34–4.44 cm for the orbits derived using DORIS and/or GPS observations and of 4.58 cm for the orbits derived using only SLR observations. The standard deviation of radial errors is of 0.99–1.09 cm for the orbits based on DORIS and/or GPS observations and of 1.24 cm for the SLR-only orbits. The standard deviation of geographically correlated errors is of 0.12–0.18 cm for the orbit solutions tested. For all solutions, positive errors are visible in the Western Pacific and in the South Atlantic Ocean, while the geographically correlated errors are negative west of South America, in the northern Atlantic and south of Africa.

A single-satellite crossover analysis of the orbits for all 11 altimetry missions based on the POE-F (consistent) standards (CNES POE-F and GFZ VER13) shows that the standard deviation of the single-satellite crossover differences is 4.1 cm for Sentinel-3A and Sentinel-3B, 4.2 cm for Jason-3 and Cryosat-2, 4.3 cm for Jason-2 and SARAL, 4.5 cm for Jason-1 and Envisat, 4.9 cm for TOPEX, 5.5 cm for ERS-1, and 5.6 cm for ERS-2. The standard deviations of radial errors for these missions vary between 1.0 cm (Sentinel-3A, Sentinel-3B, Jason-3, Jason-2), 1.1 cm (Jason-1, Cryosat-2, SARAL, Envisat), 1.3 cm (TOPEX), 1.5 cm (ERS-1), and 1.7 cm (ERS-2).

We have found that geographically correlated errors are most pronounced for ERS-1 (0.27 cm standard deviation of GCE) and ERS-2 (0.25 cm), followed by Sentinel-3B (0.20 cm), SARAL and Envisat (0.18 cm). TOPEX, Cryosat-2, and Sentinel-3 yield values of about 0.16 cm, whereas the Jason missions show the smallest GCE pattern of only about 0.12 to 0.13 cm. When interpreting the results of MMXO, it is important to keep in mind that the numbers themselves not only include orbit errors but may also contain instrumental or geophysical effects (such as measurement errors or ocean variability).

So, significant progress has been reached in POD of altimetry satellites in the recent decades. Radial orbit errors of altimetry satellites reduced (improved) from 48 cm for Seasat in 1985 to the 1 cm level for contemporary altimetry missions at the beginning of 2020s. They still vary between different missions. Based on the results presented in this study, we conclude that the main contributions to the improvements of altimetry satellite orbit quality in the recent decades were the use of, in addition to SLR, GPS and DORIS measurements, technological advances in measurement methods, improvements in modeling the Earth time-variable gravity and improvements in reference frame realizations. However, sea level (and trend) estimates computed using different up-to-date orbit solutions, types of observations and up-to-date models still exceed the requirements of the Global Climate Observing System (GCOS) for the regional sea level (< 1 cm) and its trend (< 1 mm/year, https://gcos.wmo.int/en/essential-climate-variables/about/requirements). Taking into account that orbit radial errors are just a part of radial errors impacting regional sea level, the GCOS requirement for the regional sea level (< 1 cm) does not seem to be met yet. For reliable sea level products, the geodetic datum of the altimetry satellite orbits should meet the requirements of the Global Geodetic Observing System (GGOS, < 1 mm for positions, < 0.1 mm/year for trends, Gross et al. (2009)) in addition to those of GCOS. Further elaboration of the background models for POD of altimetry satellites together with possible tracking system improvements should aim for a further reduction of radial orbit errors of altimetry satellites and, as result, improvement of the orbit quality to reach the requirements of GCOS and GGOS. Additional attempts should be made to reduce geographically correlated errors.