Abstract
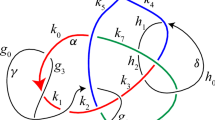
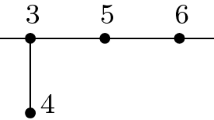
An R-link is an n-component link L in \(S^3\) such that Dehn surgery on L yields \(\#^n(S^1 \times S^2)\). Every R-link L gives rise to a geometrically simply-connected homotopy 4-sphere \(X_L\), which in turn can be used to produce a balanced presentation of the trivial group. Adapting work of Gompf, Scharlemann, and Thompson, Meier and Zupan produced a family of R-links L(p, q; c/d), where the pairs (p, q) and (c, d) are relatively prime and c is even. Within this family, \(L(3,2;2n/(2n+1))\) induces the infamous trivial group presentation \(\langle x,y \, | \, xyx=yxy, x^{n+1}=y^n \rangle \), a popular collection of potential counterexamples to the Andrews–Curtis conjecture for \(n \ge 3\). In this paper, we use 4-manifold trisections to show that the group presentations corresponding to a different subfamily, L(3, 2; 4/d), are Andrews–Curtis trivial for all d.







Similar content being viewed by others
References
Akbulut, S., Kirby, R.: A potential smooth counterexample in dimension \(4\) to the Poincaré conjecture, the Schoenflies conjecture, and the Andrews–Curtis conjecture. Topology 24(4), 375–390 (1985). https://doi.org/10.1016/0040-9383(85)90010-2
Andrews, J.J., Curtis, M.L.: Free groups and handlebodies. Proc. Amer. Math. Soc. 16, 192–195 (1965). https://doi.org/10.2307/2033843
Burns, R.G., Macedońska, O.: Balanced presentations of the trivial group. Bull. Lond. Math. Soc. 25(6), 513–526 (1993). https://doi.org/10.1112/blms/25.6.513
Farb, B., Margalit, D.: A Primer on Mapping Class Groups, Princeton Mathematical Series, vol. 49. Princeton University Press, Princeton (2012)
Fernández, X.: Morse Theory for Group Presentations. arXiv e-prints arXiv:1912.00115 (2019). https://doi.org/10.48550/arXiv.1912.00115
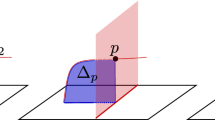
Gay, D., Kirby, R.: Trisecting 4-manifolds. Geom. Topol. 20(6), 3097–3132 (2016). https://doi.org/10.2140/gt.2016.20.3097
Gompf, R.E.: Killing the Akbulut-Kirby \(4\)-sphere, with relevance to the Andrews–Curtis and Schoenflies problems. Topology 30(1), 97–115 (1991). https://doi.org/10.1016/0040-9383(91)90036-4
Gompf, R.E., Scharlemann, M., Thompson, A.: Fibered knots and potential counterexamples to the property 2R and slice-ribbon conjectures. Geom. Topol. 14(4), 2305–2347 (2010). https://doi.org/10.2140/gt.2010.14.2305
Gompf, R.E., Stipsicz, A.I.: \(4\)-manifolds and Kirby calculus. In: Graduate Studies in Mathematics, vol. 20. American Mathematical Society, Providence (1999). https://doi.org/10.1090/gsm/020. https://doi.org/10.1090/gsm/020
Hoffman, H., Nakagawa, K., Potter, R., Zupan, A.: Knots in the fibers of generalized square knots. In preparation
Meier, J., Schirmer, T., Zupan, A.: Classification of trisections and the generalized property R conjecture. Proc. Amer. Math. Soc. 144(11), 4983–4997 (2016). https://doi.org/10.1090/proc/13105
Meier, J., Zupan, A.: Presentations of the trivial group and generalized square knots. In preparation
Meier, J., Zupan, A.: Bridge trisections of knotted surfaces in \(S^4\). Trans. Amer. Math. Soc. 369(10), 7343–7386 (2017). https://doi.org/10.1090/tran/6934
Meier, J., Zupan, A.: Characterizing Dehn surgeries on links via trisections. Proc. Natl. Acad. Sci. USA 115(43), 10887–10893 (2018). https://doi.org/10.1073/pnas.1717187115
Meier, J., Zupan, A.: Generalized square knots and homotopy 4-spheres. J. Differ. Geom. 122(1), 69–129 (2022). https://doi.org/10.4310/jdg/1668186788
Metzler, W.: Äquivalenzklassen von Gruppenbeschreibungen, Identitäten und einfacher Homotopietyp in niederen Dimensionen. In: Homological Group Theory (Proc. Sympos., Durham, 1977), London Math. Soc. Lecture Note Ser., vol. 36, pp. 291–326. Cambridge Univ. Press, Cambridge-New York (1979)
Metzler, W.: On the Andrews–Curtis conjecture and related problems. In: Combinatorial Methods in Topology and Algebraic Geometry (Rochester, N.Y., 1982), Contemp. Math., vol. 44, pp. 35–50. Amer. Math. Soc., Providence (1985). https://doi.org/10.1090/conm/044/813099. https://doi-org.libproxy.unl.edu/10.1090/conm/044/813099
Miasnikov, A.D.: Genetic algorithms and the Andrews–Curtis conjecture. Internat. J. Algebra Comput. 9(6), 671–686 (1999). https://doi.org/10.1142/S0218196799000370
Myasnikov, A.D., Myasnikov, A.G., Shpilrain, V.: On the Andrews–Curtis equivalence. In: Combinatorial and Geometric Group Theory (New York, 2000/Hoboken, NJ, 2001), Contemp. Math., vol. 296, pp. 183–198. Amer. Math. Soc., Providence (2002). https://doi.org/10.1090/conm/296/05074. https://doi.org/10.1090/conm/296/05074
Panteleev, D., Ushakov, A.: Conjugacy search problem and the Andrews–Curtis conjecture. Groups Complex. Cryptol. 11(1), 43–60 (2019). https://doi.org/10.1515/gcc-2019-2005
Scharlemann, M.: Proposed property 2R counterexamples examined. Illinois J. Math. 60(1), 207–250 (2016)
Acknowledgements
We are grateful to Jeffrey Meier for helpful conversations and for comments on an earlier draft of this paper. AZ was supported by NSF awards DMS-1664578 and DMS-2005518 and a Simons Fellowship during the completion of this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Romary, E., Zupan, A. A family of Andrews–Curtis trivializations via 4-manifold trisections. Geom Dedicata 218, 45 (2024). https://doi.org/10.1007/s10711-024-00891-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10711-024-00891-6