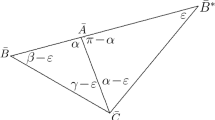
Abstract
We study the problem of determining the least symmetric triangle, which arises both from pure geometry and from the study of molecular chirality in chemistry. Using the correspondence between planar n-gons and points in the Grassmannian of 2-planes in real n-space introduced by Hausmann and Knutson, this corresponds to finding the point in the fundamental domain of the hyperoctahedral group action on the Grassmannian which is furthest from the boundary, which we compute exactly. We also determine the least symmetric obtuse and acute triangles. These calculations provide prototypes for computations on polygon and shape spaces.












Similar content being viewed by others
Notes
Here ordered means that the order of edges in the n-gon matters: e.g., a triangle with edges ordered from shortest to longest is distinct from the same triangle with edges ordered from longest to shortest.
Strictly speaking, scalene triangles are only chiral when viewed as living in a two-dimensional universe. In three dimensions a scalene triangle and its mirror image are related by a rotation.
Here the 1 should be thought of as the semiperimeter of the triangle. This is why we fixed the perimeter to be 2.
With a view towards generalizations to n-gons in \(\mathbb {R}^3\) and questions like “What is the probability that a random n-gon is knotted”, which is of interest for modeling ring polymers.
Note that a triangle can also be doubly-degenerate, with two sides of length 1 and one of length 0. This means that two vertices coincide.
Rassat and Fowler [14] showed that any non-isosceles triangle is the most chiral triangle according to some chirality measure in a particular family, but their chirality measures are slightly unnatural to define on the sphere.
Meaning furthest from the subset of unknotted polygons.
References
Bowden, L., Haynes, A., Shonkwiler, C., Shukert, A.: Spherical Geometry and the Most Scalene Triangle: Supplementary Materials. http://www.math.colostate.edu/~clayton/research/ScaleneTriangles (2017)
Buda, A.B., der Heyde, T.A., Mislow, K.: On quantifying chirality. Angew. Chem. Int. Ed. 31(8), 989–1007 (1992)
Buda, A.B., Mislow, K.: On geometric measures of chirality. J. Mol. Struct. Theochem 232, 1–12 (1991)
Cantarella, J., Deguchi, T., Shonkwiler, C.: Probability theory of random polygons from the quaternionic viewpoint. Commun. Pure Appl. Math. 67(10), 1658–1699 (2014)
Cantarella, J., Needham, T., Shonkwiler, C., Stewart, G.: Random triangles and polygons in the plane. Preprint, arXiv:1702.01027 [math.MG] (2017)
Chauvin, R.: Entropy in dissimilarity and chirality measures. J. Math. Chem. 19(2), 147–174 (1996)
Deguchi, T., Uehara, E.: Statistical and dynamical properties of topological polymers with graphs and ring polymers with knots. Polymers 9(7), 252 (2017)
Hausmann, J.-C., Knutson, A.: Polygon spaces and Grassmannians. L’Enseign. Math. 43, 173–198 (1997)
Hermann, R.: On the existence of a fundamental domain for Riemannian transformation groups. Proc. Am. Math. Soc. 13(3), 489–494 (1962)
Needham, T.: Kähler structures on spaces of framed curves. Ann. Glob. Anal. Geom. https://doi.org/10.1007/s10455-018-9595-3 (2018)
O’Hara, J.: Renormalization of potentials and generalized centers. Adv. Appl. Math. 48(2), 365–392 (2012)
Portnoy, S.: A Lewis Carroll pillow problem: probability of an obtuse triangle. Stat. Sci. 9(2), 279–284 (1994)
Prelog, V.: Chirality in chemistry. Science 193(4247), 17–24 (1976)
Rassat, A., Fowler, P.W.: Any scalene triangle is the most chiral triangle. Helv. Chim. Acta 86(5), 1728–1740 (2003)
Robin, A.C.: The most scalene triangle. Math. Gazette 93(527), 331–338 (2009)
Suzuki, T., Yamamoto, T., Tezuka, Y.: Constructing a macromolecular \({\rm K}_{3,3}\) graph through electrostatic self-assembly and covalent fixation with a dendritic polymer precursor. J. Am. Chem. Soc. 136(28), 10148–10155 (2014)
Uehara, E., Tanaka, R., Inoue, M., Hirose, F., Deguchi, T.: Mean-square radius of gyration and hydrodynamic radius for topological polymers evaluated through the quaternionic algorithm. React. Funct. Polym. 80, 48–56 (2014)
Younes, L., Michor, P.W., Shah, J., Mumford, D.: A metric on shape space with explicit geodesics. Atti della Accademia Nazionale dei Lincei. Classe di Scienze Fisiche, Matematiche e Naturali. Rendiconti Lincei. Serie IX. Matematica e Applicazioni 19(1), 25–57 (2008)
Acknowledgements
We would like to thank Vance Blankers, Jason Cantarella, Renzo Cavalieri, Andy Fry, Tom Needham, Eric Rawdon, and Gavin Stewart for stimulating conversations about the geometry of polygon space. We are especially grateful to Noah Otterstetter for his participation in our early conversations about this project and to the anonymous referee for their very helpful suggestions for improving this paper. This work was supported by a grant from the Simons Foundation (#354225, CS).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Bowden, L., Haynes, A., Shonkwiler, C. et al. Spherical geometry and the least symmetric triangle. Geom Dedicata 198, 19–34 (2019). https://doi.org/10.1007/s10711-018-0327-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10711-018-0327-4