1 Introduction

Rock engineering properties are considered to be the most important parameters in the design of ground works. Two important mechanical parameters, uniaxial compressive strength (σc) and elastic modulus of rock (E) should be estimated correctly. There are different empirical relations between σc and E obtained for limestones, agglomerates, dolomites, chalks, sandstones, and basalts (Vásárhelyi 2005; Palchik 2007; Ocak 2008; Vásárhelyi and Davarpanah 2018; Asszonyi et al. 2016), among the others.

Hypothetical stress–strain curves for three different types of rock are presented in Fig. 1. by Ramamurthy et al. (2017). Based on the figure, curves OA, OB and OC represent three stress–strain curves with failure occurring at A, B and C, respectively. According to their sample, curves OA and OB have the same modulus but different strengths and strains at failure, whereas the curves OA and OC have the same strength but different modulus and strains at failure. It means, neither strength nor modulus alone could be chosen to represent the overall quality of rock. Therefore, strength and modulus together will give a realistic understanding of the rock response to engineering usage. This approaching of defining the quality of intact rocks was proposed by Deere and Miller (1966) considering the modulus ratio (MR), which is defined as the ratio of tangent modulus of intact rock (E) at 50% of failure strength to its compressive strength (σc).

Fig. 1
figure 1

Hypothetical stress–strain curves (Ramamurthy et al. 2017)

Full size image

The modulus ratio (MR = E/σc) between the modulus of elasticity (E) and uniaxial compressive strength (σc) for intact rock samples varies from 106 to 1600 (Palmström and Singh 2001). For most rocks MR is between 250 and 500 with average MR = 400, E = 400 σc.

Palchik (2011) examined the MR values for 11 heterogeneous carbonate rocks from different regions of Israel. The investigated dolomites, limestones and chalks had weak to very strong strength with wide range of elastic modulus. He found that MR is closely related to the maximum axial strain (εa,max) at the uniaxial strength of the rock (σc) and the following relationship was found (see Fig. 2):

$${MR = \frac{2k}{{\varepsilon_{a,\hbox{max} } \left( {1 + e^{{ - \varepsilon_{a,\hbox{max} } }} } \right)}}}$$
(1)

where k is a conversion coefficient equal to 100, and εa,max is in  %. When MR is known, εa,max (%) is obtained from Eq. (1) as:

Fig. 2
figure 2

Relationship between modulus ratio (MR) and maximum axial strain (εa,max) using different carbonate rocks (Palchik 2011)

Full size image
$${\varepsilon_{a,\hbox{max} } = \frac{k}{MR - 0.46k}}$$
(2)

Since the expansion of the expression 2/(1 + \(e^{{\varepsilon_{a.\hbox{max} } }}\)) using Taylor’s theorem shows the value of 2/(1 + \(e^{{\varepsilon_{a.\hbox{max} } }}\)) = 1 + 0.46 εa,max (Palchik 2013).

The goal of this paper is to check Eq. (1) for Hungarian granitic rock samples and study relations between characteristic compressive stress level, strain and mechanical properties, as well. Additionally, the validity of recently proposed mathematical model by Palchik (2019) for granitic rock samples was investigated. These granitic rock samples were investigated previously by Vásárhelyi et al. (2013) using multiple failure state triaxial tests (Figs. 3, 4).

Fig. 3
figure 3

Main types of rock samples. a, b megacryst-bearing, medium-grained, biotite-monzogranites, c medium-grained, biotite-monzogranites with elongated monzonitic enclaves, d quartz monzonite

Full size image
Fig. 4
figure 4

A prepared sample in the beginning of the UCS test

Full size image

2 Laboratory Investigations and Analysing

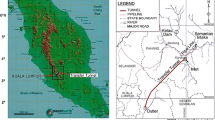
Laboratory samples originated from research boreholes deepened in carboniferous Mórágy Granite Formation during the research and construction phases of deep geological repository of low and intermediate level radioactive waste. This granite formation is a carboniferous intruded and displaced Variscan granite pluton situated in South-West Hungary. The main rock types are mainly microcline megacryst-bearing, medium-grained, biotite-monzogranites, and quartz monzonites (Buda 1985). In spatial viewpoint the monzogranitic rocks contain generally ovalshaped, variably elongated monzonite enclaves (predominantly amphibole-biotite monzonites, diorites, and syenites) of various size (from a few cm to several hundred metres) reflecting the mixing and mingling of two magmas with different composition. Feldspar-quartz rich leucocratic dykes belonging to the late-stage magmatic evolution and Late Cretaceous trachyte and tephryte dykes crosscut all of the previously described rock types (Király and Koroknai 2004). In general fractured but fresh rock is the common which is sparsely intersected by fault zones with few meter thick clay gauges. Intense clay mineralization in the fault cores indicates a low-grade hydrothermal alteration.

The samples were tested by using a computer controlled servo-hydraulic machine in continuous load control mode. The magnitude of loading was settled in kN with 0.01 accuracy, rate of loading was 0.6 kN/s. Axial and tangential deformation were measured by strain gauges, that measures the deformation between ¼ and ¾ of the sample’s height.

Fifty uniaxial compressive tests were performed in the rock mechanics laboratory at RockStudy Ltd. The D = 50 mm sized cylindrical rock samples having the ratio L/D = 2/1 (here L and D is the length and diameter of a sample, respectively) were prepared. Mechanical properties of granitic rock samples are summarized in Table 1.

Table 1 Mechanical properties of investigated Mórágy granitic rock samples
Full size table

Table 1 shows the value of Modulus of elasticity (E), Modulus of rigidity (G) and Bulk modulus (K), uniaxial compressive strength (σc), Poisson’s ratio (ν), Axial failure strain (εamax), and MR for each of the studied granitic samples.

The values of Tangent Young’s modulus (\(E_{tan} )\) is defined as the slope of a line tangent to the stress–strain curve at a fixed percentage (50%) of the ultimate strength, the value of Average Young’s modulus \(\left( E \right)\) is defined as the slope of the straight-line part of the stress–strain curve, the value of Secant Young’s modulus \(\left( {E_{sec} } \right)\) is defined as as the slope of the line from the origin (usually point (0; 0)) to some fixed percentage of ultimate strength, usually 50% and Poisson’s ratio (\(\nu\)) were calculated by using linear regressions along linear portions of stress–axial strain curves and radial strain–axial strain curves, respectively The International Society for Rock Mechanics suggests three standard methods for its determination (Ulusay and Hudson 2007). The value of \(G_{tan}\), \(G_{sec}\) and \(K_{tan}\), \(K_{sec}\) are calculated based on the following equations.

$$G_{tan, sec} = \frac{{E_{tan,sec} }}{{2\left( {1 + \vartheta_{tan,sec} } \right)}}$$
(3)
$$K_{tan,sec} = \frac{{E_{tan,sec} }}{{3\left( {1 - 2\vartheta_{tan,sec} } \right)}}$$
(4)

The values of crack initiation stress (σci) and crack damage stress (σcd) were calculated based on the following methods:

2.1 Onset Dilatancy Method

Brace et al. (1966) illustrated that crack initiation threshold is visible on the axial–volumetric strain curve when it diverges from the straight line (Fig. 5). In practice small deviation of the stress–volumetric strain curve from the straight line can make some difficulties to define one point determining the threshold of crack initiation.

Fig. 5
figure 5

Axial stress–volumetric strain curve with the threshold of crack initiation and crack damage and failure stress for Hungarian granitic samples (uniaxial compression case)

Full size image

2.2 Crack Volumetric Strain Method

Martin and Chandler (1994) proposed that crack initiation could be determined using a plot of crack volumetric strain versus axial strain (Fig. 6). Crack volumetric strain εVcr is calculated as a difference of the elastic volumetric strain εVel and volumetric strain εV determined in the test,

Fig. 6
figure 6

Crack volumetric strain method for crack initiation threshold determination for Hungarian granitic rock sample (uniaxial compression case)

Full size image
$$\varepsilon_{\text{V}} = \varepsilon_{1} + 2\varepsilon_{\text{l}} ,\left( \% \right)$$
(5)
$$\varepsilon_{Vcr} = \varepsilon_{V} - \varepsilon_{Vel} ,\left( \% \right)$$
(6)
$$\varepsilon_{Vel} = \frac{1 - 2\nu }{E}\left( {\sigma_{1} + 2\sigma_{3} } \right),\left( \% \right)$$
(7)

  • εa, εl: axial and lateral strain, (%)

  • σ1, σ3: axial and confining stress, (MPa)

  • E, ν; Young’s modulus and Poisson’s ratio, respectively, (GPa), (–)

Crack volumetric strain is calculated on the basis of these two elastic constants and is strongly sensitive to its value. This is probably why this method does not give objective values.

2.3 Change of Poisson’s Ratio Method

Diederichs (2007) proposed a method of crack initiation threshold identification based on change of Poisson’s ratio. The onset of crack initiation can be identified by analysis of the relation of Poisson’s ratio, evaluated locally, to the log of the axial stress (Fig. 7).

Fig. 7
figure 7

Poisson’s ratio method for crack initiation threshold determination for Hungarian granitic rock samples (uniaxial compression case)

Full size image

However, in this paper, the results obtained from the first method were used for further analysis. The reason is that, based on the findings by Cieslik (2014), this method gives more precise results for granitic rock samples.

The value of MR in each of 50 studied granitic rock samples is between 326.4 and 597.4 with the mean of 439.4. The range of MR obtained by Deere (1968) is between 250 and 700 with the mean of 420 for limestone and dolomites. The range of MR obtained by Palchik (2011) is between 60.9 and 1011.4 with the mean value of 380.5 for carbonated rock samples. The mean value of MR in this study is similar to the mean value of MR obtained by Deere (1968) and Palchik (2011). Figure 8 shows the value of MR for all studied samples in this study. As it can be seen from Fig. 5, the range of MR = 326.4–597.4, observed in this study is narrower than the range of MR obtained by Deere (1968) and Palchik (2011).

Fig. 8
figure 8

Observed values of modulus ratio (MR) in each of 50 examined rock samples

Full size image

The ranges of the elastic modulus (E), Poisson’s ratio (ν), crack damage stress (σcd) and uniaxial compressive strength (σc), axial failure strain (εa max) and maximum volumetric strain (εcd), crack initiation stress (σci) and crack initiation strain (εci) for the studied 50 samples are presented as following (Davarpanah et al. 2019). The histogram of measured parameters is exhibited in Fig. 9.

Fig. 9
figure 9

Histogram of measured parameters

Full size image
$$\begin{aligned} & 57.425\;{\text{GPa}} < {\text{E}} < 88.937\;{\text{GPa}} \\ & 0.18 < \nu < 0.32 \\ & 30\;{\text{MPa}} < \sigma_{\text{ci}} < 90\;{\text{MPa}} \\ & 77\;{\text{MPa}} < \sigma_{\text{cd}} < 182\;{\text{MPa}} \\ & 133.34\;{\text{MPa}} < \sigma_{\text{c}} < 213.04\;{\text{MPa}} \\ & 0.02 < \varepsilon_{\text{ci}} < 0.06 \\ & 0.18 \, < \varepsilon_{\text{a,max}} < \, 0.19 \\ & 0.04 \, < \varepsilon_{\text{cd}} < \, 0.14 \\ \end{aligned}$$

3 Relationship Between Mechanical Parameters and Deformation Constants

The relationship between uniaxial compressive strength (σc), MR and E is shown in Fig. 10.

Fig. 10
figure 10

The Influence of uniaxial compressive strength (σc) on elastic modulus (E) and the value of MR for all studied samples

Full size image

As it is clear, the elastic modulus is related to (σc), (with R2 = 0.06 very small). It also demonstrates that increase in the value of σc from 133 to 213 MPa doesn’t influence E value. It can be seen from Fig. 10 that MR is related to (σc), (with R2 = 0.61). These values, however, are different from the values found by Palchik (2011) for carbonated rocks. In his studies the elastic modulus is partly related to uniaxial compressive strength with R2 = 0.55 and increase in the value of σc doesn’t influence \({\text{M}}_{\text{R}}\) value (R2 = 0.021 is very small).

The observed and analytical (Eq. 1) relationships between εa max and MR for all rock samples exhibiting εa max < 1% is plotted in Fig. 11. It is clear that the calculated (Eq. 1) and observed values of MR for studied rock samples are similar. Figure 12 presents relative and root-mean square errors between the calculated (Eq. 1) and observed MR at εa max < 1%. As it is clear, the relative error \(\left( {\varsigma ,\% } \right)\) for studied samples is between 0.28 and 25% and root-mean square error is (χ = 50). Compare the values with the results obtained by Palchik (2011) for carbonate rock samples, the relative error is between 0.08 and 10.8% and the root-mean square error is 43.6. The relative \(\left( {\varsigma , \% } \right)\) and root-mean-square (χ) errors between the observed and calculated parameter \(\varPi\) have been calculated as:

$$\varsigma_{\left( m \right)} = \frac{{2\left| {\prod_{{{\text{obs}}\left( j \right)}} - \prod_{{{\text{cal}}\left( j \right)}} } \right|}}{{\prod_{{{\text{obs}}\left( j \right)}} + \prod_{{{\text{cal}}\left( j \right)}} }} \times 100$$
(8)
$$\chi_{\left( m \right)} = \sqrt {\frac{{\sum\limits_{j = 1}^{n} {\left[ {\prod_{{{\text{obs}}\left( j \right)}} - \prod_{{{\text{cal}}\left( j \right)}} } \right]^{2} } }}{n - 1}}$$
(9)

where \(\varPi_{obs\left( j \right)}\) is the observed value of parameter in jth sample, here is MR, \(\varPi_{cal\left( j \right)}\) is the calculated value of parameter in jth sample, j = 1, 2,…, n, is the number of tested samples, here is 50.

Fig. 11
figure 11

The observed and analytical (Eq. 1) relationship between εa max and MR

Full size image
Fig. 12
figure 12

Relative \(\left( {\varsigma , \% } \right)\) and root-mean-square (χ) errors between calculated (Eq. 1) and observed MR

Full size image

4 Relationship Between Deformation Constants (E, G, K, ν, MR)

Correlation between Tangant Young’s modulus \(\left( {E_{tan} } \right)\) and Secant Young’s modulus, Tangant Modulus of rigidity (\(G_{tan}\)) and Secant Modulus of rigidity (\(G_{sec}\)), Tangant Bulk modulus (\(K_{tan}\)) and Secant Bulk Modulus (\(K_{sec}\)), Tangant Poisson’s ratio (\(\vartheta_{tan}\)) and Secant Poisson’s ratio (\(\vartheta_{sec}\)), Tangant Modulus ratio (\(M_{Rtan}\)) and Secant Modulus ratio (\(M_{Rsec}\)) were investigated (Fig. 13).

Fig. 13
figure 13

Relationships between deformation constants (E, G, K, ν, MR)

Full size image

According to Fig. 13a, we can see good linear correlation between tan and secant Young’s modulus \(,\) tan and secant modulus of rigidity (Fig. 13b), tan and secant modulus ratio (Fig. 13e), tan Young’s modulus and rigidity modulus (Fig. 13f), secant Young’s modulus and rigidity modulus (Fig. 13g).

5 Investigation of the Validity of Mathematical Model Proposed by Palchik (2019) for Granitic Rock Samples

Palchik (2019) proposed a simple stress–strain model for very strong (\(\sigma_{c} > 100\;{\text{MPa}}\)) carbonate rocks based on Haldane’s distribution function (Haldane 1919).

$$\sigma_{a} = \sigma_{c} \left( {\frac{{1 - e^{{ - s\varepsilon_{a} }} }}{{1 - e^{ - \theta } }}} \right)$$
(10)

where \(\sigma_{a}\) is a current axial stress (MPa), \(\varepsilon_{a}\) is a current axial strain (%) at the axial stress \(\sigma_{a}\), \(\sigma_{c}\) is a uniaxial compressive strength (MPa), parameter (s) is a constant involved in a canonical form of Haldane’s function. For very strong limestones and dolomites (\(\sigma_{c} > 100\;{\text{MPa}}\)) the value of s is between 0.5 and 1, and exponent \(\theta\) is defined as follows

$$\theta = - ln\left[ {1 - \frac{{\sigma_{c} }}{{\sigma_{a} }}\left( {1 - e^{{ - 0.5\varepsilon_{a} }} } \right)} \right]$$
(11)

And can be presented in the following form by using Taylor’s series expansion:

$$\theta = \emptyset + \frac{{\emptyset^{2} }}{2} + \frac{{\emptyset^{3} }}{3}$$
(12)
$$\emptyset = \left( {\frac{{\sigma_{c} }}{{\sigma_{a1} }}} \right)\left( {1 - e^{{ - 0.5\varepsilon_{a1} }} } \right)$$
(13)

when s = 1.1:

$$\sigma_{a} = \sigma_{c} \left( {\frac{{1 - e^{{ - 1.1\varepsilon_{a} }} }}{{1 - e^{ - \psi } }}} \right)$$
(14)
$$\psi = - ln\left[ {1 - \frac{{\sigma_{c} }}{{\sigma_{a} }}\left( {1 - e^{{ - 1.1\varepsilon_{a} }} } \right)} \right]$$
(15)
$$\psi = \upsilon + \frac{{\upsilon^{2} }}{2} + \frac{{\upsilon^{3} }}{3}$$
(16)
$$\upsilon = \left( {\frac{{\sigma_{c} }}{{\sigma_{a1} }}} \right)\left( {1 - e^{{ - 1.1\varepsilon_{a1} }} } \right)$$
(17)

The estimated and observed stress–strain relationships for four granitic rock samples are presented in Fig. 14. The relevant modelling parameters used in Fig. 14. are followings:

Fig. 14
figure 14

Examples of comparison of stress–strain models [Eqs. (10), (14)] and stress–strain relationships observed in this study for very strong (σc > 100 MPa) granitic rock samples (a, b, c, d)

Full size image

  • Sample(a1):\(\sigma_{c} = 181.05 \;{\text{MPa}}\), \(\sigma_{a1} = 27.8 \;{\text{MPa}}\) at \(\varepsilon_{a1} = 0.037\%\)

  • Sample(b4):\(\sigma_{c} = 184.48\;{\text{MPa}}\), \(\sigma_{a1} = 22.22 \;{\text{MPa}}\) at \(\varepsilon_{a1} = 0.042\%\)

  • Sample(c6):\(\sigma_{c} = 148.39\;{\text{MPa}}\), \(\sigma_{a1} = 34.44 \;{\text{MPa}}\) at \(\varepsilon_{a1} = 0.045\%\)

  • Sample(d8):\(\sigma_{c} = 204.23 \;{\text{MPa}}\), \(\sigma_{a1} = 28.93\;{\text{MPa}}\) at \(\varepsilon_{a1} = 0.032\%\)

According to our calculations, the proposed model by Palchik (2019) for very strong limestones and dolomites is in good agreement with the elastic region of stress–strain relationships observed in this study for very strong granitic rock samples. However, there is a significant difference in non-linear part of stress–strain relationships between the observed and estimated values.

Comparison between estimated [Eqs. (10) and (14)], and observed axial stresses for studied rock samples shows a very good linear correlation between these stresses, and thus, Eq. 10 can predict stresses well (Fig. 15).

Fig. 15
figure 15

Linear correlation between observed and estimated (Eq. 10) axial stresses for granitic rock samples

Full size image

6 Discussion

The laboratory compressive tests, statistical analysis, and empirical and analytical relations have been used to estimate the values of MR = E/σc and its relationship with other mechanical parameters for granitic rocks. Studied rock samples exhibiting the wide range of mechanical properties (57.425 GPa < E < 88.937 GPa, 0.18 < ν < 0.32, 77.3 MPa < σcd < 212.42 MPa, 133.34 MPa < σc < 213.04 MPa, 0.18 < εa max < 0.19, 0.04 < εcd < 0.14). The ranges of \(\frac{{\varepsilon_{a max} }}{{\varepsilon_{cd} }}\) and \(\frac{{\sigma_{cd} }}{{\sigma_{c} }}\) and \(\frac{{\sigma_{ci} }}{{\sigma_{c} }}\) ratios are 1.49–5.28 and 0.5–0.9 and 0.2–0.5, respectively. These values are different from the values of \(\frac{{\sigma_{cd} }}{{\sigma_{c} }}\) = 0.5–1.0 and \(\frac{{\varepsilon_{a max} }}{{\varepsilon_{cd} }} =\) 1.51–6.91 obtained by Palchik (2011). They are also different from the values of \(\frac{{\sigma_{cd} }}{{\sigma_{c} }}\) = 0.71–0.84 obtained by Brace et al. (1966), Bieniawski (1967), Martin (1993), Pettitt et al. (1998), Eberhardt et al. (1999), Heo et al. (2001), Katz and Reches (2004) for granites, sandstones and quartzite. The range of \(\frac{{\sigma_{ci} }}{{\sigma_{c} }}\) for most rocks falls in the range of 0.3 to 0.5. Moreover, the relative and root-mean square errors between the calculated (Eq. 1) and observed MR at εa max < 1% were calculated. The relative error \(\left( {\varsigma , \% } \right)\) for studied samples is between 0.28 and 25% and root-mean square error is (χ = 50), while Palchik (2011) calculated the relative error is between 0.08 and 10.8% and the root-mean square error is 43.6. Furthermore, the relationships between deformation constants were investigated. Based on our analyses, there is correlation between tan and secant Young’s modulus (R2 = 0.91), tan and secant modulus of rigidity (R2 = 0.90), tan and secant modulus ratio (R2 = 0.95), tan Young’s modulus and rigidity modulus (R2 = 0.96), secant Young’s modulus and rigidity modulus (R2 = 0.95), Tangant Modulus ratio (\(M_{Rtan}\)) and Secant Modulus ratio (\(M_{Rsec}\)) with the value of (R2 = 0.95). The estimated [Eqs. (10) and (14)] and observed stress–strain relations were plotted for all studied granitic rock samples. The values of the root-mean-square errors (χ), was also calculated for samples (based on Eq. (9)). For sample(a), this value is 2.3 MPa and 1.91 MPa, for sample(b), this value is 18.71 MPa and 21.39 MPa, for sample(c), this value is 7.32 MPa and 4.97 MPa, for sample(d), this value is 34.7 MPa and 21.87 MPa. Palchik (2019) observed a very good linear correlation (0.983 < \(R^{2}\) < 0.99) between estimated and observed axial stresses for very strong (\(\sigma_{c} > 100 \;{\text{Mpa}}\)) carbonate rocks, his results are in good agreement with our obtain results (0.997 < R2 < 0.999) for granitic rock samples.

7 Conclusion

From the results of this study, the following main conclusions are made:

  • The mean value of (MR mean = 439) for all granitic rock samples observed in this study and the mean value of (MR mean = 420) obtained by Deere (1968) for limestone and dolomite and the mean value of (MR mean = 380.5) obtained by Palchik (2011) for carbonate rock samples are similar. However, the range of (MR = 326.42–597.42) obtained in this study is narrower than the range of (MR = 250–700) obtained by Deere (1968) and the range of (MR = 60–1600) obtained by Palchik (2011).

  • The observation confirms that there is no general empirical correlation (with reliable R2) between elastic modulus (E) and uniaxial compressive strength (σc), MR and maximum volumetric strain (εcd), MR and crack damage stress σcd.

  • The analytical relationship (Eq. 1) between εa max and MR offered by Palchik (2011) for carbonate rock samples were investigated for granitic rock samples in this study. It is observed that this relationship can also be used for granitic rocks. The relative error \(\left( {\varsigma , \% } \right)\) for studied samples is between 0.2 and 24.5% and root-mean square error is \(\left( {\chi = 50} \right)\). Compare the values with the result obtained by Palchik (2011) for carbonate rock samples, the relative error is between 0.08 and 10.8% and the root-mean square error is 43.6.

  • The observed correlation between MR and \(\varepsilon_{cd}\) for studied granitic rock sample is (R2 = 0.20). Palchik (2011); however, found a good relationship (R2 = 0.85) between these two parameters for carbonate rock samples.

  • A mathematical model proposed by Palchik (2019) for very strong (σc > 100 MPa) carbonate rocks based on Haldane’s distribution function has a good predictive capability for the linear part of observed stress–strain relation of studied granitic rock samples; however, when it comes to non-linearity behaviour there is a significant difference.

  • Based on proposed mathematical model by Palchik (2019), there is a very good linear correlation between observed and estimated stresses for studied granitic rock samples with the value of R2 = 0.99.

Notably, for a more precise and fundamental description of the mechanical behaviour of rock, one should apply nonequilibrium continuum thermodynamics along the lines of Asszonyi et al. (2015) and beyond. These relationships can be used for determining the mechanical parameters of the rock mass, as well (Vásárhelyi and Kovács 2017).