Probabilistic Characterization of Hoek–Brown Constant m_i of Rock Using Hoek’s Guideline Chart, Regression Model and Uniaxial Compression Test

Abstract

The Hoek–Brown constant m_i is a key input parameter in the Hoek–Brown failure criterion developed for estimating rock mass properties. The Hoek–Brown constant m_i values are traditionally estimated from results of triaxial compression tests, but these tests are time-consuming and expensive. In the absence of laboratory test data, guideline chart and empirical regression models have been proposed in the literature to estimate m_i values, and they give a general trend of m_i. Instead of only using either the guideline chart or regression models, information from both sources can be systematically integrated to improve estimates of m_i. In this study, a Bayesian approach is developed for probabilistic characterization of m_i, using information from guideline chart, regression model and site-specific uniaxial compression strength (UCS) test values. The probabilistic characterization of m_i provides a large number of m_i samples for conventional statistical analysis of m_i, including its full probability distribution. The proposed approach is illustrated and validated using real UCS and triaxial compression test data from a granite site at Forsmark, Sweden. To evaluate the reliability of the proposed method, m_i values estimated from the proposed method are compared with those predicted from a separate analysis which uses triaxial compression tests data. In addition, a sensitivity study is performed to explore the effect of site-specific input on the evolution of m_i. The approach provides reasonable statistics and probability distribution of m_i at a specific site, and the m_i samples can be directly used in rock engineering design and analysis, especially in Hoek–Brown failure criterion to predict rock failure.

1 Introduction

The Hoek–brown failure criterion (Hoek and Brown 1980) is widely used in rock engineering for the determination of rock mass properties such as rock mass strength and deformation modulus (e.g., Peng et al. 2014). The rock mass strength and deformation modulus are important parameters for evaluating the stability of engineering structures in or on rock, such as slopes, foundations, tunnels, and underground caverns. The Hoek–Brown failure criterion is also linked with the Mohr–Coulomb criterion to estimate friction angle and cohesion of rock mass. The criterion has been updated several times in response to experience gained with its use and to address certain practical limitations associated with its usage (e.g., Hoek and Brown 1988; Hoek et al. 1992, 1995, 2002). The generalized Hoek–Brown criterion for jointed rock mass is expressed as (Hoek et al. 2002):

$$\sigma_{1} = \sigma_{3} + \sigma_{ci} \left( {m_{b} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + s} \right)^{a}$$

(1)

where $\sigma_{1}$ and $\sigma_{3}$ are the major and minor principal stresses, respectively, $\sigma_{ci}$ is the uniaxial compressive strength (UCS) of intact rock, and m_b, s, and a are constants for the rock mass. The rock mass constants (i.e., m_b, s, and a) can be calculated as (Hoek et al. 2002):

$$m_{b} = m_{i} \exp \left( {\frac{GSI - 100}{28 - 14D}} \right)$$

(2)

$$s = \exp \left( {\frac{GSI - 100}{9 - 3D}} \right)$$

(3)

$$a = \frac{1}{2} + \frac{1}{6}\left( {\exp ( -\,GSI/15) - \exp ( - \,20/3)} \right)$$

(4)

where GSI, D and m_i are geological strength index (GSI), damage factor and Hoek–Brown constant, respectively. For intact rocks, s and a are equal to 1 and 0.5, respectively, while $m_{b} = m_{i}$. Therefore, for intact rocks, Eq. (1) reduces to:

$$\sigma_{1} = \sigma_{3} + \sigma_{ci} \left( {m_{i} \frac{{\sigma_{3} }}{{\sigma_{ci} }} + 1} \right)^{0.5}$$

(5)

Thus, UCS, GSI and m_i are important parameters required in the Hoek–Brown failure criterion to estimate rock mass properties. While many practical, empirical and probabilistic approaches have been developed in the literature to estimate UCS and GSI (e.g., Hoek and Brown 1997; Hoek et al. 2013; Diamantis et al. 2009; Russo 2009; Aksoy et al. 2012; Kahraman 2014; Wang and Aladejare 2015, 2016a, b; Wong et al. 2015; Aladejare 2016), the determination of m_i remains a difficult task. m_i depends on the frictional characteristics of the component minerals in the intact rock, and it has a significant influence on rock strength (Hoek and Marinos 2000).

Different approaches have been proposed in the literature to estimate m_i. For example, one approach is the determination of m_i through analysis of series of triaxial compression tests (Hoek and Brown 1997). Another approach is guideline chart developed for obtaining m_i values in the absence of laboratory triaxial test data (Hoek and Brown 1997; Hoek 2007). Another approach is R index, which estimates m_i value as a ratio of UCS to tensile strength (e.g., Cai 2010; Read and Richards 2011). The limitations to these approaches are that triaxial tests require time-consuming procedures, and they are not always routinely conducted at the early stage of a project (Cai 2010). The guideline chart represents general information, which does not necessarily reflect exact information from a specific site. Also, direct tensile tests are not frequently carried out as standard procedures in many rock testing laboratories, because of the difficulty in specimen preparation. To solve this problem, different empirical models have been proposed in the literature to estimate m_i from parameters like crack initiation stress and UCS etc. (e.g., Cai 2010; Peng et al. 2014; Shen and Karakus 2014; Vasarhelyi et al. 2016). Specifically, estimating m_i from UCS has gained prominence due to UCS availability in most rock mechanics databases, and also because of the possibility to estimate UCS from other rock properties like point load index, when UCS data are not available from laboratory test (e.g., Wang and Aladejare 2015). When triaxial test results are not available at a project site, rock engineers and engineering practitioners frequently adopt the guideline chart proposed by Hoek (2007) or regression models available in the literature for predicting values of m_i. Instead of only using information from either the guideline chart or regression models available in the literature, information from both sources can be systematically synthesized and integrated to improve predictions of m_i values. This is consistent with the suggestion of Shen and Karakus (2014) that the correlations between UCS and m_i available in the literature can be used together with the guideline chart for preliminary estimation of m_i in the absence of triaxial test data. Bayesian method provides a rational vehicle for such combination, as it can integrate information from different sources to improve predictions in terms of statistics and full probability distribution of m_i.

This paper develops a Bayesian approach for probabilistic characterization of Hoek–Brown constant m_i through Bayesian integration of information from Hoek’s guideline chart, regression model and site-specific UCS data. The proposed Bayesian approach provides a logical route to determine the characteristic values and full probability distribution of m_i when extensive triaxial testing cannot be performed, which is often the case for a majority of rock engineering projects, particularly those of small to medium sizes. This study briefly reviews the existing methods in the literature for estimating m_i. Then, probabilistic modelling of the inherent variability of the Hoek–Brown constant m_i at a site and transformation uncertainty associated with the regression between m_i and UCS are presented, followed by the development of the proposed Bayesian approach. The proposed approach derives the probability density function (PDF) of m_i based on the integration of Hoek’s guideline chart, regression model and site-specific UCS data, under a Bayesian framework. A large number of equivalent samples of m_i are generated from the PDF using Markov chain Monte Carlo (MCMC) simulation. Conventional statistical analysis of the equivalent examples is subsequently carried out to determine the statistics of m_i and its characteristic values. The proposed approach is illustrated using a set of real UCS data obtained from a granite site at Forsmark, Sweden. In addition, several sets of simulated data are used to explore the evolution of m_i as the number of site-specific data increases.

2 Existing Methods for Estimating Hoek–Brown Constant m _i

The Hoek–Brown constant m_i defines the nonlinear strength envelope of intact rocks. The parameter m_i depends on the frictional characteristics of the component minerals in intact rock and it has significant influence on rock strength (Hoek and Marinos 2000). Some methods have been reported in the literature for estimating m_i at a site.

For example, one method introduced for estimating m_i is through the analysis of a series of triaxial compression tests. Hoek and Brown (1997) suggested that the values of m_i be estimated by applying different confining stress ($\sigma_{3}$) from 0 to 0.5UCS, with at least five sets of triaxial tests included in the analysis. For n number of triaxial data sets, the Hoek–Brown constant m_i can be calculated using Eqs. (6) and (7).

$$\sigma_{ci} = \sqrt {\frac{\sum y}{n} - \left[ {\frac{\sum xy - (\sum x\sum y/n)}{{\sum x^{2} - [(\sum x)^{2} /n]}}} \right]\frac{\sum x}{n}}$$

(6)

$$m_{i} = \frac{1}{{\sigma_{ci} }}\left[ {\frac{\sum xy - (\sum x\sum y/n)}{{\sum x^{2} - [(\sum x)^{2} /n]}}} \right]$$

(7)

where $x = \sigma_{3}$ and $y = (\sigma_{1} - \sigma_{3} )^{2}$. Note that the value of $\sigma_{ci}$ in Eq. (6) is calculated from triaxial data and is different from UCS estimated from uniaxial compression tests. Singh et al. (2011), Peng et al. (2014), and Shen and Karakus (2014) explained that the reliability of m_i values calculated from triaxial test analysis depends on the quality and quantity of test data used in the analysis. They concluded that the range of $\sigma_{3}$ can have a significant influence on the calculation of m_i. In addition, triaxial tests require time-consuming procedures, and they are not always routinely conducted in a significant number especially at small to medium project sites and at the early stage of a project.

In the absence of triaxial tests or when the number of triaxial test results available is not sufficient for estimating m_i, Hoek et al. (2007) proposed a guideline chart, which is based on a more detailed lithologic classification of rocks and geologic description of rock types. Table 1 shows the guideline chart for estimating m_i values of intact rock, by rock group. The guideline chart, however, represents general information, acquired through engineering experience which does not necessarily reflect exact information of m_i at a specific site.

Table 1 Values of m_i for intact rock, by rock group (after Hoek 2007)

In order to determine m_i at a specific site when there are no triaxial test results, some regression models have been developed and reported in the literature to estimate m_i from results of uniaxial compression tests (i.e., UCS values) (e.g., Shen and Karakus 2014; Vasarhelyi et al. 2016). They developed regression models with a general format, as expressed in Eq. (8).

$$m_{in} = a{\text{UCS}}^{b}$$

(8)

where $m_{in} = m_{i} /{\text{UCS}}$ = normalized m_i (the unit for m_in is 1/MPa). From Eq. (8) and $m_{in} = m_{i} /{\text{UCS}}$, m_i can be estimated using UCS values, as expressed in Eq. (9).

$$m_{i} = a{\text{UCS}}^{b + 1}$$

(9)

where a and b are rock type specific model constants, and they were derived by their respective authors.

3 Probabilistic Modelling of Inherent Variability in m _i

Probability theory (e.g., Ang and Tang 2007; Wang and Aladejare 2015; Aladejare and Wang 2018) is applied in this study to model the inherent variability of Hoek–Brown constant m_i of rock at a rock deposit or project site. Consider, for example, the Hoek–brown constant m_i, of a rock deposit, which is a continuous variable and must be strictly non-negative. To explicitly model the inherent variability, m_i is taken as a lognormal random variable with a mean $\mu$ and standard deviation $\sigma ,$ and it is expressed as (e.g., Ang and Tang 2007; Wang and Cao 2013):

$$m_{i} = \exp (\mu_{N} + \sigma_{N} z)$$

(10)

where z is a standard Gaussian random variable; $\mu_{N} = \ln \mu - 0.5\sigma_{N}^{2}$ and $\sigma_{N} = \sqrt {\ln (1 + (\sigma /\mu )^{2} }$ are the mean and standard deviation of the logarithm of m_i (i.e., $\ln (m_{i} )$), respectively. Since m_i is lognormally distributed, $\ln (m_{i} )$ is normally distributed, and it is expressed as:

$$\ln (m_{i} ) = \mu_{N} + \sigma_{N} z$$

(11)

Both $\sigma$ of $m_{i}$ and $\sigma_{N}$ of $\ln (m_{i} )$ represent the inherent variability of the Hoek–brown constant at a rock deposit or project site.

4 Transformation Uncertainty in the m _i and UCS Regression

The Hoek–Brown constant m_i of rock can be estimated from other rock properties when the required sets of triaxial tests are not readily available at a project site. Among the rock properties that have been proposed to estimate m_i, UCS is readily available in the literature or could be estimated from other properties like point load index (e.g., Bell and Lindsay 1999; Tsiambaos and Sabatakakis 2004; Sabatakakis et al. 2008; Wang and Aladejare 2015; Aladejare 2016). Therefore, the model for estimating m_i from UCS is considered in the development of the proposed Bayesian approach. Take, for instance, the empirical model proposed by Vasarhelyi et al. (2016) for estimating m_i of granitic rocks from UCS as expressed in Eqs. (8) or (9), in which a = 216 and b = − 1.53. Equation (9) can be rewritten in a log–log scale as:

$$\ln ({\text{UCS}}) = \frac{1}{b + 1}\ln (m_{i} ) - \frac{1}{b + 1}\ln (a) + \varepsilon$$

(12)

where $\ln ({\text{UCS}})$ denotes the UCS values in a log scale, $\varepsilon$ is the transformation uncertainty associated with the regression for estimating m_i from UCS in Eq. (12). $\varepsilon$ is a Gaussian random variable with a mean of $\mu_{\varepsilon } = 0$ and standard deviation of $\sigma_{\varepsilon } = 0.467$, calculated from the original dataset that was used to develop the model. Combining Eqs. (11) and (12) leads to:

$$\ln ({\text{UCS}}) = \left( {\frac{{\mu_{N} - \ln (a)}}{b + 1}} \right) + \frac{{\sigma_{N} z}}{b + 1} + \varepsilon$$

(13)

The inherent variability is from the spatial variability in m_i (e.g., Aladejare and Wang 2017) while the transformation uncertainty is from the empirical model for estimating m_i from UCS. The inherent variability and transformation uncertainty are from different sources and can be assumed to be independent of each other (i.e., z is independent of $\varepsilon$). Therefore, ln(UCS) is taken as a Gaussian random variable with a mean $\left( {\frac{{\mu_{N}- \ln (a)}}{b + 1}}\right)$ and standard deviation $\sqrt {\left( {\frac{{\sigma_{N} }}{b + 1}} \right)^{2} + (\sigma_{\varepsilon } )^{2} }$.

5 Bayesian Quantification of Probabilistic Model Parameters for Hoek–Brown Constant m _i

As defined by Eqs. (10) or (11), the Hoek–Brown constant is modelled by a lognormally distributed random variable m_i with a mean $\mu$ and standard deviation $\sigma$. The information on the model parameters (i.e., $\mu$ and $\sigma$) is required for probabilistic characterization of Hoek–Brown constant m_i. Such information is unknown and can be determined using site observation data (e.g., UCS data) and guideline chart on m_i reported in the literature. The information on m_i from the guideline chart is used as prior information in this study, to reflect the knowledge on m_i before site observation data are obtained. For a given set of the prior knowledge (i.e., information from the Hoek’s guideline chart) and site-specific UCS data, there are many sets of possible combinations of $\mu$ and $\sigma$. Each set of $\mu$ and $\sigma$ has its corresponding occurrence probability, which is defined by a joint conditional probability density function (PDF), $P(\mu ,\sigma \left| {Data,Prior} \right.)$.

Under a Bayesian framework, the updated knowledge (i.e., posterior knowledge) on model parameters $\mu$ and $\sigma$ (i.e., $P(\mu ,\sigma \left| {Data,Prior} \right.)$) is simplified as $P(\mu ,\sigma \left| {Data} \right.)$. Using Bayes’ theorem, $P(\mu ,\sigma \left| {Data} \right.)$ is expressed as (e.g., Ang and Tang 2007; Wang et al. 2016; Wang and Aladejare 2016a, b):

$$P(\mu ,\sigma \left| {Data} \right.) = KP(Data{\kern 1pt} \left| {\mu ,\sigma } \right.)P(\mu ,\sigma )$$

(14)

where $K = P(Data) = (\iint {P(Data{\kern 1pt} \left| {\mu ,\sigma } \right.)P(\mu ,\sigma )d\mu d\sigma )^{ - 1} }$ is a normalizing constant such that the area under the updated PDF is unity, $Data = \{ \ln ({\text{UCS}})_{i} ,\;i = 1,{\kern 1pt} 2, \ldots ,n_{k} \}$ is a set of UCS data with a total of $n_{k}$ ln(UCS) values obtained at a specific project site, $P(Data{\kern 1pt} \left| {\mu ,\sigma } \right.)$ is the likelihood function, which reflects the model fit with the Data.$P(\mu ,\sigma )$ is the prior distribution of $\mu$ and $\sigma$, which reflects the prior knowledge on $\mu$ and $\sigma$ to express the user’s judgment about the relative plausibility of the values of $\mu$ and $\sigma$ in the absence of observation data at a project site. The prior information on $\mu$ and $\sigma$ is obtained from the Hoek’s guideline chart on m_i.

As described in Sect. 4, ln(UCS) is a Gaussian random variable with a mean $\left(\frac{{\mu_{N} - \ln (a)}}{b + 1}\right)$ and standard deviation $\sqrt {(\frac{{\sigma_{N} }}{b + 1})^{2} + (\sigma_{\varepsilon } )^{2} }$. The samples for estimating UCS are often obtained at a rock site by grab sampling or by drilling in discrete manner at considerable distance between drilled holes, and hence, the site-specific UCS data points can be considered to be independent of each other. Therefore, the site-specific UCS data (i.e., $Data = \{ \ln ({\text{UCS}})_{i} ,\;i = 1,2, \ldots ,{\kern 1pt} n_{k} \}$) can be simplified as $n_{k}$ independent realizations of the Gaussian random variable ln(UCS). Then, the likelihood function $P(Data{\kern 1pt} \left| {\mu ,\sigma } \right.)$ is a product of the data points of ln(UCS), which is expressed as:

$$P(Data{\kern 1pt} \left| {\mu ,\sigma } \right.) = \prod\limits_{i = 1}^{{n_{k} }} {\frac{1}{{\sqrt {2\pi } \sqrt {(\frac{{\sigma_{N} }}{b + 1})^{2} + (\sigma_{\varepsilon } )^{2} } }}} \exp \left\{ { - \frac{1}{2}\left[ {\frac{{\ln ({\text{UCS}})_{i} - \left(\frac{{\mu_{N} - \ln (a)}}{b + 1}\right)}}{{\sqrt {(\frac{{\sigma_{N} }}{b + 1})^{2} + (\sigma_{\varepsilon } )^{2} } }}} \right]^{2} } \right\}$$

(15)

When there is no prevailing prior knowledge of $\mu$ and $\sigma$, a non-informative prior distribution can be employed so that the prior PDF can be absorbed into the normalizing constant. With this type of prior distribution, the Bayesian inference on $\mu$ and $\sigma$ will rely solely on the likelihood function. The prior distribution can be simply assumed as a joint uniform distribution of $\mu$ and $\sigma$ with respective minimum values of $\mu_{\hbox{min} }$ and $\sigma_{\hbox{min} }$ and respective maximum values of $\mu_{\hbox{max} }$ and $\sigma_{\hbox{max} }$ and it is expressed as (e.g., Ang and Tang 2007; Cao et al. 2016):

$$P(\mu ,\sigma ) = \left\{ {\begin{array}{*{20}l} {\frac{1}{{(\mu_{\hbox{max} } - \mu_{\hbox{min} } ) \times (\sigma_{\hbox{max} } - \sigma_{\hbox{min} } )}}} \hfill & {\begin{array}{*{20}c} {\quad {\text{for}}\;\mu \in [\mu_{\hbox{min} } ,\mu_{\hbox{max} } ]} \\ {\quad {\text{and}}\;\sigma \in [\sigma_{\hbox{min} } ,\sigma_{\hbox{max} } ]} \\ \end{array} } \hfill \\ 0 \hfill & {\quad {\text{others}}} \hfill \\ \end{array} } \right.$$

(16)

Only the possible ranges (i.e., $\mu_{\hbox{min} }$, $\mu_{\hbox{max} }$, $\sigma_{\hbox{min} }$ and $\sigma_{\hbox{max} }$) of the model parameters are needed to completely define a uniform prior distribution presented in Eq. (16). The values of $\mu_{\hbox{min} }$, $\mu_{\hbox{max} }$, $\sigma_{\hbox{min} }$ and $\sigma_{\hbox{max} }$ are obtained from the information contained in the Hoek’s guideline chart (Hoek 2007). Consider, for example, the information of m_i reported for granite in the Hoek’s guideline chart. m_i of granite is reported to have a range of 32 ± 3. Therefore, $\mu_{\hbox{min} }$ and $\mu_{\hbox{max} }$ are taken as the lower and upper bound of the ranges of $m_{i}$ (i.e., 32 ± 3) reported in the Hoek’s guideline chart. Hence, $\mu_{\hbox{min} }$ = 29 and $\mu_{\hbox{max} }$ = 35, $\sigma_{\hbox{min} }$ = 0 to reflect the non-negative physical meaning of the standard deviation of m_i. Since there is no $\sigma_{\hbox{max} }$ reported in literature, this study adopted $\sigma_{\hbox{max} }$ as a factor of the range of m_i reported in the Hoek’s guideline chart. As suggested by Cao et al. (2016), when there is lack of confident information, a relatively large range shall be used as prior information in Bayesian method. Therefore, $\sigma_{\hbox{max} }$ is taken as twice the range of values of m_i reported by Hoek (2007) (i.e., $\sigma_{\hbox{max} }$ = 12). For non-informative prior knowledge like the one adopted in this study, uniform prior distribution is sufficient to quantitatively reflect the engineering common sense and judgment. These typical ranges (i.e., $\mu$: [29, 35] and $\sigma$: [0, 12]) obtained from the Hoek’s guideline chart is integrated with site-specific UCS data (i.e., $Data = \{ \ln ({\text{UCS}})_{i} ,\;i = 1,2, \ldots ,{\kern 1pt} n_{k} \}$) to update information on m_i. In the next section, the updated distribution of model parameters of m_i is used in formulating the PDF of m_i.

6 Probability Density Function of Hoek–Brown Constant m _i

As earlier discussed in Sect. 5, for a given prior knowledge and site-specific data, there are many possible combinations of $\mu$ and $\sigma$. Using the theorem of total probability (e.g., Ang and Tang 2007) and the updated distribution of model parameters of m_i obtained in Sect. 5, the PDF of the Hoek–Brown constant m_i for a given set of prior knowledge (obtained from guideline chart) and site-specific UCS data is denoted as $P(m_{i} \left| {Data,Prior} \right.)$, and expressed as:

$$P(m_{i} \left| {Data,Prior} \right.) = \iint {P(m_{i} \left| {\mu ,\sigma } \right.)}P(\mu ,\sigma \left| {Data,Prior} \right.)d\mu d\sigma$$

(17)

Using the updated knowledge of the model parameters given by Eq. (14), the PDF of Hoek–Brown constant m_i (i.e., Eq. 17) is rewritten as:

$$P(m_{i} \left| {Data,Prior} \right.) = K\iint {P(m_{i} \left| {\mu ,\sigma } \right.})P(Data\left| {\mu ,\sigma } \right.)P(\mu ,\sigma )d\mu d\sigma$$

(18)

$P(m_{i} \left| {\mu ,\sigma )} \right.$ is the conditional PDF of m_i for a given set of model parameters (i.e., $\mu$ and $\sigma$). Since m_i is lognormally distributed, $P(m_{i} \left| {\mu ,\sigma )} \right.$ is expressed as (e.g., Ang and Tang 2007):

$$P(m_{i} \left| {\mu ,\sigma } \right.) = \frac{1}{{\sqrt {2\pi } \sigma_{N} m_{i} }}\exp \left\{ { - \frac{1}{2}\left[ {\frac{{\ln (m_{i} ) - \mu_{N} }}{{\sigma_{N} }}} \right]^{2} } \right\}$$

(19)

Note that both $\mu_{N}$ and $\sigma_{N}$ are functions of $\mu$ and $\sigma$ (see Sect. 2). Equation (18) gives the PDF of m_i for a given set of prior knowledge (i.e., information of m_i on specific rock type available in the Hoek’s guideline chart) and site-specific UCS data (i.e., Data). The PDF obtained using Eq. (18) is incorporated into MCMC simulation to improve its robustness and practicality and make the proposed approach readily applicable to general choices of prior distributions (e.g., normal prior distribution, an arbitrary histogram type of prior distribution etc.). Metropolis–Hastings (MH) algorithm (Metropolis et al. 1953; Hastings 1970) is adopted in the MCMC simulation to generate a sequence of large number of m_i samples from Eq. (18). Then, using conventional statistical methods, the equivalent samples of m_i simulated through MCMC simulation are used to construct a histogram and cumulative frequency diagram for proper estimations of the PDF and cumulative distribution function (CDF) of m_i and to estimate the statistics (e.g., mean, standard deviation, and percentiles) of m_i. Finally, the characteristic values of m_i are determined from the statistics accordingly. Details of the MH algorithm used in MCMC simulation for generating samples from arbitrary and complicated PDF like Eq. (18) have been reported in the literature (e.g., Wang and Cao 2013; Wang and Aladejare 2016a).

7 Illustrative Example

This section illustrates the proposed Bayesian approach using a set of real-life UCS data of granite from uniaxial compression test of cylindrical specimens obtained from borehole KFM05A at Forsmark, Sweden (Jacobsson 2005a). Note that reported data from sophisticated laboratory and field tests on Forsmark, Sweden have been previously used in rock engineering studies (e.g., Peng et al. 2014). In addition, Jacobsson (2005b) reported results of triaxial compression tests (i.e., 8 data pairs of $\sigma_{1}$ and $\sigma_{3}$) of cylindrical specimens obtained from borehole KFM05A at Forsmark, Sweden. These data (i.e., $\sigma_{1}$ and $\sigma_{3}$) are of great value, as they are used in this study for separate analysis in order to validate the results obtained from the proposed Bayesian approach. This section aims to illustrate how the proposed Bayesian approach is used together with only 10 UCS data points to provide a probabilistic characterization of m_i, which is practically identical to a m_i characterization obtained from a separate analysis using triaxial compression test results from the site. Note that, quite often, the triaixal compression tests are not available for a majority of rock engineering projects, because of limited resources or testing condition requirements.

Table 2 presents the 10 UCS data in the second column while Table 3 presents eight data pairs of $\sigma_{3}$ and $\sigma_{1}$ from triaxial compression tests in the second and third columns, respectively. To validate the results of the proposed Bayesian approach, a bootstrap analysis is performed using results of the triaxial compression tests from the site with Eqs. (6) and (7) proposed by Hoek and Brown (1997) to obtain m_i. The bootstrap method is especially advantageous for the situation when the distributions of property of interest are unknown and/or the sample size is insufficient (e.g., Luo et al. 2012). Using the original set of observations (i.e., $\sigma_{1}$ and $\sigma_{3}$) presented in Table 3, bootstrapping begins with random sampling of a data point (i.e., a pair of $\sigma_{1}$ and $\sigma_{3}$) with replacement until the total number of sample pair is equal to the original sample pairs in Table 3 (i.e., n = 8). In the bootstrapping, the size of a bootstrap sample pairs in a single resampling is set to the original sample size, n. This is because if the size of each bootstrap sample pairs is set to be smaller or greater than the original sample size, the sample statistics may be overestimated or underestimated (e.g., Johnson 2001). The 8 bootstrap sample pairs of $\sigma_{1}$ and $\sigma_{3}$ are then used in Eqs. (6) and (7) to calculate m_i. These processes of bootstrapping and calculation of m_i are repeated 1000 times to obtain 1000 data points of m_i, for separate estimation of the statistics and probability distribution of m_i. The choice of 1000 simulations samples of m_i is consistent with some geotechnical engineering studies that have successfully used 1000 bootstrapped samples in geotechnical applications, like comparing soil depth profiles (Keith et al. 2016), predicting the soil–water retention curve (Babaeian et al. 2015) etc. The scatter plot of the 1000 data points of m_i obtained from the bootstrap analysis using results of the triaxial compression tests in Eqs. (6) and (7) are shown in Fig. 1. The bootstrapping of a limited number of triaxial data set of $\sigma_{1}$ and $\sigma_{3}$ is used as independent test results to validate the proposed Bayesian method, because the proposed method does not use triaxial data set of $\sigma_{1}$ and $\sigma_{3}$. In addition, since the sampled data set of $\sigma_{1}$ and $\sigma_{3}$ obtained from the original data set are in different order, they can be taken as independent test results in this study. Therefore, the data points of m_i shown in Fig. 1, which are estimated from bootstrapped data sets of $\sigma_{1}$ and $\sigma_{3}$ are used as independent test results. They are used to compare and validate the results from the proposed Bayesian approach.

Table 2 Results of uniaxial compression tests on granite from borehole KFM05A, Forsmark site, Sweden (after Jacobsson 2005a)

Table 3 Results of triaxial compression tests on granite from borehole KFM05A, Forsmark site, Sweden (after Jacobsson 2005b)

Fig. 1

Bootstrap samples of m_i of granite from borehole KFM05A, Forsmark, Sweden, obtained using triaxial compression test results

7.1 Equivalent Samples of Hoek–Brown Constant m _i

In this illustrative example, the 10 UCS data points in Table 2, regression model for estimating m_i and the information on m_i reported in the Hoek’s guideline chart are systematically synthesized and integrated as input in the proposed Bayesian approach. An MCMC simulation is performed to simulate 30,000 equivalent samples of m_i. Figure 2 shows a scatter plot for the 30,000 equivalent samples of m_i obtained through the proposed Bayesian approach. 27,930 equivalent samples (i.e., around 93% of the 30,000 equivalent samples) of m_i are less than 48. The equivalent samples become growingly sparse when m_i > 48. To examine the statistical distribution of the equivalent samples, the corresponding histogram is constructed, as shown in Fig. 3. The histogram peaks at a m_i value of around 30, and roughly about 27,479 out of the total 30,000 samples representing about 91.5% are within m_i range of [18, 48]. Therefore, the 90% inter-percentile range of m_i is roughly between m_i values of 18 and 48.

Fig. 2

Scatter plot of Hoek–Brown constant m_i samples from Bayesian approach

Fig. 3

Histogram of the equivalent samples for Hoek–Brown constant m_i from Bayesian approach

7.2 Probability Distribution of Hoek–Brown Constant m_i

Figure 4 shows the PDF of m_i estimated through the histogram (see Fig. 3) of the equivalent samples from Bayesian approach by a solid line. Figure 4 also includes the histogram of the 1000 m_i samples obtained from bootstrap analysis using triaxial compression test results in Eqs. (6) and (7). 913 out of the 1000 values of m_i provided by the bootstrap analysis using triaxial compression test results in Eqs. (6) and (7) fall within a $m_{i}$ range of [18, 48], i.e., around the 90% inter-percentile range of m_i estimated from the equivalent samples through the Bayesian approach. It can be observed that the probability distribution of the 30,000 samples of m_i from Bayesian approach is consistent with the distribution of the 1000 samples of m_i estimated from bootstrap analysis by using the site-specific triaxial compression test results in Eqs. (6) and (7). The PDF line estimated from 30,000 samples of m_i from Bayesian approach peaks at the same region of the peak of the histogram estimated from 1000 samples of m_i estimated from bootstrap analysis using triaxial compression test results in Eqs. (6) and (7). In addition, the spread of the PDF line is consistent with that of the histogram of 1000 m_i samples obtained from the bootstrap analysis. The consistency indicates that the proposed Bayesian approach provides a reasonable representation of the distribution of m_i at the site.

Fig. 4

Probability distribution of Hoek–Brown constant m_i

Figure 5 plots the CDFs of m_i estimated from the cumulative frequency diagrams of the 30,000 equivalent samples (see Fig. 2) obtained through Bayesian approach and the 1000 m_i samples obtained through bootstrap analysis using triaxial compression test results in Eqs. (6) and (7) (see Fig. 1) by a solid line and dashed line, respectively. The solid line plots closely to the dashed line, which indicates good agreement between them. The CDF of m_i estimated from the equivalent samples compares favourably with that obtained from the 1000 m_i samples obtained through the bootstrap analysis. Such a good agreement suggests that the information contained in the equivalent samples from Bayesian approach is consistent with that obtained from bootstrap analysis, which uses triaxial compression test results. The equivalent samples of m_i from Bayesian approach contain combined information of site-specific UCS data, regression model and guideline on the typical ranges of m_i reported in the Hoek’s guideline chart. Based on the regression model, limited uniaxial compression test data (i.e., 10 UCS values) and guideline chart on m_i reported in the literature, the Bayesian approach provides a reasonable estimate of the statistical distribution of m_i at the site. Such probabilistic characterization is often difficult to obtain from direct triaxial compression tests because of a large amount of data required, and the associated cost, time and equipment set-up. Many times, triaxial compression tests are not performed at mining project sites or at most the number of triaxial compression tests performed are not sufficient to obtain distribution of m_i. The approach developed in this study helps to bypass the difficulty in obtaining probability distribution of m_i from limited test data. The full probability distribution of Hoek–Brown constant m_i is helpful in estimating rock mass properties through Hoek–Brown failure criterion, especially when probabilistic assessment of rock properties is required.

Fig. 5

Validation of the probability distribution of Hoek–Brown constant m_i from Bayesian equivalent samples

7.3 Statistics of Hoek–Brown Constant, m_i

Table 4 summarizes the estimates of the mean and standard deviation of the 30,000 equivalent samples of m_i from the Bayesian approach in the second column. The mean and standard deviation of m_i from the 30,000 equivalent samples are calculated as 29.37 and 11.37, respectively. Table 4 also includes the mean and standard deviation of the 1000 samples of m_i obtained through the bootstrap analysis using triaxial compression test results in the third column, calculated as 28.79 and 10.52, respectively.

Table 4 Summary of the statistics of Hoek–Brown constant, m_i

The absolute difference between the mean values estimated from the equivalent samples of Bayesian approach and samples from the bootstrap analysis using triaxial compression test results is 0.58, which represents a relative difference of 2.1%. The absolute difference between their standard deviation values is 0.85, which represents a relative difference of 8.1%. The small relative differences in the mean and standard deviation values suggest that the Bayesian approach proposed in this study properly characterizes the m_i at the site, using information from guideline chart, regression model and available site-specific UCS data. This tackles the difficulty in estimating the statistics of m_i, especially when triaxial compression test results are not available or when available in small quantities, which is often the case for most rock engineering projects.

With the statistics of m_i obtained, design calculations involving the use of m_i values can be carried out accordingly. The m_i samples from the proposed approach can be used in preliminary design and construction stage when triaxial compression tests data are not available, or when they are only available in limited quantity for meaningful statistics of m_i to be made. In addition, the m_i samples obtained through the proposed approach can be used directly in probability-based estimation of rock mass properties through the Hoek–Brown failure criterion.

8 Sensitivity Study on Site-Specific Test Data

In this section, a sensitivity study is performed to explore the evolution of m_i as the number of test data increases. The equivalent samples of m_i generated through the approach developed in this study use site-specific test data and information from guideline chart as input data, it is therefore logical that the results from the approach may be affected by the test data and guideline chart used. While the guideline chart represents general information about m_i existing in the literature, the site-specific test data can be obtained for different sites and are different from site to site. To perform the sensitivity study, simulated UCS data are used, which are simulated using the uncertainty model given by Eq. (13) with $\mu = 30.0$ and $\sigma = 10.0$, while the information from the guideline chart are kept constant as used in Sect. 5. 10 data sets each of UCS data are simulated for different number of UCS test values (i.e. ${\kern 1pt} n_{k}$) at ${\kern 1pt} n_{k}$ = 1, 3, 5, 10, 20, and 30 resulting in a total of 60 sets of UCS data with 10 sets for each ${\kern 1pt} n_{k}$. For example, Fig. 6 shows 10 sets of the simulated UCS data with 10 UCS values in each data set (i.e., data quantity ${\kern 1pt} n_{k}$ = 10 in each data set). Each of the 60 data sets of simulated UCS data is used as site-specific test data in the Bayesian approach, together with the information from guideline chart used in Sect. 5 to generate 30,000 equivalent samples of m_i. This leads to 60 sets of the probabilistic characterization of m_i including estimates of mean and standard deviation for each data set, which are compared with the true mean and standard deviation (i.e., $\mu = 30.00$ and $\sigma = 10.00$) in the next subsections.

Fig. 6

Ten sets of simulated UCS data

8.1 Effect of Data Quantity on the Mean of m _i

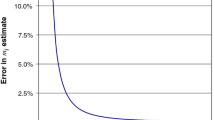
Table 5 presents the summary of the mean values of m_i from probabilistic characterization using the 60 simulated data sets. The ranges of the mean values of m_i from probabilistic characterizations using different data quantity (i.e., ${\kern 1pt} n_{k}$ = 1, 3, 5, 10, 20, and 30) are presented. The ranges presented for each ${\kern 1pt} n_{k}$ in Table 5 are from 10 estimates of mean obtained by using 10 data sets of ${\kern 1pt} n_{k}$ = 1, 3, 5, 10, 20, and 30 in the proposed approach for probabilistic characterization of m_i. The maximum difference of the mean values for each ${\kern 1pt} n_{k}$ is included in parenthesis. Table 5 also includes the averages of the mean values of m_i from using different number of input data, and their absolute and relative differences. The true value of mean (i.e., $\mu = 30.00$) is included in the footnote of Table 5 for comparison with the results from the proposed approach. It is observed that when ${\kern 1pt} n_{k}$ = 1, 3 and 5, the equivalent samples of m_i from Bayesian approach are dominated by information in the guideline chart. The average mean values of m_i when ${\kern 1pt} n_{k}$ = 1, 3 and 5 are close to the mid value of the m_i range (i.e., 32.00) in the guideline chart. As the number of input data increases, the mean values of m_i begin to approach the true mean (i.e., 30.00). Also, it is observed that the scatterness of the mean values of m_i reduces as the number of input data increases. The absolute and relative differences in the mean values of m_i reduce as the number of input data increases, from 7.67% at ${\kern 1pt} n_{k}$ = 1 to 0.40% at ${\kern 1pt} n_{k}$ = 30. At ${\kern 1pt} n_{k}$ = 10, the relative difference is as small as 2.17%, indicating closeness in the estimates of the mean values of m_i from the proposed approach with the true value of m_i.

Table 5 Effect of the data quantity on mean of m_i

In addition, Fig. 7 plots the mean values from each probabilistic characterization by open circles, and the true mean value by dashed lines. It is observed that the spread of the mean values is wide and above the true value before ${\kern 1pt} n_{k}$ = 10. At ${\kern 1pt} n_{k}$ = 10 and above, the spread of the mean values reduces drastically and clustered more around the true mean. This shows that the estimates of the mean of m_i become more consistent as the number of input data increases. The uncertainty arising from limited number of data reduces as the number of input data increases. This is because as the number of input data increases, the equivalent samples of m_i from the proposed approach reflects more of information from the site-specific test data than the guideline chart. At ${\kern 1pt} n_{k}$ = 30, the mean estimates from the proposed approach clustered closely to the true mean value of m_i, which was used to simulate the UCS data used in the probabilistic characterizations. From the results, it is deduced that as from ${\kern 1pt} n_{k}$ = 10, the proposed approach provides characterization of m_i which reflects the information from the site. Thus, at such a limited number of site-specific data, the proposed approach provides a full probability distribution of m_i, therefore bypassing the prevalent problem of non-availability of triaxial compression tests data for estimation of m_i at most rock engineering project sites.

Fig. 7

Sensitivity results on the mean of Hoek–Brown constant m_i

8.2 Effect of Data Quantity on the Standard Deviation of m _i

Table 6 presents the summary of the standard deviation values of m_i from probabilistic characterization using the 60 simulated data sets. The ranges of the standard deviation values of m_i from probabilistic characterization using different data quantity (i.e., ${\kern 1pt} n_{k}$ = 1, 3, 5, 10, 20, and 30) are presented. The ranges presented for each ${\kern 1pt} n_{k}$ in Table 6 are obtained from 10 estimates of standard deviation obtained by using 10 data sets of ${\kern 1pt} n_{k}$ = 1, 3, 5, 10, 20, and 30 in the proposed approach for probabilistic characterization of m_i. The maximum difference of the standard deviation values for each ${\kern 1pt} n_{k}$ is included in parenthesis. Table 6 also includes the averages of the standard deviation values of m_i from using different number of input data, and the absolute and relative differences. The true value of standard deviation (i.e., $\sigma = 10.00$) is included in the footnote to Table 6 for comparison with the results from the proposed approach. In a similar trend to the estimates of the mean of m_i, the estimates of the standard deviation of m_i are affected by the number of input data. At ${\kern 1pt} n_{k}$ = 1, 3 and 5, most estimates of the standard deviation of m_i are far from the true standard deviation. As ${\kern 1pt} n_{k}$ increases the estimates of the standard deviation of m_i continue to approach the true standard deviation. In addition, the average values of the standard deviations in each ${\kern 1pt} n_{k}$ continue to approach the true standard deviation as ${\kern 1pt} n_{k}$ increases from 1 to 30. Most of the estimates of the standard deviation are far from the true standard deviation until at ${\kern 1pt} n_{k}$ = 10, when the average standard deviation is 10.44, which is quite close to the true standard deviation of 10.00. The average standard deviation improves as the number of input data increases. As ${\kern 1pt} n_{k}$ increases from 1 to 30, the maximum difference between the standard deviation values for each ${\kern 1pt} n_{k}$ reduces from 4.25 to 0.40. Also, the absolute and relative differences decrease as the input data increase, with the relative difference decreasing from 26.00% at ${\kern 1pt} n_{k}$ = 1 to 2.10% at ${\kern 1pt} n_{k}$ = 30. In a similar trend to mean estimates, the relative difference in the standard deviation values as from ${\kern 1pt} n_{k}$ = 10 is less than 5%.

Table 6 Effect of the data quantity on standard deviation of m_i

Furthermore, Fig. 8 plots the standard deviation values from each probabilistic characterization by open circles, and the true standard deviation value by dashed lines. It is observed that the spread of the standard deviation values is wide and mostly fall below the true standard deviation value before ${\kern 1pt} n_{k}$ = 10. At ${\kern 1pt} n_{k}$ = 10 and above, the spread of the standard deviation values reduces drastically and clustered more around the true standard deviation. This shows that the estimates of the standard deviation of m_i become more consistent as the number of input data increases. At ${\kern 1pt} n_{k}$ < 10, there is underestimation of the standard deviation of m_i, which may be due to insufficient information from the available site input data. As from ${\kern 1pt} n_{k}$ = 10, the estimates of the standard deviation of m_i become more consistent with the true standard deviation of m_i. This indicates that as the number of input data increases, the estimates of the standard deviation from the proposed approach becomes more confident and reliable, reflecting the characteristics of the true standard deviation of m_i, which was used to simulate the UCS data used in the probabilistic characterizations. The clustering of the standard deviation values around the true standard deviation as from ${\kern 1pt} n_{k}$ = 10 to 30 indicates that the equivalent samples of m_i from the proposed approach become more dominated by the information contained in the input data, which is more consistent across different data sets as the number of input data increases.

Fig. 8

Sensitivity results on the standard deviation of Hoek–Brown constant m_i

9 Summary and Conclusions

This study tackled the difficulty involved in characterization of Hoek–Brown constant m_i when triaxial data sets are not available at a project site. A Bayesian approach is developed for probabilistic characterization of Hoek–Brown constant m_i, which systematically synthesizes and integrates information from regression model, site-specific UCS data and ranges of m_i reported in Hoek’s guideline chart, to give better predictions of m_i values. The proposed approach provides a systematic way to obtain the statistics and full probability distribution of m_i when extensive triaxial compression test cannot be performed, which is mainly the case for small to medium-sized rock engineering projects. Regression model relating m_i to UCS is used in the Bayesian approach to systematically integrate the site-specific UCS data and information available on m_i in the Hoek’s guideline chart for probabilistic characterization of m_i. The integrated information from Hoek’s guideline chart and site-specific test data is transformed into a large number, as many as needed, of equivalent m_i samples using MCMC simulation. Conventional statistical analysis of the equivalent samples is subsequently performed to obtain the statistics and probability distributions of m_i, for rock engineering analysis and design, particularly those using Hoek–Brown failure criterion. The proposed approach effectively tackles the problem of inability to estimate site-specific statistics and probability distributions of Hoek–Brown constant m_i when triaxial compression test data are not available or when they are available in limited quantity. The m_i samples can be directly used in rock engineering design and analysis, especially in Hoek–Brown failure criterion to predict rock failure. The site-specific statistics and probability distribution of m_i can also be used in probability-based estimation of rock mass properties through the Hoek–Brown failure criterion.

Equations were derived for the proposed Bayesian approach, and the proposed approach was illustrated using real-life UCS data of granite obtained from borehole KFM05A at Forsmark, Sweden. Based on the available UCS data (i.e., 10 UCS values), regression model and the ranges of m_i reported in Hoek’s guideline chart, the Bayesian approach provides reasonable statistics and full probability distribution of m_i. Such probabilistic characterization used to require a large number of triaxial compression tests, which are quite often not available for most rock engineering projects. The difficulty in obtaining full distribution of m_i at project sites from limited triaxial compression tests is rationally tackled by the proposed approach.

A sensitivity study was performed to explore the effect of quantity of site-specific test data on the evolution of m_i through the proposed approach. It has been shown that the information from the equivalent samples of m_i from the proposed approach becomes more consistent and informative as the number of input data increases. At relatively limited number of input data, the samples are dominated by information contained in the guideline chart. As the input data increases, the dominance of information from the guideline chart gradually disappears leading to the equivalent samples reflecting more of information from the input data.