Modal analysis of the dynamic crack growth and arrest in a DCB specimen

Abstract

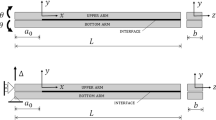
This paper discusses dynamic crack growth and arrest in an elastic double cantilever beam (DCB) specimen, simulated using the Bernoulli–Euler beam theory. The specimen is made from two different materials. The section of interest, where the dynamic crack growth takes place, is made from a material, the fracture energy of which will be denoted $2\Gamma _1$. The initial crack grows slowly in a starter material with a fracture energy $2\Gamma _{0} \;(\Gamma _{0} >\Gamma _1 )$, while opposed displacements on both arms of the specimen are continuously increased. As the crack reaches the material interface at $\ell =\ell _c$, the loading displacement is instantly suspended, and the crack suddenly propagates through the test zone, until it stops at $\ell =\ell _A$. During this process, the energy $2\Gamma _1 (\ell _A -\ell _c )$ is dissipated. The beam motion and the fracture process during the fast crack growth stage are investigated, based on the balance energy associated to the Griffith criterion. The motion equations are approximated using a modal decomposition up to order $N$ of the beam deflection (the analysis has been performed up to $N=10$ but in most cases $N=5$ is sufficient to obtain an accurate solution). This process leads to a set of N second order differential equations whose unknowns are the mode amplitudes and their derivatives, and another equation the unknowns of which are the current crack length $\ell (t)$, velocity $\dot{\ell }(t)$ and acceleration $\ddot{\ell }(t)$. To demonstrate the accuracy of this method, it is first tested on a one dimensional peeling stretched film problem, with an insignificant bending energy. An exact solution exists, accurately approximated by the modal solution. The method is then applied to the DCB specimen described above. Despite the rather crude nature of the Bernoulli–Euler model, the results crack kinematics, and specially the arrest length, correspond well to those obtained by the combined use of finite elements and cohesive zone models, even for a few modes. Moreover, for the basic mode $N=0$ (also referred to as Mott solution), even if the crack kinematics is not accurately reproduced, the prediction of the crack arrest length remains correct for moderate ratios. Some parametric studies about the beam geometry and the initial crack velocity are performed. The relative crack arrest $\ell _A /\ell _c$ appears to be almost insensitive to these parameters, and is mainly governed by the ratio $R=\Gamma _{0} /\Gamma _1$ which is the key parameter to predict the crack arrest.

Appendix: Energy derivation for the DCB test

Local motion equations derived from the enrgy balance:

$$\begin{aligned} \frac{dH}{dt}&= \frac{\partial H}{\partial q_i }\dot{q}_i +\frac{\partial H}{\partial \dot{q}_i }\ddot{q}_i =0\\ \frac{dH(q_i ,\dot{q}_i )}{dt}&= \frac{\partial U}{\partial q_i }\dot{q}_i +\frac{\partial K}{\partial q_i }\dot{q}_i\\&+\,\frac{\partial K}{\partial \dot{q}_i }\ddot{q}_i +\Gamma _1 \dot{\ell }=0\quad (I) \end{aligned}$$

It is deduced that:

$$\begin{aligned} \frac{\partial K}{\partial \dot{q}_i }\ddot{q}_i =\frac{d}{dt}\left( \frac{\partial K}{\partial \dot{q}_i }\dot{q}_i \right) -\dot{q}_i \frac{d}{dt}\left( \frac{\partial K}{\partial \dot{q}_i }\right) \end{aligned}$$

and that $\frac{\partial K}{\partial \dot{q}_i }\dot{q}_i =2K$ (for the stationary crack the kinetic energy is a quadratic form, for the growing crack, this property cancels but the energy keeps the property $\frac{\partial K}{\partial \dot{a}_i }\dot{a}_i +\frac{\partial K}{\partial \dot{\ell }}\dot{\ell }=2K)$

That leads to:

$$\begin{aligned} \frac{\partial K}{\partial \dot{q}_i }\ddot{q}_i&= -\frac{d}{dt}(2U)-2\Gamma _1 \dot{\ell }-\dot{q}_i \frac{d}{dt}\left( \frac{\partial K}{\partial \dot{q}_i}\right) \\&= -2\frac{\partial U}{\partial q_i }\dot{q}_i -2\Gamma _1 \dot{\ell }-\dot{q}_i \frac{d}{dt}\left( \frac{\partial K}{\partial \dot{q}_i }\right) \end{aligned}$$

Inserting this relation in (I), it comes:

$$\begin{aligned}&\frac{\partial U}{\partial q_i }\dot{q}_i +\frac{\partial K}{\partial q_i }\dot{q}_i -2\frac{\partial U}{\partial q_i }\dot{q}_i -2\Gamma _1 \dot{\ell }\\&\quad -\dot{q}_i \frac{d}{dt}(\frac{\partial K}{\partial \dot{q}_i })+2\Gamma _1 \dot{\ell }=0 \end{aligned}$$

That says:

$$\begin{aligned}&\left[ {\frac{\partial (K-U)}{\partial q_i }-\frac{d}{dt}(\frac{\partial K}{\partial \dot{q}_i })} \right] \dot{q}_i -\Gamma _1 \dot{\ell }=0,\\&\quad i=1,N\quad (II) \end{aligned}$$

Selecting an arbitrary number of modes $N$, and making the difference of the relations (II) for $N$ and $N+1 \quad \dot{q}_i$, the following relations hold for each occurrence:

$$\begin{aligned}&\left[ {\frac{\partial (K-U)}{\partial a_i }-\frac{d}{dt}\left( \frac{\partial K}{\partial \dot{a}_i }\right) } \right] =0,\quad \forall i=1,N\\&\left[ {\frac{\partial (K-U)}{\partial \ell }-\frac{d}{dt}\left( \frac{\partial K}{\partial \dot{\ell }}\right) } \right] -\Gamma _1 \dot{\ell }=0, \end{aligned}$$

Application to the DCB test:

Using the relation (8), the kinetic and elastic energy relations for N modes are expressed as (with the Einstein summation convention):

$$\begin{aligned} K&= \frac{\rho A\dot{\ell }^{2}}{2\ell }\int \limits _0^1 \left( Xw_{stat}^{\prime } \left( X \right) +Xa_i \left( t \right) {\phi }'_i \left( X \right) \right. \\&\left. -\frac{\ell }{\dot{\ell }}\dot{a}_i \left( t \right) \phi _i \left( X \right) \right) ^{2} dX \quad i=1,\ldots N\\ U&= \frac{EI}{2\ell ^{3}}\int \limits _0^1 {\left( {w_{stat}^{{\prime }{\prime }} \left( X \right) +a_i \left( t \right) {\phi }''_i \left( X \right) } \right) } ^{2}dX \end{aligned}$$

The above expression of $K(a_i ,\dot{a}_i ,\ell ,\dot{\ell })$ is clearly a $2^\mathrm{nd}$ order homogeneous function of $(\dot{a}_i ,\dot{\ell })$.

Deriving $K-U$ with respect to $(\dot{a}_i ,a_i )$ leads to :

$$\begin{aligned}&\frac{\partial (K-U)}{\partial a_i }=\rho A\left[ \frac{\dot{\ell }^{2}}{\ell }\int \limits _0^1 {(X^{2}\phi ^{{\prime }}_i w_{stat}^{\prime } +X^{2}\phi ^{{\prime }}_i \phi ^{{\prime }}_j a_j )dX}\right. \\&\quad \left. -\dot{\ell }\int \limits _0^1 {X\phi ^{{\prime }}_i \phi _j \dot{a}_j dX} \right] +\frac{EI}{\ell ^{3}}\int \limits _0^1 {(-\phi ^{{\prime }{\prime }}_i w_{stat}^{{\prime }{\prime }} -\phi ^{{\prime }{\prime }}_i \phi ^{{\prime }{\prime }}_j a_j )dX}\\&\frac{d}{dt}\frac{\partial (K-U)}{\partial \dot{a}_i }=\rho A\left[ \ddot{\ell }\int \limits _0^1 {(-X\phi _i w_{stat}^{{\prime }{\prime }} -X\phi _i \phi ^{{\prime }}_j a_j )dX}\right. \\&\quad \left. +\dot{\ell }\int \limits _0^1 {(-X\phi _i \phi ^{{\prime }}_j \dot{a}_j +\phi _i \phi _j \dot{a}_j )dX} +\ell \int \limits _0^1 {\phi _i \phi _j \ddot{a}_j dX} \right] \\&\frac{\partial (K-U)}{\partial a_i }=\rho A\left[ \frac{\dot{\ell }^{2}}{\ell }\int \limits _0^1 {(X^{2}\phi ^{{\prime }}_i w_{stat}^{\prime } +X^{2}\phi ^{{\prime }}_i \phi ^{{\prime }}_j a_j )dX}\right. \\&\quad \left. -\dot{\ell }\int \limits _0^1 {X\phi ^{{\prime }}_i \phi _j \dot{a}_j dX} \right] +\frac{EI}{\ell ^{3}}\int \limits _0^1 {(\phi ^{{\prime }{\prime }}_i w_{stat}^{{\prime }{\prime }} +\phi ^{{\prime }{\prime }}_i \phi ^{{\prime }{\prime }}_j a_j )dX}\\&\quad \frac{d}{dt}\frac{\partial (K-U)}{\partial \dot{a}_i }=\rho A\left[ \ddot{\ell }\int \limits _0^1 {(-X\phi _i w_{stat}^{{\prime }{\prime }} -X\phi _i \phi ^{{\prime }}_j a_j )dX}\right. \\&\quad \left. +\dot{\ell }\int \limits _0^1 {(-X\phi _i \phi ^{{\prime }}_j \dot{a}_j +\phi _i \phi _j \dot{a}_j )dX} +\ell \int \limits _0^1 {\phi _i \phi _j \ddot{a}_j dX} \right] \end{aligned}$$

Therefore, the Eq. (24) lead to the following differential system (using the Einstein summation convention on the index j):

$$\begin{aligned} \ddot{a}_i&= \frac{\ddot{\ell }}{\ell }\left( {C_3^i +a_j C_4^{ij} } \right) +\frac{2\dot{\ell }}{\ell }\dot{a}_j C_4^{ij}\\&\quad +\frac{\dot{\ell }^{2}}{\ell ^{2}}\left( {C_2^i +a_j C_1^{ij} } \right) -\frac{1}{\ell ^{4}}\frac{EI}{\rho A}a_i \mu _i ^{4},\;\forall i=1,N \end{aligned}$$

with the following coefficients :

$$\begin{aligned} C_1^{ij} =\int \limits _0^1 {X^{2}{\phi }'_i } \phi _j ^{\prime }dX\\ C_2^i =\int \limits _0^1 {X^{2}w^{{eq}{\prime }}{\phi }'_i } dX\\ C_3^i =\int \limits _0^1 {Xw^{{eq}{\prime }}\phi _i } dX\\ C_4^{ij} =\int \limits _0^1 {X{\phi }'_i } \phi _j dX \end{aligned}$$

In the same way, deriving $H=K+U+\Gamma _1 (\ell -\ell _c )$ with respect to $(\ell ,\dot{\ell })$ leads to :

$$\begin{aligned}&\frac{\partial (K-U)}{\partial \ell }=\rho A\left[ -\frac{\dot{\ell }^{2}}{\ell ^{2}}\int \limits _0^1 (+\frac{1}{2}X^{2}\phi ^{{\prime }}_i (w_{stat}^{\prime } )^{2}\right. \\&\quad \left. +X^{2}w_{stat}^{\prime } \phi ^{{\prime }}_i a_i +X^{2}\phi ^{{\prime }}_i \phi ^{{\prime }}_j a_i a_j )dX +\frac{1}{2}\int \limits _0^1 {\phi _i \phi _j \dot{a}_i \dot{a}_j dX} \right] \\&\quad +\frac{3EI}{2\ell ^{4}}\int \limits _0^1 {((w_{stat}^{{\prime }{\prime }} )^{2}+2w_{stat}^{{\prime }{\prime }} \phi ^{{\prime }{\prime }}_i a_i +\phi ^{{\prime }{\prime }}_i \phi ^{{\prime }{\prime }}_j a_i a_j )dX}\\&\frac{d}{dt}\frac{\partial (K-U)}{\partial \dot{\ell }}=\rho A-\frac{\dot{\ell }^{2}}{\ell ^{2}}\int \limits _0^1 (X^{2}(w_{stat}^{\prime } )^{2}\\&\quad +2X^{2}w_{stat}^{\prime } \phi ^{{\prime }}_i a_i +X^{2}\phi ^{{\prime }}_i \phi ^{{\prime }}_j a_i a_j )dX \\&-\int \limits _0^1 {(X\phi _i \phi ^{{\prime }}_j \dot{a}_i \dot{a}_j +Xw_{stat}^{\prime } \phi _i \ddot{a}_i +X\phi ^{{\prime }}_i \phi _j a_i \ddot{a}_j )dX}\\&\quad +\frac{\dot{\ell }}{\ell }\int \limits _0^1 {(2X^{2}w_{stat}^{\prime } \phi ^{{\prime }}_i \dot{a}_i +2X^{2}\phi ^{{\prime }}_i \phi ^{{\prime }}_j a_i \dot{a}_j )dX} \\&+\frac{\ddot{\ell }}{\ell }\int \limits _0^1 {(X^{2}(w_{stat}^{\prime } )^{2}+2X^{2}w_{stat}^{\prime } \phi ^{{\prime }}_i a_i +X^{2}\phi ^{{\prime }}_i \phi ^{{\prime }}_j a_i a_j )dX} \\ \end{aligned}$$

The equation relative to the Griffith criterion leads to the single differential equation:

$$\begin{aligned} \ddot{\ell }&= \frac{\dot{\ell }^{2}}{2\ell }+\frac{\dot{\ell }}{\Delta }\left( {-2\dot{a}_j C_2^j -2\dot{a}_j a_i C_1^{ij} } \right) \\&+\frac{3EI}{2\ell ^{3}\Delta \rho A}\left( {3(w^c )^{2}+a^{2}_i \mu ^{4}_i } \right) \\&+\frac{\ell }{\Delta }\left( {\ddot{a}_i C_3^i +\ddot{a}_i a_j C_4^{ij} -\frac{\Gamma _1 }{2\rho A}} \right) , \end{aligned}$$

with $\Delta =C_1 +a_i a_j C_2^{ij} +2a_i C_3^i$.

Application to the peeling test:

the kinetic and elastic energy relations for N modes are expressed as (using the Einstein summation convention) :

$$\begin{aligned} K&= \frac{\rho \dot{\ell }^{2}}{2\ell ^{2}}\int \limits _0^1 {(\frac{dw}{dt}} )^{2}dX\\&= \frac{\rho \dot{\ell }^{2}}{2\ell ^{2}}\int \limits _0^1 {(W^{0}X+\frac{\ell }{\dot{\ell }}} \dot{a}_i (t)\phi _i (X)-Xa_i (t)\phi ^{\prime }_i (X))^{2}dX\\ U&= \frac{N}{2\ell (t)}\int \limits _0^1 {\left( {\frac{\partial w}{\partial X}} \right) dX=} ^{2}\frac{N}{2\ell (t)}(W^{0^{2}}+a_i a_j (i\pi )^{2}\delta _{ij} ) \end{aligned}$$

Applying the same process than for the DCB case, and deriving $K-U-D$ with respect to $(a_i ,\dot{a}_i )$ and to $(\ell ,\dot{\ell })$, the following equations hold :

$$\begin{aligned} \ddot{a}_i&= \frac{\ddot{\ell }}{\ell }\left( {-\int \limits _0^1 {XW^0 \phi _i } dX+a_j \int \limits _0^1 {X\phi ^{\prime }_j \phi _i } dX} \right) \\&+\frac{2\dot{\ell }}{\ell }\dot{a}_j \int \limits _0^1 {X\phi _i \phi _j^{\prime } dX} -\frac{\dot{\ell }^{2}}{\ell ^{2}}\int \limits _0^1 {(W^{0}-a_j \phi _j^{\prime } )X^{2}\phi _i^{\prime } dX}\\&-\frac{1}{\ell ^{2}}\frac{N}{\rho }a_i \mu _i ^{2},\;i=1,N\\ \ddot{\ell }&= \frac{\dot{\ell }^{2}}{2\ell }+\frac{\dot{\ell }\dot{a}_i }{\Delta }\left( {\int \limits _0^1 {2X^{2}(W^0 \phi ^{\prime }_i } -a_j \phi ^{\prime }_i \phi ^{\prime }_j )dX} \right) \\&+\frac{N}{2\rho \ell \Delta }\left( {(W^0 )^{2}+a_i a_j \delta _{ij} \mu ^{2}_i } \right) \\&+\frac{\ell }{\Delta }\left( {-\ddot{a}_i \int \limits _0^1 {XW^0 \phi _i } dX+\ddot{a}_i a_j \int \limits _0^1 {X\phi ^{\prime }_j \phi _i } dX-\frac{\Gamma _1 }{\rho }} \right) \\ \Delta&= (W^0 )^{2}/3+a_i a_j \int \limits _0^1 {X^{2}\phi ^{\prime }_j \phi ^{\prime }_i } dX-2a_i W^0 \int \limits _0^1 {X^{2}\phi ^{\prime }_i } dX \end{aligned}$$