Uncertain random data envelopment analysis for technical efficiency

Abstract

Data envelopment analysis (DEA) is a classical and prevailing tool for estimating relative efficiencies of multiple decision making units (DMUs). However, sometimes DMUs’ inputs and outputs cannot be observed accurately in practical cases, and hence this paper attempts to propose an uncertain random DEA model to evaluate the efficiencies of DMUs with uncertain random inputs and outputs. The sensitivity and stability of this new model are further analyzed with the aim to figure out the stability radius of each DMU. Finally, a numerical example is presented for illustrating the proposed uncertain random DEA model.

Appendices

Uncertainty theory

Liu (2007) set up uncertainty theory to analyze the belief degree in 2007 and then Liu (2009) perfected it in 2009. In this appendix, some helpful knowledge is provided which is beneficial to this article. The set function on a $\sigma$-algebra ${\mathcal {L}}$ over a nonempty set $\varGamma$ is named uncertain measure provided that it meets three axioms below:

• 1. Normality Axiom: For the universal set $\varGamma$, .

• 2. Duality Axiom: For any event $\varLambda$, .

• 3. Subadditivity Axiom: For every countable sequence of events $\varLambda _1, \varLambda _2, \cdots$, we obtain

  

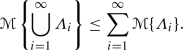
  Then, Liu (2009) proposed product axiom in 2009.

• 4. Product Axiom: The product uncertain measure in uncertainty spaces is an uncertain measure meeting

  

  where $\varLambda _k$ are arbitrarily chosen events from ${\mathcal {L}}_{k}$ for $k=1, 2, \cdots$, respectively.

Definition 2

(Liu 2007) An uncertain variable is a function $\xi$ from an uncertainty space ($\varGamma$, ${\mathcal {L}}$, ) to the set of real numbers such that $\{\xi \in B \}$ is an event for any Borel set B of real numbers.

Definition 3

(Liu 2007) For an uncertain variable $\xi$, its uncertainty distribution $\varPhi$ is

for any real number x.

Based on the definitions above, a frequently used uncertainty distribution can be expressed below:

$$\begin{aligned} \varPhi (x) = \left\{ \begin{array}{ll} \displaystyle 0, &{} \quad \text{ if } x \le a \\ \displaystyle \frac{x - a}{b - a}, &{} \quad \text{ if } a < x \le b \\ \displaystyle 1, &{} \quad \text{ if } x > b \end{array} \right. \end{aligned}$$

which is named linear uncertainty distribution and labeled with ${\mathcal {L}}(a,b)$.

Definition 4

(Liu 2009) Uncertain variables $\xi _1$, $\xi _2$, $\cdots$, $\xi _n$ are said to be independent if

for any Borel sets $B_{1}$, $B_{2}$, $\cdots$, $B_{n}$ of real numbers.

If an uncertain variable $\xi$ has a regular uncertainty distribution $\varPhi (x)$, then the inverse function $\varPhi ^{-1}(\alpha )$ is named the inverse uncertainty distribution of $\xi$ (Liu 2010).

Theorem 6

(Liu 2010) Assume $\xi _{1}, \xi _{2}, \ldots , \xi _{n}$ are independent uncertain variables with regular uncertainty distributions $\varPhi _{1}, \varPhi _{2},\ldots , \varPhi _{n},$ respectively. When $f(x_{1}, x_{2}, \ldots , x_{n})$ is continuous, strictly increasing with respect to $x_{1}, x_{2}, \ldots , x_{m}$ and strictly decreasing with respect to $x_{m+1}, x_{m+2}, \ldots , x_{n}$, then $\xi = f(\xi _{1}, \xi _{2}, \ldots , \xi _{n})$ has an inverse uncertainty distribution

$$\begin{aligned} \begin{aligned}&\displaystyle \varPsi ^{-1}(\alpha ) = f(\varPhi ^{-1}_{1}(\alpha ), \cdots , \varPhi ^{-1}_{m}(\alpha ), \varPhi ^{-1}_{m+1}(1-\alpha ), \cdots , \varPhi ^{-1}_{n}(1-\alpha )). \end{aligned} \end{aligned}$$

For the uncertain variable $\xi$, its expected value can be figured out by following formula:

$$\begin{aligned} \displaystyle E[\xi ] = \int _{0}^{1} \varPhi ^{-1}(\alpha ) \mathrm {d} \alpha \end{aligned}$$

if $\xi$ has a regular uncertainty distribution $\varPhi$ (Liu 2010).

Theorem 7

(Liu and Ha 2010) Suppose $\xi _{1}, \xi _{2}, \ldots , \xi _{n}$ are independent uncertain variables with regular uncertainty distributions $\varPhi _{1}, \varPhi _{2}, \ldots , \varPhi _{n},$ respectively. When $f(\xi _{1}, \xi _{2}, \ldots , \xi _{n})$ is strictly increasing with respect to $\xi _{1}, \xi _{2}, \ldots , \xi _{m}$ and strictly decreasing with respect to $\xi _{m+1}, \xi _{m+2}, \ldots , \xi _{n}$, then

$$\begin{aligned} \begin{aligned}&\displaystyle E[\xi ] = \int _{0}^{1} f(\varPhi _{1}^{-1}(\alpha ), \cdots , \varPhi _{m}^{-1}(\alpha ), \varPhi _{m+1}^{-1}(1-\alpha ), \cdots , \varPhi _{n}^{-1}(1-\alpha )) \mathrm {d} \alpha \end{aligned} \end{aligned}$$

is the expected value of $f(\xi _{1}, \xi _{2}, \ldots , \xi _{n})$.

Chance theory

Liu (2013b) created chance theory for modeling the phenomenon that uncertainty and randomness simultaneously appear in a system. Some essential definitions and theorems are given in this appendix.

Definition 5

(Liu 2013b) The chance measure of event $\varTheta$ is

where $\varTheta \in {\mathcal {L}} \times {\mathcal {A}}$ is an event in a chance space .

Definition 6

(Liu 2013b) An uncertain random variable is a function $\xi$ from a chance space to the set of real numbers such that $\{\xi \in B \}$ is an event in ${\mathcal {L}} \times {\mathcal {A}}$ for any Borel set B of real numbers.

Definition 7

(Liu 2013b) Let $\xi$ be an uncertain random variable. Then its chance distribution is defined by

$$\begin{aligned} \varPhi (x)=\mathrm {Ch}\{ \xi \le x\} \end{aligned}$$

for any $x \in \mathfrak {R}.$

Theorem 8

(Liu 2013a) Let ${\eta }_{1},{\eta }_{2},\ldots ,{\eta }_{m}$ be independent random variables with probability distributions $\varPsi _{1},\varPsi _{2},\ldots ,\varPsi _{m}$, and let ${\tau }_{1},{\tau }_{2},\ldots ,{\tau }_{n}$ be independent uncertain variables with regular uncertainty distributions $\varUpsilon _{1},\varUpsilon _{2},\ldots ,\varUpsilon _{n}$, respectively. Assume $f({\eta }_{1},{\eta }_{2},\ldots ,{\eta }_{m},{\tau }_{1},{\tau }_{2},\ldots ,{\tau }_{n})$ is continuous, strictly increasing with respect to ${\tau }_{1},{\tau }_{2},\ldots ,{\tau }_{k}$ and strictly decreasing with respect to ${\tau }_{k+1},{\tau }_{k+2},\ldots ,{\tau }_{n}$. Then the uncertain random variable

$$\begin{aligned} \xi =f({\eta }_{1},{\eta }_{2},\ldots ,{\eta }_{m},{\tau }_{1},{\tau }_{2},\ldots ,{\tau }_{n}) \end{aligned}$$

has a chance distribution

$$\begin{aligned} \varPhi (x)=\int _{\mathfrak {R}^{m}}F(x;{y}_{1},{y}_{2},\ldots ,{y}_{m})\mathrm {d} \varPsi _{1}({y}_{1})\mathrm {d}\varPsi _{2}({y}_{2}) \ldots \mathrm {d}\varPsi _{m}({y}_{m}) \end{aligned}$$

where $F(x;{y}_{1},{y}_{2},\ldots ,{y}_{m})$ is the root $\alpha$ of the equation

$$\begin{aligned} f({y}_{1},{y}_{2},\ldots ,{y}_{m},\varUpsilon _{1}^{-1}(\alpha ),\ldots , \varUpsilon _{k}^{-1}(\alpha ),\varUpsilon _{k+1}^{-1}(1-\alpha ), \ldots ,\varUpsilon _{n}^{-1}(1-\alpha ))=x. \end{aligned}$$

For the uncertain random variable $\xi$, its expected value can be figured out by the theorem below.

Theorem 9

(Liu 2013a) Assume ${\eta }_{1}, {\eta }_{2}, \ldots , {\eta }_{m}$ are independent random variables with probability distributions $\varPsi _{1}, \varPsi _{2}, \ldots , \varPsi _{m}$, and assume ${\tau }_{1}, {\tau }_{2}, \ldots , {\tau }_{n}$ are independent uncertain variables with uncertainty distributions $\varUpsilon _{1}, \varUpsilon _{2}, \ldots , \varUpsilon _{n}$, respectively. If f is a measurable function, then

$$\begin{aligned} \begin{aligned} \xi =f({\eta }_{1},{\eta }_{2},\ldots ,{\eta }_{m},{\tau }_{1},{\tau }_{2},\ldots ,{\tau }_{n}) \end{aligned} \end{aligned}$$

has an expected value

$$\begin{aligned} E[\xi ]=\int _{\mathfrak {R}^{m}}{G({y}_{1},{y}_{2},\ldots ,{y}_{m})\mathrm {d} \varPsi _{1}({y}_{1})\mathrm {d}\varPsi _{2}({y}_{2}) \ldots \mathrm {d}\varPsi _{m}({y}_{m})} \end{aligned}$$

where

$$\begin{aligned} G({y}_{1},{y}_{2},\ldots ,{y}_{m})=E[f({y}_{1},{y}_{2},\ldots ,{y}_{m}, {\tau }_{1},{\tau }_{2},\ldots ,{\tau }_{n})] \end{aligned}$$

is the expected value of the function $f({y}_{1},{y}_{2},\ldots ,{y}_{m},{\tau }_{1},{\tau }_{2},\ldots , {\tau }_{n})$ for any real numbers ${y}_{1},{y}_{2}$, $\ldots ,{y}_{m}$, and is determined by $\varUpsilon _{1}, \varUpsilon _{2},\ldots ,\varUpsilon _{n}$.