A restless bandit approach for capacitated condition based maintenance scheduling

Abstract

This paper considers the maintenance scheduling problem of multiple non-identical machines deteriorating over time. The deterioration gradually decreases a machine’s performance, which results in revenue losses due to lower output quality. The maintenance cost is dependent on the degradation state, and the number of maintenance activities that can be carried out simultaneously is restricted by the number of maintenance workers. Our main goal is to propose a heuristic with low complexity that consistently produces solutions close to the optimal strategy for problems of real size. We cast the problem as a restless bandit problem and propose an index based heuristic (Whittle’s index policy) which can be computed efficiently. We also provide a lower bound that can be computed by linear programming. We numerically compare the performance of the index heuristic with alternative policies. In addition to achieving superior performance over failure-based and threshold policies, Whittle’s policy numerically converges to our lower bound when the number of machines is moderately high and/or maintenance workload is high.

1 Introduction

The machine repairman problem, also called the machine interference problem, is characterized by a collection of M machines subject to random failures and R repairmen ($R \le M$). Its classical formulation determines the optimal sequence of machines to be assigned to the repair crew [see Haque and Armstrong (2007) for a detailed review of studies in this direction]. It has been extensively studied in the literature as this type of problem arises not only in maintenance operations but also in manufacturing, transportation, telecommunication, and computer systems (Wang 1994; Desruelle and Steudel 1996; Bunday et al. 1997; Kryvinska 2004; Armstrong 2002).

In this paper, we consider a machine repairman problem in which each machine gradually deteriorates over time rather than experiencing sudden breaks downs. Each machine eventually fails unless there is a maintenance intervention. The failure of a machine results in high costs related to production losses and delays, safety issues and unplanned intervention on the machine. The deterioration level of a machine can be directly measured by techniques such as vibration analysis or wear monitoring. Thus, it is reasonable to schedule maintenance actions based on the degradation statuses of machines. This maintenance scheme falls into the category of condition-based maintenance (CBM). Under such a scheme, maintenance decisions are taken prior to any predicted failures using the information collected via continuous monitoring or inspections. Early work on CBM has shown that it reduces maintenance costs, improves system reliability and reduces the number of failures.

The conditions of the machines can be expressed through states based on the data collected. A machine follows a stochastic degradation process over a finite number of discrete states starting from the as good as new state and ending in the failed state. During maintenance, necessary overhaul, replacement, and repair operations are carried out to bring the machine into the ‘as good as new’ condition. The performance of the machines is assessed by output quality and it is a non-increasing function of the accumulated degradation. This setup is especially relevant for high-precision machining and heavy machine tooling that is utilized in many sectors such as aerospace, electronics, defense, and medical technology (Akcay et al. 2021). Degradation increases revenue losses due to decreasing output quality and also the likelihood of failure. The maintenance interventions mitigate the risk of costly machine breakdown as well as escalating revenue losses due to machine deterioration. When a factory has several machines but there is only a limited number of repairmen, it is important to effectively utilize the repairmen. Hence, the problem is to determine which machines to maintain at each decision point to ensure a high performance level at minimum cost.

A primary approach to exploit maintenance optimization and resource allocation problems is to formulate them as a Markov Decision Process (MDP). A MDP formulation can be solved exactly through standard techniques such as value iteration or policy improvement (Puterman 2014). However, these algorithms are computationally intractable for large-scale real life problems. Naturally, the development of heuristics that can find near-optimal solutions in a time efficient manner is an area of interest. Our problem relates to the restless bandit problem (RBP) which has been introduced by Whittle (1988). The problem deals with the sequential allocation of resources to a collection of stochastic reward-generating projects. As it cannot be solved analytically except for some small problems, Whittle (1988) has developed an index based heuristic that emerges from a relaxation of the problem in which the resource capacity constraint at any decision time is replaced with its time-averaged version. In literature, the heuristic is referred to as Whittle’s index policy, which is applicable to a particular problem if a technical condition called the indexability property holds. Note that this property is not trivial to establish in general. The index heuristic relies on the computation of indices or scores for all projects and choosing the projects with the highest index values at each decision point. Although Whittle (1988) conjectures asymptotic optimality of the policy for RBPs under indexability in a limiting regime, Weber and Weiss (1990) have shown that this asymptotic optimality requires that the differential equation characterizing the dynamics of Whittle’s index in a certain fluid limit have a globally stable equilibrium.

In this paper, we present two approaches to solve condition-based maintenance scheduling of deteriorating machines. We assume that the degradation process can be modeled by a continuous time Markov chain and that maintenance times are exponentially distributed. Also, it is allowed for the maintenance intervention decisions to be made dynamically at any decision epoch. We first develop an average cost MDP formulation of the problem, which enables us to obtain the optimal policy and cost for sufficiently small problem instances. Then, we cast the problem as a RBP. We show that the indexability property holds and that the optimal policy for the relaxed RBP is a threshold type. Under a threshold policy, a maintenance action is initiated as soon as the degradation level of the machine exceeds a certain threshold. Next, a closed form expression for the Whittle indices is derived in terms of the problem parameters. Thus with a translation into a RBP, we obtain the index heuristic which can be easily applied to very large problem instances. We further propose a linear programming formulation that can be used to find a lower bound on the cost for our problem. This formulation can also be used to obtain lower bounds for restless bandits problems where the optimal policy for the relaxed problem is a threshold policy. Finally, we carry out a numerical performance evaluation of the index heuristic. Small sized settings are considered to perform a comparison with the optimal policy, and medium and large sized systems are employed for comparison with two benchmark policies as well as the lower bound. The first benchmark policy is an obvious one, the failure based policy, under which failed machines are maintained on a FCFS basis. The second benchmark policy is referred to as a naive policy as it determines the threshold wear degree levels of intervention with no consideration of capacity. This policy is applied with the first come first served (FCFS) discipline. The index heuristic shows superior performance compared to the benchmark policies for all instances. The cost-saving achieved by the proposed policy is more remarkable when the system size is large and the maintenance workload is high. Moreover, the performance is robust with respect to changes in the forms of maintenance cost and revenue loss. The numerical experiments are consistent with the conjecture that the index heuristic is asymptotically optimal as the number of machines and repairmen grow in a fixed proportion, especially when the maintenance capacity is heavily utilized.

In this paper, we consider a rich capacitated condition based maintenance scheduling (CBMS) problem that has received little attention in literature so far. Only two other papers, Glazebrook et al. (2005) and Ruiz-Hernández et al. (2020), have addressed a similarly complex problem. Specifically, our paper makes the following contributions: (1) we show how to efficiently compute an index heuristic based on recent mathematical results for restless bandit problems and the Whittle index policy. (2) We develop a new linear programming model which finds a lower bound on the performance of the optimal policy. (3) We solve problem instances of industrial size and show that the index heuristic has small optimality gaps for small, moderate, and large problem instances and that it requires low computation times, even for large problem instances with up to 160 machines and 16 repairmen. (4) We provide numerical evidence that the optimality gap of our index heuristic becomes very small for large scale problems with many machines and repair men.

The remainder of this article is structured as follows. In Sect. 2, we review the related literature focusing on condition-based maintenance scheduling and RBPs. The details of the MDP and RBP models developed are explained in Sects. 3.2 and 3.3, respectively. Section 3.4 presents the linear program that provides a lower bound on the expected cost of the optimal policy. Next, in Sect. 4, we present a numerical study to investigate the performance of the proposed policy. Finally, the conclusions are stated in Sect. 5.

2 Literature review

We structure the discussion of related literature as follows. We begin with discussing CBMS problems, the methodologies used, and the most relevant articles. Thereafter, we review RBP problems and Whittle’s index theory to establish the essentials of our model. Lastly, we focus on studies which cast the CBMS problem as a RBP.

2.1 CBMS

Maintenance optimization problems have been extensively studied in the literature in the past several decades. Cho and Parlar (1991), Wang (2002), Alaswad and Xiang (2017), Olde Keizer et al. (2017) and de Jonge and Scarf (2020) survey and summarize the research and practice in this field for different time periods using different classification schemes. These classifications include single vs. multiple machines, discrete vs. continuous state degradation, and with or without capacity constraints for maintenance scheduling. Our paper considers a problem with multiple machines, discrete state degradation, and finite maintenance capacity. Markovian deterioration models such as the Poisson process are a common class used in many old and new maintenance applications (Kolesar 1966; Kao 1973; Tian et al. 2021; Drent et al. 2023; Soltani et al. 2024; Bansal et al. 2024). Ye and Xie (2015) provide a comprehensive overview of deterioration models. The standard approach for problems with multiple machines, discrete state Markovian degradation, and finite maintenance capacity is to formulate the problem as a MDP or one of its extensions. This MDP can then be solved with standard algorithms such as policy and value iteration or approximately with custom designed scheduling rules (e.g. shortest mean residual life first).

Within the stream of single-component/machine CBM models, the goal is to determine the threshold level beyond which it is optimal to maintain/replace the machine/component. Kolesar (1966) and Kao (1973) are early studies on a single machine system subject to discrete state Markovian deterioration. They show that a control limit type policy is optimal, i.e. the machine is maintained whenever its wear status exceeds a certain level. As the concept of CBM has become more established, various extensions and variations of models have been proposed for the single-machine setting (e.g. Grall et al. 2002; Kurt and Kharoufeh 2010; van der Weide and Pandey 2011; Fouladirad and Grall 2015; Zhu et al. 2017; Havinga and de Jonge 2020; Tian et al. 2021; Drent et al. 2023). Single-machine models have also been applied in settings with multiple machines (Zhu et al. 2010; Tian and Liao 2011; Tian et al. 2011). Such applications require that there is limited or no dependency between machines.

In literature, four types of dependencies between machines are recognized, which are economic, structural, stochastic, and resource dependencies (Olde Keizer et al. 2017; de Jonge and Scarf 2020). In our study, we consider resource dependency which applies when multiple machines rely on a limited number of maintenance engineers to perform maintenance. Despite its practical relevance, only a small number of studies have addressed resource dependency under a CBM regime. Liu et al. (2014) propose a dynamic CBM policy for a multi-component system maintained by a single worker. The case with multiple maintenance workers is investigated by Marseguerra et al. (2002) and Koochaki et al. (2013) for a system including only three components. Marseguerra et al. (2002) calculate threshold degradation levels beyond which maintenance has to be performed based on a combination of a genetic algorithm and Monte Carlo simulation. Koochaki et al. (2013) compare the performance of CBM and age-based maintenance in the opportunistic maintenance framework under three different workforce limitation scenarios, which are without worker constraint, with a single worker, and with multiple external workers subject to a certain response time. Recently, Soltani et al. (2024) show optimality of a threshold replacement policy for multiple turbines in a wind farm under both stochastic and economic dependencies.

The complex multi-component/machine environment of industrial systems can be hardly captured by the aforementioned studies. They find a CBM regime by optimizing either or both of the two typical objectives, that are maintenance cost and availability, while ignoring the effect of machine’s performance loss on any cost factor. In addition, their numerical experiments indicate that those methods have high computational complexity even for a three component system. Thus, their computational requirements are prohibitive for industrial scale application.

2.2 Restless bandit approach to CBMS

The RBP is a generalization of the multi-armed bandit problem (MABP) (Gittins 1979; Whittle 1988). In the MABP, the decision maker is presented with a set of bandits and each bandit has a finite state space. At each discrete time instant, the decision maker needs to select one of the bandits to activate so that the expected total discounted reward will be maximized. Only an active bandit earns reward and changes state. Gittins (1979) has shown the optimality of index policies for MABPs, which directs the key resource to the bandit with the largest index value. On the other hand, in the RBP the decision maker can activate a number of bandits, and inactive bandits can also change states and generate rewards (referred to as passive rewards). The restless bandit model has gained attention lately due to its applicability to many real-life problems.

Despite providing a powerful modeling framework, RBPs are PSPACE-Hard (Papadimitriou and Tsitsiklis 1999), which puts the computation of optimal policies out of reach. Thus, a relaxed version of the problem is considered in the literature, where the constraint on the maximum number of active bandits at any moment is relaxed to its time average. This relaxation makes the problem analytically amenable as it allows for a decomposition to one problem per bandit. The optimal solution of the relaxed problem is defined in terms of index values per bandit depending on the state and transition rates of the bandit. The index values for the relaxed problem serve as a heuristic for the original problem, called Whittle’s index policy, where the bandits with the highest Whittle index values are activated at each decision point. These index values reduce to the Gittins’ index values if the bandits are static and yield no reward in the passive phase (Whittle 1988). More importantly, the Whittle index policy has been shown to be asymptotically optimal under certain conditions and performs well in practice. In spite of its practicality, application of the Whittle index involves two difficulties, (i) showing a technical property called indexability; (ii) the calculation of the index function itself. Recently, Larranaga et al. (2016) and Ayesta et al. (2021) have established indexability for a family of problems and also derived closed form Whittle’s index expressions. We base our analysis on the results of Ayesta et al. (2021) for sufficient conditions of indexability and index function derivation.

A limited number of studies has mapped CBMS as a RBP. Abbou and Makis (2019) consider group maintenance interventions in a RBP framework, which is a more general case of our problem. Glazebrook et al. (2013) and Akbarzadeh and Mahajan (2019) use machine maintenance as an application domain for restless bandits. For the specific restless bandit type considered, both studies present a general indexability result and derive the index function under certain monotonicity conditions. Ayesta et al. (2021) use a simple machine repairmen problem in continuous time to illustrate their framework to compute Whittle’s indices for modified birth-death restless bandit problems. They do not numerically benchmark how well their models perform compared to other approaches or a lower bound. In contrast our paper provides such a comparison for both with respect to competing heuristics and a new lower bound for industry size instances. In addition there are differences in the modeling set-up as Ayesta et al. (2021) create a problem such that all features of their framework can be illustrated, while our modeling is based on our experience working with industry. Glazebrook et al. (2005) and Ruiz-Hernández et al. (2020) have studied an equally rich CBMS problem as we do. Different from us, Glazebrook et al. (2005) consider a discrete time setting, whereas Ruiz-Hernández et al. (2020) allow maintenance interventions to be imperfect. However, neither of them include the impact of a deteriorating machine’s performance loss. Also, their numerical experiments are limited to small problem sizes. Specifically, Glazebrook et al. (2005) use problem instances with 4 machines and 2 repairmen and 5 machines and 3 repairmen, and Ruiz-Hernández et al. (2020) consider problem sizes of up to 50 machines and 3 repairmen. In sum, our paper is richer than the previous studies in terms of the problem environment and numerical experiment for larger problem instances with up to 160 machines and 16 repairmen. Through our new lower bound we can benchmark the performance of our policy for these large industrial scale instances. Our results indicate the the performance of our heuristic relative to the lower bound improves as the problem scale increases.

3 Model

3.1 Problem description

A team of R repairmen is responsible for the maintenance of M non-identical deteriorating machines, where $1 \le R < M$. Each machine runs continuously while being subject to a stochastic degradation process. A machine eventually fails if no preventive maintenance is performed. As the number of repairmen is smaller than the number of machines, all machines cannot be maintained simultaneously. Thus, the decision maker needs to select which machines to maintain at each decision epoch, which corresponds to the moments of state change. Maintenance interventions follow a condition based scheme using the degradation statuses of the machines. Consequently, the conditions of the machines are continuously monitored. The repairmen have the ability to switch between maintenance operations quickly and perform maintenance continuously.

We describe the degradation process of each machine by discrete state degradation. Specifically, a finite number of states are used to denote the condition of the machine, which starts in the new state and ends in the failed state. After every maintenance action, the machine returns to its “as good as new” condition and then gradually deteriorates to worse states. Machines evolve independently from each other. In addition to providing information about the likelihood of failure, the degradation state also impacts a machine’s operational efficiency. The higher the degradation state, the lower the output quality of a machine. This decrease in the output quality results in revenue loss due to producing lower quality products that are less suitable for sale/use. Thus, we incorporate decreasing operational performance of a machine as revenue loss in our setting. Both revenue loss and maintenance costs are non-decreasing with the state of the machine. Furthermore, there is a higher probability of failing at a higher degradation level for all machines. The maintenance interventions are intended to restore the machine to a good-as-new state. Its rate is independent of the wear level as it is designed as a standard protocol, however the maintenance cost may increase with the degradation level. The decision maker can initiate the maintenance at any moment. The machine is non-operational when it undergoes maintenance. Although any number of repairmen might be working at any time, a single repairman can conduct maintenance on one individual machine only.

The model is applicable to systems where the time it takes for repairmen to switch between machines is insignificant compared to the time between two degradation increments, and the repairmen are cross-trained to maintain all types of machines.

3.2 MDP formulation

We first use MDP methodology in order to model the problem described above. A summary of notation used by both the MDP and Restless Bandit Problem formulation is presented in Table 1.

Table 1 Notation

We denote the degradation state of machine m by $n_m$, where $m\in \{1,\ldots , M\}$ and $n_m \in \{0, 1, \ldots \, B_m\}$ with 0 being the as-good-as-new state and $B_m \in {\mathbb {N}}$ being the state where the revenue generated from the manufactured product is (close to) zero. Then, the system state is given by $\pmb {n}=(n_1,n_2, \ldots , n_M)$. If a repairman is assigned to machine m, it returns to pristine state 0 with exponential repair rate $\mu _m$ while incurring a lump-sum maintenance cost of $Y_m(n_m)$. Otherwise if machine m is unattended, its degradation state transitions from $n_m$ to $n_m+1$ with an exponential rate of $\lambda _m(n_m)$. In this case, there is a revenue loss rate of $R_m(n_m)$ due to operating in state $n_m$ instead of the as good as new state.

We assume that $\lambda _m(n_m)$ is non-decreasing in $n_m$ for all machines. Then the sum of the transition rates under any state $\pmb {n}$ is bounded from above by $\Delta =\sum _{m=1}^M \lambda _m(B_m-1) + \sum _{m=1}^M \mu _m$. Thus, we can formulate this continuous time MDP as a discrete time MDP with $\Delta$ as the mean time between events. In any state $\pmb {n}$, the decision maker can take an action $\pmb {a}=(a_1, \ldots , a_M)$, where $a_m=1$ indicates that a repairman is assigned to machine m and $a_m=0$ indicates that machine m continues operation. Let ${\mathbb {A}}$ denote the set of feasible actions that satisfy the condition $\sum _{i=1}^M a_i \le R$. The transition probability of going from state $\pmb {n}$ to state $\pmb {n'}$ given a feasible action $\pmb {a}$ is denoted by $p(\pmb {n'}|\pmb {n},\pmb {a})$, where

$$\begin{aligned} p(\pmb {n'}|\pmb {n},\pmb {a}) = {\left\{ \begin{array}{ll} \lambda _m(n_m)/\Delta &{}\hbox {if } a_m=0 \hbox { and } \pmb {n'}=\pmb {n}+e_m\, \text { for } \, m\in \{1,\ldots , M\},~ 0\le n_m \le B_m-1,\\ \mu _m/\Delta &{}\hbox {if } a_m=1 \hbox { and } \pmb {n'}=\pmb {n} - n_m e_m \text { for }\, m\in \{1,\ldots , M\},~ 1\le n_m \le B_m,\\ \frac{\lambda _m(B_m-1)-\lambda _m(n_m)+\mu _m}{\Delta } &{}\hbox {if }\,a_m=0 \,\text { and }\, \pmb {n'}=\pmb {n},\\ \frac{\lambda _m(B_m-1)}{\Delta } &\hbox {if }\,~ a_m=1\, \text { and }\, \pmb {n'}=\pmb {n},\\ 0 &{}\text {otherwise}, \end{array}\right. } \end{aligned}$$

where $e_m$ is a unit vector in ${\textbf{R}}^{M}$ with all elements 0 except the $m^{th}$ element.

Let $C^{\pmb {a}}(\pmb {n})$ denote the cost for choosing action $\pmb {a}$ at state $\pmb {n},$

$$\begin{aligned} C^{\pmb {a}}(\pmb {n}) = \sum _{m=1}^{M} \left[ {\mathbb {I}}\{a_m=0\} R_m(n_m) + {\mathbb {I}}\{a_m=1\} (R_m(B_m)+\mu _m Y_m(n_m)) \right] \end{aligned}$$

The immediate cost associated with choosing an action for each machine can be elucidated as follows. When the action $a_m=0$ is selected for machine m at state $n_m$, the cost per unit time is only the revenue loss rate $R_m(n_m)$. However, selecting $a_m=1$ includes both the maximum revenue loss rate associated with not operating the machine, $R_m(B_m)$, and the maintenance cost per unit time.

Accordingly, the Bellman optimality equations of the MDP are given by

$$\begin{aligned} \gamma +V(\pmb {n})= \min _{\pmb {a} \in {\mathbb {A}}} \left[ \sum _{\pmb {n'} \in \pmb {S}} p(\pmb {n'} \mid \pmb {n},\pmb {a}) (C^{\pmb {a}}(\pmb {n}) +V(\pmb {n'})) \right] , \quad \forall \pmb {n} \end{aligned}$$

(1)

where $V(\pmb {n})$ is the relative value function representing the relative cost of starting in state $\pmb {n}$, and $\gamma$ is the optimal cost rate.

The MDP formulation given in (1) can be solved by implementing one of the well-known approaches such as value iteration or policy improvement. However, the computational complexity grows with the number of machines and repairmen. Hence, we employ this model only to generate optimal solutions to problems of small sizes in Sect. 4.2.

3.3 RBP formulation

Independent evolution of the machines allows us to cast the problem as a RBP and utilize Whittle’s index theory to obtain a well-performing heuristic. To formulate the problem as a RBP, we represent each individual machine with a bandit, where the state of bandit m, $n_m$, is the degradation level. Decision epochs are defined as the moments when a bandit undergoes a state change. At each decision epoch, the controller can choose one of two actions for each bandit: action $a = 0$ to render the bandit passive, or action $a = 1$ to render the bandit active. For our problem, activation of bandit m corresponds to performing maintenance on machine m. The transition dynamics of a bandit are dependent on the action chosen, but are independent of the other bandits. When one of the R repairmen is maintaining machine m, it makes a transition from state $n_m$ ($>0$) to state 0 after a duration with exponential rate $\mu _m$. Else, if machine m is unattended, it experiences a deterioration from state $n_m$ $(<B_m)$ to state $n_m+1$ with an exponential rate $\lambda _m(n_m)$. Let $\tau _m^{a}(i,j)$ represent the transition rate from state i to j for bandit m under action a, then the transition rate function can be expressed as

$$\begin{aligned} \tau _m^{a}(i,j) = {\left\{ \begin{array}{ll} \mu _m &{} \text {if }\, a_m=1,\, j=0,\, 1\le i \le B_m, \\ \lambda _m(i) &{} \text {if }\, a_m=0,\, j=i+1,\, 0\le i < B_m,\\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(2)

For bandit m, the cost per unit of time when in state i under action a, $C_m^{a}(i)$, can be written as

$$\begin{aligned} C_m^{a}(i) = {\left\{ \begin{array}{ll} R_m(B_m)+\mu _m Y_m(i) &{} \hbox { if}\;a_m=1\\ R_m(i) &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(3)

Note that the cost of activating a bandit (i.e. maintaining a machine) has two components, which can be explained as follows: (i) $R_m(B_m)$ is the revenue loss rate due to not operating during maintenance (i.e., equal to the maximum revenue that can be realized per unit of time), and (ii) $\mu _m Y_m(i)$ is the maintenance cost per unit of time.

The decision maker is interested in finding a policy $\phi$, which decides on bandits to activate such that at most R out of M bandits are active at any moment in time. For our specific problem, we seek a policy $\phi$ that determines the machines to maintain while ensuring that at most R repairmen are occupied any time. Given the policy $\phi$, $X_m^{\phi } (t)$ stands for the state of bandit m at time t and $X^{\phi }(t)=(X_1^{\phi } (t), X_2^{\phi } (t), \ldots X_M^{\phi } (t))$. $Z_m(X^{\phi }(t))$ takes value 1 if bandit m is made active at time t under policy $\phi$ and 0 otherwise. A policy $\phi$ is called feasible if the following constraint is satisfied.

$$\begin{aligned} \sum _{m=1}^M Z_m(X^{\phi }(t)) \le R \quad \forall t \end{aligned}$$

(4)

The collection of feasible policies satisfying constraint (4) is denoted by U and $U \ne \emptyset$. The original optimization problem can be represented in the following form:

$$\begin{aligned}&\min ~\lim \sup _{T \rightarrow \infty } \sum _{m=1}^{M} \frac{1}{T} E \left[ \int _0^T C_m^{ Z_m(X^{\phi }(t))} (X_m^{\phi } (t) ) dt \right] \end{aligned}$$

(5)

$$\begin{aligned}&\text{ s.t. } ~~ \phi \in U . \end{aligned}$$

(6)

where the objective function is to minimize long-run average cost. Given the intractability of the problem, we relax it in two steps following the approach in Whittle (1988) to obtain an efficient solution. We first relax the class of policies from those which activate at most R bandits in every decision epoch into those which activate at most R bandits on average. This is equivalent to limiting the number of busy repairmen by R on average in our setting. Specifically, we replace constraint (4) with (7).

$$\begin{aligned} \lim \sup _{T \rightarrow \infty } \frac{1}{T} E \left[ \int _0^T \sum _{m=1}^M Z_m(X^{\phi }(t)) dt \right] \le R \end{aligned}$$

(7)

Then, the corresponding relaxed problem is to solve (5) under constraint (7), which turns out to be tractable. The Lagrangian relaxation of the optimization problem can be expressed as the following unconstrained minimization problem:

$$\begin{aligned} \lim \sup _{T \rightarrow \infty } \frac{1}{T} E \left[ \int _0^T \sum _{m=1}^M C_m^{ Z_m(X^{\phi }(t))} (X_m^{\phi } (t) ) - W \left( R-\sum _{m=1}^M Z_m(X^{\phi }(t)) \right) ~ dt \right] , \end{aligned}$$

(8)

where W is the Lagrange multiplier. Problem (8) yields decomposition into M sub-problems, one for each bandit m, that is:

$$\begin{aligned} \min \lim \sup _{T \rightarrow \infty } \frac{1}{T} E \left[ \int _0^T C_m^{ Z_m(X^{\phi }(t))} (X_m^{\phi } (t) ) - W \left( 1-Z_m(X^{\phi }(t)) \right) ~ dt \right] \quad m\in \{1,\ldots ,M\}. \end{aligned}$$

(9)

In other words, optimal policies for M bandits found by (9) operate as a solution to the relaxed problem (8). Due to the unchain nature of the problem, the sub-problem for each bandit becomes equivalent to minimizing

$$\begin{aligned} E\left[ C_m^{ Z_m(X^{\phi }(t))} (X_m^{\phi } (t) ) \right] - W E[{\mathbb {I}}\{Z_m(X^{\phi }(t))=0\}]. \end{aligned}$$

(10)

The optimal solutions of the relaxed problem facilitate the development of the Whittle’s heuristic for the original problem in (5). The heuristic relies on establishing a technical property known as indexability. A bandit is indexable if the set of states in which it is optimal to take a passive action increases in W. Given that indexability holds, Whittle’s index value for bandit m at state n, $W_m(n)$, is defined as the minimum subsidy that makes the passive and active actions equally rewarding at state n for problem (10). Note that indexability is not a trivial property to prove and it is not always possible to obtain a closed-form expression for Whittle’s index. In order to analyze our problem structure, we adapt the results of Ayesta et al. (2021) for Markovian restless bandits of birth-death type.

Lemma 1

An optimal solution of (10) is of a 0–1 threshold type with threshold $t_m$. That is, when machine m is in a state $n_m\le t_m$, the optimal decision is to continue operating the machine, otherwise the optimal decision is to maintain the machine.

Fig. 1

Transition diagram for machine m under the threshold policy n

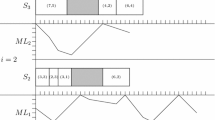
The lemma follows from Proposition 1 in Ayesta et al. (2021), which gives conditions on the transition rates that are sufficient for a threshold policy to be optimal. We can analyze the behavior of each machine under a threshold policy in isolation of the others. Let $\pi _m^n(.)$ denote steady state probabilities for machine m under threshold policy $t_m=n$. The transition diagram corresponding to threshold policy $t_m=n$ for machine m is presented in Fig. 1. Action $a=0$ is taken in states $0,1,2,\ldots ,n$, whereas action $a=1$ is taken in states $n+1,n+2,\ldots , B_m$.

The balance equations to find the stationary distribution of machine m are given by

$$\begin{aligned}&\lambda _m(0) \pi _m^{n}(0)=\mu _m \pi _m^{n}(n+1)&\\&\lambda _m(i) \pi _m^{n}(i)= \lambda _m(i-1) \pi _m^{n}(i-1),\quad \text{ for }~~ i=1,\ldots , n&\\&\mu _m \pi _m^{n} (n+1)=\lambda _m(n) \pi ^{n}(n),&\\&\sum _{i=0}^{n+1} \pi _m^{n} (i)=1. \end{aligned}$$

From the set of equations given above, we obtain the following expressions:

$$\begin{aligned}&\pi _m^{n}(i)=\frac{1}{\lambda _m(i) (\sum _{j=0}^{n}\frac{1}{\lambda _m(j)} + \frac{1}{\mu _m} )}, \quad \text{ for } ~~i=0,1,\ldots n&\end{aligned}$$

(11)

$$\begin{aligned}&\pi _m^{n}(n+1)=\frac{1}{\mu _m (\sum _{j=0}^{n}\frac{1}{\lambda _m(j)} + \frac{1}{\mu _m} )}, \end{aligned}$$

(12)

$$\begin{aligned}&\pi _m^{n}(i)=0,\quad \text{ for } ~~i=n+2,\ldots B_m&\end{aligned}$$

(13)

Lemma 2

(a) Problem (10) is indexable, if $E[{\mathbb {I}}\{Z_m^{n}(X_m^{n})=0\}]= \sum _{j=0}^n \pi _m^{n} (j)$ is non-negative and strictly increasing in n. (b) Let $C_m^{n}(i)$ denote the cost rate of bandit m in state i under threshold policy $t_m=n$. Whittle’s index for machine m at state n, $W_m(n)$ is given by

$$\begin{aligned} \frac{E[C_m^{n}(i)]-E[C_m^{n-1}(i)]}{\sum _{j=0}^{n} \pi _m^{n} (j) - \sum _{j=0}^{n-1} \pi _m^{n-1} (j)}, \end{aligned}$$

(14)

provided that (14) is a monotone function in n.

Proof

(a) As $\pi _m^{n}(i)=0$ for $i\ge n+2$, $\sum _{j=0}^n \pi _m^{n} (j)$ being strictly increasing in n is equivalent to $\pi _m^{n} (n+1)$ being strictly decreasing in n. We then obtain

$$\begin{aligned} \pi _m^{n}(n+1) - \pi _m^{n-1}(n) = \frac{1}{\mu _m \left( \sum _{j=0}^{n}\frac{1}{\lambda _m(j)} + \frac{1}{\mu _m} \right) } - \frac{1}{\mu _m \left( \sum _{j=0}^{n-1}\frac{1}{\lambda _m(j)} + \frac{1}{\mu _m}\right) } ~, \end{aligned}$$

(15)

which is negative. So, the result follows. (b) It follows from Proposition 3 in Ayesta et al. (2021). $\square$

Although we could not prove that $W_m(n)$ is a monotonic function of n, we observe that this always holds in the numerical experiments.

Note that the expected cost of implementing threshold policy $t_m=n$ for machine m is given by

$$\begin{aligned} E[C_m^{n}(i)] = \sum _{j=1}^{n} R_m(j) \pi _m^{n}(j) + R_m(B_m) \pi _m^{n}(n+1) + \mu _m Y_m(n+1) \pi _m^{n}(n+1) \end{aligned}$$

(16)

Given index values, one can implement the index heuristic to determine for which machines to conduct maintenance. At any decision point, the policy decides to intervene up to R machines with the highest non-negative index values at their current states, $W_m(n)$. If all machines have negative index values, then none of them will be worked on.

Several remarks should be made at this point about Whittle’s index and its corresponding policy. The index value is quite intuitive and easy to compute. Given that a machine is at state n, the first term in the numerator of Eq. (14) represents the expected cost of continuing operating and then performing maintenance in state $n+1$; and the second term corresponds to the expected cost of performing the maintenance now. The difference between them gives us the expected cost savings realized if the maintenance is carried out immediately. The denominator of the expression calculates the difference in the fraction of time spent under threshold policy n and $(n-1)$, respectively. Thus, (14) calculates the expected cost saving per unit time due to maintaining the machine immediately. This also brings an intuitive interpretation to the index heuristic, which is to select machines to work on that would result in higher cost savings. Another advantage of the policy is its flexibility. As the index values are found independently for each machine, any change in the problem environment can be handled easily. Examples include the purchase of a new machine, removal of a machine, and changes in the availability of repairmen.

3.4 Lower bound on the performance of an optimal policy

The dimensionality problem of the MDP formulation hinders the sub-optimality assessment of the index heuristic for relatively large sized instances. Therefore, we now proceed to develop a performance bound that can be used to assess the strength of the policy. We develop a linear programming model of the threshold policy n, which meets the constraint on the number of machines at maintenance on average. It yields an optimal solution to the relaxed RBP formulated by (5) and (7), hence a lower bound on the performance of the optimal policy.

To formulate the problem, we introduce variable $x_m^{n}$ to represent the fraction of time that machine m is undergoing maintenance when it is controlled by a threshold policy with parameter n. Recall that under the n-threshold policy, maintenance is carried on the machine when its wear state exceeds n. The threshold n can take values in $\{0,1,\ldots , B_m\}$. $n=B_m$ corresponds to the situation where a machine is never maintained and remains inoperable.

We compute the stationary distribution and expected costs of threshold policies using results in the preceding section [i.e., equations (11)–(13) and (16)]. A linear program allows us to select the correct thresholds for each machine to minimize (5) subject to (7).

$$\begin{aligned} \text {(LB)}:{} & {} \min \sum _{m=1}^{M} \sum _{n=0}^{B_m} x_m^{n} E[C_m^{n}(i)] \end{aligned}$$

(17)

$$\begin{aligned} \text {s.t.}{} ~~& {} \sum _{n=0}^{B_m} x_m^{n} =1 \quad \forall m \in \{1,\ldots , M\} \end{aligned}$$

(18)

$$\begin{aligned}{} & {} \sum _{m=1}^{M} \sum _{n=0}^{B_m-1} x_m^{n} \pi _m^{n}(n+1) \le R \end{aligned}$$

(19)

$$\begin{aligned}{} & {} 0 \le x_m^{n} \le 1 \quad \forall m \in \{1,\ldots , M\},\quad \forall n \in \{0,1,\ldots , B_m-1\} . \end{aligned}$$

(20)

The formulation determines the threshold deterioration degrees that trigger an intervention decision for each machine together with the percentage of time that threshold levels are used. The objective of the model is to minimize the expected cost of exercising such a policy while ensuring that on the average at most R repairmen are working.

4 Numerical experiments

In this section, we study the performance of the index heuristic through an extensive numerical experiment. The first phase of our analysis centres on small scale problems for which it is possible to investigate the optimality gap of the policy. In the second phase, we continue with larger instances to assess the strength of the policy with problem sizes of practical interest. Given that aim, we benchmark the proposed policy against the lower bound presented in Sect. 3.4 and two other simpler policies, a failure based one and a naive one. In order to evaluate the average cost of implementing any policy, it is necessary to simulate the system. The set-up of the simulation study is included in B.

4.1 Instance generation

We consider non-identical machines whose characteristics will be individually generated. The degradation is modelled so as to have an increasing drift toward higher value states in which higher revenue loss rates and maintenance costs are incurred. We model the maintenance cost as a linear function of the state, which is given by $Y_m(j)=\alpha _m+b_m j$, where $\alpha _m$ and $b_m$ are non-negative constants. The function comprises a fixed component ($\alpha _m$), which is associated with the setup cost, and a variable component ($\alpha _m$) accounting for the expenses related to labor cost, replaced parts and the use of specialized tools. Revenue loss rates are selected so that $R_m$ is 0 for the initial two states, where the degradation level and its impact on the revenue loss is minimal, and assumed to be linearly increasing for the subsequent states. Specifically, $R_m(j)=0$ for $j=0,1$, and $R_m(j)=(j-1)f_m$, where $f_m$ is a positive constant. The parameters $\alpha _m$, $b_m$, and $f_m$ are drawn from distinct uniform distributions, for which the details are given in Sects. 4.2 and 4.3. Note that these parameters are generated randomly to facilitate for a comprehensive numerical experiment. The deterioration rates are sampled as follows: $\lambda _m(0) \sim U[0,1]$ and $\lambda _m(j)=\lambda (j-1) + U[0,1]$ for $j=1, \ldots B_m-1$. Then, $\lambda _m(j)$ values are scaled so that the mean time to failure is equal to a specified value. This approach is used only for illustrative purposes, as a detailed analysis of the machines’ deteriorating processes is essential for practical application.

We are interested in the impact of different levels of maintenance workload (i.e. utilization of repairmen) on the performance of the index heuristic. Higher maintenance workload may result in queues for repairmen and consequently maintenance delays. Thus, it is critical to identify whether the policy is robust in a congested setting. Note that the maintenance workload depends on the chosen policy and deriving an exact expression, even under the failure-based policy, is challenging. Thus, we examine the workload under the failure-based policy using closed queueing network theory and use it as a proxy for the workload. A higher proxy value indicates a higher actual workload. To facilitate application of the theory, we assume that the maintenance rate is independent of the machine, $\mu _m=\mu$ for all m. We first formulate a multi-class closed queueing network model of the system operating under a failure based policy and then use the SCAT algorithm to calculate the utilization for a given maintenance rate (Lavenberg and Reiser 1980; Neuse and Chandy 1981). $\mu$ is calibrated for each instance to achieve the target utilization level. The details of the queueing model and calibration procedure are presented in A. The proxy for the maintenance workload, $\rho$, is chosen from $\{0.8, 0.85, 0.9, 0.95\}$ by controlling the maintenance rate.

As indicated in Sect. 3.3, the index value is determined by (14), provided that it is non-decreasing with respect to the wear state. Therefore, we ensure this condition is met for each randomly generated parameter set before conducting the simulation experiment.

4.2 Small sized systems

The index heuristic can be easily applied to systems with a large number of machines, however it is not generally tractable to evaluate the MDP formulation in such systems. Therefore, we restrict ourselves to small sized instances to assess the optimality gap of the index heuristic. The optimal cost is obtained by means of a standard value iteration algorithm with a tolerance limit of $10^{-5}$ (Puterman 2014).

First of all, we investigate the behavior of the Whittle index on a small example with 3 machines and 7 degradation levels. We employ linear configurations for the revenue loss and maintenance cost functions as explained in the previous section. The specific parameter set considered is presented in Table 2. Notice that the deterioration rates are generated as described in Sect. 4.1. Whittle index values are calculated by Eq. (14) and reported in Table 3. The index values show that ordering machines by degradation level does not necessarily yield the same sequence as the one found by index values. This difference occurs because the Whittle index also incorporates information about the evolution of degradation processes and cost differentials between machines.

Table 2 Parameters for the illustrative example

Table 3 Whittle index values for the illustrative example

Table 4 Input parameters for optimality gap analysis

Thereafter, we explore the optimality gap of the index heuristic based on 20 randomly generated instances (i.e., deterioration rates) for 3 machines and 1 repairmen. In the RBP framework, our problem translates into selecting R machines to maintain at any decision point, which corresponds preemptive scheduling rule. Consequently, we conduct the optimality gap analysis using simulation results of the index heuristic under both non-preemptive and preemptive scheduling rules. Under preemption, the maintenance of a machine can be interrupted by another machine with a higher index value at any decision point. We use the instance generation process explained in Sect. 4.1. The results of the dataset presented in Table 4 are summarized in Table 5. In this table, we report the minimum, mean, and maximum percentages of the optimality gap for both scheduling rules.

The majority of instances have a cost rate within 3% of optimality. The optimality gap decreases with the utilization proxy, which is a strong endorsement of the index heuristic for congested systems. Moreover, the performance of the policy under preemptive and non-preemptive scheduling rules are very close to each other. This shows applicability of the policy for practical situations where non-preemptive scheduling is preferable. Thus, we only consider the performance of the index heuristic under non-preemptive scheduling in the next section.

Table 5 Results of optimality gap analysis

4.3 Large sized systems

In this section, we subject the proposed policy to numerical investigation for large sized instances, which preclude the use of the value iteration algorithm to find an optimal policy. Therefore, the performance comparison of interest is conducted between the index heuristic exercised with non-preemptive scheduling rule, the lower bound on the optimal solution (formulation LB), and two other scheduling policies that emerge in practice. These two policies are: (1) failure based policy: Only the failed machines are maintained under a first come first served (FCFS) discipline. This policy is reasonable if there is no information regarding the conditions of the machines. It acts as a basic benchmark since any decent degradation state dependent policy should perform better. (2) Naive policy: The machines exceeding their deterioration thresholds are maintained on a FCFS basis. The threshold level of a machine is determined as the degradation state that minimizes the cost expression (16). Note that the thresholds are found with no consideration of maintenance capacity.

Table 6 Input parameters for simulation study

We set up a test bed including instances that are obtained through the parameter values displayed in Table 6. Four possible values for the number of machines and repairmen are explored. While selecting (M, R) combinations, we maintain a constant ratio between them to numerically evaluate the convergence rate for the asymptotic optimality of the index heuristic. All of the machines have 7 degradation states (i.e. $\{0,1, \ldots , 6\}$) and have a mean life time of 10. To vary the cost levels of the machines, $a_m$, $b_m$, and $f_m$ parameters are sampled as shown in Table 6. For each (M, R) scenario, we follow the data generation procedure explained in Sect. 4.1.

In total, 480 problem instances are randomly generated and simulated. There are 6 configurations of maintenance cost and revenue loss and 4 different utilization proxy - $\rho$ values. This makes 24 scenarios for each pair of (M, R) values and 5 experiments are conducted for each scenario. Those 5 experiments differ in the values of the parameters of maintenance cost and revenue loss, and degradation rates. For every simulated instance and policy, the average cost rate is recorded and subsequently the percentage gap between the lower bound is calculated as a performance metric. Specifically, we are interested in $\%GAP_\Pi = (C_\Pi -C_{LB})/C_{LB} \times 100$, where $C_{LB}$ is the lower bound on the optimal average cost and $C_\Pi$, $\Pi =\{WI,F,N\}$ is the average cost under Whittle’s index, failure based, and naive policies, respectively. In Tables 7, 8, 9 and 10, we summarize outcomes by categorizing problem instances with respect to system size, cost configurations (i.e., MC denotes maintenance cost and RL denotes revenue loss) and approximate workload levels. We present the minimum, average, and maximum $\%GAP_\Pi$ for each policy $\Pi =\{WI,F,N\}$.

Table 7 Results of gap analysis for $(M,R)=(10,1)$

Table 8 Results of gap analysis for $(M,R)=(40,4)$

The results in Tables 7, 8, 9, and 10 confirm that the performance of the failure-based policy is the weakest and the index heuristic is consistently the strongest. Specifically, the suboptimality of the index heuristic is the lowest among all policies for all problem instances which shows that it is robust to changes in cost parameters. Even though it outperforms failure-based and naive policies, the index heuristic produces rather weak results when the system size is small (i.e. $M=10,40$) and workload is relatively low ($\rho =0.8,0.85$). However, its consistency and robustness in performance, relative to the lower bound for relatively larger system sizes that exist in practice, makes it stand out. For the scenarios including 160 machines, its overall worst case performance is at most 4.9%, while the value for the other policies are 50.88%. The superior performance of the index heuristic is due to its ability to dynamically react to deterioration levels of machines while also considering workload. Ignoring both the conditions of the machines and the maintenance capacity while scheduling maintenance can be quite costly, as gaps with the lower bound up to 50.88% are observed under the failure based policy. Although taking maintenance actions based on degradation levels of machines is beneficial, failing to consider maintenance capacity leads to gaps of up to 19.43% under the naive policy. Also, the index heuristic performs better against the lower bound as the system size increases, which provides numerical evidence that index heuristic may be asymptotically optimal.

Table 9 Results of gap analysis for $(M,R)=(80,8)$

Table 10 Results of gap analysis for $(M,R)=(160,16)$

Fig. 2

Average cost per machine as a function of M

Fig. 3

$\%$ gap in lower bound as a function of M

Following the general discussions of the results, our focus shifts to investigate whether the numerical results are consistent with the conjecture of asymptotic optimality when the number of machines approaches infinity with a fixed proportion to the number of repairmen. This is equivalent to exploring the convergence rate of the policy to the lower bound on the optimal solution as the number of machines grows. For this purpose, we plot the average cost per machine under the index heuristic and the lower bound as a function of the number of machines at different levels of utilization proxy. We also incorporate average cost behavior of benchmark policies to the plots for the completeness of the analysis. Even though, the plots are drawn for a single scenario, one can observe similar behaviors for other instances as well. Figure 2 depicts empirical support for the fact that the performance of the index heuristic converges to the lower bound quite fast with the increase in the number of machines. Although the convergence rate is high up to 80 machines, the rate of the increase slows down as the number of machines grows, which is as expected. The gaps up to 80 machines when utilization proxy $\rho$ is 0.8 and 0.85 are lower than the ones when it is 0.9 and 0.95. For the same instances, we also plot the percentage gap with the lower bound for all policies with respect to the number of machines (i.e. see Fig. 3). Both figures indicate that the performance of the index heuristic becomes increasingly promising for systems with higher maintenance workload and larger number of machines.

5 Conclusion

In this paper, we have considered the maintenance scheduling of deteriorating machines so that a limited number of repairmen is effectively utilized. We have first formulated the problem with a MDP, which is computationally restrictive for problems of practical size. Thus, we instead used the RBP approach to derive maintenance policies based on characteristics of the individual machines. We showed that the indexability property holds for our problem and the optimal maintenance policy for a relaxed version of the problem follows a 0–1 threshold structure. We developed an index based heuristic for our problem, which emerges from closed form expressions of the Whittle’s index values of each machine. Furthermore, we formulated a linear programming model to find a lower bound on the performance of the optimal policy. We conducted a comprehensive numerical study to show superior performance of the Whittle’s index heuristic compared to failure-based and naive policies. Furthermore, we have shown that the index heuristic performs close to the optimal solution when the number of machines is high and/or maintenance workload is high. An interesting extension is to study multiple deteriorating components for each individual machine.

Appendices

Appendix A: Multi-class closed queueing network model

In this section, we consider our problem under the use of the failure based policy. This scenario is modelled as a multi-class queueing network and the product form analysis of it is adapted to ensure an efficient analysis. We start with the description of the model and proceed with presenting the algorithm to find the mean system throughput.

Fig. 4

Closed queueing network diagram with M customer classes and $M+1$ stations

We consider a network consisting of machine bases and a maintenance facility. Figure 4 provides a pictorial illustration of the network. M non-identical machines are characterized as M machine bases with a single machine. Also, each machine is associated with a separate class of customers to use a multi-class queueing network framework. We represent the maintenance facility as Station 0 and machine base m as Station m, $m=1, \ldots , M$. The operating time of base m is assumed to be exponentially distributed with mean $\Lambda _m$, the mean time to failure for machine m. In the maintenance facility, R identical repairmen are retained to service the failed machines. The service times of each repairmen follow an exponential distribution with rate $\mu$. Once the repair of machine m is completed, it is directly sent to machine base m. Let $p_{ij}(r)$ express the probability that machine m that departs Station i will next visit Station j. Note that $p_{0m}(m)=1$ and $p_{m0}(m)=1$ $\forall m$; and all other transitions have zero probability.

The network is described with state $\pmb {u}=(\pmb {u_0}, \pmb {u_1}, \ldots , \pmb {u_m})$, where $\pmb {u_i}=(u_{i1},u_{i2},\ldots , u_{iM})$ and $u_{im}$ is the number of type m machines at Station i for $i=0,1,\ldots ,M$ and $m=1,\ldots , M$. Note that $U_m=\sum _{i=0}^M u_{im} =1$ $\forall r$. Suppose that $e_{im}$ expresses the relative frequency of visits to Station i by machine type m. It can be found by using the following M sets of linear equations:

$$\begin{aligned} e_{im}=\sum _{j=0}^M e_{jm} p_{ji} (m), \quad i \in 0,1,\ldots ,M, ~m \in 1,\ldots , M \end{aligned}$$

(21)

Evaluating (21) with the routing information gives us ($i,m \in 1,\ldots , M$)

$$\begin{aligned} e_{im} = {\left\{ \begin{array}{ll} e_{0m} &{} \text {if}\; m=i,\\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(22)

We continue our analysis by setting $e_{0m}$ to 1, for $m \in 1,\ldots , M$.

Mean value analysis is an exact technique to obtain solutions for the product-form closed queueing networks. However, its computational complexity increases very rapidly with the number of job classes. So, several algorithms have been developed over the years for computing approximate solutions. We adapt an early significant method referred to as SCAT, which allowed approximate analysis of queueing network models with multiple job classes and multiple servers for the first time (Neuse and Chandy 1981). The method is an iterative procedure to calculate the mean number of jobs, mean residence time and average system throughput.

The notation is summarized in Table 11 and the general form of the algorithm adapted for our problem is outlined below (Tables 12, 13, 14).

Table 11 Notation used in SCAT algorithm

Table 12 Core algorithm

Table 13 SCAT algorithm

Following, we obtain mean number of machine m maintained at Station 0 with the formula $Y_{m}=k_{0m}/t_{0m}$, which allows us to calculate utilization of the Station 0, $\rho =\sum _{m=1}^M \frac{Y_m}{R \mu }$.

Lastly, we present steps of calibration procedure for $\mu$ to achieve a certain utilization of repairmen.

Table 14 Calibration of $\mu$

Appendix B: Details of the simulation study

In this part, we explain how we set up our discrete event simulations. We use the non-overlapping batch means approach for which an extensive description is provided in Steiger and Wilson (2001). After analyzing sample scenarios, the number of batches and the batch size are determined. Accordingly, each simulation run is divided in 201 batches each with 10,000 maintenance completions. The simulation is started in the state with all machines working and the first batch is disregarded to eliminate the initial bias. The average cost values are recorded for the remaining 200 batches and then the corresponding confidence interval is constructed. For each data instance, we confirm that 95% confidence interval half-widths are less than 1% of the average estimate.