Abstract
Improving access to care in medically under-served areas (MUA) is an important task for public health policy in many countries. A lack of access to care in MUAs is often addressed by establishing new service providers, which improves the accessibility in those regions in a geographic sense. However, the geographic accessibility is only a necessary condition for relieving the regions from being under-served; new service providers must be sufficiently attractive for care consumers to use so that the new establishment effectively translates to actual improvement in accessibility to care in the MUAs. In this paper, we first develop a location-allocation model for healthcare facilities that incorporates a choice model to represent care consumers’ preferences and choice decisions on the care facilities. Then we expand the model such that some of the attribute variables in the consumer utility function can be handled as decision variables in the location-allocation optimization. Thus, the proposed model determines the attributes variables of open facilities as well as their locations. Utility of the proposed model is demonstrated by using the Korea’s MUA support program for perinatal care.







Similar content being viewed by others
Notes
In this paper, we use the terms “perinatal care capacity” and “perinatal care provider” interchangeably.
\(V_{i0}\) is constant since care units represented by index 0 are existing hospitals, for which we do not change any attribute therein.
The minimum limit is a regulatory requirement; the maximum limit, on the other hand, is needed due to a technical reason—we use \(\hat{l}\) to define the number of pieces in the piecewise linear function, and \(\hat{l}\) requires both minimum and maximum value for \(z_{ij}\).
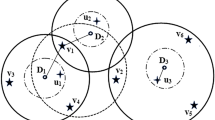
Delivery records from the data suggest that most delivery cases are serviced in an obstetrics care provider within 90-minute of their residence; thus, when we establish a new care capacity in an MUA, those providers within 90-min of the MUA should be considered competing for the demand in the MUA.
References
Aros-Vera F, Marianov V, Mitchell JE (2013) p-hub approach for the optimal park-and-ride facility location problem. Eur J Oper Res 226(2):277–285
Avijit GSM, Craig CS (1995) Multifacility retail networks. In: Drezner Z (ed) Facility location: a survey of applications and methods. Springer, New York, pp 301–330
Benati S, Hansen P (2002) The maximum capture problem with random utilities: problem formulation and algorithms. Eur J Oper Res 143(3):518–530
Bornstein BH, Marcus D, Cassidy W (2000) Choosing a doctor: an exploratory study of factors influencing patients’ choice of a primary care doctor. J Eval Clin Pract 6(3):255–262
Castillo-López I, López-Ospina HA (2015) School location and capacity modification considering the existence of externalities in students school choice. Comput Ind Eng 80:284–294
Current J, Min H, Schilling D (1990) Multi-objective analysis of facility location decisions. Eur J Oper Res 49(3):295–307
Dan T, Marcotte P (2017) Competitive facility location with selfish users and queues. CIRRELT, Centre interuniversitaire de recherche sur les réseaux d’entreprise, la logistique et le transport = Interuniversity Research Centre on Enterprise Networks, Logistics and Transportation
Drezner T (1995) Competitive facility location in the plane. In: Drezner Z (ed) Facility location: a survey of applications and methods. Springer, New York, pp 285–300
Eiselt HA, Laporte G (1995) Objectives in location problems. In: Drezner Z (ed) Facility location: a survey of applications and methods. Springer, New York, pp 151–180
Fotheringham AS, Brunsdon C, Charlton M (2000) Quantitative geography: perspectives on spatial data analysis. Sage
Haase K (2009) Discrete location planning. Institute of Transport and Logistics Studies
Haase K, Müller S (2015) Insights into clients’ choice in preventive health care facility location planning. OR Spectrum 37(1):273–291
Hwang K, Jang H, Lee T, Kim M, Shin H, Lee T (2017) A choice model for estimating realized accessibility: case study for obstetrics care in Korea. In: International conference on health care systems engineering, Springer, pp 73–85
Jang H, Hwang K, Lee T, Kim M, Shin H, Lee T (2017) A location problem for medically under-served areas in Korea. In: International conference on health care systems engineering, Springer, pp 61–71
Jang H, Hwang K, Lee T, Lee T (2019) Designing robust rollout plan for better rural perinatal care system in Korea. Eur J Oper Res 274(2):730–742
Khan AA (1992) An integrated approach to measuring potential spatial access to health care services. Socio-Econ Plan Sci 26(4):275–287
Koppelman FS, Bhat C (2006) A self instructing course in mode choice modeling: multinomial and nested logit models
Ljubić I, Moreno E (2018) Outer approximation and submodular cuts for maximum capture facility location problems with random utilities. Eur J Oper Res 266(1):46–56
Marianov V, Ríos M, Icaza MJ (2008) Facility location for market capture when users rank facilities by shorter travel and waiting times. Eur J Oper Res 191(1):32–44
Marschak J et al (1959) Binary choice constraints on random utility indicators. Cowles Foundation for Research in Economics, Yale University, Tech. rep
McFadden D (1973) Conditional logit analysis of qualitative choice behaviour. In: Zarembka P (ed) Frontiers in econometrics. Academic Press, New York, pp 105–142
O’Kelly ME (1987) Spatial interaction based location-allocation models. In: Ghosh AGR (ed) Spatial analysis and location-allocation models, van Nostrand Reinhold, New York, pp 302–326
Pellegrini PA, Fotheringham AS (2002) Modelling spatial choice: a review and synthesis in a migration context. Prog Hum Geogr 26(4):487–510
Radman M, Eshghi K (2018) Designing a multi-service healthcare network based on the impact of patients’ flow among medical services. OR Spectrum pp 1–42
Rahmaniani R, Rahmaniani G, Jabbarzadeh A (2014) Variable neighborhood search based evolutionary algorithm and several approximations for balanced location-allocation design problem. Int J Adv Manuf Tech 72(1–4):145–159
Roy JR, Thill JC (2003) Spatial interaction modelling. Pap Reg Sci 83(1):339–361
Sherali HD, Tuncbilek CH (1992) A global optimization algorithm for polynomial programming problems using a reformulation-linearization technique. J Global Optim 2(1):101–112
Victoor A, Delnoij DM, Friele RD, Rademakers JJ (2012) Determinants of patient choice of healthcare providers: a scoping review. BMC Health Serv Res 12(1):272
Zhang Y (2015) Designing a retail store network with strategic pricing in a competitive environment. Int J Prod Econ 159:265–273
Zhang Y, Berman O, Verter V (2012) The impact of client choice on preventive healthcare facility network design. OR Spectrum 34(2):349–370
Zhang Y, Liang L, Liu E, Chen C, Atkins D (2016) Patient choice analysis and demand prediction for a health care diagnostics company. Eur J Oper Res 251(1):198–205
Acknowledgements
Funding was provided by National Research Foundation of Korea (Grant No. 2019-R1A2C1088302).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix: A. Proof of linearization for choice constraints
We follow Aros-Vera et al. (2013) to linearize the original constraint on choice probability, (12) and (13). This linearization results in (14)–(16), and in this “Appendix”, we show that they are equivalent to the original constraints. For ease of reference, (12)–(16) are reproduced here.
Proof
For any two alternatives j and k, the ratio of the choice probabilities \(x_{ij}\) and \(x_{ik}\) is
This ratio is independent from other alternatives than j and k, and is said to be independent from irrelevant alternatives (IIA). A logit model naturally exhibits this IIA property. By definition of probability, we have
With the IIA property a logit model, we can write choice probability \(x_{ij}\) as
Now, substitute (A.2) into (A.1), and we obtain the following:
Then (A.2) can be rewritten as
Note that the equality (A.2) can be split to upper and lower inequality:
Thus, we have the following relationships:
(A.1), (A.2) \(\leftrightarrow\) (A.1), (A.5) , (A.6) \(\leftrightarrow\) (A.3), (A.4).
Now, we take into account \(y_j\) in (12). Specifically, we need make sure that (1) if \(y_{j}=0\) then \(x_{ij}=0\), and (2) if \(y_{j}=1\) then \(x_{ij}=e^{V_{ij} }/ (\sum _{m\in J} e^{V_{im}} y_{m} + e^{V_{i0}})\).
In Constraint (11), we require \(x_{ij} \le y_{j}\), and this ensures condition (1). For (2), it is evidently satisfied when \(y_j\) = 1. Note that, since \(e^{V_{ij}-V_{i0}} x_{i0}\) is always positive, if \(x_{ij}=0\), (A.6) is invalid while constraint (A.5) is valid. To relieve this invalidity, we add the \(-(y_{j}-1)\) term. This ensures that if \(y_{j}=1\), constraint (16) is same as (A.6) and that if \(y_{j}=0\), constraint (16) is valid. Finally,
Constraint (12) \(\leftrightarrow\) Constraint (A.4),
Constraint (13) \(\leftrightarrow\) Constraint (A.3),
Constraint (14) \(\leftrightarrow\) Constraint (A.1),
Constraint (15) \(\leftrightarrow\) Constraint (A.5),
Constraint (16) \(\leftrightarrow\) Constraint (A.6).
Since constraint (A.1), (A.5), (A.6) \(\leftrightarrow\) constraint (A.3), (A.4), constraint (14), (15), (16) \(\leftrightarrow\) constraint (12), (13). For more detail, we refer readers to Aros-Vera et al. (2013). \(\square\)
Appendix: B. Full formulation of \(P_{MUA}\)
Rights and permissions
About this article
Cite this article
Hwang, K., Asif, T.B. & Lee, T. Choice-driven location-allocation model for healthcare facility location problem. Flex Serv Manuf J 34, 1040–1065 (2022). https://doi.org/10.1007/s10696-021-09441-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10696-021-09441-8