Pricing and greening strategies for a dual-channel closed-loop green supply chain

Abstract

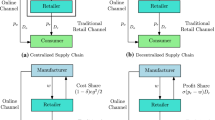
This article considers a closed-loop green supply chain with both forward and reverse dual-channels, where a manufacturer produces and sells a single green product to the potential customers through both the direct online channel (e-tail/internet) and the traditional retail channel in the forward dual-channel, and collects the used products for remanufacturing from the customers through both the retail and the direct online channels in the reverse dual-channel (Model II). The pricing and greening strategies for the channel members and the whole supply chain are derived both analytically and numerically under centralized and three decentralized scenarios viz. manufacturer-led and retailer-led decentralized scenarios and Nash game. These results are compared with those in the case when reverse logistic does not exist (Model I). Two special cases are examined when the products are returned through only online channel and only retail channel. Sensitivity analysis is performed to explore the effect of key model-parameters on optimal decisions. From numerical analysis, it is observed that the retail price in the centralized scenario is higher than that in the decentralized scenario, which contradicts the result due to double marginalization, and the retailer-led decentralized policy provides higher profit than the other decentralized policies. Model II gives better result in terms of profit of the whole supply chain, whereas Model I suggests a more environment-friendly product. It is also observed that the channel members gain more profit when the retailer only collects the used products.

Appendix

Proof of Proposition 1

From (6), we have

$$\begin{aligned} \frac{\partial \Pi ^{IC}}{\partial p_0} &= - 2 p_0 \alpha _0 + 2 p \beta + c_m (\alpha _0 - \beta ) + \gamma _0 \theta + a (1 - \rho ); \frac{\partial ^2\Pi ^{IC}}{\partial p^2_0} = - 2 \alpha _0;\\ \frac{\partial \Pi ^{IC}}{\partial \theta }&= p_0 \gamma _0 + p \gamma _1 - c_m (\gamma _0 + \gamma _1) - 2 \theta \lambda ;\\ \frac{\partial ^2\Pi ^{IC}}{\partial \theta ^2}&= - 2 \lambda ; \frac{\partial \Pi ^{IC}}{\partial p} = - 2 p \alpha _1 + 2 p_0 \beta + c_m (\alpha _1 - \beta ) + \gamma _1 \theta + a \rho ;\\ \frac{\partial ^2\Pi ^{IC}}{\partial p^2}&= - 2 \alpha _1; \frac{\partial ^2\Pi ^{IC}}{\partial p_0\partial \theta } = \gamma _0; \frac{\partial ^2\Pi ^{IC}}{\partial p_0\partial p} = 2 \beta ;\\ \frac{\partial ^2\Pi ^{IC}}{\partial \theta \partial p}&= \gamma _1 \end{aligned}$$

The Hessian matrix is given by

$$\begin{aligned} H^{IC}=\left( \begin{array}{lll} \frac{\partial ^2\Pi ^{IC}}{\partial p^2_0} &{}\quad \frac{\partial ^2\Pi ^{IC}}{\partial p_0\partial \theta } &{}\quad \frac{\partial ^2\Pi ^{IC}}{\partial p_0\partial p} \\ \frac{\partial ^2\Pi ^{IC}}{\partial \theta \partial p_0} &{}\quad \frac{\partial ^2\Pi ^{IC}}{\partial \theta ^2} &{}\quad \frac{\partial ^2\Pi ^{IC}}{\partial \theta \partial p} \\ \frac{\partial ^2\Pi ^{IC}}{\partial p\partial p_0} &{}\quad \frac{\partial ^2\Pi ^{IC}}{\partial p\partial \theta } &{}\quad \frac{\partial ^2\Pi ^{IC}}{\partial p^2} \end{array} \right) =\left( \begin{array}{lll} - 2 \alpha _0 &{}\quad \gamma _0 &{}\quad 2 \beta \\ \gamma _0 &{}\quad - 2 \lambda &{}\quad \gamma _1 \\ 2 \beta &{}\quad \gamma _1 &{} \quad - 2 \alpha _1 \end{array} \right) \end{aligned}$$

Now, $|H^{IC}_1| = - 2 \alpha _0 < 0$,

$$\begin{aligned} |H^{IC}_2| = 4 \alpha _0 \lambda - \gamma _0^2>0, \hbox {if}\, \lambda > \frac{\gamma _0^2}{4 \alpha _0} . \end{aligned}$$

Again, $|H^{IC}| = 2 [\alpha _1 \gamma _0^2 + 2 \beta \gamma _0 \gamma _1 + \alpha _0 \gamma _1^2 - 4 \lambda ( \alpha _0 \alpha _1 - \beta ^2 )]$.

$< 0, \hbox {if}\, \lambda > \frac{\alpha _1 \gamma _0^2 + 2 \beta \gamma _0 \gamma _1 + \alpha _0 \gamma _1^2}{4 (\alpha _0 \alpha _1 - \beta ^2) }.$

Therefore, $H^{IC}$ is negative definite if and only if $\lambda > \hbox {max}\{\frac{\gamma _0^2}{4 \alpha _0},\frac{\alpha _1 \gamma _0^2 + 2 \beta \gamma _0 \gamma _1 + \alpha _0 \gamma _1^2}{4 (\alpha _0 \alpha _1 - \beta ^2)}\}.$

If the Hessian matrix is negative definite then there exists a unique optimal solution which can be obtained by solving $\frac{\partial \Pi ^{IC}}{\partial p_0} = 0,\frac{\partial \Pi ^{IC}}{\partial \theta } = 0 \,\hbox {and}\, \frac{\partial \Pi ^{IC}}{\partial p} = 0$ simultainously, as given in Proposition 1. $\square$

Proof of Proposition 2

The retailer’s reaction

From (5), we have the second order sufficient condition $\frac{\partial ^2\Pi _r^{IM}}{\partial p^2} = - 2 \alpha _1 < 0$, which ensures that unique optimal solution exists. From the first order optimality condition $\frac{\partial \Pi _r^{IM}}{\partial p} = 0$, we get the optimal reaction as $p^{IM} = \frac{ \rho a + \beta p_0 + \gamma _1 \theta + \alpha _1 w}{2 \alpha _1}.$

The manufacturer’s reaction

After getting the reaction of the retailer, the manufacturer maximizes his profit and determines the optimal decisions. The Hessian matrix associated with the profit function $\Pi _m^{IM}$ is given by

$$\begin{aligned} H^{IM}=\left( \begin{array}{lll} - \alpha _1 &{}\quad \beta &{}\quad \frac{\gamma _1}{2}\\ \beta &{}\quad - 2 \alpha _0 + \frac{\beta ^2}{\alpha _1} &{}\quad \frac{\beta \gamma _1}{2 \alpha _1} + \gamma _0 \\ \frac{\gamma _1}{2} &{}\quad \frac{\beta \gamma _1}{2 \alpha _1} + \gamma _0 &{}\quad - 2 \lambda \end{array} \right) \end{aligned}$$

Now, $|H^{IM}_2| = \frac{8 (\alpha _0 \alpha _1 - \beta ^2)}{4}$. As  $\alpha _i > \beta _i\, (i = 0,1)$, $|H^{IM}_2| > 0$.

Again, $|H^{IM}| = \frac{(2 \alpha _1^2 \gamma _0^2 + 4 \alpha _1 \beta \gamma _0 \gamma _1 + (\beta ^2 + \alpha _0 \alpha _1) \gamma _1^2) - 8 \alpha _1 \lambda ( \alpha _0 \alpha _1 - \beta ^2)}{2 \alpha _1}$

$< 0, \hbox {if}\, \lambda > \frac{(2 \alpha _1^2 \gamma _0^2 + 4 \alpha _1 \beta \gamma _0 \gamma _1 + (\beta ^2 + \alpha _0 \alpha _1) \gamma _1^2) }{8 \alpha _1 ( \alpha _0 \alpha _1 - \beta ^2) }$.

Therefore, $H^{IM}$ is negative definite if and only if $\lambda > \frac{(2 \alpha _1^2 \gamma _0^2 + 4 \alpha _1 \beta \gamma _0 \gamma _1 + (\beta ^2 + \alpha _0 \alpha _1) \gamma _1^2) }{8 \alpha _1 ( \alpha _0 \alpha _1 - \beta ^2) }$. Under this condition, the unique optimal solution can be obtained from the first order optimality conditions as given in Proposition 2. $\square$

Proof of Proposition 3

The manufacturer’s reaction

The Hessian matrix associated with the profit function $\Pi _m^{IR}$ is given by

$$\begin{aligned} H^{IR}=\left( \begin{array}{ll} - 2 \alpha _0 &{}\quad \gamma _0\\ \gamma _0 &{}\quad - 2 \lambda \end{array} \right) \end{aligned}$$

It is clear that $|H_1^{IR}| < 0$ and $|H^{IR}| = 4 \alpha _0 \lambda - \gamma _0^2 > 0$, if $\lambda > \frac{\gamma _0^2}{4 \alpha _0}$. Therefore, $H^{IR}$ is negative definite if and only if $\lambda > \frac{\gamma _0^2}{4 \alpha _0}$ and the unique optimal decisions of the manufacturer is then given by

$$\begin{aligned} p_0^{IR} &= \frac{4 a \lambda (1 - \rho ) + c_m[ 4 \alpha _0 \lambda - 2 \beta \lambda - \gamma _0(2 \gamma _0 + \gamma _1)] + ( \gamma _0 \gamma _1 + 6 \beta \lambda ) p^{IR}}{2 (4 \alpha _0 \lambda - \gamma _0^2)}\\ \theta ^{IR} &= \frac{2 a \gamma _0 (1 - \rho ) - c_m[(2 \alpha _0 + \beta ) \gamma _0 + 2 \alpha _0 \gamma _1] + ( 3 \beta \gamma _0 + 2 \alpha _0 \gamma _1)p^{IR}}{2 (4 \alpha _0 \lambda - \gamma _0^2)}\\ w^{IR} &= (p^{IR} + c_m)/2. \end{aligned}$$

The retailer’s reaction

After getting the reaction of the manufacturer, the retailer optimizes his profit and determines his/her optimal decision. We have $\frac{\partial ^2\Pi _r^{IR}}{\partial p^2} = \frac{\big (\alpha _1 \gamma _0^2 + 2 \beta \gamma _0 \gamma _1 + \alpha _0 \gamma _1^2 \big ) - \lambda \big ( 4 \alpha _0 \alpha _1 - 3 \beta ^2 \big )}{ ( 4 \alpha _0 \lambda - \gamma _0^2)} < 0$,

if $\lambda > \frac{\big (\alpha _1 \gamma _0^2 + 2 \beta \gamma _0 \gamma _1 + \alpha _0 \gamma _1^2 \big )}{(4 \alpha _0 \alpha _1 - 3 \beta ^2)}.$

So, with this restriction on $\lambda ,$ the unique optimal decision of the retailer is obtained as

$$\begin{aligned} p^{IR}= & {} \frac{1}{2 \Psi _3}\Big [ c_m\Big [ \Psi _3 + \beta \lambda (2 \alpha _0 - \beta ) - (\beta \gamma _0^2 + (\alpha _0 + \beta ) \gamma _0 \gamma _1 + \alpha _0 \gamma _1^2)\Big ] \\&+\, a\Big [(\gamma _0 \gamma _1 + 2 \beta \lambda )(1 - \rho ) + \rho ( 4 \alpha _0 \lambda - \gamma _0^2)\Big ] \Big ] \end{aligned}$$

where $\Psi _3 = \lambda (4 \alpha _0 \alpha _1 - 3 \beta ^2) - (\alpha _1 \gamma _0^2 + 2 \beta \gamma _0 \gamma _1 + \alpha _0 \gamma _1^2 ).$$\square$

Proof of Proposition 4

It is easy to see that $\frac{\partial ^2\Pi _r^{ID}}{\partial p^2} = - \alpha _1 < 0$, $\frac{\partial ^2\Pi _m^{ID}}{\partial p^2_0} = - 2 \alpha _0 < 0$ and $\frac{\partial ^2\Pi _m^{ID}}{\partial \theta ^2} = - 2 \lambda < 0$. The associated Hessian matrix is given by

$$\begin{aligned} H^{ID}=\left( \begin{array}{ll} - 2 \alpha _0 &{}\quad \gamma _0\\ \gamma _0 &{}\quad - 2 \lambda \end{array} \right) \end{aligned}$$

which is negative definite if $\lambda > \frac{\gamma _0^2}{4 \alpha _0}$.

Then, from the first order condition of optimality, the optimal decisions $(p_0^{ID}, \theta ^{ID}, p^{ID}, w^{ID})$ of the decentralized policy can be obtained as given in Proposition 4. $\square$

Proof of Property 1

From (3), using the first order optimality condition of $\Pi ^{C}$, we get p in terms of $p_0$. Now $\frac{\partial p^{C}}{\partial p_0} = \frac{\gamma _0 \gamma _1 + 4 \lambda \beta }{4 \alpha _1 \lambda - \gamma _1^2} > 0$.

Again from (3), using the first order optimality condition of $\Pi ^{C}$, we get $p_0$ in terms of p. Now $\frac{\partial p_0^{C}}{\partial p} = \frac{\gamma _0 \gamma _1 + 4 \lambda \beta }{4 \alpha _0 \lambda - \gamma _0^2} > 0$.

Also, $\frac{\partial p^{C}}{\partial \theta } = \frac{ \alpha _0 \gamma _1 + \beta \gamma _0}{2(\alpha _0 \alpha _1 - \beta ^2)} > 0$.

and $\frac{\partial p_0^{C}}{\partial \theta } = \frac{ \alpha _1 \gamma _0 + \beta \gamma _1 }{2(\alpha _0 \alpha _1 - \beta ^2)} > 0$.

From (1), using the first order optimality condition of $\Pi _m$, we get $p_0$ and $\theta$ in terms of p. Also $\frac{\partial p_0^{IIR}}{\partial p} = \frac{\gamma _0 \gamma _1 + 6 \lambda \beta }{2 (4 \alpha _0 - \gamma _0^2)} > 0$ and $\frac{\partial \theta ^{IIR}}{\partial p} = \frac{2 \alpha _0 \gamma _1 + 3 \gamma _0 \beta }{2 (4 \alpha _0 - \gamma _0^2)} > 0$. $\square$

Proof of Property 2

From (2), using the first order optimality condition of $\Pi _r$, we get $p^M = \frac{\rho a + \beta p_0 + \gamma _1 \theta + \alpha _1 w}{2 \alpha _1}$. Now $\frac{\partial p^M}{\partial \theta } = \frac{\gamma _1}{2 \alpha _1} > 0$.

Putting this value of $p^M$ in Eq. (1), and using the first order optimality condition we get,

$w^M=\frac{c_m \alpha _0 \alpha _1 + a \beta - c_m \beta ^2 + \beta \gamma _0 \theta + \alpha _0 \gamma _1 \theta + a (\alpha _0 - \beta ) \rho }{2 \alpha _0 \alpha _1 - 2 \beta ^2}$ and $p_0^M=\frac{c_m \alpha _0 \alpha _1 - c_m \beta ^2 + \alpha _1 \gamma _0 \theta + \beta \gamma _1 \theta + a (\alpha _1 - \alpha _1 \rho + \beta \rho )}{2 \alpha _0 \alpha _1 - 2 \beta ^2}$. Then $\frac{\partial w^M}{\partial \theta } = \frac{ \alpha _0 \gamma _1 + \beta \gamma _0}{2(\alpha _0 \alpha _1 - \beta ^2)} > 0$. and $\frac{\partial p_0^M}{\partial \theta } = \frac{ \alpha _1 \gamma _0 + \beta \gamma _1 }{2(\alpha _0 \alpha _1 - \beta ^2)} > 0$.

Again from (2), $\frac{\partial \Pi _r^M}{\partial \theta } = \frac{\gamma _1 (\rho a + \beta p_0 + \gamma _1 \theta - \alpha _1 w )}{2 \alpha _1} > 0 \, \hbox {if} \, w < \frac{\rho a + \beta p_0 + \gamma _1 \theta }{\alpha _1}$. $\square$