1 Introduction

We here detail the four modelling frameworks used by “Team Yalla” to win the Conference Data Challenge organised for the 13\(^\text {th}\) International Conference on Extreme Value Analysis (EVA; 2023); full details are provided in the editorial (Rohrbeck et al. 2023). The challenge comprised four sub-challenges that each required prediction of exceedance probabilities or quantiles for data simulated from highly complex statistical models. Our frameworks combined classical EVA methods with modern modelling techniques, including additive models (Chavez-Demoulin and Davison 2005; Youngman 2019), deep learning-based inference (Sainsbury-Dale et al. 2024; Richards et al. 2023), non-stationary conditional extremal dependence models (Heffernan and Tawn 2004; Winter et al. 2016), and non-parametric probability estimators (Krupskii and Joe 2019). While the data considered in this work are simulated, the data were constructed to be representative of real observations of an environmental process (sampled from the fantasy country of “Utopia”), and so exhibit realistic characteristics, such as sparsity, non-stationarity, and missingness. Moreover, as the true values of the challenge predictands are known, our predictions can be easily validated. Hence, we expect our proposed frameworks to perform well, in practice, with real data. The code used for implementing our models is available at https://github.com/matheusguerrero/yalla.

The novelty of our work is threefold: i) we propose an amortised neural Bayes estimator for univariate quantiles; ii) we generalise the non-parametric multivariate exceedance probability estimator of Krupskii and Joe (2019); and iii) we illustrate the efficacy of the extreme value regression models proposed by Winter et al. (2016) and Youngman (2019) when applied to simulated data. The remainder of the paper is organised as follows: Section 2 describes the methodology we adopt to address the data challenge, with Sections 2.1–2.2 and 2.3–2.5 focusing on univariate and multivariate extremes, respectively. In Section 3, we apply our proposed methodology to the data. Section 4 provides a concise discussion and suggests avenues for further work.

2 Methodology

In this section, we present the methodological details of our approaches. Throughout, we adopt the notation Y and \(\textbf{Y}:=(Y_1,\dots ,Y_d)^{\prime }\) to denote a random response variable and random d-vector of response variables, respectively. Covariates are denoted by \(\textbf{X}:=(X_1,\dots ,X_l)^{\prime }\in \mathbb {R}^l\) for \(l\in \mathbb {N}\). Where appropriate, we use the subscript \(t\in \{1,\dots ,n\}\) to denote temporal replicates of the response (i.e., \(Y_t\) or \(\textbf{Y}_t:=(Y_{1,t},\dots ,Y_{d,t})^{\prime }\)) or covariates (i.e., \(\textbf{X}_t:=(X_{1,t},\dots ,X_{l,t})^{\prime }\)) and lowercase notation to denote observations. The values of l, d, and sample size n differ throughout the paper. Sub-challenges C1/C2 and C3/C4 (see Rohrbeck et al. 2023) concern univariate and multivariate modelling, respectively. In the univariate setting with \(d=1\) and \(n=21000\), the covariate vector \(\textbf{X}\) comprises \(l=8\) variables: wind direction, wind speed, atmosphere, season, and four unnamed variables (denoted \(V_1,\dots ,V_4)\). For C3 and C4, we have \(d=3\) and \(d=50\), respectively, and \(n=21000\) and \(n=10000\), respectively, with the response vector \(\textbf{Y}\) known to have standard Gumbel margins. The response vector for C3, \((Y_1,Y_2,Y_3)\), is accompanied by the atmosphere and season covariates mentioned above; hence, \(l=2\) for C3. No covariates accompany the 50 response variables that comprise the data for C4 (i.e., \(l=0\)).

Sections 2.1 and 2.2 detail methodology for estimating univariate extreme quantiles, while Sections 2.3–2.5 concern methodology for modelling extremal dependence. Section 2.1 describes peaks-over-threshold modelling using the generalised Pareto distribution and generalised additive models, which we used to address sub-challenge C1. Section 2.2 describes a likelihood-free neural Bayes estimator for point estimation of the extreme quantiles for sub-challenge C2. Section 2.3 describes a non-stationary model for conditional extremal dependence (sub-challenge C3), while Section 2.4 details a bivariate extremal dependence measure. Section 2.5 concludes with details of a non-parametric estimator for tail probabilities, used in sub-challenge C4.

2.1 Peaks-over-threshold models

Sub-challenge C1 required the prediction of a \(50\%\) confidence interval for the q-quantile of \(Y\mid (\textbf{X}=\textbf{x}^*_j)\) for 100 test covariate sets \(\{\textbf{x}^*_j:j=1,\dots ,100\},\) and for \(q=0.9999\) corresponding to an extreme conditional quantile. To this end, we adopt a peaks-over-threshold regression model. The upper tails of the distribution of a random variable can be modelled in this framework using the generalised Pareto distribution (GPD), see, for example, Davison and Smith (1990). For a random variable Y, we assume that there exists some high threshold u such that the distribution of exceedances \((Y-u)\mid ( Y > u)\) can be characterised by the GPD, denoted by GPD\((\sigma _u,\xi )\), \(\sigma _u>0,\xi \in \mathbb {R}\), with distribution function

$$\begin{aligned} H(y) := {\left\{ \begin{array}{ll} 1-(1+\xi y /\sigma _u)^{-1/\xi }, \quad & \xi \ne 0, \\ 1-\exp (-y/\sigma _u), \quad & \xi =0, \end{array}\right. } \end{aligned}$$

where \(y \ge 0\) for \(\xi \ge 0 \) and \(0 \le y \le -\sigma _u/\xi \) for \(\xi < 0\).

We model the conditional distribution \((Y-u(\textbf{x}))\mid {( Y > u(\textbf{x}),\textbf{X}=\textbf{x})}\) as \(\text{ GPD }(\sigma _u(\textbf{x}),\xi (\textbf{x}))\), where the exceedance threshold u and GPD scale and shape parameters, \(\sigma _u\) and \(\xi \), are functions of covariates. We follow Youngman (2019) and use a generalised additive model (GAM) representation, with \(\sigma _u(\textbf{x})\) and \(\xi (\textbf{x})\) modelled via a basis of splines. The threshold \(u(\textbf{x})\) is taken to be the intermediate \(\lambda \)-quantile of \(Y\mid (\textbf{X}=\textbf{x})\) for \(\lambda < 0.9999\) and this is modelled using additive quantile regression (Fasiolo et al. 2021).

2.2 Neural point estimation

Sub-challenge C2 required estimation of the q-quantile of Y for \({q=1-(6\times 10^4)^{-1}}\), that is, estimating \(\theta \) such that \(\Pr \{Y>\theta \}=1-q\). However, inference for \(\theta \) should seek to minimise the conservative asymmetric loss function

$$\begin{aligned} L(\theta ,\widehat{\theta }):= {\left\{ \begin{array}{ll} 0.9(0.99\theta -\widehat{\theta }),\quad & \text {if } 0.99\theta > \widehat{\theta },\\ 0,\quad & \text {if } \vert \theta -\widehat{\theta }\vert \le 0.01\theta ,\\ 0.1(\widehat{\theta }-1.01\theta ),\quad & \text {if } 1.01\theta < \widehat{\theta }, \end{array}\right. } \end{aligned}$$
(1)

where \(\widehat{\theta }\) denotes estimates of \(\theta \) and \(\vert \cdot \vert \) denotes the absolute value; this loss function is illustrated in Fig. 2. The loss function in Eq. 1 provides a larger penalty for under-estimates of \(\theta \), relative to over-estimates, in order to encourage conservative estimates of the quantile. We construct such an estimator using neural networks.

Neural point estimators, that is, neural networks that are trained to map input data to parameter point estimates, have shown recent success as a likelihood-free inference approach for statistical models. Although they have been typically used for inference with classical spatial processes (see, e.g., Zammit-Mangion and Wikle 2020; Gerber and Nychka 2021) and spatial extremal processes (see, e.g., Lenzi et al. 2023; Lenzi and Rue 2023; Sainsbury-Dale et al. 2023, 2024; Richards et al. 2023), they can be exploited in a univariate setting. For example, Rai et al. (2024) use a neural point estimator to make inference with the univariate generalised extreme value distribution (see Coles 2001). We construct a neural point estimator to perform single quantile estimation for a random variable Z. In particular, we follow Sainsbury-Dale et al. (2024) and construct a neural Bayes estimator (NBE).

Define a set of univariate probability distributions \(\mathcal {P}\) on a sample space, taken to be \(\mathbb {R}\), which are parameterised by a parameter \({\theta }\in \mathbb {R}\) such that \(\mathcal {P}:= \{P_{{\theta }}:{\theta }\in \Theta \}\), where \(\Theta \) is the parameter space; then \(\mathcal {P}\) defines a parametric statistical model (see McCullagh 2002). Denote \(\textbf{Z}:=({Z}_1,\dots ,{Z}_n)^{\prime }\) as n mutually independent realisations of the random variable Z from distribution \(P_{{\theta }} \in \mathcal {P}\). A point estimator \(\widehat{{\theta }}(\cdot )\) for model \(\mathcal {P}\) is any mapping from \(\mathbb {R}^n\) to \(\Theta \), and the output of such an estimator, for a given \({\theta }\) and \(\textbf{Z}\), can be assessed using a non-negative loss function \(L({\theta },\widehat{{\theta }}(\textbf{Z}))\). The risk of this point estimator, evaluated at \({\theta }\), \(R({\theta },\widehat{{\theta }}(\cdot )),\) is the loss \(L(\cdot ,\cdot )\) averaged over all possible realisations of \(\textbf{Z}\), that is,

$$\begin{aligned} R({\theta },\widehat{{\theta }}(\cdot )):= \int _{\mathbb {R}^n}L({\theta },\widehat{{\theta }}(\textbf{z}))f(\textbf{z}\mid {\theta })\, \text {d}\textbf{z}, \end{aligned}$$
(2)

where \(f(\textbf{z}\mid {\theta })\) is the density function of the data. We define the Bayes risk \(r_\pi (\cdot )\) as the weighted average of Eq. 2 over all \({\theta }\in \Theta \), with respect to some prior measure \(\pi (\cdot )\), as

$$\begin{aligned} r_\pi (\widehat{{\theta }}(\cdot )):=\int _\Theta R({\theta },\widehat{{\theta }}(\cdot ))\,\text {d}\pi ({\theta }). \end{aligned}$$
(3)

If the estimator \(\widehat{{\theta }}(\cdot )\) minimises Eq. (3), we term it a Bayes estimator with respect to the loss \(L(\cdot ,\cdot )\) and prior measure \(\pi (\cdot )\). Note that in the context of the prediction task, the parameter \({\theta }\) is taken to be the q-quantile of the distribution(s) \(P_\theta \) and the loss function is \(L(\theta ,\widehat{\theta })\) in Eq. 1 (illustrated in Fig. 2). Details on the construction of the prior measure \(\pi (\cdot )\) and the statistical model \(\mathcal {P}\) will follow.

A neural Bayes estimator (NBE) is a neural network designed to approximately minimise (3). Sainsbury-Dale et al. (2024) construct NBEs by leveraging the DeepSets neural network architecture (Zaheer et al. 2017). Consider functions \(\varvec{\psi }:\mathbb {R}\mapsto \mathbb {R}^Q\) and \({\phi }:\mathbb {R}^Q\mapsto \mathbb {R}\), and a permutation-invariant set function \(\textbf{a}:(\mathbb {R}^Q)^n\mapsto \mathbb {R}^Q\), where the j-th component of \(\textbf{a}\), \(a_j(\cdot ),\) returns the element-wise average over its input set for \(j=1,\dots ,Q\). We represent \({\phi }(\cdot )\) and \(\varvec{\psi }(\cdot )\) as neural networks, and collect in \(\varvec{\gamma }:= (\varvec{\gamma }_\phi ^{\prime },\varvec{\gamma }_{\varvec{\psi }}^{\prime })^{\prime }\) their estimable “weights” and “biases”. Our NBE is of the form

$$\begin{aligned} \widehat{{\theta }}(\textbf{Z}; \varvec{\gamma })={\phi }(\textbf{T}(\textbf{Z}; \varvec{\gamma }_{{\varvec{\psi }}}); \varvec{\gamma }_{{\phi }}),\text { with }\textbf{T}(\textbf{Z}; \varvec{\gamma }_{\varvec{\psi }}):=\textbf{a}(\{\varvec{\psi }(Z_t; \varvec{\gamma }_{\varvec{\psi }}):t=1,\dots ,n\}). \end{aligned}$$
(4)

We use a densely-connected neural network to model both \({\phi }(\cdot )\) and \(\varvec{\psi }(\cdot )\). The NBE is built by obtaining neural network weights \(\varvec{\gamma }^*\) that minimise the Bayes risk in the estimator space spanned by \(\widehat{{\theta }}(\cdot ,\varvec{\gamma })\). As we cannot directly evaluate (3), it is approximated using Monte Carlo methods. For a set of K parameter values \(\{\theta ^{(k)}:k=1,\dots ,K\}\) drawn from the prior \(\pi (\cdot )\), we simulate, for each k, a set of n mutually independent realisations \(\textbf{z}^{(k)}\) from \(P_{{\theta }}\). The Bayes risk in Eq. 3 is then approximated by

$$ \widehat{r}_\pi (\widehat{{\theta }}(\cdot ;\varvec{\gamma })):=\frac{1}{K}\sum _{k=1}^KL({\theta }^{(k)},\widehat{{\theta }}(\textbf{z}^{(k)};\varvec{\gamma }))\approx {r}_\pi (\widehat{{\theta }}(\cdot ;\varvec{\gamma })). $$

We obtain estimates \(\varvec{\gamma }^{*}:=\text {argmin}_{\varvec{\gamma }}\widehat{r}_\pi (\widehat{{\theta }}(\cdot ;\varvec{\gamma }))\) using the package NeuralEstimators (Sainsbury-Dale et al. 2024) in \(\texttt {Julia}\) (Bezanson et al. 2017).

Specifying a prior measure on the q-quantile, \(\theta \in \Theta \), for a random variable Z is nontrivial, as the mapping from the model \(\mathcal {P}\) to the parameter space \(\Theta \) is not guaranteed to be surjective; for a fixed level q, multiple probability distributions can have the same q-quantile \(\theta \), and so simulating Z conditional on \(\theta \) is not necessarily feasible. In this case, \(P_\theta \) would define a set of distributions with equal q-quantile, rather than a single probability distribution (as in Sainsbury-Dale et al. 2024). Thus, instead of placing a prior directly on \(\theta \), we assume that \(P_\theta \) is determined by some hyper-parameters (for simplicity, we omit the dependency of \(P_\theta \) on hyper-parameters from our notation). We then construct a general prior measure for these hyper-parameters, which consequently induces a prior measure on \(\theta \). As we are interested in \(\theta \) when q is close to one, our choice of the class of feasible models \(\mathcal {P}\) is motivated by extreme value theory, and we exploit the univariate peaks-over-threshold models described in Section 2.1.

Rohrbeck et al. (2023) note that our data \(\{Y_t:t=1,\dots ,n\},\) from which we wish to infer \(\theta \), are non-stationary over time. We reflect this property in our construction for the prior measure on the hyper-parameters of \(P_\theta \): for \(t=1,\dots ,n\), let \((Y_t-u_t)\mid (Y_t > u_t)\sim \text{ GPD }(\sigma _t,\xi _t)\) and let \(Y_t\mid {(Y_t \le u_t)}\sim F^\le _t(\cdot )\) for threshold \(u_t\in \mathbb {R}\), scale \(\sigma _t>0,\) and shape \(\xi _t \in \mathbb {R}\), and where \(\Pr \{Y_t \le u_t\} = \lambda \) for \(\lambda \in [0,1]\). For simplicity, we hereafter treat \(\lambda \) and the distribution of non-exceedances \(F^\le _t(\cdot )\) as fixed. After placing a suitable prior measure on the hyper-parameters \(\{(u_t,\sigma _t,\xi _t): t=1,\dots ,n\}\) and specifying \(\lambda \) and \(F^\le _t(\cdot )\) (see Section 3.1), we can simulate data \(\{y^*_t:t=1,\dots ,n^*\}\) from the model above and store this in a vector \(\textbf{z}^*\) with the index t removed from each entry. In this way, we consider \(\textbf{z}^*\) as \(n^*\) independent draws from the distribution of Z, unconditional on t, as we have marginalised out the effect of this covariate (see, e.g., Rohrbeck et al. 2018). Note that \(n^*\) need not satisfy \(n^*=n\), where n is the sample size.

The prior measure on the hyper-parameter set \(\{(u_t,\sigma _t,\xi _t): t=1,\dots ,n\}\) induces a prior on \(\theta \), which is the q-quantile of Z. As there is no closed-form expression for \(\theta \), we compute it using Monte Carlo methods. That is, we set \(n^*\) large and derive \(\theta \) empirically from realisations \(\textbf{z}^*\). A single entry to the training data for our NBE then consists of the pair \((\textbf{z},\theta )\), where \(\textbf{z}\) is a sub-sample from \(\textbf{z}^*\) of length n; this procedure is repeated for a total of K entries. Note that, we could instead construct a prior on \(\theta \) using a stationary GPD model, that is, with \(n=1\), but our approach produces a more diffuse prior on \(\theta \) by increasing the prior support for the hyper-parameters of \({P}_\theta \). It also exploits knowledge about the data-generating distribution, which produces more realistic models for Z.

When choosing larger values of \(\lambda \), fewer new observations are generated for training of the NBE; a bigger proportion of the training data will comprise resamples from the observations. Smaller \(\lambda \) will produce a more diffuse prior on the distributional models for Z (particularly with regards to the upper-tail behaviour of Z) and, hence, the q-quantile of Z. A larger variety in the training data is also likely to increase the reliability of our estimator when generalising to unseen data. However, when \(\lambda \) is too small, the threshold \(u_t\) may be too low to safely assume that \((Y_t-u_t)\mid (Y_t > u_t)\) follows a GPD. In this case, our estimator would not benefit from being trained on well-specified models for \(Y_t\). Hence, we advocate taking \(\lambda \) as low as possible while still obtaining reasonable fits for the non-stationary GPD model, even if this value is not optimal. In our application, we take \(\lambda =0.6\) but note that this is lower than the optimal \(\lambda \) (in terms of providing the best fit for the model described in Section 2.1).

2.3 Conditional extremes models

Sub-challenge C3 required estimation of

$$\begin{aligned} p_1&:= \Pr \{Y_1> 6, Y_2> 6, Y_3> 6\},\\\nonumber p_2&:= \Pr \{Y_1> 7, Y_2 > 7, Y_3 < -\log {(\log {2})} \}, \end{aligned}$$
(5)

where \( -\log {(\log {2})}\) is the median of the standard Gumbel distribution. To estimate these extreme exceedance probabilities, we construct a non-stationary extremal dependence model for random vectors. Proposed by Heffernan and Tawn (2004) and later generalised by Heffernan and Resnick (2007), the conditional extremes framework models the behaviour of a random vector, conditional on one of its components being extreme. We adopt this model as its inference is typically less computationally demanding than that of other models for multivariate extremal dependence (Huser and Wadsworth 2022). Additionally, it is capable of capturing both asymptotic dependence and asymptotic independence in a parsimonious manner. To accommodate non-stationarity in the extremal dependence structure of our data, we utilise the extension of the Heffernan and Tawn (2004) model proposed by Winter et al. (2016). This extension represents the dependence parameters as a linear function (subject to some non-linear link transformation) of the covariates.

Let the random vector \(\textbf{Y}^{(\mathcal {L})}_t:=(Y^{(\mathcal {L})}_{1,t},Y^{(\mathcal {L})}_{2,t},Y^{(\mathcal {L})}_{3,t})^{\prime }\) for \(t={1,\dots ,n}\) have standard Laplace margins (Keef et al. 2013). It is noteworthy that our original data \(\textbf{Y}_t\) are known to possess standard Gumbel marginal; therefore, we transform these to standard Laplace. Then, denote by \(\textbf{Y}^{(\mathcal {L})}_{-i,t}\) as the vector \(\textbf{Y}^{(\mathcal {L})}_t\) with its i-th component removed. Note that all vector operations hereafter are taken component-wise. We then follow Winter et al. (2016) and assume that there exist vectors of coefficients \(\varvec{\alpha }_{-i,t}:=\{\alpha _{j\mid i,t}: j\in (1,2,3) \setminus i\}\in [-1,1]^{2}\) and \(\varvec{\beta }_{-i,t}:=\{\beta _{j\mid i,t}: j\in (1,2,3)\setminus i\}\in [0,1)^{2}\) such that, for \(\textbf{z}\in \mathbb {R}^{2},\) \(y>0,\) and as \(u\rightarrow \infty \),

$$\begin{aligned} \Pr \left\{ \frac{\textbf{Y}^{(\mathcal {L})}_{-i,t}-\varvec{\alpha }_{-i,t}Y^{(\mathcal {L})}_{i,t}}{\{Y_{i,t}^{(\mathcal {L})}\}^{\varvec{\beta }_{-i,t}}}\le \textbf{z}, Y^{(\mathcal {L})}_{i,t}-u> y \;\;\bigg \vert \;\; Y^{(\mathcal {L})}_{i,t} > u\right\} \rightarrow G_{-i,t}(\textbf{z})\exp (-y), \end{aligned}$$
(6)

with \(G_{-i,t}(\cdot )\) a non-degenerate bivariate distribution function. The values of the dependence parameters \(\varvec{\alpha }_{-i,t}\) and \(\varvec{\beta }_{-i,t}\) determine the strength and class of extremal dependence exhibited between \(Y^{(\mathcal {L})}_{i,t}\) and the corresponding component of \(\textbf{Y}^{(\mathcal {L})}_{-i,t}\); for details, see Keef et al. (2013). We allow these parameters to vary with covariates \(\textbf{x}_t\) by letting

$$\begin{aligned} \tanh ^{-1}(\varvec{\alpha }_{-i,t})=\varvec{\alpha }^{(0)}_{-i}+\varvec{\alpha }^{(1)}_{-i}\textbf{x}_t,\quad \text {logit}(\varvec{\beta }_{-i,t})=\varvec{\beta }^{(0)}_{-i}+\varvec{\beta }^{(1)}_{-i}\textbf{x}_t, \end{aligned}$$
(7)

with coefficients \(\varvec{\alpha }^{(0)}_{-i}\),\(\;\varvec{\beta }^{(0)}_{-i}\in \mathbb {R}^2\) and \(\varvec{\alpha }^{(1)}_{-i}\),\(\;\varvec{\beta }^{(1)}_{-i}\in \mathbb {R}^{2\times l},\) where l is the number of covariates. Note that the \(\tanh (\cdot )\) and \(\text {logit}(\cdot )\) link functions are used to ensure that the parameter values are constrained to their correct ranges.

Modelling follows under the assumption that the limit in Eq. 6 holds in equality for all \(Y^{(\mathcal {L})}_{i,t} > u\) for some sufficiently high threshold \(u>0\). In this case, rearranging (6) provides the model

$$\begin{aligned} \textbf{Y}^{(\mathcal {L})}_{-i,t}=\varvec{\alpha }_{-i,t}Y^{(\mathcal {L})}_{i,t}+\{Y_{i,t}^{(\mathcal {L})}\}^{\varvec{\beta }_{-i,t}}\textbf{Z}_{-i,t}\; \big \vert \; (Y^{(\mathcal {L})}_{i,t} > u), \end{aligned}$$
(8)

where the residual random vector \(\textbf{Z}_{-i,t}:=\{Z_{j \mid i,t}: j\in (1,2,3)\setminus i\}\sim G_{-i,t}\) is independent of \(Y^{(\mathcal {L})}_{i,t}\). For inference, we make the working assumption that \(G_{-i,t}(\cdot )\) does not depend on time t and follows a bivariate standard Gaussian copula with correlation \(\rho _i\in (-1,1)\) and delta-Laplace margins (see, e.g., Shooter et al. 2021). We hereafter drop the subscript t from the notation. A random variable that follows the delta-Laplace distribution with location, scale, and shape parameters \(\mu \in \mathbb {R},\;\sigma >0,\) and \(\delta >0\), respectively, has density function \(f(z)=\delta (2k\sigma \Gamma (\delta ^{-1}))^{-1}\exp \{-(|z-\mu |/(k\sigma ))^{\delta }\}\) for \(k^2=\Gamma (\delta ^{-1})/\Gamma (3\delta ^{-1}),\) where \(\Gamma (\cdot )\) denotes the gamma function. Note that when \(\delta =1\) and \(\delta =2\), f(z) corresponds to the Laplace and Gaussian densities, respectively.

Inference proceeds via maximum likelihood estimation. The model is fitted separately for each conditioning variable with index \(i=1,2,3\). For each i, we have eight parameters in \(\varvec{\alpha }^{(0)}_{-i}\),\(\;\varvec{\alpha }^{(1)}_{-i}\),\(\;\varvec{\beta }^{(0)}_{-i}\),\(\;\varvec{\beta }^{(1)}_{-i},\) as well as the seven parameters that characterise \(G_{-i}\), that is, the correlation \(\rho _i\) and the three marginal parameters for each component of \(\textbf{Z}_{-i,t}\). After estimation of the parameters, we no longer require the working Gaussian copula assumption for \(\textbf{Z}_{-i,t}\). We instead use observations \({\textbf{y}}^{(\mathcal {L})}_{-i,t}\) and \({{y}}^{(\mathcal {L})}_{i,t}\) of \({\textbf{Y}}^{(\mathcal {L})}_{-i,t}\) and \({{Y}}^{(\mathcal {L})}_{i,t}\), respectively, to derive the empirical residual vector

$$ \widehat{\textbf{z}}_{-i,t}:=({\textbf{y}}^{(\mathcal {L})}_{-i,t}-\widehat{\varvec{\alpha }}_{-i,t}{y}^{(\mathcal {L})}_{i,t})/{\{{y}}^{(\mathcal {L})}_{i,t}\}^{\widehat{\varvec{\beta }}_{-i,t}}, $$

where \(\widehat{\varvec{\alpha }}_{-i,t}\) and \(\widehat{\varvec{\beta }}_{-i,t}\) denote estimates of \({\varvec{\alpha }_{-i,t}}\) and \({\varvec{\beta }_{-i,t}}\), respectively. Assuming independence across time, we use the empirical residuals to provide an empirical estimate \(\widehat{G}_{-i}(\cdot )\) of \(G_{-i}(\cdot )\).

We estimate the necessary exceedance probabilities, \(p_1\) and \(p_2\) in Eq. (5), via the following Monte-Carlo procedure. We first note that, for fixed \(t\in \{1,\dots ,n\}\), we require realisations of \(\textbf{Y}^{(\mathcal {L})}_t\), that is, unconditional on an exceedance. We follow, for example, Richards et al. (2022) and Richards et al. (2023) and obtain these realisations by drawing a realisation from

$$\begin{aligned} \textbf{Y}^{(\mathcal {L})}_{t} \;\bigg \vert \left( \max _{i=1,2,3}Y^{(\mathcal {L})}_{i,t} > u\right) , \end{aligned}$$
(9)

with probability

$$\begin{aligned} \Pr \left\{ \max _{i=1,2,3}Y^{(\mathcal {L})}_{i,t} > u\right\} , \end{aligned}$$
(10)

and, otherwise, drawing a realisation of \(\textbf{Y}^{(\mathcal {L})}_{t} \mid (\max _{i=1,2,3}Y^{(\mathcal {L})}_{i,t} < u)\). As realisations of the latter are unlikely to significantly impact estimates of \(p_1\) and \(p_2\), we draw them empirically (see Richards et al. 2022). In practice, we also replace the probability in Eq. 10 with an empirical estimate; as both \(\textbf{Y}^{(\mathcal {L})}_{t} \mid (\max _{i=1,2,3}Y^{(\mathcal {L})}_{i,t} < u)\) and the probability in Eq. 10 depend on t, we estimate them empirically by assuming stationarity over time. Further discussion of this modelling simplification is provided in Section 4.

To simulate from Eq. 9, we must first draw realisations of the conditional exceedance model, \(\textbf{Y}^{(\mathcal {L})}_{-i,t} \mid (Y^{(\mathcal {L})}_{i,t} > u)\) in Eq. 8, using Algorithm 1.

Algorithm 1
figure a

Simulating from Eq. 8.

Full size image

We then combine realisations from the three separate conditional exceedance models, that is, \(\textbf{Y}^{(\mathcal {L})}_{-i,t} \mid (Y^{(\mathcal {L})}_{i,t} > u)\) for each \(i=1,2,3\), into a single realisation of Eq. 9 using importance sampling (Wadsworth and Tawn 2022). While this can be achieved for a single fixed value of t, we note that \(p_1\) and \(p_2\) in Eq. 5 do not depend on the time t. Hence, we treat t as random during simulation and average over all times \(t\in \{1,\dots ,n\}\) to produce approximate realisations of \(\textbf{Y}^{(\mathcal {L})}\) with t marginalised out. The full simulation algorithm is detailed in Algorithm 2. Note that we back-transform from standard Laplace to standard Gumbel margins after simulation, as the original data has the latter.

Algorithm 2
figure b

Simulating from \(\{(Y^{(\mathcal {L})}_{1,t},Y^{(\mathcal {L})}_{2,t},Y^{(\mathcal {L})}_{3,t}):t\in \{1,\dots ,n\}\}\).

Full size image

2.4 Extremal dependence measure

A number of pairwise measures have been proposed to quantify the strength of extremal dependence between random variables \(Y_1\) and \(Y_2\), see, for example, Heffernan (2000). We adopt the extremal dependence measure (EDM) proposed by Resnick (2004) and Larsson and Resnick (2012), which has been extended to a multivariate setting by Cooley and Thibaud (2019). Let \((Y_1,Y_2)\in [0,\infty )^2\) be a regularly-varying random vector with index \(\alpha >0\); for full details on regular variation, see Resnick (2007). Then, there exists a sequence \(b_n\rightarrow \infty \) and limit measure \(\nu (\cdot )\) supported on the cone \(\mathbb {E}^2_+:=[0,\infty ]^2\setminus {\{\varvec{0}\}}\), such that, as \(n\rightarrow \infty \),

$$ n\Pr \{b_n^{-1}(Y_1,Y_2)\in \cdot \}\xrightarrow {v} \nu (\cdot ), $$

where \(\xrightarrow {v}\) denotes vague convergence. For some symmetric norm \(\Vert \cdot \Vert \) on \([0,\infty )^2\), define the transformation \((R,\varvec{\Omega }):=(\Vert (Y_1,Y_2)\Vert ,(Y_1,Y_2)/\Vert (Y_1,Y_2)\Vert )\). Then, for \(r>0\), we can express the limit measure \(\nu (\cdot )\) as

$${\nu (\{(y_1,y_2)\in \mathbb {E}^2_+: ||(y_1,y_2)||\ge r, (y_1,y_2)/||(y_1,y_2)||\in \mathcal {B} \})}=r^{-\alpha }H(\mathcal {B}),$$

where \(\mathcal {B} \subset \mathcal {S}_+ \) is a Borel subset of the positive part of the unit circle, \(\mathcal {S}_+:={\{\textbf{y} \in [0,\infty )^2\setminus \{\textbf{0}\}: \Vert \textbf{y}\Vert =1\},}\) and the angular measure \(H(\cdot )\) controls the stochastic behaviour of \(\varvec{\Omega }=(\Omega _1,\Omega _2)\in \mathcal {S}_+\). The extremal dependence measure between \(Y_1\) and \(Y_2\) is then

$$ \text {EDM}(Y_1,Y_2):=\int _{\mathcal {S}_+}\omega _1\omega _2\,\text {d}H(\varvec{\omega })=\lim _{r\rightarrow \infty }\mathbb {E}\left[ \Omega _1\Omega _2 \mid R > r\right] . $$

Note that \(\text{ EDM }(Y_1,Y_2)\in [0,1]\) quantifies the strength of extreme dependence between \(Y_1\) and \(Y_2\). If \(\text{ EDM }(Y_1,Y_2) = 0\), then H concentrates all mass along the axes and hence \(Y_1\) and \(Y_2\) are asymptotically independent (Resnick 2007). Conversely, \(\text{ EDM }(Y_1,Y_2)\) is maximal if and only if \((Y_1,Y_2)\) has full asymptotic dependence, or H places all mass on the diagonal. Larsson and Resnick (2012) propose the empirical estimator

$$\begin{aligned} \widehat{\text {EDM}}\left( Y_1, Y_2\right) :=\frac{1}{N_n} \sum _{t=1}^n \frac{y_{1 , t}}{r_t} \frac{y_{2, t}}{r_t} \mathbbm {1}{\left\{ r_t>u\right\} }, \end{aligned}$$
(11)

where \(\{\left( y_{1, t}, y_{2,t}\right) \}^n_{t=1}\) is an independent and identically distributed sample from \(\left( Y_1, Y_2\right) \), \(r_t=\left\| \varvec{y}_t\right\| \), and \(N_{n}=\sum _{t=1}^{n} \mathbbm {1}{\left\{ r_t>u\right\} }\) is the number of exceedances of \(\{r_t\}^n_{t=1}\) above some high threshold \(u>0\). In Section 3.2, we use EDM estimates to investigate the extremal dependence structure of a high-dimensional random vector and then decompose it into subvectors of strongly tail-dependent variables.

2.5 Non-parametric tail probability estimation

Sub-challenge C4 requires estimation of the two exceedance probabilities

$$\begin{aligned} p_3&:= \Pr \{Y_1>s_1, \dots , Y_{50}>s_1\},\nonumber \\ p_4&:= \Pr \{Y_1> s_1,\dots ,Y_{25}>s_1,Y_{26}> s_2,\dots ,Y_{50}>s_2\}, \end{aligned}$$
(12)

where \(s_j,j=1,2,\) is the \((1-\phi _j)\)-quantile of the standard Gumbel distribution with \(\phi _1=1/300\) and \(\phi _2=12\phi _1\). Hence, \(p_3\) corresponds to an exceedance probability with all components of \(\textbf{Y}\) being equally extreme, that is, concurrently exceeding the same marginal quantile, while, for \(p_4\), the first 25 components of \(\textbf{Y}\) exceed a higher quantile, that is, are more extreme, than the latter 25 components. Thus, we seek an estimator for exceedance probabilities of high-dimensional random vectors \(\textbf{Y}\in \mathbb {R}^d\). While scalable parametric models for high-dimensional multivariate extremes do exist, as exemplified by Engelke and Ivanovs (2021) and Lederer and Oesting (2023), they often impose restrictive assumptions about extremal dependence of \(\textbf{Y}\), particularly as the dimension d grows large. Examples include regular or hidden regular variation (Resnick 2002). As our goal is point estimation of exceedance probabilities, rather than a full characterisation of the joint upper tail of \(\textbf{Y}\), we choose instead to use a non-parametric estimator for exceedance probabilities that makes few assumptions on the joint upper tails. In particular, we adopt the non-parametric multivariate tail probability estimator proposed by Krupskii and Joe (2019).

Denote by \(F_i(\cdot )\) the distribution functionFootnote 1 of \(Y_i\) and let \(U_i=F_i(Y_i)\) for \(i=1,\dots ,d\). Then, for \(\phi \in (0,1)\), let

$$\begin{aligned} p(\phi ) := \Pr \{U_1> 1-\phi , \ldots , U_{d} > 1-\phi \}=\Pr \{U_{\text {max}} < \phi \}, \end{aligned}$$
(13)

where \(U_{\text {max}}:=\max (U_1,\dots ,U_d)\). Denote by \(C:[0,1]^d\mapsto \mathbb {R}\) the copula associated with \(\textbf{Y}\) and by \(\bar{C}\) the corresponding survival copula, such that \(p(\phi )=\bar{C}(1-\phi ,\dots ,1-\phi )\). Krupskii and Joe (2019) constructed estimators of \(p(\phi )\) for small \(\phi >0\) by making assumptions about the joint tail decay of C. In particular, they assumed that C (and \(\bar{C}\)) has continuous partial derivatives and, as \(\phi \downarrow 0\), that

$$\begin{aligned} p(\phi )&=\Pr \{U_{\text {max}}<\phi \}= \lambda _1 \phi +\lambda _2 \phi ^{1/\eta } \ell (\phi )+o\{\phi ^{1/\eta } \ell (\phi )\},\nonumber \\ \frac{\text {d} p(\phi )}{\text {d}\phi }&= \lambda _1+\lambda _2 \phi ^{1/\eta -1}\ell (\phi )/\eta +o\{\phi ^{1/\eta -1} \ell (\phi )\}, \end{aligned}$$
(14)

for \(\lambda _1,\lambda _2 \ge 0,\) and \(\eta <1\), and where \(\ell (\cdot )\) is a slowly-varying function at zero such that, for all \(s>0\), \(\ell (s\phi )/\ell (\phi )\rightarrow 0\) as \(\phi \downarrow 0\); these regularity assumptions hold for a number of popular parametric copulas (see Krupskii and Joe 2019). We note that, when \(d=2\), \(\eta \) corresponds to the coefficient of tail dependence proposed by Ledford and Tawn (1996); the extension to d-dimensions is described by Eastoe and Tawn (2012).

Under the model in Eq. 14, the parameters \(\lambda _1,\lambda _2,\) and \(\eta \) can be estimated by defining a small threshold \(\phi _*>\phi \) and considering \(U_{\text {max}} \mid U_{\text {max}} <\phi _*\). Then, as \(\phi \downarrow 0\),

$$\begin{aligned} \Pr \{U_{\text {max}}< \phi \mid U_{\text {max}} < \phi _*\}=p(\phi )/p(\phi _*)\sim k_1 \phi + k_2 \phi ^{1/\eta }, \end{aligned}$$
(15)

where \(k_1:=\lambda _1/(\lambda _1\phi _*+\lambda \phi _*^{1/\eta })\) and \(k_2:=(1-k_1\phi _*)/\phi _*^{1/\eta }\). By fixing \(\phi _*\) and assuming equality between the left and right-hand sides of Eq. 15, parameter estimates \(\widehat{k}_1\) and \(\widehat{\eta }_1\) can be computed using maximum likelihood methods. Then, our estimate of \(p(\phi )\) is

$$\begin{aligned} \widehat{p(\phi )}:=\{\widehat{k}_1\phi +(1-\widehat{k}_1\phi _*)\phi ^{1/\widehat{\eta }}\}\widehat{p(\phi _*)}, \end{aligned}$$
(16)

where \(\widehat{p(\phi _*)}\) is the empirical estimate of the probability \(p(\phi _*)=\Pr \{U_{\text {max}}<\phi _*\}\).

Estimator (16) can be directly used to estimate \(p_3\) in Eq. 12 by setting \(\phi =\phi _1=1/300\). However, it cannot be used to estimate \(p_4\), as the formulation of the joint survival probability in Eq. 13 does not account for different levels of marginal tail decay for each component of \(\textbf{Y}\). In fact, we require an adaptation of \(p(\phi )\) such that each component \(U_i,i=1,\dots ,d,\) exceeds a scaled value of the form \(1-c_i\phi \) for \(0<c_i<1/\phi \). Setting \(c_i=1\) for \(i=1,\dots ,25\) and \(c_i=12\), otherwise, yields \(p_4\) in Eq. 12. We construct such an estimator by considering, for \(\textbf{c}:=(c_1,\dots ,c_d)^{\prime }\), the probability

$$\begin{aligned} p(\phi , \textbf{c}) := \Pr \{U_1> 1-c_1\phi , \ldots , U_{d} > 1-c_d\phi \}=\Pr \{U_{\text {max}}(\textbf{c}) < \phi \}, \end{aligned}$$
(17)

for weighted maxima \(U_{\text {max}}(\textbf{c}):=\max \{(1-U_1)/c_1,\dots ,(1-U_d)/c_d\}\); note that when \(\textbf{c}=(1,\dots ,1)'\), we have equivalence between (13) and (17). An estimator of the form in Eq. 17 was alluded to by Krupskii and Joe (2019); however, they did not provide theoretical results for its asymptotic behaviour. We choose to estimate \(p(\phi , \textbf{c})\) by assuming that, as \(\phi \downarrow 0\), \(\Pr \{U_{\text {max}}(\textbf{c}) < \phi \}\) has the same parametric form as \(p(\phi )\) in Eq. 14. Inference for \(p(\phi , \textbf{c})\) then follows in a similar manner as for \(p(\phi )\), only with samples of \(U_{\text {max}}(\textbf{c}) \mid (U_{\text {max}}(\textbf{c}) > \phi _*)\) (rather than \(U_{\text {max}} \mid (U_{\text {max}} > \phi _*)\)) used for inference.

3 Results

3.1 Univariate quantile estimation

We now describe estimation of the univariate conditional quantiles required for sub-challenge C1 (Rohrbeck et al. 2023). To estimate the conditional q-quantile of \(Y \mid (\textbf{X}=\textbf{x})\) for \(q=0.9999\), we fit the GPD-GAM model described in Section 2.1. The structure of \(u(\textbf{x})\), \(\sigma _u(\textbf{x})\), and \(\xi (\textbf{x})\) are optimised, for a fixed value of \(\lambda \), by minimising the model’s BIC for different additive combinations of linear and smooth functions of the covariates. All smooth terms are centered at zero and represented as univariate thin-plate splines, with their degrees of freedom optimised automatically using the default penalisation options available in the R package evgam (Youngman 2022). Missing covariate values are imputed to the marginal mean of the observed values and missingness is treated as a factor variable. That is, smooth terms in a model output one of two values, depending on whether or not the input covariate is missing.

We optimise \(\lambda \) by using the threshold selection scheme proposed by Varty et al. (2021) and extended by Murphy et al. (2024). We first follow Heffernan and Tawn (2001) and use the quantile and GPD-GAM model estimates to transform all data onto standard exponential margins. Then, we define a grid of n equally spaced probabilities, \(\{0<\lambda _1<...<\lambda _{n}<1\)}, with \(\lambda _n:=1-(\lambda _2-\lambda _1)\). Let \(F_E(\cdot )\) be the standard exponential distribution function and \(\lambda _* \in (0,1)\) be a pre-specified cut-off threshold. We define a vector of weights \(\textbf{w}:=(w_1,\dots ,w_n)^{\prime }\) with components \(w_i:=F_{E}^{-1}(\lambda _i)/\sum ^n_{j=1}F_{E}^{-1}(\lambda _j)\) for \(\lambda _i>\lambda _*\) and zero, otherwise, for all \(i=1,\dots ,n\). We then define the tail-weighted standardised mean absolute deviance (twsMAD) by \((1/n)\sum ^n_{i=1}w_i|\tilde{\theta }(\lambda _i)-F_E^{-1}(\lambda _i)|,\) where \(\tilde{\theta }(\lambda _i),i=1,\dots ,n,\) denotes the empirical \(\lambda _i\)-quantile of the standardised data. We set \(\lambda _*=0.99\) and evaluate the twsMAD for a range of candidate \(\lambda \) values satisfying \(\lambda <\lambda _*\). We then choose the optimal value which minimises this metric.

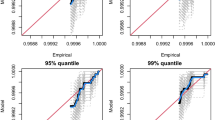
Using the BIC and twsMAD, our optimal model uses \(\lambda =0.972\) and, for the covariates, we include: season and wind speed as linear terms in \(u(\textbf{x})\), \(\sigma _u(\textbf{x}),\) and \(\xi (\textbf{x})\); \(V_2\), \(V_3\), \(V_4\), and wind direction as smooth terms in \(u(\textbf{x})\) and \(\sigma _u(\textbf{x})\); for a comparison with the significant covariate effects included in the true data-generating distribution, see Section 4. The median and the \(50\%\) confidence intervals for the test conditional q-quantiles (see Section 2.1) are estimated using the empirical quantiles over 2500 non-parametric bootstrap samples, and presented in Fig. 1. The true values of the quantiles were provided by Rohrbeck et al. (2023). We observe good predictions of the conditional quantiles, with our estimates close to the true values. Our framework attains a \(38\%\) coverage rate, which is a slight underestimation of the nominal \(50\%\).

Fig. 1
figure 1

Predicted conditional quantiles against true values for the 100 test covariate sets for sub-challenge C1. Vertical error bars denote the \(50\%\) confidence interval, with the black points denoting the median over bootstrap samples

Full size image

To estimate the required extreme q-quantile \(\theta \) of Y, we use the NBE framework detailed in Section 2.2 with \(n=21000\) independent replicates. Neural networks are trained using the Adaptive Moment Estimation (Adam) algorithm (Kingma and Ba 2014) with a mini-batch size of 32 and, in order to improve numerical stability, input data are standardised prior to training by subtracting and dividing by the mean and standard deviation (evaluated over the entire training data set), respectively. We use \(K=350,000\) and K/5 parameter values for training and validation, respectively, with \(n^*=4\times 10^7\) replicates used to estimate the theoretical q-quantiles for the training data (\(\theta \); see Section 2.2). When producing training data, we use an empirical prior distribution for the hyper-parameter set \(\{(u_t,\sigma _t,\xi _t): t=1,\dots ,n\}\). To construct this prior, we estimate the GPD-GAM model as described above but with \(\lambda =0.6\) (see Section 2.2 for details), across 750 bootstrap samples. Draws from the empirical prior on \(\{(u_t,\sigma _t,\xi _t):t=1,\dots ,n\}\) then correspond to a sample from all bootstrap parameter estimates. To increase the variety of candidate distributions (and hence, quantiles) used to train the estimator, we permute the values of \(u_t\), \(\sigma _t,\) and \(\xi _t\) across \(\{(u_t,\sigma _t,\xi _t): t=1,\dots ,n\}\) when constructing the training and validation data. As small values of \(Y_t < u_t\) are unlikely to impact the high q-quantile we seek to infer, we take the distribution of non-exceedances \(F^\le _t(\cdot )\) to be the empirical distribution of observations \(\{{y}_t:{y}_t \le u_t, t=1,\dots ,n\}\), that is, all observations that subceed the time-varying threshold \(u_t\). We note that this distribution does not vary over t, but does vary with the prior draw from \(\{u_t: t=1,\dots ,n\}\).

The estimator is trained using early stopping (see, e.g., Prechelt 2002); the validation loss is recorded at each epoch during training, which halts if the validation loss has not decreased for 10 epochs. We choose the optimal architecture for the neural networks, \(\phi \) and \(\varvec{\psi }\) in Eq. 4, by minimising the risk for a test set of 1000 parameter values (not used in training); the architecture is provided in Table 1.

Table 1 Optimal DNN architecture used in Section 3.1
Full size table

NBEs are trained on GPUs that are randomly selected from KAUST’s Ibex cluster, see https://www.hpc.kaust.edu.sa/ibex/gpu_nodes for details (last accessed 13/07/2023).

To illustrate the efficacy of our estimator, Fig. 2 presents extreme quantile estimates for 1000 test data sets. We observe that estimates are generally aligned to the left of the diagonal, that is, the majority of estimates are overestimates. This is a consequence of the asymmetric loss function (also presented in Fig. 2), which favours conservative estimation of quantiles. We estimate the q-quantile for \(q=1-(6\times 10^4)^{-1}\) to be 201.25. A 95% confidence interval of (200.79, 201.73) was derived using a non-parametric bootstrap; due to the amortised nature of our neural estimator, non-parametric bootstrap-based uncertainty estimation is extremely fast, as the estimator does not need to be retrained for every new sample.

Fig. 2
figure 2

Left: Extreme quantile estimates for 1000 test data sets. Dark blue points denote those for which \(L(\theta ,\widehat{\theta })=0\). Right: Loss function, \(L(\theta _0,\widehat{\theta })\) in Eq. 1, for \(\theta _0:=200\)

Full size image

3.2 Extremal dependence modelling

For sub-challenge C3, we estimate \(p_1\) and \(p_2\) in Eq. 5 using the non-stationary conditional extremes model described in Section 2.3. We perform model selection to identify the best covariates to include in the linear model for the dependence parameters, \(\varvec{\alpha }_{-i,t}\) and \(\varvec{\beta }_{-i,t}\) in Eq. 7, by minimising the AIC over the three separate model fits, that is, \(\textbf{Y}^{(\mathcal {L})}_{-i,t} \mid (Y^{(\mathcal {L})}_{i,t} > u), i=1,2,3\), with u set to the \(90\%\) standard Laplace quantile. The best fitting model did not include any transformation (e.g., \(\log \) or square) of the covariates and uses a homogeneous \(\varvec{\beta }_{-i,t}\) function, that is, with \(\varvec{\beta }_{-i,t}=\varvec{\beta }_{-i}\) for all \(t=1,\dots ,n,\) and for \(i=1,2,3\).

We use a visual diagnostic to optimise the exceedance threshold u. We fit the three conditional models for a grid of u values, use Algorithm 2 (with \(N'=5N\)) to simulate \(N=10^7\) realisations from the fitted model for \(\textbf{Y}=(Y_1,Y_2,Y_3),\) that is, on standard Gumbel margins and with time t marginalised out, and then compute realisations of \(R:=Y_{1}+Y_{2}+Y_{3}\). The upper tails of the aggregate random variable R are heavily influenced by the extremal dependence structure of the random vector \((Y_{1},Y_{2},Y_{3})\) (see, e.g., Richards and Tawn 2022). Hence, we can exploit the empirical distribution of the aggregate as a diagnostic measure for the quality of the dependence model fit. We choose the optimal u as that which provides the best estimates for extreme quantiles of R; this is achieved through visual inspection of a Q-Q plot (see, also, Richards et al. 2022, 2023). For brevity, we test only two values of u: the \(90\%\) and \(95\%\) standard Laplace quantiles. We found the optimal u to be the latter, and we illustrate the corresponding Q-Q plot in Fig. 3. Table 2 provides the corresponding parameters estimates \({\widehat{\varvec{\alpha }}^{(0)}_{-i}}, {\widehat{\varvec{\alpha }}^{(1)}_{-i}},\) and \(\widehat{\varvec{\beta }}_{-i}\), for \(i=1,2,3\).

Fig. 3
figure 3

Top-left panel: Q-Q plot for the simulated and empirical sum \(R=Y_{1}+Y_{2}+Y_{3}\). Other panels provide scatter plots of (black) observations and (blue) realisations from the fitted conditional extremal dependence models. Red vertical and horizontal lines correspond to the exceedance threshold u, i.e., the \(95\%\) marginal quantile

Full size image

Example realisations from the fitted model are illustrated in Fig. 3. Good model fit is illustrated, as the realisations mimic the extremal characteristics of the observed data. Probabilities \(p_1\) and \(p_2\) are estimated empirically from the aforementioned \({N=10^7}\)realisations of \((Y_1,Y_2,Y_3)\), and found to be \(\widehat{p}_1=3.13\times 10^{-5}\) and \(\widehat{p}_2=2.29\times 10^{-5}\), respectively.

For sub-challenge C4, we estimate \(p_3\) and \(p_4\) in Eq. 12 using the non-parametric tail probability estimators defined in Eqs. 16 and 17, respectively. However, we first seek to decompose the high-dimensional random vector \(\textbf{Y}\) into strongly tail-dependent sub-vectors. Our reasoning is threefold: i) the estimator in Eq. 17 requires strong assumptions about the joint upper tail decay of the random vector \(\textbf{Y}\) which are unlikely to hold for high dimension d; ii) reliable estimation of the intermediate exceedance probability, \(\widehat{p(\phi _*)}\) in Eq. 16, becomes difficult as d grows large; iii) (Krupskii and Joe 2019) observed through simulations that the estimator in Eq. 16 provides more accurate estimates when the true value of \(\eta \) is close to one, that is, when \(\textbf{Y}\) exhibits strong upper tail dependence.

Table 2 Sub-challenge C3: Parameter estimates \({\widehat{\varvec{\alpha }}^{(0)}_{-i}}, {\widehat{\varvec{\alpha }}^{(1)}_{-i}},\) and \(\widehat{\varvec{\beta }}_{-i}\), for the conditional extremal dependence model, \(\textbf{Y}^{(\mathcal {L})}_{-i,t} \mid Y^{(\mathcal {L})}_{i,t}>u\), \(i=1,2,3\)
Full size table

We identify sub-vectors by estimating the EDM between all pairs of components of \(\textbf{Y}\), with \(\alpha =2\), \(\Vert \cdot \Vert \) set to the \(L_2\) norm, and with u in Eq. 11 taken to be the empirical 0.99-quantile. Estimates are presented in a heatmap in Fig. 4, with values grouped using hierarchical clustering. An appropriate grouping can be found by visual inspection of Fig. 4; the clustered heatmap produces a block-diagonal matrix with five blocks (with size ranging from 8–13 components), and with elements of the off-diagonal blocks close to zero. For less well-behaved data, the number of clusters (and sub-vectors of \(\textbf{Y}\)) can instead be determined by placing a cut-off at an appropriate point on the clustering dendrogram.

Fig. 4
figure 4

Left: Heatmap of pairwise EDM estimates grouped using hierarchical clustering, alongside the corresponding dendrogram. Right: Threshold stability plots of estimated log-exceedance probabilities, \(\log (\widehat{p_3})\) and \(\log (\widehat{p_4}),\) against the intermediate quantile \(\phi _*\) used in their estimation. Red horizontal lines denote the optimal choice of \(\phi _*\)

Full size image

We decompose \(\textbf{Y}\) into the five sub-vectors suggested by Fig. 4, which we denote by \(\mathcal {Y}_i\) for \(i=1,\dots ,5\). Estimation of \(p_3\) then follows under the approximation

$$\begin{aligned} p_3 =\Pr \{Y_1>s_1, \dots , Y_{50}>s_1\}\approx \prod _{i=1}^5\Pr \left\{ \bigcap \limits _{Y\in \mathcal {Y}_i} Y > s_1 \right\} , \end{aligned}$$

and similarly for \(p_4\) (with the exceedance value \(s_1\) or \(s_2\) chosen appropriately). That is, we assume complete independence between the sub-vectors \(\mathcal {Y}_i,i=1,\dots ,5,\) of \(\textbf{Y}\) to approximate \(p_3\) and \(p_4\). Exceedance probabilities for each sub-vector are estimated using the methodology described in Section 2.5. We fix the intermediate quantile level \(\phi _*\) in Eq. 16 across all sub-vectors and for estimation of both \(p_3\) and \(p_4\). An optimal value \(\widehat{\phi }_*\) is chosen via a threshold stability plot (see, e.g., Coles 2001). In Fig. 4, we present estimates of \(\log (p_3)\) and \(\log (p_4)\) for a sequence of \(\phi _*\) values in [0.1, 0.4]. We choose \(\widehat{\phi }_*\) as the smallest \(\phi _*\) such that there is visual stability in Fig. 4 for estimates of both \(\log (p_3)\) and \(\log (p_4)\) when \(\phi _* >\widehat{\phi }_*\). In this case, we adopt \(\widehat{\phi }_*=0.25\) as the optimal value. We use a non-parametric bootstrap with 200 samples to assess uncertainty in estimates of \(p_3\) and \(p_4\). The resulting medianFootnote 2 bootstrap estimates of \(\log (p_3)\) and \(\log (p_4\)) (and their estimated 95% confidence intervals) are \(-59.38\) \((-68.46, -49.82)\) and \(-55.24\) \((-60.12,-49.79)\), respectively.

4 Discussion

We proposed four frameworks for the estimation of exceedance probabilities and levels associated with extreme events. To estimate extreme conditional quantiles, we adopted an additive model that represents parameters in a peaks-over-threshold model as splines. To estimate univariate quantiles in an unconditional setting, we constructed a neural Bayes estimator that estimates a quantile subject to a conservative asymmetric loss function. Our new approach to quantile estimation is amortised, likelihood-free, and requires few parametric assumptions about the underlying distribution. For multivariate data, we considered two frameworks: i) in the presence of covariates, we adopted a non-stationary conditional extremal dependence model to capture linear trends in extremal dependence parameters and ii) in the absence of covariates, we proposed a non-parametric estimator of multivariate tail probabilities that can be applied to high-dimensional (\(d=50)\) data via a sparse decomposition using pairwise extremal dependence measures. We validated these modelling approaches by using them to win the EVA (2023) Conference Data Challenge (Rohrbeck et al. 2023).

For sub-challenge C1, we illustrated the efficacy of additive GPD regression models for estimating extreme conditional quantiles. The sub-challenge data were generated using a GPD regression model with the upper tails of the conditional response variable, \(Y \mid (\textbf{X}=\textbf{x})\), dependent on three covariates: \(V_2\), \(V_3\), and wind speed; the bulk of \(Y \mid (\textbf{X}=\textbf{x})\) was dependent on season and wind direction as well (see Rohrbeck et al. 2023). We further note that the true GPD model used to generate these data had a fixed shape parameter, \(\xi \), independent of all covariates. In our analysis, we used a model selection scheme to choose the covariates and the functional forms for the GPD parameters (see Section 3.1). While our model selection scheme correctly identified all five of the aforementioned significant covariate effects, it misidentified \(V_4\) as having a significant effect and favoured a model with \(\xi \) represented as a function of season and wind speed. These slight differences between our fitted model and the true data-generating model suggest that our quantile estimates for sub-challenge C1 could be improved with a more rigorous testing procedure. Finally, we note that our approach to C1 benefited from a model with smoothly varying regression parameters, as the data were generated using a model with a similarly smooth representation. In cases where parameters are not a smooth function of covariates, machine learning-based extreme quantile regression models using, for example, random forests (Gnecco et al. 2024), gradient boosting (Velthoen et al. 2023), or neural networks (Pasche and Engelke 2022; Richards and Huser 2022; Richards et al. 2023; Cisneros et al. 2024), may offer a more flexible alternative to additive spline-based regression models.

We designed a neural Bayes estimator (NBE) to perform simulation-based inference for extreme quantiles. To train this estimator, we constructed an empirical prior measure \(\pi (\cdot )\) for the extreme quantile, by simulating from a family of pre-defined peaks-over-threshold models. The resulting NBE was optimal with respect to the prior measure \(\pi (\cdot )\). While our estimator performed well in the application, the underlying truth was a peaks-over-threshold model (Rohrbeck et al. 2023), and, hence, the true distribution was contained within the class of distributions spanned by \(\pi (\cdot )\). We note that our estimator may not perform as well when the converse holds, and the true distribution of Y is not approximated well by any family used to construct \(\pi (\cdot )\). Further study of the optimality properties of our proposed NBE is required and, in particular, its efficacy under model misspecification.

We proposed an extension of the conditional extremal dependence regression model of Winter et al. (2016) and highlighted its efficacy for estimation of extreme exceedance probabilities. Our conditional model performed well in practice, but alternative non-stationary extremal dependence regression models which rely on more classical assumptions about extremes of \(\textbf{Y}\), for example, regular or hidden regular variation, could have been tested (see, e.g., Cooley et al. 2012; de Carvalho et al. 2022; Murphy-Barltrop and Wadsworth 2022). In our application, we tested only two values for the threshold u in Eq. 6, and quantified goodness-of-fit through visual inspection of Q-Q plots for the aggregate variable R (see Fig. 3). A more rigorous testing procedure could be employed, whereby a grid of u values are tested and the optimal u is taken to minimise some numerical measure of fit; see, for example, Murphy et al. (2024), who proposed an automated threshold selection procedure for peaks-over-threshold models. Finally, we assumed that only the distribution of exceedances was non-stationary with respect to covariates (see Eq. 9); for simplicity, we assumed stationarity of the distribution of non-exceedances (i.e., the bulk and lower tail of the distribution; see Eq. 10). When compared to the true data-generating distribution, this assumption is seen to be false (see Rohrbeck et al. 2023). However, even under this false assumption, our model still provided good estimates of the probabilities required for sub-challenge C3. Further extensions of our framework, that employ parametric regression models for the bulk of the distribution (e.g., a logistic regression model for the probability in Eq. 10), may lead to improvements in our results.

Finally, we proposed an extension of the non-parametric tail probability estimator of Krupskii and Joe (2019) to account for different levels of marginal decay for components of a random vector. While we were able to showcase the efficacy of our estimator by using it to win sub-challenge C4 of the EVA (2023) Conference Data Challenge, we have not provided any theoretical guarantees for the estimator; we leave this as a future endeavour.