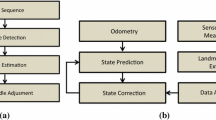
Abstract
The design and usability of a fully autonomous robotic control system (SunbYte - Sheffield University Balloon “lYfted” TElescope) for solar tracking and observational applications onboard high-altitude balloons are addressed here. The design is based on a six-step development plan balancing scientific objectives and practical engineering requirements. The high-altitude solar observational system includes low-cost components such as a Cassegrain-type telescope, stepper motors, harmonic drives, USB cameras and microprocessors. OpenCV installed from ROS (Robotic Operating System), python and C facilitated the collection, compression, and processing of housekeeping and scientific data. This processed data was then transmitted to the ground station through the launch vehicle’s telecommunication link. The SunbYte system allows the brightest spot in the sky, the sun, to be identified, and a telescope pointed towards it with high enough accuracy that a scientific camera can capture images. This paper gathers and presents the results from primarily two missions with the High-Altitude Student Platform (HASP, NASA Balloon Program office and LaSpace). Additionally, a discussion will be made comparing these with an earlier iteration flown with the German-Swedish “REXUS/BEXUS” programme coordinated by the European Space Agency. By capturing and analysing a series of tracking images with the location of the Sun at the calibrated centre, the system demonstrated the tracking capabilities on an unstable balloon during ascent. Housekeeping sensor data was collected to further analyse the thermal and mechanical performance. The low temperature increased friction in the drive train and reduced the responsiveness of the harmonic drive actuation system. This caused some issues which require further work in future missions, for example, with SunbYte 4 and its work when flying with the HEMERA ZPB (Zero Pressure Balloon) program.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Studies indicate that geomagnetic storms during the modern era can have devastating economic and social impacts on society [1, 2]. This was first observed in 1859 when amateur astronomers Hodgson and Carrington recorded one of the largest geomagnetic storms ever known to date [3,4,5]. Widespread blackouts and failures in telegraph systems happened across Europe and North America. Since then, thousands of solar flares have been observed and recorded by a variety of different techniques across the spectrum of wavelengths. It is a matter of luck that a storm of the same magnitude has not hit Earth since then. In 2022, 40 out of 49 SpaceX Starlink satellites failed due to the aftereffects of a geomagnetic storm [6]. As satellites are vital for navigation, telecommunications and Earth Observation, the loss of critical space infrastructure directly places many typical human activities at risk. This is why in 2019 at the UN General Assembly, the UK government quadrupled its investment into Space Weather Operations at the Met Office [7].
Geomagnetic storms originating from the Sun have two constituents, solar flares and Corona Mass Ejections (CMEs). Solar flares are X-ray and other high energy emissions which travel at the speed of light. These take approximately 8 minutes to reach Earth. Since they travel at the speed of light, the first visible sign that they have occurred is when the light arrives at Earth. Solar observatories near the Sun which observe these cannot notify Earth fast enough since the notification signals also travels at the speed of light. On the other hand, CMEs are particles with mass which travel over a period of several days before reaching Earth. These are likely to cause more damage but due to their slower speed, there is also more advance notice. CMEs are normally preceded by a strong flare however, the fundamental cause of flares are not clear. Which flares will result in CMEs and which will not?
In 2001, Shibata and Magara postulated that the key physical process for producing a solar flare was due to a series of events [8]: Firstly, a magnetic field emerges from the solar interior to the solar atmosphere (flux emergence). This causes a local enhancement of electric current in the Sun’s corona (current sheet” formation). Secondly, the sudden enhancement leads to rapid dissipation of the enhanced electric current through magnetic re-connection that causes the effects associated with solar flare, shock heating and CMEs. Although solar flare theoretical modelling was developed under real observations, the details of the flaring process and CMEs are still not yet fully understood.
Traditionally, ground-based telescopes are situated at high altitudes where atmospheric effects such as absorption and wavefront aberrations are minimised. A prime example is the Gemini Observatory, consisting of twin telescopes located in Hawaii and Chile - areas known for their minimal light pollution [9]. According to [10], the total construction cost for both telescopes was $184 million [10].
Both pointing accuracy and the ability to capture enough light information are important solar telescope parameters as they are essential for obtaining high-resolution temporal and spatial observational data. The McMath-Pierce telescope, for instance, was among the largest solar telescopes at the time of its completion in 1962. Its theoretical angular resolution is reported to be 0.07 arcsec at a wavelength of 500 nm [11, 12].
Over time, telescopes have become larger and required higher pointing precision. The Daniel K. Inouye Solar Telescope (DKIST) began construction in 2013 and was completed 8 years later, in 2021. This telescope featured a 4-meter mirror but boasts a theoretical angular resolution of 0.03 arcseconds [13]. Table 1 contains an explanation of all the acronyms used in the paper.
Building large ground observatories is an expensive endeavour. The European Solar Telescope (EST), a European project aimed at constructing a next-generation 4-meter class solar telescope, will be located in the Canary Islands [14]. The design and construction of the EST are estimated to cost €150 million (approximately $171 million), with projected annual operational costs of about €6.5 million (around $7.4 million) [15].
Numerous ground-based solar telescopes are in operation around the world. For instance, the Dunn Solar Telescope, with its 0.76-meter aperture, is located in New Mexico, USA [16]. In China, the Fuxian Solar Observatory houses the 1-meter New Vacuum Solar Telescope [17]. The Teide Observatory in Tenerife is home to the 1.5-meter GREGOR telescope [18], while the 1.6-meter New Solar Telescope can be found at the Big Bear Solar Observatory in California, USA [19, 20].
However, even telescopes located at higher altitudes still face atmospheric absorption and wavefront aberrations. These factors limit observations to wavelengths above 315 nm, as the Earth’s atmosphere absorbs everything below this threshold. In an innovative move during the 1950s and 60s, the first solar telescopes were hoisted into the stratosphere using weather balloons to mitigate these issues [21]. Building on this, subsequent decades saw the launch of the first free-flying space telescopes into orbit, enabling the detection of wavelengths across the entire electromagnetic spectrum.
The Hinode space solar telescope, launched in 2006, was equipped with a 50 cm Gregorian Solar Optical Telescope. It was specifically designed to study the interactions between the Sun’s magnetic field and its corona [22]. One of its remarkable features is the image stabilisation system, which enabled a performance better than 0.01 arcsec rms, with an angular resolution of up to 0.25 arcsec.
Following this, the Parker Solar Probe was launched in 2018 with the objective of observing the Sun’s outer corona [23]. It carries the Wide-Field Imager for Solar Probe (WISPR), which includes two telescopes. These telescopes have an optical resolution of 4.2 arcmin and 5.3 arcmin, respectively [24].
The most recent milestone in solar observation came with the launch of the Solar Orbiter in February 2020. Its mission is to study the inner heliosphere and the solar wind [25]. Aboard the Solar Orbiter, the Extreme Ultraviolet Imager (EUI) is equipped with two telescopes that capture high-resolution extreme-ultraviolet images of the corona [26].
While space telescopes benefit from the absence of atmospheric distortion, this advantage must be carefully weighed against the considerable commissioning challenges they face. These include the harsh conditions of space and the complexity of design and verification processes which often result in very high costs [27]. Comparing the costs and capabilities of space and ground instruments directly might be more complex than a simple trade-off. Specifically, for certain high-performance requirements, ground-based instruments might become prohibitively expensive or even technically unfeasible due to gravitational effects warping ground-based optics. This makes space telescopes the only viable option despite their cost disadvantages. Though one advantage of ground-based telescopes are that they can be more easily maintained and upgraded, unlike telescopes up in space travelling at over 10,000 mph.
Balloon-borne telescopes combine some advantages of space and ground telescopes. These types of systems ascend to floating altitudes between 30 to 35 km, positioning them above the ozone layer. This elevated position enables them to observe a wider array of wavelengths, free from the atmospheric constraints faced by telescopes on the Earth’s surface [28, 29]. They can also be upgraded between flights and overall costs are generally much lower, making these much more accessible to a wide range of institutions and scientists.
Several projects have been using balloon platforms in the stratosphere to observe and study the Sun. The technology was pioneered by Statoscope I which was first flown in 1957 [30], the same year as when Sputnik was launched into orbit. The 12-inch balloon-borne telescope flew six times in 1957-59 with the aim of studying the turbulence and granulation in the Sun’s photosphere. The pointing accuracy of 10 arc mins was achieved.
A different instrument, flown in 1975, Spektro-Stratoskop, was a solar spectrometer with an aperture of 30 cm [31, 32]. The system weighed under one ton and was guided with an accuracy of 0.1 arcsec during an exposure time of up to 30 seconds.
The Soviet Stratospheric Observatory (SSO) was launched four times during 1966-1973, and was equipped with a 50 cm primary mirror as well as with a 1m mirror during its last flight, with the highest resolution achieved as 0.24 arc seconds [33].
More recently, the Flare Genesis Experiment flew twice in 1996 and 2000 to acquire high-resolution filtergrams and vector magnetograms of the solar photosphere and chromosphere [34]. The experiment featured an 80 cm telescope, achieving a resolution of 0.2 arcseconds, and was designed for stable pointing within a 5-arcsecond range in any direction.
The Solar Bolometric Imager was designed to provide the first bolometric maps of the solar photosphere in the range from 280 nm (ultraviolet, UV) to 2600 nm (near-infrared, NIR) [35]. It was equipped with a 30 cm telescope, achieving an angular resolution of 2.86 arcseconds, and utilise sed the same pointing platform as the Flare Genesis Experiment during its three flights in 2003, 2006, and 2007.
The Sunrise telescope, one of the largest and most powerful solar telescopes to be lifted into the Earth’s upper atmosphere, featured a 1-meter primary mirror with a Gregory-type reflector [36, 37]. This design enabled it to capture ultraviolet spectrum images of the Sun. The telescope flew twice, in 2009 and 2013. Additionally, the tracking accuracy requirement was set at \(\pm 7.5\) arcseconds RMS [38]. Beyond the telescope itself, the Sunrise mission included additional scientific instruments, such as the Sunrise Filter Imager (SuFI) and the Imaging Magnetograph eXperiment (IMaX). A third Sunrise mission is planned for launch in 2024, featuring a new gondola and updated scientific instruments [39].
Table 2 summaries key balloon-borne telescope missions and their parameters.
Finally, sounding rockets have the potential to play a crucial role in conducting solar research. During a suborbital flight, payloads are elevated above the Earth’s atmosphere, enabling the collection of high-resolution data without the distortion caused by atmospheric interference. Sounding rockets provide a lower cost and a more flexible alternative to space-based observation missions. However, when compared to balloon-borne missions, a suborbital flight via sounding rockets provides less time above the atmosphere and is more expensive. Notably, several missions have utilized sounding rockets to carry scientific instruments aimed at observing various celestial phenomena, including the study of supernova remnants [40, 41].
Despite the lower cost of balloon-borne telescopes compared to their space counterparts, these advanced balloon-borne solar telescopes remain inaccessible to most amateur astronomers and local university groups. They are too large, require huge balloons, extensive ground support teams and are consequently too expensive.
To address this, researchers such as [42] have attempted to create lower cost variants [42]. In the US, a student team from the Colorado Space Grant Consortium developed the High Elevation Light Intensity Observation System (HELIOS) that carried an Orion Maksutov-Cassegrain telescope, a Hydrogen-Alpha filter, a focus reducer, and an Image Source camera [43]. A two-stage tracking system was implemented with the coarse tracking being achieved using photodiodes and the fine tracking using solar object video identification. Unfortunately, their telescope’s focus was changed during the flight which resulted in the scientific images becoming unclear. Only a few photographs of the sun was partially captured on the left side of the images [43]. Thus, to date, to our knowledge, there is not any low-cost balloon-borne solar telescope platform that has been able to clearly capture solar images in a way that can be used for scientific research.
This paper presents the results of the SunbYte programme. SunbYte (Sheffield University Nova Balloon Lifted Telescope) is a series of student-led projects founded in 2016. The SunbYte programme aims to acquire scientifically valuable observations of the Sun whilst inspiring and training the next generation of space engineers and scientists. The objectives are to design and develop a low-cost solar telescope capable of tracking and observing the Sun autonomously whilst surviving in the harsh environment of near space.
Such stabilised platforms could also be adapted for Earth Observation, telecommunication and wider astronomy applications. The programme involved researchers and students from the University of Sheffield across many disciplines and stages of education. This was supported by other researchers at the University of Hong Kong, the University of Hull, the University of Northumbria and Queen’s University Belfast. During the programme, the teams also established connections with several industrial partners such as Harmonic AG, a German manufacturer, developer, and designer of mechatronic drive systems/precision gears. The projects hardware was flown through the REXUS/BEXUS and HASP programme which provided transportation to the upper atmosphere.
The REXUS/BEXUS programme is realised under a bilateral Agency Agreement between the German Aerospace centre (DLR) and the Swedish National Space Agency (SNSA) [44]. The Swedish share of the payload has been made available to students from other European countries through a collaboration with the European Space Agency (ESA). EuroLaunch, a cooperation between the Esrange Space centre of Swedish Space Corporation (SSC) and the Mobile Rocket Base (MORABA) of DLR, is responsible for the campaign management and operations of the launch vehicles. Experts from DLR, ZARM, SSC and ESA provide technical support to the student teams throughout the project.
The High Altitude Student Platform (HASP) is a United States-based programme led by the Louisiana Space Consortium (LaSPACE) and supported by the National Aeronautics and Space Administration (NASA) Balloon Program Office (BPO). Each balloon flight is designed to carry up to twelve student payloads to an altitude of about 36 kilometres with a flight duration of 15 to 20 hours using zero-pressure balloons [45, 46].
SunbYte I was flown on REXUS/BEXUS in 2017, whilst SunbYte II and III were flown on NASA HASP in 2018 and 2019 respectively. The results and analysis of the SunbYte I mission are presented in a separate paper [47]. The main aim of this current paper is to present the lessons learnt through the analysis of the tracking system for SunbYte II and III. Discussions related to the other missions may also be presented to maximise benefit to the reader.
This paper is structured as follows: In Section 2, the general configuration of the three missions is described. The results of these missions are presented and analysed in Section 3. In Section 4, lessons learnt are generalised from the missions flown and evaluated to create a six-step roadmap that will allow readers to quickly configure the design of a stabilised platform for inexpensive solar high-altitude balloon-based solar observations.
2 Methodology
In order to address the educational and scientific objectives of the project, a set of requirements was created. These are based on our understanding of the science needs, the available space on the launch vehicle, as well as constraints on the cost and lead time of suppliers. Because the same launch vehicle was used in SunbYte II and III, these requirements have generally remained unchanged throughout each design iteration. On a high-level, the optics assembly required for observing the Sun must include an optical telescope, camera, and h-alpha filter setup. This filter and wavelength was selected as it is commonly used on the ground so the images taken can be compared more easily. The ADCS (Attitude Determination and Control System) is responsible for the tracking and control of the telescope, utilising motors, tracking sensors, and control feedback. This system works in conjunction with other control systems that keep the payload within its temperature limits and communicate with the ground station and personnel
2.1 General configuration
SunbYte I flew with the BEXUS platform, specifically on BEXUS-25, which allowed for flexibility in payload size and location. This flexibility enabled the use of larger motors and cameras, resulting in higher power consumption compared to later missions with HASP. The payloads were integrated into the launch vehicle uniquely depending on its individual needs and discussions with other payload teams sharing the flight. There was no standard “absolute” limit on mass, size or power, though a summary of the basic technical parameters of each of the SunbYte missions is shown in Table 3.
The SunbYte I experiment had dimensions of \(910\times 730\times 1546\) mm, making it much larger when compared to later flights. This size allowed for a 203.2 mm aperture Schmidt-Cassegrain telescope. A powerful Andor Zyla sCMOS Camera was paired with this. The BEXUS platform enabled both the telescope and the accompanying tracking platform to be cantilevered from the side of the balloon gondola as shown in Fig. 1.
SunbYte I payload. The telescope and tracking platform were cantilevered from the edge of the balloon gondola for increased visibility and clearance to other objects. The flight computers which did not need to be near the tracking platform were placed inside the balloon gondola for better thermal protection
The system used two 7 W, five-phase stepper motors, each with a step angle of 0.36 deg/step. Micro-stepping was also tested and demonstrated an accuracy of 0.00288 deg/micro-step (10.368 arcsec). However, to the larger and heavier optical system, this increased torque loading and motor requirements. To meet the torque requirement, zero backlash harmonic drives (model: CPL2A HFUC - 2UH) with a 1:160 gear ratio from Harmonic Drive AG were used. This also further increasing the pointing precision to 8.1 arcsec/step [48].
To operate the scientific camera, a powerful Kaby Lake i7 7500U Mini PC with 16GB of RAM was necessary. This was used to conduct high-speed and high-resolution image capture. The demanding processing required led to some issues around thermal management, power consumption and spatial constraints [47].
For more detailed information on the flight configuration, please refer to Table 3.
SunbYte II flew with NASA HASP, which imposed more stringent payload constraints based on the large/small class your experiment fit into. Each large-class payload was required to conform to a maximum volume of \(380\times 300\times 300\) mm and not exceed the mass of 20 kg (in part to ensure compatibility with the thermal vacuum testing facilities). To meet these requirements, the telescope and science camera were significantly downsized with just a simple Dielectric energy rejection filter (D-ERF). This allowed the use of stepper motors with half the number of windings. A CAD model can be seen in Fig. 2. The smaller motors also facilitated a minimization of some electronic components. Despite these changes, the same harmonic drives were used as in the SunbYte I mission [47].
On HASP flights, power (2.5 amps at 30 VDC) and telecommunications are provided. A serial downlink of 4800 bps, is available using the RS232 protocol and a DB9 connector. To initiate a command uplink, the team was required to provide the HASP operator with the payload ID number and two bytes in hexadecimal format for transmission. The HASP operator will transmit commands during a limited window of time every hour.
SunbYte III was launched aboard the same HASP vehicle but with some upgrades such as the use of a Hydrogen-\(\alpha \) (\(H_{\alpha }\)) filter at 656.28 nm wavelength. The main aim of this was to help students to gain experience with the use of solar filters and to potentially obtain high-quality images of the solar chromosphere that will not be distorted by the Earth’s atmosphere.
Figure 3 shows the configuration of the SunbYte III payload, with the specific components covered in Table 3. The science camera, the ASI120MM, had a maximum resolution of \(1280 \times 960\) pixels, with a maximum readout speed of 35 frames per second (FPS). The \(H_{\alpha }\) filter was tuned for optimal performance under the anticipated flight conditions before launch. Images were recorded and stored on a 750 GB SSD. The positioning of the telescope was updated by the ‘tracking camera’, image processing tasks were handled by a Raspberry Pi (RPi) and a Teensy 3.6 microcontroller unit (MCU) was used for controlling pitch and yaw movements. The telescope was capable of pitching up to a maximum of 65 degrees, ensuring that the system could capture images of the Sun consistently throughout the flight. The yaw and pitch actuation lines are shown in Fig. 4.
All three designs of the telescope used similar tracking and pointing mechanisms which will be explained in the following section.
2.2 Attitude determination and control system
The objective of the Attitude Determination and Control Systems (ADCS) was to maintain the Sun within the Field of View of the telescope’s science camera and stabilise the image during the exposure time. To achieve this, the system’s tracking camera needed to identify the location of the Sun and continuously point the telescope at it.
Whilst the rotational and oscillation behaviour of NASA HASP launch vehicles (used in SunbYte II and SunbYte III) has not been published, similarities can be drawn from other launch programmes which utilise similar-sized balloons and payloads. For example, SunbYte I flew as part of the BEXUS programme. According to [49], the BEXUS manual [50], and the HEMERA manual [51]; the gondola rotates at \(\sim \)0.05 Hz with some oscillation around its centre of gravity between 0.5 Hz to 1.0 Hz with an amplitude of 0.1 degrees to 0.5 degrees. Furthermore, NASA video footage for the SunbYte II and III flight supports this information. During the ascent, the balloon can rotate up to once per several minutes (depending on the wind), but during the stabilised floating phase, this rotation reduces to once per ten to thirty minutes. This is further supported by the tracking image data during parts of the flight when the actuation of the tracking was stopped. In that scenario, the tracking camera acts as a static point on the gondola watching the sky as it rotates.
In SunbYte III, the stepper motors move at 800 rpm to provide a max 5 rpm rotation. This meets the max (yaw) rotational speed of the gondola during ascent. The rate at which the Sun moves up and down the sky over time is much less significant that the rotational performance, meaning that the speed requirements on the yaw axis will set the benchmark for the system.
The following section will detail the tracking algorithm and the hardware used for precise actuation.
2.2.1 Tracking algorithm
As the rotation of the balloon vehicle is highly dependent on the winds, SunbYte utilises a tracking system to identify the location of the Sun and point the telescope towards it.
The tracking algorithm, as a part of ADCS, was necessary to identify the location of the Sun. The system utilized a Logitech C920 tracking camera with a solar filter to obtain images at 1 FPS. Tracking was carried out in two steps. In the first phase, the pitch and yaw motors swept across the sky. Meanwhile, the image processing algorithm processed the incoming stream of images, identifying the largest and the brightest objectswhich exceed a predefined threshold value. The sweeping continued until such a object was detected. Upon detection, the algorithm transitioned to the second phase, centering the telescope on the disk of the Sun by continuously adjusting the pitch and yaw positions. The tracking algorithm used a proportional controller in both pitch (vertical) and yaw (horizontal) axes to convert the offset in pixels into stepper motor steps.
During development, other potential tracking algorithms were developed and tested. For example, an estimation of the Sun’s initial position based on magnetometer and GPS data was intended to be used as a starting point for the Sun’s position search. However, testing revealed that the stepper motors introduced significant magnetic interference with the inertial measurement unit (IMU) and this positioning method was discarded. In the future, MEMS IMU sensors could be tested as an alternative instead. This could reduce the workload compared to tracking cameras as the amount of incoming data is less.
A proposed alternative method entailed employing multiple tracking cameras alongside a fisheye camera. Nonetheless, this approach increased the computational demand as the computer had to unwrap the fisheye image for tracking, thereby complicating the tracking algorithm. Considering the gradual rotation of the balloon vehicle at float altitude, incorporating additional tracking cameras was deemed unnecessary at this developmental phase.
Furthermore, acquiring a space-qualified MOEMS sun sensor proved costly and exceeded project budget constraints. Although SunbYte II had explored light intensity sensors, they lacked the precision of camera tracking, leading to the rejection of the idea. In summary, camera tracking remains the most accurate and cost-effective method for our educational experiment.
2.3 Optics system
2.3.1 Science camera
The science camera flown on SunbYte II and III was a ZWO ASI MINI 120 mm monochromatic CMOS camera. This was powered through a 5 V USB-C connection, it is compact, low-cost, and consumes minimal power. It utilises a rolling-shutter AR0130CS sensor, providing 12bit pixel depth, a QE peak of 78%, a maximum readout speed of 35 FPS and a sensor size of is 4.8mm by 3.6mm. The stated operating temperature is between -5°C to 45°C.
2.3.2 \(H_{\alpha }\) filter
For SunbYte III, an \(H_{\alpha }\) Daystar Quark chromosphere filter was added to the telescope. The power supply was facilitated through a 5 V USB connector.
2.3.3 Mirrors
The volume constraints of the HASP platform mentioned in the section on General configuration necessitated the use of two diagonal mirrors in order to fit within the permitted volume. Figure 5 illustrates the optical setup for SunbYte III.
The following section will focus on the tracking results of SunbYte II and III, for more information regarding results and analysis of the SunbYte I mission, please refer to [47].
3 Results
3.1 SunbYte II
SunbYte II launched on the 4th of September 2018 at 14:03:22 UTC from Fort Sumner, New Mexico, USA. A total of 33436 pictures were taken and saved on an SD card onboard the flight computer. According to the in-flight tracking images, the tracking was successful with 3358 images containing the Sun, this corresponds to approximately 10% of images. There were 874 images where the Sun was at the calibrated centre point. No uplink commands were issued during the mission flight as it was full autonomous.
Figure 6 shows examples of the Sun images taken by the tracking camera. The red dot indicates the location of the Sun as calculated by the tracking algorithm. The yellow circle is an estimate of the Sun’s diameter.
Figure 7 is a 2D scatter plot with concentration colour bar readings of all 3358 images with the Sun presence. The x axis represents the horizontal pixel location within the tracking camera whilst the y axis represents the vertical pixel location. The calibrated centre point is at pixel position (354, 298) and red lines mark the centre lines intersecting this coordinate point. At this position, the telescope is aligned to point correctly at the Sun.
Sun concentration location SunbYte II - red box indicates the target location - where the calibrated centre is at pixel (297, 353). Paths ‘A’, ‘B’ and ‘C’ are tracking paths made by the system. ‘A’ and ‘B’ represent the successful movement of the robotic telescope towards the Sun whilst ‘C’ is only partially successful. Generated using custom MATLAB Data Density plot function [52]
There are several distinct Sun’s tracking paths moving towards the calibrated centre point. These paths describe the motion of the gimbal as it attempts to centre the Sun. As the HASP gondola is constantly rotating, it takes some time to accurately centre the image. Some of the paths indicate that the motor was not rotating fast enough to capture the Sun movement.
As the Sun will only rise to a fixed angle, a future improvement could be to discard this area from the tracking cameras images to prevent unnecessary searching, or to align the calibrated centre of the tracking camera at the top of the sensor, so that the rest of image can be used to determine the suns location.
A closeup of the centre is also shown in Fig. 7. There were more than 90 images when the Sun was in the middle of the image. One pixel below this, there are an additional 50 images. By projection, there are 9 pixels in the tracking camera which fall within the field of view of the telescope and should be considered as the “correct” location of the Sun. If we take this area into account, there are more than 400 images which locate the Sun correctly.
Due to a technical issue with the science camera system, it was not able to return any scientific images. During the final late access period, the scientific images folder was emptied to maximise space for the flight data. Unfortunately, the folder itself was also removed and thus no longer on the file path. As a result, the computer was unable to write the images to the folder as the folder no longer existed. An error prevention system that auto-creates a missing folder would have solved this problem. In addition more robust pre-flight checklist would also help prevent such problems in the future.
3.2 SunbYte III
SunbYte III launched on the 5th of September 2019 at 13:03:15 UTC from Fort Sumner, New Mexico, USA. The flight time was 7 hours and 37 minutes. A total of 387643 data points were collected based on 13367 telemetry messages from 29 different sources, including 19 sensors and various status indicators. 53726 tracking images were recorded at a rate of \(\approx 2\) FPS.
Approximately 20% of the tracking images contained the Sun. This is in contrast to SunbYte II which captured the Sun in 10% of its tracking images. Since both systems flew on missions with similar duration and used the same tracking camera with the same Field of View; initial assessment would suggest the SunbYte III system performed better. Figure 8 shows some examples of the images containing the Sun.
There were 2 uplink commands made throughout the flight in the mission: the first time was after losing power during the flight, the calibration became out of sync requiring a command to reset it. The second command lowered the speed and acceleration of the motors.
As with SunbYte II, Figure 9 shows the detected Sun locations stacked onto a single scatter plot for SunbYte III. As before, the red cross-hairs indicate the centre of the telescope within the tracking camera for calibration of the target. The point markers form many distinct curved lines in the image that show the path of the Sun during the flight time. The curvature is the path of the Sun passing through the sky as seen by the tracking camera.
The telemetry housekeeping data presented in Figs. 12, 17, 18, 15 will be used in conjunction with these tracking images to determine the behaviour and performance of the tracking system. There was a power supply interruption on the launch vehicle from T+02:12:33 until T+02:35:34 so data during this time was not collected.
2D scatter plot of Sun locations within the tracking images (Sunbyte III). Generated using custom MATLAB Data Density plot function [52]
The ambient temperature near the pitch axis is shown in red in Fig. 18. It can be used as a rough measure of when the tracking system was working effectively because of its location on the side of the payload. If there are minimal temperature fluctuations, it means the sensor is in a stationary position relative to the Sun. If it fluctuates over a period of minutes, this matches the typical oscillatory period of the balloon rotation and suggests the tracking is not working effectively.
Figure 10 is a 3D scatter plot with time as the vertical z axis. This enables the temporal and spatial distribution of the sun locations to be displayed simultaneously. To compare with Fig. 9, the equivalent 2D scatter plot would be a top view looking down onto the x and y axis. Taking different horizontal slices of time this Figure, the behaviour of the tracking throughout various periods of the flight can be dissected for closer analysis.
At the early stage of the launch in Fig. 11 (left), the Sun’s location within the tracking image was largely concentrated around the calibrated centre point at pixel coordinates (150, 110). This indicates the experiment was tracking correctly and the few points not in the centre were taken as the tracking was moving towards the centre point. It can be seen that in this time period, both the yaw and pitch were functioning as expected.
Next, Figure 11 (right) contains several curved paths showing the Sun moving steadily across the tracking camera captured at regular intervals as the gondola rotates. This was because the response became slow so the system was manually powered off for the remainder of the ascent. It is likely the motor or gearing was affected by the low temperatures and this is supported by the yaw position sensor shown in Fig. 12. The flight profile takes the payload through a region of cold air and causes a significant increase in the torque required for the motors to move. Float started at approximately 15:40:37 UTC, 2 hours and 37 minutes into the flight. As the float phase began, the system resumed as planned, sweeping successfully multiple times, and then tracking the Sun.
In Figure 13 (left), the Sun location slowly moved upwards with some zigzag pattern. It represents some motion in the yaw and pitch direction. The density of the points (located close to each other), suggests that some tracking was taking place. However, the movement is not significant enough to confirm since the tracking should place the Sun at the calibrated centre of the image (the red cross-hair).
In Figure 13 (right), the telescope attempted to correct the yaw and pitch position. The telescope moved the Sun from pixel position (100, 230) to (150, 170). The yaw position is located in the correct place (150 pixels on the X-axis).
Figure 14 shows the Sun entering the image at pixel position (0, 130) on the far left of the image (see path 1). It then moves towards the left in a distinct pattern of sporadic nature. The curves with sporadic points followed by a distinct cluster of points (e.g. pixel position (130, 180)) indicate the yaw tracking system was working successfully and pointed at the same position over a period of time (see paths 2 and 4 on the same image). The curves with a consistent density of points such as those in path 3 of Fig. 14 suggest no tracking.
Based on the video footage, the gondola changed the direction of yaw rotation several times throughout the flight. This is reflected in the zigzag pattern in some of the figures; for example, the right-hand side of Fig. 14.
At some points during the flight, the view of the Sun is blocked by other devices installed on the balloon gondola. This can be observed on the tracking images as a gap in the Sun position (see Figs. 11 (right) and 15 (left)). Figure 16 (left) shows a snapshot of the video footage when this occurs whilst Fig. 16 (right) illustrates this obstruction from the telescope’s point of view.
Figure 17 shows current, voltage fluctuation and power data from the current sensors located on the 12 V, 5 V and 3.3 V lines, alongside the RPi power input. The current and voltage fluctuate during the flight due to high power components being switched on and off (for example, the motors). A moving mean with a window of 200 samples is used to show overall trends. The current, voltage and power readings are within nominal range. Larger fluctuations are present on the 12 V line as it provides power to the motors. This demonstrates how the power draw of the motors changes when movement is required.
Figure 15 (right) indicates the operation of 4 on-board heaters. The primary heater is programmed to turn on below 40 degrees Celsius whilst the secondary heater is programmed to turn on below 20 degrees Celsius. More heating was required on the yaw motor than the pitch motor. The secondary heaters for the pitch motor were barely used. The second yaw heater was on in the early phases of the flight as the temperature dropped (see Fig. 18). This demonstrated SunbYte III heating system was operating as designed. The slowdown in the performance of the tracking appears to be due to cold temperatures in the harmonic drive gears causing a mechanical seizure. As the flight environment is a near vacuum, only radiation and conduction heat transfer can be used. Therefore, a future improvement could be to prioritise additional space for insulation around the harmonic drives and apply heaters directly to them. Careful attention should also be paid to any heat bridges.
There was a power loss in the HASP system between T+02:30 Hr to T+02:45 Hr, this affected the payload with the system unable to record and downlink data. In the future, on-board backup power could be implemented to ensure the data can continue to be written to the local on-board backup storage. This would require qualification and acceptance with the launch providers.
SunbYte III has partially fulfilled the experiment requirements. The active heating system was an improvement compared to SunbYte II. The tracking system was able to identify, locate and point the telescope at the Sun for a minimal period. During power loss, the payload loses active heating, more insulation could have been used to maintain the payload temperature. Due to this, the calibration point was lost. This meant the tracking centre target was no longer aligned towards the center of the sun and the pointing system no longer knew where it was relative to the yaw limits. This suggested that a fixed calibrated centre might be a better choice. In SunbYte II the calibrated centre is saved inside the code, and is supplemented with the use of physical limit switches. Both SunbYte II and III could benefit from more robust thermal systems, as conditions during the flight can become quite harsh.
3.3 Overall system discussion
The essential lesson from both SunbYte II and III underscores the significance of maintaining simplicity within systems. There are more pictures by SunbYte III compared to SunbYte II (53,726 vs 33,436 pictures). SunbYte II has approximately 10 % of the tracking images with the Sun whilst SunbYte III has approximately 20 % of the tracking images containing the Sun.
While an increase in recorded data may suggest improved functionality, it does not necessarily indicate successful sun tracking. Despite recording less data, SunbYte 2 has effectively demonstrated three distinct tracking paths (A, B, and C) both are leading to the calibrated centre, as depicted in Fig 7.
By contrast, the scatter plot of SunbYte 3 in Fig. 9 does not reveal any clear tracking path. Further examination in Fig. 10 with spatial analysis also lacks consistent evidence of the system guiding the sun toward the calibrated centre or any specific points (one except being in Fig. 11 (right)).
From this comparison, it can be concluded that SunbYte II boasts a superior overall system design. Despite being slower to respond, recording less data, and without a heating system, it fulfils the fundamental requirement of stabilisation, i.e., guiding the sun to the centre point as long as possible. SunbYte III’s hardware improvements over SunbYte II are commendable, but the system falls short of meeting the basic requirement. This deficiency may stem from three primary reasons:
Firstly, the calibration point appears to be variable, possibly adjusted during flight. This oversight is critical since the calibrated centre serves as the offset between the physical positions of the tracking camera and the telescope. This distance remains constant and must be calibrated and fixed beforehand. Failure to re-calibrate the system resulted in tracking errors, impeding its ability to follow the sun accurately.
Secondly, SunbYte II features four limiting switches at the ends of each side of the pitch and yaw motors. This provides active feedback preventing the system from ever moving beyond acceptable limits. This is vital to prevent cable entanglement and ensures that even in the event of a power loss, the resumption of power will not lead to skipped step counting. Conversely, SunbYte III lacks such a design feature. This disparity proves to be a significant difference between the two missions. Post-flight assessments emphasise the necessity of having limiting switches or similar systems to establish precise motor positions for effective tracking. Without reference points for the motors, the tracking system faces challenges, leading to erratic patterns like those seen in the Sunbyte III mission.
The hallmark of successful tracking lies in maintaining the sun at the calibrated centre for as long as possible. SunbYte II demonstrates numerous successful attempts at this, whereas SunbYte III exhibits behaviour indicative of losing control.
The third lesson learned is the importance of full autonomy. SunbYte II operates autonomously without requiring ground control or input, unlike SunbYte III, where attempts were made to correct calibration discrepancies and adjust speed and accelerations through manual uplink commands. This reliance on human intervention poses risks, as demonstrated by calibration issues and power loss affecting system stability. It is suggested that designing a more autonomous system reduces dependency on human intervention and ensures consistent system performance.
In short, the calibration point must remain fixed overall in flight duration, a mechanism should exist to track the motor’s location at some point in flight, and the system should strive for full autonomy. SunbYte II has outstanding tracking algorithms and SunbYte III has a better hardware system. The key lesson from both SunbYte II and III highlights the criticality of simplicity in system design.
4 Proposed design framework
This section uses the lessons learnt from the SunbYte program to establish a framework for developing an initial design of a low-cost solar telescope tracking system. It is intended to be a guide for readers on how to create initial design specifications. Since improving one aspect of a system’s design (e.g. higher resolution science camera), can negatively impact several other design parameters e.g. power consumption, computing requirements), it is important to have a clear design flow. A flow chart illustrating the recommended optimal design process for a typical low-cost solar telescope tracking platform is shown in Fig. 24. Firstly we shall select the science image requirement and the telescope sizes. Based on the telescope’s field-of-view, we can select the tracking camera and actuation system. Finally, the wider supporting system can be specified based on these driving requirements.
4.1 Resolution requirements
The first step in assessing the required resolution is to identify the size of the features and wavelength of light chosen for observation. For example, to resolve the solar features with the size, f of 1000 km and by taking into account the distance, l between the Earth and Sun (149.84 million km), the minimum angular resolution, \(\theta \) can be calculated using (1).
Figure 19 shows solar images with different filters. For example, the wavelength of \(H{\alpha }\) in a vacuum is 656.461 nm. Note, that this differs from the wavelength of \(H{\alpha }\) in the air which is 656.281 nm.
It is possible to estimate the minimum telescope aperture needed using the Rayleigh criterion
with the angular resolution in radians, \(\theta \) = \(6.593 \times 10^{-6}\) rad and wavelength being measured, \(\lambda \) = 656.461 nm. Using these two variables, the minimum diameter of the telescope lens aperture, D is 121 mm.
4.2 Determining tracking accuracy requirements
The size of the solar disk within the telescope’s field of view greatly affects the pointing requirements (see Fig. 20). For an initial design, it is recommended to image the whole disk as this greatly reduces the required tracking accuracy. Providing a larger margin of error in case of poor tracking performance or misalignment. In Figure 20, the angular resolution of the Sun is 32’. To be able to capture the Sun confidently using a four-factor margin of error, a horizontal resolution of 128’ is necessary.
The Sun in different wavelengths. Visible light (left), Ca-K at 393.4 nm (center), \(H{\alpha }\) at 656.281 nm (right) [53]
The same stabilisation system should be used throughout the integration and flight time, to make sure the system remains unchanged.
This means the telescope and the tracking system can move up to 48 arcmin either way in the horizontal direction before the Sun begins to disappear from the edge of the image. As a result, the system’s tracking accuracy could be as low as ± 48 arcmin.
The two-stage tracking cycle consists of a sweep phase when the Sun is not in the field of view of the tracking camera; and a tracking phase when the Sun is within the field of view of the tracking camera. Three main steps as shown in Fig. 21.
-
1.
The tracking camera takes images.
-
2.
Those images are sent to the computer for Sun tracking calculation. If no Sun is found, it defaults to a sweeping mode to move the camera in a systematic pattern until the Sun can be found.
-
3.
When the Sun is found, the offset will be calculated and sent to the motor drivers to move the telescope.
Each of these procedures has its own timing and they will affect the overall tracking accuracy and latency of the system. Hence, there is a trade-off between the computer’s physical size, speed and thermal output, and also between the processing speed and accuracy of the tracking mechanism.
The motor is required to operate at sufficient speed to chase the Sun. However, if it outperforms the computer processing speed, it is a waste of performance and if it is too slow, it becomes a bottleneck of the system. A demonstration of the types of images obtained during tracking can be seen in Fig. 22. These factors define the total response time for the entire sensing and correction tracking cycle.
During the tracking process, the Baader solar filter filters out 99% of the light, meaning the remaining light must come from very bright objects (i.e, the Sun). SunbYte uses an OpenCV function - “Hough Circle Transform” to further check that the bright object is circular. It then calculates the pixel differences between the centre of the circle to the calibrated centre of the system.
4.3 Selecting on-board flight computers
The system has to be able to handle the speed of writing the images to a local storage drive as well as operate the tracking algorithm. Some extra margin is recommended to enable the computer(s) to do additional tasks such as data compression and communication with the ground or other flight systems.
It is difficult to estimate the performance of a computer without real-life testing, especially as it depends on the exact tracking algorithm implementation, available computational resources, camera resolution and environmental conditions (such as heat dissipation). A comparison to other missions and projects with similar imaging requirements can be conducted to identify analogies. For example, a Raspberry Pi computer was used for the Pan-Tilt HAT project’s tracking system with TensorFlow for computer vision [54]. Out of the box, it was benchmarked to operate at 8 FPS. A USB Accelerator containing an Edge TPU was then added which further increased the frame rate up to 24 FPS. On another project using OpenCV for deep learning object detection, Python’s multiprocessing module along with a Raspberry Pi camera achieved an FPS of 27.83 [55].
Most of these examples demonstrate that the Commercial-Off-The-Shelf (COTS) processors operate typical cameras up to 30 FPS. In the previous example, multiple objects were being tracked, hence solar tracking should be considered computationally easier than object tracking so Raspberry Pi should be a suitable computer if the camera resolution is not excessively high (above \(720\times 1280\)). There are also many online resources on utilising Raspberry Pi as an image-tracking processor which makes it a great choice for students and citizen scientists who may benefit from enhanced community support [56]. The focus for the development of the tracking system should therefore be the frequency of updates the motor drivers can receive to correct the telescope pointing position.
4.4 Selecting actuation components
4.4.1 Angular resolution requirements
As a guide, based on the resolution of the science camera being 128 arcmin, the authors suggest the pointing system must be able to have a per step angular resolution of around 10 arcmin to get the telescope pointing in a position that enables the Sunlight to enter the science camera. From this requirement alone, it will be very difficult for any motor to achieve this kind of precision without some type of gear.
The challenge with gears is that backlash reduces pointing tolerances. Harmonic drives provide a low-backlash solution. A 1:100 gear ratio with a 10 arcmin output results in the input stepper motor shaft only needing a angular resolution of 1000 arcmin, or 17 deg. This significantly eases the requirements for motor selection.
4.4.2 Torque requirements
The motor and gear must be powerful enough to move the telescope assembly in both the pitch and yaw directions. Whilst the pitch axis is more likely to encounter eccentric loads, depending on the design, the yaw axis may need to rotate more components as well as the pitch actuation mechanism. Therefore, it is worth carefully designing the system in a way that enables identical motors and gears to be used and minimises part variety. The motor needs to overcome friction as well as the static moment of inertia before it can move the telescope assembly.
4.4.3 Pitch requirements
Figure 23 shows an example of an under-slung telescope system. Since gravity acts vertically, the moment acting on the pivot is the weight of the system multiplied by the horizontal distance between the centre of mass and the pivot. At a resting neutral position, the telescope will naturally point upwards at a positive angle due to the rear of the telescope assembly being heavier. This coincidentally also minimises the power necessary to pitch the telescope up. Depending on the availability of space and other limitations, the position of the centre of mass can be optimised to minimise the pitch necessary and reduce the torque requirements (e.g. without power, the telescope could point at 30 degrees up).
Since gravity acts vertically, the pitch angle which causes maximum torque is when the centre of mass is furthest away from the pivot as shown in the last diagram.
For systems where the centre of mass lies above the fulcrum, the position of maximum torque will be when the centre of mass forms a horizontal line with the fulcrum. This is only likely to occur when the Sun is at the highest point in the sky. If it is suitable an under-slung system is recommended as it will reduce the pointing power requirements as it is inherently more stable.
The torque, T exerted on the actuation shaft can be calculated as:
where m is the mass in kg, d is the horizontal distance between the fulcrum in metres and g is the acceleration due to gravity (9.81 m/s2). d can be calculated using simple trigonometry if the radial distance, r between the centre of mass and the fulcrum is known.
4.4.4 Yaw requirements
Designing for the yaw is normally easier as the motor rotation is perpendicular to gravity so the motor does not need to fight gravitational force. The motor only needs to overcome the moment of inertia.
The presence of the gearing ratio means very little torque is usually required from the motor to actuate the system. The pitch is normally the axis that requires the most torque, using the same motor and gearing for both axes will ensure the yaw actuation can operate successfully.
4.4.5 Rotational speed requirement
The gondola, attached to the balloon, can have a yaw rotation of up to \(\phi \) times per minute, this becomes the worst possible operating case and becomes the minimum speed required for the tracking system. This speed must account for the time to point, determined by the motor setup, and the time to find, which is the time taken for an image to be captured, tracking information identified from that image and sent to the motor controllers for movement. As balloon movement is continuous, the tracking system must update frequently enough to ensure that the view of the telescope is over the sun. The size of these adjustments will influence the minimum shutter speed of the scientific camera, with smaller adjustments permitting slower shutter speeds.
If the gondolas rotation is \(\phi \), in rotations per minute, the rotation, \(\omega \) in degrees per seconds, can be calculated by \(\omega = \phi /6\). As the motors drive the yaw and pitch of the gondola through harmonic drives, the actual motor speed \(\zeta \) can be determined by the Gear Ratio (GR) and the minimum speed of tracking \(\omega \).
Assuming that there was 1 full rotation of the gondola per minute with a gear ratio of 1:100, then the motors driving the yaw would need to have a minimum top speed of 600 degrees per second or 100 rpm.
4.5 Systems budget and specification
Knowing all of the scientific parameters and converting them into physical engineering specifications means that the electrical, optical and mechanical components for the project can be chosen to fulfil the mass and power budget provided. Table 4 demonstrates the variety of mass and power parameters that can be found among the different subsystems.
The 20% mass margin includes many staple components, including bolts, wiring and other miscellaneous sensors. An initial power margin of 20% was also included for the potential power draw from components operating in cold conditions, as well as from other critical systems, such as focusing, and non-critical systems, such as housekeeping sensors.
5 Conclusions
A flow chart illustrating the recommended optimal design process for a typical low-cost solar telescope tracking platform is shown in Fig. 24. During the project life, if new requirements are imposed or where the budget increases or decreases, changes to the design should always start again following the beginning of the design flow shown in Fig. 24. This will ensure the system does not become unbalanced, as improving one subsystem, such as a larger aperture telescope, may impact the technical requirements of other subsystems, requiring motors with more torque and electrical power to move it. Such an ability to quickly achieve an optimal design using the least resources available will be invaluable to educational institutions and companies looking to develop low-cost entry-level solar tracking platforms for education, research and commercial purposes.
6 Recent developments
SunbYte IV has been flown with the HEMERA program (funded by the Horizon 2020 [57]), the new payload volume allowed for a larger Williams Optics GT-71 II 2019 to be fitted and the refracting prisms removed, reducing the number of potential optical artefacts [58]. Additionally, the science camera was upgraded to a ZWO ASI183MM, which as well as supporting a higher resolution of 20.18 megapixels, and an improved readout speed of 19 FPS; also has improved quantum efficiency of \(84\%\) in the \(H\alpha \) channel and a better read noise of 1.6e. The system underwent a new design cycle following the guidelines presented in Section 4. Some highlights include replacing the Raspberry Pi with a more powerful Single Board Computer (SBC), the Odroid M1. This tracked the sun and saved the images taken by the science camera. The Teensy MCU was replaced with an Ethernet-capable Arduino which interpreted UDP packets to drive the Pitch and Yaw motors. The onboard software was also completely rewritten in C++ to further improve processing speed. Future work will analyse the data generated from this later flight and evaluate the impact of the upgrades on the tracking performance and scientific output.
Availability of data and materials
Please contact Yun-Hang Cho at yun-hang@hotmail.com for requests regarding the data.
References
Societal, Committee On The.: Economic Impacts Of Severe Space Weather Events: Severe Space Weather Events-Understanding Societal and Economic Impacts: A Workshop Report. Understanding Societal and Economic Impacts Workshop Report, Severe Space Weather Events (2008)
Schulte In Den Baeumen, H., Cairns, I.: Global economic impacts of severe Space Weather. In: 40th COSPAR Scientific Assembly, vol. 40, pp. 3–15414 (2014)
Carrington, R.C.: Description of a Singular Appearance seen in the Sun on September 1, 1859. Monthly Notices of the Royal Astronomical Society. 20, 13–15 (1859). https://doi.org/10.1093/mnras/20.1.13
Carrington, R.C.: On certain Phenomena in the Motions of Solar Spots. Monthly Notices of the Royal Astronomical Society. 19, 81–84 (1859). https://doi.org/10.1093/mnras/19.3.81
Hodgson, R.: On a curious Appearance seen in the Sun. Monthly Notices of the Royal Astronomical Society. 20, 15–16 (1859). https://doi.org/10.1093/mnras/20.1.15
Gulati, I., Dlay, S., Gulati, I., Dlay, S.: Analysis of a solar geomagnetic storm that doomed 40 satellites. 44th COSPAR Scientific Assembly. 44, 725 (2022)
Office, P.M.: £20 million to accelerate British research into forecasting space weather (2019). https://www.gov.uk/government/news/20-million-to-accelerate-british-research-into-forecasting-space-weather
Shibata, K., Magara, T.: Solar flares: Magnetohydrodynamic processes. Living Reviews in Solar Physics. 8, 6 (2011). https://doi.org/10.12942/lrsp-2011-6
Carrasco, E.R., Edwards, M.L., McGregor, P.J., Winge, C., Young, P.J., Doolan, M.C., van Harmelen, J., Rigaut, F.J., Neichel, B., Trancho, G., Artigau, E., Pessev, P., Colazo, F., Tigner, J., Mauro, F., Lührs, J., Rambold, W.N.: Results from the commissioning of the Gemini South Adaptive Optics Imager (GSAOI) at Gemini South Observatory. In: Ellerbroek, B.L., Marchetti, E., Véran, J.-P. (eds.) Adaptive Optics Systems III. Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, vol. 8447, p. 84470 (2012). https://doi.org/10.1117/12.926240
Michaud, P.: Gemini Press Release MediaFacts. http://www.gemini.edu/media/mediafacts.html
Pierce, A.K.: The mcmath solar telescope of kitt peak national observatory. Appl. Opt. 3(12), 1337–1346 (1964). https://doi.org/10.1364/AO.3.001337
Plymate, C.: A History of the McMath-Pierce Solar Telescope. National Solar Observatory,(2001). http://nsokp.nso.edu/sites/nsokp.nso.edu/files/files/history/McM-P_History.pdf
Rast, M.P., Bello González, N., Bellot Rubio, L., Cao, W., Cauzzi, G., Deluca, E., de Pontieu, B., Fletcher, L., Gibson, S.E., Judge, P.G., Katsukawa, Y., Kazachenko, M.D., Khomenko, E., Landi, E., Martínez Pillet, V., Petrie, G.J.D., Qiu, J., Rachmeler, L.A., Rempel, M., Schmidt, W., Scullion, E., Sun, X., Welsch, B.T., Andretta, V., Antolin, P., Ayres, T.R., Balasubramaniam, K.S., Ballai, I., Berger, T.E., Bradshaw, S.J., Campbell, R.J., Carlsson, M., Casini, R., Centeno, R., Cranmer, S.R., Criscuoli, S., Deforest, C., Deng, Y., Erdélyi, R., Fedun, V., Fischer, C.E., González Manrique, S.J., Hahn, M., Harra, L., Henriques, V.M.J., Hurlburt, N.E., Jaeggli, S., Jafarzadeh, S., Jain, R., Jefferies, S.M., Keys, P.H., Kowalski, A.F., Kuckein, C., Kuhn, J.R., Kuridze, D., Liu, J., Liu, W., Longcope, D., Mathioudakis, M., McAteer, R.T.J., McIntosh, S.W., McKenzie, D.E., Miralles, M.P., Morton, R.J., Muglach, K., Nelson, C.J., Panesar, N.K., Parenti, S., Parnell, C.E., Poduval, B., Reardon, K.P., Reep, J.W., Schad, T.A., Schmit, D., Sharma, R., Socas-Navarro, H., Srivastava, A.K., Sterling, A.C., Suematsu, Y., Tarr, L.A., Tiwari, S., Tritschler, A., Verth, G., Vourlidas, A., Wang, H., Wang, Y.-M., NSO and DKIST Project, DKIST Instrument Scientists, DKIST Science Working Group, DKIST Critical Science Plan Community: Critical Science Plan for the Daniel K. Inouye Solar Telescope (DKIST). Solar Physics. 296(4), 70 (2021) https://doi.org/10.1007/s11207-021-01789-2, arXiv:2008.08203
Sánchez Capuchino, J., Collados, M., Soltau, D., López, R., Rasilla, J.L., Gelly, B.: Current concept for the 4m European Solar Telescope (EST) optical design. In: Bentley, J., Gupta, A., Youngworth, R.N. (eds.) International Optical Design Conference 2010. Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, vol. 7652, p. 76520 (2010). https://doi.org/10.1117/12.871604
EST: European Solar Telescope Funding Sources. https://est-east.eu/funding
Dunn, R.B.: Sacramento Peak’s New Solar Telescope. Sky and Telescope. 38, 368 (1969)
Liu, Z.: From NVST to CGST. In: Nagendra, K.N., Stenflo, J.O., Qu, Z.Q., Sampoorna, M. (eds.) Solar Polarization 7. Astronomical Society of the Pacific Conference Series, vol. 489, p. 247 (2014)
Schmidt, W., von der Lühe, O., Volkmer, R., Denker, C., Solanki, S.K., Balthasar, H., Bello González, N., Berkefeld, T., Collados Vera, M., Hofmann, A., Kneer, F., Lagg, A., Puschmann, K.G., Schmidt, D., Sobotka, M., Soltau, D., Strassmeier, K.G.: The GREGOR Solar Telescope on Tenerife. In: Rimmele, T.R., Tritschler, A., Wöger, F., Collados Vera, M., Socas-Navarro, H., Schlichenmaier, R., Carlsson, M., Berger, T., Cadavid, A., Gilbert, P.R., Goode, P.R., Knölker, M. (eds.) Second ATST-EAST Meeting: Magnetic Fields from the Photosphere to the Corona. Astronomical Society of the Pacific Conference Series, vol. 463, p. 365 (2012)
Cao, W., Gorceix, N., Coulter, R., Ahn, K., Rimmele, T.R., Goode, P.R.: Scientific instrumentation for the 1.6 m New Solar Telescope in Big Bear. Astronomische Nachrichten. 331(6), 636 (2010). https://doi.org/10.1002/asna.201011390
Zirin, H.: The Big Bear Solar Observatory. Sky and Telescope. 39, 215 (1970)
Martin, Schwarzschild: B.: Balloon astronomy. Scientific American. 200, 52–59 (1959). https://doi.org/10.1038/scientificamerican0559-52
Tsuneta, S., Ichimoto, K., Katsukawa, Y., Nagata, S., Otsubo, M., Shimizu, T., Suematsu, Y., Nakagiri, M., Noguchi, M., Tarbell, T., Title, A., Shine, R., Rosenberg, W., Hoffmann, C., Jurcevich, B., Kushner, G., Levay, M., Lites, B., Elmore, D., Matsushita, T., Kawaguchi, N., Saito, H., Mikami, I., Hill, L.D., Owens, J.K.: The Solar Optical Telescope for the Hinode Mission: An Overview. Solar Physics. 249(2), 167–196 (2008). https://doi.org/10.1007/s11207-008-9174-z. arXiv:0711.1715
Pecora, F., Servidio, S., Greco, A., Matthaeus, W.H., McComas, D.J., Giacalone, J., Joyce, C.J., Getachew, T., Cohen, C.M.S., Leske, R.A., Wiedenbeck, M.E., McNutt, R.L., Hill, M.E., Mitchell, D.G., Christian, E.R., Roelof, E.C., Schwadron, N.A., Bale, S.D.: Parker Solar Probe observations of helical structures as boundaries for energetic particles. Monthly Notices of the Royal Astronomical Society. 508(2), 2114–2122 (2021). https://doi.org/10.1093/mnras/stab2659, arXiv:2109.04571
Vourlidas, A., Howard, R.A., Plunkett, S.P., Korendyke, C.M., Thernisien, A.F.R., Wang, D., Rich, N., Carter, M.T., Chua, D.H., Socker, D.G., Linton, M.G., Morrill, J.S., Lynch, S., Thurn, A., Van Duyne, P., Hagood, R., Clifford, G., Grey, P.J., Velli, M., Liewer, P.C., Hall, J.R., DeJong, E.M., Mikic, Z., Rochus, P., Mazy, E., Bothmer, V., Rodmann, J.: The Wide-Field Imager for Solar Probe Plus (WISPR). Space Science Reviews. 204(1–4), 83–130 (2016). https://doi.org/10.1007/s11214-014-0114-y
Müller, D., St. Cyr, O.C., Zouganelis, I., Gilbert, H.R., Marsden, R., Nieves-Chinchilla, T., Antonucci, E., Auchère, F., Berghmans, D., Horbury, T.S., Howard, R.A., Krucker, S., Maksimovic, M., Owen, C.J., Rochus, P., Rodriguez-Pacheco, J., Romoli, M., Solanki, S.K., Bruno, R., Carlsson, M., Fludra, A., Harra, L., Hassler, D.M., Livi, S., Louarn, P., Peter, H., Schühle, U., Teriaca, L., del Toro Iniesta, J.C., Wimmer-Schweingruber, R.F., Marsch, E., Velli, M., De Groof, A., Walsh, A., Williams, D.: The Solar Orbiter mission. Science overview. Astronomy & Astrophysics. 642, 1 (2020). https://doi.org/10.1051/0004-6361/202038467arXiv:2009.00861
Rochus, P., Auchère, F., Berghmans, D., Harra, L., Schmutz, W., Schühle, U., Addison, P., Appourchaux, T., Aznar Cuadrado, R., Baker, D., Barbay, J., Bates, D., BenMoussa, A., Bergmann, M., Beurthe, C., Borgo, B., Bonte, K., Bouzit, M., Bradley, L., Büchel, V., Buchlin, E., Büchner, J., Cabé, F., Cadiergues, L., Chaigneau, M., Chares, B., Choque Cortez, C., Coker, P., Condamin, M., Coumar, S., Curdt, W., Cutler, J., Davies, D., Davison, G., Defise, J.-M., Del Zanna, G., Delmotte, F., Delouille, V., Dolla, L., Dumesnil, C., Dürig, F., Enge, R., François, S., Fourmond, J.-J., Gillis, J.-M., Giordanengo, B., Gissot, S., Green, L.M., Guerreiro, N., Guilbaud, A., Gyo, M., Haberreiter, M., Hafiz, A., Hailey, M., Halain, J.-P., Hansotte, J., Hecquet, C., Heerlein, K., Hellin, M.-L., Hemsley, S., Hermans, A., Hervier, V., Hochedez, J.-F., Houbrechts, Y., Ihsan, K., Jacques, L., Jérôme, A., Jones, J., Kahle, M., Kennedy, T., Klaproth, M., Kolleck, M., Koller, S., Kotsialos, E., Kraaikamp, E., Langer, P., Lawrenson, A., Le Clech’, J.-C., Lenaerts, C., Liebecq, S., Linder, D., Long, D.M., Mampaey, B., Markiewicz-Innes, D., Marquet, B., Marsch, E., Matthews, S., Mazy, E., Mazzoli, A., Meining, S., Meltchakov, E., Mercier, R., Meyer, S., Monecke, M., Monfort, F., Morinaud, G., Moron, F., Mountney, L., Müller, R., Nicula, B., Parenti, S., Peter, H., Pfiffner, D., Philippon, A., Phillips, I., Plesseria, J.-Y., Pylyser, E., Rabecki, F., Ravet-Krill, M.-F., Rebellato, J., Renotte, E., Rodriguez, L., Roose, S., Rosin, J., Rossi, L., Roth, P., Rouesnel, F., Roulliay, M., Rousseau, A., Ruane, K., Scanlan, J., Schlatter, P., Seaton, D.B., Silliman, K., Smit, S., Smith, P.J., Solanki, S.K., Spescha, M., Spencer, A., Stegen, K., Stockman, Y., Szwec, N., Tamiatto, C., Tandy, J., Teriaca, L., Theobald, C., Tychon, I., van Driel-Gesztelyi, L., Verbeeck, C., Vial, J.-C., Werner, S., West, M.J., Westwood, D., Wiegelmann, T., Willis, G., Winter, B., Zerr, A., Zhang, X., Zhukov, A.N.: The Solar Orbiter EUI instrument: The Extreme Ultraviolet Imager. Astronomy & Astrophysics. 642, 8 (2020). https://doi.org/10.1051/0004-6361/201936663
Rogerson, J.B.: The Orbiting Astronomical Observatories. Space Science Reviews. 2(5), 621–652 (1963). https://doi.org/10.1007/BF00172442
Young, E.F., Hibbitts, C., Emery, J., Hendrix, A., Merline, W., Grundy, W., Retherford, K.: Balloon-borne telescopes for planetary science: Imaging and photometry. Technical report, Southwest Research Institute, Space Studies, Boulder, United States (2017). https://solarsystem.nasa.gov/studies/155/balloon-borne-telescopes-for-planetary-science-imaging-and-photometry/
Young, E.: NASA’s GHAPS Project: A Balloon-Borne Telescope for Planetary Science. In: EGU General Assembly Conference Abstracts. EGU General Assembly Conference Abstracts, p. 17953 (2017)
Schwarzschild, M.: Photographs of the solar granulation taken from the stratosphere. The Astrophysical Journal. 130, 345 (1959). https://doi.org/10.1086/146725
Kiepenheuer, K.O., Mehltretter, J.P.: Spectrostratoscope: A balloon-borne solar observatory. Applied Optics. 3, 1359 (1964). https://doi.org/10.1364/ao.3.001359
Mehltretter, J.P.: Balloon-borne imagery of the solar granulation. II. The lifetime of solar granulation. Astronomy and Astrophysics. 62(3), 311–316 (1978)
Krat, V.A.: Solar research at the Pulkovo Astronomical Observatory. Solar Physics. 73(2), 405–409 (1981). https://doi.org/10.1007/BF00151690
Rust, D.M., Murphy, G., Strohbehn, K., Keller, C.U.: Balloon-Borne Polarimetry. Solar Physics. 164(1–2), 403–415 (1996). https://doi.org/10.1007/BF00146652
Bernasconi, P.N., Eaton, H.A.C., Foukal, P., Rust, D.M.: The solar bolometric imager. Advances in Space Research. 33(10), 1746–1754 (2004). https://doi.org/10.1016/j.asr.2003.08.028
Solanki, S.K., Barthol, P., Danilovic, S., Feller, A., Gandorfer, A., Hirzberger, J., Riethmüller, T.L., Schüssler, M., Bonet, J.A., Martínez Pillet, V., del Toro Iniesta, J.C., Domingo, V., Palacios, J., Knölker, M., Bello González, N., Berkefeld, T., Franz, M., Schmidt, W., Title, A.M.: SUNRISE: Instrument, Mission, Data, and First Results. The Astrophysical Journal Letters. 723(2), 127–133 (2010). https://doi.org/10.1088/2041-8205/723/2/L127. arXiv:1008.3460
Bittner, H., Erdmann, M., Haberler, P., Hartel, K.-R., Barthol, P., Curdt, W.: Baseline design of the sunrise telescope. Ground-based Telescopes. 5489, 927 (2004). https://doi.org/10.1117/12.552007
The sunrise mission: Barthol, P., Gandorfer, A., Solanki, S.K., Schüssler, M., Chares, B., Curdt, W., Deutsch, W., Feller, A., Germerott, D., Grauf, B., Heerlein, K., Hirzberger, J., Kolleck, M., Meller, R., Müller, R., Riethmüller, T.L., Tomasch, G., Knölker, M., Lites, B.W., Card, G., Elmore, D., Fox, J., Lecinski, A., Nelson, P., Summers, R., Watt, A., Pillet, V.M., Bonet, J.A., Schmidt, W., Berkefeld, T., Title, A.M., Domingo, V., Blesa, J.L.G., Toro Iniesta, J.C., Jiménez, A.L., Álvarez-Herrero, A., Sabau-Graziati, L., Widani, C., Haberler, P., Härtel, K., Kampf, D., Levin, T., Grande, I.P., Sanz-Andrés, A., Schmidt, E. Solar Physics. 268, 1–34 (2010). https://doi.org/10.1007/s11207-010-9662-9
Max Planck Institute for Solar System Research: SUNRISE III: a balloon-borne Solar Observatory. https://www.mps.mpg.de/solar-physics/sunrise. Accessed: insert-date-here
Urban, M., Nentvich, O., Báča, T., Veřtát, I., Maršíková, V., Doubravová, D., Dániel, V., Inneman, A., Pína, L., Sieger, L., McEntaffer, R.L.: Rex: X-ray experiment on the water recovery rocket. Acta Astronautica. 184, 1–10 (2021)
Stehlikova, V., Urban, M., Nentvich, O., Daniel, V., Sieger, L., Tutt, J.: Hard x-ray vela supernova observation on rocket experiment wrx-r. Contributions of the Astronomical Observatory Skalnate Pleso. 47, 165–169 (2017)
Nirmal, K., Sreejith, A.G., Mathew, J., Sarpotdar, M., Ambily, S., Prakash, A., Safonova, M., Murthy, J.: Pointing system for the balloon-borne astronomical payloads. Journal of Astronomical Telescopes, Instruments, and Systems. (2016)
Beatty, D., Flaherty, H., Kloetzel, R., Nystrom, V.: High elevation light intensity observation system v. Technical report, University of Colorado at Boulder (2016)
Fittock, M., Stamminger, A., Maria, R., Dannenberg, K., Page, H.: REXUS/BEXUS: launching student experiments -a step towards a stronger space science community. In: 38th COSPAR Scientific Assembly, vol. 38, p. 6 (2010)
High Altitude Student Payload: High Altitude Student Payload Website. https://laspace.lsu.edu/hasp/index.php
Guzik, T.G., Granger, D., Fairbrother, D., Canfield, A., Franco, H., Salter, R., Hays, J.R.: Leading University Students to the Edge of Space. In: 43rd COSPAR Scientific Assembly. Held 28 January-4 February, vol. 43, p. 2299 (2021)
Cho, Y.-H., Heung, G.S.Y., Verth, G., Fedun, V.: Sheffield university solar balloon lifted telescope (sunbyte-bexus 25). 2nd Symposium on Space Educational Activities. (2018)
Drive AG: Engineering Data HFUC-2UH Units. https://harmonicdrive.de/fileadmin/user_upload/2014_12_ED_1019644_HFUC_2UH.pdf
Aubin, F., Bayman, B., Hanany, S., Franco, H., Marsh, J., Didier, J., Miller, A.D.: Torsional balloon flight line oscillations: Comparison of modelling to flight data. Advances in Space Research. 60 (2017). https://doi.org/10.1016/j.asr.2017.05.003
Krämer, S., Kinnaird, A., Newie, N., Inga, M., Schmidt, A., Siegl, M., Fittock, M., Uitendaal, M.: Bexus user manual. (2016)
Vargas, A.: User manual for zpb infrastructure access. (2019)
McLean, M.: Data Density Plot. https://uk.mathworks.com/matlabcentral/fileexchange/31726-data-density-plot
Damian, A.: The Sun in Baader, CaK, and H-alpha Filters. http://www.cnyo.org/2013/09/
Johnson, L.: Real-time Object Tracking with TensorFlow, Raspberry Pi, and Pan-Tilt HAT. Portable Computer Vision and Motion Tracking on a Budget. https://towardsdatascience.com/real-time-object-tracking-with-tensorflow-raspberry-pi-and-pan-tilt-hat-2aeaef47e134
Rosebrock, A.: Raspberry Pi: Deep Learning Object Detection with OpenCV. https://pyimagesearch.com/2017/10/16/raspberry-pi-deep-learning-object-detection-with-opencv/
Zeevi, S.: Build a Faster OpenCV for Raspberry Pi3. https://www.theimpossiblecode.com/blog/build-faster-opencv-raspberry-pi3/
SPATIALES, C.N.D.: Integrated Access to Balloon-borne Platforms for Innovative Research and Technology. https://doi.org/10.3030/730970 . https://cordis.europa.eu/project/id/730970
Middleton, J.E.G., Janiak, I.A., Wege, S.: Developing low-cost, reusable solar observation platforms to advance sustainable heliophysics research. 4th Symposium on Space Educational Activities. (2022). https://doi.org/10.5821/CONFERENCE-9788419184405.109
Acknowledgements
The authors thank our balloon launch vehicle providers: Dr Guzik and his team at the Louisiana State University and NASA Balloon Program Office for running the HASP programme; to the team at the European Space Agency, German Aerospace centre, Swedish National Space Board (now renamed to Swedish National Space Agency) for organising the REXUS/BEXUS programme. Further thanks to all the engineers, scientists, technicians and students who participated in the SunbYte Programme. Personal thanks to Professor Tony Ryan, Professor Mike Hounslow, Professor Wyn Morgan and Dr Stuart Fraser for their support of our student-led learning initiatives at the University of Sheffield.
Funding
We would like to express our appreciation to the University of Sheffield’s Alumni Fund, the Higher Education Innovation Fund (HEiF) as well as the Faculty of Engineering’s Departments of Automatic Controls and Systems Engineering, Mechanical Engineering, Electronic and Electrical Engineering, Aerospace Engineering; and the Faculty of Science’s Department of Physics and School of Mathematics and Statistics. To the iForge makerspace at the Diamond for their in-kind support and the Mercure research centre for their metal 3D printing support. In addition, we would like to thank the Professional Engineering Institutions: Institution of Mechanical Engineers, IMechE (ESAC/REPRECGOOD/17/096) and the Institution of Engineering Technology, IET for their funding and support. YHC would like to express his gratitude to the UK Space Agency for financial support via the Space Placements in Industry (SPIN) programme. GH is thankful to the Croucher Foundation for their financial funding to the University of Hong Kong (Ref: 18J049, 18J050 & 18J051). Many thanks to industry companies 3DS, Harmonic Drive AG, Andor Oxford Instruments and Rother Valley Optics for their technical support and/or in-part contribution.
Author information
Authors and Affiliations
Contributions
Yun-Hang Cho (YHC) wrote the main manuscript. YHC and Gianni Heung (GH) prepared the figures. Yakov Bobrov (YB) assisted with the literature review. Joseph Middleton participated in the conclusions and recent developments sections. Viktor Fedun (VF) and Gary Verth (GV) participated in the paper writing, reviewing and provided academic support.
Corresponding author
Ethics declarations
Competing interests
The authors declare no known conflicts of interest.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cho, YH., Heung, G., Bobrov, Y. et al. SunbYte: an autonomous pointing framework for low-cost robotic solar telescopes on high altitude balloons. Exp Astron 57, 27 (2024). https://doi.org/10.1007/s10686-024-09944-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10686-024-09944-w