1 GRB simulations and cross-correlation analysis

We have used cross-correlation techniques to investigate the temporal delays between the light-curves of a given GRB in different energy bands. The light-curve of a bright long GRB observed by Fermi-GBM is shown in Fig. 1, Panel a. The bright Long GRB lasted for ΔtGRB = 40 s, with an average flux in the 50–300 keV energy band of ϕGRB = 6.5 photons/s/cm2, and a background flux of ϕBCK = 2.8 photons/s/cm2. Moreover, the GRB was characterised by variability on timescale of the order of \(\sim \) 5 ms.

Fig. 1
figure 1

GRB130502327 observed by Fermi-GBM. Panel a) GRB light-curve. Panel b) Template at one millisecond resolution (detail of the main peak)

Full size image

Starting from this, we derived a template with millisecond resolution (see [1] for more details). Figure 1, Panel b, shows the detail of the main peak of the GRB template where the timescale of the fast variability is about 5 ms. Using Monte-Carlo simulations, we generated light-curves as seen by detectors of different effective areas. Since the number of photons collected in a given energy energy band is a fraction of the total number of photons collected, light-curves obtained from detectors of different areas are equivalent - w.r.t. cross-correlation accuracies - to light-curves in different energy bands providing that the number of photons expected in a given energy band is equal to the number of photons detected with a detector of a given area. We performed cross-correlation analysis between pairs of simulated GRB with the aim to investigate the capability to reconstruct time delays between the observed signals. As an example, the cross-correlation function at 1 μ s resolution for a pair of detectors of 100 m2 area is shown in Fig. 2, Panel a. Panel b shows the detail of the cross-correlation function around the peak and the best fit Gaussian. To determine a reliable estimation of the accuracy achievable using cross-correlation analysis, we repeated the procedure described 1000 times, and we then fitted the distribution with a Gaussian model, from which we estimated an accuracy of 0.27 μ s. Distributions for different effective areas, 56 cm2 (HERMES, see [2, 3] for more details on the HERMES project), 125 cm2 (Fermi-GBM), 1 m2, 10 m2, 50 m2, and 100 m2, are shown in the six panels of Fig. 3, top panel. The bottom panel shows the one sigma delay accuracy as a function of the effective area. The accuracy scales as the inverse of the effective area A to the power of 0.6, close but slightly better than the theoretical lower limit of 0.5 (derived from counting statistics).

Fig. 2
figure 2

Cross–correlation analysis of a simulated GRB seen by two identical detectors. Panel a) Cross–correlation function. Panel b) Detail of the cross–correlation function at 1 μ s around the main peak

Full size image
Fig. 3
figure 3

Accuracy in cross correlation derived from Monte-Carlo simulations of GRBs. Top panel) Distributions of the delays obtained from cross-correlation analysis between 1000 pairs of simulated light-curves of identical detectors, for different effective areas, 56 cm2 (HERMES), 125 cm2 (Fermi-GBM), 1 m2, 10 m2, 50 m2, and 100 m2. Bottom panel) Logarithmic plot of the one sigma delay accuracy as a function of the effective area and best linear fit

Full size image

The best fit formula is:

$$ \sigma_{\text{cross}} \sim \sigma_{{\Delta} t} = 3.3 \mu\mathrm{s} \times \left( \frac{A}{1 \mathrm{m}^{2}} \right)^{-0.58}. $$
(1)

In terms of the number of collected photons N (adopting the same \(0.8/6.5 \sim 40\%\) overall background) we obtain:

$$ \sigma_{\text{cross}} \sim \sigma_{{\Delta} t} = 3.3 \mu\mathrm{s} \times \left( \frac{N}{3.7 \times 10^{6}} \right)^{-0.58}. $$
(2)

2 A shallow dive into quantum gravity: minimal length hypothesis, Lorentz invariance violation, and dispersion relation for photons in vacuo

Several theories proposed to describe quantum Space-Time, for instance some String Theories, predict the existence of a minimal length for space of the order of Planck length, \(\ell _{\text {PLANCK}} = \sqrt {G \hbar /c^{3}} = 1.6 \times 10^{-33}\) cm (see e.g. [4] for a review). This implies the following facts:

  • these theories predict a Lorentz Invariance Violation (LIV, hereafter). According to Special Relativity, a proper length, ℓ, is Lorentz contracted by a factor γ− 1 = [1 − (v/c)2]1/2 when observed from a reference system moving at speed v w.r.t. the reference system in which ℓ is at rest. If ℓMIN = αℓPLANCK (where \(\alpha \sim 1\) is a dimensionless constant that depends on the particular theory under consideration) is the minimal length physically conceivable (in String Theories ℓMIN is the String length), no further Lorentz contraction must occur, at this scale. This is a violation of the Lorentz invariance.

  • These theories predict the remarkable fact that the space has, somehow, the structure of a crystal lattice, at Planck scale.

  • In perfect analogy with the propagation of light in crystals, these theories predict the existence of a dispersion law for photons in vacuo [5]. Since, for photons, energy scales as the inverse of the wavelength, this dispersion law can be expressed as a function of the energy of photons in units of the Quantum Gravity energy scale, which is the energy at which the quantum nature of gravity becomes relevant: EQG = ζmPLANCKc2 = ζEPLANCK, where \(\zeta \sim \alpha ^{-1} \sim 1\) is a dimensionless constant that depends on the particular theory under consideration, \(m_{\text {PLANCK}} = \sqrt {c \hbar /G} = 2.2 \times 10^{-5}\) g is the Planck mass, and the Planck energy is EPLANCK = 1.2 × 1019 GeV. We have:

    $$ |v_{\text{PHOT}}/c - 1| \approx \xi \left( \frac{E_{\text{PHOT}}}{\zeta m_{\text{PLANCK}} c^{2}} \right)^{n} $$
    (3)

    where \(\xi \sim 1\) is a dimensionless constant that depends on the particular theory under consideration, vPHOT is the group velocity of the photon wave-packet, and EPHOT is the photon energy. The index n is the order of the first relevant term in the expansion in the small parameter 𝜖 = EPHOT/(ζmPLANCKc2). In several theories that predict the existence of a minimal length, typically, n = 1. Finally, the modulus is present in (3) takes into account the possibility (predicted by different LIV theories) that higher energy photons are faster or slower than lower energy photons (discussed as sub-luminal, + 1, or super-luminal, − 1, as in [6]).

We stress that not all the theories proposed to quantise gravity predict a LIV at some scale. This is certainly the case for Loop Quantum Gravity (see e.g. [7,8,9]). No LIV is expected as a consequence of the recently proposed Space-Time Uncertainty Principle [10] and in the Quantum Space-Time [11]. In some of these theories it is possible to conceive a photon dispersion relation that does not violate Lorentz invariance, although the first relevant term is quadratic in the ratio photon energy over EQG, i.e. n = 2 in this case. We explicitly note that, since \(E_{\text {QG}} \sim 10^{19}\) GeV, second order effects are almost not relevant even for photons of at 0.1 PeV energies (1014 eV), the highest energy photons ever recorded, recently confirmed to be emitted by the Crab Nebula [12]. Indeed also for these extreme photons \((E_{\text {PHOT}}/E_{\text {QG}})^{2} \sim 10^{-28}\).

2.1 Dispersion relation for photons in vacuo

During motion at constant velocity, travel time is the ratio between the distance travelled DTRAV and the speed. Therefore, differences in speed result in differences in the arrival times ΔtQG of photons of different energies ΔEPHOT departing from the same point at the same time, such as those emitted during a GRB event. For small speed differences, as those predicted by the dispersion relations discussed above, these delays scales with the same order n – in the ratio ΔEPHOT/EQG – as that between photon energy and Quantum Gravity energy scale:

$$ {\Delta} t_{\text{QG}} = \pm \xi \left( \frac{D_{\text{TRAV}}}{c} \right) \left( \frac{{\Delta} E_{\text{PHOT}}}{\zeta m_{\text{PLANCK}} c^{2}} \right)^{n}, $$
(4)

where \(\xi \sim 1\) is a dimensionless constant that depends on the particular theory under consideration and the sign ± takes into account the possibility (predicted by different LIV theories) that higher energy photons are faster or slower than lower energy photons respectively, as discussed above [6].

On the other hand, the distance traveled has to take into account the cosmological expansion, being a function of cosmological parameters and redshift. The comoving trajectory of a particle is obtained by writing its Hamiltonian in terms of the comoving momentum [13]. The computation of the delays has to take into account the fact that the proper distance varies as the universe expands. Photons of different energies are affected by different delays along the path, so, because of cosmological expansion, a delay produced further back in the path amounts to a larger delay on Earth. Taking into account these effects this modified “distance traveled” DEXP can be computed [13].

More specifically we adopted the so called Lambda Cold Dark Matter Cosmology (ΛCDM) with the following values [14]: H0 = 67.74(46) km s− 1Mpc− 1, Ωk = 0, curvature k = 0 that implies a flat Universe, ΩR = 0, radiation = 0 that implies a cold Universe, w = − 1, negative pressure Equation of State for the so called Dark Energy that implies an accelerating Universe, ΩΛ = 0.6911(62) and ΩMatter = 0.3089(62) (see [14], for the parameters and related uncertainties).

With these values we have:

$$ \frac{D_{\text{EXP}}}{c} = \frac{1}{H_{0}} {{\int}_{\!\!\!\!0}^{z}} dz \frac{(1+z)}{\sqrt{{\Omega}_{{\Lambda}} + (1+z)^{3}{\Omega}_{\text{Matter}}}}, $$
(5)

where z is the redshift.

Substituting DTRAV of (4) with DEXP derived in (5) we finally obtain the delays between the time of arrival of photons of different energies as a function of the specific Dispersion Relation adopted, the specific Cosmology adopted, and the redshift:

$$ {\Delta} t_{\text{QG}} = \pm \xi \left( \frac{1}{H_{0}} {{\int}_{0}^{z}} dz \frac{(1+z)}{\sqrt{{\Omega}_{{\Lambda}} + (1+z)^{3}{\Omega}_{\text{Matter}}}} \right) \left( \frac{{\Delta} E_{\text{PHOT}}}{\zeta m_{\text{PLANCK}} c^{2}} \right)^{n}. $$
(6)

2.2 Computation of the expected delays: long GRB at different redshifts

We considered a bright Long GRB lasted for ΔtGRB = 40 s, with average flux in the 50–300 keV energy band ϕGRB = 6.5 photons/s/cm2, background flux of ϕBCK = 2.8 photons/s/cm2, and variability timescale \(\sim 5\) ms discussed in Section 1.

We selected eight consecutive energy bands from 5 to 50 MeV. For an overall collecting area of 100 m2, the number of detected photons in each band was computed adopting a Band function, an empirical function that well fits GRB spectra [16]:

$$ \frac{dN_{E}(E)}{dA dt} = F \times \left\{ \begin{array}{lr} \left( \frac{E}{E_{\mathrm{B}}} \right)^{\alpha} \exp\{-(\alpha - \beta)E/E_{\mathrm{B}}\}, & E \le E_{\mathrm{B}}\\ \left( \frac{E}{E_{\mathrm{B}}} \right)^{\beta} \exp\{-(\alpha - \beta) \}, & E \ge E_{\mathrm{B}}, \end{array} \right. $$
(7)

where E is the photon energy, dNE(E)/(dAdt) is the photon intensity energy distribution in units of photons/cm2/s/keV, F is a normalisation constant in units of photons/cm2/s/keV, EB is the break energy, and EP = [(2 + α)/(α − β)]EB is the peak energy. For most GRBs: \(\alpha \sim -1\), \(\beta \sim -2.0 \div -2.5\), and \(E_{\mathrm {B}} \sim 225\) keV that implies \(E_{\mathrm {P}} \sim 150\) keV. We considered soft and hard cases (β = − 2.5 and β = − 2.0, respectively). Once the number of photons collected in each band N is computed, the one sigma accuracy in the delays of the ToA of photons in a given energy band, ECC(N), is computed adopting the results of cross-correlation analysis performed on pairs of Monte-Carlo simulated GRBs in Section 1 and expressed in (2) adopting the most conservative assumption that ECC(N) scales as (N/3.7 × 106)− 0.5 (as expected from counting statistics) and not as (N/3.7 × 106)− 0.58 of (2). We adopted the geometric mean of the lower and upper limits of a given energy band, \(E_{\min \limits }\) and \(E_{\max \limits }\) respectively, as representative of the average energy of the photons in that given band \(E_{\text {AVE}} = \sqrt {E_{\min \limits } \times E_{\max \limits }}\). With this, the energy difference between photons of different energy bands w.r.t. photons of very low energy \(E_{\text {AVE}} \sim 0\), are ΔEPHOT = EAVE. We adopted the cosmology described in Section 2.1, a first order dispersion relation i.e. n = 1, and, finally, ξ = 1 and ζ = 1. The Quantum Gravity delays of the time of arrival of photons of different energy bands were computed with (6), for values of the redshift z = 0.1,0.5,1.0,3.0, typical of GRBs as shown in Fig. 4. The results are shown in Table 1. Numbers in red and blue refer to delays below and just above one sigma accuracy, respectively. Numbers in black are above three sigma.

Fig. 4
figure 4

Distribution of 219 GRBs detected by Swift as a function of the redshift in bins of Δz = 0.2. Figure from [15]

Full size image
Table 1 Photon fluence and expected delays induced by a Quantum Gravity first order Dispersion Relation for the bright Long GRB described in Section 1 and observed with a detector of cumulative effective area of 100 m2 (e.g. obtained by adding the photons collected by N = 104 nano–satellites of 100 cm2 each)
Full size table

2.3 Intrinsic delays or quantum gravity delays?

Because of unknown details on the Fireball model, intrinsic delays in the emission of photons of different energy bands are possible. For a given GRB, these intrinsic delays can mix to, or even mimic, a genuine quantum gravity effect, making its detection impossible. However, intrinsic delays in the emission mechanism are independent of the distance of the GRB. On the other hand, the delays induced by a photon dispersion law are proportional both to the distance traveled (known function of redshift) and to the differences in energy of the photons. This double dependence on energy and redshift is the unique signature of a genuine Quantum Gravity effect. This behaviour, shown in Table 1, demonstrates that, given an adequate collecting area, GRBs are indeed excellent tools to effectively search for a first order dispersion law for photons, once their redshifts are known.

3 Testing LIV theories with THESEUS

3.1 The sample

We considered a sample of long GRBs detectable by THESEUS in one year of mission as derived from the mock catalogue of 2 millions of long GRB produced by Ghirlanda et al. (see Ghirlanda et al., 2021, for details). Moreover we considered the fraction of long GRBs in the adopted mock catalogue that are detectable by THESEUS for which a measure of the redshift is obtainable according to the sensitivity of the mission and the conditions under which a good redshift measurement is possible (see Mereghetti et al., 2021, for details). This gave us a sample of about 200 long GRBs per year. In order to apply the accuracy in delays of (2), derived in the hypothesis of a signal-to-background ratio \(\sim \) 2, we further selected the GRBs that fulfil these criteria (\(\sim \) 4 per year). It is possible, in principle, to use the whole sample of 200 GRBs per year, however, for GRBs with signal-to-background ratio < 2, the accuracy in computing the delays has a much more complex dependence on the number of photons in the GRB, than that expressed in (2). In this case further studies are required to obtain a reliable relation that express the accuracy in computing the delays as a function of the number of photons in the GRB and the number of photons in the background. The inclusion of the whole sample of GRBs in our analysis is possible once this more complex relation is adequately investigated, but this is beyond the scope of this short report and will be discussed elsewhere. Finally we considered two scenarios: a mission lasting for its nominal duration, 3 years lifetime (13 GRBs in the sample), and an extended mission, lasting for 7.5 years (27 GRBs in the sample).Footnote 1

3.2 The analysis

We firstly explored, for each GRB in a given energy band, ΔEPHOT i, i = 1,...,Nbands, where Nbands is the total number of energy bands adopted, the dependence of the delays on the redshift. This, according to (6) with n = 1 and \(\xi \sim 1\) is:

$$ {\Delta} t_{\text{QG i}} = \frac{1}{H_{0}} \left( \frac{{\Delta} E_{\text{PHOT i}}}{\zeta m_{\text{PLANCK}} c^{2}} \right) \times f(z) $$
(8)

where

$$ f(z) = {{\int}_{0}^{z}} dz \frac{(1+z)}{\sqrt{{\Omega}_{{\Lambda}} + (1+z)^{3}{\Omega}_{\text{Matter}}}}. $$
(9)

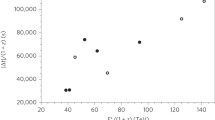
Fits of (8) as a function of f(z), are shown in Fig. 5, for the eight energy bands chosen to cover the whole energy range of THESEUS, from 10 keV to 10 MeV. In particular these energy bands are: 2–25 keV; 25–50 keV; 50–150 keV; 150–300 keV; 300–1000 keV; 1000–2000 keV; 2000–5000 keV; 5000–10000 keV.

Fig. 5
figure 5

The eight panels show the delays \(H_{0}^{-1} \left ({\Delta } E_{\text {PHOT i}}/(\zeta m_{\text {PLANCK}} c^{2}) \right )\) (i.e. the expected delays normalised to a redshift function f(z) = 1) vs. the redshift function f(z) defined in (9) in the text, for the eight energy bands chosen to cover the whole energy range of THESEUS, from 10 keV to 10 MeV. The best fit slope of each panel are the values si defined in (10) in the text

Full size image

The slopes of these linear fits represent the eight values of the quantities

$$ s_{\mathrm{i}} = \frac{1}{\zeta} \frac{1}{H_{0}} g(E_{\text{PHOT i}}) $$
(10)

where

$$ g(E_{\text{PHOT i}}) = \left( \frac{{\Delta} E_{\text{PHOT i}}}{m_{\text{PLANCK}} c^{2}} \right) $$
(11)

for i = 1,...,Nbands. Fit of (10) as a function of h(EPHOT i) = g(EPHOT i)/H0, are shown in Fig. 5, for the eight energy bands chosen to cover the whole energy range of THESEUS, from 10 keV to 10 MeV. The slope of this linear fit gives the quantity

$$ \mu = \frac{1}{\zeta} $$
(12)

As it is customary in this field, the parameter μ express the strength of the LIV effect. The higher the μ, the greater the effect of Quantum Gravity, in the sense that a value of e.g. μ = 5 implies that the effects of Quantum Gravity are already relevant at energies equal to 1/5 of Planck energy, mPLANCKc2.

To quantify the capability of THESEUS in deriving a robust upper limit (or detection) of a LIV effect, we injected, in our sample, a LIV parametrised by a dummy value of μ. In particular we adopted μ = 30 in the simulations performed. The three sigma upper limit on μ has been computed from the one sigma error on the slope quoted in the fit.

To be conservative, in performing this last fit we made two assumptions:

  • i) we artificially amplified by one order of magnitude the statistical errors on the quantities si w.r.t. obtained by applying (2) derived from our Monte-Carlo simulations of long GRBs. This is done to take into account several effects that could worsen the statistical accuracies. Among these the most relevant is the unknown (a priori) variation of the shape of the GRB light-curve in different energy bands that could bias the value of the cross correlation;

  • ii) we considered two scenarios, the first in which the similarity of the light-curves is guaranteed over the whole THESEUS energy band 2 keV–10 MeV. In this case all the si were included in our analysis. In a more conservative approach, we assumed that the similarity of the light-curves holds only for energies ≤ 1 MeV and, consequently, all the si above this threshold were excluded from our analysis.

Our results are shown in Fig. 6 where we explored the two scenarios mentioned above, namely a mission lasting for its nominal duration, 3 years (13 GRBs in the sample), and an extended mission, lasting for 7.5 years (27 GRBs in the sample).

Fig. 6
figure 6

Distributions of the Monte-Carlo simulations performed to explored the μ parameter for the two mission scenarios described in the text: i.e. nominal mission duration, 3 years (13 GRBs in the sample), and an extended mission, 7.5 years (27 GRBs in the sample). We adopted μ = 30 for generating a dummy LIV effect and, as an upper limit to the value of the μ parameter, three times the one sigma uncertainty obtained from the distribution of 1000 Monte-Carlo simulations

Full size image

We compare our results with and [17] who set a robust constraint on LIV using Fermi-LAT GRB data. Applying different estimations procedures developed on the basis of statistical measures to the eight observed GRBs relatively bright in multi-GeV energies detected by Fermi-LAT, they constrained μ ≥ 50 and μ ≥ 15 depending on different hypotheses and statistical methods adopted. For a mission lasting for its nominal duration, 3 years, the results are a three sigma upper limit on μ ≤ 9, considering the whole energy range (2 keV–10 MeV) and a three sigma upper limit on μ ≤ 20, considering an energy range 2 keV–1 MeV. For a mission lasting for an extended duration, 7.5 years, the results are a three sigma upper limit on μ ≤ 7, considering the whole energy range (2 keV–10 MeV) and a three sigma upper limit on μ ≤ 15, considering an energy range 2 keV–1 MeV.