Contracting under asymmetric information and externalities: an experimental study

Abstract

We investigate contract negotiations in the presence of externalities and asymmetric information in a controlled laboratory experiment. In our setup, it is commonly known that it is always ex post efficient for player A to implement a project that has a positive external effect on player B. However, player A has private information about whether or not it is in player A’s self-interest to implement the project even when no agreement with player B is reached. Theoretically, an ex post efficient agreement can always be reached if the externality is large, whereas this is not the case if the externality is small. We vary the size of the externality and the bargaining process. The experimental results are broadly in line with the theoretical predictions. However, even when the externality is large, the players fail to achieve ex post efficiency in a substantial fraction of the observations. This finding holds in ultimatum-game bargaining as well as in unstructured bargaining with free-form communication.

1 Introduction

Externalities are ubiquitous in the public and the private sector. For instance, a nation’s climate policy can impact other nations. A city’s expenditures on infrastructure, such as public schools and hospitals, can benefit citizens in neighboring cities. A manufacturer’s decision to invest in new production technologies may reduce the harm caused by pollution in a nearby community. A firm’s research and development activities may have positive spillovers on other firms. When a country modernizes its defense capabilities, this may also improve the security of allied countries.

In a seminal article, Coase (1960) pointed out that externalities need not lead to inefficiencies when transaction costs are low enough that the parties involved can negotiate a suitable contract.¹ Specifically, suppose a decision maker can implement a project (e.g., infrastructure investments, measures to reduce pollution, R &D activities, etc.) that is socially desirable because the decision maker’s costs are smaller than the total benefits generated by the project. In some cases, it may be that the decision maker’s own benefit is larger than the project’s cost; thus, the project may be implemented even when no compensation payments are made. However, in other cases, without a contract the decision maker would not implement the project because the decision maker’s own benefit is smaller than the project’s cost. Whether or not the project would be implemented without compensation may well be private information of the decision maker. Thus, the question arises whether the transaction costs are low enough for the parties involved to agree on a contract specifying suitable transfer payments, ensuring that the project will always be implemented.

Contract theory has identified asymmetric information as a major source of transaction costs.² In particular, starting with Myerson and Satterthwaite (1983) several impossibility theorems have been proven in the contract-theoretic literature. In this context, an impossibility theorem shows that under certain circumstances rational parties will not be able to voluntarily agree on a contract that specifies an ex post efficient outcome, regardless of the bargaining protocol governing the negotiations. However, most impossibility results in the literature do not consider situations with externalities, where in the case of disagreement, one party can unilaterally make a decision that affects another party’s payoff. An important exception is Klibanoff and Morduch (1995).³ Somewhat surprisingly, they point out that the classical argument, according to which small externalities lead to small problems and large externalities give rise to large problems, can be violated. In particular, they show that it may be impossible to achieve ex post efficiency when the externality is relatively small, whereas ex post efficiency can be attained when the externality is sufficiently large. Intuitively, in the case of a small externality, an affected party may be unwilling to pay the decision maker in exchange for a specific decision if there is a good chance that the decision maker will make the same decision even without receiving a payment. In contrast, in the case of a large externality, the affected party may be more inclined to contractually agree to a suitable payment to ensure that the decision maker will make the efficient decision.

Reaching agreements to overcome externalities in the presence of asymmetric information can be of utmost importance for society, particularly regarding health, safety, security, and environmental issues. Understanding if and how agreements ensuring ex post efficient outcomes can be reached is therefore crucial. In the present paper, we use a controlled laboratory experiment to study behavior in contract negotiations with externalities and private information.⁴ In addition to studying a very simple and exogenously given bargaining game, we also explore unstructured negotiations in which individuals can freely communicate.

Our experimental design follows Klibanoff and Morduch’s (1995) basic setup. We consider two parties, player A and player B. Player A can either implement or not implement a project. Player A’s payoff v from implementing the project can be either positive or negative. While the distribution of v is commonly known, only player A knows the realization. When the project is implemented, then there is an externality of a commonly known size $w>0$ on player B.⁵ It is always ex post efficient to implement the project; i.e., the sum $v+w$ of player A’s payoff and the externality on player B is positive, even when player A’s payoff v is negative. The two parties can negotiate a contract, according to which player B makes a payment to player A and the project is implemented. If no agreement is reached, player A is free to decide whether or not to implement the project. Note that when the parties negotiate a contract, player B may be reluctant to make a payment to player A, because player A might implement the project even when no agreement is reached.

We use a 2$\times$2 design, varying the bargaining procedure and the size of the externality. In two of our four treatments, we exogenously specify a simple bargaining protocol, namely an ultimatum game where player B can make a take-it-or-leave-it offer to player A. In the other two treatments, in order to impose as few restrictions as possible on the contract negotiations, we allow for unstructured bargaining with free-form communication. In each case, we are particularly interested in comparing the effects of a small externality to those of a large externality.

In the good state (i.e., when player A’s payoff v is positive), the theoretical prediction is that the project will always be implemented, regardless of the size of the externality. In the bad state (i.e., when player A’s payoff v is negative), the predictions depend on whether or not we impose an ultimatum bargaining protocol.

In the case of the ultimatum game, the theoretical prediction in the bad state is that the project will never be implemented if the size of the externality w is small, whereas it will always be implemented if the externality is large.

The experimental results of the ultimatum game treatments are broadly in line with the predictions. In the good state, the project is implemented in the overwhelming majority of the cases. In the bad state, implementation of the project is very rare when the externality is small. The most substantial deviation of our experimental findings from the theoretical predictions occurs in the bad state when the externality is large. While the project is implemented in a majority of the cases, the implementation frequency is substantially smaller than predicted. Mild inequity aversion of player A and mistakes by player B both contribute to this deviation. However, regarding player B’s behavior, we observe some learning over time.

In the case of free-form bargaining, according to theory it is possible (but not necessary) that in the bad state the parties always reach an agreement to implement the project when the externality is large. In contrast, when the externality is small, an impossibility result holds. No matter what bargaining procedure the parties choose, they will not be able to always implement the project in the bad state. Specifically, our parameters are chosen such that according to theory, the project will not be implemented in more than 50% of the cases in the bad state.

Indeed, the experimental results of the free-form bargaining treatments show that in the good state the project is implemented in the overwhelming majority of the cases, whereas in the bad state it is implemented in approximately half of the cases when the externality is small. When in the bad state the externality is large, the implementation frequency is substantially below the theoretically possible 100%, but significantly larger than in the case of the ultimatum game. The fact that the implementation frequency is much smaller than 100% when in the bad state the externality is large can be partially explained by low offers made by player B, particularly in the first rounds of the experiment. We observe some learning effects over time. The analysis of the free-form communication shows that to reach an agreement in the bad state, it can help when player A explicitly points out that the state is bad, mentioning honesty and trust. In contrast, if player A discusses fairness issues, this reduces the likelihood that the project will be implemented.

1.1 Related literature

To the best of our knowledge, our paper presents the first experimental investigation of contracting under asymmetric information in the presence of externalities as theoretically studied by Klibanoff and Morduch (1995).

We explore behavior in a situation in which, according to theory, an impossibility result holds; i.e., ex post efficiency cannot always be achieved by voluntary negotiations, regardless of the bargaining protocol.⁶ The most famous impossibility result was shown by Myerson and Satterthwaite (1983). They consider a buyer and a seller who can trade an indivisible object. Only the buyer knows his valuation and only the seller knows her cost. It turns out that if valuation and cost are continuous random variables that are independently distributed and their supports overlap (so it is ex ante uncertain whether or not trade is ex post efficient), then it is impossible to come up with a bargaining mechanism that always results in the ex post efficient trade decision.⁷

There is by now a large contract-theoretic literature on possibility and impossibility results following Myerson and Satterthwaite (1983); see, e.g., Mailath and Postlewaite (1990), Makowski and Mezzetti (1994), Williams (1999), Schweizer (2006), Segal and Whinston (2011), and Segal and Whinston (2013). In this literature, it is usually assumed that when no agreement between the parties is reached, there is no trade; i.e., the allocation is then given by a commonly known status quo.

In contrast, building on Klibanoff and Morduch (1995), we consider a setup where in the case of disagreement one party can make a unilateral decision that has an external effect on the other party. The impossibility result in our setting is quite different from that of Myerson and Satterthwaite (1983). In particular, there is only one-sided private information and there are only two types. The simplicity of this setup makes it particularly suitable for an experimental investigation. Moreover, the impossibility result is stronger in the sense that it holds even though it is commonly known that it is always ex post efficient to implement the project.

While we are unaware of any experimental work exploring real human behavior in such a setting, there are some studies in the experimental literature that were motivated by Myerson and Satterthwaite’s (1983) original impossibility theorem. In particular, McKelvey and Page (2000) compare bargaining under two-sided private information to bargaining under complete information. They allow for unstructured bargaining, but rule out communication. In line with Myerson and Satterthwaite (1983), their results corroborate that there is more inefficiency in the case of private information. Valley et al. (2002) also study bargaining under two-sided private information, but exogenously specify the bargaining protocol using a double auction. They find that pre-play communication can increase the fraction of cases in which the ex post efficient decision is taken.⁸

There are also experimental studies that explore settings with one-sided private information without externalities, where according to standard theory it would be possible to achieve ex post efficiency with suitable bargaining protocols. In particular, starting with Mitzkewitz and Nagel (1993), several authors have explored ultimatum games with asymmetric information; see, e.g., Straub and Murnighan (1995), Croson (1996), Güth et al. (1996), Kagel et al. (1996), Rapoport and Sundali (1996), Güth and Van Damme (1998), and Harstad and Nagel (2004).⁹ Kriss et al. (2013) study different forms of communication in ultimatum bargaining with incomplete information. Note that in a standard ultimatum game the pie to be divided is destroyed when the responder rejects the proposer’s offer. In contrast, in our setup, after rejecting the proposer’s offer, the privately informed responder is free to unilaterally decide whether or not to implement the project.

1.2 Organization of the paper

The remainder of the paper is organized as follows. In the next section, we introduce the theoretical framework that provides the starting point for our experimental study. We describe our experimental design in Sect. 3 and we derive predictions in Sect. 4. We present and analyze our experimental results in Sect. 5. Finally, concluding remarks follow in Sect. 6. Some technical details and further data analyses have been relegated to the Online Appendix and to the Supplementary Material.

2 The theoretical framework

2.1 The model

In this section, we present a stripped-down (binary) version of Klibanoff and Morduch’s (1995) model.¹⁰ There are two risk-neutral parties, player A (he) and player B (she). Player A has the right to make a decision $Q\in \{0,1\}$. The decision $Q=0$ means that we stick to the status quo, where both parties’ payoffs are zero. The decision $Q=1$ means that player A implements a project that has a direct externality on player B. Specifically, player A’s valuation of the project is $v\in \{v_{L},v_{H}\}$, where $v_{L}<0<v_{H}$, whereas player B’s valuation of the project is $w>0$.

Hence, when player B makes a transfer payment t to player A, then player A’s payoff is¹¹

$$\begin{aligned} u_{A}(Q,t)=vQ+t \end{aligned}$$

and player B’s payoff is

$$\begin{aligned} u_{B}(Q,t)=wQ-t. \end{aligned}$$

In a first-best world with symmetric information, according to the Coase Theorem the parties would agree on implementing the project whenever $v+w$ is positive. However, we are interested in the case in which player A has private information about his valuation v. In particular, v is a random variable with $\Pr \{v=v_{H}\}=p$, where $p\in (0,1)$. Following Klibanoff and Morduch (1995), we assume that only player A knows the realization of v, whereas all other elements of the model (including the size of the externality w) are common knowledge.

The sequence of events is as follows. In the first stage, player A privately learns the realization of his valuation v. In the second stage, the two parties can bargain with each other. If the parties reach an agreement about a decision Q and a transfer payment t, then the agreement will be enforced and the game is over. If the parties do not reach an agreement, then the third stage is reached. In this case, player A can choose $Q\in \{0,1\}$ unilaterally and no payment is made.

Note that when the third stage is reached, player A will implement the project if and only if $v=v_{H}$. Thus, when the externality is trivially small, $w<-v_{L}$, then player A’s decision in the case of disagreement always corresponds to the first-best outcome. In what follows, we will focus on the interesting case in which player A will not always take the first-best decision already in the absence of an agreement.

Assumption 1

Let $w>-v_{L}$.

Specifically, Assumption 1 means that it is common knowledge that in a first-best world the project would always be implemented, regardless of the state of the world.

2.2 A simple ultimatum game

Before we look at general bargaining mechanisms, let us first study a simple ultimatum game. Specifically, suppose that in the second stage player B can offer a price X that she will pay to player A when player A agrees to choose $Q=1$. If player A accepts the take-it-or-leave-it offer, the decision $Q=1$ and the payment of X will be enforced. If player A rejects the offer, the third stage is reached. Player A can then freely choose $Q\in \{0,1\}$ and no payment is made.

Recall that in the case of disagreement, in the third stage player A will set $Q=1$ if and only if $v=v_{H}$. Therefore, if in the first stage player A has learned that $v=v_{H}$, he will accept any price $X\ge 0$ in the second stage. If player A has learned that $v=v_{L}$, he will accept any price $X\ge -v_{L}$.

Since player B does not know the realization of v, anticipating player A’s reaction it is optimal for player B to propose $X=-v_{L}$ if $w+v_{L}\ge pw$, and $X=0$ otherwise.

Therefore, the first-best solution will always be attained if the externality is sufficiently large, $w\ge -v_{L}/(1-p)$. However, if the externality is relatively small, $w<-v_{L}/(1-p)$, then the project will be implemented only in the good state of the world ($v=v_{H}$), but not in the bad state of the world ($v=v_{L}$). Thus, in the latter case the first-best outcome will not be achieved.

2.3 General analysis

The simple ultimatum game we studied in the previous section is just one example of a bargaining game that the parties could play in the second stage. There are countless ways to modify and extend the ultimatum game. For instance, when player A rejects player B’s offer, he might have the possibility to make a counteroffer. It might also be the case that player A can make the first offer, and there could be many rounds with alternating offers. In general, bargaining games can have multiple equilibria, including equilibria in mixed strategies (see, e.g., Muthoo, 1999).

To characterize what can be achieved by voluntary negotiations in general, we can invoke the revelation principle (cf. Myerson, 1982). According to the revelation principle, whatever the parties can achieve with any conceivable bargaining mechanism could also be achieved with a corresponding direct revelation mechanism. In such a mechanism, player A is directly asked about his valuation, and it is in player A’s self-interest to tell the truth.¹²

In the general analysis we allow for randomization, so let $q\in [0,1]$ denote the probability that the decision $Q=1$ is taken. In the present context, a direct revelation mechanism is given by a menu of contracts $(q_{H},t_{H}),$ $(q_{L},t_{L})$, where $(q_{i},t_{i})$ are the probability of implementing the project and the transfer payment when player A claims that $v=v_{i}$, where $i\in \{L,H\}$.

The incentive-compatibility constraints that ensure truth-telling by player A are

$$\begin{aligned} q_{H}v_{H}+t_{H}&\ge q_{L}v_{H}+t_{L}, \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad {(IC_H)}\\ q_{L}v_{L}+t_{L}&\ge q_{H}v_{L}+t_{H}. \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad {(IC_L)} \end{aligned}$$

The constraint $(IC_{i})$ means that it is in the self-interest of type $i\in \{L,H\}$ of player A to pick the contract that is intended for him. The constraints that ensure voluntary participation are

$$\begin{aligned} q_{H}v_{H}+t_{H}&\ge v_{H}, \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {(PC_H^A)}\\ q_{L}v_{L}+t_{L}&\ge 0,\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad {(PC_L^A)}\\ p(q_{H}w-t_{H})+(1-p)(q_{L}w-t_{L})&\ge pw. \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad {(PC^B)} \end{aligned}$$

To see this, recall that if in the second stage no agreement is reached, then in the third stage player A will implement the project if and only if $v=v_{H}$. Hence, the constraint $(PC_{H}^{A})$ ensures that when type H of player A agrees to the mechanism, then he obtains at least $v_{H}$, whereas the constraint $(PC_{L}^{A})$ ensures that type L obtains at least zero. Recall that player B does not know the realization of v. Hence, the constraint $(PC^{B})$ ensures that player B’s expected payoff when she participates in the mechanism is larger than her expected payoff when she does not participate.

Under Assumption 1, it is common knowledge that the project would always be implemented in a first-best world ($q_{H}^{FB}=q_{L}^{FB}=1$). Under what circumstances can the first-best solution be attained in a second-best world with asymmetric information? Note that when $q_{H}=q_{L}=1$, the incentive-compatibility constraints imply $t_{H}=t_{L}=:X$. Intuitively, when the project will be implemented regardless of player A’s message, player A would always announce the state of the world that leads to a larger payment, so truth-telling requires that the payments are independent of the state. The participation constraint $(PC_{H}^{A})$ can then be rewritten as $X\ge 0$, whereas $(PC_{L}^{A})$ becomes $X\ge -v_{L}$, and $(PC^{B})$ now reads $X\le (1-p)w$. A transfer payment X that satisfies these constraints exists if and only if $w\ge -v_{L}/(1-p)$. Therefore, the first-best solution can be attained whenever the externality is sufficiently large. However, if $w<-v_{L}/(1-p)$, then it is impossible to construct a direct revelation mechanism that achieves the first-best solution and in which the parties participate voluntarily. Hence, the revelation principle implies that in this case it is impossible to achieve the first-best solution with voluntary negotiations, no matter what bargaining mechanism one might come up with.

The following proposition summarizes our results and also characterizes what in general can best be achieved when $w<-v_{L}/(1-p)$ holds.

Proposition 1

• (i) In the case of a sufficiently large externality, i.e. if $w\ge -\frac{1}{1-p}v_{L}$, the first-best solution $(q_{H}^{FB}=q_{L}^{FB}=1)$ can be achieved.

• (ii) In the case of a relatively small externality, i.e. if $w<-\frac{1}{1-p}v_{L}$, it is impossible to attain the first-best solution $(q_{H} ^{FB}=q_{L}^{FB}=1)$ with voluntary negotiations. The maximum attainable expected total surplus is achieved by $q_{H}=1$, $q_{L}=\frac{pv_{H}}{pv_{H}-v_{L}-(1-p)w}$.

Proof

See the Online Appendix. $\square$

Hence, even though it is commonly known that in a first-best world the project would always be implemented, due to asymmetric information it is impossible for the parties to voluntarily agree on a mechanism that implements the project more frequently than stated in the proposition.

3 Experimental design

3.1 Procedure

Our experiment consists of four treatments. We implemented a between-subjects design with 80 participants in each treatment; i.e., in total 320 subjects participated in the experiment.¹³ The experiment was conducted at the Karlsruhe Decision and Design Lab (KD²Lab) and all subjects were students at the Karlsruhe Institute of Technology enrolled in various fields of study.¹⁴ No subject was allowed to participate in more than one session. All interactions were anonymous; i.e., the subjects did not learn the identities of the subjects with whom they were matched.

At the beginning of each session, all subjects received identical written instructions, and they were required to answer several comprehension questions.¹⁵ Each subject was randomly assigned to a role and maintained this role throughout the session. Half of the subjects in each treatment were in the role of player A, and the remaining were in the role of player B. Each session lasted between 60 and 90 minutes. We made use of the experimental currency unit ECU, with an exchange rate of 5 ECU to one euro. On average, a subject earned 17.26 euro across the whole experiment.

To give the subjects the opportunity to gain some experience, we used a perfect stranger matching protocol with eight rounds. In particular, each subject knew that he or she would interact only once with another subject.¹⁶ This procedure leads to five independent matching groups (consisting of eight subjects in the role of player A and eight subjects in the role of player B) for each treatment. We paid all eight rounds.

After the main part of the experiment, we elicited various control variables. Specifically, we collected information on risk attitudes (Dohmen et al., 2009), social value orientation (Murphy et al., 2011), and reciprocity (Dohmen et al., 2009). Moreover, we implemented the subscale for the Honesty-Humility domain from the HEXACO personality inventory. The Honesty-Humility domain captures the facets fairness, sincerity, modesty, and greed avoidance (Ashton & Lee, 2009). We also collected demographic information from our subjects.¹⁷

3.2 Treatments

In each treatment, player A can implement a project. Player A has private information about his or her valuation v of the project, which can be either $v=v_{H}=6$ or $v=v_{L}=-10$, with equal probability ($p=1/2$). When the project is implemented, it has a commonly known externality w on player B.

We used a 2x2 design, varying both the size of the externality and the bargaining procedure (cf. Table 1). Specifically, we compare the case of a small externality ($w=14$) to the case of a large externality ($w=24$). Moreover, we consider a simple ultimatum game (in which player B can make a take-it-or-leave-it offer to player A) as well as free-form bargaining (i.e., unstructured bargaining with free-form communication).

Table 1 The four treatments

In the following, we describe our four treatments in more detail. At the beginning of each round, two subjects with different roles are matched in one group. Each round consists of up to three stages.

• Ultimatum Game with Small Externality (Treatment UG-14): In the first stage, the computer software randomly decides whether the state is “good” or “bad”.¹⁸ Both players know that the probability of each state is 50%. Player A is informed about whether the state is “good” or “bad”, whereas player B is not informed about the state. In the second stage, player B can offer a payment X, where X can be any integer between 0 and 14. If player A accepts the offer, the payment is made and the project is implemented, so player A’s payoff is X ECU $+$ 6 ECU in the “good” state and X ECU − 10 ECU in the “bad” state, whereas player B’s payoff is 14 ECU − X ECU. In this case, the round is over. If player A rejects the offer, no payment is made and the third stage is reached. In the third stage, player A can unilaterally decide whether or not to implement the project. If player A implements the project, player A’s payoff is 6 ECU in the “good” state and $-10$ ECU in the “bad” state, whereas player B’s payoff is 14 ECU. If player A does not implement the project, both players receive zero ECU.

• Ultimatum Game with Large Externality (Treatment UG-24): This treatment is identical to treatment UG-14, except that “14” is replaced by “24”.

• Free-Form Bargaining with Small Externality (Treatment FF-14): The first stage is identical to the first stage in treatment UG-14. In the second stage, the players have three minutes in which they can freely bargain about a payment X to be made from player B to player A (where X can be any integer between 0 and 14). Specifically, the players can make binding offers with regard to X and they can freely communicate by sending each other chat messages.¹⁹ Neither the number of offers nor the number of chat messages is limited. Each player can accept an offer made by the other player by clicking on an “accept” button. Moreover, each player can click on a button to break off the negotiations. In addition, players can retract offers they have made as long as the offer has not been accepted. If the players reach an agreement (i.e., one of the players accepts an offer made by the other player), then the agreed-upon payment is made and the project is implemented, so player A’s payoff is X ECU $+$ 6 ECU in the “good” state and X ECU − 10 ECU in the “bad” state, whereas player B’s payoff is 14 ECU − X ECU. Then the round is over. If the players do not reach an agreement (i.e., no player has clicked on the “accept” button within the three minutes or a player has clicked on the “break off” button), then no payment is made and the third stage is reached. The third stage is the same as that in treatment UG-14.

• Free-Form Bargaining with Large Externality (Treatment FF-24): This treatment is identical to treatment FF-14, except that “14” is replaced by “24”.

4 Predictions

Recall that in each treatment all players had the necessary information to conclude that it is always ex post efficient to implement the project, regardless of the state of the world.²⁰ Our main interest is to find out how often the project will actually be implemented and to what extent the treatment variations demonstrate the theoretically predicted effects.

In the ultimatum game treatments, the theoretical predictions are very clear. As explained in Sect. 2.2, in the case of a small externality ($w=14<-v_{L} /(1-p)=20$), player B offers a payment of zero. Hence, in the bad state player A rejects the offer and never implements the project. In the good state, the project will always be implemented (either player A accepts the offer, or player A rejects and implements the project in the third stage). In the case of a large externality ($w=24>-v_{L}/(1-p)=20$), in equilibrium player B offers a payment of 10 which player A accepts, so the project is always implemented.²¹

In the free-form bargaining treatments, it is also the case that according to theory the project will always be implemented in the good state.²² Without specifying the bargaining game, we cannot make point predictions regarding project implementation in the bad state. However, the analysis of Sect. 2.3 shows that in the case of a small externality ($w=14$) an impossibility result holds; i.e., no matter what bargaining game the players play, it is impossible that the project will always be implemented in the bad state. Specifically, according to Proposition 1, the probability that the project will be implemented cannot be larger than $\frac{pv_{H}}{pv_{H}-v_{L}-(1-p)w}=50\%$. In contrast, in the case of a large externality ($w=24$), it is possible (but not necessary) that the project will always be implemented in the bad state. The theoretically predicted implementation frequencies are summarized in Table 2.

Table 2 The theoretically predicted implementation frequencies

5 Results

5.1 Overview

We start with a short summary of our central results. Table 3 provides an overview of the main descriptive statistics.

First, we look at the prime variable of interest, the relative implementation frequency of the project. In all treatments, the project is implemented in over $94\%$ of the cases in the good state of the world, which is reasonably close to the theoretical prediction of $100\%$. In the bad state of the world, the project is implemented in only $9\%$ of the cases in UG-14 and in $56\%$ of the cases in FF-14. These results are not too far from the theoretical upper bounds of $0\%$ and $50\%$, respectively. Overall, the findings are thus broadly in line with the theoretical predictions if the externality is small.

In contrast, the implementation frequency in the bad state is only $51\%$ in UG-24, which is substantially below the theoretical prediction of $100\%$ given the large externality. Moreover, in FF-24 the implementation frequency in the bad state is $69\%$, whereas up to $100\%$ would be theoretically possible. Hence, when the externality is large then in the bad state there are unexploited gains from trade. According to theory these gains could be realized despite the presence of asymmetric information.

Table 3 Descriptive statistics

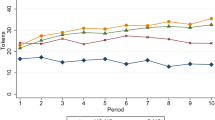
To investigate potential learning over time, we examine the implementation frequencies in all eight rounds depicted in Fig. 1. In the second half of the experiment, the implementation frequencies in the bad state in UG-24 and FF-24 are larger than those in the early rounds. Specifically, in rounds $5-8$ in the bad state the project is implemented in $61\%$ of all cases in UG-24 and in $81\%$ of all cases in FF-24. Thus, over the rounds, the subjects appeared to learn, leaving fewer gains from trade unrealized in the bad state when the externality is large. In contrast, the implementation frequencies in the good state are very similar between rounds $1-4$ and rounds $5-8$ across all treatments.

Fig. 1

The relative frequencies with which the project was implemented in each treatment, conditional on whether the state was good or bad

In the good state, the implementation frequencies do not differ significantly when we vary the size of the externality or the bargaining procedure ($p\ge 0.280$, cf. Table A1 in the Online Appendix), which is in line with the theoretical predictions.²³ Also as predicted, in the bad state the implementation frequencies differ significantly between UG-14 and UG-24 ($p=0.045$). The implementation frequencies in the bad state do not differ significantly between FF-14 and FF-24 when we consider all eight rounds ($p=0.125$). However, when we consider only experienced subjects (rounds $5-8$), the implementation frequencies in the bad state differ significantly between FF-14 and FF-24 ($p=0.048$). Moreover, regardless of whether the externality is small or large, free-form bargaining leads to significantly higher implementation frequencies in the bad state than the ultimatum game ($p\le 0.077)$.

Table 4 Random-effects logit regression with the implementation decision as the dependent variable for all treatments in the bad state

These impressions for the bad state are supported by a series of random-effects logit regressions with the implementation decision as the dependent variable displayed in Table 4. Both the coefficient of the large externality dummy variable (UG-14 vs. UG-24) and the coefficient of the Free-form (FF) dummy variable (UG-14 vs. FF-14) are significantly different from zero in all models. In addition, we observed a significant difference between the FF-14 and FF-24 treatments (Wald test $p\le 0.053$ for all models) as well as between the UG-24 and FF-24 treatments (Wald test $p\le 0.014$ for all models). Interestingly, the interaction effect between the larger externality dummy variable and the FF dummy variable is negative. The bargaining procedure and the size of the externality seem to act as substitutes rather than complements regarding their impact on the implementation decision. While we observe some learning over the rounds, we find no impact of demographic variables or individual or social preferences on the implementation decision.²⁴

To add controls for offers made by both players and chat behavior, we must split the dataset into the UG and FF treatments. The respective results are discussed in the following sections.

Finally, Table 3 also shows whether the project was implemented due to an agreement between the players in stage 2 or due to player A’s unilateral decision in stage 3. If no second-stage agreement was reached in the bad state, as predicted, the project was never implemented in the third stage, except for in one case in FF-24. Moreover, when no second-stage agreement was reached in the good state, player A implemented the project in the third stage in at least $75\%$ of the cases, whereas player A would always do so according to theory.

In the following sections, we take a closer look at the offers, the acceptance behavior, player A’s third-stage implementation decisions, and the resulting payoffs. In particular, we want to shed further light on the experimental findings that deviate from the theoretical predictions.

5.2 Ultimatum game

5.2.1 Offers and reactions to the offers

Recall that according to the theoretical predictions, when the third stage is reached, player A implements the project if and only if the state is good. In the second stage, player A accepts any offer (strictly) larger than 10 in the bad state, and any offer (strictly) larger than 0 in the good state.²⁵ Note that player A has a relatively simple task in the ultimatum game, and player A’s optimal behavior does not depend on the size of the externality. In contrast, player B’s task is more difficult. Not knowing the state of the world and anticipating player A’s behavior, according to theory it is optimal for player B to offer 0 in treatment UG-14 and 10 or 11 in treatment UG-24. Figure 2 shows the offers the subjects in the role of player B actually made and how the subjects in the role of player A reacted to these offers. We first take a closer look at player A’s behavior (depicted in the lower part of Fig. 2) and subsequently investigate player B’s behavior (shown in the upper part of Fig. 2).

Player A’s behavior Consider first player A’s behavior in the bad state. As predicted, there is not a single case in which player A rejects player B’s offer and subsequently implements the project in the third stage. Moreover, it is extremely rare that player A accepts an offer smaller than 10. This never happens in treatment UG-24 and in less than $3\%$ of the cases (4/145) in treatment UG-14. If player B offers 10, we observe both rejections and acceptances by player A; the acceptance rate is 2/6 ($33\%$) in UG-14 and 3/19 ($16\%$) in UG-24. An offer of 11 or larger is always accepted in treatment UG-14. Thus far, the behavior of subjects in the role of player A is very close to the theoretical predictions.

The most notable deviation is the fact that in treatment UG-24, an offer of 11 was rejected in $38\%$ of the cases. We observe some learning, as rejections of the offer 11 dropped from $50\%$ (13/26) in the first half of the experiment to only $31\%$ (12/39) in the second half.²⁶ Apparently, some subjects in the role of player A disliked the extremely inequitable outcome when an offer of 11 was accepted in the bad state. In this case, player A’s payoff is 1 and player B’s payoff is 13. Some A-players prefer to punish player B for making this offer, which is reminiscent of responder behavior in standard ultimatum games. However, note that in the present context inequity aversion seems to be rather mild, since offers weakly larger than 12 were always accepted also in UG-24 (i.e., subjects in the role of player A found it acceptable to have a payoff of only 2, whereas player B’s payoff is 12).

Further insights can be derived from the random-effects logit regressions with the implementation decision as the dependent variable focusing on the bad state reported in Table A2 in the Online Appendix. In line with the theory, an offer above 9 significantly increases the likelihood that the project is implemented. Given that the offers vary across treatments, inserting a control for the offer renders the large externality dummy variable insignificant. We find no significant learning effects in the UG-treatments. Interestingly, we observe a significant effect that players characterized as prosocial (based on SVO) are more likely to implement the project.

Fig. 2

Ultimatum game. The distribution of the offers made by player B, and player A’s reaction conditional on the state of the world

This effect is driven by players in the UG-24 treatment and can also be found if we restrict the dataset to observations with offers above 9.²⁷ This finding indicates that some subjects prefer to punish and not implement the project based on their social value orientation. The remaining controls for demographics as well as individual or social preferences have no significant impact on the decision to implement the project.

Next, consider player A’s behavior in the good state displayed in Fig. 2. As predicted, an offer strictly larger than 0 was almost always accepted.²⁸ When player B offered 0, rejections occurred frequently. However, by far most subjects in the role of player A subsequently implemented the project in the third stage (which leads to the same payoffs as accepting the offer 0). Specifically, there are only four cases in UG-14 and two cases in UG-24 in which the project was not implemented in the good state. Hence, with very few exceptions the behavior of the subjects in the role of player A in the good state is in line with the theoretical predictions.²⁹

Player B’s behavior Next, we consider player B’s behavior, which is shown in the upper part of Fig. 2.³⁰ Given that player B’s task was more difficult, it is remarkable that the most frequent offers correspond to the theoretical predictions. Specifically, in treatment UG-14 the most frequently made offer is 0, which was made in $35\%$ of the cases. Moreover, in treatment UG-24 the most frequently made offer is 11, which was made in $40\%$ of the cases (and the offer 10, which can also be optimal according to theory, was made in $13\%$ of the cases). The offers made in UG-14 and UG-24 are significantly different ($p=0.005$), with a mean of 2.88 in UG-14 and 9.95 in UG-24.

In treatment UG-14, only very few subjects in the role of player B aim to implement the project in the bad state. Specifically, less than $9\%$ of the offers are weakly larger than 10. Thus, as predicted the overwhelming majority of subjects in the role of player B made offers that player A had to reject in the bad state to avoid making a loss. Given that the offer will be accepted in the good state only, both players have equal payoffs if the offer is 4 (so that in the good state each player’s payoff is 10). This offer was made in $16\%$ of the cases.³¹

In treatment UG-24, by far most subjects in the role of player B seem to aim at implementation of the project in the bad state. However, $19\%$ of the offers are strictly smaller than 10, so in theses cases player A would make a loss when implementing the project in the bad state. We observe some learning over time, because $23\%$ of the offers are strictly smaller than 10 in rounds $1-4$, whereas this percentage drops to $16\%$ in rounds $5-8$. Given that the project will be implemented in the good state only, both players have equal payoffs when the offer is 9. This offer was made in only $3\%$ of the cases. Given that the project will always be implemented, both players have the same expected payoff when the offer is 13. This offer was made in only $5\%$ of the cases. Overall, the B-players do not seem to aim to equalize the players’ payoffs.

We use random-effects tobit regressions with the offer as the dependent variable to investigate the impact of social preferences, risk attitude, and learning over time on player B’s behavior (cf. Table A3 in the Online Appendix). First, we observe that the effect of higher offers in UG-24 than in UG-14 is robust if we add various control variables. Second, we find that offers increase over time indicating learning effects. A further analysis reveals that this effect is driven by players in UG-24, whereas we do not find systematic patterns for the UG-14 treatment.³² Third, individual or social preferences and demographic controls have no systematic impact on the offer.

5.2.2 Payoffs

Taken together, the players’ behavior in treatment UG-14 reflects the theoretical considerations quite well. Note that according to theory, both players’ payoffs are zero in the bad state, whereas player A obtains 6 and player B obtains 14 in the good state. The actual payoffs (cf. Table 3) are, on average, not too far from these predictions. However, player B’s offers are somewhat more generous; thus, in the good state player A’s payoff is larger and player B’s payoff is smaller than predicted. In treatment UG-24, the predicted offer is 10 or 11, so in the good state player A’s payoff is 16 or 17, whereas player B’s payoff is 14 or 13. The actual payoffs in the good state are remarkably close to these predictions. Yet, in the bad state theory predicts a payoff of 0 or 1 for player A and of 14 or 13 for player B. While player A’s payoff is as predicted, player B’s payoff is much smaller.

The latter observation reflects that in our ultimatum game treatments, the main deviation between theory and experimental results is the fact that the project is not implemented in almost half of the cases in the bad state in UG-24. As we have seen, this deviation can be attributed to two factors. First, $19\%$ of the offers made by player B are so small that player A must reject them to avoid a loss. Second, in the bad state the offer 10 (where according to theory player A is indifferent) is rejected in $84\%$ of the cases, and the offer 11 is rejected in $38\%$ of the cases. The fact that player B sometimes makes an offer strictly smaller than 10 is most likely attributable to decision errors and we indeed observe fewer such offers over time. As noted above, the fact that player A sometimes rejects an offer of 11 can be attributed to (rather mild) inequity aversion. Both facts together lead to a smaller-than-predicted implementation frequency in the bad state in UG-24.

5.3 Free-form bargaining

5.3.1 Offers and reactions to the offers

We now take a closer look at the offers, the decisions regarding whether or not to accept, and the third-stage implementation decisions in the free-form bargaining treatments. As there is no exogenously fixed bargaining protocol in these treatments, in what follows we particularly focus on the opening offers and the final offers. Note that when we refer to an “offer” we mean a binding offer that was entered by a player in the offer box.³³

We define an offer as an opening offer if it is the first offer made. Table 5 shows the frequencies with which the opening offer was made by player A and by player B and the means of these offers, conditional on the treatment and the state of the world. The upper parts of Figs. 3 and 4 show the distributions of the opening offers.

We define an offer as a final offer if it was either accepted or ultimately rejected by the other player. The latter case occurs when, after receiving the offer, the other player broke off the negotiations (by clicking on the break-off button) or the other player waited until the three-minute bargaining stage was over (and no new offers were made).³⁴ The lower parts of Figs. 3 and 4 show the distributions of the final offers and the reactions to these offers.

Note that the average number of offers is relatively small, varying between 1.85 and 2.89. This is not surprising since the players could use the free-form chat communication to coordinate on an offer. In a few cases the players concluded in their chat that they cannot reach an agreement, so no offer was made at all (which happened in almost $8\%$ of the cases in the bad state in FF-14). Overall, in $34\%$ of the cases only one offer was made.

As shown in Table 5, in each treatment and in each state of the world, on average a final offer made by player A was smaller than an opening offer made by player A. Similarly, in each treatment and in each state, on average a final offer made by player B was larger than an opening offer made by player B. Hence, when players made more than one offer, they typically made concessions by adjusting the offer to make it more attractive for the other player.³⁵

Table 5 Offers in the free-form bargaining treatments

Before we discuss the offers in detail, we first take a closer look at the impact of these offers on the implementation decision in general. As in the ultimatum game treatments, we run random-effects logit regressions with the decision to implement the project focusing on the data from the bad state (cf. Table A4 in the Online Appendix). In Model 1, we control only for the externality and find a small effect that a higher externality leads to higher implementation rates. If we add controls for the number of offers by each player and controls for the last offer by both players if they submitted any, the results show that the externality has no significant impact on the implementation decision. Note that not all players submitted offers. Therefore, our dataset is restricted to the subsample of players making offers if we add these controls. We observe no significant learning effects in general over both treatments. The offers made by player A do not have an economically strong impact on the implementation decision.³⁶ However, higher offers by player B increase the chance of implementation, whereas more frequent offers by player B decrease the chance. We do not find an impact of prosocial traits on the decision to implement, but players with higher scores on the honesty-humility domain are less likely to implement the project. In addition, there is a weakly significant impact of age on the implementation frequency.

In Table A9, we also control for selected chat content.³⁷ Again, we restrict the sample to observations in the bad state. The likelihood that the project is implemented increases if player A claims that the state is bad. The likelihood of implementation also increases if A-players use more arguments related to trust and honesty. In contrast, mentioning fairness more often is an indicator that the bargaining might not be successful. Additionally, a higher number of messages by A-players decreases the chance of project implementation. Our findings that higher scores on the honesty-humility scale and mentioning fairness more often decreases the chance of implementation, whereas mentioning honesty and trust enhances the chance, indicate that inequity aversion and fairness concerns influence the decision to implement the project in the bad state. If A-players feel the need to send more messages, this indicates that the bargaining process is more likely to fail. The chat content of player B has no significant impact on the outcome of the process.

Offers made by player B We start with Fig. 3, which depicts the distributions of the offers made by player B. In contrast to the ultimatum game treatments, player B’s offers can now be influenced by claims about the state of the world made by player A in the free-form text messages.

Consider first player B’s behavior in treatment FF-14, where the externality is small. Recall that both players have the same payoffs if they agree on the payment 12 in the bad state and on the payment 4 in the good state.³⁸ Note that in the bad state, the most frequent opening offers by player B are 4 (made in $34\%$ of the cases) and 12 (made in $22\%$ of the cases). In the good state, the opening offer 4 is made in $56\%$ of the cases, whereas the opening offer 12 is made in only $8\%$ of the cases. Hence, we already see an impact of communication when the opening offer is made. Now compare these numbers to the final offers made by player B, which are depicted in the lower part of Fig. 3. In the bad state, the two most frequent offers are now 12 (made in $38\%$ of the cases) and 11 (made in $30\%$ of the cases), whereas the offer 4 is made in only $6\%$ of the cases. Thus, player A often seems to be successful during the negotiations in persuading player B that the state is bad.³⁹ In the good state, the most frequent offer is still 4, which is made in $41\%$ of the cases.

Fig. 3

Free-form bargaining. Opening and final offers made by player B

Now consider player B’s behavior in treatment FF-24, where the externality is large. The offer 9 yields an equal split of the surplus if it is accepted in the good state, whereas the offer 17 yields an equal split of the surplus if it is accepted in the bad state. In the good state, 9 is indeed the most frequent opening offer (made in $18\%$ of the cases) and the most frequent final offer (made in $22\%$ of the cases). In the bad state, the opening offers are more evenly distributed, and the most frequent final offers are 12, 15, and 17 (made in $18\%$, $17\%$, and $17\%$ of the cases, respectively). We observe some learning in the bad state, because $14\%$ of the final offers are 10 or below in rounds $1-4$, whereas only $4\%$ are 10 or below in rounds $5-8$.

Observe that the colors in the lower part of Fig. 3 indicate how player A reacted when the final offer was made by player B. As predicted, when player A rejected player B’s offer in the bad state, then player A never implemented the project in the third stage. With the exception of only one case, in the bad state all offers strictly smaller than 10 were rejected. Note that whereas in UG-24 offers weakly larger than 12 were always accepted, this is not the case in FF-24. While player B’s ability to make a take-it-or-leave-it offer in the ultimatum game has put player B in a strong bargaining position, player A apparently feels entitled to a larger share of the pie in the case of free-form bargaining. Observe also that in the good state there are several cases in which player A rejects a strictly positive offer and nevertheless implements the project in the third stage (3 out of 4 cases in FF-14 and 6 out of 9 cases in FF-24). Apparently, the negotiations annoyed some players, but self-interest often prevailed in the end.

We also execute random-effects tobit regressions with the final offer of player B as the dependent variable. Note that not all B-players submitted a final offer, which restricts the dataset. Similar to the ultimatum game treatments, we control for individual or social preferences and demographic characteristics, but also add information about the state and the number of offers by each player as controls (cf. Table A5). We observe that B-players submit higher final offers if the state is bad or if the externality is large, whereas the number of offers has no significant impact. A higher risk aversion triggers higher offers by player B, presumably because more risk-averse players want to increase the implementation likelihood by offering a higher share to A-players. In Table A10, we control for chat content and observe higher offers by B-players if A-players claim that the state is bad, whereas the mentioning of fairness or honesty by player A has no such effect. In addition, we observe higher offers if player A suggests splitting the revenue evenly in case of a bad state. Interestingly, the offers are also slightly higher if player B raises doubts about the honesty of player A. It seems that outspoken concerns and doubts can be addressed during the bargaining process, whereas a higher number of messages by player A correlates with lower offers. Thus, more messages by A-players harm the outcome of the negotiations in the bad state in two ways. First, more messages mean lower offers by B-players, and we know from the results in Table A4 that lower offers decrease the chance of implementation. Second, more messages by A-players also decrease the likelihood of implementation directly, as shown in Table A9.

Offers made by player A Fig. 4 shows the distributions of offers made by player A. In the bad state of FF-14, player A makes the opening offer 12 in $83\%$ of the cases, whereas player A makes some concessions in the final offers, where the offers 12 and 11 are made in $67\%$ and $26\%$ of the cases, respectively. It is remarkable that in the good state of FF-14, the most frequent opening offer is 12 (made in $49\%$ of the cases). Thus, in the good state player A often tries to persuade player B that the state is bad.⁴⁰ When player A makes the final offer, then in the good state of FF-14 the offer 12 is still made in $37\%$ of the cases, whereas the equal-split offer 4 is made in $22\%$ of the cases.

In the bad state of treatment FF-24, player A’s opening offer is 17 in $61\%$ of the cases, whereas player A makes some concessions in the final offers (where the offer 17 is made in $32\%$ of the cases). In the good state of FF-24, player A again often tries to convince player B that the state is bad, so the most frequent opening offer is 17 (made in $40\%$ of the cases).⁴¹ However, during the negotiations player A often gives in, so in the final offers the equal-split offer 9 is most frequently made (in $26\%$ of the cases).

The colors in the lower part of Fig. 4 indicate whether the final offer made by player A was accepted or rejected by player B, and in the latter case whether or not player A subsequently implemented the project in the third stage. When player B rejected player A’s final offer in the bad state, then with only one exception player A never implemented the project in the third stage. Observe that in the bad state player B rejects the equal-split offers in a substantial fraction of the cases, so player B often does not trust player A’s claim that they are in the bad state. In the good state, when player B rejects player A’s final offer, then in most cases player A implements the project in the third stage.

Table A6 shows random-effects tobit regressions with the final offer of player A as the dependent variable. We observe that player A demands a higher payment if the state is bad or if the externality is large. In addition, a higher number of offers by player A increases the likelihood of a lower final offer, indicating that player A often announces a high demand and later gives in. Individual or social preferences and demographic characteristics do not play a major role.⁴² Regarding the content of the chat, we observe a similar pattern as for offers by player B (cf. Table A11).

Fig. 4

Free-form bargaining. Opening and final offers made by player A

Announcing a bad state, demanding an equal split in the bad state, and doubts by player B predict a higher final offer, whereas other chat content has no significant impact.

5.3.2 Payoffs

Taken together, the results show that in the bad state of the world, both parties benefit from the fact that with free-form bargaining the project is more often implemented than in the case of the ultimatum game (see the players’ payoffs reported in Table 3). However, in the good state of the world, player B’s payoff is smaller in the case of free-form bargaining than in the corresponding ultimatum game, because player B was exogenously put in a stronger bargaining position in the ultimatum game. As we have seen, even when it is player B who makes the final offer in the case of free-form bargaining, the offers are on average larger than those in the ultimatum game.

6 Concluding remarks

Over sixty years ago, Coase (1960) discussed how the problems caused by externalities can be solved through voluntary contracting between the involved parties. His lead example was building a fence when straying cattle may destroy crops on neighboring land. The topic of externalities has lost none of its relevance. A nation’s measures to contain the outbreak of a virus may save other nations from a deadly pandemic. When EU member states at the external border crack down on illegal immigration, this can also reduce crime and the burden on the social security system in other EU member states. When the hiring and training of police officers is improved in one city, this may help to prevent violent riots and looting also in other cities.

However, even when it is commonly known that it would be efficient to implement certain measures, in the presence of externalities decision makers might be unable to reach an agreement due to asymmetric information. Thus, it is important to explore how subjects behave in contract negotiations when both externalities and private information come into play.

As a first step, we conducted a controlled laboratory experiment. It turns out that the concerns first formalized by Klibanoff and Morduch (1995) are well-founded. When the size of the externality is relatively small, the parties reach an agreement in the bad state only slightly more often than theoretically predicted. In particular, allowing for unstructured bargaining with free-form communication, we were able to broadly corroborate the impossibility result proved by Klibanoff and Morduch (1995). When the size of the externality is large, then as expected the subjects reach an agreement in the bad state more often than when the externality is small. Yet, there is still a substantial fraction of cases in which the subjects do not reach an agreement. While this finding does not contradict theory in the case of free-form bargaining, it is a deviation from theory in the case of ultimatum-game bargaining.

Our analysis revealed that the deviation from theory in treatment UG-24 results from two contributing factors. First, B-players sometimes make offers that must be rejected by A-players when they want to avoid making a loss. It seems plausible that such offers are mainly due to decision errors, which is in line with the observation that the number of such offers declines over time. Second, sometimes offers of 11 are rejected by A-players in the bad state, which can be explained by inequity aversion. However, offers weakly larger than 12 are always accepted; thus, the degree of inequity aversion seems to be rather small.

Specifically, let us consider the formal model of inequity aversion proposed by Fehr and Schmidt (1999). They argue that when $u_{A}$ is the monetary payoff of player A and $u_{B}\ge u_{A}$ is the monetary payoff of player B, then player A’s utility is $u_{A}-\alpha (u_{B}-u_{A})$, where $\alpha$ measures the degree of aversion against disadvantageous inequity.⁴³ Note that when player A accepts the offer X, then in the bad state of UG-24 we have $u_{A}=-10+X$ and $u_{B}=24-X$, whereas $u_{A}=u_{B}=0$ when the offer is rejected. Therefore, player A accepts the offer whenever $X\ge \frac{1}{1+2\alpha }\left( 10+34\alpha \right)$. The fact that some A-players rejected an offer of 11 can be explained when $\alpha >0.08{\bar{3}}$, whereas the fact that all offers weakly larger than 12 were accepted implies that $\alpha \le 0.2$ must hold. For comparison, based on their analysis of standard ultimatum game data, Fehr and Schmidt (1999) argued that $\alpha$ can be between 0 and 4, with an average of 0.85.

Thus, in our setup inequity aversion seems to play a less pronounced role than in the literature on ultimatum games under symmetric information. This finding can be explained if player A’s fairness views take into consideration that player B does not know the state of the world when making an offer (cf. Cappelen et al., 2013). Our finding is in line with some other studies exploring the role of social preferences when there is asymmetric information. In particular, Hoppe and Schmitz (2013, 2015) experimentally studied adverse selection problems without externalities. The average $\alpha$ according to their estimates is between 0.07 and 0.25, which is consistent with our results.⁴⁴

In future research, it might be interesting to explore whether it is possible to further increase the implementation frequencies in the bad state when the externality is large. In particular, it might be worthwhile to conduct treatments with more rounds, such that the subjects have more opportunities to learn. It is plausible that in settings with asymmetric information subjects need more time to learn, because they have to gain experience with different types of players. Moreover, it would be interesting to have groups of subjects make the decisions, so that discussions within the groups might foster learning and provide insights into the subjects’ reasoning.⁴⁵ Furthermore, another promising avenue for future research might be to explore how the implementation frequencies would change if the externality were even larger.

Recall that in the case of free-form bargaining, where no specific bargaining protocol has been specified, Bayesian mechanism design theory tells us that in the case of a large externality it is possible to always implement the project in the bad state, but the theory does not say that this is the necessary outcome. However, if the mechanism is proposed by a mediator who aims to maximize the expected total surplus, theory would predict that the efficiency frontier would be reached. Thus, in follow-up research it might be worthwhile to conduct treatments where a mediator can propose a mechanism to the players.

Going beyond laboratory experiments, in future research, it would be desirable to investigate to what extent our findings also hold true in the field. Fréchette et al. (2022) report on experimental studies comparing the behaviors of university students and representative samples of the U.S. population. The findings suggest that experiments utilizing undergraduate students allow generalizable inferences and are thus indeed a useful first step to generate insights into the behavioral effects of a public policy.⁴⁶ Regarding Myerson and Satterthwaite’s (1983) original impossibility theorem, researchers have begun only recently to take the second step and explore its relevance in the field (see Larsen, 2021).⁴⁷ So far, we are unaware of any attempts to explore contracting under asymmetric information in the presence of externalities using field data. We hope that our contribution helps to spur more research on this important topic.