1 Introduction

The increased need for freshwater is one of the most significant challenges confronting both developing and developed countries (Ghandourah et al., 2022; Zayed et al., 2021). Therefore, governments and researchers worldwide are searching for and seeking new strategies to ensure the long-term abundance of sustainable resources of freshwater. One of the greatest techniques used to generate pure water from seawater or brackish water is solar desalination (Aboelmaaref et al., 2020; El-Agouz et al., 2022a). The desalination processes are classified into two substantial types: membrane and thermal procedures (Najid et al., 2021; Shoeibi et al., 2022a).

Incorporating the benefits of membrane and thermal distillation, membrane distillation (MD) is a potential approach for saltwater distillation (Lim et al., 2021; Shoeibi et al., 2022b). It is a thermally procedure through which the cold stream (permeate side) and hot stream (saltwater feeding side) take the powerful energy via the vapor pressure difference resulting from the temperature changes through the surface of the membrane. Thereafter, mass and heat transport phenomena concurrently take place from the warm heated side to the feed side (Lutze & Gorak, 2013; Shalaby et al., 2023). MD distinguishes itself from thermal desalination techniques with a variety of benefits. Firstly, by utilizing such limited excess heat, MD could perform at reduced feed temperatures. Secondly, compared to conventional thermal desalination arrangements, it allows for a compact small system design (Susanto, 2011). However, the two major obstacles that prevent MD from being commercialized in the worldwide seawater desalination field are the scarcity of affordable membranes and the excessive use of energy (Susanto, 2011). This feed heating temperature allows for the potential connection of MD and solar energy sources to provide the necessary energy for warming the MD system's feed water. MD processes are supplied by heat energy by solar collectors which include solar flat plate collectors (SFPCs), solar vacuumed tubes collectors (SVTCs), concentrated solar collectors, and PV-integrated solar heaters (Almodfer et al., 2022; González et al., 2017).

To examine the energy performance of solar-integrated MD for the desalination of saltwater, numerous experimental investigations, mathematical models, and economic assessments have been developed. Koschikowski et al. (2003a) conducted a numerical investigation on the MD system combined with additional heat recovery. The SFPC total area measured was 5.90 m2, and the overall membrane surface area utilized was 8.0 m2. The daily pure water yield varied from 11 L/m2 of SFPC in the winter to 22 L/m2 of SFPC in the summer. Modeling of DCMDS powered by SFPCs was conducted by Duong et al. (2017). The results revealed that the total freshwater yield was 6.40 L/day per m2 of both membrane and SFPC area. A 7.2 m2 spiral wound DCMD coupled with a 22.6 m2 SFPC system can produce approximately 140 kg of freshwater per day under real-world meteorological conditions, which translates to a daily pure water yield of 6.30 kg/m2 of SFPC or 19.72 kg/m2 of the membrane. Wang et al. (2009) examined the potential of a solar-powered vacuumed type MD system for producing potable water in Hangzhou, south China. The system's results showed that its pure water flux was 32.20 kg/m2/h, and its specific permeate flux was greater than 1.96 kg/m2 of SFPC per day. Khiadani and Shafieian (2019) investigated the dynamic performance of DCMD powered by SVTCs experimentally. Three different types were investigated under Perth, Australia's meteorological circumstances: Case A without and Case B with a cooler in the summer, and Case C without a cooler in the winter. The solar system's maximum energy and exergy efficiency during the summer were 78% and 5%, correspondingly. Moreover, Cases A, B, and C had the highest pure water productivity rates of 2.78, 3.82, and 2.13 L/h.m2, respectively. A multi-channel air gap MD (AGMD) with a total surface area of 14.4 m2 operated by both SVTC and SFPC was investigated by Kim et al. (2013) and Sandid et al., (2021). In comparison with the SFPC, the AGMD with SVTC had a freshwater flow that was 18.81–30.44% higher while costing 22.48% less. The specific thermal energy consumption of the suggested AGMD system ranged from 156 and 347 kWh/m3. The maximum acquired output ratio is estimated as 4.40, as well as the AGMD system's energy efficiency, reached 72% at 52 °C.

Solar collectors combined with photovoltaic (PV) panels may supply the grid with heat and electricity, making it entirely self-sufficient. In a study by Selvi and Baskaran (2014), a solar MD scheme was examined, in which a typical PV module was utilized to generate power, and the electricity was then stored by batteries to be utilized for the hybrid system's erratic functioning. An SFPC (6.0 m2) and PV (1.64 m2) driven modular DCMD desalination system with a 10 m2 membrane size was constructed by Zarzouom et al. (2019). It was drawn that an overall freshwater productivity of 86 L may be produced via latent heat recovered by warming the feed salt water with the condenser. Few investigations have considered the cost of solar MD systems. The distilled water cost of the solar MD was appreciated to be 15–18 $/m3 (Ma et al., 2021), while the distilled water cost of solar multi-effect distillation and PV-RO were lower undoubtedly than solar MD systems, which were 2.6–6.5 $/m3 and 6.5–9.1 $/m3, respectively (Abdelkareem et al., 2018).

According to the survey explained previously, it is declared that the MD technologies have been combined and powered by diversified kinds of solar collecting units including, flat frame solar collectors, vacuumed tubes solar collectors, concentrated solar collectors, and PV-integrated solar heaters, and indicated an unpretentious accessibility in the energy consumption savings and rates of freshwater yield. The survey shows also that the influences of the solar collecting areas on the production performance of the membrane desalinating systems are scarcely investigated in almost all of the summed-up studies in the above review. Additionally, in the industry of desalination, solar-driven MD has little chance of competing with other solar distillation systems from an economic standpoint.

In this research, we introduce a mathematical analysis and dynamic performance assessment for a small-scale SDCMDS powered by vacuumed tube solar collectors (VTSCs) for efficient freshwater production. The effects of the solar collecting area on the energy performance of the proposed SDCMDS for improving the feed inlet temperature of the saline water and augmenting the freshwater product of the system are studied. For numerous seasonal situations, a thorough theoretical model based on opto-geometric and thermodynamic analyses is built and implemented in MATLAB software to dynamically simulate the SDCMDS operation and examine its performance in Tanta City, Egypt, under real-world weather circumstances.

2 Research methods

2.1 Hybrid system description

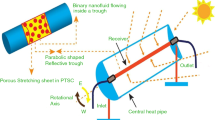
Membrane distillation is a challenging physical procedure that involves both mass and heat transmission. A micro-porous membrane serves as a physical barrier separating a warm liquid from a cooler compartment that carries either a liquid or a gas in this thermally driven process. Since the mechanism is non-isothermal, vapor particles from the high will go through the membrane pores, as depicted in Fig. 1 (Alsebaeai & Ahmad, 2020). Simultaneously, conduction and flux are the essential parameters for heat transfer via the membrane. More specifically, three key mechanisms dominate the heat transport in MD, which are Poiseuille flow, Knudsen diffusion, and molecular diffusion. In addition, momentum transfer also causes various kinds of resistance to mass transport on the membrane (Elzahaby et al., 2016a). The heat subsequently moves through the membrane via heat conduction and vapor latent heat. Convection then removes the energy from the surface of the membrane on the cool side through the boundary layer.

Fig. 1
figure 1

Schematic representation of MD principle

Full size image

In this study, two solar configurations within the proposed SDCMDS are modeled, designed, and investigated for summer and winter seasonal scenarios under the real weather conditions of Tanta, Egypt. The first configuration is an SDCMD with two identical VTSCs (1.80 m2 for each unit) as displayed in Fig. 2a, which are employed to provide the required heat to the amount of 180.0 L of saline water stored in the collector tank. While, the second configuration is an SDCMD with four identical VTSCs (1.8 m2 for each unit) as presented in Fig. 2b, which are utilized to preheat the same amount of saline water capacity (180 L) that is stored in the collector tank to further promote and improve the feed water temperature that thereafter fed to the membrane.

Fig. 2
figure 2

Schematic description of the proposed SDCMDS: a SDCMDS with two vacuumed tube solar collectors; b SDCMDS with four vacuumed tube solar

Full size image

The SDCMDS system employed in this study utilized a tubular membrane module consisting of forty-six porous tubes made from polypropylene, with a pore size of 0.2 μm. The total membrane area measured 1.0 m2 and had a porosity of 75%. The adapted membrane module featured a 1.27 m-long shell with an outer diameter of 9.0 cm. Furthermore, the external and internal pores of each membrane tube had dimensions of 8.50 mm and 5.50 mm, respectively. The key technical specifications of the proposed SDCMDS system, powered by VTSCs, are outlined in Table 1.

Table 1 Technical characteristics and design dimensions of the studied SDCMDS
Full size table

The solar heated loop, membrane permeate loop, and membrane feeding loop are the three key loops that make up the SDCMDS. The solar loop's main advantage is its capacity to transform solar energy into thermal energy and transmit that heat gain to the seawater in the feed tank. This loop's use of vacuum tubes and heat pipes minimized the thermal losses in the collectors while simultaneously producing efficient heat transfer. Through the membrane feed loop, hot salt water is supplied to the DCMD module (feed channel). In the meantime, the DCMD module's permeate channel is being compelled to receive the cold permeate water (membrane permeate loop).

2.2 Meteorological data and site selection

Tanta is a big city in the north of Egypt. Tanta is the capital of Gharbia governate, which lies in the middle of Delta, North of Egypt. Geographically, it is located at 30°47′28″ North and 30°59′53″ East. Egypt, like other sun-belt nations, receives significant amounts of annual direct solar radiation of 2000–3200 kWh/m2 from north to south, according to the solar map indicated in Fig. 3 (Kapica et al., 2021).

Fig. 3
figure 3

Global solar map of Tanta city, Egypt (Kapica et al., 2021)

Full size image

The entire daily incident shortwave solar radiation that reaches the surface of the earth over a large area is covered in this part, with full consideration given to seasonal fluctuations in day length, sun elevation above the horizon, and absorption by clouds and other atmospheric components. UV and visible light are examples of shortwave radiation (https://weatherspark.com/y/129118/Average-Weather-in-Tanta-Indonesia-Year-Round#Figures-SolarEnergy). During the whole year, the average daily incident shortwave solar energy per square meter for Tanta city stays relatively constant, ranging between 0.5 and 4.8 kilowatt-hours as illustrated in Fig. 4.

Fig. 4
figure 4

Average daily incident shortwave solar energy in Tanta (https://weatherspark.com/y/129118/Average-Weather-in-Tanta-Indonesia-Year-Round#Figures-SolarEnergy)

Full size image

Rapid population growth in Egypt raises water stress levels by increasing the amount of water needed for home use and increasing agricultural water use to keep up with rising food demands (Dakkak, 2016). In the Middle East, Egypt has one of the fastest rates of population increase. The population of the nation increased threefold between 1970 and 2023, from 35.3 million to about 105 million people (Roudi-Fahimi, et al., 2002). Water shortage is viewed as a critical problem in Egypt and will likely remain so for some time. Seven billion cubic meters of water are lost annually in Egypt, and by 2025 when 1.80 billion people globally are predicted to live in complete water scarcity (UNEP, 2014), the country may run out of water. A major contributing factor to this issue is climate change. Regarding Tanta city, Tanta is a crowded city that mainly depends on agriculture and industry which requires a huge amount of water to meet its needs. In addition, Tanta lacks potable freshwater sources such as the Nile River and underground water. So, the most appropriate solution for this water shortage problem in Tanta is water desalination assisted with solar energy introduced in the proposed SDCMDS, which is considered as a case study of this research.

The behavior of the hybrid SDCMDS is analyzed, from 8:00 a.m. to 7:00 p.m. at the weather circumstances of Tanta, Egypt (30.47° N and 31° E) for two various seasonal scenarios to contrast the thermal performance and distillate yield enhancement of the investigated SDCMDS under the two different applied configurations. Four cases of the proposed SDCMDS are investigated: two identical VTSCs of 1.80 m2 each unit in summer (Case I), two identical VTSCs in winter (Case II), four identical VTSCs in summer (Case III), and four identical VTSCs in winter (Case IV).

3 Mathematical models

A numerical study was conducted to simulate the hybrid SDCMDS integrated with VTSCs. MATLAB software was used to build the model and to perform related calculations. A coupled analytical modeling based on heat transfer, mass transport, and thermodynamic analysis is created to dynamically simulate the studied SDCMDS driven by VTSCs to analyze its performance, under real weather in Tanta, Egypt. In the following sections, the construction and formation of the developed models applied in the present investigation are well described.

3.1 Heat transport modeling

As seen in Fig. 5, synchronous mass transport and heat transfer occurrences happen from the hotter to the colder side. Firstly, the mass transfer between vapor and liquid is initiated because of the feed water evaporating at the membrane's surface boundaries. Due to the non-isothermal nature of the procedure, heat is transferred from the hot saltwater side across the thermal boundary thickness of the module surface to the cooler side in a convection form by vapor atoms moving through the membrane from the heated side to the cold side. The heat subsequently travels across the membrane by latent heat of vaporization as well as conduction heat transfer. Lastly, following the occurrence of condensation on the cold side, the pressure decline of the vapor can accelerate the propagation of the vapor atoms through the membrane.

Fig. 5
figure 5

Schematic diagram of heat transfer process occurs through SDCMDS

Full size image

The assumptions for the governing formulation are taken into account in this model as given: (i) one-dimensional and steady-state heat transfer flow, (ii) a parabolic or constant velocity distribution accomplished in the permeate and feed sides, (iii) constant thermo-physical characteristics, (iv) no chemical reactions, (iv) the thermal losses to the surrounding are negligible, and (v) the concentration polarization in the saltwater feed solution is ignored.

For each step \(Q_{{\text{f}}}\) on the feed side, the transmitted convection flux is depicted as follows (Elzahaby et al., 2016b):

$$Q_{{\text{f}}} = \left( {T_{{\text{f}}} - {\text{T}}_{{{\text{fm}}}} } \right) \cdot h_{{\text{f }}}$$
(1)

where \(h_{{\text{f}}}\) is the coefficient of heat transfer by convection on the feed side, \(T_{{\text{fm }}}\) is the temperature of the membrane at the feed side, and \(T_{{\text{f}}}\) is the temperature of bulk feed water.

The vaporization latent heat induced by the migration of vapor particles \(Q_{{{\text{vap}}}}\) and the conduction heat passing over the membrane \(Q_{{{\text{cond}}}}\) are expressed as (Elzahaby et al., 2016b):

$$\begin{aligned} & Q_{{\text{m}}} = Q_{{{\text{vap}}}} + Q_{{{\text{cond}}}} \\ & Q_{{\text{m}}} = J \cdot \Delta H_{{\text{v}}} + h_{{\text{m }}} \left( {T_{{{\text{fm}}}} - T_{{{\text{pm}}}} } \right){ } \\ \end{aligned}$$
(2)

Here, \(h_{{\text{m }}}\) is the membrane conduction heat transfer coefficient, \(\Delta H_{{\text{v}}} { }\) is the rate of vaporization, J is the permeate pure water flux, and \(T_{{{\text{pm}}}} { }\) is the temperature of the membrane of a cold stream.

The relationship between the thermal conductivity of membrane \(k_{{\text{m}}}\) and thickness of membrane \(\delta_{{\text{m}}}\) can be used to compute the membrane conduction heat transfer coefficient \(h_{{\text{m }}}\) as follow (Elzahaby et al., 2016b):

$$h_{{\text{m }}} { } = { }\frac{{k_{{\text{m}}} }}{{\delta_{{\text{m}}} }}$$
(3)

According to the iso-strain approach, the conductivity of two-phase MD module material is determined by:

$$k_{{\text{m}}} = \left( {1 - \emptyset } \right) \cdot k_{{{\text{sm}}}} + \emptyset \cdot k_{{\text{g}}}$$
(4)

where \(k_{{{\text{sm}}}}\) is the solid membrane material's thermal conductivity and \(k_{{\text{g}}}\) represents the air and water vapor thermal conductivity. The porosity of the membrane \(\emptyset\) is defined as (Elzahaby et al., 2016a):

$$\emptyset = \frac{{{\text{Avoid}}\;{\text{ volume}}}}{{{\text{Overall }}\;{\text{volume}}\;{\text{ of }}\;{\text{the }}\;{\text{membrane }}}}{ }$$
(5)

On the opposite side, the heat transferred by convection in the permeate side is calculated by:

$$Q_{{\text{p}}} = \left( {T_{{{\text{pm}}}} - T_{{\text{p}}} } \right) \cdot h_{{\text{p}}} { }$$
(6)

where \(h_{{\text{p}}}\) is the coefficient of heat transfer by convection in the permeate side, and \(T_{{\text{p}}}\) is the temperature of bulk permeate water.

Due to the steady-state heat flow consideration, the heat transfer rate through membrane, feed, and permeate boundary layers are equal (Elzahaby et al., 2020). So:

$$\begin{aligned} & Q = Q_{{\text{m}}} = Q_{{\text{p}}} = Q_{{\text{f}}} \\ & J \cdot \Delta H_{{\text{v}}} + h_{{\text{m }}} \left( {T_{{{\text{fm}}}} - T_{{{\text{pm}}}} } \right) = \left( {T_{{{\text{pm}}}} - T_{{\text{p}}} } \right) \cdot h_{{\text{p}}} = \left( {T_{{\text{f}}} - T_{{{\text{fm}}}} } \right) \cdot h_{{\text{f }}} \\ \end{aligned}$$
(7)

From the previous equations, the following formulas are used to determine the temperatures of the membrane at the feed and permeate sides:

$$T_{{{\text{fm}}}} = \frac{{h_{{\text{f}}} \cdot T_{{\text{f}}} - J \cdot \Delta H_{{\text{v}}} + h_{{\text{m}}} \left( {T_{{\text{p}}} + T_{{\text{f}}} \cdot h_{{\text{f}}} /h_{{\text{p}}} } \right)}}{{h_{{\text{f}}} \left( {1 + h_{{\text{m}}} /h_{{\text{f}}} } \right) + h_{{\text{m}}} }}$$
(8)
$$T_{{{\text{pm}}}} = \frac{{h_{{\text{p}}} \cdot T_{{\text{p}}} + J \cdot \Delta H_{{\text{v}}} + h_{{\text{m}}} \cdot \left( {T_{{\text{f}}} + T_{{\text{p}}} \cdot h_{{\text{p}}} /h_{{\text{f}}} } \right)}}{{h_{{\text{p}}} \left( {1 + h_{{\text{m}}} /h_{{\text{p}}} } \right) + h_{{\text{m}}} }}$$
(9)

3.2 Mass transport modeling

The semi-model published by Loydis and Lawson empirically describes the mass transferred through the suggested TDCMD module (Lawson et al., 1996). According to this method, the permeate water mass flux \(J\) is determined, as indicated:

$$J = C{*}\left( {P_{{{\text{m}}1}} - P_{{{\text{m}}2}} } \right)$$
(10)

In this context, \(P_{{{\text{m}}1}}\) and \(P_{{{\text{m}}2}}\) stand for the pressure of pure water vapor at the permeate and saline feed streams, respectively. However, C is the membrane coefficient.

The molecular diffusion model can potentially take into account the membrane mass transfer coefficient (C) that is adjusted to be 0.000000047 kg/m2 Pa s (Shalaby et al., 2022). Antoine's relation is used to calculate the partial vapor pressure of pure water as follows (Phattaranawik & Jiraratananon, 2001):

$$p_{{\text{v}}} = \exp \left[ {23.238 - \frac{3841}{{\left( {T - 45} \right)}}} \right]$$
(11)

Herein, T represents the temperature of either the heated saltwater or the cold distilled water in (K). As Raoult's law interprets a reduction in the vapor pressure caused by a salt concentration of saltwater in relation to the salt molecularly fraction (SMF) within the surface of the membrane, \(x_{{\text{ms }}}\) (Phattaranawik & Jiraratananon, 2001):

$${ }\dot{p}_{{\text{v}}} = p_{{\text{v}}} \cdot \left( {1 - x_{{{\text{ms}}}} } \right){ }$$
(12)

where the SMF of the surface of the membrane, \(x_{{ms{ }}}\) is obtained from Lawal and Khalifa (2014):

$$x_{{{\text{ms}}}} = x_{{{\text{bs}}}} \cdot \exp \left( {\frac{J}{{K_{{\text{s}}} \cdot \rho }}} \right)$$
(13)

where \(\rho ,x_{{{\text{ms}}}}\) and \(x_{{{\text{bs}}}}\) are the overall density, SMF at the surface, and the bulk of the surface of the membrane, respectively.

By performing an analogue between heat and mass transfer as set out, the Boelter–Dittus equations are applied to calculate the salt mass coefficient \(K_{{\text{s}}}\) as followed (Salehi & Rostamani, 2013):

For heat transfer:

$${\text{Nu}} = 0.023*\Pr^{0.33} *{\text{Re}}^{0.83} = \frac{{d_{{\text{h}}} \cdot h}}{k}$$
(14)

For mass transfer:

$${\text{Sh}} = 0.023*{\text{Sc}}^{0.33} *{\text{Re}}^{0.83} = \frac{{d_{{\text{h}}} \cdot K_{{\text{s}}} }}{{D_{{{\text{wa}}}} }}$$
(15)

where \(d_{{\text{h}}}\) is the hydraulic diameter, \({\text{Sh}}\) is Sherwood number, and \({\text{Sc}}\) is Schmidt number.

Schmidt number \({\text{Sc}}\) is calculated from El-Agouz et al., 2022b:

$${\text{Sc}} = \frac{\upsilon }{{D_{{{\text{wa}}}} }} = \frac{\mu }{{D_{{{\text{wa}}}} \cdot \rho }}$$
(16)

The diffusive coefficient of water vapor in stagnated air \(D_{{{\text{wa}}}}\) can be determined as given (Rezaei et al., 2018; Schofield et al., 1990):

$$D_{{{\text{wa}}}} = \frac{{0.01013 T^{1.75} \left( {\frac{1}{{M_{{\text{a}}} }} + \frac{1}{{M_{{\text{w}}} }}} \right)^{0.5} }}{{P \cdot \left( {v_{{\text{a}}}^{1/3} + v_{{\text{w}}}^{1/3} } \right)^{2} }}$$
(17)

where \(M_{{\text{w}}}\) and \(M_{{\text{a}}}\) are the molecular masses of water and air, which are adapted 18 and 29 kg/kmol for water and air, respectively. While \(v_{{\text{a}}}\) and \(v_{{\text{w}}}\) are the atomic diffusion volumes (12.7 for water and 20.1 for air).

From the previous equations, the salt mass coefficient \(K_{{\text{s}}}\) can be calculated from the following equation (El-Agouz et al., 2022b):

$$K_{{\text{s}}} = 0.023*{\text{Sc}}^{0.33} *{\text{Re}}^{0.83} \cdot \frac{{D_{{{\text{wa}}}} }}{{d_{{\text{h}}} }}$$
(18)

3.3 Feed saltwater tank modeling

The energy balance of the feed saltwater tank can be formulated mathematically as follows (El-Agouz et al., 2022c; Schofield et al., 1990):

$$T_{{\text{tank, new }}} = \frac{{(Q_{{{\text{solar}}}} + Q_{{{\text{elec}}}} - Q_{{{\text{loss}}}} + m_{{{\text{tank}}}} C T_{{{\text{tank}}}} + m_{2} C T_{{\text{f,out}}} + m_{3} C T_{{{\text{make}}\;{\text{up}}}} )}}{{\left( {m_{{{\text{Tank}}}} + m_{1} } \right)}}$$
(19)
$$T_{dh } = T_{{f,{\text{in}}}} = \frac{{Q_{dh} }}{{\left( {m_{1} *4180} \right)}} + T_{{{\text{solar }}\;{\text{col, out}}}}$$
(20)

3.4 Thermal performance indexes of the SDCMDS

The thermal analyses and freshwater accessibility of the hybrid SDCMDS under the four studied solar arrangements have been evaluated in terms of feed water inlet temperature, product permeate flux, accumulative freshwater product, gained output ratio (GOR), and total efficiency of the SDCMDS.

Performance of MD can be assessed by the gained output ratio (GOR) which is represented as the ratio of the latent heat required for the evaporation process by the supplied heat energy (Eq. 21), the higher the \({\text{GOR}}\) means better performance of the system (Alkhudhiri et al., 2018; Koschikowski et al., 2003b);

$${\text{GOR}} = \frac{{\dot{m}_{{\text{d}}} {*}h_{{\text{v}}} }}{{\dot{m}_{{\text{f}}} {*}C_{{{\text{pf}}}} {*}\left( {T_{{{\text{fi}}}} - T_{{{\text{fo}}}} } \right)}}$$
(21)

Thermal efficiency is the ratio between heat gain for saltwater vaporization across the membrane and the overall available solar power transferred to the membrane (Zayed et al., 2019). It can be computed as:

$$\eta_{{\text{t}}} = \frac{{JH_{{\text{v}}} A_{{\text{m}}} }}{{Q_{{{\text{total}}}} }}$$
(22)

Herein, \(J\) is water product flux (kg/s m2), \(A_{{\text{m}}}\) is the projected area of the membrane (m2), and \(H_{{\text{v}}}\) is the vaporization latent heat (kJ/kg).

The overall available solar power transferred to the membrane \(Q_{{{\text{total}}}}\) can be exemplified as (Aboelmaaref et al., 2023a, 2023b):

$$Q_{{{\text{total}}}} = { }\dot{m}_{{\text{f}}} {*}C_{{{\text{pf}}}} {*}\left( {T_{{{\text{fi}}}} - T_{{{\text{fo}}}} } \right)$$
(23)

where \(\dot{m}_{f}\) is the mass flowrate of the feed saltwater (kg/s) and \(T_{{{\text{fi}}}}\) and \(T_{{{\text{fo}}}} { }\) are the entry and exit feed water temperatures (°C), respectively.

Another important parameter in the MD systems is the specific heat energy consumption (SHEC) which is described as the energy required for producing one m3 of desalinated water (Aboelmaaref et al., 2023b; Zaragoza et al., 2014).

$${\text{STEC}} = \frac{{\rho *Q_{{{\text{total}}}} }}{{JA_{{\text{m}}} }}/3600$$
(24)

3.5 Solution approach, system variables, and limitations

The SDCMDS incorporated with VTSCs is simulated in conjunction with the sequential method depicted in Fig. 6. A mathematical model is created based on assessments of heat and mass transport and thermodynamic balances of the SDCMDS elements. The modeling is created using MATLAB software, which is also used to carry out the modeling algorithm's computations. The algorithm relies on the fundamentals of heat, and mass transport related to the SDCMDS combined with the VTSCs, which were discussed in the preceding subsections. To investigate mathematically the impacts of the quantity of solar collectors being used (solar collection area) on the thermal performance of the SDCMDS. The energy performance of the suggested solar SDCMDS is simulated under various design and operative settings under the realistic environmental conditions of Tanta, Egypt considering four operational seasons for the SDCMDS.

Fig. 6
figure 6

Schematic of the sequential solution method of the integrated SDCMDS modeling

Full size image

3.6 Model verification

A theoretical simulation was conducted to evaluate the thermal performance of SDCMDS and then compared with the experimental results from Shafieian and Khiadani (2019), as seen in Fig. 7. This comparison was based on identical climatic data, operating conditions for seawater feed, permeate, and cooling water, as well as input parameters for the membrane and solar collectors (1.80 m2 VTSC). The purpose was to verify the accuracy of our developed model. In Fig. 8, we present a comparison between the inlet feed temperature measured from SDCMDS (experimental data) and the corresponding values predicted by our research model. This comparison is made concerning solar irradiation. Notably, our model effectively captures the instantaneous changes in the trend of the inlet seawater feed temperature. Comparing the results, we find a satisfactory agreement with a maximum, average, and minimum relative error of 11.1%, 5.50%, and 0.432%, respectively, between the experimental and theoretical data. It's important to note that the deviations observed in the findings may be attributed to the omission of certain design parameters, such as the mass transport coefficient of the membrane, salt mass coefficient, and molecular fractions at the bulk and surface of the membrane, which were not addressed in the existing literature. From Fig. 8, it's evident that he SDCMDS model effectively validates against the experimental results.

Fig. 7
figure 7

Comparison between the measured inlet-feed temperature of the SDCMDS and their corresponding ones computed by the proposed model

Full size image
Fig. 8
figure 8

Variations in the hourly inlet saltwater feed temperature of the membrane with time for the two feeding configurations of SDCMDS

Full size image

4 Results and discussion

The performance of the hybrid SDCMDS driven by vacuumed tube solar collectors (VTSCs) is assessed under two different configurations considering the impact of the solar collecting area, i.e., the number of solar collectors (n). The performance of the hybrid SDCMDS is simulated and analyzed based on the real climate of Tanta, Egypt for two various seasonal scenarios (summer 15-6-2021 and winter 15-12-2021) for the two applied SDCMDS configurations. The first configuration is an SDCMDS with two identical VTSCs (1.8 m2 each unit). The second configuration is an SDCMDS with four identical VTSCs (1.8 m2 each unit). The research aims to compare the thermal behavior and the distillation yield improvement of the SDCMDS under the two applied configurations in summer and winter conditions. The proposed SDCMDS are analyzed based on diversified parameters; including, feed saltwater inlet temperature, product permeate flux (distillation yield per solar collection area), accumulative freshwater product, gained output ratio (GOR), and total efficiency of the SDCMDS.

Figure 8 presents the variation of inlet feed temperature feeding the membrane with time under two different system configurations in summer and winter at a feed flowrate of 0.20 kg/s. The results show that the utilization of four VTSCs connected in series significantly improved the feed seawater temperature range from 30.0 to 70.50 °C in summer (Case III) and from 26.0 to 63.3 °C in winter (Case IV) compared to a feed temperature range of 26.0 to 49.2 °C in summer (Case I) and from 26.0 to 44.7 °C in winter (Case II) was achievable by utilizing only two VTSCs at a feed flowrate of 0.20 kg/s. This is attributed to the significant increase in the useful heat gain to the feed water compared to the thermal losses by increasing the solar collecting area (No. of solar collectors) for preheating the same amount of saline water capacity (180 L) that is stored in the collector tank and thus remarkably improved the feed water temperature that thereafter fed to the membrane. This refers to the applicability of the two configurations of solar systems to drive the SDCMDS in both summer and winter. These results had a good a agreement with findings obtained by Shafieiun and Khiadanii (2019), Kim et al., (2013) and Sandid et al., (2021).

To fairly explore the effect of a solar collecting area (No. of solar collectors) on the freshwater distillation yield of the SDCMDS. Figure 9 shows the variation of permeate product flux with time for the two solar configurations of SDCMDS in summer and winter. It is identified that the SDCMDS with four VTSCs in a series connected is much more efficient for promoting the permeate flux than the SDCMDS with two VTSCs at different times for all seasons for the same reasons stated before. Moreover, for the two investigated SDCMDS, the product water fluxes are obtained higher in summer than in winter, due to the higher input available power and longer day times on hot days in summer than cold days in winter. Furthermore, the results show that the peak hourly permeate flux was 0.34, 0.25, 0.53, and 0.40 L/m2.h for Cases I, II, III, and IV, respectively. Moreover, it is found that the daily averaged permeate flux was 2.21, 1.29, 3.41, and 2.07 L/day per m2 of solar collecting area for Cases I, II, III, and IV, respectively, at a feed flowrate of 0.20 kg/s.

Fig. 9
figure 9

Changes in the hourly permeate product flux with time for the two configurations of SDCMDS

Full size image

Figure 10 highlights the accumulated daily quantities of freshwater productivity for the SDCMDS by using two and four solar collectors in summer and winter. It is clear that the SDCMDS with four vacuumed tubes collectors yielded the maximum cumulative distilled production compared to the SDCMDS with two evacuated collectors in both summer and winter, for the same reasons sated before. It is concluded that the maximal collective distillate product is obtained to be 23.04 and 14.78 L/day for the SDCMDS with four evacuated collectors in summer and winter, respectively. While, the conforming for the SDCMDS with only two evacuated collectors is about 7.48, and 4.60 L/day, in summer and winter, respectively, at the same feed flowrate of 0.20 kg/s. This is pointed out that the daily accumulated pure water production of the hybrid SDCMDS is improved by 208.0% and 221.0% in summer and winter, respectively, by increasing the number of solar vacuumed tubes collectors from (two collectors, 3.60 m2 solar collecting area) to (four collectors, 7.20 m2).

Fig. 10
figure 10

Variations of hourly collective freshwater product with time for the two configurations of SDCMDS

Full size image

Variations of the overall efficiency of the SDCMDS versus time with using two and four solar collectors within the SDCMDS in the winter and summer seasons are presented in Fig. 11. The total efficiency of the SDCMDS increases with time which reaches its maximal value at sunset time. This is due to the remarkably obtained yield of pure water at low periods of solar radiation at the end of the examination day compared to the other periods of the daytime. It is also clear that the SDCMDS with four evacuated collectors achieved higher overall efficiencies compared to the SDCMDS with two evacuated collectors in both summer and winter, for the same reasons earlier stated Shafieiun and Khiadanii (2019). As seen in Fig. 11, the average totally efficiency of the SDCMDS is estimated to be 24.95% and 22.50% for the SDCMDS with four evacuated collectors in summer and winter, respectively, at a feed flowrate of 0.20 kg/s. Whereas, it is found to be about 14.71% and 12.50% for the SDCMDS with only two evacuated collectors in summer and winter, respectively, at the same feed flowrate.

Fig. 11
figure 11

Variation of hourly system overall efficiency with time for the two configurations of SDCMDS

Full size image

Figure 12 displays the variation of hourly GOR with time under the two different SDCMDS configurations (with two solar collectors, and with four solar collectors). It is obvious that in all studied cases, the GOR had an increment tendency in the early morning and reached the highest values at the midday time corresponding to the highest setpoint feed inlet temperature. Then, it started to remarkably decrease till evening which is mainly due to the feed inlet temperature decrement and its consequent influence on the hourly productivity for solar operative configuration. The results show that the peak hourly GOR was 0.20, 0.13, 0.30, and 0.27 for Cases I, II, III, and IV, respectively. Moreover, it is found that the daily averaged GOR was 0.153, 0.132, 0.234, and 0.207 for Cases I, II, III, and IV, respectively, at a feed flowrate of 0.20 kg/s.

Fig. 12
figure 12

Variation of hourly GOR with time for the two configurations of SDCMDS

Full size image

The evaluation of the effects of climate season and the number of VTSCs on the energic performance and daily freshwater output of SDCMDS is comprehensively analyzed in terms of the SDCMDS's daily water yield, average daily energic efficacy, and mean daily inlet feed temperature, as highlighted in Fig. 13. It is shown that when using four VTSCs, the SDCMDS's daily water yield, average daily energic efficacy, and mean daily inlet feed temperature is found as 23.04 kg/day, 24.95%, and 50.35 °C in summer, and 14.78 kg/day, 22.5%, and 44.78 °C, in winter, respectively, at a feed flowrate of 0.20 kg/s. Hence, it can be concluded the SDCMDS's daily water yield, average daily energic efficacy, and mean daily inlet feed temperature are improved by 55.95%, 10.90%, and 12.44% for the summer operation of the SDCMDS compared to the winter operation, respectively, using four VTSCs and 0.20 kg/s inlet feed flowrate. While, when using only two VTSCs, these performance parameters significantly decreased for the same reasons stated above. It is estimated as 7.48 kg/day, 14.71% and 37.8 °C in summer, and 4.60, 12.50%, and 35.30 °C, in winter, respectively.

Fig. 13
figure 13

Daily performance for the proposed SDCMDS in terms of daily water yield, average daily energic efficacy, and mean daily inlet feed temperature for the different investigated cases

Full size image

Conclusively, it can be suggested that the SDCMDS with four vacuumed solar collectors is the best design configuration from both freshwater production and energy consumption saving considerations compared to the SDCMDS with two evacuated collectors in both summer and winter.

5 Comparative discussion of the proposed work with published similar studies

The theoretical results of the proposed SDCMDS obtained from the conducted model are compared with those corresponding ones of other similar research works, particularly the MD studies that utilized VTSCs as a solar preheating technique for the MD configurations. A comparative view between the findings of the present study with those of other relevant studies established in VTSCs-powered MD systems has been demonstrated in Table 2. The obtained findings in flux water production exhibited a good performance compared to those revealed by other previous works.

Table 2 Comparison between the findings of the present work and previous relevant studies in the performance of MD systems powered VTSCs
Full size table

6 Conclusions

The solar collecting area versus the vaporization latent heat from the produced freshwater distillation yield within the solar membrane distillation systems is the essential challenge that inhibits their energy performance. In this study, mathematical modeling of an improved solar direct contact membrane desalination system (SDCMDS) powered by vacuumed tube solar collectors (VTSCs) was conducted to explore the effects of the solar collecting area on the performance of the proposed SDCMDS. The heat transfer behavior and energy performance of the hybrid SDCMDS were investigated under two various solar collecting configurations in the real seasonal conditions of Tanta, Egypt. Four cases of the proposed SDCMDS are investigated: two identical VTSCs of 1.80 m2 each unit in summer (Case I), two identical VTSCs in winter (Case II), four identical VTSCs in summer (Case III), and four identical VTSCs in winter (Case IV). A detailed thermal analysis of the performances of the two investigated solar DCMD systems was performed. The following outcomes can be deduced:

  1. 1.

    The SDCMDS with four evacuated collectors is the best design configuration from both freshwater production and energy consumption saving considerations compared to the SDCMDS with two evacuated collectors in both summer and winter.

  2. 2.

    The utilization of four VTSCs connected in series significantly improved the feed seawater temperature range from 30.0 to 70.50 °C in summer (Case III) and from 26.0 to 63.3 °C in winter (Case IV) compared to a feed temperature range of 26.0–49.2 °C in summer (Case I) and from 26.0 to 44.7 °C in winter (Case II) was achievable by utilizing only two VTSCs at a feed flowrate of 0.20 kg/s. This is inferred from the applicability of the two configurations of solar systems to drive the SDCMDS in both summer and winter conditions.

  3. 3.

    The daily averaged permeate flux were 2.21, 1.29, 3.41, and 2.07 L/day per m2 of solar collecting area with total daily freshwater production of 7.48, 4.60, 23.04, and 14.78 L/day for Cases I, II, III, and IV, respectively, at a feed flowrate of 0.20 kg/s.

  4. 4.

    The overall accumulative distillate of the modified SDCMDS is improved by 208.0% and 221.0% in summer and winter, respectively, by increasing the number of solar vacuumed tube collectors from (two collectors, 3.60 m2 solar collecting area) to (four collectors, 7.20 m2).

  5. 5.

    The average overall efficiency of the system is estimated to be 24.95% and 22.50% for the SDCMDS with four evacuated collectors in summer and winter, respectively, at a feed flowrate of 0.20 kg/s. While it is found to be about 14.71% and 12.50% for the SDCMDS with only two evacuated collectors in summer and winter, respectively.

For future aspects, the low economic potential of solar-MD systems due to the higher overall capital costs of the SDCMDS is still challenging. Therefore, accurate techno-economic based on actual long-term experimentations and extreme degree of uncertainties concerning the lifetime and performance of the membranes are highly recommended for future research. Additionally, to improve the modular operation of the SDCMDS, the controlled working of the solar field should be administered to balance the competing influences between excess solar intensity, feed water temperature, and intermittent natural solar energy toward optimizing the performance of the SDCMDS.