Skip to main content
SpringerLink
Log in

Modeling doppler ultrasound blood flow signals in vessels with various stenosis degrees

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Abstract

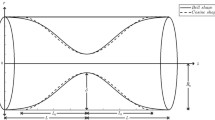
The Doppler ultrasound technique is used to detect vascular stenosis as a non-invasive procedure. To look for characteristics of Doppler ultrasound signals that are susceptible to stenosis, an accurate model of the Doppler ultrasound signal is required. This study models Doppler ultrasound waves from blood flow through stenotic arteries of varying degrees. In this model, it was expected that random scattering points will move based on their velocity. The Doppler influence was also included by modifying the form of the scattered signal at any time. Modeling the blood flow pattern through arteries helped identify the scattering point’s velocity profile and Doppler spectrum. The Tu and Devil model was used to consider a cosine stenosis shape because it is sufficiently similar to the natural shape of stenosis in the arteries. According to the Womersley model, the input flow to the stenotic zone was the same as the pulsatile blood flow in the vessel. As a result, the flow amplitude and Reynolds number changes will be near to reality. The fluid was deemed as non-Newtonian in the form of the power law to provide a more precise approximation to blood. When the calculated velocity profile was compared to the applied input value, the error rate was 6% for both normal and stenotic (70%) situations, validating the model’s accuracy in mimicking Doppler signals. This new computer model can be used to evaluate spectral analysis methods on simulated Doppler signals with clinically important underlying flow patterns.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Pontrelli G (1998) Pulsatile blood flow in a pipe. Comput Fluids 27:367–380

    Article  MATH  Google Scholar 

  2. Pashaei A, Fatouraee N (2009) An analytical phantom for the evaluation of medical flow imaging algorithms. Phys Med Biol 54:1791

    Article  Google Scholar 

  3. Tu C, Deville M (1996) Pulsatile flow of non-Newtonian fluids through arterial stenoses. J Biomech 29:899–908

    Article  Google Scholar 

  4. Wajihah SA, Sankar DS, Nagar AK (2022) Effects of catheter, stenosis and thrombosis in non-Newtonian blood flow through narrow arteries with clinical applications: a mathematical model. Int J Appl Comput Math 8:1–27

    Article  MathSciNet  MATH  Google Scholar 

  5. Ghofrani S, Ayatollahi A, Shamsollahi MB (2003) Modifying the cosine model for non-stationary blood-flow signal simulation. J Ultrasound Med 22:281–285

    Article  Google Scholar 

  6. Ghofrani S, Jahed-Motlagh MR, Ayatollahi A (2001) An adaptive speckle suppression filter based on Nakagami distribution. Int Conf Trends Commun 1:84–87

    Google Scholar 

  7. Strandness DE Jr, Schultz RD, Sumner DS, Rushmer RF (1967) Ultrasonic flow detection: a useful technique in the evaluation of peripheral vascular disease. Am J Surg 113:311–320

    Article  Google Scholar 

  8. Ahmed SA, Giddens DP (1984) Pulsatile flow studies with laser Doppler anemometry. J Biomech 17:695–705

    Article  Google Scholar 

  9. Siouffi M, Peronneau P, Wildt E, Pelissier R (1977) Modifications of flow patterns induced by a vascular stenosis. Proc Euromech 92:73–88

    Google Scholar 

  10. Chen X, Zhan Y, Fu YI, Lin J, Ji Y, Zhao C, Fang Y, Wu J (2021). The effect of stenosis rate and Reynolds number on local flow characteristics and plaque formation around the atherosclerotic stenosis. Acta Bioeng Biomech 23

  11. Tu C, Deville M, Dheur L, Vanderschuren L (1992) Finite element simulation of pulsatile flow through arterial stenoses. J Biomech 25:1141–1152

    Article  Google Scholar 

  12. Khan M, Sardar H, Gulzar MM, Alshomrani AS (2018) On multiple solutions of non-Newtonian Carreau fluid flow over an inclined shrinking sheet. Result Phys 8:926–932

    Article  Google Scholar 

  13. Marshall I, Zhao S, Papathanasopoulou P, Hoskins P, Xu XY (2004) MRI and CFD studies of pulsatile flow in healthy and stenotic carotid bifurcation models. J Biomech 37:679–687

    Article  Google Scholar 

  14. Steinman DA, Thomas JB, Ladak HM, Milner JS, Rutt BK, Spence JD (2002) Reconstruction of carotid bifurcation hemodynamics and wall thickness using computational fluid dynamics and MRI. Magn Reson Med 47:149–159

    Article  Google Scholar 

  15. Forrester JH, Young DF (1970) Flow through a converging-diverging tube and its implications in occlusive vascular disease-II: theoretical and experimental results and their implications. J Biomech 3:307–316

    Article  Google Scholar 

  16. Sharifi Asl M, Toghraie D, Azimian A (2018) Numerical simulation of convective heat transfer in a turbulant non-Newtonian nanofluid flow through a horizontal circular tube. J Model Eng 16:113–120

    Google Scholar 

  17. Buchanan JR Jr, Kleinstreuer C, Comer JK (2000) Rheological effects on pulsatile hemodynamics in a stenotic tube. Comput Fluids 29:695–724

    Article  MATH  Google Scholar 

  18. Eslami S, Mohseni M (2019) Effect of turbulence model on numerical simulation of turbulent flow of nanofluids in a horizontal pipe. J Model Eng 17:279–293

    Google Scholar 

  19. Neuwirth JG (1977) Pressure and velocity fluctuations associated with the flow through a stenosis with upstream roughness. IEEE Trans Biomed Eng 24:269–727

    Article  Google Scholar 

  20. Jensen JA (1996) Estimation of blood velocities using ultrasound: a signal processing approach, 2nd edn. Cambridge University Press, Cambridge

    Google Scholar 

  21. Yamaguchi H (2008) Engineering fluid mechanics, 2nd edn. Springer, Berlin

    MATH  Google Scholar 

  22. Bohme G (1987) Non-Newtonian fluid mechanics, 2nd edn. Elsevier, London

    MATH  Google Scholar 

  23. Hajjam A, Behnam H (2008) A modified time-domain approach for modelling the ultrasound signal from blood-flow. Ultrasound 16:160–164

    Article  Google Scholar 

  24. Khodabakhshi MB, Behnam H (2010) A new method for simulation of emblic signal in ultrasound blood flow signals. In 2010 17th Iranian conference of biomedical engineering, vol 17, pp 1–3

  25. Lehmann EL, Casella G (2006) Theory of point estimation, 2nd edn. Springer, Berlin

    MATH  Google Scholar 

  26. Spiegel MR, Schiller JJ, Srinivasan RA, LeVan M (1980) Probability and statistics, 2nd edn. Mcgraw-Hill, New York

    Google Scholar 

Download references

Funding

No funding was received for conducting this study.

Author information

Authors and Affiliations

  1. Radiation Application Research School, Nuclear Science and Technology Research Institute, P.O.BOX: 11365-8486, Tehran, Iran

    Mohsen Mehrabi & Sara Vosoughi

  2. Nuclear Fuel Cycle Research School, Nuclear Science and Technology Research Institute, P.O.BOX: 11365-8486, Tehran, Iran

    Nafise Salek & Hassan Ranjbar

Authors
  1. Mohsen Mehrabi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Nafise Salek
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sara Vosoughi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hassan Ranjbar
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed to the study conception and design. Material preparation, data collection, and analysis were performed by Mohsen Mehrabi, Nafise Salek, Sara Vosoughi, and Hassan Ranjbar. The first draft of the manuscript was written by Mohsen Mehrabi and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Mohsen Mehrabi.

Ethics declarations

Conflict of interest

The authors have no competing interests to declare that are relevant to the content of this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mehrabi, M., Salek, N., Vosoughi, S. et al. Modeling doppler ultrasound blood flow signals in vessels with various stenosis degrees. J Eng Math 138, 7 (2023). https://doi.org/10.1007/s10665-022-10250-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10665-022-10250-7

Keywords

Search

Navigation