Dissimilar nonhomogeneous magnetoelectroelastic layers with moving crack at the interface

Abstract

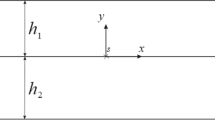
In this paper, the dynamic fracture problem of multiple moving cracks at the interface of two dissimilar functionally graded magnetoelectroelastic (FGMEE) layers subjected to anti-plane mechanical and in-plane magnetoelectrical loads is considered. The magnetoelectromechanical properties are assumed to vary exponentially with the coordinate perpendicular to the cracks. The integral transform technique is employed to solve the moving crack problem at the interface of dissimilar FGMEE layers. Numerical values for the field intensity factors are graphically presented and the effects of the crack velocity, nonhomogeneity parameter, and material volume fraction on the field intensity factor are examined.

Appendix A

The coefficients of Eq. (14) are

$$\begin{aligned} A_{2}^{(2)} (\omega )= & {} \frac{b_{z} }{P\hat{{R}}-\hat{{P}}}(\pi \delta (\omega )-\mathrm{i} \big / \omega ), \nonumber \\ B_{2}^{(2)} (\omega )= & {} \frac{mb_{z} -b_{\varphi } }{\hat{{Q}}-QR}(\pi \delta (\omega )-\mathrm{i} \big / \omega ), \nonumber \\ C_{2}^{(2)} (\omega )= & {} \frac{nb_{z} -b_{\psi } }{\hat{{Q}}-QR}(\pi \delta (\omega )-\mathrm{i} \big / \omega ), \nonumber \\ A_{1}^{(2)} (\omega )= & {} -\mathrm{e}^{-2\gamma _{3} h_{2} }\frac{\lambda -\gamma _{3} }{\lambda +\gamma _{3} }\frac{b_{z} }{P\hat{{R}}-\hat{{P}}}(\pi \delta (\omega )-\mathrm{i} \big / \omega ), \nonumber \\ B_{1}^{(2)} (\omega )= & {} -\mathrm{e}^{-2\gamma _{4} h_{2} }\frac{\lambda -\gamma _{4} }{\lambda +\gamma _{4} }\frac{mb_{z} -b_{\varphi } }{\hat{{Q}}-QR}(\pi \delta (\omega )-\mathrm{i} \big / \omega ), \nonumber \\ C_{1}^{(2)} (\omega )= & {} -\mathrm{e}^{-2\gamma _{4} h_{2} }\frac{\lambda -\gamma _{4} }{\lambda +\gamma _{4} }\frac{nb_{z} -b_{\psi } }{\hat{{Q}}-QR}(\pi \delta (\omega )-\mathrm{i} \big / \omega ). \end{aligned}$$

(A-1)

In the above equations

$$\begin{aligned} P= & {} 1-\mathrm{e}^{-2\gamma _{1} h_{1} }\frac{\beta +\gamma _{1} }{\beta -\gamma _{1} },\quad \quad \hat{{P}}=1-\mathrm{e}^{-2\gamma _{3} h_{2} }\frac{\lambda -\gamma _{3} }{\lambda +\gamma _{3} }, \end{aligned}$$

(A-2)

$$\begin{aligned} Q= & {} 1-\mathrm{e}^{-2\gamma _{2} h_{1} }\frac{\beta +\gamma _{2} }{\beta -\gamma _{2} },\quad \quad \hat{{Q}}=1-\mathrm{e}^{-2\gamma _{4} h_{2} }\frac{\lambda -\gamma _{4} }{\lambda +\gamma _{4} }, \end{aligned}$$

(A-3)

$$\begin{aligned} R= & {} \frac{(\lambda -\gamma _{4} )(1-\mathrm{e}^{-2\gamma _{4} h_{2} })}{(\beta +\gamma _{2} )(1-\mathrm{e}^{-2\gamma _{2} h_{1} })},\quad \quad \hat{{R}}=\frac{(\lambda -\gamma _{3} )(1-\mathrm{e}^{-2\gamma _{3} h_{2} })}{(\beta +\gamma _{1} )(1-\mathrm{e}^{-2\gamma _{1} h_{1} })}, \end{aligned}$$

(A-4)

the following functions are used in the field components.

$$\begin{aligned} T_{1} (\gamma _{1} ,\gamma _{3} )= & {} \int \limits _0^{+\infty } {(\mathrm{e}^{\gamma _{3} y}-\mathrm{e}^{-\gamma _{3} (y+2h_{2} )})\frac{\lambda -\gamma _{3} }{\omega (P\hat{{R}}-\hat{{P}})}\sin \omega x\,\mathrm{d}\omega }, \end{aligned}$$

(A-5)

$$\begin{aligned} T_{2} (\gamma _{2} ,\gamma _{4} )= & {} \int \limits _0^{+\infty } {(\mathrm{e}^{\gamma _{4} y}-\mathrm{e}^{-2\gamma _{4} h_{2} }\mathrm{e}^{-\gamma _{4} y})\frac{\lambda -\gamma _{4} }{\omega (\hat{{Q}}-QR)}\sin \omega x\,\mathrm{d}\omega }, \end{aligned}$$

(A-6)

$$\begin{aligned} T_{3} (\gamma _{1} ,\gamma _{3} )= & {} \int \limits _0^{+\infty } {\left[ (\mathrm{e}^{\gamma _{3} y}-\mathrm{e}^{-\gamma _{3} (y+2h_{2} )})\frac{\lambda -\gamma _{3} }{\omega (P\hat{{R}}-\hat{{P}})}-\frac{K}{2}\mathrm{e}^{K\omega y}\right] \sin \omega x\,\mathrm{d}\omega }, \end{aligned}$$

(A-7)

$$\begin{aligned} T_{4} (\gamma _{2} ,\gamma _{4} )= & {} \int \limits _0^{+\infty } {\left( (\mathrm{e}^{\gamma _{4} y}-\mathrm{e}^{-\gamma _{4} (y+2h_{2} )})\frac{\lambda -\gamma _{4} }{\omega (\hat{{Q}}-QR)}+\frac{\mathrm{e}^{\omega y}}{2}\right) \sin \omega x\,\mathrm{d}\omega }, \end{aligned}$$

(A-8)

The kernels of singular integral equations (18) are:

$$\begin{aligned} K_{ij}^{11} (s,t)= & {} \,\,-\frac{K\mathrm{e}^{\lambda (y_{i} -y_{j} )}}{2\pi }\frac{x_{i} -x_{j} }{(x_{i} -x_{j} )^{2}+[K(y_{i} -y_{j} )]^{2}}+\frac{[(e_{150} m+h_{150} n)]\mathrm{e}^{\lambda (y_{i} -y_{j} )}}{2\pi \tilde{{c}}_{44} }\frac{x_{i} -x_{j} }{(x_{i} -x_{j} )^{2}+(y_{i} -y_{j} )^{2}}, \nonumber \\&\quad -\int \limits _0^{+\infty } {\left[ \frac{(\lambda -\gamma _{3} )(\mathrm{e}^{\gamma _{3} (y_{i} -y_{j} )}-\mathrm{e}^{-\gamma _{3} ((y_{i} -y_{j} )+2h_{2} )})}{\omega (P\hat{{R}}-\hat{{P}})}-\frac{K}{2}\mathrm{e}^{k\omega (y_{i} -y_{j} )}\right] \sin \omega (x_{i} -x_{j} )\mathrm{d}\omega }, \nonumber \\&\quad -\frac{(e_{150} m+h_{150} n)\mathrm{e}^{\lambda (y_{i} -y_{j} )}}{\pi \tilde{{c}}_{44} }\int \limits _0^{+\infty } \left[ \frac{(\lambda -\gamma _{4} )(\mathrm{e}^{\gamma _{4} (y_{i} -y_{j} )}-\mathrm{e}^{-\gamma _{4} ((y_{i} -y_{j} )+2h_{2} )})}{\omega (\hat{{Q}}-QR)}+\frac{1}{2}\mathrm{e}^{\omega (y_{i} -y_{j} )}\right] \nonumber \\&\qquad \times \sin \omega (x_{i} -x_{j} )\mathrm{d}\omega , \nonumber \\ K_{ij}^{12} (s,t)= & {} \,\,-\frac{e_{150} \mathrm{e}^{\lambda (y_{i} -y_{j} )}}{2\pi \tilde{{c}}_{44} }\frac{x_{i} -x_{j} }{(x_{i} -x_{j} )^{2}+(y_{i} -y_{j} )^{2}}+\frac{e_{150} \mathrm{e}^{\lambda (y_{i} -y_{j} )}}{\pi \tilde{{c}}_{44} }, \nonumber \\&\quad \times \,\int \limits _0^{+\infty } {\left[ \frac{(\lambda -\gamma _{4} )(\mathrm{e}^{\gamma _{4} (y_{i} -y_{j} )}-\mathrm{e}^{-\gamma _{4} ((y_{i} -y_{j} )+2h_{2} )})}{\omega (\hat{{Q}}-QR)}+\frac{1}{2}\mathrm{e}^{\omega (y_{i} -y_{j} )}\right] \sin \omega (x_{i} -x_{j} )\mathrm{d}\omega }, \nonumber \\ K_{ij}^{13} (s,t)= & {} \,\,-\frac{h_{150} \mathrm{e}^{\lambda (y_{i} -y_{j} )}}{2\pi \tilde{{c}}_{44} }\frac{x_{i} -x_{j} }{(x_{i} -x_{j} )^{2}+(y_{i} -y_{j} )^{2}}+\frac{h_{150} \mathrm{e}^{\lambda (y_{i} -y_{j} )}}{\pi \tilde{{c}}_{44} } \nonumber \\&\quad \times \,\int \limits _0^{+\infty } {\left[ \frac{(\lambda -\gamma _{4} )(\mathrm{e}^{\gamma _{4} (y_{i} -y_{j} )}-\mathrm{e}^{-\gamma _{4} ((y_{i} -y_{j} )+2h_{2} )})}{\omega (\hat{{Q}}-QR)}+\frac{\mathrm{e}^{\omega (y_{i} -y_{j} )}}{2}\right] \sin \omega (x_{i} -x_{j} )\mathrm{d}\omega }, \nonumber \end{aligned}$$

$$\begin{aligned} K_{ij}^{21} (s,t)= & {} \,\,\frac{\mathrm{e}^{\lambda (y_{i} -y_{j} )}}{2\pi }\frac{x_{i} -x_{j} }{(x_{i} -x_{j} )^{2}+(y_{i} -y_{j} )^{2}}+\frac{\mathrm{e}^{\lambda (y_{i} -y_{j} )}}{\pi } \nonumber \\&\quad \times \int \limits _0^{+\infty } {\left[ \frac{(\lambda -\gamma _{4} )(\mathrm{e}^{\gamma _{4} (y_{i} -y_{j} )}-\mathrm{e}^{-\gamma _{4} ((y_{i} -y_{j} )+2h_{2} )})}{\omega (\hat{{Q}}-QR)}+\frac{\mathrm{e}^{\omega (y_{i} -y_{j} )}}{2}\right] \sin \omega (x_{i} -x_{j} )\mathrm{d}\omega }, \nonumber \\ K_{ij}^{22} (s,t)= & {} \,\,\frac{d_{110} \mathrm{e}^{\lambda (y_{i} -y_{j} )}}{2\pi (d_{110} m+\beta _{110} n)}\frac{x_{i} -x_{j} }{(x_{i} -x_{j} )^{2}+(y_{i} -y_{j} )^{2}}-\frac{d_{110} \mathrm{e}^{\lambda (y_{i} -y_{j} )}}{\pi (d_{110} m+\beta _{110} n)}, \nonumber \\&\quad \times \int \limits _0^{+\infty } {\left[ \frac{(\lambda -\gamma _{4} )(\mathrm{e}^{\gamma _{4} (y_{i} -y_{j} )}-\mathrm{e}^{-\gamma _{4} ((y_{i} -y_{j} )+2h_{2} )})}{\omega (\hat{{Q}}-QR)}+\frac{\mathrm{e}^{\omega (y_{i} -y_{j} )}}{2}\right] \sin \omega (x_{i} -x_{j} )\mathrm{d}\omega }, \nonumber \\ K_{ij}^{23} (s,t)= & {} \,\,\frac{\beta _{110} \mathrm{e}^{\lambda (y_{i} -y_{j} )}}{2\pi (d_{110} m+\beta _{110} n)}\frac{x_{i} -x_{j} }{(x_{i} -x_{j} )^{2}+(y_{i} -y_{j} )^{2}}-\frac{\beta _{110} \mathrm{e}^{\lambda (y_{i} -y_{j} )}}{\pi (d_{110} m+\beta _{110} n)}, \nonumber \\&\quad \times \,\int \limits _0^{+\infty } {[\frac{(\lambda -\gamma _{4} )(\mathrm{e}^{\gamma _{4} (y_{i} -y_{j} )}-\mathrm{e}^{-\gamma _{4} ((y_{i} -y_{j} )+2h_{2} )})}{\omega (\hat{{Q}}-QR)}+\frac{\mathrm{e}^{\omega (y_{i} -y_{j} )}}{2}]\sin \omega (x_{i} -x_{j} )\mathrm{d}\omega } \nonumber \\ K_{ij}^{31} (s,t)= & {} \,\,\frac{\mathrm{e}^{\lambda (y_{i} -y_{j} )}}{2\pi }\frac{x_{i} -x_{j} }{(x_{i} -x_{j} )^{2}+(y_{i} -y_{j} )^{2}}+\frac{\mathrm{e}^{\lambda (y_{i} -y_{j} )}}{\pi }, \nonumber \\&\quad \times \int \limits _0^{+\infty } {\left[ \frac{(\lambda -\gamma _{4} )(\mathrm{e}^{\gamma _{4} (y_{i} -y_{j} )}-\mathrm{e}^{-\gamma _{4} ((y_{i} -y_{j} )+2h_{2} )})}{\omega (\hat{{Q}}-QR)}+\frac{\mathrm{e}^{\omega (y_{i} -y_{j} )}}{2}\right] \sin \omega (x_{i} -x_{j} )\mathrm{d}\omega }, \nonumber \\ K_{ij}^{32} (s,t)= & {} \,\,\frac{\beta _{110} \mathrm{e}^{\lambda (y_{i} -y_{j} )}}{2\pi (\beta _{110} m+\gamma _{110} n)}\frac{x_{i} -x_{j} }{(x_{i} -x_{j} )^{2}+(y_{i} -y_{j} )^{2}}\,-\frac{\beta _{110} \mathrm{e}^{\lambda (y_{i} -y_{j} )}}{\pi (\beta _{110} m+\gamma _{110} n)}, \nonumber \\&\quad \times \int \limits _0^{+\infty } {\left[ \frac{(\lambda -\gamma _{4} )(\mathrm{e}^{\gamma _{4} (y_{i} -y_{j} )}-\mathrm{e}^{-\gamma _{4} ((y_{i} -y_{j} )+2h_{2} )})}{\omega (\hat{{Q}}-QR)}+\frac{\mathrm{e}^{\omega (y_{i} -y_{j} )}}{2}\right] \sin \omega (x_{i} -x_{j} )\mathrm{d}\omega }, \nonumber \\ K_{ij}^{33} (s,t)= & {} \,\,\frac{\gamma _{110} \mathrm{e}^{\lambda (y_{i} -y_{j} )}}{2\pi (\beta _{110} m+\gamma _{110} n)}\frac{x_{i} -x_{j} }{(x_{i} -x_{j} )^{2}+(y_{i} -y_{j} )^{2}}-\frac{\gamma _{110} \mathrm{e}^{\lambda (y_{i} -y_{j} )}}{\pi (\beta _{110} m+\gamma _{110} n)}, \nonumber \\&\quad \times \int \limits _0^{+\infty } {\left[ \frac{(\lambda -\gamma _{4} )(\mathrm{e}^{\gamma _{4} (y_{i} -y_{j} )}-\mathrm{e}^{-\gamma _{4} ((y_{i} -y_{j} )+2h_{2} )})}{\omega (\hat{{Q}}-QR)}+\frac{\mathrm{e}^{\omega (y_{i} -y_{j} )}}{2}\right] \sin \omega (x_{i} -x_{j} )\mathrm{d}\omega }. \end{aligned}$$

(A-9)