Skimming impacts and rebounds of smoothly shaped bodies on shallow liquid layers

Abstract

Investigated in this paper is the coupled fluid–body motion of a thin solid body undergoing a skimming impact on a shallow-water layer. The underbody shape (the region that makes contact with the liquid layer) is described by a smooth polynomic curve for which the magnitude of underbody thickness is represented by the scale parameter C. The body undergoes an oblique impact (where the horizontal speed of the body is much greater than its vertical speed) onto a liquid layer with the underbody’s trailing edge making the initial contact. This downstream contact point of the wetted region is modelled as fixed (relative to the body) throughout the skimming motion with the liquid layer assumed to detach smoothly from this sharp trailing edge. There are two geometrical scenarios of interest: the concave case ($C<0$ producing a hooked underbody) and the convex case ($C > 0$ producing a rounded underbody). As C is varied the rebound dynamics of the motion are predicted. Analyses of small-time water entry and of water exit are presented and are shown to be broadly in agreement with the computational results of the shallow-water model. Reduced analysis and physical insights are also presented in each case alongside numerical investigations and comparisons as C is varied, indicating qualitative analytical/numerical agreement. Increased body thickness substantially changes the interaction structure and accentuates inertial forces in the fluid flow.

1 Introduction

The notion of an object skimming across the surface of a liquid layer is likely to be familiar to many. A main point of reference is the childhood game of ducks and drakes or stone skimming, where smooth stones are thrown across a body of water in an attempt to cause the stone to bounce off of the surface. Thrown with a significant horizontal velocity, the stone, as it skips, descends initially into the liquid layer with a small downward velocity. As it impacts, pressure on the body from the liquid layer increases producing a positive lift, carrying the stone back out of the water. Subsequent bounces may occur thereafter. In addition to this toy example, there are several other scientific and industrial occurrences of such dynamics, many noted in [1].

One key motivation is aircraft icing, a real-world application that admits many avenues for mathematical research. This includes the analytical study of fluid–body interaction in boundary-layer flow, such as [2, 3] and the references therein, and a wealth of experimental, scientific and numerical studies in numerous research programmes around the world—notably work conducted by NASA Lewis Research Centre, Royal Aerospace Establishment (RAE), Defence Evaluation and Research Agency (DERA), Official National d’Etudes et de Recherches Aérospatiales (ONERA) and CIRA. For an in-depth overview of modelling within aircraft icing, see [4]. Regarding experimentation, a range of scenarios have been investigated over the years relating to airframe icing (the investigation of ice forming on the external surfaces of a vehicle, e.g [5]) and engine icing (the investigation of jet engine power-loss events due to ice crystal ingestion [6]). To evaluate these scenarios the field requires a combination of computational analysis (e.g. [7, 8]), wind tunnel testing (e.g. [9]) and flight testing (e.g. [10]) to produce holistic analysis of the aircraft system (e.g. [11]). The purpose of these experiments varies and includes the investigation of topics such as ice crystal or droplet impingement/ingestion; the formation and growth of ice on the aircraft/within vital aircraft components; and the design, placement and effectiveness of anti-icing and de-icing systems.

In this industrial context, the primary motivation is the impact of ice crystals onto a liquid-coated aircraft surface. As aircraft pass through convective cloud systems, they may be impacted by ice crystals or supercooled large droplets, which may cause ice formations to accrete on key components such as engines, pitot tubes and wings. It is also possible for these impacts to create thin sheets of water on the aircraft, especially on the aircraft’s warm components, or when ice melts. Subsequently, other ice crystals may continue to impact the aircraft, and may now impact upon this wetted surface. This leads to potentially new and noteworthy dynamics as an interaction occurs between these solid (ice) bodies and the shallow liquid layer. Notably, there is a large range of shapes that are relevant to ice crystals [12] and may have increasingly different physical responses to the water layer as a result.

This study investigates the skimming impacts of thin bodies (such as particles or ice crystals) with smooth underbody shapes (as described by a polynomial and with an arbitrary overbody shape, within reason) on a shallow liquid layer. Of note, in considering thin bodies, the horizontal scale of the body is far larger than the vertical, and a further important assumption is that the body is only considered to be inclined at small angles of $\theta$. This work extends the analysis presented in [13] in order to understand and treat a wider range of shapes and scales for the system of non-linear ordinary differential equations (ODEs) that govern the vertical height of the body, its rotation and the extent of the wetted region throughout the skimming process (as derived in the aforementioned paper). For an overview of the research that forms the basis of the derived model, see the introductions to [1, 13]. A variety of scenarios have previously been studied for skimming bodies including those featuring deep water impacts [14,15,16,17,18,19,20,21,22,23], multiple bodies [24, 25] and repeated oblique impacts [1].

By considering bodies with smooth polynomic undersides and the range of geometric scenarios and constraints this admits, of chief concern is how the scaled size of a body’s underside curvature (as represented by a scaling parameter C) affects its progression through the water layer and its subsequent trajectory upon exit.

Section 2 provides the background to the modelled system, briefly covering the derivation of the model and its foundational equations. Section 3 introduces the smooth polynomic underbody shape for which the six ODE system is derived. Following this set-up, several analytical results for general underbody shapes are discussed. This includes the small-time asymptotic entry condition, conditions for body exit, and insight into the expected effect of increased scaled underbody curvature on the body’s skimming motion. In Sect. 5 an in-depth numerical investigation of three different scenarios is performed. The cases considered are as presented in Fig. 1: a concave underbody $(C<0)$ (curving away from the liquid layer), and two cases for a convex underbody with either a fixed air angle $(C>0)$ (where an initial angle, say ${\hat{\theta }}_0$ between the body and the water layer is fixed for all values of C) or a fixed body angle $(C>0)$ (where an initial angle, say $\theta _0$ between the body midline and the water layer is fixed). The results in Sect. 5 prompt a corresponding analysis for increased body thickness which is presented in Sect. 6 for concave and convex shapes. Concluding remarks and observations are in Sect. 7.

Fig. 1

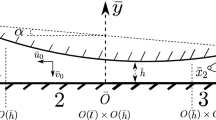
The three skimming scenarios considered in this paper: a a hook-shaped body $(C<0)$; b a fixed air angle ${\hat{\theta }}_0, (C>0)$; c a fixed body angle $\theta _0, (C>0)$; and d an illustration of a body skimming over a shallow liquid layer. The solid arrows indicate the direction of the flow in a frame of reference in which the body does not appear to move horizontally. The leading contact position, $x_1$, varies with time, while the trailing edge of the body and wetted region, $x_0$, remains fixed. (These figures are not to scale with the angle of incidence accentuated)

2 Background model

The analysis presented in this paper follows from the foundational work of [13] on the unsteady two-dimensional interactions that occur in the coupled fluid–body motion of a thin body skimming on a liquid layer (to re-emphasise, the major differences in this current work are the detailed analysis of curved underbodies and the range of geometrical scenarios that these shapes admit). The initial set-up and assumptions are the same as in [13], and are outlined in [1] as the two-dimensionality of the entire fluid–body interaction, the neglect of air effects, the incompressibility of the inviscid fluid (water), the shallowness of the water layer and the smallness of the body’s inclination ($\theta$) during the motion. For the full details of the model development see [13]. Of potential interest to the reader are the steps taken to non-dimensionalise and derive the system of equations that govern the fluid–body interaction. The non-dimensionalisation is based on the distance L from the centre of mass of the thin body to its trailing edge, the component U of the body velocity parallel to the undisturbed water surface, the convective time scale L/U and the pressure scale $\rho U^2$ where $\rho$ is the water density. It is then assumed that the water layer thickness H is small relative to the representative length L. The body inclination (as previously mentioned) is modelled based on the small ratio H/L in effect (where in reality the body inclination is $H/L \theta$).

Consequently the shallow-water equations (i.e. unsteady inviscid boundary-layer equations) nominally apply to the fluid flow in this scenario due to the large Reynolds number, Froude number and Weber number, in practice [1]. Hence, at leading order the effects of viscosity, gravity and surface tension are negligible. In addition, working with a frame of reference centred on the body, we study scenarios where the underbody depth is far less than that of the liquid layer, and the body is typically of uniform density. The non-dimensional form of the system also leads to a horizontal velocity, body half-length and typical convective time of order unity.

Considered throughout the analysis presented here are bodies where the underside shape is described by a smooth polynomic curve, subject to the existence of a prescribed trailing edge. The topside of the body is assumed to be of an arbitrary shape that has negligible effect on the skimming motion since this is governed by the displacement of the liquid layer below the body, Fig. 1d (and given the body’s prescribed thinness and the assumption that aerodynamic effects are negligible).

Now, consider a body with leading edge at $x_F$ and trailing edge at $x_R = x_0$, see Fig. 2. The trailing edge is considered to be sharp (as remarked earlier) with the liquid free surface detaching there. Furthermore, the centre of mass is assumed to be located at a fixed distance $x_0 - x_{cm}$ from the trailing edge (which follows due to the consideration of only small angles in the set-up).

Fig. 2

A curved body skimming over a shallow liquid layer: the distance between the body’s leading edge ($x_F$) and trailing edge ($x_R$) is significantly larger than the typical vertical depth (in y) of the liquid, and the representative angles of inclination of the plate from the horizontal are small. The solid arrow indicates the direction of liquid motion in a frame of reference in which the solid body does not appear to move in the horizontal direction

Regarding the location of the centre of mass and horizontal body extent, there is no loss in generality by considering a body with symmetrical horizontal extent about a centre of mass at $x=0$. Firstly, the choice of the centre of mass is somewhat arbitrary since, in theory, the centre of mass may be moved around freely (in both the x and y directions) by either adjusting the density distribution of the body or by adjusting the upper surface of the body (both of which are admissible in the modelling development and framework). As a result, the system may be rescaled accordingly such that $x_{cm}$ is considered to be zero in all cases and that $x_R = x_0$ and $x_F$ may vary independently (if one wishes to study a non-zero centre of mass, the solution to the system of equations is perturbed by a constant). Secondly, given the above and the subsequent analysis, the system of equations that govern the trajectory of the body is independent of the choice of $x_F$ since this is essentially the maximal value of $x_1$ and is thus a limit for the physical interpretation of the model. Hence, the following results will hold for bodies of equal length about the centre of mass and those that are unequal. With this in mind, we consider a horizontal extent of $2x_0$ and $x_{cm} = 0$ to make clearer the details of the skimming interaction.

Defining h as the unknown height of the body’s underside within the water sheet as measured from the bottom of the liquid layer; u as the horizontal flow velocity; p as the fluid pressure; Y as the vertical position of the body’s centre of mass; $\theta$ as the inclination of the body to the flow; and $T = T(x)$ as the function of underside body shape, the following holds:

$$\begin{aligned} (h, u, p, Y, \theta , T) = (1, 1, 0, 1, 0, 0) + \left( {\tilde{h}}, {\tilde{u}}, {\tilde{p}}, {\tilde{Y}}, {\tilde{\theta }}, {\tilde{T}} \right) + \cdots , \end{aligned}$$

(1)

where the terms with tildes are small.

For a body of scaled underside geometry ${\tilde{T}}(x)$ the free surface height under the body, within the wetted region, is given by

$$\begin{aligned} {\tilde{h}}(x,t) = {\tilde{Y}}(t) + (x - x_{cm}) {\tilde{\theta }}(t) - {\tilde{T}}(x) . \end{aligned}$$

(2)

Since the flow is irrotational, the scaling of (1) when used in the horizontal momentum and mass conservation equations provides the shallow-water equations:

$$\begin{aligned}&{\tilde{u}}_t + {\tilde{u}}_x = -{\tilde{p}}_x, \quad \;\;\; x_1 \le x \le x_0, \end{aligned}$$

(3a)

$$\begin{aligned}&{\tilde{h}}_t + {\tilde{h}}_x + {\tilde{u}}_x = 0, \quad x_1 \le x \le x_0. \end{aligned}$$

(3b)

Here $x_0$ is the known trailing edge of the wetted region/body and $x_1 = x_1(t) \in [-x_0, x_0]$ is the unknown leading contact point between the body and liquid layer and is typically O(1). At $x_0$ the equi-pressure Kutta condition implies that ${\tilde{p}}(x_0, t) = 0$.

Under (1) and as in [13, 26] the jump conditions at $x_1$ are

$$\begin{aligned} {\tilde{p}}(x_1,t) + \left( 1 - x_1^\prime \right) {\tilde{u}}(x_1,t) = 0, \end{aligned}$$

(4)

with

$$\begin{aligned} {\tilde{u}}(x_1,t) = -\left( 1-x_1^\prime \right) {\tilde{h}}(x_1,t). \end{aligned}$$

(5)

Note that the prime notation refers to a time derivative throughout. From Newton’s second law, the vertical motion equation for the body simplifies to

$$\begin{aligned} M {\tilde{Y}}^{\prime \prime } = \int _{x_1}^{x_0} {\tilde{p}}(x,t) \mathrm{{d}}x, \end{aligned}$$

(6)

Here $M \,(= {\tilde{H}} {\tilde{m}}/{\tilde{\rho }}{\tilde{L}}^3)$ is the scaled mass of the body with ${\tilde{m}}$ the dimensional mass. In addition, the rotational motion equation of the body may also be simplified to

$$\begin{aligned} I {\tilde{\theta }}^{\prime \prime } = \int _{x_1}^{x_0} x {\tilde{p}}(x,t) \mathrm{{d}}x, \end{aligned}$$

(7)

where $I\, (= {\tilde{H}} {\tilde{i}}/{\tilde{\rho }}{\tilde{L}}^5)$ is the scaled moment of inertia for the body with ${\tilde{i}}$ the dimensional moment of inertia.

Of primary interest is the wetted region $[x_1, x_0]$. In particular, investigations of how $x_1$ evolves throughout the skimming process will be carried out under varying geometric considerations. Additionally, the responses of ${\tilde{Y}}, {\tilde{V}}, {\tilde{\theta }}, {\tilde{\omega }}$ and ${\tilde{p}}$ are evaluated. Here ${\tilde{V}}$ is the vertical velocity of the initially downward moving body, and ${\tilde{\omega }}$ is the angular velocity induced by the skimming action. For ease of notation we omit the tildes in the following sections.

3 Equations of motion for a body of general smooth shape

The aim of the current and subsequent sections is to extend the existing theory by generalising the previous work to a body with a smooth polynomic underside and hence determine the physical implications of different underbody shapes. The underbody shape is described by a polynomial T(x) of order n defined across the body’s horizontal extent $x \in [-x_0,x_0]$.

The underbody thickness function satisfies $T(x_0) = T(-x_0) = 0$, to maintain the physicality of the model (that the initial touchdown occurs at the trailing edge, with the trailing edge of the contact region remaining fixed at $x_0$ throughout the skimming motion, and that the body makes contact with the liquid layer over a single region). Furthermore, $x_0$ must be a simple root of T(x) (the reasoning is explained later). Thus

$$\begin{aligned} T(x) = (x_0 - x)\left( \sum _{m = 0}^{n-1} a_m x^m \right) , \qquad \sum _{m = 0}^{n-1} a_m (-x_0)^m = 0. \end{aligned}$$

(8)

If $n = 1$ then $T(x) = 0$ giving the flat plate case as in [13]. As a result, cases where $n = 2,3,\ldots$ are of interest since these correspond to a curved body. To understand the motion of the body through the water layer, consider the flow response in the wetted region $[x_1,x_0]$. Given the definition of the body geometry (8),  (3a) and (3b) imply that $p_{xx}$ has powers of at most $x^{n-2}$ for $n>2$ and is linear for $n = 1, 2$ (due to the $x \theta$ term in (2)). Hence the pressure response can be written as a polynomial:

$$\begin{aligned} p = {\left\{ \begin{array}{ll} \sum _{m = 0}^{n} \gamma _m x^m, &{} n > 2, \\ \sum _{m = 0}^{3} \gamma _m x^m, &{} n \le 2. \end{array}\right. } \end{aligned}$$

(9)

Here the coefficients $\gamma _m$ are unknown functions of time. Without loss of generality, the case where $n > 2$ is assumed throughout the remainder of this paper unless otherwise stated (for $n \le 2$, the coefficients of T(x) can be defined as $a_k = 0$ for $k = 2$ or $k = 3$, such that the following holds).

The pressure at the leading edge of the wetted region can be found by substituting (9) into the jump conditions (4) and (5). Combining these two equations leads to

$$\begin{aligned} p(x_1) = \sum _{m = 0}^{n} \gamma _m x_1^m = \left( Y + x_1 \theta - T(x_1) \right) \left( 1 - x_1^\prime \right) ^{2} . \end{aligned}$$

(10)

Next, by integrating (3b) with (2) and (9)

$$\begin{aligned} u(x,t) = D(t) - \frac{1}{2} \theta ^{\prime } x^2 - x \left( Y^\prime + \theta \right) + \sum _{m = 0}^{n-1} (x_0 a_{m+1} - a_{m}) x^{m+1}, \end{aligned}$$

(11)

where D(t) is a function of time to be determined. Note that $u(0,t)=D(t)$. In addition to (10), a second equation for the pressure at the leading contact position is gained by substituting the velocity profile (11) at $x = x_1$ and (2) into the jump condition (4) to obtain

$$\begin{aligned} \begin{aligned} \sum _{m = 0}^{n} \gamma _m x_1^m =\left( -D + \frac{1}{2} {\theta }^{\prime } x_1^2 + x_1 \left( {Y}^\prime + {\theta } \right) - \sum _{m = 0}^{n-1} (x_0 a_{m+1} - a_{m}) x_1^{m+1} \right) (1-x_1^\prime ) . \end{aligned} \end{aligned}$$

(12)

Finally, definitions of $\gamma _m, \; m = 0, 1, 2,\ldots n$ follow from (9) and the velocity profile (11) when substituted into (3a) such that the matching of coefficients requires

$$\begin{aligned}&\gamma _1 = -D^{\prime } + {Y}^{\prime } + {\theta } + a_0 - x_0 a_1 ,&\end{aligned}$$

(13a)

$$\begin{aligned}&2 \gamma _2 = {Y}^{\prime \prime } + 2 \theta ^\prime + 2 (a_1 - x_0 a_2) ,&\end{aligned}$$

(13b)

$$\begin{aligned}&6 \gamma _3 = {\theta }^{\prime \prime } + 6 (a_2 - x_0 a_3) ,&\end{aligned}$$

(13c)

$$\begin{aligned}&m \gamma _m = m (a_{m-1} - x_0 a_m) \quad \text {for } m = 4,5,\ldots ,n \text { and } a_n = 0 . \end{aligned}$$

(13d)

At the trailing edge the equi-pressure (Kutta) condition implies

$$\begin{aligned} p(x_0) = \sum _{m = 0}^{n} \gamma _m x_0^m = 0 , \end{aligned}$$

(14)

such that $\gamma _0$ can be found using (13a)–(13d) alongside (10) and (12). Finally, the vertical and rotational equations of motion can be found in terms of the $\gamma _m$ functions as

$$\begin{aligned} \begin{aligned} M {Y}^{\prime \prime } = \sum _{m = 0}^{n} \frac{\gamma _m}{m+1} \left( x_0^{m+1} - x_1^{m+1} \right) \end{aligned} \end{aligned}$$

(15)

and

$$\begin{aligned} \begin{aligned} I {\theta }^{\prime \prime } = \sum _{m = 0}^{n} \frac{\gamma _m}{m+2} \left( x_0^{m+2} - x_1^{m+2} \right) , \end{aligned} \end{aligned}$$

(16)

from  (6), (7) and (9).

Altogether, for the sake of clarity, the system of equations that will be used to model the body motion are as follows:

$$\begin{aligned} {Y}^\prime&= V, \end{aligned}$$

(17)

$$\begin{aligned} {\theta }^\prime&= \omega , \end{aligned}$$

(18)

$$\begin{aligned} {V}^\prime&= \sum _{m = 0}^{n} \frac{\gamma _m}{M(m+1)} \left( x_0^{m+1} - x_1^{m+1} \right) , \end{aligned}$$

(19)

$$\begin{aligned} {\omega }^\prime&= \sum _{m = 0}^{n} \frac{\gamma _m}{I(m+2)} \left( x_0^{m+2} - x_1^{m+2} \right) . \end{aligned}$$

(20)

Furthermore, substituting ${Y}^\prime$ into (13a) and rearranging gives

$$\begin{aligned} {D}^\prime = {V} + {\theta } - \gamma _1 - a_1 x_0 + a_0. \end{aligned}$$

(21)

Now to obtain the equation for the evolution of $x_1$, (10) can be rearranged to give

$$\begin{aligned} x_1^\prime = 1 - \left[ \frac{\sum _{m = 0}^{n} \gamma _m x_1^m}{Y + x_1 {\theta } - T(x_1)}\right] ^{1/2}. \end{aligned}$$

(22)

Finally for the functions $\gamma _m$, a system of linear equations can be formulated. The first equation is gained by eliminating $x_1^\prime$ from (10) and (12)

$$\begin{aligned} \sum _{m = 0}^{n} \gamma _m x_1^m = \frac{\left[ D - \frac{1}{2} \omega x_1^2 - x_1 \left( Y^\prime + {\theta } \right) + \sum _{m = 0}^{n-1} (x_0 a_{m + 1} - a_{m}) x_1^{m + 1} \right] ^{2}}{Y + x_1 {\theta } - T(x_1)}. \end{aligned}$$

(23)

The second by rearranging and substituting (13b) into (15) yields

$$\begin{aligned} \gamma _2 - \omega - (a_1 - x_0 a_2) = \sum _{m = 0}^{n} \frac{\gamma _m}{2M(m+1)} \left( x_0^{m+1} - x_1^{m+1} \right) . \end{aligned}$$

(24)

The third is from (13c) and (20) such that

$$\begin{aligned} \gamma _3 - (a_2 - x_0 a_3)= \sum _{m = 0}^{n} \frac{\gamma _m}{6I(m+2)} \left( x_0^{m+2} - x_1^{m+2} \right) . \end{aligned}$$

(25)

The fourth is the pressure response at $x_0$, Eq. (14), to complete the system. Hence the body and fluid motions are described by a non-linear system of six ODEs (17)–(22) for $Y, V, \theta , \omega , D$ and $x_1$, and a linear system of equations comprising (14) and (23)–(25).

Given the non-linearity and the number of equations and parameters, numerical investigation of this system is required to gain insight into how each equation relates to the others and each influences the body’s trajectory. At this stage, we should remark that choosing T(x) to be a polynomial is convenient for studying effects of underbody shape. Notably, other shapes could be considered of an even more general form and a similar set-up used, so long as there is zero thickness at the leading and trailing edges of the underbody. Some prior analysis is now presented to inform the direction of the numerical work and provide initial insight into the possible behaviour of the results.

4 Entry and exit results for general body shapes

We now explore two aspects of the model that hold for bodies of general underside shape as defined by (8). These aspects are the small-time entry and the exit behaviour. Subsequently the possible behaviour of the model as the scaled underbody curvature increases will be investigated.

4.1 Small-time entry solution

Small-time solutions for the body’s entry into the water layer are used to initialise the computational calculations. Here we outline the key details of the asymptotic solution, with the full details provided in Appendix A.

Assuming that the initial configuration of the body upon impact is known, the key parameters are asymptotically expanded according to their initial value. Explicitly, these are the vertical extent of the body’s centre of mass $Y_0$; the body’s vertical velocity $V_0$; the angle of the body $\theta _0$; the horizontal position of the body’s trailing edge $x_0$; and the initial angular velocity of the body $\omega _0$. For small times after entry, the leading contact point of the body with the water will move in a negative x direction, away from the trailing edge (initial point of contact) as the plate begins to submerge. Hence in the expansion of $x_1$ ($x_1 = x_0 + {\check{x}}_1 t + {\check{x}}_2 t^2 +\cdots$), the constant ${\check{x}}_1$ is expected to be negative.

Working through the analysis in a similar manner to [13], three key geometric observations are gained at leading order. Firstly, we observe that $Y_0 + x_0 \theta _0 = 0$ giving a geometric constraint for the body entering an initially undisturbed water layer. Importantly, this result is unchanged from [13] since $T(x_0) = 0$. Secondly, we also deduce that $D_0 = x_0^2 \omega _0/2 + x_0 (V_0 + \theta _0 + a_0)$, providing a constraint relating the initial fluid velocity at $x = 0$ to the initial trailing-edge position of the body, angular momentum of the body, inclination of the body, velocity of the body, and the constant term of the underbody-shape function. Having found these two conditions, the third relates to the constant ${\check{x}}_1$, where

$$\begin{aligned} {\check{x}}_1 = \frac{-3(x_0 \omega _0 + V_0) + \sqrt{9(x_0 \omega _0 + V_0)^2 + 8 \left( \theta _0 + \sum _{m = 0}^{n-1} a_m x_0^m\right) (x_0 \omega _0 + V_0)}}{4 \left( \theta _0 + \sum _{m = 0}^{n-1} a_m x_0^m\right) }. \end{aligned}$$

(26)

Since (26) takes into account the tangential angle of the body geometry at the trailing edge, the entry motion of the body is dependent on an effective angle of entry, say ${\tilde{\theta }}_0 = \left( \theta _0 + \sum _{m = 0}^{n-1} a_m x_0^m\right)$. This effective angle consists of the angle of inclination for the body’s longitudinal line, $\theta _0$, plus the initial gradient of the body’s scaled underbody at the trailing edge ($\mathrm{{d}}T(x_0)/\mathrm{{d}}x = \sum _{m = 0}^{n-1} a_m x_0^m$). We remark that, when $a_m = 0, m = 0,1,2,\ldots ,n$, (26) is the same as the straight plate case in [13], as might be expected.

Moreover, if the $x_0$ root in T(x) has a multiplicity $k > 1$, the body shape has no influence on the entry condition of the body at leading order.

We make a further observation regarding the initial inclination of the body. Given the assumptions of the model, this needs to be carefully considered to ensure that the initial touchdown occurs at the trailing edge of the body, with the trailing edge of the contact region remaining fixed there throughout the duration of the skimming motion. As a result, we may need to set a larger initial $\theta$ than seen in [13] to account for the underbody geometry. In the numerical results presented in Sect. 5, $T(x) = C(x_0 - x_1)(x_0 + x_1)$ in most cases, where C is a given constant. Hence the choice of initial $\theta$ depends on the value of |C|.

Firstly, take the concave (hooked underbody) example stated earlier where $C<0$ in the T(x) above. The height of the water layer at the leading contact point at any time t during the skim is given by

$$\begin{aligned} {h}(x_1,t) = {Y}(t) + x_1 {\theta }(t) - C(x_0 - x_1)(x_0 + x_1) . \end{aligned}$$

To ensure that the result is physical ${h}(x_1,t)$ must always be less than the liquid-layer height required for the leading edge of the body to become wet, $h(-x_0,t)$. Hence, by the definition of $h(x_1,t)$ we have that

$$\begin{aligned} {Y}(t) + x_1 {\theta }(t) - C(x_0 - x_1)(x_0 + x_1) < {Y}(t) - x_0 {\theta }(t), \end{aligned}$$

which results in the constraint that

$$\begin{aligned} C(x_0 - x_1) > {\theta }(t) \end{aligned}$$

throughout the skimming motion. This is a property that is best evaluated numerically when the initial conditions are varied due to the coupling of the system of equations and effect of each parameter on the system. Increasing |C| further would lead the present model to give unphysical results as the leading edge of the body enters the water without the whole body being wetted. Thus, the choice of $\theta _0$ limits the extent to which |C| may be increased in the future analysis.

Secondly, considering the convex case, it is important that the trailing edge is the last point of contact as the body exits the liquid layer. In certain scenarios this may not occur due to the body undergoing a rotation. As a result it must be ensured that $\theta + \mathrm{{d}}T/\mathrm{{d}}x(x_0) \ge 0$ as exit is approached by setting the initial inclination of the body to be sufficiently large enough. Again, this is a property that is best evaluated numerically after each analysis of the system.

4.2 Exit-time behaviour

As the body progresses it begins to descend into the liquid layer with a positive pressure across the wetted region of the body’s underside increasing up to a point in time after which the pressure falls and the body begins to ascend back out of the layer. During this latter phase the leading contact position of the wetted region $x_1$ tends back towards $x_0$ as the body rises. At some point the body exits the liquid layer when $x_1$ equals $x_0$. We now refer to an analytical solution describing the behaviour of $x_1$ and the pressure under the body as exit is approached.

The exit solution and behaviour for $\gamma _0, \gamma _1, x_1$ and the pressure at the leading contact point found in [13] still hold in the general case. Particularly, the same unbounded response in $\gamma _0$ and $\gamma _1$ is expected since their definitions are analogous in the general polynomic case. Likewise, the definitions of $\gamma _m, m = 2,3,\ldots ,n$, imply that these responses remain bounded throughout (as confirmed by the numerical examples in Appendix B). Furthermore, since $(x_1 - x_0) (\sum _{a=0}^{n-1} a_m x_1^m)$ is small as the body approaches water exit, the body shape does not affect the arguments discussed in [13], and thus as one might anticipate their results are valid for the general polynomial case.

Therefore, in theory, for some time $t_e$, with the subscript e denoting a quantity at unknown water exit, the asymptotic solution ${{x}_1}_e = x_0 - (t_e - t) + \cdots + O((t_e - t)^2)$ holds for the exit asymptote (notably this may hold over a very short time period). This comes from an analysis of (10) near exit where the left-hand side $\sum _{m = 0}^{n} \gamma _m x_1^m$ is shown to be small. Since on the right-hand side $\left( Y + x_1 \theta - (x_0 - x_1)\left( \sum _{m = 0}^{n-1} a_m x_1^m \right) \right)$ is large, $\left( 1 - x_1^\prime \right)$ should be small to balance the equation, providing the above result. Also

$$\begin{aligned} p_1 = \frac{Y_{e,0} + x_{e,0} \theta _{e,0}}{\log (\alpha (t_e - t))^2} + \cdots , \end{aligned}$$

indicating that a rapid change in pressure is expected towards water exit, with the constant of integration $\alpha$ estimated graphically by considering the function [13]

$$\begin{aligned} \frac{1}{(t_e - t)} \exp \left( \frac{Y_{e,0} + x_{e,0} \theta _{e,0}}{D - D_{e,0}} \right) \rightarrow \alpha \end{aligned}$$

as $t \rightarrow t_e$. The logarithmic effect present implies a sensitive response here as in [13] but the response fits reasonably well with numerical findings over a short time frame as we will see in Sect. 6.

5 Computations for bodies with increasing underbody curvature

Before tackling the general case in Sect. 5.4 we consider first, in Sects. 5.1–5.3, the quadratic body-shape case where the thickness $T(x) = C(x_0 - x)(x_0 + x)$, with $x_0 = 1$ such that $n = 2, a_0 = C, a_1 = C, a_2 = 0$ and $x \in [-1,1]$. Two geometric configurations are of interest: negative and positive C, respectively, for which numerical and analytical calculations are now shown.

Numerical solutions for the system of equations (17)–(22) are produced using a seventh and eighth-order Runge–Kutta adaptive step-size integration [27] starting from the small-time solution derived in Sect. 4.

5.1 A concave underbody

First consider $C \le 0$, producing a concave or hooked body that curves towards the liquid layer. The geometry of the skimming body is as shown in Fig. 3. Unless otherwise stated, the following initial conditions are used for each case: $Y_0 = 20, V_0 = -1, \theta _0 = -20, \omega _0 = 0$ with $D_0 = x_0^2 \omega _0/2 + x_0 (V_0 + \theta _0 + a_0)$ and $M = 2, I = 1$. Of note throughout, it could be expected that aerodynamic effects may be influential on the non-wetted parts of the body surface and may be worth considering in greater detail in future studies; however, we treat these as negligible in the following calculations.

Fig. 3

Geometric configuration for concave underbody shape $T(x) = C(x_0 - x)(x_0 + x), C < 0$. Here $\theta _0$ refers to the angle made between the water surface and the line connecting the body’s ends

Fig. 4

Evolution of $x_1$ as a function of time for varying $C < 0$. The linear asymptotic behaviour at small time and for exit (dashed lines) are shown with a blow-up of the exit-time behaviour included

The initial $Y_0$ and $\theta _0$ are each larger than the cases shown in [13] to keep the resulting analysis geometrically and physically valid, as noted in Sect. 4.1. For example, since we are considering a downward hook, it is possible for the body to undergo a significant rotation such that $\theta$ becomes positive and the body moves into a nose down formation. Unlike a straight plate it is possible that both the leading edge and trailing edge of the body be submerged yet the rest of the body remain dry, which is not taken into account within the model given the definition of wetted region herein. Thus, as previously stated, a larger $\theta _0$ can help avoid this situation.

The evolution of the leading contact position of the wetter region $x_1$ throughout an impact is shown in Fig. 4 for $C = 0, -10, -50, -100, -200$. In this study some large values of C or |C| may be thought to be not sensible physically because of the underlying scaling argument discussed in Sect. 2 but they are taken in order to highlight solution trends. The same qualitative behaviour of the body as in $C = 0$ (the straight plate case) is seen for each case as |C| increases. That is, the leading contact position is initially close to the trailing edge at touch down and immediately begins to move in the negative direction as the body descends into the water film. Eventually a maximum wetted region is reached after which the body tends to rebound with the leading contact position moving downstream and returning to the trailing-edge position as water exit is approached. The physical limitation of the rebound is $x_1 \in \left[ -1,1 \right]$.

The time to body exit remains remarkably similar as |C| increases, marginally increasing with |C| as the extent of body wetting decreases (as measured from $x_1$ to $x_0$). Overall the small-time solution holds well throughout the body entry, displaying the trend of shallower entry gradient with increasing magnitude of C, as discussed in Sect. 4.2. The exit solution however only matches over increasingly short time frames with increasing magnitude of C (a phenomenon that involves the delicate effect of the logarithm and will be explained by asymptotic analysis in Sect. 6).

We further investigate the vertical height of the body’s centre of mass and its rotational progression to explain why the above dynamics occur. Figure 5 presents the height Y of the body’s centre of mass and the vertical velocity V of the body. In each case, Y initially falls as downward momentum carries the body into the liquid layer with the body beginning to rise out of the water as the pressure on the wetted region increases: see Fig. 7. Likewise while |C| grows larger the body leaves the liquid layer at a greater depth indicating a larger displacement of the water layer. In addition, the velocity of the body as it leaves is of a similar but positive value for each |C|. Again, the vertical velocity continues to increase throughout the majority of the skimming motion as the pressure falls away. This also helps to explain why the exit asymptote only holds within a short time frame (previously in [13] the body stopped accelerating at some earlier time before exit), as confirmed in the next section.

Fig. 5

Left: evolution of Y as a function of time for varying $C < 0$. Right: evolution of V as a function of time for varying $C < 0$

The discrepancy between entry and exit height Y can be understood by the rotational behaviour of the body, as shown in Fig. 6. As the body progresses through the liquid layer, there is an anti-clockwise moment due to a positive pressure over the wetted region. This causes the body’s angle of inclination to retreat throughout its skimming motion. Simultaneously the angular velocity accelerates rapidly throughout, reaching a constant near exit.

Since, geometrically, Y and $\theta$ are closely related, the reduced inclination of the body contributes to the smaller Y value upon exit. Physically, the body is descending into the water layer, undergoing a significant rotation which acts to lift the rear of the body out of the water. This causes the leading contact position of the wetted region to move towards the trailing edge producing the rapid decrease in the wetted region towards body exit. Thus, in this hooked body case, the trailing edge lifts out of the water before the body has completed the full “traditional” rebound (as discussed in [28]).

Fig. 6

Left: evolution of $\theta$ as a function of time for varying $C < 0$. Right: evolution of $\omega$ as a function of time for varying $C < 0$

As discussed in Sect. 4.2, the rapid change in the pressure at $x_1$ as exit is approached is still seen as |C| becomes large. Qualitatively the profile of the curve changes to a more parabolic shape with larger negative C, Fig. 7. The figure suggests the pressure may asymptotically approach the underbody-shape value at the leading contact point. The pressure initially increases until a maximum is reached after which it begins to fall with an increasingly sharp gradient until exit. This rapid plunge in pressure causes the shortness of the period in which the vertical and angular accelerations diminish. Section 6 describes analysis and comparisons for the current concave case.

Fig. 7

Evolution of the pressure on the body at $x_1$ as a function of time for varying $C < 0$. The corresponding body thickness at $x_1$ is shown for each case (dashed lines) for comparison

Fig. 8

Geometric configuration for convex underbody shape $T(x) = C(x_0 - x)(x_0 + x), C = C_1, C_2;$ $C_2>C_1>0$. Here the air angle ${\hat{\theta }}_0$ refers to the angle made between the water surface and the tangent of the underbody at $x_0$. For varying C, $\theta _0$ is the body angle and increases with C according to $\theta _0 = {\hat{\theta }}_0 - \frac{\mathrm{{d}}T}{\mathrm{{d}}x}(x_0)$

5.2 A convex underbody with fixed air angle

Now consider $C > 0$, for a convex body that curves away from the water layer. The physical geometry may be analysed in two ways. The first scenario to consider is for a fixed air angle. In this case an initial angle, say ${\hat{\theta }}_0$, between the underbody at the trailing edge and the water layer is fixed for all values of C. Thus, for increased C, $\theta _0$ must increase to maintain ${\hat{\theta }}_0$, i.e. $\theta _0 = {\hat{\theta }}_0 - \frac{\mathrm{{d}}T}{\mathrm{{d}}x}(x_0)$. This is shown in Fig. 8. In this scenario, the size of C is not limited since $\theta _0$ accounts for the change in geometry.

The evolution of $x_1$ throughout an impact is shown in Fig. 9 for $C = 0, 10, 50, 100, 200$ with $\theta _0 = -20, -40, -120, -220, -420$, respectively. Again the flat place case where $C = 0$ is computed for comparison. The same qualitative behaviour of the body rebound is seen in each case of varying C. Here again analysis is called for (see in Sect. 6) to explain the overall effects of increasing C as well as the changes in responses near entry and exit.

As C becomes large the extent of underbody wetting decreases, showing the dynamics explained in Sect. 4. In this case, the small-time solution is the same for each value of C since $\theta _0 + \sum _{m = 0}^{n-1} a_m x_0^m = {\hat{\theta }}_0$ in (26) which is the fixed air angle. For large C the body’s trajectory quickly deviates from the small-time solution and a similar trend of rapid body exit is shown. The results suggest that both the variation in Y and the velocity V remain of O(1) as C increases.

Despite the difference in small-time response compared to the $C<0$ cases, the dynamics of the body rebound are otherwise similar—as seen in Figs. 10 and 11. Notably, the Y and $\theta$ responses are translated by $\frac{\mathrm{{d}}T}{\mathrm{{d}}x}(x_0)$ for Y and $-\frac{\mathrm{{d}}T}{\mathrm{{d}}x}(x_0)$ for $\theta$ for each value of C, respectively. The body again undergoes significant rotation and as a result exits the water film with a positive vertical velocity at a smaller height than its entered height.

The initial angle must still be set large enough such that the body position does not become nose down ($\theta < 0$). A nose down formation will allow the trailing edge of the body to lift out of the water with the body remaining in contact with the liquid layer, creating a chord across two points away from the trailing edge. In this case the body may remain in contact with the water sheet while the trailing edge detaches giving the impression of a completed skim. Thus, $\theta _0$ must be large enough to prevent this happening.

Fig. 9

Evolution of $x_1$ as a function of time for varying $C > 0$, fixed air angle case. The linear asymptotic behaviour at exit (dashed lines) are shown

Fig. 10

Left: evolution of Y as a function of time for varying $C > 0$, fixed air angle case. Right: evolution of V as a function of time for varying $C > 0$, fixed air angle case

Fig. 11

Left: evolution of $\theta$ as a function of time for varying $C > 0$, fixed air angle case. Right: evolution of $\omega$ as a function of time for varying $C > 0$, fixed air angle case

Finally, the rapid change in the pressure at $x_1$ as exit is approached is seen as C becomes large, Fig. 12. The rapid plunge in pressure causes similar characteristics to before, with a shorter period in which the body’s acceleration slows as it exits the water layer.

5.3 A convex underbody with fixed body angle

The second scenario for $C > 0$ is to consider a fixed body angle. In this case an initial angle, say ${\theta }(0)$, between the body midline and the water layer is fixed. Thus, for increased C, the initial air angle ${\hat{\theta }}_0$ reduces as C increases since ${\hat{\theta }}_0 = {\theta }_0 - \frac{\mathrm{{d}}T}{\mathrm{{d}}x}(x_0)$. This is shown in Fig. 13. In this scenario, the size of C is limited since $\theta + \sum _{m = 1}^n a_m x_1^m > 0$. Hence, considering the quadratic body shape: $C<\theta _0/2$.

Fig. 12

Evolution of the pressure on the body at $x_1$ as a function of time for varying $C > 0$, fixed air angle case

Fig. 13

Geometric configuration for a convex underbody shape $T(x) = C(x_0 - x)(x_0 + x), C >0$. Here $\theta _0$ refers to the angle made between the water surface and a straight line that connects the body’s maxima. For increasing C, the effective body angle ${\hat{\theta }}_0 = \theta _0 - T_x(x_0)$ decreases

Fig. 14

Evolution of $x_1$ as a function of time with $\theta _0 = -2$ and $C = 0, 0.33, 0.66$ and 0.99, for fixed body angle. The linear asymptotic behaviour at small time and for exit are also shown

Fig. 15

Evolution of the pressure on the body at $x_1$ as a function of time for $\theta _0 = -2$ and $C = 0, 0.33, 0.66$ and 0.99, fixed body angle case. The inset shows the rapid decrease in leading edge pressure as exit is approached

The evolution of $x_1$ throughout the skimming impact is shown in Fig. 14 for $C=0,0.33,0.66,0.99$ with $Y(0) = Y_0 = 2, V_0 = -1, \theta _0 = -2, \omega _0 = 0$ with $D_0 = x_0^2 \omega _0/2 + x_0 (V_0 + \theta _0 + a_0)$ and $M = 2, I = 1$. Notably, for $C=0$ this is the same straight plate case studied in [13]. As C increases the dynamics seen are very different to the previous two cases. While qualitatively the same, as C increases the time to exit is delayed with the body penetrating further into the water layer with an increasingly skewed trajectory (fast entry to rebound with a slower progression towards exit). Here, the largest C corresponds to a very shallow air angle upon entry which has not been seen previously. In addition, the agreement between exit asymptotes and numerical solutions is closer than in the cases presented earlier in Sects. 5.1 and 5.2.

Furthermore, the underbody curvature is important here. An equivalent case of a straight plate at a shallow angle of entry $\theta _0 = -0.02$ gives an unphysical result with the body becoming fully submerged early into the skim. One reason for this is that the initial vertical height of the plate is small, $Y_0 = 0.02$, and hence the denominator in (22) is small to begin with, inducing the rapid decent into the liquid layer. Thus, the underbody curvature helps to balance this equation and sustain a skim that is within the physical bounds of the model. To understand the rebound further, the pressure at $x_1$ on the body is presented in Fig. 15.

Fig. 16

Evolution of the pressure across the wetted region of the body at several time intervals for $\theta _0 = -2$ and $C = 0$ and $C = 0.99$, fixed body angle case. The inset in the $C = 0$ plot shows the $t = 4.5, 5.0, 5.5$ curves for clarity

The profile is very different to the previous cases. Given the need for a larger initial $\theta$ for the previous two cases, the shape of the pressure profile seen in [13] was lost. Now however, a similar qualitative shape is seen in each case with the pressure initially increasing steeply and reaching a peak after which it falls again as exit is approached, and quickly plummeting on exit. As C becomes larger the initial increase in pressure is sharper, while after the peak the pressure falls more slowly, matching and explaining the behaviour of $x_1$ progression. A larger positive pressure is sustained for longer throughout the skimming process and declines more slowly inducing a slower lift back through the liquid layer. Interestingly the peak value of each curve is similar and the plunge in pressure to zero is seen for each C. When the pressure over the whole body is compared for the $C = 0$ case and $C = 0.99$ case, it is clear that a larger pressure is maintained during the skim for a larger C, Fig. 16. The consequences of these differences in pressure are seen in Fig. 17, regarding the rotation of the body and its vertical velocity.

For $\theta$ and $\omega$, when $C = 0$, the body undergoes a positive rotation, decreasing the body’s angle of inclination. As C increases however the behaviour changes dramatically. When $C = 0.33$ the same rotational behaviour is seen as an anti-clockwise rotation acts on the body, yet this is less than the $C = 0$ case and the body maintains a larger negative angle of inclination. As C grows larger, at some point during the skim the body’s angular velocity now becomes negative, induced by the slow decline in positive pressure. As a result an clockwise rotation acts on the body increasing its inclination to the flow. For the largest C the body’s angle more than doubles. When compared to the pressure at $x_1$, the changes in angular velocity closely match the changes in gradient of the pressure profile, showing how the body responds to the variation of pressure due to underbody shape.

The response of the body’s vertical height Y and vertical velocity V are also significant. Before, rotation led to the body exiting the water layer at a lower height; here a super-elastic response is seen where the velocity and vertical height are of greater magnitude upon exit for increased C. The underbody pressure is once again instructive as the delayed exit and slower decline in pressure lead to this response, pushing the body out of the water with greater velocity and height. This is in accordance with observations from empirical studies [29].

Fig. 17

Top left: evolution of Y as a function of time. Top Right: Evolution of V as a function of time. Bottom Left: Evolution of $\theta$ as a function of time. Bottom Right: Evolution of $\omega$ as a function of time, for fixed body angle

5.4 Arbitrary underbody

Results for a more general body shape are presented here for the sake of completeness and for subsequent analysis. Figure 18 displays a fixed angle case with $T(x) = (x_0 - x)(0.1625 + 0.1625 x - 0.5 x^2 - 0.5 x^3 + x^4 + x^5)$, giving the $x_1$ trajectory, while Fig. 19 shows the corresponding pressure response at the leading edge. The trends for increasing C values are the same as in the cases of the simpler curved shapes in previous figures.

We turn next to an analysis of the influences of increased C or |C| values.

6 Analysis and comparisons

Asymptotic analysis is described here for relatively large underbody curvature, as guided by the numerical results and trends of the previous section, and this is accompanied by comparisons between the numerical and the analytical findings. Section 6.1 addresses the concave shape and Sect. 6.2 the convex shape.

Fig. 18

Evolution of $x_1$ as a function of time for a more general convex body shape for varying $C > 0$, with a fixed air angle. The dashed lines are the entry and exit asymptotes for each case

Fig. 19

Evolution of pressure on the body at $x_1$ as a function of time for a more general convex body shape for varying $C > 0$, with a fixed air angle

6.1 For concave underbodies

The present description is based on the approach laid out in Sect. 3 for a general body shape with concavity. Of interest is the result that the pressure under a hooked body equals the displacement of the liquid layer for large |C|. This is evaluated analytically below for any generic polynomic body shape where $a_m = {\hat{a}}_m C, m = 0,1,2,\ldots ,n$. In fact, as C grows large, the pressure across the wetted region for any point, $x \in [x_1, x_0]$ say, tends towards the body thickness at x throughout the rebounding process, shown particularly for the leading contact position of the wetted region in Fig. 7. This is due to the definition of pressure in (10). As $|{C}| \rightarrow \infty$, $Y, Y^\prime , \theta , \theta ^\prime , D, D^\prime$ are all O(1), and only $a_m \sim C, m = 0,1,2,\ldots ,n$, so that the pressure approximates to

$$\begin{aligned} p(x) = \sum _{m = 0}^{n} \gamma _m x^m =&\left( -D^\prime + Y^\prime + \theta \right) \left( x - x_0 \right) + \left( \frac{Y^{\prime \prime }}{2} + \theta ^\prime \right) \left( x^2 - x_0^2 \right) \\&+ \left( \frac{\theta ^{\prime \prime }}{6} \right) \left( x^3 - x_0^3 \right) + \sum _{m =1}^n \left( a_{m-1} - x_0 a_m \right) \left( x^m - x_0^m \right) , \\ \rightarrow&- (x - x_0)\left( \sum _{m = 0}^{n-1} a_m x^m \right) = T(x) . \end{aligned}$$

This result holds for all concave body shapes. It is partly for this reason that the exit asymptote holds over decreasingly short time periods as $|{C}| \rightarrow \infty$. Explicitly, substituting this result in to (22) we have that

$$\begin{aligned} x_1^\prime \rightarrow 1 - \left( \frac{T(x_1)}{Y + x_1 \theta + T(x_1)}\right) ^{1/2}. \end{aligned}$$

Since $T(x_1)$ takes larger values as $|{C}| \rightarrow \infty$, the $T(x_1)$ remains larger over a longer time period and dominates the $Y + x_1 \theta + T(x_1)$ term in the denominator. However, at some point in time as exit is approached, $T(x_1)$ becomes smaller than $Y + x_1 \theta + T(x_1)$ (which remains non-zero) and $x_1^\prime$ quickly tends to the exit asymptote value of 1 with $T(x_1)$ eventually diminishing to 0.

Further understanding is gained for arbitrary bodies when the shallow-water equation (3a) is considered with (11). Integrating (3a) with respect to x, we obtain

$$\begin{aligned} \int _{x_0}^x {u}_t \ \mathrm{{d}}x + {u} = -{p}, \; x_1 \le x \le x_0. \end{aligned}$$

At leading order the term u only contributes T(x) as per (11). The remaining integral provides

$$\begin{aligned} \int _{x_0}^x D^\prime (t) - \frac{1}{2} \theta ^{\prime \prime } x^2 - \theta ^{\prime } x^\prime x - x \left( Y^{\prime \prime } + \theta ^\prime \right) - x^\prime \left( Y^{\prime } + \theta \right) + \sum _{m = 0}^{n-1} (m+1)(x_0 a_{m+1} - a_{m}) x^\prime x^{m} \mathrm{{d}}x. \end{aligned}$$

Each term is O(1) other than the $a_m$ coefficients; however, $x^\prime \rightarrow 0$ as |C| becomes large (from Sect. 4). Thus at leading order the above integral is negligible and only the body thickness at $x \in \left[ x_1, x_0\right]$ contributes to the pressure response at x.

The broad implication here is that, for the thicker bodies of present interest, the skimming process becomes quasi-steady as far as the fluid flow is concerned, whereas the body motion remains fully unsteady. Thus the time derivatives in (3a, 3b) become negligible and so we have simply

$$\begin{aligned} u_x = - p_x, \qquad h_x + u_x = 0. \end{aligned}$$

Hence to within additive constants the balance $p = - u = h$ holds, confirming the simple relation found above between the scaled pressure and the scaled shape: see for example the results in Figs. 7, 9, 18. This simplification should be of much interest in further exploration of the skimming effects due to much thicker bodies: see also the next section. The latter would include cases where the body thickness is comparable with the liquid-layer depth, negating the expansion (1) and making the fluid–body interaction fully non-linear throughout, similar in form to the interactions studied by [1, 2, 25, 30,31,32,33] in various contexts. Here the change in interaction structure and the connection with other settings are interesting features in terms of the original applications discussed in the introduction.

Considering all of the above, there is still much dynamical interest in understanding how hooked bodies skim. In the next section investigations are made into how the effects of scaled size of underbody curvature and its initial inclination may be approximated.

6.1.1 Large negative C and analogy with large initial $\theta$

The equations will now be studied for large negative C to find the limiting behaviour and a reduced system of equations. Considering a general underbody shape, substituting (23) into (22) gives the evolution of $x_1$ as governed by

$$\begin{aligned} x_1^\prime = 1 - \frac{\left[ - D + \frac{1}{2} \omega x_1^2 + x_1 \left( V + {\theta } \right) - \sum _{m = 1}^{n} (x_0 a_m - a_{m-1}) x_1^m \right] }{Y + x_1 {\theta } - (x_0 - x_1)\left( \sum _{m = 0}^{n-1} a_m x_1^m \right) }. \end{aligned}$$

(27)

Since the wetted region remains small for large-scaled underbody curvature such that $x_1 \sim x_0$, then $\sum _{m = 0}^{n-1} a_m x_1^m$ may be approximated by $\sum _{m = 0}^{n-1} a_m x_0^m$, which is the derivative of T(x) at $x_0$, such that (27) becomes

$$\begin{aligned} x_1^\prime \approx 1 - \frac{- \left( D + \sum _{m = 0}^{n-1} x_0 a_m x_0^m - x_0 a_0\right) + \frac{1}{2} \omega x_1^2 + x_1 Y^\prime + x_1 \left( {\theta } +\sum _{m = 0}^{n} a_{m} x_0^{m} \right) }{ \left( Y - x_0 \sum _{m = 0}^{n-1} a_m x_0^m \right) + x_1 \left( {\theta } + \sum _{m = 0}^{n-1} a_m x_0^m \right) }. \end{aligned}$$

(28)

We define

$$\begin{aligned} {\bar{D}}&= D + \sum _{m = 0}^{n-1} x_0 a_m x_0^m - x_0 a_0 = D + \frac{\mathrm{{d}}T}{\mathrm{{d}}x}(x_0) - x_0 a_0 \\ {\bar{Y}}&= Y - x_0 \sum _{m = 0}^{n-1} a_m x_0^m = Y - x_0 \frac{\mathrm{{d}}T}{\mathrm{{d}}x}(x_0) \\ {\bar{\theta }}&= {\theta } +\sum _{m = 0}^{n} a_{m} x_0^{m} = {\theta } + \frac{\mathrm{{d}}T}{\mathrm{{d}}x}(x_0) \\ x_1^\prime&\approx 1 - \frac{-{\bar{D}} + \frac{1}{2} \omega x_1^2 + x_1 Y^\prime + x_1 {\bar{\theta }}}{ {\bar{Y}} + x_1 {\bar{\theta }}}. \end{aligned}$$

Geometrically, as C grows large, the above shows that the skimming action of the trailing edge of any concave-shaped body may be approximated by that of a straight plate at an increased initial angle $\theta _0$.

This can be seen numerically in Figs. 20–22. Illustrated again by the quadratic case, for $C < 0$ such that $a_0 = C x_0, a_1 = C$ and $a_m = 0, m > 1$, the result for $x_1$ is analogous to the case where $T(x) = 0$, ${\bar{\theta }}_0 = -2 + 2C, {\bar{Y}}_0 = 2 - 2C$ and ${\bar{D}}_0 = -2 + 2C + V_0 = {\bar{\theta }}_0 + V_0$.

In Fig. 20, the evolution of $x_1$ for varying $C < 0$ and the equivalent straight plate cases match closely. It is observed in particular that the time to body exit is captured well as is the rebound behaviour. Figure 21 shows that the pressure response at the leading contact position of the wetted region is similar to that for the flat plate. Another comparison given in Fig. 21 is with the body-thickness function (in view of the analysis above), indicating quite close agreement especially as the negative effective underbody curvature increases. Finally, Fig. 22 shows that the vertical position of the body’s centre of mass, its vertical velocity, its inclination and its rotational velocity closely match the straight plate.

Given the above results, the system of equations can now be reduced and used to model either a steep flat plate or a downward hooked underbody of large-scaled underbody curvature since they act very similarly as one would expect. Consider a straight plate at a large angle $\theta$ that corresponds to a concave underbody shape with some $C<0$ (as defined above). In the straight plate case $a_m = 0, m = 0,1,2,\ldots ,n$ and ${\theta }, {Y}, D \sim C$ while all other parameters are O(1) throughout. Notably, ${D}^\prime , \gamma _0$ and $\gamma _{1}$ each become large when exit is approached; however, this is only over a very short time scale in principle such that they can be treated as O(1) quantities for the majority of the evolution.

Fig. 20

Evolution of $x_1$ as a function of time for: $C = -\,200, -\,50$ and $-\,10$ with $\theta _0 = -\,20$ (curved underbody, solid lines) and for $C = 0$ with $\theta _0 = -\,420, -\,120$ and $-\,40$ (straight underbody, dotted lines)

Fig. 21

Evolution of pressure on the body at $x_1$ as a function of time for $C = -\,200, -\,50$ and $-\,10$ with $\theta _0 = -\,20$ (curved underbody, solid lines) and for $C = 0$ with $\theta _0 = -\,420, -\,120$ and $-\,40$ (straight underbody, dotted lines). The corresponding body thicknesses at $x_1$ are shown for comparison (dashed lines)

Fig. 22

Top left: evolution of Y as a function of time. Top right: evolution of V as a function of time. Bottom Left: Evolution of $\theta$ as a function of time. Bottom Right: Evolution of $\omega$ as a function of time. For $C = -\,50$ with $\theta _0 = -\,20$ and with $C = 0$ with $\theta _0 = -\,120$

6.2 For convex underbodies—fixed air angle

The detailed account below returns to consider the original equations of Sect. 2 when the body becomes thicker in the sense of its convex underbody becoming more curved. (A similar account applies for the concave case.)

The solution for $C \gg 1$ with air angle and initial velocity V(0) of order unity is found to involve three distinct successive stages as follows.

6.2.1 Stage 1—early times

The first stage occurs soon after entry. Orders of magnitude indicate the small scale $x - x_0 = C^{-1} x^*$ near the entry point with $x^*$ of O(1), with the time scaling $t = C^{-1} t^*$ proving important in the development since it corresponds to the contact speed being of order unity: physically this comparability between horizontal body speed and wetting speed is the distinguishing feature of the first stage. Here the underbody function T is $O(C^{-1})$, while M, I are assumed to be of order unity and we expect the variations in $u, p, h, Y, \theta$ to all be $O(C^{-1})$. The reason for these orders stems from the initial body velocity being O(1) and the body surface being highly curved which admits a balance between the dominant shape proportional to $C(x - x_0)^2$ and the $O(C^{-1})$ effect above.

The expansion applying here is

$$\begin{aligned} (p, h, u, T)&= (C^{-1} p^*, C^{-1} h^*, C^{-1} u^*, \sigma _1 x^* + C^{-1} (k_3 x^* + T^*)) + \cdots , \end{aligned}$$

(29a)

$$\begin{aligned} (Y, \theta )&= (C \sigma _2 + \sigma _4 + C^{-1} Y^*, C \sigma _1 + \sigma _3 + C^{-1} \theta ^*) + \cdots , \end{aligned}$$

(29b)

where $\sigma _1$ to $\sigma _4$ are typically O(1) constants satisfying $\sigma _2 + x_0 \sigma _1 = 0, \sigma _4 + x_0 \sigma _3 = 0$, from the initial impact conditions, and $-C \sigma _1$ is the large slope of the underbody at the trailing edge, whereas $C \sigma _1$ is the large body angle at leading order. Smaller constants can be added to the $Y, \theta$ expansions satisfying the initial impact requirement, while the constant $k_3$ is an O(1) body angle correction and the contribution $T^*$ represents the main effect of the body curvature. From substitution into (2) and with $x_{cm}, x_0$ taken as 0, 1, respectively, we have, after some cancellation,

$$\begin{aligned} h^*(x^*, t^*) = Y^*(t^*) + \theta ^*(t^*) - T^{**}(x^*) , \end{aligned}$$

(30)

at order $C^{-1}$, where $T^{**} = T^* + s x^*$ and the constant $s = k_3 - \sigma _3$ is a given relative angle. So the kinematic requirement (3b) on integration implies that

$$\begin{aligned} u^* = T^{**}(x^*) - ({Y^*}^\prime (t^*) + {\theta ^*}^\prime (t^*)) x^* + f_1^*(t^*), \end{aligned}$$

(31)

where $f_1^*(t^*)$ is an unknown function. Then the x-momentum equation (3a) gives

$$\begin{aligned} p^* = \frac{1}{2} ({Y^*}^{\prime \prime }(t^*) + {\theta ^*}^{\prime \prime }(t^*)) {x^*}^2 + ({Y^*}^\prime (t^*) + {\theta ^*}^\prime - {f_1^*}^\prime (t^*)) x^* - T^{**}(x^*) + f_2^*(t^*) \end{aligned}$$

(32)

on integration, with $f_2^*(t^*)$ an unknown function of $t^*$. The Kutta condition at the trailing edge $x^* = 0$ now requires however that $f_2^*(t^*)$ must be identically zero, and hence the two leading edge conditions (5, 6) applied at the current unknown contact location $x^* = x_1^*(t^*)$ become

$$\begin{aligned}&\frac{1}{2} ({Y^*}^{\prime \prime }(t^*) + {\theta ^*}^{\prime \prime }(t^*)) {x_1^*}^2 + ({Y^*}^\prime (t^*) + {\theta ^*}^\prime - {f_1^*}^\prime (t^*)) x_1^* - T^{**}(x_1^*) \nonumber \\&\quad =-\,(1 - {x_1^*}^\prime ) [T^{**}(x_1^*) - ({Y^*}^\prime (t^*) + {\theta ^*}^\prime (t^*)) x_1^* + f_1^*(t^*)] , \end{aligned}$$

(33a)

$$\begin{aligned}&[T^{**}(x_1^*) - ({Y^*}^\prime (t^*) + {\theta ^*}^\prime (t^*)) x_1^* + f_1^*(t^*)] \nonumber \\&\quad =-\,(1 - {x_1^*}^\prime )\lbrace Y^*(t^*) + \theta ^*(t^*) - T^{**}(x_1^*)\rbrace , \end{aligned}$$

(33b)

successively.

On the other hand the body-motion equations (7), (8) have contributions O(C) on the left but only $O(C^{-2})$ on the right and so they yield simply $M {Y^*}^{\prime \prime } = 0$ and $I {\theta ^*}^{\prime \prime } = 0$. In consequence

$$\begin{aligned} Y^*&= Y_0^* + V^* t^*, \end{aligned}$$

(34a)

$$\begin{aligned} \theta ^*&= \theta _0^* + \omega _0^* t^* . \end{aligned}$$

(34b)

Here the initial values $Y^*_0 , V^*, \theta ^*_0 , \omega ^*_0$ are known O(1) constants and $Y^*_0 + \theta ^*_0 = 0$ since $h^*$ must be zero initially at the trailing edge. Use of (34a) and  (34b) in  (33a) and  (33b) leaves us with two equations for the evolution of $f_1^*(t^*), x_1^*(t^*)$. The influence of the local underbody curve is given by

$$\begin{aligned} T^*(x^*) = q {x^*}^2,\text { so } T^{**}(x^{**}) = s x^* + q {x^*}^2 , \end{aligned}$$

(35a)

with q a constant O(1) coefficient. The solution of (33a), (33b), where $Y^*, \theta ^*, T^*$ are given by (34a), (34b), (35a), is displayed in Fig. 23. A single non-linear equation for $\chi (t^*) = x_1^*(t^*)$ can be written down, namely

$$\begin{aligned} (\tau - V^{**}t^*) \chi \chi ^{\prime \prime } + \lbrace \chi \tau ^\prime - 2 V^{**} \chi + (\tau - V^{**} t^*)( \chi ^\prime - 2) \rbrace \chi ^\prime + 2V^{**} \chi = V^{**}t^* \end{aligned}$$

(35b)

(here $\tau (t^*)$ denotes $T^{**}(x_1^*(t^*))$ and the constant $V^{**} = V^* + \omega ^*_0$ ), and this can be normalised to the case where q, $V^{**}$ are both $-1$ by working in terms of $qt^*/V^{**}$, $q x_1^*/V^{**}$. The only parameter in effect is $s/V^{**}$. Solving (35b) numerically gives the result in the figure.

Fig. 23

Results from large-C analysis in Sect. 6.2, for the entry phase (stage 1) of a convex underbody. Plots of $x_1^*$ (blue) and its derivative (red) versus scaled time $t^*$. Here $s/V^{**} = 1$. Also shown are the asymptotes for large $t^*$ (dashed). (Color figure online)

Fig. 24

Large-C analysis, the middle phase (stage 2), convex underbody. Graphs of the function Z (blue), the contact-point correction $X_1$ (red, dash) and the pressure term $p_0$ at the contact point (yellow, dash) versus t

The response at small times $t^*$ essentially retrieves the form discussed in Sect. 4.1, as required, verifying the dependence on $s/V^{**}$. The response at large $t^*$ by contrast exhibits the growth

$$\begin{aligned} x_1^* \sim \lambda {t^*}^{2/3} + \cdots , \qquad f_1^* \sim \mu t^* + \cdots , \; (t^* \rightarrow \infty ), \end{aligned}$$

(36a)

where $\lambda = - (3V^{**}/(4q))^{1/3}, \mu = 2q\lambda ^3/3$. The reduction in downward velocity of the contact point compared with that at small times is sensible physically for such a thick body. Along with this the other properties behave according to

$$\begin{aligned} (u^*, p^*, h^*, T^*) \sim q \lambda ^2 (1, -1, -1, 1) {t^*}^{4/3} + O(t^*) , \end{aligned}$$

(36b)

from (30), (32), while $Y^*, \theta ^*$ are given by (34a), (34b).

6.2.2 Stage 2—time for the majority of the skim

The next stage is associated physically with the lift and moment on the body becoming significant. Stage 2 takes place when t rises to O(1). In this stage as inferred from the behaviour in (36a), (36b) we have $x - 1 = C^{-1/3} X$ with X of O(1) and the expansion of the solution along with the underbody shape now takes the form

$$\begin{aligned}&x_1(t) - 1 = C^{-1/3}X_1(t) + C^{-2/3} X_{11}(t) + \cdots , \end{aligned}$$

(37a)

$$\begin{aligned}&(p, h, u, T - C^{2/3} \sigma _1 X) = C^{1/3} ({\bar{p}}_0, {\bar{h}}_0, {\bar{u}}_0, {\bar{T}}_0) + ({\bar{p}}_1, \bar{h_1}, {\bar{u}}_1, {\bar{T}}_1) + \cdots , \end{aligned}$$

(37b)

$$\begin{aligned}&(Y, \theta ) = (C \sigma _2 + {\bar{Y}}_0, C \sigma _1 + {\bar{\theta }}_0) + \cdots . \end{aligned}$$

(37c)

We substitute the expansion into (2), (3), (4)–(7) and obtain the following reduced equations. At leading order, the unknown terms having subscript zero together with $X_1$ are seen to satisfy

$$\begin{aligned}&{{\bar{h}}_{0_X}} + {{\bar{u}}_{0_X}} = 0 , \end{aligned}$$

(38a)

$$\begin{aligned}&{{\bar{u}}_{0_X}} = -\,{{\bar{p}}_{0_X}} , \end{aligned}$$

(38b)

$$\begin{aligned} {\bar{h}}_0 = -\,{\bar{T}}_0(X) \end{aligned}$$

(39)

$$\begin{aligned}&\text {at } X = 0: \; {\bar{p}}_0 = 0, \end{aligned}$$

(40a)

$$\begin{aligned}&\text {at } X = X_1: \; {\bar{p}}_0 = -{\bar{u}}_0, \end{aligned}$$

(40b)

$$\begin{aligned}&\text {at } X = X_1: \; {\bar{u}}_0 = -{\bar{h}}_0, \end{aligned}$$

(40c)

$$\begin{aligned} M {\bar{Y}}_0^{\prime \prime }&= \int _{X_1}^0 {\bar{p}}_0(X, t) \mathrm{{d}}x; \end{aligned}$$

(41a)

$$\begin{aligned} I {\bar{\theta }}_0^{\prime \prime }&= \int _{X_1}^0 {\bar{p}}_0(X, t) \mathrm{{d}}x . \end{aligned}$$

(41b)

The equality of the scaled lift and moment are notable. Solving gives only very little explicit time dependence at this level, with

$$\begin{aligned} {\bar{u}}_0&= {\bar{u}}_0(X) = -{\bar{h}}_0 = -{\bar{h}}_0(X), \end{aligned}$$

(42a)

$$\begin{aligned}&= -{\bar{p}}_0 = -\,{\bar{p}}_0(X), \end{aligned}$$

(42b)

$$\begin{aligned}&= {\bar{T}}_0(X), \end{aligned}$$

(42c)

which satisfy (38a)–(40c), while (41a), (41b) give us

$$\begin{aligned} M {\bar{Y}}_0^{\prime \prime }&= -\int _{X_1}^0 {\bar{T}}_0(X) \mathrm{{d}}x; \end{aligned}$$

(43a)

$$\begin{aligned} I {\bar{\theta }}_0^{\prime \prime }&= -\int _{X_1}^0 {\bar{T}}_0(X) \mathrm{{d}}x . \end{aligned}$$

(43b)

The integral contributions immediately above are, to repeat, the aspects that distinguish the present time scale from the earlier one. However we are one equation short since (43a), (43b) yield two equations for three unknown functions of t, namely ${\bar{Y}}_0, {\bar{\theta }}_0, X_1$. We continue to the next order to derive the third equation.

At the next order, the unknowns with subscript unity and the correction term $X_{11}$ take effect in the form

$$\begin{aligned}&{{\bar{h}}_{0_t}} + {{\bar{h}}_{1_X}} + {{\bar{u}}_{1_X}} = 0, \end{aligned}$$

(44a)

$$\begin{aligned}&{{\bar{u}}_{0_t}} + {{\bar{u}}_{1_X}} = -{{\bar{p}}_{1_X}} , \end{aligned}$$

(44b)

$$\begin{aligned} {\bar{h}}_1 = -{\bar{T}}_1(X) + {\bar{Y}}_0(t) + {\bar{\theta }}_0(t) , \end{aligned}$$

(45)

$$\begin{aligned}&\text {at } X = 0: \; {\bar{p}}_1 = 0; \end{aligned}$$

(46a)

$$\begin{aligned}&\text {at } X = X_1: \; {\bar{p}}_1 + X_{11} {\bar{p}}_0^\prime (X_1) = -{\bar{u}}_1 - X_{11} {\bar{u}}_0^\prime (X_1) + X_1^\prime {\bar{u}}_0(X_1) , \end{aligned}$$

(46b)

$$\begin{aligned}&\text {at } X = X_1: \; {\bar{u}}_1 + X_{11} {\bar{u}}_0^\prime (X_1) = -{\bar{h}}_1 - X_{11} {\bar{h}}_0^\prime (X_1) + X_1^\prime {\bar{h}}_0(X_1) . \end{aligned}$$

(46c)

Therefore solving gives, from (44a) and (44b),

$$\begin{aligned} {\bar{u}}_1(X, t)&= -{\bar{h}}_1(X, t) + G_0 (t), \end{aligned}$$

(47a)

$$\begin{aligned} {\bar{p}}_1(X, t)&= {\bar{h}}_1(X, t) + G_2(t), \end{aligned}$$

(47b)

where the Kutta condition leaves us with $G_2(t) = -{\bar{h}}_1(0, t)$. Then when we impose (46b), (46c) we find much cancellation takes place and leads to the two equations

$$\begin{aligned} G_2(t)&= - G_0 (t) + X_1^\prime {\bar{T}}_0(X_1),\\ G_0(t)&= - X_1^\prime {\bar{T}}_0(X_1), \end{aligned}$$

respectively. Hence we obtain, after also using (45) and the fact that ${\bar{T}}_1(0)$ is zero,

$$\begin{aligned} - ( {\bar{Y}}_0(t) + {\bar{\theta }}_0 (t)) = 2 X_1^\prime (t) {\bar{T}}_0(X_1) \end{aligned}$$

(48)

as the third equation. (This agrees with the previous temporal stage involving $x_1^*$ at large $t^*$.)

Hence our non-linear problem in this second stage reduces to solving (43a), (43b), and (48). We take the local shape to be ${\bar{T}}_0(X) = q X^2$ as the main example as above. Remarkably the solution is then determined by a linear ODE since putting $Z = X_1^3$ leads to Z(t) satisfying

$$\begin{aligned} Z^{\prime \prime \prime } = -c_1 Z. \end{aligned}$$

(49a)

Here $c_1 = (I + M) /(2 I M)$ is a positive constant. The initial condition to match the trend (36a) emerging from the first stage is

$$\begin{aligned} Z \sim \lambda ^3 t^2 \text { as } t \rightarrow 0^+, \end{aligned}$$

(49b)

where we comment that $\lambda ^3 = - 3 V^{**} / (4q)$ is negative. The analytical solution is plotted in Fig. 24. The Z curve matches with (49b) at small t, reaches a minimum at a finite value of t and subsequently it approaches zero, where we find a terminal time $t_F$ which is dependent only on the coefficient c, i.e. on the M, I values, not on the shape factor q or the initial velocity V(0) (or indeed on C provided C is large). The approach of Z is linear in terms of $t_F - t$ and therefore $p, h, u, T, X_1$ vary as 2/3 powers and $X_1$ as the 1/3 power of $t_F - t$ locally.

6.2.3 Stage 3—time to exit

The final stage has the contact point approaching the trailing edge closely and at a speed comparable with the original body speed. The ending of the previous stage as the function Z tends linearly to zero, forcing $X_1$ into an irregular (1/3 power) trend, points to the appropriate scales in stage 3 which yield $t = t_F + C^{-1/2} {\hat{t}}, x - 1 = C^{-1/2} {\hat{x}}$ with ${\hat{t}}, {\hat{x}}$ of order unity and, in terms of asymptotic expansion,

$$\begin{aligned}&x_1 - 1 = C^{-1/2} {\hat{x}}_1(t) + \cdots , \end{aligned}$$

(50a)

$$\begin{aligned}&(p, h, u, T-C^{1/2} \sigma _1 {\hat{x}}) = ({\hat{p}}, {\hat{h}}, {\hat{u}}, {\hat{T}}) + \cdots , \end{aligned}$$

(50b)

$$\begin{aligned}&(Y, \theta ) = (C \sigma _2 + {\hat{Y}}, C \sigma _1 + {\hat{\theta }}) + \cdots . \end{aligned}$$

(50c)

Substitution into the original equations (2), (3), (4)–(7) leaves us at leading order with the reduced system

$$\begin{aligned}&{\hat{h}}_t + {\hat{h}}_x + {\hat{u}}_x = 0 , \end{aligned}$$

(51a)

$$\begin{aligned}&{\hat{u}}_t + {\hat{u}}_x = -{\hat{p}}_x , \end{aligned}$$

(51b)

$$\begin{aligned} {\hat{h}}({\hat{x}}, {\hat{t}}) = Y(t) + \theta (t) - {\hat{T}}({\hat{x}}) , \end{aligned}$$

(52)

$$\begin{aligned}&\text {at } {\hat{x}} = 0: \; {\hat{p}} = 0; \end{aligned}$$

(53a)

$$\begin{aligned}&\text {at } {\hat{x}} = {\hat{x}}_1: \; {\hat{p}} = - (1 - \mathrm{{d}}{\hat{x}}_1/\mathrm{{d}}{\hat{t}}) {\hat{u}} , \end{aligned}$$

(53b)

$$\begin{aligned}&\text {at } {\hat{x}} = {\hat{x}}_1: \; {\hat{u}} = - (1 - \mathrm{{d}}{\hat{x}}_1/\mathrm{{d}}{\hat{t}}) {\hat{h}} ; \end{aligned}$$

(53c)

$$\begin{aligned}&M {\hat{Y}}^{\prime \prime } = 0 , \end{aligned}$$

(54a)

$$\begin{aligned}&I {\hat{\theta }}^{\prime \prime } = 0 . \end{aligned}$$

(54b)

The system is effectively the same as that in the first stage except that the initial conditions are different as here they require matching with stage 2 when ${\hat{t}}$ is large and negative. The match also establishes that ${\hat{Y}}, {\hat{\theta }}$ remain constant throughout and their sum (denoted by $\gamma$) is positive as implied by the end of stage 2: see (48). Thus, working through as in (30)–(33b) and setting $\tau ({\hat{t}}) = {\hat{T}}({\hat{x}}_1({\hat{t}}))$ now, we obtain the non-linear ODE

$$\begin{aligned} (\tau - \gamma ) \chi \chi ^{\prime \prime } + \lbrace \chi \tau ^\prime + (\tau - \gamma )( \chi ^\prime - 2) \rbrace \chi ^\prime = \gamma , \end{aligned}$$

(55a)

for $\chi ({\hat{t}}) = {\hat{x}}_1({\hat{t}})$ subject to the incident condition, since ${\hat{T}}({\hat{x}}) = q {\hat{x}}^2$ here,

$$\begin{aligned} \chi \sim - (3 \gamma {\hat{t}} /(2q))^{1/3} \text { as } {\hat{t}} \rightarrow -\infty . \end{aligned}$$

(55b)

The problem can be normalised such that $\gamma$, q may be replaced by $1, - 1$, respectively, without loss of generality. The solution is shown in Fig. 25. The match (55b) is observed at large negative ${\hat{t}}$ values. At exit however, as ${\hat{t}}$ tends to some finite value $\hat{t_E}$, the contact point $\chi = {\hat{x}}_1$ tends to zero, implying that $\tau = {\hat{T}}$ approaches zero relatively fast and so (55a) is clearly dominated by the sub-system with $\tau$ replaced by zero. This integrates to

$$\begin{aligned} (\chi ^\prime - 2) \chi = ({\hat{t}}_E - {\hat{t}}) \end{aligned}$$

(56)

on the assumption that $\chi ^\prime \chi$ tends to zero, which is justifiable afterwards. The solution can be found implicitly from integration of $d\alpha /d\beta = - (1 + \beta )^{-2} \beta$, where $\chi = ({\hat{t}}_E - {\hat{t}}) \beta (\alpha )$ and $({\hat{t}}_E - {\hat{t}}) = \exp (\alpha )$, and from this integration we readily obtain the final exit behaviour (as $\alpha$ tends to $-\infty$)

$$\begin{aligned} \chi = {\hat{x}}_1 \sim -({\hat{t}}_E - {\hat{t}}) \lbrace 1 + (\ln ({\hat{t}}_E - {\hat{t}}))^{-1}\rbrace + \cdots \text { at exit}. \end{aligned}$$

(57)

The implicit solution of (56) and Eq. (57) are shown in Fig. 26. In particular, Fig. 26 and the result (57) agree with and confirm the exit response shown in Sect. 4.2: this logarithmic form originally obtained in [13, 25] only appears in the present large-C scenario when stage 3 is encountered, very near to exit, a feature which explains the last-gasp behaviour seen in the full numerical results of the figures throughout Sect. 5.2.

Fig. 25

Large-C analysis, the exit stage (stage 3), convex underbody. Graphs of ${\hat{x}}_1$ (blue) and its derivative (red) versus scaled time ${\hat{t}}$, along with asymptotes (dashed) at large negative ${\hat{t}}$ values ((55b) and its derivative) and at near-exit times ${\hat{t}}$ values ((57) and its derivative). The former asymptote agrees with that in Sect. 4.2. The inset shows a close-up view near exit (see also (56) and Fig. 26)

Fig. 26

Exact solution $\alpha = - \ln (\beta +1) - 1/(\beta +1) + c$ (blue) of the local exit equation (56). Here $\chi = (t_E - t) \beta$, $t_E - t = \exp (\alpha )$ and the constant c is taken as unity. The final asymptote (57) is also shown (red)

6.2.4 Comparisons

The main comparisons concern the movement of the contact point, the duration of the skim and the evolution of the leading edge pressure. Figure 27 shows comparisons between the present asymptotic analysis and full simulation results as regards the motion of the contact point for increasing C. The agreement on trends is clear. This includes the behaviour near entry, taking place rapidly in stage 1, the more gradual development during stage 2 and then the acceleration into stage 3 leading on to exit. We mention again the last-gasp nature of the final behaviour just before exit as stage 3 above comes into play and admits the final form in (57).

Fig. 27

Comparison between the present asymptotic analysis ($Z^{1/3}$, from (49a)) and transformed full simulation ($C^{1/3}(x_1 - x_0)$) results versus time for increasing C as regards the motion of the contact point. Here the asymptotic result is the limiting result as C grows larger. The arrow indicates the exit time predicted by analysis

Fig. 28

Comparison between the present asymptotic analysis ($Z^{2/3}$, from (49a)) and transformed full simulation ($C^{-1/3} p(x_1)$) results versus time for increasing C as regards the motion of the contact point pressure. Here the asymptotic result is the limiting result as C grows larger. The arrow shows the analytical prediction of the exit time

The next comparisons are on the time from entry to exit, which is predicted by the solution of (49a), (49b) in terms of the cube roots of $-1$ as being

$$\begin{aligned} t = t_E = 4.65 \text { approx.} \end{aligned}$$

(58)

This is for the case of the present simulations which have $M = 2, I = 1$ and so $c_1 = 3/4$, giving the exit time as above. The asymptote (58) is very close to the full simulation findings in all of the relevant figures, including Figs. 27 and 28, indicating reasonable agreement for C values as low as 1. We observe that since (58) is independent of the shape coefficient q it applies formally to concave as well as convex underbodies. Figure 28 presents comparisons for the contact-point pressure versus time. Here again there is quite close agreement on trends as C increases. Similar agreement is seen in previous figures where in particular the pressure curve is closely approximated by the body function, in keeping with the prediction (42a)–(42c). Finally here we should perhaps re-emphasise the point that in parts of this paper we allow rather large values of $C, \theta$ or Y to be used in order to help illustrate trends more clearly where necessary and to help understanding. There is little doubt that some of these values may strictly violate the basic physical assumptions of the model in practice such as the true angles ($\theta H /L$) of the body shape as well as its motion remaining of order H/L or broadly small as described in Sect. 2 but this is in the nature of asymptotic analysis. The analysis works well over a surprisingly large range for certain cases and less so for others: an example of the former is the fact that the asymptotic prediction (58) for large C applies well even at small or zero C values. Quantitative agreement should perhaps not be expected at moderate values of C since the analysis in the present subsection involves –1/3 powers of C. Nevertheless qualitative agreement exists for moderate C values in regard to the trends of location and pressure curves (Figs. 27, 28) and quantitative agreement applies to the skim duration (see arrows in Figs. 27, 28).

7 Conclusion

An immediate observation concerns the potentially valuable insights gained from direct computation and asymptotic analysis together, supplementary to those given at the end of the previous section. The analysis for large underbody curvature confirms among other things that the scaled contact-pressure and body-shape curves are virtually identical and that the curve of the contact-point location versus time is steeper on approaching exit than it is just after entry. The findings are for initial downward velocities of the body which are of order unity but can be scaled up for larger velocities. By virtue of the three-phased progress of the skim found in this work, i.e. the entry, middle and exit stages, the analysis also explains why in general the entry slope formula and the exit slope formula often apply accurately only very close indeed to entry and exit, respectively. Along with this the logarithmic effect at exit, which is a sensitive effect, is itself surrounded by the relatively short exit stage of the progress. An enhanced formula capturing this effect for the final stage prior to exit is provided in implicit form by the $\alpha -\beta$ formulation (Fig. 26) described near the end of the previous section.

Considered more broadly, the original model and analysis of a straight plate undergoing an oblique skimming impact on a shallow liquid layer have been extended here to a body of smooth polynomic shape. In each of the analysed cases, the trailing edge of the body initially descends into the water layer with an increasing wetted region. A point is reached at which the pressure underneath the body becomes sufficiently large to raise the body back out of the water layer with the body leaving the liquid layer in finite time. Throughout the motion the body undergoes changes to its vertical position, vertical velocity, inclination and rotational velocity in response to the changes in pressure. After the body rebounds out of the layer into the air it may continue to a subsequent skimming impact with the liquid layer under the influence of gravity.

Three geometric cases have been analysed in this paper. In each case the skimming motion is qualitatively similar; however, increasing underbody curvature has a markedly different influence in each scenario. For a concave body and a convex body with fixed air angle (where the initial angle between the underside of the body and the water layer is kept fixed for all values of C), a significant rotation occurs causing the body to leave the liquid layer at a height smaller than that at which it entered. For a convex body with fixed body angle (where the initial angle between the body midline and the water layer is fixed as C is varied) a super-elastic response occurs with increased scaled underbody curvature.

For each case we have determined the asymptotic behaviour of the body upon entering the layer, accounting for body thickness. For the concave and fixed air angle scenarios reduced order systems for the skimming motion have also been derived and shown to be in agreement for increasing scaled underbody curvature. Likewise, in the case of a concave underbody, it has been shown that the trailing-edge behaviour may be approximated by a straight plate at an equivalently steep inclination. This analogy can thus also be used to reduce the order of the system of equations and simplify the model.

The asymptotic results provide physical understanding of the skimming interaction and of the solution trends, helping to add clarity to the overall process given the complexity of the coupled system of non-linear equations (17)–(22) and linear system of equations (14), (23)–(25). In general the asymptotics and reduced order analysis hold well in each case, for the entry, middle and exit parts of the skim (with the logarithmic feature of the exit process being explained at the end of the previous section).

In each of the geometric cases careful considerations are required to ensure physical results. In the concave case, setting the initial angle at too shallow of a pitch leads to the front end of body entering the liquid layer ahead of the wetted region, trapping a pocket of gas. With falling pressure across the plate during the skimming process, it would be useful to investigate the possibility of cavitation if below ambient pressures are induced. Initially, re-parametrisation of the model to include the front-end behaviour would be an interesting direction for such future work. Regarding the fixed air angle case, the smoothly varying body shape towards the trailing edge allows $x_0$ to move if the effective body angle becomes positive, which is again of interest.

Subsequent work could allow for the trailing edge to move freely, and in this case the model would be extended to incorporate an additional momentum jump condition at the trailing edge. As noted in [13], this allows solutions with splash jets both in front and behind the body, as in [16]. Furthermore such issues with moving $x_0$ for ellipsoid-like bodies are considered in [28]. Further extensions to this work include the incorporation of gravity effects for larger bodies or the consideration of a series of impacts for variously shaped bodies, extending the work presented in [1].

Appendices

Appendix A: Full details of small-time asymptotic solution

The configuration of the plate upon impact is given by the initial values of: the vertical extent of the body’s centre of mass $Y_0$; the body’s vertical velocity $V_0$; angle of the body $\theta _0$; the horizontal position of the body’s trailing edge $x_0$, and the initial angular momentum of the body $\omega _0$. Hence, the following asymptotic expansions are used:

$$\begin{aligned} Y&= Y_0 + V_0 t + O(t^4), \end{aligned}$$

(59a)

$$\begin{aligned} \theta&= \theta _0 + \omega _0 t + O(t^4), \end{aligned}$$

(59b)

$$\begin{aligned} x_1&= x_0 + {\hat{x}}_1 t + {\hat{x}}_2 t^2 + O(t^3), \end{aligned}$$

(59c)

$$\begin{aligned} D&= D_0 + D_1 t + O(t^2). \end{aligned}$$

(59d)

For small times after entry, the leading contact position will move in a negative x direction as the plate begins to submerge, hence it is expected that ${\hat{x}}_1<0$.

Expanding the $\gamma _m, \; m = 0, 1, 2,\ldots , n$ functions by Taylor theorem:

$$\begin{aligned} \gamma _m = \gamma _{m(0)} + \gamma _{m(1)}t + O(t^2). \end{aligned}$$

(60)

Substitution into (14) gives key relations between these functions at each order:

$$\begin{aligned} \sum _{m = 0}^n \gamma _{m(k)} x_0^m = 0, \qquad k = 0,1,2,\ldots , \end{aligned}$$

(61)

Furthermore, substituting (60) into the pressure at $x_1$ term $p_1 = \sum _{m = 0}^n \gamma _{m} x_1^m$ and using (61):

$$\begin{aligned} {\hat{p}}_1 = t \left( \sum _{m = 1}^{n} m \gamma _{m(0)} x_0^{m-1} {\hat{x}}_1\right) + O(t^2). \end{aligned}$$

(62)

This indicates a small pressure at the leading point of the contact region when the plate enters the liquid layer for the first time.

Substituting (59a)–(59d) and (62) into (10):

$$\begin{aligned} {\hat{p}}_1 = \left( (Y_0 + V_0 t) + (x_0 + {\hat{x}}_1 t)(\theta _0 + \omega _0 t) + {\hat{x}}_1 t \sum _{m = 0}^{n-1} a_m (x_0 + {\hat{x}}_1 t)^m \right) (1-{\hat{x}}_1)^2. \end{aligned}$$

(63)

Since the left-hand side of (63) is O(t), we observe that $Y_0 + x_0 \theta _0 = 0$ giving a geometric constraint for the body entering an initially undisturbed water layer. The body shape does not feature in this constraint however since $T(x_0) = 0$. The remaining terms at O(t) are

$$\begin{aligned} \sum _{m = 1}^{n} m \gamma _{m(0)} x_0^{m-1} {\hat{x}}_1 = \left( V_0 + x_0 \omega _0 + \theta _0 {\hat{x}}_1 + {\hat{x}}_1 \left( \sum _{m = 0}^{n-1} a_m x_0^m \right) \right) (1-{\hat{x}}_1)^2. \end{aligned}$$

(64)

Similarly, substituting into (12) leads to

$$\begin{aligned} \begin{aligned} {\hat{p}}_1 =&\Bigg ((x_0 + {\hat{x}}_1 t)^2 \frac{\omega _0}{2} + (x_0 + {\hat{x}}_1 t)(V_0 + \theta _0 + \omega _0 t) - D_0 - D_1 t \\&\left. - \sum _{m = 1}^{n} (x_0 a_m - a_{m-1}) (x_0 + {\hat{x}}_1 t)^m \right) (1-{\hat{x}}_1) + O(t) . \end{aligned} \end{aligned}$$

(65)

Again, since the right-hand side must be at most O(t), we deduce that $D_0 = x_0^2 \omega _0/2 + x_0 (V_0 + \theta _0 + a_0)$ since $-\sum _{m = 1}^{n} (x_0 a_m - a_{m-1}) x_0^m = -x_0\left( \sum _{m = 1}^{n} x_0^{m} a_m - \sum _{m = 0}^{n-1} a_{m} x_0^{m} \right) = x_0 a_0$. Hence, matching terms at order t gives

$$\begin{aligned} \begin{aligned} \sum _{m = 1}^{n} m \gamma _{m(0)} x_0^{m-1} {\hat{x}}_1 = \left( x_0 {\hat{x}}_1 \omega _0 + x_0 \omega _0 + (V_0 + \theta _0) {\hat{x}}_1 - D_1 +\sum _{m = 0}^{n-1} a_m x_0^m {\hat{x}}_1 \right) (1-{\hat{x}}_1) . \end{aligned} \end{aligned}$$

(66)

Notably, (61) with (15) and (16) give that neither Y nor $\theta$ has any $O(t^2)$ or $O(t^3)$ terms. Comparing (64) and (66) an expression for $D_1$ is found to be

$$\begin{aligned} D_1 = {\hat{x}}_1^2 \left( \theta _0 + \sum _{m = 0}^{n-1} a_m x_0^m \right) + 2 {\hat{x}}_1 (x_0 \omega _0 +V_0) - V_0, \end{aligned}$$

(67)

where $\sum _{m = 0}^{n-1} a_m x_0^m$ is the derivative of T(x) at $x = x_0$.

Now seeking an expression for ${\hat{x}}_1$, first consider expressions for the functions $\gamma _m, \; m = 0, 1, 2,\ldots , n$. Firstly, from (13a) we find that

$$\begin{aligned} \gamma _{1(0)} + \gamma _{1(1)} t = -D_1 - 2D_2 t + V_0 + \theta _0 + \omega _0 t + a_0 - x_0 a_1 . \end{aligned}$$

(68)

This, when balancing at leading order, leads to

$$\begin{aligned} \gamma _{1(0)} = -D_1 + V_0 + \theta _0 + a_0 - x_0 a_1 . \end{aligned}$$

(69)

Secondly, from (13b) it follows that

$$\begin{aligned} 2(\gamma _{2(0)} + \gamma _{2(1)} t) = 2 \omega _0 + 2 a_1 - 2 x_0 a_2 . \end{aligned}$$

(70)

Again, when matching at leading order, we obtain

$$\begin{aligned} \gamma _{2(0)} = \omega _0 + a_1 - x_0 a_2 . \end{aligned}$$

(71)

Finally, when considering both (13c) and (13d) at leading order, we find that

$$\begin{aligned} \gamma _{m(0)} = a_{m-1} - x_0 a_m \end{aligned}$$

(72)

for $m = 3, 4, \ldots ,n$.

Substituting the above results for the $\gamma _m, \; m = 0, 1, 2,\ldots , n$ functions and $D_1$ into (64) we have

$$\begin{aligned} \begin{aligned}&\Bigg [ -D_1 + V_0 + \theta _0 + 2\omega _0 x_0 + \sum _{m = 1}^{n} m x_0^{m-1} (a_{m-1} - x_0 a_m)\Bigg ] {\hat{x}}_1\\&\quad = \left( V_0 + x_0 \omega _0 + \theta _0 {\hat{x}}_1 + {\hat{x}}_1 \left( \sum _{m = 0}^{n-1} a_m x_0^m \right) \right) (1-{\hat{x}}_1)^2 . \end{aligned} \end{aligned}$$

(73)

Rearranging gives

$$\begin{aligned} 2 \left( \theta _0 + \sum _{m = 0}^{n-1} a_m x_0^m\right) {\hat{x}}_1^2 + 3(x_0 \omega _0 + V_0) {\hat{x}}_1 - (x_0 \omega _0 + V_0) = 0 . \end{aligned}$$

(74)

Thus

$$\begin{aligned} {\hat{x}}_1 = \frac{-3(x_0 \omega _0 + V_0) - \sqrt{9(x_0 \omega _0 + V_0)^2 + 8 \left( \theta _0 + \sum _{m = 0}^{n-1} a_m x_0^m\right) (x_0 \omega _0 + V_0)}}{4 \left( \theta _0 + \sum _{m = 0}^{n-1} a_m x_0^m\right) } \end{aligned}$$

(75)

giving the final constraint that is required for initialising the computation.

Appendix B: Unbounded response in $D, \gamma _0$ and $\gamma _1$ for a general body shape

As noted in Sect. 4 for the exit-time solution, the evolutions of D and the functions $\gamma _m, m=0,1,2,\ldots$ follow that of the straight plate. Here we present examples of this behaviour for each of these parameters for the general body case discussed in Sect. 6. As exit is approached there are unbounded responses in the gradients of D (in Fig. 29), and of $\gamma _0$ and $\gamma _1$ (in Fig. 30). This illustrates that the qualitative observations used to understand the exit-time behaviour for a straight plate in [13] are still applicable for a general body. Furthermore, all other $\gamma _m$ functions remain bounded, a property which follows from (13b)–(13d).

Fig. 29

Example of unbounded response in the gradient of D as the body nears exit from the liquid layer for a fixed air angle case with $T(x) = (x_0 - x)(0.1625 + 0.1625 x - 0.5 x^2 - 0.5 x^2 + x^3 + x^4)$

Fig. 30

Example of unbounded response in gradients of $\gamma _0$ and $\gamma _1$ as the body nears exit from the liquid layer for a fixed air angle case with $T(x) = (x_0 - x)(0.1625 + 0.1625 x - 0.5 x^2 - 0.5 x^2 + x^3 + x^4)$

Figures 29 and 30 and the discussion here are included to provide examples of the body’s behaviour and aspects of the fluid–body interaction that were discussed within the paper and used in order to analyse the system at leading order. Specifically, we used these arguments when applying the exit solution from [13], and for the leading-order arguments made throughout Sect. 5 for the reduced order analysis.