Closed form expression for the surface temperature in wet grinding: application to maximum temperature evaluation

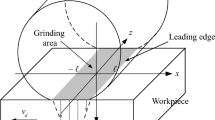
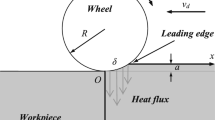
Abstract

Considering the classical modelling of heat transfer in wet flat grinding [DesRuisseaux and Zerkle, J Heat Transf 92:456–464, 1970], we have calculated a closed-form expression for the surface temperature in the stationary regime. For any Peclet number and for small Biot numbers this closed expression can be computed much more rapidly than its equivalent integral form given in the literature. As an application, this result can be used to compute the maximum temperature of the workpiece very rapidly. We have seen that the numerical maximization of the surface temperature using the integral form given in the literature is extremely slow and sometimes fails. However, to prevent thermal damage, a fast computation of the maximum temperature is highly desirable for on-line monitoring in industrial grinding.

Appendix A

1.1 A.1 The $\mathrm {Yu}\!\left( x\right)$ function

In the literature, we find [22, Eq. 13]

$$\begin{aligned}&\displaystyle \int \limits _{0}^{x}\mathrm{e}^{\pm u}\ u^{\nu }K_{\nu }\!\left( u\right) \ \mathrm{d}u =\frac{\mathrm{e}^{\pm x}x^{\nu +1}}{2\nu +1}\left[ K_{\nu }\!\left( x\right) \pm K_{\nu +1}\!\left( x\right) \right] \mp \frac{2^{\nu }\Gamma \!\left( \nu +1\right) }{ 2\nu +1}. \end{aligned}$$

(106)

From (106) we can calculate the $\mathrm {Yu}\!\left( x\right)$ function defined by the following integral:

$$\begin{aligned} \mathrm {Yu}{}_{\nu }\!\left( x\right) :=\int \limits _{0}^{x}\mathrm{e}^{u}\left| u\right| ^{\nu }K_{\nu }\!\left( \left| u\right| \right) \ \mathrm{d}u. \end{aligned}$$

1.1.1 A.1.1 $x>0$

Directly from (106) we have

$$\begin{aligned} \mathrm {Yu}{}_{\nu }\!\left( x\right)&= \int \limits _{0}^{x}\mathrm{e}^{u}u^{\nu }K_{\nu }\!\left( u\right) \ \mathrm{d}u=\frac{\mathrm{e}^{x}x^{\nu +1}}{2n+1}\left[ K_{\nu }\!\left( x\right) +K_{\nu +1}\!\left( x\right) \right] -\frac{2^{\nu }\Gamma \! \left( \nu +1\right) }{2\nu +1}. \end{aligned}$$

(107)

1.1.2 A.1.2 $x<0$

Performing the change of variables $u=-u^{\prime }$,

$$\begin{aligned} \mathrm {Yu}{}_{\nu }\!\left( x\right)&= \int \limits _{0}^{x}\mathrm{e}^{u}\ \left( -u\right) ^{\nu }K_{\nu }\!\left( -u\right) \ \mathrm{d}u=-\int \limits _{0}^{-x}\mathrm{e}^{-u^{\prime }}\!\left( u^{\prime }\right) ^{\nu }\ K_{\nu }\!\left( u^{\prime }\right) \ \mathrm{d}u^{\prime }, \end{aligned}$$

and applying again (106), we have

$$\begin{aligned} \mathrm {Yu}{}_{\nu }\!\left( x\right)&=-\left\{ \frac{\left( -x\right) ^{\nu +1}\mathrm{e}^{-\left( -x\right) }}{2\nu +1}\left[ K_{\nu }\!\left( -x\right) -K_{\nu +1}\!\left( -x\right) \right] +\frac{2^{\nu }\Gamma \!\left( \nu +1\right) }{ 2\nu +1}\right\} \nonumber \\&=-\frac{\left( -x\right) ^{\nu +1}\mathrm{e}^{x}}{2\nu +1}\left[ K_{\nu }\!\left( -x\right) -K_{\nu +1}\!\left( -x\right) \right] -\frac{2^{\nu }\Gamma \!\left( \nu +1\right) }{2\nu +1}. \end{aligned}$$

(108)

1.1.3 A.1.3 $x\ne 0$

For $x\ne 0$ we can unify the results given in (107) and (108) as follows:

$$\begin{aligned} \mathrm {Yu}{}_{\nu }\!\left( x\right) =\frac{x\left| x\right| ^{\nu }\mathrm{e}^{x}}{2\nu +1}\ \left[ K_{\nu }\!\left( \left| x\right| \right) + \mathrm {sign}\!\left( x\right) K_{\nu +1}\!\left( \left| x\right| \right) \right] -\frac{2^{\nu }\Gamma \! \left( \nu +1\right) }{2\nu +1}, \end{aligned}$$

(109)

where

$$\begin{aligned} \mathrm {sign}\!\left( x\right) =\frac{\left| x\right| }{x}. \end{aligned}$$

(110)

1.1.4 A.1.4 $x=0$

To evaluate $\mathrm {Yu}{}_{\nu }\!\left( 0\right)$, let us calculate the following limit:

$$\begin{aligned} \mathrm {Yu}{}_{\nu }\!\left( 0\right)&= \frac{1}{2\nu +1}\underset{ x\rightarrow 0}{\lim }\ x\left| x\right| ^{\nu }\mathrm{e}^{x}\ \left[ K_{\nu }\!\left( \left| x\right| \right) +\mathrm {sign}\!\left( x\right) K_{\nu +1}\!\left( \left| x\right| \right) \right] -\frac{2^{\nu }\Gamma \! \left( \nu +1\right) }{2\nu +1}. \end{aligned}$$

(111)

On the one hand, when $\nu =0$, we have

$$\begin{aligned} \mathrm {Yu}{}_{0}\!\left( 0\right) =\underset{x\rightarrow 0}{\lim }\ x\ \left[ K_{0}\!\left( \left| x\right| \right) +\mathrm {sign}\!\left( x\right) K_{1}\!\left( \left| x\right| \right) \right] -1. \end{aligned}$$

Applying the asymptotic formulas [23, Eq. 5.16.4]

$$\begin{aligned}&K_{0}\!\left( x\right) \approx \log \left( \frac{2}{x}\right) ,\qquad x\rightarrow 0, \end{aligned}$$

(112)

$$\begin{aligned}&K_{\nu }\!\left( x\right) \approx \frac{2^{\nu -1}\Gamma \! \left( \nu \right) }{ x^{\nu }},\qquad x\rightarrow 0, \end{aligned}$$

(113)

and taking into account (110), we have

$$\begin{aligned} \mathrm {Yu}{}_{0}\!\left( 0\right)&=\underset{x\rightarrow 0^{+}}{\lim }\ x\ \left[ \log \left( \frac{2}{\left| x\right| }\right) +\frac{ \left| x\right| }{x}\frac{1}{\left| x\right| }\right] -1=\underset{x\rightarrow 0^{+}}{\lim }\ -x\log \left( \frac{\left| x\right| }{2}\right) =0. \end{aligned}$$

(114)

On the other hand, when $\nu \ne 0$, we can apply in (111) the asymptotic formula (113), so that

$$\begin{aligned} \mathrm {Yu}{}_{\nu }\!\left( 0\right)&= \frac{1}{2\nu +1}\underset{ x\rightarrow 0^{+}}{\lim }\ x\left| x\right| ^{\nu }\left[ \frac{ 2^{\nu -1}\Gamma \! \left( \nu \right) }{\left| x\right| ^{\nu }}+\frac{ \left| x\right| }{x}\frac{2^{\nu }\Gamma \! \left( \nu +1\right) }{ \left| x\right| ^{\nu +1}}\right] -\frac{2^{\nu }\Gamma \! \left( \nu +1\right) }{2\nu +1}=0,\qquad \nu \ne 0. \end{aligned}$$

(115)

Therefore, according to (109), (114) and (115), we can express the $\mathrm {Yu}{}_{\nu }\!\left( x\right)$ function as follows:

$$\begin{aligned} \begin{array}{l} \displaystyle \mathrm {Yu}{}_{\nu }\!\left( x\right) :=\int \limits _{0}^{x}\mathrm{e}^{u}\ \left| u\right| ^{\nu }K_{\nu }\!\left( \left| u\right| \right) \ \mathrm{d}u \\ \qquad \qquad \,\,=\left\{ \begin{array}{ll} \displaystyle \frac{x\left| x\right| ^{\nu }\mathrm{e}^{x}}{2\nu +1}\ \left[ K_{\nu }\!\left( \left| x\right| \right) +\mathrm {sign}\!\left( x\right) K_{\nu +1}\!\left( \left| x\right| \right) \right] -\frac{2^{\nu }\Gamma \!\left( \nu +1\right) }{2\nu +1} &{} \quad x\ne 0, \\ 0 &{}\quad x=0. \end{array} \ \right. \end{array} \ \end{aligned}$$

(116)

1.2 A.2 Convergence condition for $\mathcal {T}\!\left( X,0\right)$

According to [27, theorem 10.6], if a series $\sum _{n=0}^{\infty }a_{n}$ converges, then $\lim _{{n\rightarrow \infty }}a_{n}=0$. Therefore, the series given in (39),

$$\begin{aligned} \mathcal {T}\!\left( X,0\right) =\sqrt{\pi }\sum _{n=0}^{\infty }\frac{\left( -H/ \sqrt{2}\right) ^{n}}{\Gamma \left( \frac{n+1}{2}\right) } \widetilde{ \mathrm {Yu}}{}_{n/2}\!\left( u\right) \left. \!\! \right| _{X-L}^{X+L}, \end{aligned}$$

converges if

$$\begin{aligned} \underset{n\rightarrow \infty }{\lim }\frac{\left( -H/\sqrt{2}\right) ^{n}}{ \Gamma \left( \frac{n+1}{2}\right) } \widetilde{\mathrm {Yu}}{} _{n/2}(u) \left. \!\! \right| _{X-L}^{X+L}. \end{aligned}$$

(117)

Notice that according to (36),

$$\begin{aligned} \widetilde{\mathrm {Yu}}{}_{\nu }\!\left( u\right) \left. \!\! \right| _{X-L}^{X+L}=\int \limits _{X-L}^{X+L}\mathrm{e}^{u}\left| u\right| ^{\nu }K_{\nu }\!\left( \left| u\right| \right) \mathrm{d}u, \end{aligned}$$

and, according to [28, Eq. 10.41.2],

$$\begin{aligned} K_{\nu }\!\left( z\right) \approx \sqrt{\frac{\pi }{2\nu }}\left( \frac{\mathrm{e}z}{ 2\nu }\right) ^{-\nu },\qquad \nu \rightarrow \infty , \end{aligned}$$

and thus

$$\begin{aligned} \underset{\nu \rightarrow \infty }{\lim } \widetilde{\mathrm {Yu}}{} _{\nu }\!\left( u\right) \left. \!\! \right| _{X-L}^{X+L}&= \underset{\nu \rightarrow \infty }{\lim }\sqrt{\frac{\pi }{2\nu }}\left( \frac{\mathrm{e}}{2\nu }\right) ^{-\nu }\int \limits _{X-L}^{X+L}\mathrm{e}^{u}\mathrm{d}u=2\mathrm{e}^{X}\sinh L\underset{\nu \rightarrow \infty }{\lim }\sqrt{\frac{\pi }{ 2\nu }}\left( \frac{\mathrm{e}}{2\nu }\right) ^{-\nu }. \end{aligned}$$

(118)

Notice as well that, according to Stirling’s formula [20, Eq. 6.1.37],

$$\begin{aligned} \Gamma \!\left( \nu \right) \approx \left( \frac{\nu }{\mathrm{e}}\right) ^{\nu }\sqrt{ \frac{2\pi }{\nu }},\qquad \nu \rightarrow \infty , \end{aligned}$$

(119)

so that from (118) and (119) we have

$$\begin{aligned} \underset{\nu \rightarrow \infty }{\lim }\frac{ \widetilde{\mathrm {Yu} }{}_{\nu }\!\left( u\right) \left. \!\! \right| _{X-L}^{X+L}}{\Gamma \! \left( \nu \right) }=\mathrm{e}^{X}\sinh L\underset{\nu \rightarrow \infty }{\lim }2^{\nu }. \end{aligned}$$

(120)

Therefore, taking $\nu =n/2$ in (120), we can calculate the following limit:

$$\begin{aligned} \varLambda&= \underset{n\rightarrow \infty }{\lim }\frac{\left( -H/\sqrt{2} \right) ^{n}}{\Gamma \left( \frac{n+1}{2}\right) } \widetilde{\mathrm { Yu}}{}_{n/2}\!\left( u\right) \left. \!\! \right| _{X-L}^{X+L}=\mathrm{e}^{X}\sinh L\underset{n\rightarrow \infty }{\lim }\!\left( -H\right) ^{n}. \end{aligned}$$

Thus, the condition given in (117) is satisfied when

$$\begin{aligned} H<1. \end{aligned}$$

1.3 A.3 Inequality for modified Bessel function of third kind

Let us consider the following integral representation of the modified Bessel function of the third kind [23, Eq. 5.10.23]:

$$\begin{aligned} K_{\nu }\!\left( z\right) =\int \limits _{0}^{\infty }\exp \!\left( -z\cosh \alpha \right) \cosh \nu \alpha \ \mathrm{d}\alpha . \end{aligned}$$

(121)

Notice that the $\cosh x$ function is a positive increasing function for $x>0$; thus,

$$\begin{aligned} \nu >\mu >0,\ \alpha >0,\ \forall z\quad \rightarrow \quad \mathrm{e}^{-z\cosh \alpha }\cosh \nu \alpha >\mathrm{e}^{-z\cosh \alpha }\cosh \mu \alpha >0. \end{aligned}$$

(122)

Therefore, integrating in (122) and taking into account (121), we have

$$\begin{aligned} \nu >\mu >0\quad \rightarrow \quad K_{\nu }\!\left( z\right) >K_{\mu }\!\left( z\right) >0. \end{aligned}$$

(123)