1 Introduction

China opened its economy to the world in 1978, thereafter structural reforms, it has become the world’s fastest-growing economy (Garnaut et al. 2018). Export remains the main driving force behind this inspiring growth (He and Zhang 2010). In the 1980s, China adopted a low-priced leadership strategy, viz. low labor cost and high production capacity, which allowed the operation with low-profit margins. Accordingly, China managed to increase its share in the global commodity market from 1.9% in 2000 to 11.4% in 2017. Using this strategy, Chinese companies targeted middle- and low-income countries, where competition is considerably intense, and rapidly increased their global export market share (Lew and Sulaiman 2014; Martin and Mejean 2014; Obeng 2019). However, the widespread adoption of a low-priced leadership strategy by exporting companies led consumers to associate Chinese products with low quality (Karanfil 2015; Zhang and Su 2009). Researchers have presented the existing perception by comparing Chinese goods to both domestic and foreign goods in several countries (Franco and Roach 2018; Khan and Ahmed 2012; Kim et al. 2015; Laforet and Chen 2012; Schniederjans et al. 2004; Srivastava 2015; Watung 2014). Over time, consumers generalized this perception about all Chinese products, including those of higher quality (Barney and Zhang 2008). Other significant developments increased the negative perception of Chinese products around the world. In 2007 and 2008 specifically, reports were issued about Chinese goods that led to food and product safety concerns (e.g., toys dyed with lead paint; melamine in wheat gluten, rice protein, and infant milk powder; harmful pet foods; toothpaste with toxic content; and hazardous drug residues in farm shrimp species) (Becker 2007; Gale and Buzby 2009; Obeng 2019; Peijuan et al. 2009; Watung 2014; Wu and Chen 2013).

Although China has improved the quality of its exports in recent years, this improvement has not been sufficient to change the general perception of low quality. This can be due to the heterogeneous distribution of exporting sectors without spreading across the whole export basket (Zhang and Dai 2018). The negative perceptions toward Chinese products affect the country’s export performance (Cagé and Rouzet 2015; Rodrik 2006), considering the perception of consumers towards a particular commodity are more determinative of individual preferences than of actual product quality (Zeithaml et al. 1988). Within this scope, existing studies show outgrowth in income level influences consumers to relatively buy higher-priced products, branded (Üstüner and Holt 2010), luxurious (Madinga et al. 2016), healthy and safe (Hwang and Choe 2016), environmentally friendly (Brécard et al. 2009), organic (Smith et al. 2009), hedonic and snobby (Kambiz and Fereshteh 2013) sophisticated and complicated (Hausmann et al. 2014), and personalized goods. Such goods are sold at a higher price and are relatively perceived by consumers as higher-quality goods (Erickson and Johansson 1985; Lichtenstein et al. 1988; Lichtenstein et al. 1993; Widell 2005; Azhar and Elliott 2006; Hallak 2006; Wiedmann et al. 2009; Ray and Vatan 2013; Pham and Ali 2016). Linder (1961) developed a demand-side approach for foreign trade by addressing this relationship between quality and income, which was revealed through microeconomic studies in the context of foreign trade. According to Linder, changes in income indicate changing demand structures—thus, with increased income, countries spend a higher portion of their income on high-quality products (Linder 1961). This implies consumers tend to buy lower-priced products within the same product segment when income depreciates with time. Linder’s hypothesis that implies countries experiencing an increase in income level mount up their demand for quality products was analyzed by Hummels and Skiba (2004), Hummels and Klenow (2005), Hallak and Schott (2011), Brambilla and Porto (2016) and Hummels and Lee (2017). Thus, the development in demand structures that occurred during the global crisis of 2008–2009 further supports this hypothesis. The negative income shock during the global crisis increased demand for lower-priced products within the same product segment, whereas demand for comparable higher-priced products decreased significantly. Given that price represents quality (Dodds et al. 1991), the shift indicates a transition from high-quality products to low-quality products (“flight from quality”) (Fajgelbaum et al. 2011; Levchenko et al. 2011). Because the fall in Chinese imports was less than that of other countries during the global crisis (Behrens et al. 2013; Lattemann et al. 2012; Levchenko et al. 2011), China was comparatively less affected by the global recession. China had an increase in real income of 8.5% and 8.8%—during and after the global crisis, respectively. These dynamics reveal that the perceived quality of Chinese products impacts exports.

Considering the general global perception of Chinese products as less sophisticated than the same product segment from other countries, and demand for higher-quality goods increases with income growth—it is likely Chinese exports could increase to a specific threshold of income level in partner countries. If this threshold is exceeded, Chinese exports might then decrease. This mechanism suggests the relationship between China’s exports and the income of partner countries is synonymous with the “U”Footnote 1 concept proposed by Kuznets (1955)—which explains the relationship between income inequality and per capita income. The approach expounded by Kuznets was widely accepted by researchers and saw fruition in economics, viz., the relationship between environmental degradation and economic growth (see Grossman and Krueger 1991) or the relationship between democracy and income distribution (see Chong 2004). In this study, we investigate how Chinese export and income dynamics across partner countries interact over time by utilizing the U concept—by proposing the quadratic nexus between real income and real exports as the “Trading Kuznets Curve” (TKC) hypothesis.

There is a dynamic relationship between exports and income depending on many factors, including preferences, quality of relevant goods, and consumer habits. If a trade-off relationship exists between exports of one country and the income level of its partner countries, it is crucial to establish a threshold income level for partner countries and ascertain the market direction after it surpasses the country-specific income level. However, existing studies that examine the relationship between exports and income of partner countries are based on a monotonic assumption—ignoring the possibility of an inverse U-shaped relationship. In other words, if the estimated income coefficient of a partner country is positive (negative), it is assumed that income growth would increase (decrease) exports. Such an approach may hinder the development of effective export strategies for markets with various income levels. Therefore, it is necessary to investigate the possibility of a dynamic relationship between exports and income across partner countries rather than assuming only a monotonic relationship. From this perspective, the purpose of this study is to investigate whether a quadratic relationship exists between China’s real exports to 154 partner countries and income of these countries for the period 1996–2019. Such an approach will help China develop effective export strategies, specify target markets, determine quality diversification policies suitable for its target markets, and sustain the country’s trade competitiveness. The study will contribute to the existing literature on export–the income relationship as follows:

  • First, to the best of our knowledge, no existing studies examine the export–income relationship using a quadratic model for China or other countries. The quadratic approach will allow for empirical testing of the dynamic interaction between export of China and the income level of its trading partners. The findings will be significant in terms of estimating the validity of an inverted U-shaped nexus between China’s export and the income level of its trading partner—by understanding the export dynamics of China. This is essential to determine which markets and up to which income level China can maintain its competitive power.

  • Second, the vast majority of studies investigating China’s export demand function failed to account for the cross-sectional dependence phenomenon frequently encountered in panel data analysis. Hence, ignoring cross-section dependence may lead to biased estimates and undesirable policy results. For this reason, panel data analysis methods that account for cross-section dependence are employed in this study. This study contributes to the existing literature in subject, concept, sample, and method.

2 Literature review

China experienced extraordinary economic growth because of its Open-Door Policy that was implemented in the late 1970s. Of great importance were economic reforms like the export-based growth model, which was applied in other East Asian economies, including Taiwan and South Korea (Peng et al. 2018). Because China experienced an economic miracle with the help of the export-based growth model (Jinjun 1995), determinants of China’s exports have been examined by many researchers. These studies focusing on China’s export demand function can be examined under several topics.

The first group of studies focuses on one of the widely-known components of the export demand function of China. This group investigated the income effect of partner countries on Chinese export (see Senhadji and Montenegro 1999; Li et al. 2006; Kumar 2009; Cheung et al. 2009; Thorbecke and Smith 2010; Chen et al. 2011; Yao et al. 2013; Peng et al. 2018; Xing 2018; Nasrullah et al. 2020; Baek and Nam 2021). The salient point of these papers shows an increase in income level improves the purchasing power of partner countries, hence, fostering Chinese export. The second group focuses on effects of exchange rate, appreciation and depreciation of RMB on Chinese export demand (see Dèes 2001; Bénassy-Quéré and Lahrèche-Révil 2003; Lau et al. 2004; Marquez and Schindler 2006; Li et al. 2006; Garcia-Herrero and Koivu 2008; Kumar 2009; Cheung et al. 2009; Xing 2018; Guan 2020; Nasrullah et al. 2020). The majority of these studies showed that RMB depreciation increases the international competitive capacity of the Chinese economy, whereas appreciation of RMB decreases demand for Chinese products. Moreover, Li et al. (2006) emphasized that real exchange rate volatility and misalignment reduce Chinese export, while Baek and Nam (2021) showed that fluctuations in exchange rates might have asymmetric effects on the export level of the Chinese economy.

The third group focuses on other economic determinants of Chinese export characteristics alongside purchasing power of partner countries and exchange rates such as relative prices (Senhadji and Montenegro 1999), effect of international demand for Chinese products (see Dèes 2001; Lau et al. 2004; Garcia-Herrero and Koivu 2008; Aiello et al. 2015), effect of FDI (see Chen et al. 2011; Charoenrat and Amornkitvikai 2021), tax and capacity utilization (Garcia-Herrero and Koivu 2008) capital stock, foreign investment stock, wages, research and development (R and D) innovation, skilled labor, foreign direct investments (FDI), wages, import duty, total factor productivity, and recession (see Thorbecke and Smith 2010; Peng et al. 2018; Xing 2018; Guan 2020; Xie and Hue 2020; Charoenrat and Amornkitvikai 2021; Hou et al. 2021). The brief results of these studies are presented in the literature table (see Table 1).

Table 1 Data definition and sources
Full size table

The fourth group investigates the effect of non-economic factors on Chinese exports. Guan (2020) and Nasrullah et al. (2020) emphasized the increase in partner countries’ populations enhances the level of exports in China, whereas Nasrullah et al. (2020) and Yu et al. (2020) indicated that the increasing distance between China and its trading partners reduces the level of Chinese exports. Lin and Zhang (2020) reported mixed results about the effect of COVID-19 on Chinese agricultural export. Charoenrat and Amornkitvikai (2021) revealed that a female chief executive officer (CEO) at the firm level might improve Chinese exports; however, the firm’s longevity has no statistically significant effect on exports.

The salient points in the existing literature can be outlined as follows: first, there is a consensus that an increase in the income of China’s trading partners stimulates Chinese exports, whereas an appreciation of the RMB decreases China’s exports. Second, no existing studies appear to examine the export-income relationship using the quadratic model for China. Third, studies that examine China’s export structure with second-generational econometric analysis—such as accounting for cross-section dependence are limited. This study seeks to contribute to the literature by empirically examining the validity of the TKC hypothesis in China via second-generational econometric analysis for the period spanning 1996–2019.

3 Data description

Due to data availability, we employed a balanced panel data of 154 countries (see Table 2) with trade relations with China for the period 1996 to 2019. Table 3 provides detailed definitions and data sources of all sampled variables in the empirical analysis. Table 4 presents the descriptive statistics and correlation matrix for all variables.

Table 2 Cross-sectional dependency and homogeneity tests results
Full size table
Table 3 CCEMG results
Full size table
Table 4 CCEMG results
Full size table

The majority of existing studies used either price of a specific commodity group or the aggregate commodity price index to estimate the country-specific real export level. However, the adoption of such a methodology may have some weaknesses. For example, (1) the use of one commodity price index will be enough in the case of the existence of a country specialized in a specific commodity; thus, the use of an aggregate price index may result in model misspecification; (2) there could be significant price variations within aggregate commodity categories. Therefore, the aggregate price index may poorly reflect price variations of particular commodities; (3) trade measures could capture non-commodity price fluctuations and are affected by the composition of export; (4) international commodity prices may serve better at capturing the effects of trade shocks for exporter countries (Chen and Rogoff 2003; Deaton and Miller 1995; Grus 2014). In this regard, Deaton and Miller (1995) proposed a country-specific export price index combining international price levels and country-specific data based on the export volumes of individual commodities. It allows changes in the share of any specific commodity over time by using three-year rolling averages of trade values and lagged-one year. Hence, fluctuations in the price index reflect variations in commodity prices rather than endogenous changes in volumes. This in turn, considers the time-varying nature of the export characteristics of the given country. It is widely known that price shocks of imported goods may reduce economic growth by reducing the profitability of local firms or the disposable income of households. Therefore, Grus (2014) modified the country-specific export price index of Deaton and Miller (1995) by using the net export of each country as weights and labeled it as commodity net export price index (CNEPI). Similar to Deaton and Miller (1995), Grus (2014) considered possible price fluctuations of different commodities in past years to obtain CNEPI. This is the core advantage of the CNEPI compared to the standard commodity price index (Agarwal et al. 2020). In addition, the CNEPI is based on the international prices of 45 different commodities under four main categories, namely energy, metals, food and beverages, and agricultural raw materials, respectively (see Grus and Kebraj 2019: 6–7). Based on these theoretical explanations, we utilized CNEPI to decouple the price effects. The value of China’s real export to partner countries is estimated using the specification:

$$REXP_{CNEPI} = \frac{EXP}{{CNEPI_{ch} }}$$
(1)

where \(EXP\) is China’s exports to partner countries and \(CNEPI_{ch}\) is the commodity net export price index of China. Moreover, CNEPI can be estimated as follows (Grus 2014):

$$CNEPI = \sum\limits_{j = 1}^{J} {P_{t} } (\tau_{i,j,t} )$$
(2)

where \(P_{t}\) is the real logarithmic price of commodity j in year t (in U.S. dollars and divided by the IMF’s unit value index for manufactured exports and time-varying weights), and \(\tau_{i,j,t}\) denotes country-specific time-varying weights for each commodity price for country i. \(\tau_{i,j,t}\) can be estimated by using the following specification (Grus and Kebraj 2019):

$$\tau_{i,j,t} = \frac{1}{3}\sum\limits_{s = 1}^{3} {\frac{{x_{i,j,t} - m_{i,j,t} }}{{GDP_{i,t} }}}$$
(3)

where \(x_{i,j,t}\) and \(m_{i,j,t}\) shows the export and import value of commodity j from country i in year t (in US$), respectively. \(GDP_{i,t}\) represents nominal GDP (in U.S. dollars) of a given country in year t. It should be noted that utilizing net exports to weigh individual commodities enables us to consider price variations of imported commodities (Agarwal et al. 2020; Gruss and Kebhaj 2019). As emphasized by Gruss and Kebhaj (2019), the use of a country-specific net export price index would allow for consideration of the price fluctuations of each commodity, which may have moved differently.

The annual-bilateral real exchange rate was estimated using the following specification:

$$R_{CNEPI} = \frac{{CNEPI_{ch} }}{{e \times CNEPI_{i} }}$$
(4)

where \(e\) is the nominal exchange rate \(CNEPI_{ch}\) is the commodity net export price index of China, and \(CNEPI_{i}\) is the commodity net export price index of given countries. Because the nominal exchange rate does not reflect relative price differences among countries, the real exchange rate of RMB was used as an indicator of its real value. In general, a consumer price index (CPI) is used to deflate real exchange rates in the literature. However, it must be noted that CPI includes the price effects of formerly imported goods and non-traded goods and services (Kang and Dagli 2018). Furthermore, the International Monetary Fund (IMF) points out that CPI-deflated indicators may lead to biased estimation (2015). To hinder spurious estimation results, CNEPI was used to deflate nominal exchange rates. An appreciation in the exchange rate shown in Eq. (4) refers to the increase of RMB’s purchasing power and loss of competitive export capacity, while depreciation in exchange rate refers to a decrease in RMB’s purchasing power and increase of competitive export capacity.

China's real exports and annual-bilateral real exchange rate are constructed with the CPI for robustness check by using the following specifications:

$$REXP_{CPI} = \frac{EXP}{{CPI_{ch} }}$$
(5)
$$R_{{CPI_{{}} }} = \frac{{CPI_{ch} }}{{e \times CPI_{i} }}$$
(6)

where \(EXP\) is China’s exports to partner countries, \(CPI_{ch}\) is the consumer price index of China, and \(e\) is the nominal exchange rate of given countries.\(YP_{sd}\) is the standardized GDP per capita estimated via the method suggested by Kim and Dong-Ku (2011), and \(YP_{sd}^{2}\) is the standardized quadratic of GDP per capita. The standardized GDP per capita is estimated using the following specification:

$$YP_{sd} = \frac{{(YP - \overline{YP} )}}{{S_{YP} }}$$
(7)

where \(YP\) is the GDP per capita (PPP), \(\overline{YP}\) is the mean of GDP per capita (PPP), and \(S_{YP}\) is the standard deviations of the GDP per capita (PPP).

4 Methodology

To evaluate the effect of the GDP per capita square (purchasing power parity, PPP) across partner countries on China’s real exports, we adopt the reduced form of the imperfect substitute model proposed by Goldstein and Khan (1985). Our methodology is based on the literature, which focuses on estimations of the related income and price elasticities in export and import demand. According to traditional theory, the export demand for a product is influenced by income of importing countries, and export price of the product is relative to prices of like products in importing countries. In this, we follow the procedure presented in Sawyer and Sprinkle (1996), Bahmani-Oskooee and Niroomand (1998), Garcia-Herrero and Koivu (2008), Matsubayashi and Hamori (2009), Thorbecke and Smith (2010), Thorbecke (2011), Yin and Hamori (2011), Aiello et al. (2015), Dash et al. (2018), Thuy and Thuy (2019). The annual data analyzed in this study cover the period from 1996 to 2019 in 154 countries with trade ties with China. We employ panel data estimation techniques to calculate the effect of price, income, and the GDP per capita square (PPP) of partner countries on China’s real exports. The common correlated effects mean group estimator (CCEMG) can be used as a forecasting method—allowing cross-section dependence between countries and heterogeneous parameter estimation across countries. We adapted a logarithmic base model to estimate the export demand function for China in relation to the GDP per capita (PPP) square of partner countries and it can be specified as:

$$\ln REXP_{CNEPI} = \beta_{0} + \beta_{1} \ln YP_{it} + \beta_{2} \ln YP_{it}^{2} + \beta_{3} \ln R_{{CNEPI_{it} }} + \varepsilon_{it}$$
(8)

where \(REXP_{CNEPI}\) denotes China’s real exports to 154 partner countries, \(YP\) shows GDP per capita (PPP) of partner countries, \(YP^{2}\) represents the quadratic of GDP per capita (PPP) of partner countries, and \(R_{CNEPI}\) shows the bilateral real exchange rate.

It is well known in the empirical literature that ignoring possible cross-section dependence—which frequently occurs in panel data analysis, could cause biased estimations and false hypothesis testing (Chudik and Pesaran 2013; Erdogan et al. 2020; Sarafidis et al. 2009). Hence, initial analyses are required before implementing panel data analysis. To this end, cross-section dependence and slope homogeneity tests are executed. First, we use the Bias-adjusted LM (\(LM_{adj}\)) test developed by Pesaran et al. (2008) to make inferences on the existence of cross-section dependence. Pesaran et al. developed \(LM_{adj}\) procedure based on the standard LM method (Breusch and Pagan 1980). \(LM_{adj}\) method modifies the LM approach by using mean and variance to solve size distortions when N is relatively larger than T. Thus, \(LM_{adj}\) statistic can be estimated as:

$$LM_{adj} = \sqrt {\frac{2}{N(N - 1)}} \sum\limits_{i = 1}^{N - 1} {\sum\limits_{j = i + 1}^{N} {\frac{{\left( {T - k} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{ij}^{2} - \mu_{Tij} }}{{\upsilon_{Tij} }}} }$$
(9)

where k is the number of regressors, \(\mu_{Tij}\) and \(\upsilon_{Tij}\) are mean and variance, respectively. The \(LM_{adj}\) approach adopts” \(H_{0} :Cov(u_{it} ,u_{jt} ) = 0\)-for all t and \(i \ne j\)- in null hypothesis against alternative of \(H_{1} :Cov(u_{it} ,u_{jt} ) \ne 0\) -at least one pair of \(i \ne j\). Furthermore, the slope homogeneity is tested by using Delta tests proposed by Pesaran and Yamagata (2008). Delta approach tests slope homogeneity (\(H_{0} :\beta_{i} = \beta\) for all i) in null against slope heterogeneity (\(H_{1} :\beta_{i} \ne \beta_{j}\)) in the alternative. Delta tests have a good performance when \(N,T \to \infty\) and normal distribution is valid. The \(\tilde{\Delta }\) statistics (6) perform satisfactorily for large samples, while bias-adjusted version (\(\tilde{\Delta }_{adj}\)) of \(\tilde{\Delta }\) performs well for small samples: \(\tilde{\Delta }_{adj}\) version (7):

$$\tilde{\Delta } = \sqrt N \left( {\frac{{N^{ - 1} \tilde{S} - k}}{{\sqrt {2k} }}} \right)$$
(10)
$$\tilde{\Delta }_{adj} = \tilde{\Delta } = \sqrt N \left( {\frac{{N^{ - 1} \tilde{S} - E(\tilde{z}_{iT} )}}{{\sqrt {Var(\tilde{z}_{iT} )} }}} \right)$$
(11)

Conventional panel estimators known as the first-generation panel data methods, such as fixed or random effects can cause misleading inferences and even inconsistent estimators, depending on the extent of cross-sectional dependence and the source generating the cross-sectional dependence (such as an unobserved common shock) is correlated with regressors (Phillips and Sul 2003, 2007; Andrews 2005; Sarafidis and Robertson 2009; Chudik and Pesaran 2013). Moreover, while fixed and random effect methods allow intercept shifts, the estimators constrain slope parameters equal over countries. These homogeneity restrictions imply that the ‘turning point’ level (per capita GDP) in all counties is identical (Perman and Stern 2003). The country and time-specific effects merely alter the level of real export at this turning point. Finally, the fixed effects estimator for non-stationary data is asymptotically normal, yet the results are biased (Kao et al. 1999; Fidrmuc 2009). Therefore, to estimate long-run relationships between variables, we implement the common correlated effects estimator (CCE) proposed by Pesaran (2006). In principle, the CCE approach allows the stationarity of unobserved factors and individual-specific errors. However, the number of unobserved factors is not required to be estimated. Besides, the CCE method performs well regardless of whether variables are stationary or non-stationary, cointegrated or non-cointegrated—exhibit structural breaks, or have challenges with endogeneity. The CCE approach has satisfactory small sample properties even under a substantial degree of heterogeneity and dynamics and for relatively small values of N and T (Acaravci and Akalin 2017; Eberhardt and Teal 2013). Pesaran (2006) proposed two estimation procedures which are Pooled CCE (CCEP) and Mean Group CCE (CCEMG), respectively. The CCEP \((\widehat{b}p)\) method is based on the idea of homogeneity of individual slope coefficients \((\beta_{i} )\), while the CCEMG \((\widehat{b}_{MG} )\) method is based on a simple average of individual CCE estimators. Both statistics can be estimated as follows (Pesaran 2006):

$$\widehat{b}p = \left( {\sum\limits_{i = 1}^{N} {\theta_{i} X_{i}^{^{\prime}} \overline{M}_{\omega } } X_{i} } \right)^{ - 1} \sum\limits_{i = 1}^{N} {\theta_{i} } X_{i}^{^{\prime}} \overline{M} \omega y_{i}$$
(12)
$$\widehat{b}_{MG} = N^{ - 1} \sum\limits_{i = 1}^{N} {\widehat{b}_{i} }$$
(13)

Ultimately, we estimate the turning point (TP) of GDP across partner countries in export demand function expressed as:

$$TP = - {{\beta_{YP} } \mathord{\left/ {\vphantom {{\beta_{YP} } {2\beta_{{YP^{2} }} }}} \right. \kern-\nulldelimiterspace} {2\beta_{{YP^{2} }} }}$$
(14)

5 Results and discussion

We began our analysis by implementing \(LM_{adj}\) and delta (\(\widetilde{\Delta }\)) tests and results reported in Table 5. According to the \(LM_{adj}\) findings, the null hypothesis of no cross-section dependence is strongly rejected at p-value < 0.01 for both models. This refers to the existence of cross-section dependence between China and its partner countries; thus, a possible shock in one country could affect the other. The factors leading to cross-sectional dependence can be summarized as follows: (a) shared institutions such as the World Trade Organization, WB, IMF, and UNCTAD, (b) multilateral trade agreements, and (c) common trade policies from international treaties (2019). The delta test findings show the null hypothesis of slope homogeneity is strongly rejected—validating heterogeneous coefficients across countries.

Due to the existence of cross-sectional dependence and slope heterogeneity, we employed CCEMG to estimate long-run relationships between variables. The CCEMG results reported in Table 6 show the real exchange rate has a negative and statistically significant effect on real Chinese exports. Therefore, 1% increase in the real exchange rate (i.e., an appreciation of RMB) will decrease Chinese exports by 0.206%. The main reason for the negative correlation between real exchange rate and export levels may be attributed to the positive effect of RMB depreciation on China’s export competition capacity. Appreciation of RMB may increase purchasing power, which may make Chinese goods and services more expensive. This may further decrease the volume of Chinese exports, thus, confirming the results presented in Dèes (2001), Bénassy-Quéré and Lahrèche-Révil (2003), Lau et al. (2004), Marquez and Schindler (2006), Li et al. (2006), Garcia-Herrero and Koivu (2008), Kumar (2009), Thorbecke and Smith (2010), Chen et al. (2011), Aiello et al. (2015), Peng et al. (2018) and Xing (2018), while contradicting the results reported in Cheung et al. (2009).

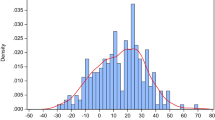
The GDP per capita (PPP) of partner countries has a positive effect on China’s real exports. This finding confirms the majority of previous literature and theoretical expectations. In contrast, the GDP per capita square (PPP) of partner countries has negative and statistically significant effects on China’s real exports. According to the F-based joint significance test, GDP per capita (PPP) and the GDP per capita square (PPP) affect China's real exports jointly as well. When one compares \(Adj.R^{2}\) of the quadratic and linear models, it can be inferred that the power of the quadratic model to explain China's real export performance is higher than the linear model. These findings indicate the existence of an inverted U-shaped relationship between China’s real exports and the income level of partner countries—confirming the validity of the TKC hypothesis in China. Figure 1 shows the structure of the estimated export demand function. The estimated function describes the validity of TKC, where China’s exports may increase until the income of partner countries reaches the estimated turning point, viz. US$ 11.827Footnote 2 (anti ln of 9.37) and decreases thereafter. In this regard, the 1% increase in partner countries' GDP per capita (PPP) averagely increases China’s real exports by 4.91% before the turning point, while 1% increase in GDP per capita (PPP) of partner countries averagely decreases China’s real exports by 2.47% after the turning point. We further observe that the magnitude of China’s exports is stimulated across the ranks of income groups (i.e., high > upper-middle > lower-middle > low-income economies).

Fig. 1
figure 1

Trading Kuznets curve for China. (The dashed line denotes the turning point at 9.37.)

Full size image

The inverted U-shaped relationship and corresponding turning point have several policy implications.

First, growth in China’s exports at low levels of income is related to an increase in purchasing power across partner countries and its stimulating effect on import levels. Second, the inverted U-shape explains the relationship between China's exports and the income level of its trading partners better than the conventional linear relationship. Therefore, studies on estimating the export demand function should not ignore the inverted-U relationship. This finding shows that the income level of partner countries is closely related to China’s export level; thus, decreasing demand for Chinese goods after a certain threshold of income level is achieved by partner countries. Third, China has international competitive power not only in low- or lower-middle-income countries but also across most upper-middle-income countries. Indeed, China has the opportunity to increase its real exports and market share in 84/154 countries. Fourth, China may lose its competitive power after passing the turning point in 70/154 countries, and this number is too large to ignore.

6 Robustness check for empirical estimations

As mentioned, we utilized CNEPI to decouple price effects on China's export and obtain real exchange rates for the base model. The CNEPI, a newly developed price index, has some advantages explained in the earlier section compared to CPI. However, CPI is a widely used measure of the price level in the literature, and it is pretty standardized among countries. Therefore, to check the robustness of empirical results, we used CPI to construct the real exchange rate and China's export level for model 3, employed for the robustness of the estimated model. The CCEMG results in Table 7 show that GDP per capita and quadratic GDP per capita have significant positive and negative coefficients, respectively, while the real exchange rate has a statistically significant negative coefficient. Besides, the turning point of the new model is broadly consistent with former findings of the base model.

On the other hand, one might query the existence of multicollinearity problems in the case of the quadratic model. One of the main approaches to control multicollinearity is to standardize the linear and quadratic terms in the polynomial regression. However, the squared term is not standardized independently but calculated using the square of the standardized linear term. In this regard, we standardized GDP per capita (\(YP_{sd}\)) in the first step and obtained the standardized GDP per capita square (\(YP_{sd}^{2}\)) in the second step. As observed in Table 4, the correlation coefficient between the linear term and the quadratic term drops significantly. In the third step, we estimated model 4 by using standardized data and reported it in Table 7. The empirical findings show that GDP per capita and quadratic GDP per capita have positive and negative coefficients, respectively, whereas the real exchange rate has a significant negative coefficient. Therefore, estimations obtained using model 4 are primarily consistent with our former findings. Consequently, all three different estimations indicate the existence of an inverted U-shaped relationship between China's exports and the income of partner countries.

7 Conclusion

The impact of exports on macroeconomic indicators has been widely scrutinized by researchers since the late 1970s. Indeed, many countries adopted the export-led industrialization strategy to increase economic growth and welfare. China was also affected by the export-oriented industrialization wave and adopted its Open-Door Policy. Within these parameters, China achieved unprecedented economic growth rates; thus, this stride has motivated researchers to investigate the determinants of the demand for Chinese exports. In general, studies have focused on productivity levels, exchange rates, product diversification, and income level of partner countries—as determinants of Chinese export demand. The income level of partner countries is the only exogenous variable that China cannot directly control. However, one of the most significant factors that determine China’s export performance is the income level of partner countries. Some studies report the effect of the income level of partner countries on China’s export performance is much stronger than other effects. However, the rest of the studies assume a monotonic relationship between China’s exports and the income level of partner countries—ignoring the possibility of a quadratic relationship. Assuming the global perception that Chinese products are less sophisticated than other countries and demand for more sophisticated, healthy, and quality products increases with income growth—it becomes difficult to satisfy the presumption of monotony. Within this scope, this study investigated the quadratic relationship between China’s real exports to 154 partner countries and income for the period 1996 to 2019. We adopted a dynamic modeling strategy using second-generation panel data estimation methods. According to the empirical results, an increase in GDP per capita (PPP) of partner countries has a positive effect on China’s real exports, whereas the GDP per capita (PPP) square of partner countries has a negative and statistically significant effect. This implies the existence of an inverted U-shaped nexus between income levels of trading partners and China’s real export level. On the other hand, the appreciation of RMB decreases export level.

As of 2019, China exported 4,423 varieties of goods to its 215 partner countries [HS-6-digit products]. China’s exports of food products, minerals, fuels, chemicals, plastic or rubber, textiles and clothing, stone and glass, metals, transportation, intermediate goods, and raw materials have significantly increased in countries with sub-threshold income while decreasing in countries with up-threshold income for the period 1996 to 2019 (World Bank 2019c). The loss of competitive power in up-threshold income countries is in line with our empirical findings, and this decrease may be related to the notorious low-quality perception of Chinese products and shifting preferences with increasing income (Franco and Roach 2018; Khan and Ahmed 2012; Kim et al. 2015; Laforet and Chen 2012; Schniederjans et al. 2004; Srivastava 2015; Watung 2014). Although China has increased the quality of its exports in recent years, the increase was not enough to diminish the country’s reputation for low-quality goods. Undoubtedly, it could take significant time for China to improve its quality image, which affects consumers' decisions and trust. Therefore, decisions by trade policymakers could support image-building efforts. It is important to note, however, that image building alone may not increase China’s export share in its trade partner countries once income level passes over a specific threshold. Decision-makers could expect dynamic changes in export demand when income increases in their partner countries. Knowing this, Chinese policymakers could develop quality improvement policies in line with the income of individual partner countries.

Based on the empirical findings, the appreciation of the RMB poses significant risks for the sustainability of China’s real exports. Thus, the Chinese monetary authority could take strict measures to hinder the appreciation of the RMB—to preserve the country’s international competitiveness. Moreover, an extreme devaluation of the RMB may raise the risks of a trade war, which threatens the sustainability of international trade. Therefore, stabilizing the value of the RMB will ensure the competitive power of China and prevent trade wars.

Regardless of our findings, this paper has several limitations. First, due to data availability, we examined the existence of quadratic nexus between the Chinese export level and the income of its trade partners for the period 1996 to 2019. Hence, the size and power of the panel data estimations may have been affected by the time span. Therefore, future studies may consider testing the validity of TKC using extended proxy data. Second, we examined the existence of the quadratic nexus of income of trade partners and China’s aggregate export level. The presence of quadratic nexus may vary in different product groups or sectors in China. Therefore, future studies could consider testing specific sectors or product categories. This may help to understand whether the existence of quadratic nexus is valid at the sectoral or product level and establish product and industry-based export strategies. Third, future studies may consider testing quadratic nexus between export and income level for different countries. This would deepen the debate on the trading Kuznets curve with insights from other countries with different export characteristics.