Skip to main content
SpringerLink
Log in

Identification of clandestine groundwater pollution sources using heuristics optimization algorithms: a comparison between simulated annealing and particle swarm optimization

  • Published:
Environmental Monitoring and Assessment Aims and scope Submit manuscript

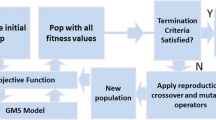
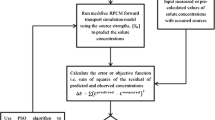
Abstract

Groundwater pollution is the biggest threat to sustainability of groundwater resources and even more difficult to detect in case of clandestine sources. At the time when pollution is first detected in randomly located sparse wells, very little is known about the pollution sources. Finding the precise locations of clandestine sources of pollution and their release flux history is the biggest challenge and often termed as a problem belonging to the class of environmental forensics. In this study, two linked simulation optimization–based novel techniques are developed to estimate locations and release flux history from clandestine point sources of groundwater pollution. Simulation model is clubbed with optimization solver to determine the locations and release flux histories of groundwater pollution sources by minimizing the residual error between observed and simulated concentration values. Simulated annealing (SA) and particle swarm optimization (PSO) are used as optimization algorithms. A detailed comparative analysis of these two meta-heuristic optimization algorithms in minimizing the residual error is presented in this study. The performance evaluation of both the algorithms in identifying the sources locations and release flux history is carried out for two synthetic cases and a real-life scenario of groundwater pollution in an aquifer in New South Wales, Australia, which has not been attempted in the past. The results of source location identification and release flux history show the selective applicability of each algorithm in solving real-life scenarios of groundwater pollution.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  • Alapati, S., & Kabala, Z. (2000). Recovering the release history of a groundwater contaminant using a non-linear least-squares method. Hydrological Processes, 14(6), 1003–1016.

    Google Scholar 

  • Amirabdollahian, M., & Datta, B. (2013). Identification of contaminant source characteristics and monitoring network design in groundwater aquifers: an overview. Journal of Environmental Protection, 4, 26–41.

    Google Scholar 

  • Aral, M.M., Guan, J., & Maslia, M.L. (2001). Identification of contaminant source location and release history in aquifers. Journal of Hydrologic Engineering, 6(3), 225–234.

    Google Scholar 

  • Ayvaz, M.T. (2010). A linked simulation–optimization model for solving the unknown groundwater pollution source identification problems. Journal of Contaminant Hydrology, 117(1-4), 46–59.

    CAS  Google Scholar 

  • Bashi-Azghadi, S.N., Kerachian, R., Bazargan-Lari, M.R., & Solouki, K. (2010). Characterizing an unknown pollution source in groundwater resources systems using PSVM and PNN. Expert Systems with Applications, 37(10), 7154–7161.

    Google Scholar 

  • Bear, J., & Cheng, A.H.D. (2010). Modeling groundwater flow and contaminant transport Vol. 23. New York : Springer Science & Business Media.

    Google Scholar 

  • collab=Černỳ V. (1985). Thermodynamical approach to the traveling salesman problem: an efficient simulation algorithm. Journal of optimization theory and applications, 45(1), 41–51.

    Google Scholar 

  • Chadalavada, S., Datta, B., & Naidu, R. (2011). Optimisation approach for pollution source identification in groundwater: an overview. International Journal of Environment and Waste Management, 8(1-2), 40–61.

    Google Scholar 

  • Chen, J.S., Liang, C.P., Liu, C.W., & Li, L.Y. (2016). An analytical model for simulating two-dimensional multispecies plume migration. Hydrology and Earth System Sciences, 20(2), 733–753.

    CAS  Google Scholar 

  • Chen, J.S., Li, L.Y., Lai, K.H., & Liang, C.P. (2017). Analytical model for advective-dispersive transport involving flexible boundary inputs, initial distributions and zero-order productions. Journal of Hydrology, 554, 187–199.

    Google Scholar 

  • Chen, J.S., Ho, Y.C., Liang, C.P., Wang, S.W., & Liu, C.W. (2019a). Semi-analytical model for coupled multispecies advective-dispersive transport subject to rate-limited sorption. Journal of Hydrology, 124164, 579.

    Google Scholar 

  • Chen, J.S., Liang, C.P., Chang, C.H., & Wan, M.H. (2019b). Simulating three-dimensional plume migration of a radionuclide decay chain through groundwater. Energies, 12(19), 3740.

    CAS  Google Scholar 

  • Clerc, M., & Kennedy, J. (2002). The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE Transactions on Evolutionary Computation, 6(1), 58–73.

    Google Scholar 

  • Datta, B., Chakrabarty, D., & Dhar, A. (2009). Optimal dynamic monitoring network design and identification of unknown groundwater pollution sources. Water Resources Management, 23 (10), 2031–2049.

    Google Scholar 

  • Datta, B., Durand, F., Laforge, S., Prakash, O., Esfahani, H.K., Chadalavada, S., & Naidu, R. (2016). Preliminary hydrogeologic modeling and optimal monitoring network design for a contaminated abandoned mine site area: application of developed monitoring network design software. Journal of Water Resource and Protection, 8(01), 46.

    Google Scholar 

  • Datta, B., Petit, C., Palliser, M., Esfahani, H.K., Prakash, O., & et al. (2017). Linking a simulated annealing based optimization model with pht3d simulation model for chemically reactive transport processes to optimally characterize unknown contaminant sources in a former mine site in Australia. Journal of Water Resource and Protection, 9(05), 432.

    CAS  Google Scholar 

  • Dokou, Z., & Pinder, G.F. (2009). Optimal search strategy for the definition of a dnapl source. Journal of Hydrology, 376(3-4), 542–556.

    CAS  Google Scholar 

  • Eberhart, R., & Kennedy, J. (1995). A new optimizer using particle swarm theory, Proceedings of the Sixth International Symposium on Micro Machine and Human Science, IEEE.

  • Elċi, A., & Ayvaz, M.T. (2014). Differential-evolution algorithm based optimization for the site selection of groundwater production wells with the consideration of the vulnerability concept. Journal of Hydrology, 511, 736–749.

    Google Scholar 

  • Fried, J.J. (1975). Groundwater pollution Vol. 4. Amsterdam: Elsevier.

    Google Scholar 

  • Gaur, S., Chahar, B.R., & Graillot, D. (2011). Analytic elements method and particle swarm optimization based simulation–optimization model for groundwater management. Journal of Hydrology, 402(3-4), 217–227.

    Google Scholar 

  • Gorelick, S.M., Evans, B., & Remson, I. (1983). Identifying sources of groundwater pollution: an optimization approach. Water Resources Research, 19(3), 779–790.

    CAS  Google Scholar 

  • Guneshwor, L., Eldho, T., & Kumar, A.V. (2018). Identification of groundwater contamination sources using meshfree rpcm simulation and particle swarm optimization. Water Resources Management, 32(4), 1517–1538.

    Google Scholar 

  • Gurarslan, G., & Karahan, H. (2015). Solving inverse problems of groundwater-pollution-source identification using a differential evolution algorithm. Hydrogeology Journal, 23(6), 1109–1119.

    CAS  Google Scholar 

  • Hou, Z., Lu, W., Chu, H., & Luo, J. (2015). Selecting parameter-optimized surrogate models in dnapl-contaminated aquifer remediation strategies. Environmental Engineering Science, 32 (12), 1016–1026.

    CAS  Google Scholar 

  • Javandel, I., Doughty, C., & Tsang, C.F. (1984). Groundwater transport: handbook of mathematical models. Tech rep., Lawrence Berkeley Lab., CA (USA).

  • Jha, M., & Datta, B. (2012). Three-dimensional groundwater contamination source identification using adaptive simulated annealing. Journal of Hydrologic Engineering, 18(3), 307–317.

    Google Scholar 

  • Jha, M.K., & Datta, B. (2011). Simulated annealing based simulation-optimization approach for identification of unknown contaminant sources in groundwater aquifers. Desalination and Water Treatment, 32(1-3), 79–85.

    Google Scholar 

  • Jiang, X., Lu, W., Hou, Z., Zhao, H., & Na, J. (2015). Ensemble of surrogates-based optimization for identifying an optimal surfactant-enhanced aquifer remediation strategy at heterogeneous dnapl-contaminated sites. Computers & Geosciences, 84, 37–45.

    CAS  Google Scholar 

  • Keshari, A.K., & Datta, B. (2001). A combined use of direct search algorithms and exterior penalty function method for groundwater pollution management. Journal of Porous Media 4(3).

  • Kirkpatrick, S., Gelatt, C.D., & Vecchi, M.P. (1983). Optimization by simulated annealing. Science, 220(4598), 671–680.

    CAS  Google Scholar 

  • Kitanidis, P.K., & VoMvoris, E.G. (1983). A geostatistical approach to the inverse problem in groundwater modeling (steady state) and one-dimensional simulations. Water Resources Research, 19(3), 677–690.

    Google Scholar 

  • Leichombam, S., & Bhattacharjya, R.K. (2018). New hybrid optimization methodology to identify pollution sources considering the source locations and source flux as unknown. Journal of Hazardous, Toxic, and Radioactive Waste, 23(1), 04018037.

    Google Scholar 

  • Li, J., Lu, W., Wang, H., Fan, Y., & Chang, Z. (2020). Groundwater contamination source identification based on a hybrid particle swarm optimization-extreme learning machine. Journal of Hydrology 124657.

  • Liu, C., & Ball, W.P. (2002). Back diffusion of chlorinated solvent contaminants from a natural aquitard to a remediated aquifer under well-controlled field conditions: Predictions and measurements. Groundwater, 40(2), 175–184.

    CAS  Google Scholar 

  • Mahar, P.S., & Datta, B. (1997). Optimal monitoring network and ground-water–pollution source identification. Journal of Water Resources Planning and Management, 123(4), 199–207.

    Google Scholar 

  • Mahar, P.S., & Datta, B. (2000). Identification of pollution sources in transient groundwater systems. Water Resources Management, 14(3), 209–227.

    Google Scholar 

  • Mahar, P.S., & Datta, B. (2001). Optimal identification of ground-water pollution sources and parameter estimation. Journal of Water Resources Planning and Management, 127(1), 20–29.

    Google Scholar 

  • Mahinthakumar, G., & Sayeed, M. (2005). Hybrid genetic algorithm—local search methods for solving groundwater source identification inverse problems. Journal of Water Resources Planning and Management, 131(1), 45–57.

    Google Scholar 

  • McDonald, M.G., & Harbaugh, A.W. (1988). A modular three-dimensional finite-difference ground-water flow model Vol. 6. Reston: US Geological Survey.

    Google Scholar 

  • Neupauer, R., & Wilson, J. (2005). Backward probability model using multiple observations of contamination to identify groundwater contamination sources at the massachusetts military reservation. Water Resources Research 41(2).

  • Prakash, O., & Datta, B. (2013). Sequential optimal monitoring network design and iterative spatial estimation of pollutant concentration for identification of unknown groundwater pollution source locations. Environmental Monitoring and Assessment, 185(7), 5611–5626.

    Google Scholar 

  • Prakash, O., & Datta, B. (2014). Characterization of groundwater pollution sources with unknown release time history. Journal of Water Resource and Protection, 6, 337–350.

    Google Scholar 

  • Prakash, O., & Datta, B. (2015). Optimal characterization of pollutant sources in contaminated aquifers by integrating sequential-monitoring-network design and source identification: methodology and an application in Australia. Hydrogeology Journal, 23(6), 1089–1107.

    CAS  Google Scholar 

  • Singh, R.M., & Datta, B. (2007). Artificial neural network modeling for identification of unknown pollution sources in groundwater with partially missing concentration observation data. Water Resources Management, 21(3), 557–572.

    Google Scholar 

  • Singh, R.M., Datta, B., & Jain, A. (2004). Identification of unknown groundwater pollution sources using artificial neural networks. Journal of Water Resources Planning and Management, 130 (6), 506–514.

    Google Scholar 

  • Skaggs, T.H., & Kabala, Z. (1994). Recovering the release history of a groundwater contaminant. Water Resources Research, 30(1), 71–79.

    Google Scholar 

  • Snodgrass, M.F., & Kitanidis, P.K. (1997). A geostatistical approach to contaminant source identification. Water Resources Research, 33(4), 537–546.

    CAS  Google Scholar 

  • Sophia, L., & Bhattacharjya, R.K. (2020). A ga based iterative model for identification of unknown groundwater pollution sources considering noisy data. In Nature-inspired methods for metaheuristics optimization (pp. 303–321): Springer.

  • Srivastava, D., & Singh, R.M. (2015). Groundwater system modeling for simultaneous identification of pollution sources and parameters with uncertainty characterization. Water Resources Management, 29(13), 4607–4627.

    Google Scholar 

  • Tikhonov, A.N., & Arsenin, V.I. (1977). Solutions of ill-posed problems Vol. 14. Springfield: Vh Winston.

    Google Scholar 

  • Xing, Z., Qu, R., Zhao, Y., Fu, Q., Ji, Y., & Lu, W. (2019). Identifying the release history of a groundwater contaminant source based on an ensemble surrogate model. Journal of Hydrology.

  • Xu, T., & Gómez-Hernández, J.J. (2016). Joint identification of contaminant source location, initial release time, and initial solute concentration in an aquifer via ensemble Kalman filtering. Water Resources Research, 52(8), 6587– 6595.

    CAS  Google Scholar 

  • Yan, S., & Minsker, B. (2006). Optimal groundwater remediation design using an adaptive neural network genetic algorithm. Water Resources Research 42(5).

  • Yan, X., Dong, W., An, Y., & Lu, W. (2019). A Bayesian-based integrated approach for identifying groundwater contamination sources. Journal of Hydrology, 579, 124160.

    CAS  Google Scholar 

  • Yeh, W.W.G. (1986). Review of parameter identification procedures in groundwater hydrology: the inverse problem. Water Resources Research, 22(2), 95–108.

    Google Scholar 

  • Zhang, S., Chen, P., Lee, L.H., Peng, C.E., & Chen, C.H. (2011). Simulation optimization using the particle swarm optimization with optimal computing budget allocation. In Proceedings of the 2011 Winter Simulation Conference (WSC) (pp. 4298–4309): IEEE.

  • Zhang, T., & Chen, Q. (2007). Identification of contaminant sources in enclosed environments by inverse CFD modeling. Indoor Air, 17(3), 167–177.

    CAS  Google Scholar 

  • Zheng, C., & Wang, P.P. (1999). Mt3dms: a modular three-dimensional multispecies transport model for simulation of advection, dispersion and chemical reactions of contaminants in groundwater systems; documentation and user’s guide. Tech. rep., Alabama Univ University.

Download references

Author information

Authors and Affiliations

  1. Civil and Environmental Engineering, Indian Institute of Technology Patna, Bihta, Bihar, India

    Anirban Chakraborty & Om Prakash

Authors
  1. Anirban Chakraborty
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Om Prakash
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Anirban Chakraborty.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chakraborty, A., Prakash, O. Identification of clandestine groundwater pollution sources using heuristics optimization algorithms: a comparison between simulated annealing and particle swarm optimization. Environ Monit Assess 192, 791 (2020). https://doi.org/10.1007/s10661-020-08691-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10661-020-08691-7

Keywords

Search

Navigation