A fuzzy multi-stakeholder multi-criteria methodology for water allocation and reuse in metropolitan areas

Abstract

In this paper, a fuzzy decision making methodology is proposed to find a socially optimal scenario for allocating effluent of wastewater treatment plants and urban and suburban runoffs to agricultural regions and recharging aquifers. The presented methodology named modified fuzzy social choice (MFSC) considers multi-stakeholder multi-criteria problems under uncertainties inherent in a decision making process utilizing a fuzzy ranking method and the fuzzy social choice (FSC) theory. A set of water and wastewater allocation scenarios are proposed for water quantity and quality management of the study area, while six main stakeholders with conflicting utilities and different negotiation powers are involved. The proposed methodology is applied to Tehran metropolitan area, the capital city of Iran with the population of about 8 million people, to examine its applicability and effectiveness. The results shows that using fuzzy multi-stakeholder multi-criteria decision making method considering equal and different negotiation powers can lead to different outcomes. Based on the results, the MFSC method, which considers a number of decision makers having different negotiation powers, degrees of importance of decision making criteria, and some important uncertainties, performs more promising in real water resources management problems.

Appendix

Fuzzy ranking

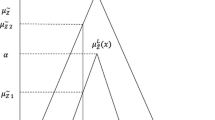
Assume a DM wants to rank m fuzzy numbers ${\overset{\sim }{A}}_1,{\overset{\sim }{A}}_2,\dots, {\overset{\sim }{A}}_m$. The kth α-cut ${\overset{\sim }{A}}_i^{\alpha_k}$ of the fuzzy number ${\overset{\sim }{A}}_i$ is defined as follows (Chen and Wang 2009):

$$ {\overset{\sim }{A}}_i^{\alpha_k}=\left\{x\ |\ {f}_{{\overset{\sim }{A}}_i}(x)\ge {\alpha}_k,x\in X\right\},{\alpha}_k=\frac{k}{n},k\in \left\{0,1,\dots, n\right\},n\in N $$

(A.1)

where n denotes the number of α-cuts. The minimal value l_{i, k} and the maximal value r_{i, k} of the kth α-cut of the fuzzy number ${\overset{\sim }{A}}_i$ are defined as follows:

$$ {l}_{i,k}=\underset{x\in X}{\mathit{\operatorname{inf}}}\left\{x\ |\ {f}_{{\overset{\sim }{A}}_i}(x)\ge {\alpha}_k\right\} $$

(A.2)

$$ {r}_{i,k}=\underset{x\in X}{\mathit{\sup}}\left\{x\ |\ {f}_{{\overset{\sim }{A}}_i}(x)\ge {\alpha}_k\right\} $$

(A.3)

The maximal barrier U and the minimal barrier L of the m fuzzy numbers ${\overset{\sim }{A}}_1,{\overset{\sim }{A}}_2,\dots, {\overset{\sim }{A}}_m$ are defined as follows:

$$ U=\underset{\forall i}{\mathit{\max}}\left\{x|x\in {\overset{\sim }{A}}_i^{\alpha },0\le \alpha \le {h}_{{\overset{\sim }{A}}_i},i=1,2,\dots, m\right\} $$

(A.4)

$$ L=\underset{\forall i}{\mathit{\min}}\left\{x|x\in {\overset{\sim }{A}}_i^{\alpha },0\le \alpha \le {h}_{{\overset{\sim }{A}}_i},i=1,2,\dots, m\right\} $$

(A.5)

where ${h}_{{\overset{\sim }{A}}_i}$ denotes the height of ${\overset{\sim }{A}}_i$ defined as ${h}_{{\overset{\sim }{A}}_i}={\mathit{\sup}}_{x\in X}{f}_{{\overset{\sim }{A}}_i}(x)$.

The signal/noise ratio ${\widehat{\eta}}_{i,k}$ of the kth α-cut of the fuzzy number ${\overset{\sim }{A}}_i$ proposed in this method is defined as follows:

$$ {\widehat{\eta}}_{i,k}=\frac{m_{i,k}-L}{\delta_{i,k}+c} $$

(A.6)

where m_{i, k} and δ_{i, k} denote the middle point and the spread of ${\overset{\sim }{A}}_i^{\alpha_k}$, respectively, and are defined as follows:

$$ {m}_{i,k}=\frac{\left({r}_{i,k}+{l}_{i,k}\right)}{2} $$

(A.7)

$$ {\delta}_{i,k}={r}_{i,k}-{l}_{i,k} $$

(A.8)

c is a parameter that should be greater than the value of R − L. The ranking index $RI\left({\overset{\sim }{A}}_i\right)$ of the fuzzy number ${\overset{\sim }{A}}_i$ is calculated as follows:

$$ RI\left({\overset{\sim }{A}}_i\right)=\frac{h_{{\overset{\sim }{A}}_i}{\sum}_{k=1}^n{\alpha}_k\times {\widehat{\eta}}_{i,k}}{\sum_{k=1}^n{\alpha}_k} $$

(A.9)

where ${\alpha}_k={h}_{{\overset{\sim }{A}}_i}\times \frac{k}{n},k\in \left\{0,1,\dots, n\right\},n\in N$, and n denotes the number of α-cuts. The larger the value of $RI\left({\overset{\sim }{A}}_i\right)$, the better the ranking of ${\overset{\sim }{A}}_i$. Details and examples about this fuzzy ranking method can be found in Chen and Wang (2009).

Fuzzy Borda count

This method is an extension of the classic Borda count method (de Borda 1781). In fuzzy Borda count, each DM assigns the following value to every alternative x_i based on its preferences and relative power (García-Lapresta and Martínez-Panero 2002):

$$ {r}_k\left({x}_i\right)={w}^k\sum \limits_{\begin{array}{c}j=1\\ {}{r}_{ij}^k>0.5\end{array}}^n{r}_{ij}^k $$

(A.10)

where w^k is the negotiation power of the kth DM. Equation A.10 indicates the sum of the entries greater than 0.5 in the row i which is multiplied by each DM’s power in the fuzzy preference relations. Then, the collective score of alternative x_i is obtained as follows:

$$ r\left({x}_i\right)=\sum \limits_{k=1}^m{r}_k\left({x}_i\right) $$

(A.11)

Thus, the highest scored alternative ($\underset{i}{\max }r\left({x}_i\right)$) will be chosen. More details and examples of this method can be found in García-Lapresta and Martínez-Panero (2002).

Fuzzy Minimax

Also known as Minimax degree set Q(β); this method is the fuzzy extension of classic Max-Min Winner (Nurmi 1988). For each alternative x_i, x_j ∈ X and each DM let (Nurmi 1981):

$$ {\upsilon}_D^k\left({x}_j\right)={w}^k\underset{i}{\max }{r}_{ij} $$

(A.12)

where w^k is the negotiation power of the kth DM. Then, we define:

$$ {\upsilon}_D\left({x}_j\right)=\underset{k}{\max }{\upsilon}_D^k\left({x}_j\right) $$

(A.13)

Now let:

$$ \underset{j}{\min }{\upsilon}_D\left({x}_j\right)=\beta $$

(A.14)

Then:

$$ Q\left(\beta \right)=\left\{{x}_i|{\upsilon}_D\left({x}_j\right)=\beta \right\} $$

(A.15)

Therefore, the alternative with the value β will be chosen. More details about this method can be found in Nurmi (1981).

Fuzzy linguistic quantifiers

This method utilizes fuzzy logic with linguistic quantifiers for group decision making. Fuzzy linguistic quantifier “most” is employed to represent a fuzzy majority. Also, two direct and indirect solutions, namely core solution and consensus winner solution, are used for selecting the best alternative. In this section, if not otherwise determined, Q = most.

Direct solution (core)

The core is defined as a set of non-dominated alternatives not defeated in pairwise comparisons by “most” DMs (Kacprzyk et al. 1992). The linguistic quantifier “most” was first presented by Zadeh (1983). In this solution, let (Kacprzyk et al. 1992):

$$ {h}_{ij}^k=\left\{\begin{array}{c}1\ if\ {r}_{ij}^k<0.5\ \\ {}0\kern0.75em \mathrm{otherwise}\end{array}\right. $$

(A.16)

where ${h}_{ij}^k$ is used to define whether alternative x_i defeats x_j or not, ∀i, j, k. Then,

$$ {h}_j^k=\frac{w^k}{n-1}\sum \limits_{i=1,i\ne j}^n{h}_{ij}^k $$

(A.17)

is the extent to which DM k with the negotiation power of w^k is not against alternative x_j. Next,

$$ {h}_j=\frac{1}{m}\sum \limits_{k=1}^m{h}_j^k $$

(A.18)

is the extent to which all the DMs are not against x_j, and

$$ {\upsilon}_Q^j={\mu}_Q\left({h}_j\right)=\left\{\begin{array}{c}1\kern1.5em for\ {h}_j\ge 0.8\\ {}2{h}_j-0.6\kern0.5em for\ 0.3<{h}_j<0.8\\ {}0\kern1.25em for\ {h}_j<0.3\end{array}\right. $$

(A.19)

is to what extent “most” DMs are not against x_j. The fuzzy Q-core is now defined as the fuzzy set:

$$ {C}_{\mathrm{Q}}={\upsilon}_Q^1/{x}_1+\dots +{\upsilon}_Q^n/{x}_n $$

(A.20)

which denotes a fuzzy set of alternatives that are not defeated by “most” DMs. If introducing a threshold on the degree of defeat in Eq. A.16, the fuzzy α/Q-core can be defined. Let

$$ {h}_{ij}^k\left(\upalpha \right)=\left\{\begin{array}{c}1\ if\ {r}_{ij}^k<\upalpha \le 0.5\ \\ {}0\kern0.75em \mathrm{otherwise}\end{array}\right. $$

(A.21)

then, following Eqs. A.17 to A.20, the fuzzy α/Q-core is defined as:

$$ {C}_{\upalpha /Q}={\upsilon}_Q^1\left(\upalpha \right)/{x}_1+\dots +{\upsilon}_Q^n\left(\upalpha \right)/{x}_n $$

(A.22)

which is a fuzzy set of alternatives that are not sufficiently defeated by “most” DMs. Also, the strength of defeat can be introduced into Eq. A.16, and the fuzzy s/Q-core can be defined. Then, the following function is introduced:

$$ {\widehat{h}}_{ij}^k=\left\{\begin{array}{c}2\left(0.5-{r}_{ij}^k\right)\ if\ {r}_{ij}^k<0.5\ \\ {}0\kern0.75em otherwise\end{array}\right. $$

(A.23)

Following Eqs. A.17 to A.20, the fuzzy s/Q-core is defined as:

$$ {C}_{\mathrm{s}/Q}={\widehat{\upsilon}}_Q^1/{x}_1+\dots +{\widehat{\upsilon}}_Q^n/{x}_n $$

(A.24)

Indirect solution (consensus winner)

In this method, first, a social fuzzy preference relation is determined which is defined by R = [r_ij], and is given by (Kacprzyk et al. 1992):

$$ {r}_{ij}=\left\{\begin{array}{c}\frac{1}{m}\sum \limits_{k=1}^m{w^k{a}^k}_{ij}\kern1em if\ i\ne j\\ {}0\kern5em \mathrm{otherwise}\end{array}\right. $$

(A.25)

where w^k is the negotiation power of the kth DM, and

$$ {a^k}_{ij}=\left\{\begin{array}{c}1\ if\ {r}_{ij}^k>0.5\ \\ {}0\kern0.75em \mathrm{otherwise}\end{array}\right. $$

(A.26)

Since the social fuzzy preference relation is calculated, the fuzzy extension of consensus winner method will be applied which is defined by:

$$ {g}_{ij}=\left\{\begin{array}{c}1\ if\ {r}_{ij}^k>0.5\ \\ {}0\kern0.75em \mathrm{otherwise}\end{array}\right. $$

(A.27)

which expresses whether or not x_i defeats x_j. Then, let:

$$ {g}_i=\frac{1}{n-1}\sum \limits_{j=1,j\ne i}^n{g}_{ij} $$

(A.28)

g_i is the mean degree to which alternative x_i is preferred to all other alternatives. Then,

$$ {z}_Q^i={\mu}_Q\left({g}_j\right)=\left\{\begin{array}{c}1\kern1.5em for\ {g}_j\ge 0.8\\ {}2{h}_j-0.6\kern0.5em for\ 0.3<{g}_j<0.8\\ {}0\kern1.25em for\ {g}_j<0.3\end{array}\right. $$

(A.29)

is the extent to which x_i is preferred to “most” other alternatives. Finally, the fuzzy Q-consensus winner is defined as:

$$ {W}_Q={z}_Q^1/{x}_1+\dots +{z}_Q^n/{x}_n $$

(A.30)

which is a fuzzy set of alternatives that are preferred to “most” other alternatives. Analogously to the case of the core solution, a threshold is introduced as:

$$ {g}_{ij}\left(\upalpha \right)=\left\{\begin{array}{c}1\ if\ {r}_{ij}^k>\upalpha \ge 0.5\ \\ {}0\kern0.75em \mathrm{otherwise}\end{array}\right. $$

(A.31)

Then, following the Eqs. A.28 and A.29, we can define the fuzzy α/Q-consensus winner as:

$$ {W}_{\upalpha /Q}={z}_Q^1\left(\upalpha \right)/{x}_1+\dots +{z}_Q^n\left(\upalpha \right)/{x}_n $$

(A.32)

which is a fuzzy set of alternatives that are preferred to “most” other alternatives. Also, the strength of preference can be introduced into Eq. A.27 by defining:

$$ {\widehat{g}}_{ij}\left(\upalpha \right)=\left\{\begin{array}{c}2\left({r}_{ij}^k-0.5\right)\ if\ {r}_{ij}^k>0.5\ \\ {}0\kern0.75em \mathrm{otherwise}\end{array}\right. $$

(A.33)

Then, following the Eqs. A.28 and A.29, the fuzzy s/Q-consensus winner is defined as:

$$ {W}_{\mathrm{s}/Q}={\widehat{z}}_Q^1/{x}_1+\dots +{\widehat{z}}_Q^n/{x}_n $$

(A.34)

which is a fuzzy set of alternatives that are strongly preferred to “most” other alternatives. More details and examples about fuzzy linguistic quantifiers method can be found in Kacprzyk et al. (1992).