Revisiting Stress Propagation in a Two-Dimensional Elastic Circular Disk Under Diametric Loading

Abstract

In this paper, we present a comprehensive investigation of stress propagation in a two-dimensional elastic circular disk. To accurately describe the displacements and stress fields within the disk, we employ a scalar and vector potential approach, representing them as sums of Bessel functions. The determination of the coefficients for these expansions is accomplished in the Laplace space, where we compare the boundary conditions. By converting the inverse Laplace transforms into complex integrals using residue calculus, we successfully derive explicit expressions for the displacements and stress fields. Notably, these expressions encompass primary, secondary, and surface waves, providing a thorough characterization of the stress propagation phenomena within the disk. Our findings contribute to the understanding of mechanical behavior in disk-shaped components and can be valuable in the design and optimization of such structures across various engineering disciplines.

Appendices

Appendix A: Derivation of Eq. (22a)–(22e)

In this Appendix, let us give the detailed derivations of the expressions of the static values (22a)–(22e). Because we are only interested in the static values, we omit $\lim _{t\to \infty}$ in Eq. (20a)–(20e) in this Appendix. Now, we focus on $\widetilde{\sigma}_{rr}^{(m)}$. To calculate the summation $\sum _{m=2,4,\ldots}\widetilde{\sigma}_{rr}^{(m)}\cos (m\theta )$, it is convenient to use the following identity:

$$\begin{aligned} \sum _{m=2,4,\ldots}r^{*m}\cos (m\theta ) &= \Re \sum _{m=2,4,\ldots}r^{*m} \mathrm{e}^{im\theta} = \Re \frac{1}{1-r^{*2}e^{2i\theta}} \\ &= \Re \frac{1}{r_{1}^{*}r_{2}^{*}}\mathrm{e}^{i(\theta _{1}-\theta _{2})} = \frac{1}{r_{1}^{*}r_{2}^{*}}\cos (\theta _{1}-\theta _{2}), \end{aligned}$$

(38)

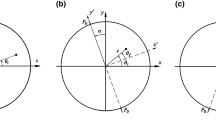
where $\Re$ represents the real part, and we have introduced $r_{1}$, $r_{2}$, $\theta _{1}$, and $\theta _{2}$ as shown in Fig. 1 in the second line of Eq. (38). From this identity, the following is also obtained:

$$\begin{aligned} \sum _{m=2,4,\ldots}m r^{*m}\cos (m\theta ) &= \Re \frac{2r^{*2}e^{2i\theta}}{\left (1-r^{*2}e^{2i\theta}\right )^{2}} = \Re \frac{2r^{*2}}{r_{1}^{*2}r_{2}^{*2}}\mathrm{e}^{2i(\theta + \theta _{1}-\theta _{2})} \\ &= \frac{2r^{*2}}{r_{1}^{*2}r_{2}^{*2}}\cos [2(\theta + \theta _{1}- \theta _{2})]. \end{aligned}$$

(39)

Using Eqs. (38) and (39), one gets

$$ \sum _{m=2,4,\ldots}\widetilde{\sigma}_{rr}^{(m)}\cos (m\theta ) = 1- \frac{\left (1-r^{*2}\right )^{2}\left [1-2r^{*2}-r^{*4}+2\cos (2\theta )\right ]}{\left [1+r^{*4}-2r^{*2}\cos (2\theta )\right ]^{2}}. $$

(40)

Now, from the definition of $r^{*1}$, $r^{*2}$, $\theta _{1}$, and $\theta _{2}$ in Eqs. (23a)–(23b), we can easily obtain

$$\begin{aligned} &\frac{\cos \theta _{1} \cos ^{2}(\theta +\theta _{1})}{r_{1}^{*}} + \frac{\cos \theta _{2} \cos ^{2}(\theta -\theta _{2})}{r_{2}^{*}} - \frac{1}{2} \end{aligned}$$

(41)

$$\begin{aligned} &\quad = \frac{\left (1-r^{*2}\right )^{2}\left [1-2r^{*2}-r^{*4}+2\cos (2\theta )\right ]}{2\left [1+r^{*4}-2r^{*2}\cos (2\theta )\right ]^{2}}. \end{aligned}$$

(42)

From Eqs. (40) and (42) with Eq. (21a), we can reach Eq. (22c). After the similar calculations, we can also derive Eqs. (22a)–(22e).

Appendix B: Stress Components in the Cartesian Coordinates

In this Appendix, we present the expressions of the stress components in the Cartesian coordinates. Once we obtain the expressions in the polar coordinates, it is straightforward to obtain those in the Cartesian coordinates as [1]

$$\begin{aligned} \widetilde{\sigma}_{xx} &= \frac{\widetilde{\sigma}_{rr}+\widetilde{\sigma}_{\theta \theta}}{2} + \frac{\widetilde{\sigma}_{rr}-\widetilde{\sigma}_{\theta \theta}}{2} \cos (2\theta ) - \widetilde{\sigma}_{r\theta}\sin (2\theta ), \end{aligned}$$

(43a)

$$\begin{aligned} \widetilde{\sigma}_{yy} &= \frac{\widetilde{\sigma}_{rr}+\widetilde{\sigma}_{\theta \theta}}{2} - \frac{\widetilde{\sigma}_{rr}-\widetilde{\sigma}_{\theta \theta}}{2} \cos (2\theta ) + \widetilde{\sigma}_{r\theta}\sin (2\theta ), \end{aligned}$$

(43b)

$$\begin{aligned} \widetilde{\sigma}_{xy} &= \widetilde{\sigma}_{r\theta}\cos (2\theta ) + \frac{\widetilde{\sigma}_{rr}-\widetilde{\sigma}_{\theta \theta}}{2} \sin (2\theta ). \end{aligned}$$

(43c)

Substituting Eqs. (22a)–(22e) into Eqs. (43a)–(43c), we can obtain

$$\begin{aligned} \widetilde{\sigma}_{xx} &= 1 -\left ( \frac{2\cos ^{3}\theta _{1}}{r_{1}} + \frac{2\cos ^{3}\theta _{2}}{r_{2}}\right ), \end{aligned}$$

(44a)

$$\begin{aligned} \widetilde{\sigma}_{yy} &= 1 - \left ( \frac{2\cos \theta _{1} \sin ^{2}\theta _{1}}{r_{1}} + \frac{2\cos \theta _{2} \sin ^{2}\theta _{2}}{r_{2}}\right ), \end{aligned}$$

(44b)

$$\begin{aligned} \widetilde{\sigma}_{xy} &= \frac{2\cos ^{2}\theta _{1} \sin \theta _{1}}{r_{1}} - \frac{2\cos ^{2}\theta _{2} \sin \theta _{2}}{r_{2}}, \end{aligned}$$

(44c)

respectively [1]. This shows that $\widetilde{\sigma}_{yy}$ becomes constant ($\widetilde{\sigma}_{yy}=1$) along the line parallel to the loading ($\theta _{1}=\theta _{2}=0$).

Appendix C: Derivation of the Speed of the Rayleigh Wave

In this Appendix, we derive the speed of the Rayleigh wave. The Rayleigh waves are produced by P- and S-waves, and propagate over the surface of the disk. Let $c$ be the speed of the Rayleigh wave. Now, it is convenient to have the origin on the surface of the disc, that is,

$$ r^{\prime }\equiv r-a, $$

(45)

and use the coordinate system $(r^{\prime}, \theta )$. Then, we assume that both the scalar and vector potentials are described by

$$\begin{aligned} \phi &= \mathcal{A}_{\mathrm{L}}(r^{\prime}) \exp \left [i\omega \left (t-\frac{a\theta}{c}\right )\right ], \end{aligned}$$

(46a)

$$\begin{aligned} A &= \mathcal{A}_{\mathrm{T}}(r^{\prime}) \exp \left [i\omega \left (t- \frac{a\theta}{c}\right )\right ], \end{aligned}$$

(46b)

respectively. Substituting Eq. (46a) into the wave equation, the amplitude $\mathcal{A}_{\mathrm{L}}$ should satisfy

$$\begin{aligned} \frac{\partial ^{2} \mathcal{A}_{\mathrm{L}}(r^{\prime})}{\partial r^{\prime 2}} +\frac{1}{a} \frac{\partial \mathcal{A}_{\mathrm{L}}(r^{\prime})}{\partial r^{\prime}} -\mathcal{A}_{\mathrm{L}}(r^{\prime}) \frac{\omega ^{2}}{c^{2} c_{\mathrm{L}}^{2}}(c_{\mathrm{L}}^{2}-c^{2}) = 0. \end{aligned}$$

(47)

We should choose a solution, which does not diverge for $r\ll 0$. After this choice, the scalar potential is written as

$$ \phi = C_{1} \exp \left [\frac{r^{\prime}}{2a}\left (\sqrt{1+4a^{2} \frac{\omega ^{2}}{c^{2} c_{\mathrm{L}}^{2}}(c_{\mathrm{L}}^{2}-c^{2})}-1 \right )\right ]\exp (i\omega t)\exp \left (- \frac{i\omega a\theta}{c}\right ). $$

(48)

Similarly, the vector potential is given by

$$ A = C_{2} \exp \left [\frac{r^{\prime}}{2a}\left (\sqrt{1+4a^{2} \frac{\omega ^{2}}{c^{2} c_{\mathrm{T}}^{2}}(c_{\mathrm{T}}^{2}-c^{2})}-1 \right )\right ]\exp (i\omega t)\exp \left (- \frac{i\omega a\theta}{c}\right ), $$

(49)

where $C_{1}$ and $C_{2}$ are constants. If the second terms in the root of Eqs. (46a) and (49) is much smaller than unity, we can rewrite them as

$$\begin{aligned} \phi &= C_{1} \exp \left [r^{\prime }a\left (\frac{\omega}{c}\right )^{2} \left (1-\frac{c^{2}}{c_{\mathrm{L}}^{2}}\right )\right ]\exp (i \omega t)\exp \left (-\frac{i\omega a\theta}{c}\right ), \end{aligned}$$

(50a)

$$\begin{aligned} A &= C_{2} \exp \left [r^{\prime }a\left (\frac{\omega}{c}\right )^{2} \left (1-\frac{c^{2}}{c_{\mathrm{T}}^{2}}\right )\right ]\exp (i \omega t)\exp \left (-\frac{i\omega a\theta}{c}\right ). \end{aligned}$$

(50b)

This solution needs to satisfy the boundary condition (1a)–(1b). After some calculations, the quantity $X\equiv c^{2}/c_{\mathrm{T}}^{2}$ should satisfy the following equation:

$$ X\left (X^{3} - 8X^{2} + 8(2+\nu )X-8(1+\nu ) \right )=0. $$

(51)

This is nothing but Eq. (35) in the main text.