Abstract
In this paper we derive the linear elastic Cosserat shell model incorporating in the variational problem effects up to order \(O(h^{5})\) in the shell thickness \(h\) as a particular case of the recently introduced geometrically nonlinear elastic Cosserat shell model. The existence and uniqueness of the solution is proven in suitable admissible sets. To this end, inequalities of Korn-type for shells are established which allow to show coercivity in the Lax-Milgram theorem. We are also showing an existence and uniqueness result for a truncated \(O(h^{3})\) model. Main issue is the suitable treatment of the curved reference configuration of the shell. Some connections to the classical Koiter membrane-bending model are highlighted.
Similar content being viewed by others
Notes
These conditions are equivalent to \(\mu >0\) and \(2\,\lambda +\mu > 0\).
Here, we have used that, since
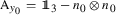 , for all \(X\in \mathbb{R}^{3\times 3}\) it holds \(\lVert X^{\perp}\rVert ^{2}=\lVert X^{T}\,n_{0}\rVert ^{2} \).
, for all \(X\in \mathbb{R}^{3\times 3}\) it holds \(\lVert X^{\perp}\rVert ^{2}=\lVert X^{T}\,n_{0}\rVert ^{2} \).
References
Acharya, A.: A nonlinear generalization of the Koiter–Sanders–Budiansky bending strain measure. Int. J. Solids Struct. 37(39), 5517–5528 (2000)
Adams, R.A.: Sobolev Spaces, 1. edn. Pure and Applied Mathematics, vol. 65. Academic Press, London (1975)
Aganović, I., Tambača, J., Tutek, Z.: Derivation and justification of the model of micropolar elastic shells from three-dimensional linearized micropolar elasticity. Asymptot. Anal. 51, 335–361 (2007)
Altenbach, H., Zhilin, P.A.: A general theory of elastic simple shells. Usp. Mekh. 11, 107–148 (1988) (in Russian)
Altenbach, H., Zhilin, P.A.: The theory of simple elastic shells. In: Kienzler, R., Altenbach, H., Ott, I. (eds.) Theories of Plates and Shells. Critical Review and New Applications. Euromech Colloquium, vol. 444, pp. 1–12. Springer, Heidelberg (2004)
Altenbach, J., Altenbach, H., Eremeyev, V.A.: On generalized Cosserat-type theories of plates and shells: a short review and bibliography. Arch. Appl. Mech. 80, 73–92 (2010)
Anicic, S., Léger, A.: Formulation bidimensionnelle exacte du modèle de coque 3D de Kirchhoff-Love. C. R. Acad. Sci. Paris, Ser. I Math. 329(8), 741–746 (1999)
Bîrsan, M.: On Saint-Venant’s principle in the theory of Cosserat elastic shells. Int. J. Eng. Sci. 45, 187–198 (2007)
Bîrsan, M.: Inequalities of Korn’s type and existence results in the theory of Cosserat elastic shells. J. Elast. 90, 227–239 (2008)
Bîrsan, M.: Thermal stresses in cylindrical Cosserat elastic shells. Eur. J. Mech. A, Solids 28, 94–101 (2009)
Bîrsan, M.: Alternative derivation of the higher-order constitutive model for six-parameter elastic shells. Z. Angew. Math. Phys. 72, 1–29 (2021)
Bîrsan, M., Altenbach, H.: A mathematical study of the linear theory for orthotropic elastic simple shells. Math. Methods Appl. Sci. 33, 1399–1413 (2010)
Bîrsan, M., Altenbach, H.: On the dynamical theory of thermoelastic simple shells. Z. Angew. Math. Mech. 91, 443–457 (2011)
Bîrsan, M., Neff, P.: Existence of minimizers in the geometrically non-linear 6-parameter resultant shell theory with drilling rotations. Math. Mech. Solids 19(4), 376–397 (2014)
Bîrsan, M., Neff, P.: Shells without drilling rotations: a representation theorem in the framework of the geometrically nonlinear 6-parameter resultant shell theory. Int. J. Eng. Sci. 80, 32–42 (2014)
Blouza, A., Le Dret, H.: Existence and uniqueness for the linear Koiter model for shells with little regularity. Q. Appl. Math. 57(2), 317–337 (1999)
Chróścielewski, J., Makowski, J., Pietraszkiewicz, W.: Statics and Dynamics of Multifold Shells: Nonlinear Theory and Finite Element Method. Wydawnictwo IPPT PAN, Warsaw (2004) (in Polish)
Chróścielewski, J., Pietraszkiewicz, W., Witkowski, W.: On shear correction factors in the non-linear theory of elastic shells. Int. J. Solids Struct. 47, 3537–3545 (2010)
Ciarlet, Ph.G.: Introduction to Linear Shell Theory, 1st edn. Series in Applied Mathematics. Gauthier-Villars, Paris (1998)
Ciarlet, Ph.G.: Mathematical Elasticity, Vol. III: Theory of Shells, 1st edn. North-Holland, Amsterdam (2000)
Ciarlet, Ph.G.: An Introduction to Differential Geometry with Applications to Elasticity. Springer, Berlin (2005)
Ciarlet, Ph.G.: An introduction to differential geometry with applications to elasticity. J. Elast. 78(1–3), 1–215 (2005)
Cosserat, E., Cosserat, F.: Sur la théorie des corps minces. C. R. Acad. Sci. 146, 169–172 (1908)
Cosserat, E., Cosserat, F.: Théorie des corps déformables. Hermann et Fils, Paris (1909) (reprint 2009)
Davini, C.: Existence of weak solutions in linear elastostatics of Cosserat surfaces. Meccanica 10, 225–231 (1975)
Eremeyev, V.A., Lebedev, L.P.: Existence theorems in the linear theory of micropolar shells. Z. Angew. Math. Mech. 91, 468–476 (2011)
Eremeyev, V.A., Pietraszkiewicz, W.: Local symmetry group in the general theory of elastic shells. J. Elast. 85, 125–152 (2006)
Ghiba, I.D., Neff, P.: Linear constrained Cosserat-shell models including terms up to \({O}(h^{5}) \). Conditional and unconditional existence and uniqueness (2022). arXiv preprint. arXiv:2211.12074
Ghiba, I.D., Bîrsan, M., Lewintan, P., Neff, P.: The isotropic Cosserat shell model including terms up to \({O}(h^{5})\). Part I: derivation in matrix notation. J. Elast. 142, 201–262 (2020)
Ghiba, I.D., Bîrsan, M., Lewintan, P., Neff, P.: The isotropic elastic Cosserat shell model including terms up to order \(O(h^{5})\) in the shell thickness. Part II: existence of minimizers. J. Elast. 142, 263–290 (2020)
Ghiba, I.D., Bîrsan, M., Lewintan, P., Neff, P.: A constrained Cosserat-shell model including terms up to \({O}(h^{5})\). J. Elast. 146(1), 83–141 (2021)
Ghiba, I.D., Lewintan, P., Neff, P.: On the deformation measures in shell models (2022). In preparation
Girault, V., Raviart, P.A.: Finite Element Approximation of the Navier-Stokes Equations Lect. Notes Math., vol. 749. Springer, Heidelberg (1979)
Green, A.E., Naghdi, P.M.: Shells in the light of generalized Cosserat continua. In: Niordson, F.I. (ed.) Theory of Thin Shells, IUTAM Symposium Copenhagen 1967, pp. 39–58. Springer, Heidelberg (1969)
Leis, R.: Initial Boundary Value Problems in Mathematical Physics. Teubner, Stuttgart (1986)
Libai, A., Simmonds, J.G.: The Nonlinear Theory of Elastic Shells, 2nd edn. Cambridge University Press, Cambridge (1998)
Naghdi, P.M.: The theory of shells and plates. In: Flügge, S. (ed.) Handbuch der Physik, Mechanics of Solids, vol. VI a/2, pp. 425–640. Springer, Berlin (1972)
Naghdi, P.M., Rubin, M.B.: Restrictions on nonlinear constitutive equations for elastic shells. J. Elast. 39, 133–163 (1995)
Neff, P.: A geometrically exact Cosserat-shell model including size effects, avoiding degeneracy in the thin shell limit. Part I: formal dimensional reduction for elastic plates and existence of minimizers for positive Cosserat couple modulus. Contin. Mech. Thermodyn. 16, 577–628 (2004)
Neff, P., Chelminski, K.: A geometrically exact Cosserat shell-model for defective elastic crystals. Justification via \(\Gamma \)-convergence. Interfaces Free Bound. 9, 455–492 (2007)
Pietraszkiewicz, W.: Consistent second approximation to the elastic strain energy of a shell. Z. Angew. Math. Mech. 59, 206–208 (1979)
Pietraszkiewicz, W.: Finite Rotations and Langrangian Description in the Non-linear Theory of Shells. Polish Sci. Publ., Warsaw-Poznań (1979)
Pietraszkiewicz, W.: Refined resultant thermomechanics of shells. Int. J. Eng. Sci. 49, 1112–1124 (2011)
Pietraszkiewicz, W., Eremeyev, V.A.: On natural strain measures of the non-linear micropolar continuum. Int. J. Solids Struct. 46, 774–787 (2009)
Pietraszkiewicz, W., Konopińska, V.: Drilling couples and refined constitutive equations in the resultant geometrically non-linear theory of elastic shells. Int. J. Solids Struct. 51, 2133–2143 (2014)
Reissner, E.: The effect of transverse shear deformation on the bending of elastic plates. J. Appl. Mech. 12, A69–A77 (1945)
Rubin, M.B.: Cosserat Theories: Shells, Rods and Points. Kluwer Academic, Dordrecht (2000)
Saem, M.M., Ghiba, I.D., Neff, P.: A geometrically nonlinear Cosserat (micropolar) curvy shell model via Gamma convergence. J. Nonlinear Sci. (2022, in press). arXiv preprint. arXiv:2207.08541
Šilhavỳ, M.: A new approach to curvature measures in linear shell theories. Math. Mech. Solids 26(9), 1241–1263 (2021)
Steigmann, D.J.: Extension of Koiter’s linear shell theory to materials exhibiting arbitrary symmetry. Int. J. Eng. Sci. 51, 216–232 (2012)
Steigmann, D.J.: Koiter’s shell theory from the perspective of three-dimensional nonlinear elasticity. J. Elast. 111, 91–107 (2013)
Tambača, J.: A new linear shell model for shells with little regularity. J. Elast. 117, 163–188 (2014)
Tambaća, J., Tutek, Z.: A new linear Naghdi type shell model for shells with little regularity. Appl. Math. Model. 40, 10549–10562 (2016)
Zhilin, P.A.: Mechanics of deformable directed surfaces. Int. J. Solids Struct. 12, 635–648 (1976)
Zhilin, P.A.: Applied Mechanics – Foundations of Shell Theory. State Polytechnical University Publisher, Sankt Petersburg (2006) (in Russian)
Acknowledgements
This research has been funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project no. 415894848: NE 902/8-1 (P. Neff) and BI 1965/2-1 (M. Bîrsan). No funding source is specified for the other author.
Author information
Authors and Affiliations
Contributions
All authors had an equal contribution in determining the results and in writing the article.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: The Classical Linear (First) Koiter Membrane-Bending Model
Appendix A: The Classical Linear (First) Koiter Membrane-Bending Model
According to [20, page 344], [22, page 154, ] in the linear (first) Koiter model, the variational problem is to find a midsurface displacement vector field \(v:\omega \subset \mathbb{R}^{2}\to \mathbb{R}^{3}\) minimizing:
where \((\mathcal{G}_{\mathrm{{Koiter}}}^{\mathrm{{lin}}})^{\flat }\) and \(\big(\mathcal{R}_{\mathrm{{Koiter}}}^{\mathrm{{lin}}}\big)^{\flat}\) are the lifted quantities of the strain measures [20] given by
and
The expression of \(\mathcal{R}_{\mathrm{{Koiter}}}^{\mathrm{{lin}}}\) involves the Christoffel symbols \(\Gamma ^{\gamma}_{\alpha \beta} \) on the surface given by \(\Gamma ^{\gamma}_{\alpha \beta}=\bigl\langle a^{\gamma}, \partial _{x_{ \alpha}} a_{\beta}\bigr\rangle =-\bigl\langle \partial _{x_{\alpha}} a^{ \gamma}, a_{\beta}\bigr\rangle =\Gamma ^{\gamma}_{\beta \alpha} \). Note that, using \(m=y_{0}+v\) and \((\nabla m)^{T}\nabla m=(\nabla y_{0})^{T}\nabla y_{0}+(\nabla y_{0})^{T} \nabla v+(\nabla v)^{T}\nabla y_{0}+\text{h.o.t}\in \mathbb{R}^{2 \times 2} \), the linear approximation of the difference \(\frac{1}{2}\big[{\mathrm{I}}_{m} - {\mathrm{I}}_{y_{0}}\big]^{\mathrm{{lin}}}\) appearing in the Koiter model can easily be obtained [20, page 92], the linear approximation of the difference \(\big[{\mathrm{II}}_{m} - {\mathrm{II}}_{y_{0}}\big]^{\mathrm{{lin}}}\) needs some more insights from differential geometry [20, page 95] and it is based on formulas of Gauß \(\partial _{x_{\alpha}} a_{\beta}= \sum _{\gamma =1,2}\Gamma _{\alpha \beta}^{\gamma }\,a_{\gamma}+b_{ \alpha \beta}a_{3}\) and \(\partial _{x_{\beta}}a^{\alpha }= - \sum _{\gamma =1,2}\Gamma ^{ \alpha}_{\gamma \beta}\,a^{\gamma }+ b^{\alpha}_{\beta}\, n_{0} \) and the formulas of Weingarten \(\partial _{x_{\alpha}} a_{3}=\partial _{x_{\alpha}} a^{3}= -\sum _{ \beta =1,2}b_{\alpha \beta}\, a^{\beta}=-\sum _{\beta =1,2} b^{\gamma}_{ \beta}\, a_{\gamma}\) together with the relations [20, page 76] \(b_{\alpha \beta}(m)=-\bigl\langle \partial _{\alpha }a_{3}(m), a_{ \beta}(m)\bigr\rangle =\bigl\langle \partial _{\alpha }a_{\beta}(m), a_{3}(m) \bigr\rangle =b_{\beta \alpha}(m) \), where \(b_{\alpha \beta}(m)\) are the components of the second fundamental form corresponding to the map \(m\), \(b_{\alpha}^{\beta}(m)\) are the components of the matrix associated to the Weingarten map (shape operator), and on the following linear approximation \(n=\,n_{0}+\frac{1}{\sqrt{\det ((\nabla y_{0})^{T}\nabla y_{0})}} \left (\partial _{x_{1}} y_{0}\times \partial _{x_{2}} v+\partial _{x_{1}} v\times \partial _{x_{2}} y_{0}+\text{h.o.t}\right ) -{\mathrm {tr}}(((\nabla y_{0})^{T} \nabla y_{0})^{-1}\, {\mathrm {sym}}((\nabla y_{0})^{T}\nabla v) )\,n_{0} \).
We note that other alternative forms of the change of metric tensor and the change of curvature tensor in [20, Page 181] are
and
respectively. Actually, on one hand, the last form of the curvature tensor will be considered when the admissible set of solutions of the variational problem will be defined. On the other hand, as noticed in [21, Page 175] by considering the form (A.3) of the change of metric tensor, we can impose substantially weaker regularity assumptions on the mapping \(y_{0}\). For the linear (first) Koiter model the existence results are given in [20, Theorem 7.1.-1 and Theorem 7.1.-2], see also [16].
While the relation between \(\mathcal{G}^{\mathrm{{lin}}}\) and \(\mathcal{G}_{\mathrm{{Koiter}}}^{\mathrm{{lin}}} \) holds in the general case, we are able to find a simple explicit relation between \(\mathcal{R}^{\mathrm{{lin}}}\) and \(\mathcal{R}_{\mathrm{{Koiter}}}^{\mathrm{{lin}}} \) only in the case of the constrained Cosserat-shell model. This is not surprising, since only symmetric stress tensors are taken into account in the classical linear Koiter model, i.e., the internal strain energy does not depend on the skew-symmetric part of the considered strain measures (since it is work conjugate to the skew-symmetric part of the stress tensor). In addition, the linear Koiter model does not consider extra degrees of freedom. In [32] we will discuss the choice of the deformation measures in shell models. We will see that the classical strain measure \(\mathcal{R}_{\mathrm{{Koiter}}}^{\mathrm{{lin}}} \) (the classical bending strain measure, also known as the change of curvature tensor) does not represent the unique choice and that some other modified expressions of the classical bending tensor may be more suitable in the modelling of a shell.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Ghiba, ID., Bîrsan, M. & Neff, P. A Linear Isotropic Cosserat Shell Model Including Terms up to \(O(h^{5})\). Existence and Uniqueness. J Elast 154, 579–605 (2023). https://doi.org/10.1007/s10659-022-09981-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-022-09981-6
Keywords
- Cosserat shell
- Micropolar shell
- 6-parameter resultant shell
- In-plane drill rotations
- Isotropy
- Existence of minimisers
- Linear theories




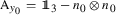 , for all
, for all