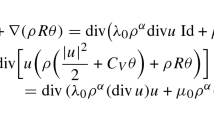On the Construction and Properties of Weak Solutions Describing Dynamic Cavitation

Abstract

We consider the problem of dynamic cavity formation in isotropic compressible nonlinear elastic media. For the equations of radial elasticity we construct self-similar weak solutions that describe a cavity emanating from a state of uniform deformation. For dimensions d=2,3 we show that cavity formation is necessarily associated with a unique precursor shock. We also study the bifurcation diagram and do a detailed analysis of the singular asymptotics associated to cavity initiation as a function of the cavity speed of the self-similar profiles. We show that for stress free cavities the critical stretching associated with dynamically cavitating solutions coincides with the critical stretching in the bifurcation diagram of equilibrium elasticity. Our analysis treats both stress-free cavities and cavities with contents.

Appendix

1.1 7.1 Gradients of Radial Functions

Consider a radial function $y:\mathbb{R}^{d} \to\mathbb{R}^{d}$ of the form

$$ y(x) = w(R) \frac{x}{R}, \quad R := |x| \mbox{ with } w(R):(0,\infty) \to\mathbb{R}. $$

(7.1)

Theorem 7.1

(J. Ball [2])

Let d>1, let 1≤p<∞ and y be given by (7.1). Then:

• (i) $y \in L^{p}_{loc}(\mathbb{R}^{d})$ if and only if

  $$ \int^{\rho}_0 R^{d-1} \bigl|w(R)\bigr|^p dR < \infty\quad\textit{for all } \rho\in(0,\infty). $$

• (ii) $y \in W^{1,p}_{loc}(\mathbb{R}^{d})$ if and only if w(R) is absolutely continuous on (0,∞) and

  $$ \int^{\rho}_0 R^{d-1} \biggl( |w_R|^p + \biggl| \frac{w}{R} \biggr|^p \biggr) dR < \infty\quad\textit{for all } \rho\in(0,\infty). $$

  (7.2)

• (iii) If (7.2) holds for (say) ρ=1 then

  $$ \bigl| w(R) \bigr|^p R^{d-p} \to0 \quad\textit{as } R \to0. $$

  (7.3)

• (iv) If $y \in W^{1,1}_{loc}(\mathbb{R}^{d})$ then

  $$ \nabla y(x) = w_R \frac{x \otimes x}{R^2} + \frac{w}{R} \biggl( {\mathbf{I}} - \frac{x \otimes x}{R^2} \biggr) \quad\textit{in } \mathcal{D}'\bigl(\mathbb{R}^d\bigr) \textit{ and a.e. } x\in \mathbb{R}^d. $$

  (7.4)

For the proofs of (i), (ii) and (iv) we refer to [2].

The proof of (iii) for p=1 goes as follows: Using the identity

$$ w(R) R^{d-2} = w(\rho) \rho^{d-2} + \int_\rho^R \biggl( w_s (s) s^{d-2} + (d-2) \frac{w(s) }{s} s^{d-2} \biggr) ds , \quad\mbox{ for } 0 < \rho< R, $$

we integrate over (0,R) and use Fubini to obtain

$$ w(R) R^{d-1} = \int_0^R \biggl( w_\rho+ (d-1) \frac{w}{\rho} \biggr) \rho^{d-1} d\rho. $$

(7.5)

This identity holds for smooth functions; then using a density argument one establishes the identity for functions $w \in W^{1,1}_{loc} (\mathbb{R}^{d})$.

For p=1, since the integral in (7.2) is finite, we have

$$ F(R) := \int_0^R \biggl( w_\rho+ (d-1) \frac{w}{\rho} \biggr) d\rho\to0 \quad \mbox{as } R \to0 $$

(in fact the function F(R) is absolutely continuous as function of R). Hence (iii) follows from (7.5) for p=1. The case p>1 is done by a similar argument.

In order to compute the distributional derivative of ∇y in (iv), one may follow the usual process of deleting a ball of small radius ε>0 around the origin, using the formula of integration by parts and passing to the limit ε→0. Then, the contribution from the surface of the ball will vanish precisely because of (7.3) and thus no delta mass appears in the formula (7.4) for dimensions d≥2.

1.2 7.2 Stored Energies

We collect here certain properties of the stored energies that are used throughout this study. As already mentioned, frame indifference and isotropy are equivalent to expressing the stored energy as

$$ W(F) = \varPhi(v_1,v_2,\dots,v_d), $$

where $\varPhi:\mathbb{R}^{d}_{++} \to\mathbb{R}$ is a symmetric function of its arguments and v ₁,…,v _d are the eigenvalues of the positive square root $(F^{\top}F)^{\frac{1}{2}}$, the so called principal stretches [1, 22].

The stored energy W(F) is said to be rank-1 convex if

$$ W\bigl(\tau F+(1-\tau)G \bigr) \leq\tau W(F) + (1-\tau) W(G), $$

(7.6)

for 0<τ<1 and for $F, G \in M^{d\times d}_{+}$ such that F−G=ξ⊗ν for some nonzero $\xi, \nu\in\mathbb{R}^{d}$. If the inequality in (7.6) is strict, then W is called strictly rank-1 convex.

It is easy to check that for $W\in C^{2}(M^{d\times d}_{+})$ rank-1 convexity is equivalent to the Legendre-Hadamard condition, that is

$$ \frac{\partial ^2 W(F)}{\partial F_{i\alpha}\partial {F_{j\beta }}} \xi^i \nu_{\alpha} \xi^j \nu_{\beta} \geq0 , \quad \forall F \in M^{d\times d}_+ \mbox{ and } \forall \xi, \nu\in\mathbb{R}^d - \{0\}. $$

For isotropic rank-1 convex functions, the stored energy Φ must satisfy certain monotonicity properties:

Proposition 7.2

(J. Ball [2])

Let $W\in C^{1}(M^{d\times d}_{+})$ be strictly rank-1 convex and isotropic. Then:

• (i) $\frac{\partial \varPhi}{\partial v_{i}}(v_{1},\dots ,v_{d})$ is a strictly increasing function of v _i when v _j , j≠i are kept fixed. If in addition $W\in C^{2}(M^{d\times d}_{+})$ then $\frac{\partial ^{2} \varPhi}{\partial v_{i}^{2}}(v_{1},\dots,v_{d})>0$.

• (ii) The Baker-Ericksen inequalities hold, that is

  $$ \biggl[\frac{v_i \frac{\partial \varPhi }{\partial v_i} - v_j \frac{\partial \varPhi}{\partial v_j}}{v_i - v_j} \biggr] > 0 \quad\textit{for } i \neq j, \ v_i \neq v_j . $$

  (7.7)

Throughout this study we work with stored energies of the special form

$$ \begin{aligned} &\varPhi(v_1, v_2, \ldots, v_d) = \sum_{i =1}^d g(v_i) + h (v_1 v_2 \dots v_d), \end{aligned} $$

(H0)

where the functions g(x)∈C ³[0,∞) and h(x)∈C ³(0,∞). One easily computes their derivatives,

$$\begin{aligned} \varPhi_{11} &= g''(v_1) + (v_2 \ldots v_d)^2 h''(v), \\ \varPhi_{12} &= (v_3 \ldots v_d) h'(v) + v_1 v_2 (v_3 \ldots v_d)^2 h''(v), \\ P = \varPhi_{12} + \frac{\varPhi_1 - \varPhi_2}{v_1 - v_2} &= \frac { g' (v_1) - g' (v_2)}{ v_1 - v_2} + (v_3 \ldots v_d) v h'' (v), \\ \varPhi_{111} &= g''' (v_1) + (v_2 \ldots v_d)^3 h''' (v), \\ \varPhi_{112} &= v_2 (v_3 \ldots v_d)^2 \bigl[ 2 h''(v) + v h''' (v) \bigr] , \end{aligned}$$

where v=v ₁ v ₂...v _d .

Due to the form of the principal stretches for radial motions (see (7.4)), in the problem of cavitation it is often needed to work for (v ₁,…,v _d ) taking values of the form (a,b,…,b) or on the diagonal (b,b,…,b). The symmetry of Φ entails certain properties on the diagonals:

$$\begin{aligned} \frac{\partial \varPhi}{\partial v_i} (a, b, \ldots, b) &= \frac{\partial \varPhi}{\partial v_j} (a, b, \ldots, b) \quad\mbox{for } i , j =2 , \ldots, d,\ i \ne j,\ \forall a, b > 0, \end{aligned}$$

(7.8)

$$\begin{aligned} \frac{\partial \varPhi}{\partial v_1} (b, b, \ldots, b) &= \frac{\partial \varPhi}{\partial v_j} (b, b, \ldots, b) \quad\mbox{for } j \ne1,\ \forall b > 0. \end{aligned}$$

(7.9)

When working with stored energies computed along the sets (a,b,…,b) we will often use the short hand notation

$$ \begin{aligned} \varPhi_1 (a, b) &\equiv \frac{\partial \varPhi}{\partial v_1} (a, b, \ldots, b) , \qquad \varPhi_2 (a, b) \equiv \frac{\partial \varPhi}{\partial v_j} (a, b, \ldots, b) , \quad j = 2, \ldots, d, \\ \varPhi_{11} (a, b) &\equiv\frac{\partial ^2 \varPhi}{\partial v_1^2} (a, b, \ldots, b) , \qquad\varPhi_{12} (a, b) \equiv\frac{\partial ^2 \varPhi }{\partial v_1 \partial v_j } (a, b, \ldots, b) , \quad j = 2, \ldots, d, \end{aligned} $$

(7.10)

and so on.

The quantity

$$ P(a,b) := \begin{cases} \varPhi_{12}( a,b, \ldots, b) + \frac{(\varPhi_1 - \varPhi_2)(a,b, \ldots, b)}{a-b}, & a<b, \\ \varPhi_{11}(b,b,\dots,b), & a=b, \end{cases} $$

appears in the defining differential equation (3.3). Using (7.10) one checks that

$$ \lim_{\substack{a\to\lambda- \\ b\to\lambda+}} P(a,b) = \lim_{\substack{a\to\lambda- \\ b\to\lambda+}} \varPhi_{11}(a,b,\dots,b)= \varPhi_{11}(\lambda,\dots, \lambda) $$

(7.11)

and thus P(a,b) is continuous up to the diagonal on the set {(a,b):0<a≤b}. Furthermore, using (7.8), (7.9) and Taylor expansions around the diagonal we easily see that

$$ \lim_{\substack{a\to\lambda- \\ b\to\lambda+}} \frac{P(a,b)-\varPhi_{11}(a,b)}{a-b} = \frac{1}{2} \bigl( \varPhi_{112}(\lambda,\lambda) - \varPhi_{111}(\lambda,\lambda) \bigr). $$

(7.12)

We list some formulas based on (H0) that are used in the text:

$$\begin{aligned} \varPhi_{11}(a,b) &= g''(a) + b^{2d-2} h''\bigl(ab^{d-1}\bigr), \\ \varPhi_{12}(a,b) &= b^{d-2} h' \bigl(ab^{d-1}\bigr) + a b^{2d-3} h'' \bigl(ab^{d-1}\bigr), \\ P(a,b) = \varPhi_{12} + \frac{\varPhi_1 - \varPhi_2}{a-b} &= \frac { g' (a) - g' (b)}{ a - b} + ab^{2d-3} h'' \bigl(ab^{d-1}\bigr), \\ Q(a,b,s) = s^2 - \varPhi_{11} & = s^2 - \bigl[ g''(a) + b^{2d-2}h'' \bigl(ab^{d-1}\bigr) \bigr], \\ \varPhi_{111}(a,b) &= g''' (a) + b^{3d-3} h''' \bigl(ab^{d-1}\bigr), \\ \varPhi_{112}(a,b) & = b^{2d-3} \bigl[ 2 h'' \bigl(ab^{d-1}\bigr) + ab^{d-1} h''' \bigl(ab^{d-1}\bigr) \bigr], \\ R(a,b,s)&= \begin{cases} \frac{\varPhi_{1}(a,b)- \varPhi_{1}(b,b)}{a-b} - s^2, &a<b, \\ \varPhi_{11}(b,b)-s^2, &a=b, \\ \end{cases} \\ &= \begin{cases} (\frac{g'(a)-g'(b)}{a-b} ) + b^{2d-2} (\frac {h'(ab^{d-1})-h'(b^d)}{ab^{d-1}-b^d} ) - s^2, &a<b, \\ g''(b)+b^{2d-2}h''(b^d)-s^2, &a=b. \\ \end{cases} \end{aligned}$$

List of Hypotheses

For the reader’s convenience, we collect the hypotheses used in the analysis of the dynamic bifurcation problem:

$$\begin{aligned} &\varPhi(v_1, v_2, \ldots, v_d) = \sum _{i =1}^d g(v_i) + h (v_1 v_2 \dots v_d) ,\quad g\in C^3[0,\infty), h \in C^3(0,\infty), \end{aligned}$$

(H0)

$$\begin{aligned} & g''(x) > 0, \qquad h''(x) > 0 , \qquad\lim_{x \to0 } h(x) = \lim_{x \to\infty} h(x) = +\infty, \end{aligned}$$

(H1)

$$\begin{aligned} &g'''(x) \leq0, \qquad h'''(x) < 0, \end{aligned}$$

(H2)

$$\begin{aligned} &\lim_{x\to\infty} \biggl(\frac{g'(x)}{x^{d-2}} \biggr) = \gamma \geq0, \end{aligned}$$

(H3)

$$\begin{aligned} &h'(x) \to-\infty\quad \mbox{as } x \to0_+ , \qquad h'(x) \to+\infty\quad \mbox{as } x \to+\infty, \end{aligned}$$

(H4)

$$\begin{aligned} &\varPhi_{11} (x, x) = g''(x) + x^{2d -2} h''\bigl( x^d \bigr) \ge \nu^2 > 0 . \end{aligned}$$

(H5)

(H0)–(H3) and (H4)₂ play a role in the existence of a weak solution with cavity, while, in addition to them, (H4)₁ and (H5) are used in the dynamic bifurcation problem. An example of stored energy that satisfies (H0)–(H5) is:

Case d≥3: g(x),h(x) in (H0) are selected by

$$ g(x) = \sum_{k=1}^K a_{k} (x+\varepsilon_k)^{\alpha_k} \quad\mbox{with } 1< \alpha_k \leq2,\ a_k,\varepsilon_k>0, $$

(7.13)

and

$$ h(x) = \sum_{m=1}^M b_{m} x^{\beta_m} + \sum_{n=1}^N c_n x^{-\mu_n} \quad\mbox{with } 1< \beta_m \leq2,\ \mu_n>0,\ b_m,c_n >0. $$

(7.14)

Case d≥2: g(x) is selected by

$$ g(x) = ax + \sum_{k=1}^K \frac{b_k}{(x+\varepsilon_k)^{\alpha_k}}\quad\mbox{with } \alpha_k, \varepsilon_k,b_k>0,\ a \geq0, $$

(7.15)

while h(x) is the same as in (7.14).

We note that ε _k , k=1,…,K, in (7.13) and (7.15), are chosen positive in order to satisfy the requirement that g∈C ³[0,∞). Thus, g″(x) cannot blow up as x→0₊ in view of the requirement that ε _k >0. This restricts the class of stored energies as compared to the class of Ogden materials [11]; see also [2, p. 593]. Also we note that h(x) defined in (7.14) satisfies lim sup _x→∞ h″(x ^d)x ^2d−2>0 for d≥2 and this together with the fact that g″(x)>0, x∈[0,∞), gives (H5).

In Sect. 5.3.2, we also used the hypotheses

$$\begin{aligned} &\frac{d}{dx} \bigl(h'\bigl(x^d \bigr)+g'(x)x^{1-d} \bigr)>0, \qquad\limsup _{x \to0_+} \bigl(h'(x)x\bigr) < 0, \end{aligned}$$

(H6)

$$\begin{aligned} & \bigl(g'(x)x \bigr)' > 0, \end{aligned}$$

(H7)

$$\begin{aligned} & \bigl( g''(x)x \bigr)' \geq0. \end{aligned}$$

(H8)

These play a very limited role, solely in establishing bounds for the critical stretching λ _cr of the equilibrium elasticity critical stretching. Namely, (H6) and (H7) are used for obtaining the bound (5.50), while (H8) is used in the derivation of the lower bound (5.51). For stored energies of class (H0), (H7) expresses the Baker-Ericksen inequality (7.7).

1.3 7.3 Numerical Computations

We now briefly discuss the numerical computation used to plot the graphs of v(s;φ ₀,H) in Fig. 1 and the bifurcation curves in Fig. 2. To obtain the solution (φ,v)(s;φ ₀,v ₀) of (3.14) we perform numerical computations employing the original (equivalent) system (3.4). As (3.4) has a geometric singularity at the origin, we initiate the solution using an analytical argument to depart from the singularity at s=0, and once we are off the singularity we continue by using a numerical solver. Below is the explanation of the approach used.

If (φ,v)(s;φ ₀,v ₀) solves (3.14) then

$$ (a,b) (s ; \varphi_0,v_0) = \biggl(\dot{\varphi}, \frac{\varphi}{s}\biggr) (s ; \varphi_0,v_0) $$

solves (3.4) and satisfies

$$ \lim_{s\to0_+} s b(s) = \varphi_0, \qquad\lim _{s\to0_+} \bigl(a b^{d-1}\bigr) (s) =v_0. $$

Moreover, in view of (H3),

$$ c_0:=\lim_{s\to0_+} \frac{d}{ds} \biggl( \dot{\varphi} \biggl(\frac{\varphi}{s}\biggr)^{d-1} \biggr) = \lim_{s\to0_+} \dot{v}(s) = \frac{(d-1)\gamma_0}{\varphi_0 h''(v_0)},\quad \gamma_0= \begin{cases} \gamma, & d \geq3, \\ \gamma-g'(0), & d=2. \end{cases} $$

Thus

$$ \frac{d}{ds} \bigl(\varphi^d(s) \bigr) = d \bigl[\dot{\varphi}\varphi^{d-1} \bigr](s)= d \bigl(v_0 s^{d-1} + c_0 s^d + o\bigl(s^d \bigr) \bigr) \quad\mbox{for } s \ll 1 $$

(7.16)

and hence

$$ \varphi(s)=\sqrt[d]{\varphi_0^d+v_0 s^d+ \biggl(\frac{d}{d+1} \biggr)c_0 s^{d+1} + o\bigl(s^d\bigr)} \quad\quad\mbox{for } s \ll 1. $$

(7.17)

Given φ ₀,v ₀>0, we construct the solution (φ,v)(s;φ ₀,v ₀) as follows: We pick a sufficiently small s ₀>0 and select the approximate values at s=s ₀>0 (following (7.16), (7.17)) by

$$ \begin{aligned} \widehat{b}(s_0)&= \frac{1}{s_0}\sqrt[d]{\varphi_0^d+v_0 s_0^d+ \biggl(\frac{d}{d+1} \biggr)c_0 s_0^{d+1}}, \\ \widehat{a}(s_0)&= \bigl(v_0 s^{d-1} + c_0 s^d \bigr) \bigl(s_0 \widehat{b}(s_0) \bigr)^{1-d}. \end{aligned} $$

We use these as initial data at s ₀ and then solve numerically (3.4) (using the standard MATLAB solver ode15) on the interval $[s_{0},\widehat{T})$, where $\widehat{T}$ is the maximal interval of existence of the approximate solution $(\widehat{a},\widehat{b})$. At $s=\widehat{T}$ computations break down due to the singularity Q=0.

We construct the dynamic bifurcation curve in Fig. 2 as follows. For a stored energy Φ with $g(x)=\frac{1}{2}x^{2}$, h(x)=(x−1)ln(x), we fix v ₀=H, where H>0 is the unique number that satisfies h′(H)=0 corresponding to a stress free cavity. Then, we pick φ ₀∈[0.05,2.7] and s ₀>0 and compute the numerical solution

$$ \bigl\{ (\widehat{a}_n,\widehat{b}_n) (s_0,\varphi_0,H)\bigr\} _{n=0}^N , \quad\mbox{on the mesh } s_0<s_1< \cdots<s_N=\widehat{T}, $$

that approximates $(\widehat{a},\widehat{b})(s ; s_{0},\varphi_{0},H)$ as described in the previous paragraph. Finally, we determine the point $s_{n_{*}} \in(s_{0},s_{N}]$ that best fits the condition

$$ s_{n_*} \approx\sqrt{ \frac{\varPhi_1( \widehat{a}_{n_*}, \widehat {b}_{n_*} )- \varPhi_1(\widehat{b}_{n_*}, \widehat{b}_{n_*} )}{\widehat {a}_{n_*}- \widehat{b}_{n_*} } } \approx\sigma\bigl( \varphi_0, V(\varphi_0)\bigr), $$

which corresponds to the Rankine-Hugoniot condition. This in turn provides the approximate value of the stretching

$$ \varLambda(\varphi_0,H) \approx\widehat{b}_{n_*}(s_0, \varphi_0,H) . $$

This procedure is repeated for a sequence of values φ ₀ values in the interval [0.05,2.7] and gives the dynamic bifurcation curve in Fig. 2.

The bifurcation curve for elastostatics (corresponding to the boundary value problem (5.44) in Sect. 5.3.2) is constructed in an analogous fashion. The only difference is that solutions are now computed for the modified system (3.4) (obtained by replacing the term s ²−Φ ₁₁ in (3.4) by the term −Φ ₁₁) on the interval (s ₀,1]. The value $\widehat{b}(1; s_{0},\varphi_{0},H)$ then gives the stretching λ(φ ₀,H) at the boundary of the unit ball. The curve in Fig. 2 is the graph of λ(φ ₀,H) with φ ₀∈[0.05,2.7].