Numerical Implementation of the Equivalent Inclusion Method for 2D Arbitrarily Shaped Inhomogeneities

Abstract

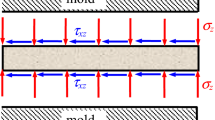
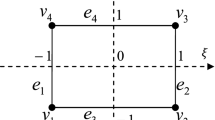
A new numerical method for solving two-dimensional arbitrarily shaped inhomogeneity problems is demonstrated in the present work. Solution is achieved through a discretization consisting of rectangular elements using newly formulated closed-form solutions. An iterative scheme for implementing the numerical equivalent inclusion method, i.e., determining the equivalent eigenstrains, is proposed. Comprehensive benchmarks on numerical convergence with respect to mesh size and iterative number are conducted to demonstrate the performance of the new numerical method. Comparative studies among results are obtained by the proposed iterative scheme, the Gaussian elimination method, and the Hutchinson approximation and show superiority of the iterative scheme. Simulations for material combinations utilizing the Dundurs α–β plane reveal its capability. A double-inhomogeneity model illustrates the ability of the new numerical method to predict the stress concentration factor for closely distributed multiple inhomogeneities.

Appendix: Analytical Solutions of Eigenstrain and Stress Concentration Factors for a Plane Medium

The analytical solution to a plane elliptical inhomogeneity problem has derived by means of the EIM by Jin et al. [10]. The results are summarized here for convenience of reference. The equivalent eigenstrain inside the inclusion domain, i.e., for (x/a)²+(y/b)²<1,

$$ \begin{aligned} \varepsilon_{xy}^{*} &= \frac{(1 + \kappa )(\alpha + \beta )(1 + t)^{2}}{\mu ( - 2t\alpha + 4t\beta + 1 + \alpha + 2t + t^{2} + t^{2}\alpha )} \tau_{xy}^{0}, \\ \left [ \begin{array}{l} \varepsilon_{xx}^{*} \\ \varepsilon_{yy}^{*} \end{array} \right ] &= \frac{1 + \kappa}{4\mu \Delta} \left [ \begin{array}{l@{\quad }l} f_{xx} & f_{xy} \\ f_{yx} & f_{yy} \end{array} \right ]\left [ \begin{array}{l} \sigma_{xx}^{0} \\ \sigma_{yy}^{0} \end{array} \right ], \end{aligned} $$

(27)

where

$$\begin{aligned} f_{xx} &= \alpha (1 + t)^{2}(1 + \alpha ) + 4t\beta (2t + 1) (\beta - \alpha ), \\ f_{xy} &= (1 + t)^{2}(1 + \alpha ) (2\beta - \alpha ) + 4t \beta (\alpha - \beta ), \\ f_{yx} &= (1 + t)^{2}(1 + \alpha ) (2\beta - \alpha ) + 4t \beta (\alpha - \beta ), \\ f_{yy} &= \alpha (1 + t)^{2}(1 + \alpha ) + 4\beta (t + 2) ( \beta - \alpha ),\\ t&=b/a,\qquad \Delta =\bigl(\alpha^2 -1\bigr)(1-t)^2+4t(\beta+1)(2\beta-\alpha-1). \end{aligned}$$

The stress concentration factors are determined by the stresses at the vertices of the ellipse. At (a,0) of the matrix side

$$ \sigma_{y}(a_{ +},0) = \frac{1}{\Delta} \bigl[ k_{ax}\sigma_{x}^{0} + k_{ay} \sigma_{y}^{0} \bigr], $$

(28)

where

$$\begin{aligned} \begin{aligned} k_{ax} &= 2(1 + \alpha ) \bigl[ (3t + 2)\beta - (2t + 1)\alpha \bigr] + 8t\beta (\alpha - \beta ), \\ k_{ay} &= \bigl(\alpha^{2} - 1\bigr) (1 + t)^{2} + (6t + 16)\beta (\beta - \alpha ) + 2\alpha (\alpha + 1) + 2t\beta (\beta + 1). \end{aligned} \end{aligned}$$

At (0,b) of the matrix side

$$ \sigma_{x}(0,b_{ +} ) = \frac{1}{\Delta} \bigl[ k_{bx}\sigma_{x}^{0} + k_{by} \sigma_{y}^{0} \bigr], $$

(29)

where

$$\begin{aligned} \begin{aligned} k_{bx} &= \bigl(\alpha^{2} - 1\bigr) (1 + t)^{2} + (6 + 16t)t\beta (\beta - \alpha ) + 2t^{2}\alpha ( \alpha + 1) + 2t\beta (\beta + 1), \\ k_{by} &= 2t(\alpha + 1) \bigl[ (3 + 2t)\beta - (t + 2)\alpha \bigr] + 8t\beta (\alpha - \beta ). \end{aligned} \end{aligned}$$