1 Introduction

The production of goods often involves environmental damage. Typically, governments adopt environmental policy measures, such as emission limits or emission taxes, to combat the damage.

Firms may react to such measures in two ways: First, they may adjust the extent of production or the way they produce. By producing less or producing in a more environmentally-friendly manner, firms may reduce the environmental impact. Second, firms may respond to environmental policy measures by relocating to countries with less strict environmental policy to avoid environmental regulation.

Relocation of firms may change the local distribution of emissions, and thus, environmental damage. If production results in local pollution, such as air pollution, soil degradation, or noise, the relocation of firms reduces local environmental damage. However, in this case, foreign pollution increases. If production results in global pollution, the damage is independent of the geographical origin of pollution. In this case, relocation changes the extent of damage neither in the home country nor in the foreign country.

The possibility of relocation, in turn, may change the strictness of environmental policy: If relocation of firms results in a welfare loss to their home countries, e.g., due to losses in tax revenue, the threat of relocation might result in relaxed environmental regulation. This applies, in particular, to global pollutants, such as greenhouse gases, because relocation of firms does not change the damage. For local pollutants, relocation has a damage-reducing effect at the original location, but a damage-increasing effect at the new location. Therefore, compared to global pollutants, the threat of relocation in the case of local pollutants provides a weaker incentive to relax the strictness of environmental regulation in the home country. Nevertheless, it may increase the strictness of environmental regulation in a foreign country, as the foreign government may try to reduce pollution or to prevent relocation.

The possibility of relocation creates a transboundary dimension even for local environmental damages and local environmental policy measures. Foreign countries are affected by local environmental policy measures in two ways: They suffer an increase in emissions, but they benefit from the inflow of firm profits, and possibly, tax revenue. These spillovers of national environmental policy result in a coordination problem for governments.

Firms do not necessarily react symmetrically to environmental policy when relocation is possible. A crucial factor for different relocation decisions of firms may be product quality differentiation. A firm that offers a higher product quality typically faces a less elastic demand than a firm that sells products of lower quality. Therefore, the firm with high-quality products is more capable of passing through the cost of environmental regulation and may be less willing to relocate. However, at the same time, a higher profit stemming from higher product quality and less elastic demand may allow a firm to pay the fixed cost of relocation more easily. Many consumer goods, such as television sets, drill machines, or lamps, are provided at different quality levels, focusing on different groups of (potential) consumers.

As the effects of an environmental policy measure may depend on the extent of quality differentiation, and thus, the competitive environment, it may be helpful to see environmental policy measures in the context of the broader institutional setting including market structure and competition policy.

We analyze the effect of environmental policy on relocation decisions in a duopoly with vertical differentiation of product quality. Production involves local environmental damage that is independent of product quality. Thus, the market is characterized by two distortions: imperfect competition and an externality caused by local pollution. We establish the relationship between an exogenous product quality markup, relocation cost, and emission taxation in a two-country-setting for three cases: An environmental tax set only by one country, non-cooperative environmental taxation in both countries, and coordinated environmental taxation. Firm relocation is typically a long-term decision which firms are not inclined to reverse too early. Democratic governments regularly lack the possibility for long-term commitment, e.g., because of limited legislative periods. Therefore, it seems plausible that environmental policy will react to relocation decisions of firms at some point.

We show that the larger the extent of quality differentiation of products, the more likely it is that at least one firm relocates. This is, the higher the product quality markup in the market, the less environmental policy instruments are able to achieve the desired effect. At the same time, product quality differentiation weakens competition and reduces quantities and, thus, emissions. Therefore, from an environmental perspective, weaker competition partly solves the environmental problem and may therefore be regarded as a substitute for environmental policy measures as both reduce emissions. However, relocation does not reduce global damage, as emissions are not reduced, but only shifted abroad.

Since the environmental policy of one country shifts emissions to another country, it seems plausible to assume that also the foreign government takes environmental damages and (re)location decisions of firms into account. Therefore, this paper also considers the environmental policy decisions of a foreign country and analyzes the interaction of two governments. Governments compete for tax revenue and firms’ profits, which has a tax rate-decreasing effect. At the same time, governments avoid environmental damage, which has a tax rate-increasing effect.

Our analysis shows that environmental taxation of the foreign country changes the optimal relocation decisions of both firms compared to unilateral environmental taxation. If both governments set environmental taxes non-cooperatively, there is no Nash equilibrium in which the firm selling the low-quality product relocates to the foreign country. If any firm relocates, it is always the firm that provides high-quality products.

If both governments set tax rates cooperatively, it is more likely that no firm relocates. Also, under cooperative taxation also equilibria exist, in which the firm selling the low-quality product relocates.

When only one firm is located in each country, the optimal emission tax is zero for the country hosting the firm that provides the high-quality product when the product quality markup is sufficiently large. In this case, the distortion from weakened competition outweighs the distortion from the externality. This holds for non-cooperative and cooperative taxation.

There are several examples for our case of local pollutants: Land consumption is an example of a primarily local environmental damage, however, spillovers may arise from habitat loss for migrating species. National environmental policy may create a transboundary spillover effect if a firm relocates, moves its production site abroad, and increases land consumption at the new location. Similar considerations apply to soil protection. Although soil protection may be closely linked to groundwater protection, a significant part of soil protection is purely local. With air pollutants, environmental damage often depends on the local concentration. The longer the distance from the source of emission is, the lower is the concentration of air pollutants and the lower is the damage. Therefore, air pollution can also be considered as a mainly local environmental problem.

These examples of local pollutants are related to basic components in consumer products, such as electrical insulation or metals, such as copper. These components are used in many products and do not differentiate products in the eye of consumers. But the products containing these components are provided at different quality levels. Concerning these components, the environmental characteristics are independent of the quality of the final product. This applies, e.g., for television sets, drill machines, or lamps, which are provided at different quality levels.

Our paper provides a new perspective on the link between competition policy and environmental policy. Since weaker competition may be seen as substitute for environmental policy, competition policy and environmental policy should be coordinated carefully. Strengthening competition may have an adverse effect on the environment. However, weaker competition makes relocation as a response to local environmental policy more likely and thereby results in emission shifting instead of emission reduction.

From a European perspective, our results indicate that even when the environmental damage is primarily local, the possibility of relocation within the single market creates a case for policy coordination. The Industrial Emissions Directive (2010/75/EU) aims at creating a level playing field within the EU, although not all pollutants covered by the directive have a transboundary impact. Soil protection is also included in the Industrial Emissions Directive (2010/75/EU). Our paper offers additional justifications for a European coordination of local environmental policy as it points to the transboundary dimension of local pollution through relocation.

The rest of the paper is organized as follows. In the next section, we provide an overview over the related literature. Section 3 presents the basic model and our main assumptions. In Sect. 4, we analyze the effect of a unilateral environmental tax on relocation decisions for both firms for a time-consistent government. Section 5 considers an alternative timing of the game, showing results for a committed government. Section 6 analyses non-cooperative and coordinated environmental tax setting in both countries. Section 7 discusses several assumptions. Section 8 concludes.

2 Related literature

The paper that is most closely related to our analysis is Ikefuji et al. (2016), who analyze the effect of environmental tax policy and relocation choices in a two country-setting. In their model, two firms offer a homogeneous good. Consumers are located only in one country. The government sets an environmental tax for production emissions. They find that the decreasing relocation cost, i.e., intensified globalization, does not necessarily result in a lower emission tax.

Our paper differs from Ikefuji et al. (2016) in two ways, marking our contribution to the literature. First, we include vertical product differentiation in our analysis, showing that it results in asymmetric incentives for firms to relocate. Also, the welfare consequences of relocation differ, depending on which firm relocates. Second, we also analyze environmental taxation in the foreign country, studying both non-coordinated and coordinated taxation. The foreign government has an incentive to respond to environmental damages. We highlight the role of the competitive environment and analyze cooperation among governments in internalizing the environmental externality versus environmental tax competition.

Ing and Nicolai (2019) study the effect of an emission tax when firms may relocate in a model with heterogeneous firms that produce a homogeneous good and compete under Cournot competition. They show that environmental damage is higher when a dirty firm relocates from a developed country to a developing country. In their paper, firm heterogeneity stems from different production technologies, while goods are perfect substitutes. Our paper complements their model by assuming homogeneous production technology and differentiated goods.

Anand and Giraud-Carrier (2020) analyze the effect of environmental policy in oligopolistic markets, where firms offer differentiated products. They show that environmental regulation is able to reduce pollution and at the same time increase firms’ profits, consumer surplus, and overall welfare. The effect is driven by the possibility of firms to use environmental policy as a device of tacit collusion and reduce production. Our paper also considers quality differentiation and allows for quantity effects, complementing the paper by Anand and Giraud-Carrier (2020) by considering relocation.

Our paper is part of the literature on environmental policy in open economies. Markusen et al. (1993) develop a model with two regions and two firms. They show that optimal environmental policy in an open economy where firms decide on their location differs from the closed economy setting. In their setting, small changes in environmental policy may result in firm relocation and large changes in welfare. Motta and Thisse (1994) also show that strict environmental policy might result in relocation of domestic firms. Rauscher (1995), however, shows that international tax competition for environmental taxes can result in tax rates that are either too low or too high from a welfare perspective. A similar finding is presented by Hoel (1997), who shows that international competition in environmental policy may result in a stricter environmental regulation than international cooperation. Greaker (2003) also shows that the possibility of firms to relocate might result in stricter environmental regulation because governments may benefit from lower damages. Heuson (2010) discusses the implications of market power on the optimal choice of environmental policy instruments and shows that an emission tax may be preferred over emission standards. His results indicate that the choice of an environmental policy instrument and its strictness depends on market structure.

While the analysis of relocation decisions as the result of environmental policy has received some attention in the literature, the consideration of product differentiation has only received little attention so far to the best of our knowledge (see Reinaud 2008 for some basic intuitions).

Our analysis is also related to the literature on the pollution haven hypothesis, which states that firms prefer to produce in countries with less stringent environmental standards as this allows them to produce at lower cost. As a result, governments might abstain from too strict environmental policy, resulting in a race to the bottom. This intuitive idea has been challenged by theoretical studies as well as by empirical findings (see Sturm 2003; Rauscher 2005, for surveys). Richter et al. (2021) show in a general equilibrium model that emission taxes are inefficiently low, when the pollutant is transboundary and firms may relocate. When the pollutant is local, governments set first-best emission taxes. Cole and Elliott (2005) confirm the pollution haven hypothesis for foreign direct investment (FDI) from the US to Brazil and Mexico for capital-intensive industries. Xing and Kolstad (2002) find that the laxity of environmental regulation is an important factor for FDI decisions for heavily polluting industries, such as chemicals and primary metals, but is not significant for other industries.

Holzinger and Sommerer (2011) analyze 17 environmental regulations in more than 20 countriesFootnote 1 for a period of 35 years and find a clear tendency for a race to the top instead of a race to the bottom. Most environmental regulations have been strengthened within this period instead of relaxed. The authors suggest that European harmonization is a major driver for this upward tendency in environmental regulation. Borghesi et al. (2020) analyze the effect of the EU Emissions Trading System (EU-ETS) on outward FDI with a special focus on Italian firms. While firms covered by the EU-ETS do not show a general tendency to relocate on average, firms exposed to international carbon leakage did increase production within their subsidiary firms abroad. This is in line with the findings by Naegele and Zaklan (2019), who do not find a tendency for carbon leakage caused by the EU-ETS. Ranocchia and Lambertini (2018) demonstrate that environmental policy measures can be designed so that firms reduce pollution, and at the same time, no incentive for relocation arises.

The counterpart of the pollution haven hypothesis is the Porter hypothesis, stating that environmental regulation has a positive effect on firms’ productivity and innovative behavior (Porter 1991).Footnote 2 Zárate-Marco and Vallés-Giménez (2015) investigate the effect of green taxes in Spain and find that environmental taxes increase productivity.

Concerning the effect of environmental policy on foreign direct investment (FDI), Elliot & Zhou (2013) present a theoretical framework showing that more stringent environmental standards may increase capital inflows. Dong et al. (2012) show in a two-country model that the effect of FDI on environmental regulation may depend on market sizes. If market sizes of both countries are small, FDI result in more stringent emission standards in the host country. If market sizes of both countries are large, FDI will not affect emission standards of the host country.

The problem of emission shifting within the EU-ETS is analyzed by Eichner and Pethig (2019). Within the EU-ETS, reducing carbon dioxide emissions by an additional instrument such as promoting green energy shifts emissions to other countries. Thus, national environmental policy in one member state increases emissions in other member states and makes decarbonization more difficult for them. Our paper differs from theirs as we do not consider a global pollutant or an additional environmental policy instrument (the EU-ETS), but analyze a local pollutant that becomes transboundary by the relocation of firms.

Ciocirlan and Yandle (2003) empirically test a political economy model of green taxation in OECD countries. They find that environmental taxes are not set in line with welfare maximization but that political economy considerations seem to play a major role. They also consider the possible relocation of firms, assuming that governments want to prevent relocation. Our paper does not focus on the positive analysis of environmental taxation but on the normative implications of relocation behavior. Therefore, we consider welfare-maximizing governments. In our setting, relocation also involves a beneficial effect for the home country, because the environmental damage is reduced.

The relationship between environmental policy, imperfect competition, and relocation also has a macroeconomic dimension. Metcalf and Stock (2020) measure the macroeconomic effect of a (carbon) emission tax and find no negative effect of the emission tax on employment and growth. De Loecker et al. (2020) show for the US that market power and the average profit rate has increased since 1980. This increase is mainly driven by an increase in markups for the firms that already have above-average market power. Their results point in the direction that the phenomenon of imperfect competition may be of increasing relevance in developed countries.

3 The model

3.1 Model setup

Consider two countries \(j=H,F\). In country H, two firms i, \(i=1,2\) sell a product with different quality levels \(s_{i}\). Assume without loss of generality that firm 1 is the firm selling the high-quality product and firm 2 is the firm selling the low-quality product, i.e. \(s_{1}>s_{2}\). In what follows, we assume an exogenous quality ranking with \(s_{1}=\lambda >s_{2}=1\). Note that \(\lambda\) also denotes the product quality markup of the high-quality product, \(\lambda =\frac{s_{1}}{s_{2}}\).Footnote 3

Firms sell their product only in H; there is no product market in country F.Footnote 4

Consumers are heterogeneous with respect to their preference for quality \(\theta\), which is distributed uniformly on the interval [0,1]. The heterogeneity in preference parameter \(\theta\) may be interpreted as differences in income, taste, or frequency of usage. Each consumer buys at most one unit of the most preferred good. The utility derived from no purchase is zero, while a consumer who buys one unit of the good obtains a net utility of

$$\begin{aligned} U=\theta s_{i}-p_{i},\text {i} = H,L\text {.} \end{aligned}$$
(1)

The marginal consumer indifferent between purchasing the high-quality good (from firm 1) and the low-quality good (from firm 2) is given by \(\theta ^{*}=\frac{p_{1}-p_{2}}{\lambda -1}\), the marginal consumer indifferent between purchasing the low-quality good and not buying is given by \(\theta ^{**}=p_{2}\). Demand is given as \(q_{1}=1-\theta ^{*}\) and \(q_{2}=\theta ^{*}-\theta ^{**}\), respectively. The market is not covered so that not all consumers necessarily buy a product. The higher product quality differentiation (and hence, market power), the larger is the share of consumers who do not buy a good. Therefore environmental policy and relocation decisions may result in quantity effects: If, e.g., environmental policy increases the equilibrium price \(p_{2}\), then ceteris paribus more consumers abstain from buying a product.

Assume that production results in emissions of a local pollutant proportional to the output, such as air pollution, soil degradation or noise.Footnote 5 Consider for the baseline scenario that emissions cause damage according to the damage function \(D=\frac{1}{2}q_{i}^{2}\), i.e., marginal damage is given by \(q_{i}\) . In the discussion section, we discuss the effect of lower and higher marginal damage.

In the baseline scenario, the government in country H may levy an environmental tax \(\tau _{H}\) on the emissions generated in H.Footnote 6 In Sect. 6 we will allow also the government in F to impose an environmental tax \(\tau _{F}\) on the emissions generated by the firms producing in F.

Both firms are initially located in country H but may relocate to country F at fixed cost \(\phi\). Therefore, a trade-off arises between bearing higher variable cost due to the environmental tax in H and paying the fixed cost of relocation \(\phi\) when relocating to and producing in F. Production technologies exhibit constant marginal costs, which are normalized to zero.

First, we analyze a scenario of a time-consistent policy, where in the first stage firms decide whether to relocate to the foreign country or not. In the second stage, the government sets a welfare-maximizing tax rate, and in the third stage, firms compete in prices. We discuss an alternative timing, where the government commits to an environmental tax rate in Sect. 5.

3.2 Main assumptions

We consider duopolistic competition in an uncovered market, i.e., quantity effects may occur. In an uncovered market not all (potential) consumers necessarily buy one unit of a good. This assumption is plausible for many consumer goods, such as television sets, drill machines, or lamps, where it can be assumed that consumers do not buy a product, if even the price of the good with the lowest quality is greater than the willingness to pay.

We assume that products are supplied at different quality levels and that the quality levels are fixed. In our context, this assumption seems to be justified as firms’ decisions on product quality are long-run decisions that are independent of environmental policy or location decisions. Product design decisions are mainly driven by expectations about consumers’ preferences and the cost of quality increases. Preferences are independent of the location of production. Thus, environmental policy affects the quantity produced but not the quality of the product.

We also assume that emissions are independent of product quality, i.e., product quality does not refer to environmental characteristics of production. So, while environmental damage is a production feature, quality is a consumption feature. This assumption seems plausible for the goods mentioned above where pollution stems from components produced by the chemical industry, e.g., electrical insulation, or metals, such as copper, that are used in products of any quality level and that do not differentiate products in the eye of consumers.

We consider a local pollutant, such as air pollution, soil degradation, land use, or noise, so that a transboundary effect stems from the relocation choice alone. Relocation is environmentally relevant only for a local pollutant because in this case, relocation has an impact on the damage in the home country and abroad.

4 Time-consistent policy

In this section, we consider a scenario where the government in H follows a time-consistent strategy. Since firm relocation is a long-term decision, the assumption seems to be plausible that the government reserves the right to react to firms’ decisions at some point. Following a committed policy in the long run requires a device for credible commitment that is hard to achieve in democratic policy making, e.g., because of limited legislative periods.

We solve the game by backward induction.

4.1 Price competition

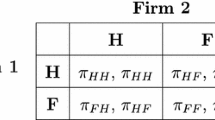
In the third stage of the game, firms compete in prices. The profit of each firm depends on its own location decision as well as on the location decision of its competitor. Therefore we consider all location equilibria that are possible from an ex-ante perspective: Both firms remain in country H (equilibrium HH), the firm selling the high-quality product remains in H, the firm selling the low-quality product relocates to F (equilibrium HF), the firm selling the high-quality product relocates to F, the firm selling the low-quality product remains in H (equilibrium FH), and both firms relocate to F (equilibrium FF). Let \(\Pi\) denote total profits and \(\pi\) operating profits (total profits net of relocation cost), with \(\Pi _{1}^{Hj}=\pi _{1}^{Hj}\), \(\Pi _{2}^{jH}=\pi _{2}^{jH}\)and \(\Pi _{1}^{Fj}=\pi _{1}^{Fj}-\phi\), \(\Pi _{2}^{jF}=\pi _{2}^{jF}-\phi\). The following payoff matrix shows profits under the four possible strategy combinations.

1,2

H

F

H

\(\Pi _{1}^{HH},\Pi _{2}^{HH}\)

\(\Pi _{1}^{HF},\Pi _{2}^{HF}\)

F

\(\Pi _{1}^{FH},\Pi _{2}^{FH}\)

\(\Pi _{1}^{FF},\Pi _{2}^{FF}\)

Equilibrium prices, quantities, and profits for the four equilibria can be found in Appendix A.1.

If both firms remain in country H (equilibrium HH), firms’ profits are

$$\begin{aligned} \Pi _{1}^{HH}=\left( p_{1}^{HH}-\tau _{H}\right) q_{1}^{HH},\Pi _{2}^{HH}=\left( p_{2}^{HH}-\tau _{H}\right) q_{2}^{HH}. \end{aligned}$$
(2)

If firm 1 remains in country H, but firm 2 relocates to country F (equilibrium HF), firms’ profits are

$$\begin{aligned} \Pi _{1}^{HF}=\left( p_{1}^{HF}-\tau _{H}\right) q_{1}^{HF}\text {, }\Pi _{2}^{HF}=p_{2}^{HF}q_{2}^{HF}-\phi \text {.} \end{aligned}$$
(3)

If firm 1 relocates to country F, but firm 2 remains in country H (equilibrium FH), firms’ profits are

$$\begin{aligned} \Pi _{1}^{FH}=p_{1}^{FH}q_{1}^{FH}-\phi \text {, }\Pi _{2}^{FH}=\left( p_{2}^{FH}-\tau _{H}\right) q_{2}^{FH}\text {.} \end{aligned}$$
(4)

If both firms relocate to country F (equilibrium FF), firms’ profits are

$$\begin{aligned} \Pi _{1}^{FF}=p_{1}^{FF}q_{1}^{FF}-\phi \text {, }\Pi _{2}^{FF}=p_{2}^{FF}q_{2}^{FF}-\phi \text {.} \end{aligned}$$
(5)

In the cases HH, FH, and FF, the quantity of firm 1 exceeds the quantity of firm 2. These findings also hold for the equilibrium HF if the product quality markup is sufficiently large. Therefore, in this case, the environmental damage resulting from the firm selling the high-quality product exceeds the environmental damage of the firm selling the low-quality product. Also, tax revenue collected from the firm selling the high-quality product in H is higher than tax revenue collected from the firm selling the low-quality product.

Firm 1 charges a higher price (\(p_{1}>p_{2}\)), with the price difference \(p_{1}-p_{2}\) increasing in the product quality markup \(\lambda\). Therefore, environmental damage and the optimal emission tax also depend on product quality differentiation.

4.2 Environmental policy

Consider that in the second stage, the government in country H taxes the emissions of each firm producing in H. The government sets a tax rate \(\tau _{H}\) to maximize social welfare, given as the sum of consumer surplus, firms’ profits, tax revenue less the environmental damage.Footnote 7 The environmental tax has four effects: It increases prices, decreases the quantity produced and thereby emissions, generates tax revenues, and may motivate one firm or both firms to relocate (and thereby reduce emissions and tax revenue in the home country).

Welfare in H and thus the welfare-maximizing choice of \(\tau _{H}\) depends on location decisions in the first stage of the game.

If both firms remain in country H (equilibrium HH), welfare is given as

$$\begin{aligned} W_{H}^{HH}=CS_{H}^{HH}+\Pi _{1}^{HH}+\Pi _{2}^{HH}+\tau _{H}^{HH}\left( q_{1}^{HH}+q_{2}^{HH}\right) -\frac{1}{2}\left( q_{1}^{HH}+q_{2}^{HH}\right) ^{2}\text {.} \end{aligned}$$
(6)

The resulting welfare maximizing tax rate is

$$\begin{aligned} \tau _{H}^{HH}=\frac{\left( 2\lambda +7\right) \lambda }{\left( \lambda +1\right) \left( 8\lambda +1\right) }\text {.} \end{aligned}$$
(7)

The equilibrium tax rate \(\tau _{H}^{HH}\) decreases in \(\lambda\). Since both firms produce in H, all production emissions are located in H. A higher degree of product differentiation weakens price competition, increases prices and profits, lowers quantities, and thereby lowers environmental damage. Thus, product differentiation can be seen as an imperfect substitute for the emission tax. As a result, the welfare-maximizing tax-rate is lower if products are more differentiated and competition is relaxed.

If firm 1 remains in country H, but firm 2 relocates to country F (equilibrium HF), welfare is given as

$$\begin{aligned} W_{H}^{HF}=CS_{H}^{HF}+\Pi _{1}^{HF}+\tau _{H}\left( q_{1}^{HF}\right) - \frac{1}{2}\left( q_{1}^{HF}\right) ^{2}\text {.} \end{aligned}$$
(8)

The welfare maximizing tax rate is

$$\begin{aligned} \tau _{H}^{HF}=\left\{ \begin{array}{ccc} \frac{\lambda \left( \lambda -1\right) (9\lambda -4\lambda ^{2}-3)}{ -3\lambda -\lambda ^{2}+4\lambda ^{3}+1} &{} \text {if } &{} \lambda <\frac{1}{8} \sqrt{33}+\frac{9}{8} \\ 0 &{} \text {if} &{} \lambda \ge \frac{1}{8}\sqrt{33}+\frac{9}{8} \end{array} \right. \text {.} \end{aligned}$$
(9)

If the product quality markup is sufficiently low (high), the welfare-maximizing tax rate \(\tau _{H}^{HF}\) increases (decreases) in \(\lambda\). Given that only firm 1 produces in H, the production emissions of firm 2 generate no environmental damage in H. Therefore, the marginal damage of production is lower compared to HH and so is the optimal tax rate. If the product quality markup is small, the optimal tax rate is also small, as a higher tax rate would drive the firm selling the high-quality product out of the market. A larger product quality markup increases the ability of firm 1 to pass-through the tax rate because demand is less elastic. Therefore the optimal tax rate increases. If the product quality markup is sufficiently large, the quantity of firm 1 is sufficiently low so that a tax is not necessary to correct an externality. The distortion from imperfect competition (lower quantity, smaller consumer surplus) outweighs the distortion from the environmental externality, so that an emission tax cannot increase welfare.

If firm 1 relocates to country F, but firm 2 remains in country H (equilibrium FH), welfare is given as

$$\begin{aligned} W_{H}^{FH}=CS_{H}^{FH}+\Pi _{2}^{FH}+\tau _{H}\left( q_{2}^{FH}\right) - \frac{1}{2}\left( q_{2}^{FH}\right) ^{2}\text {.} \end{aligned}$$
(10)

The welfare maximizing tax rate is

$$\begin{aligned} \tau _{H}^{FH}=\left\{ \begin{array}{ccc} \frac{\left( \lambda -1\right) \left( 4\lambda -2\lambda ^{2}-1\right) }{ \lambda \left( -9\lambda +8\lambda ^{2}+2\right) } &{} \text {if } &{} \lambda < \frac{1}{2}\sqrt{2}+1 \\ 0 &{} \text {if} &{} \lambda \ge \frac{1}{2}\sqrt{2}+1 \end{array} \right. \text {.} \end{aligned}$$
(11)

Again, part of the emissions are located in F, but now it is the firm selling the high quality product that produces abroad. As in the case HF, the welfare-maximizing tax rate \(\tau _{H}^{FH}\) is hump-shaped but compared to location combination FH, the government has to consider that it is the firm selling the low-quality product that produces in H. Demand for the firm selling the low-quality product is more elastic. Therefore, the optimal tax rate is lower. Also, the product quality markup, for which the optimal tax rate is zero (the distorted competition outweighs pollution), is lower than for the location choice HF.

Figure 1 shows optimal tax rates in equilibria HH (black line), HF (light gray), and FH (dark gray).

Fig. 1
figure 1

Tax rates \(\tau _{H}^{HH}\), \(\tau _{H}^{HF}\), and \(\tau _{H}^{FH}\)

Full size image

If both firms relocate to country F (equilibrium FF), there is no tax base in country H.

Optimal tax rates depend on the product quality markup as well as on location decisions, with tax rates being the highest if no firm relocates.

Product differentiation weakens competition and reduces quantities (and emissions). If both firms remain in H, the welfare-maximizing tax rate decreases in \(\lambda\) because weakened competition reduces quantities and emissions. The relocation of at least one firm decreases emissions in H, reduces the marginal damage, and lowers, therefore, the optimal tax rate. If one firm relocates to F and the level of product differentiation is sufficiently low, a positive tax rate results in market exit of the firm that remains in H because the tax increases variable cost and price competition is strong. The higher the level of product differentiation is, the higher is the optimal tax rate because the taxed firm is more capable of passing through the environmental tax to consumers. If the level of product differentiation is sufficiently high, the quantity decreases to a sufficient extent so that the optimal tax rate also decreases. For a high level of product differentiation, the quantity is sufficiently low, so that the optimal tax rate is zero.

Demand for the firm selling the low-quality product is more elastic than for the firm selling the high-quality product. Therefore optimal tax rates are always lower in the FH equilibria than in HF equilibria.

4.3 Location decision

In the first stage, firms decide whether or not to relocate to F based on expected profits, given the decision of the other firm. They anticipate the time-consistent emission tax in the second stage.

For each firm, the relocation decision is characterized by a trade-off whether to incur the variable cost of the tax levied on emissions or fixed cost of relocation and produce at zero marginal cost.

Both firms stay in H (equilibrium HH) if \(\Pi _{1}^{HH}>\Pi _{1}^{FH}\) and \(\Pi _{2}^{HH}>\Pi _{2}^{HF}\), i.e., \(\phi >\phi ^{HH}\). Firm 1 remains in H, but firm 2 relocates to F (equilibrium HF) if \(\Pi _{1}^{HF}>\Pi _{1}^{FF}\) and \(\Pi _{2}^{HF}>\Pi _{2}^{HH}\), i.e., \(\underline{\phi }^{HF}<\phi<\) \(\overline{\phi }^{HF}\). Firm 1 relocates to F and firm 2 remains in H if \(\Pi _{1}^{FH}>\Pi _{1}^{HH} {\acute{}}\) and \(\Pi _{2}^{FH}>\Pi _{2}^{FF}\), i.e., \(\underline{\phi }^{FH}<\phi<\) \(\overline{\phi }^{FH}\). Both firms relocate to F (equilibrium FF) if \(\Pi _{1}^{FF}>\Pi _{1}^{HF}\) and \(\Pi _{2}^{FF}>\Pi _{2}^{FH}\), i.e., \(\phi <\phi ^{FF}\). First stage equilibrium profits and cut-off values for \(\phi\) can be found in Appendix A.1. Figure 2 illustrates the resulting Nash equilibria depending on the product quality markup \(\lambda\) and the cost of relocation \(\phi\). We identify several combinations of \(\lambda\) and \(\phi\) with unique Nash equilibria HH (vertical dark gray stripes), FH (vertical light gray stripes), HF (horizontal light gray stripes), and FF (horizontal dark gray stripes). Also, there are regions with two Nash equilibria FH and HF (solid light gray) and a region with no Nash equilibrium in pure strategies (white region).

The product quality markup \(\lambda\) is a key driver for the relocation decision. The lower the product quality markup, the stronger is price competition between firms, resulting in lower prices, higher quantities, and lower profits. An increase in the product quality markup \(\lambda\) weakens price competition and changes the result of the trade-off between paying the tax (variable cost) or paying the relocation costs (fixed cost). The higher the product quality markup, the more likely it is that at least one firm relocates to country F. A higher product quality markup weakens competition and reduces quantities, increases prices, reduces consumer surplus, increases profits and tax revenue, and reduces damage.

If relocation cost \(\phi\) is sufficiently high, it never pays off for any firm to relocate because the advantage of the lower variable cost is more than eaten up by the high fixed cost of relocation. Therefore, HH always results as an equilibrium. If relocation cost \(\phi\) is (close to) zero and the product quality markup is sufficiently low, both firms produce large quantities so that it pays off for both firms to reduce variable cost at the expense of the (low) fixed cost of relocation (FF). As demand for the firm selling the high-quality product is less elastic than for the firm selling the low-quality product, it is more able to pass-through the emission tax to consumers. Therefore, relocating for a fixed cost and thereby reducing variable cost is more attractive for the firm selling the low-quality product than for the firm selling the high-quality product. Therefore, the firm selling the low-quality product has a stronger incentive to relocate for moderate values of \(\phi\) (HF).

Fig. 2
figure 2

Location equilibria, unilateral taxation

Full size image

As the relocation decision creates a positive externality on the remaining firm in H by lowering the equilibrium tax rate, relocation of one firm dampens the relocation incentive for the remaining firm. As a result, HF as well as FH may be equilibria for some combinations of the product quality markup and relocation cost. For some combinations of low levels of product quality markup and moderate relocation cost, no equilibrium exists. For low levels of product quality markup, price competition is strong. For intermediate values of relocation cost, it pays off for at least one firm to relocate. However, the tax-dampening-effect of the relocation of at least one firm counterbalances the advantage of relocating to F. Therefore, there is always the incentive to deviate from a given location combination for at least one firm, resulting in no equilibrium.

5 Committed policy

In this section, we present our results for the case of a committed policy, as in Ikefuji et al. (2016). We consider a case where the government commits to an environmental tax rate in the first stage of the game. Firms decide whether or not to relocate in the second stage and compete in prices in the last stage of the game. While Ikefuji et al. (2016) analyze the case of firms providing homogeneous goods, we consider differentiated goods. In the following subsections, we present the backward induction solution of the three stages.

5.1 Price ceompetition

The last stage of the game, where firms set prices, is identical to the case described in Sect. 4.

5.2 Location decision

In the second stage, firms decide whether or not to relocate to F based on expected profits, given the government’s commitment to an emission tax and the decision of the other firm. Cut-off values for \(\phi\) can be found in Appendix A.2.

Both firms remain in H if \(\Pi _{1}^{HH}>\Pi _{1}^{FH}\) and \(\Pi _{2}^{HH}>\Pi _{2}^{HF}\), i.e., \(\phi >\phi ^{HH}\). The firm selling the high-quality product relocates to F and the firm selling the low-quality product remains in H (equilibrium FH) if \(\Pi _{1}^{FH}>\Pi _{1}^{HH}\) and \(\Pi _{2}^{FH}>\Pi _{2}^{FF}\), i.e., \(\underline{\phi }^{FH}<\phi < \overline{\phi }^{FH}\). Both firms relocate to F if \(\Pi _{1}^{FF}>\Pi _{1}^{HF}\) and \(\Pi _{2}^{FF}>\Pi _{2}^{FH}\), i.e., \(\phi <\phi =\phi ^{FF}\) . There is no equilibrium in which the firm selling the high-quality product remains in H and the firm producing low quality relocates to F. For very high relocation cost, neither firm relocates. For intermediate relocation cost, it is always the firm selling the high-quality product that relocates. Both firms face a trade-off between paying the tax (variable cost) or relocating (fixed cost). Because of the higher quantity of the firm selling the high-quality product, the critical tax rate that makes relocation for a given relocation cost more favorable is lower than the critical tax rate for the firm producing low quality. Therefore, if only one firm relocates, it is always the firm selling the high-quality product but not the firm producing low quality. So the government cannot commit to a tax rate that results in the firm selling the high-quality product staying in H and the firm producing low quality relocating to F.

5.3 Environmental policy

Consider that in the first stage, the government in country H commits to a tax rate \(\tau _{H}\) to maximize social welfare, anticipating the relocation decisions in the second stage and price competition in the last stage. Equilibrium tax rates can be found in Appendix A.2.

If both firms remain in H (equilibrium HH), the welfare-maximizing tax rate \(\tau _{H}^{HH}\) is

$$\begin{aligned} \tau _{H}^{HH}=\frac{\left( 2\lambda +7\right) \lambda }{\left( \lambda +1\right) \left( 8\lambda +1\right) }\text {.} \end{aligned}$$

The welfare-maximizing tax rate under a committed policy is higher than under a time-consistent policy.

If the firm selling the high-quality product relocates to F and the firm selling the low-quality product remains in H (equilibrium FH), the welfare-maximizing tax rate \(\tau _{H}^{FH}\) is

$$\begin{aligned} \tau _{H}^{FH}=\left\{ \begin{array}{ccc} \frac{\left( \lambda -1\right) \left( 4\lambda -2\lambda ^{2}-1\right) }{ \lambda \left( -9\lambda +8\lambda ^{2}+2\right) } &{} \text {if } &{} \lambda < \frac{1}{2}\sqrt{2}+1 \\ 0 &{} \text {if} &{} \lambda \ge \frac{1}{2}\sqrt{2}+1 \end{array} \right. \text {.} \end{aligned}$$

Again, the welfare-maximizing tax rate under a committed policy is higher than under a time-consistent policy.

The difference to the scenario presented in Sect. 3 stems from the fact that under time-consistent policy, there may be a welfare-maximizing tax rate for the case that the firm selling the high-quality product has already decided to relocate and the firm selling the low-quality product has decided to stay. However, after the government has decided on a tax rate, this combination of firms’ decisions cannot be an equilibrium.

Tax rates under the committed policy for the cases where one firm relocates are higher than under the time-consistent policy. This is, under the committed policy, the government is more able to reduce local emissions by applying an emission tax than under time-consistent policy. However, from a policy perspective, long-term commitment is hard to achieve for democratic governments with limited legislative periods.

In our paper, under a committed policy, the location equilibrium HF does not exist, while it is possible in the model of Ikefuji et al. (2016) as they do not consider product quality differences. We show that under a committed policy, the firm selling the high-quality product has a higher incentive for relocation than the firm selling the low-quality good. Given that quality differentiation is a common feature in many markets, our results complement the results by Ikefuji et al. (2016).

6 Environmental taxes in both countries

So far, we have considered the case where an environmental tax is applied only in H. The government in F was assumed to be passive. This is in line with the analysis of Ikefuji et al. (2016). While this approach allows us to analyze the interaction of environmental damage, product quality markup, and relocation cost, it is plausible to assume that also the government in F applies an environmental tax. Therefore, in this section, we take environmental policy in F into account. We still abstract from consumers in F and assume that an output market exists only in H. With respect to the damage function, we assume the damage function parameter of the baseline case in both countries and further assume that there is no damage spillover.

6.1 Non-cooperative taxation

Assume that the governments in H and F set environmental taxes non-cooperatively. Hosting a firm results in profits and potential tax revenues on the one hand and harmful emissions on the other hand. The relocation trade-off for firms is different in this case because relocation does not necessarily imply not being taxed.

6.1.1 Price competition

In the third stage, firms compete in prices. Equilibrium prices, quantities, and profits for the four equilibria can be found in Appendix A.3.

If both firms remain in country H (equilibrium HH), firms’ profits are

$$\begin{aligned} \Pi _{1}^{HH}=\left( p_{1}^{HH}-\tau _{H}\right) q_{1}^{HH}\text {, }\Pi _{2}^{HH}=\left( p_{2}^{HH}-\tau _{H}\right) q_{2}^{HH}. \end{aligned}$$
(12)

If firm 1 remains in country H, but firm 2 relocates to country F (equilibrium HF), firms’ profits are

$$\begin{aligned} \Pi _{1}^{HF}=\left( p_{1}^{HF}-\tau _{H}\right) q_{1}^{HF}\text {, }\Pi _{2}^{HF}=\left( p_{2}^{HF}-\tau _{F}\right) q_{2}^{HF}-\phi . \end{aligned}$$
(13)

If firm 1 relocates to country F, but firm 2 remains in country H (equilibrium FH), firms’ profits are

$$\begin{aligned} \Pi _{1}^{FH}=\left( p_{1}^{FH}-\tau _{F}\right) q_{1}^{FH}-\phi \text {, } \Pi _{2}^{FH}=\left( p_{2}^{FH}-\tau _{H}\right) q_{2}^{FH}. \end{aligned}$$
(14)

If both firms relocate to country F (equilibrium FF), firms’ profits are

$$\begin{aligned} \Pi _{1}^{FH}=\left( p_{1}^{FH}-\tau _{F}\right) q_{1}^{FH}-\phi \text {, } \Pi _{2}^{FH}=\left( p_{2}^{FH}-\tau _{H}\right) q_{2}^{FH}. \end{aligned}$$
(15)

6.1.2 Environmental policy

Consider first that in the second stage governments set tax rates non-cooperatively. Equilibrium tax rates can be found in Appendix A.3.

If both firms remain in country H (equilibrium HH), the welfare maximizing tax rate is

$$\begin{aligned} \tau _{H}^{HH,NC}=\frac{\left( 2\lambda +7\right) \lambda }{\left( \lambda +1\right) \left( 8\lambda +1\right) }\text {,} \end{aligned}$$
(16)

which is the same as in the unilateral case (there is no tax base in country F).

If firm 1 remains in country H, but firm 2 relocates to country F (equilibrium HF), welfare in country H is given as

$$\begin{aligned} W_{H}^{HF}=CS_{H}^{HF}+\Pi _{1}^{HF}+\tau _{H}\left( q_{1}^{HF}\right) - \frac{1}{2}\left( q_{1}^{HF}\right) ^{2} \end{aligned}$$
(17)

and welfare in country F is given as

$$\begin{aligned} W_{F}^{HF}=\Pi _{2}^{HF}+\tau _{F}\left( q_{2}^{HF}\right) -\frac{1}{2} \left( q_{2}^{HF}\right) ^{2}\text {.} \end{aligned}$$
(18)

The welfare maximizing tax rates \(\tau _{H}^{HF\text {, }NC}\) and \(\tau _{F}^{HF\text {, }NC}\)are

$$\begin{aligned} \tau _{H}^{HF,NC}= & {} \left\{ \begin{array}{ccc} \frac{-6\lambda ^{3}+17\lambda ^{2}-11\lambda +1}{\lambda +6\lambda ^{2}-4} &{} \text {if } &{} \lambda<1.\,926\,7 \\ 0 &{} \text {if} &{} \lambda \ge 1.\,926\,7 \end{array} \right. \nonumber \\ \tau _{F}^{HF,NC}= & {} \left\{ \begin{array}{ccc} \frac{2\lambda ^{2}-1}{6\lambda ^{3}+\lambda ^{2}-4\lambda } &{} \text {if } &{} \lambda <1.\,926\,7 \\ \frac{\left( 2\lambda ^{2}-1\right) \left( \lambda -1\right) }{\lambda \left( 2\lambda -1\right) \left( 6\lambda -5\right) } &{} \text {if} &{} \lambda \ge 1.\,926\,7 \end{array} \right. \text {.} \end{aligned}$$
(19)

Compared to our baseline case in Sect. 3, the equilibrium tax rate in H is now higher. This is the result of the positive tax rate in F. If production of firm 2 is taxed, quantities and therefore emissions shift from country F to country H. As a result, H applies a higher equilibrium tax to correct the externality and to deter emission shifting.

If firm 1 relocates to country F, but firm 2 remains in country H (equilibrium FH), welfare in country H is given as

$$\begin{aligned} W_{H}^{FH,NC}=CS_{H}^{FH,NC}+\Pi _{2}^{FH,NC}+\tau _{H}\left( q_{2}^{FH,NC}\right) -\frac{1}{2}\left( q_{2}^{FH,NC}\right) ^{2}\text {.} \end{aligned}$$
(20)

Welfare in country F is given as

$$\begin{aligned} W_{F}^{FH,NC}=\Pi _{1}^{FH,NC}+\tau _{F}\left( q_{1}^{FH,NC}\right) -\frac{1 }{2}\left( q_{1}^{FH,NC}\right) ^{2}\text {.} \end{aligned}$$
(21)

The welfare maximizing tax rates \(\tau _{H}^{FH\text {, }NC}\) and \(\tau _{F}^{FH\text {, }NC}\) are

$$\begin{aligned} \tau _{H}^{FH,NC}= & {} \left\{ \begin{array}{ccc} \frac{\left( 2\lambda ^{3}-6\lambda ^{2}+2\lambda +1\right) }{-8\lambda ^{3}+3\lambda ^{2}+2\lambda } &{} \text {if } &{} \lambda<2.\,525\,7 \\ 0 &{} \text {if} &{} \lambda \ge 2.\,525\,7 \end{array} \right. \\ \tau _{F}^{FH,NC}= & {} \left\{ \begin{array}{ccc} \frac{\left( 6\lambda ^{2}-7\lambda +2\right) }{8\lambda ^{2}-3\lambda -2} &{} \text {if } &{} \lambda <2.\,525\,7 \\ \frac{\left( 6\lambda ^{3}-10\lambda ^{2}+4\lambda \right) }{8\lambda ^{3}-8\lambda ^{2}+1} &{} \text {if} &{} \lambda \ge 2.\,525\,7 \end{array} \right. \text {.} \end{aligned}$$

Again, equilibrium tax rates in H exceed equilibrium tax rates studied in Sect. 3 (with F assumed to be passive). The intuition is similar to the case HF. Compared to a passive government in F, taxation in F shifts emissions to H, resulting in higher taxes. In addition, taxation in F dampens the relocation incentive stemming from taxation in H, as firms now anticipate that emissions will also be taxed in F.

If both firms relocate to country F (equilibrium FF), welfare in country F is given as

$$\begin{aligned} W_{F}^{FF,NC}=\Pi _{1}^{FF,NC}+\Pi _{2}^{FF,NC}+\tau _{F}\left( q_{1}^{FF,NC}+q_{2}^{FF,NC}\right) -\frac{1}{2}\left( q_{1}^{FF,NC}+q_{2}^{FF,NC}\right) ^{2}\text {.} \end{aligned}$$
(22)

The welfare maximizing tax rate \(\tau _{F}^{FF\text {, }NC}\) is

$$\begin{aligned} \tau _{F}^{FF,NC}=\frac{2\lambda \left( 5\lambda +4\right) }{12\lambda ^{2}+14\lambda +1}. \end{aligned}$$

Note that the taxation decisions of H and F are similar if both firms produce in the respective country. But since there is no output market in F , there is no consumer surplus in F that has to be taken into account by the government.

6.1.3 Location decision

In the first stage, both firms decide whether or not to relocate by comparing equilibrium profits depending on location decisions.

First stage equilibrium profits and cut-off values for \(\phi\) can be found in Appendix A.3.

Figure 3 illustrates the resulting Nash equilibria depending on the product quality markup \(\lambda\) and the cost of relocation \(\phi\) for non-cooperative taxation in both countries.

Fig. 3
figure 3

Location equilibria, bilateral, non-cooperative taxation

Full size image

If both governments apply an environmental tax, we identify several combinations of \(\lambda\) and \(\phi\) with unique Nash equilibria HH (vertical dark gray stripes) and FH (vertical light gray stripes), and a region with no Nash equilibrium in pure strategies (white region). There is no FF-equilibrium, no HF-equilibrium, and no region characterized by multiple equilibria. For low values of \(\lambda\), there is an region where no equilibrium exists.

Similar to Fig. 2, there is an region of prohibitively high relocation cost so that no firm relocates (HH). But compared to Fig. 2, the critical relocation cost that results in the HH-equilibrium is much lower. As a result of F also taxing emissions, the difference in variable cost in case of relocation decreases. Therefore, for a given product quality markup, the critical relocation cost, which prevents the relocation of any firm, is lower.

There is no HF-equilibrium. If a firm relocates under non-cooperative taxation of both countries, it is always the firm selling the high-quality product that relocates. For a given product quality markup, the cut-off value of relocation cost for which the firm selling the high-quality product relocates at the margin (given that the firm selling the low-quality product stays at H) is higher than the cut-off value for the firm selling the low-quality product. Because of its higher profit, the firm selling the high-quality product is more inclined to relocate to the foreign country for a fixed cost than the firm selling the low-quality product. Therefore, it relocates for a higher fixed cost than the firm selling the low-quality product. The firm selling the low-quality product, in contrast, never has an incentive to relocate in equilibrium. Given that one firm (the firm selling the high-quality product) has relocated to F, country F has no incentive to attract the second firm as well.

6.2 Cooperative taxation

Consider a scenario where the governments in H and F set environmental taxes cooperatively to maximize joint welfare.

In the non-cooperative equilibrium, the environmental tax shifts emissions to the other country; this creates an incentive for high tax rates. However, relocation also shifts tax revenue, which provides a counterveiling incentive for lower tax rates. Under cooperative taxation, countries are able to balance these effects by balancing both externalities of taxation (damage shifting and revenue shifting).

6.2.1 Price competition

The third stage of the game, where firms compete in prices, is identical to our description in Sect. 3.

6.2.2 Environmental policy

Consider the case where in the second stage governments set tax rates cooperatively. Equilibrium tax rates can be found in Appendix A.4.

If both firms remain in H, welfare and the optimal tax rate are identical to the case HH under non-cooperative taxation.

If firm 1 remains in country H, but firm 2 relocates to country F (equilibrium HF), global welfare is given as

$$\begin{aligned}&W^{HF,C}=CS_{H}^{HF,C}+\Pi _{1}^{HF,C}+\Pi _{2}^{HF,C}+\tau _{H}\left( q_{1}^{HF,C}\right) +\tau _{F}\left( q_{2}^{HF,C}\right) \nonumber \\&\qquad -\frac{1}{2}\left( q_{1}^{HF,C}\right) ^{2}-\frac{1}{2}\left( q_{2}^{HF,C}\right) ^{2}\text {.} \end{aligned}$$
(23)

The welfare maximizing tax rates \(\tau _{H}^{HF\text {, }C}\) and \(\tau _{F}^{HF\text {, }C}\) are

$$\begin{aligned} \tau _{H}^{HF,C}= & {} \left\{ \begin{array}{ccc} \frac{\left( \lambda -2\right) \left( 1-2\lambda \right) }{2\lambda +1} &{} \text {if } &{} \lambda<2 \\ 0 &{} \text {if} &{} \lambda \ge 2 \end{array} \right. \\ \tau _{F}^{HF,C}= & {} \left\{ \begin{array}{ccc} \frac{1}{\lambda \left( 2\lambda +1\right) } &{} \text {if } &{} \lambda <2 \\ \frac{\left( \lambda -1\right) \left( -2\lambda +2\lambda ^{2}-1\right) }{ \lambda \left( -11\lambda +8\lambda ^{2}+5\right) } &{} \text {if} &{} \lambda \ge 2 \end{array} \right. \text {.} \end{aligned}$$

Under cooperative taxation, the government in H sets a tax rate of zero, if the product quality markup is sufficiently large (\(\lambda \ge 2\)). If the level of quality differentiation is sufficiently high and, therefore, competition is sufficiently weak, in country H, the distortion from imperfect competition (lower produced quantity, smaller consumer surplus) outweighs the distortion of damaging emissions. Therefore, the optimal tax rate in H is zero. Imperfect competition by the product quality markup is here a substitute for environmental policy.

The government in F always sets positive tax rates. The quantity of the firm providing the low-quality product is never sufficiently low to make the emission tax unnecessary.

If firm 1 relocates to country F, but firm 2 remains in country H (equilibrium FH), global welfare is given as

$$\begin{aligned}&W_{H}^{FH,C}=CS_{H}^{FH,C}+\Pi _{1}^{FH,C}+\Pi _{2}^{FH,C}+\tau _{H}\left( q_{2}^{FH,C}\right) +\tau _{F}\left( q_{1}^{FH,C}\right) \nonumber \\&\qquad -\frac{1}{2}\left( q_{2}^{FH,C}\right) ^{2}-\frac{1}{2}\left( q_{1}^{FH,C}\right) ^{2}\text {.} \end{aligned}$$
(24)

Welfare in country F is given as

$$\begin{aligned} W_{F}^{FH,C}=\Pi _{1}^{FH,C}+\tau _{F}\left( q_{1}^{FH,C}\right) -\frac{1}{2} \left( q_{1}^{FH,C}\right) ^{2}\text {.} \end{aligned}$$
(25)

The welfare maximizing tax rates \(\tau _{H}^{FH\text {, }C}\) and \(\tau _{F}^{FH\text {, }C}\) are

$$\begin{aligned} \tau _{H}^{FH,C}= & {} \left\{ \begin{array}{ccc} \frac{1}{\lambda \left( 2\lambda +1\right) } &{} \text {if } &{} \lambda<2 \\ \frac{\left( \lambda -1\right) \left( -2\lambda +2\lambda ^{2}-1\right) }{ \lambda \left( -11\lambda +8\lambda ^{2}+5\right) } &{} \text {if} &{} \lambda \ge 2 \end{array} \right. \\ \tau _{F}^{FH,C}= & {} \left\{ \begin{array}{ccc} \frac{\left( 2\lambda -1\right) \left( 2-\lambda \right) }{2\lambda +1} &{} \text {if } &{} \lambda <2 \\ 0 &{} \text {if} &{} \lambda \ge 2 \end{array} \right. \text {.} \nonumber \end{aligned}$$
(26)

Tax rates of H in equilibrium FH are identical to tax rates of F in equilibrium HF. Tax rates of H in equilibrium HF are identical to tax rates of F in equilibrium FH. This is, if each country hosts a firm under cooperation, tax rates in both countries depend only on the relative quality position of the respective domestic firm. If the product quality markup is sufficiently large (\(\lambda \ge 2\)), the optimal tax rate is zero in both cases for the country that hosts the firm selling the high-quality product 1. If the product quality markup is below this threshold level, a positive tax rate is applied.

If both firms relocate to country F (equilibrium FF), global welfare is given as

$$\begin{aligned}&W^{FF,C}=CS_{H}^{FF,C}+\Pi _{1}^{FF,C}+\Pi _{2}^{FF,C}+\tau _{F}\left( q_{1}^{FF,C}+q_{2}^{FF,C}\right) \nonumber \\&\qquad -\frac{1}{2}\left( q_{1}^{FF,C}\right) ^{2}- \frac{1}{2}\left( q_{2}^{FF,C}\right) ^{2}\text {.} \end{aligned}$$
(27)

The welfare maximizing tax rate \(\tau _{F}^{FF\text {, }C}\) is

$$\begin{aligned} \tau _{F}^{FF,C}=\frac{2\lambda \left( 5\lambda +4\right) }{12\lambda ^{2}+14\lambda +1}\text {.} \end{aligned}$$

Figures 4 and 5 show tax rates for unilateral, non-cooperative bilateral and coordinated bilateral taxation for equilibria in that one firm relocates (equilibria HF and FH).

Fig. 4
figure 4

\(\tau _{i}^{jj}\) for unilateral, non-cooperative bilateral and coordinated bilateral taxation for HF

Full size image

In the location equilibrium HF,  the tax rate in H in the case of no taxation in F is hump-shaped (see Fig. 1 and Sect. 3.2). If the product quality markup is sufficiently large, weakened competition is a substitute for the emission tax. For low levels of the product quality markup, a larger product quality markup allows for higher tax rates without forcing the firm in the home country to exit the market. If also country F taxes emissions, welfare-maximizing tax rates in H are higher than under no taxation in F because the competitive disadvantage of taxation in H is mitigated by positive tax rates in F. Tax rates in H are again hump-shaped, but optimal tax rates are now positive even in the case of no product differentiation because also the foreign country applies a tax.

If tax rates are set cooperatively, optimal tax rates in H are higher than those under no cooperation for a sufficiently large product quality markup. The reason is that cooperation allows governments to reduce the overall quantity produced without competing for tax revenues. For low levels of product differentiation, tax rates are higher under no cooperation. Here, higher taxation results in higher (domestic) welfare, given the opportunity to shift emissions to country F.

In country F, taxation is lower for low levels of product differentiation than in country H and higher for higher levels. This is a response to the decreasing tax rate in H that shifts quantities (and emissions) to F. Tax rates in F decrease in the degree of product differentiation (but at a lower rate than in H) due to the quantity effect of weakened competition. If product differentiation is sufficiently large for the tax rate in H to be zero, the optimal tax rate in F increases in the degree of product differentiation. The higher the product quality markup is, the higher is the quantity of the low-quality product and, thus, the higher are emissions. Therefore a higher tax rate is necessary to correct the externality.

Tax rates in F are higher under no cooperation than under cooperation. This mirrors the tax rates in both cases in H. If H taxes emissions less under no cooperation, F has to set higher taxes to deter the export of emissions. If H sets higher tax rates under cooperation, F responds with lower tax rates.

Fig. 5
figure 5

\(\tau _{i}^{jj}\) for unilateral, non-cooperative bilateral and coordinated bilateral taxation for FH

Full size image

In the location equilibrium FH, the optimal tax rate in H is hump-shaped in the case of unilateral taxation. If both governments tax emissions non-cooperatively, the optimal tax rate in F increases in the degree of product quality differentiation. Since there is no output market in F, there is no loss in consumer surplus in F to consider. Therefore, a higher product quality markup allows for a higher tax revenue in F and thereby transforms consumer surplus in H to tax revenue in F.

The optimal tax rate in H decreases in product quality differentiation. Prices increase because of the larger quality markup and the higher tax in F. As prices increase, the quantity produced decreases, and thus, emissions and the optimal tax rate also decrease. If the degree of product quality differentiation is sufficiently large and the quantity in H sufficiently low, the optimal tax rate in H is zero. If products are homogeneous, tax rates in both countries are identical under cooperative and non-cooperative taxation. Under cooperation, tax rates in F decrease in the degree of product differentiation if the degree of product differentiation is sufficiently high. Tax rates in H also decrease in the degree of product differentiation, but more slowly than in F. Product differentiation decreases the quantity produced and emissions. If the degree of product differentiation is sufficiently large so that the optimal tax rate in F is zero, the optimal tax rate increases in H. In this case, the tax in H compensates for the zero tax rate in F.

Under uncoordinated taxation, the emission tax is set to reduce local emissions (by reducing the quantity produced and by shifting emissions abroad) and to compete for tax revenue, while accepting a fiscal and/or environmental externality for the other country. Under coordinated taxation, governments do not compete for tax revenue or shift emissions to the other country, but they focus on the reduction and the optimal distribution of emissions, maximizing joint tax revenue, and profits. Abstaining from externalizing fiscal effects and/or environmental damage leads to a more targeted use of the tax.

6.2.3 Location decision

In the first stage, both firms decide whether or not to relocate. First stage equilibrium profits and cut-off values for \(\phi\) can be found in Appendix A.4.

Figure 6 illustrates the resulting location Nash equilibria depending on the product quality markup \(\lambda\) and the cost of relocation \(\phi\).

Fig. 6
figure 6

Location equilibria, bilateral, coordinated taxation

Full size image

If both governments apply an environmental tax in a coordinated manner to maximize joint welfare, we identify several combinations of \(\lambda\) and \(\phi\) with unique Nash equilibria HH (vertical dark gray stripes), FH (vertical light gray stripes), HF (horizontal light gray stripes), an region characterized by multiple equilibria (solid light gray) and a region with no Nash equilibrium in pure strategies (white region). There is no FF -equilibrium. In the cooperative setting, the FF-equilibrium mirror-inverted to the HH-equilibrium, but both firms pay the fixed cost of relocation. Therefore, governments avoid this equilibrium in the cooperative case.

Compared to non-cooperative taxation (please note the different scaling of the axes), the region of HH-equilibria has increased, and there is a large region in which the firm selling the low-quality product relocates to F (which is never the case under non-cooperative taxation).

The firm selling the low-quality product relocates for relatively high levels of product quality differentiation and intermediate levels of relocation cost. Compared to no taxation in F, the firm selling the low-quality product relocates only at a higher product quality markup.

Note that governments do not tax profits and that consumer surplus only results in H. Therefore, for the product quality markup being sufficiently large (and the relocation cost being sufficiently low), the firm selling the high-quality product may relocate to F. In this case, H benefits from lower pollution. F suffers from pollution, but benefits from tax revenue (the tax allows to transform consumer surplus in H to tax revenue in F).

7 Discussion

In this section, we discuss several assumptions of our model.

7.1 Global pollutant

In this paper, we consider a local pollutant. Assuming a global pollutant would mean that the damage of emissions is independent of firms’ location. In this case, relocation would affect the damage neither in the home country nor in the foreign country. Therefore, governments have no incentive to shift emissions abroad. Also, emission shifting does not result in negative spillovers for the foreign government, as also the damage in the foreign country remains unaffected by location.

For a global pollutant, a different problem arises: Governments, especially those of small countries, have no incentive to reduce emissions at all, neither through providing incentives for producing less or producing in a different way nor through providing incentives for relocation. Instead, governments have strong incentives for freeriding.

In our case of local pollutants, governments have an interest in reducing local emissions through both channels: reducing production or changing the way of production and relocation.

7.2 Consumption emissions

We consider production emissions. However, many products can also generate environmentally harmful effects during use. For instance, more energy-consuming products are more harmful to the environment during use than less energy-consuming products. Passenger cars also differ in pollution.Footnote 8

Consumption emissions are independent of production location, and governments have no interest in shifting emissions abroad. Environmental policy instruments such as a consumption related emission tax do not provide a relocation incentive. But they may have an effect on product design and market access.

7.3 Marginal damage

We consider a damage function with an increasing marginal damage. Therefore, the optimal tax rate depends on the quantity produced. Assuming a constant marginal damage would result in a lower optimal emission tax (that is independent of the quantity produced), as the optimal tax rate is equal to the marginal damage. The incentive for governments to induce relocation is lower. From a firms’ perspective, lower tax rates result ceteris paribus in lower relocation incentives.

So far, we have considered a damage function \(D=\frac{1}{2}q_{i}^{2}\) for a baseline case. A change in marginal damage affects location equilibria, but does not change the overall pattern of equilibria; see Appendix A.5 for a lower marginal damage (\(D=\frac{1}{4}q_{i}^{2}\)) and a higher marginal damage (\(D=\frac{3}{4}q_{i}^{2}\)), respectively.

For all three damage functions considered, a higher value for \(\lambda\) increases the probability that at least one firm relocates, given the optimal emission tax set by the government in H. A higher product quality markup weakens competition between firms and reduces quantities. When relocation cost is sufficiently low, it pays off for at least one firm to trade fixed cost of relocation for a lower variable cost. A higher (lower) marginal damage increases (decreases) the optimal tax rate, which, in turn, increases (decreases) the incentive of firms to relocate. Governments are more (less) interested in shifting emissions abroad when the marginal damage is higher (lower).

7.4 Quality-related damage

In this paper, pollution and environmental damage is independent of product quality. This could be the case if the environmental damage stems from product components that are similar in all products irrespective of the quality level, such as electrical insulation, metals such as copper etc. But it could also be considered that product quality is related to environmental damage. If more resources are needed for the production of high-quality products, high-quality products could be considered to cause a higher environmental damage. On the other hand, it could also be assumed that the production of low-quality products causes a more severe environmental damage, because they use low-cost production processes that involve higher emissions.

Consider that low-quality products are also produced at a low environmental quality, i.e., cause a higher damage than high-quality products. If the firm selling the low-quality product is the “brown” firm, it generates higher damage and higher tax revenue. Due to the limited ability to pass-through the environmental tax, it has higher relocation incentives than the firm that provides high-quality products.

If the firm selling the high-quality product is the “brown” firm, it causes higher damage and higher tax revenue, but it is more able to increase prices. Therefore, it has a lower relocation incentive than the firm that provides low-quality products.

When the brown firm relocates, relocation has a greater effect on emission reduction in the home country. Therefore, the government is more interested in relocation of the brown firm. However, relocation also results in a greater loss in tax revenue. The joint effect on welfare is not obvious ex ante.

Consider, e.g., that the firm selling the high-quality product emits twice the amount of pollution as the low quality firm. Then it generates twice the tax revenue but due to the increasing marginal damage four times the damage. In this case, relocation of the brown firm increases welfare. This provides an incentive for governments to set a higher tax rate to induce the relocation of the brown firm.

Since the firm selling the high-quality product is more able to pass through the tax because demand for high-quality products is less elastic than demand for low-quality products, it is easier for governments to induce relocation of the firm that sells low-quality products. If the firm that sells low-quality products is the brown firm, governments may want to induce its relocation.

7.5 Market structure

In this paper, we assume two countries, two firms, and three scenarios (one country applies the emission tax, both countries apply the emission tax, both countries cooperate in taxation). While this setting is highly stylized, it allows us to analyze relocation incentives in a tractable manner.

From the perspective of one country, the rest of the world can be perceived as the “foreign” country. Of course, this “foreign” country is not homogeneous. For instance, import cost may differ depending on from where exactly goods are shipped – but this does not change our results in principle. Considering more than two countries that set environmental taxes results in a more complex interaction of governments – but the main strategic interaction between governments can also be shown for the two-country case.

Similarly, the duopolistic case is highly stylized. In principle, market structure is to be seen as a result of an evolutionary process of entry and exit decisions in which more than two firms may be involved. However, more complex interaction with more than two firms would distract the focus from the problem under consideration.

Considering more firms and more product quality levels would intensify competition between firms because products are closer substitutes. It would be more difficult for firms to pass through the cost of environmental regulation, especially if not all firms are obliged to pay an emission tax. This increases relocation incentives. However, stronger competition decreases profits, so it is harder for firms to pay the fixed cost of relocation. This decreases relocation incentives.

7.6 Macroeconomic perspective

Our analysis is based on a microeconomic model. However, emission taxation, the choice of production location, and weakened competition may also be analyzed in a macroeconomic perspective. The emission tax considered in our paper targets a local pollutant. Therefore, this very tax could be considered of having only a modest macroeconomic impact. In addition, the tax can be considered as being only one among many other taxes. The tax would be more macro-economically relevant if it affected a key industry. If almost ubiquitous greenhouse gases were taxed, the macroeconomic impact would be more important as such a tax affects many industrial activities.

8 Conclusion

This paper has analyzed the effect of an emission tax on the relocation decisions of firms when a duopolistic market is characterized by vertical differentiation of product quality. Especially, we have focused on two distortions, weakened competition caused by a product quality markup and an externality caused by a local pollutant.

If it is only the home country applying an environmental tax in a time-consistent manner, various Nash-equilibria of location decisions exist depending on the product quality markup and relocation cost. The Nash-equilibria depend discontinuously on the cost of relocation and the product quality markup. The higher the product quality markup, the higher is the probability that at least one firm relocates to the foreign country.

If also the foreign country applies an emission tax and both governments set taxes non-cooperatively, the government in the home country cannot set a tax so that the firm selling the high-quality product relocates and the firm selling the low-quality product stays in the home country. But if both countries cooperate, this location equilibrium is possible.

Weaker competition caused by quality differentiation can be seen as a substitute for environmental policy as both reduce emissions. However, weaker competition makes firm relocation more likely, which results in emission shifting instead of emission reduction.

Our results also point at a link between competition policy and environmental policy. Strengthening competition may have an adverse effect on the environment. However, weaker competition makes relocation as a response to local environmental policy more likely and thereby results in emission shifting instead of emission reduction. Weaker competition may therefore need to be accompanied by a higher degree of policy coordination.

The possibility of relocation creates a transboundary dimension even for local environmental damages and local environmental policy measures. Therefore, international coordination of environmental policy may be needed even for local pollutants to avoid emission shifting. The Industrial Emissions Directive of the European Union may be seen as an attempt to coordinate environmental policy measures also for local pollutants within the European Union.