1 Introduction

Negative steps, such as weirs and sills, have been installed in rivers for water intake, riverbed degradation prevention, and riverbed gradient stabilization [1]. Several cross-sectional structures exhibiting characteristics akin to negative steps with abrupt width widening include weir notches and the confluences of small streams with a step. These steps facilitate the transition of water flow by generating jumps with intense turbulent motion, connecting flows with different energy heads upstream and downstream of the step, thereby causing the water to lose its kinetic energy [2,3,4,5]. The process of energy loss through these spontaneous jumps has attracted significant interest due to its aesthetic appeal and its practical significance as an efficient mechanism for downstream energy dissipation [6, 7]. The determination of the jump form based on the disparity in energy head between upstream and downstream flow conditions serves as a robust benchmark for validating numerical models, particularly those focused on water surface and turbulent behavior [5, 8]. In addition, the risk of erosion damage to surrounding river structures during the energy loss process is high [9]; therefore, understanding the hydraulic jump mechanism is of great engineering importance.

The form of a jump on a flatbed without a step is determined by the Froude number (F) just upstream of the jump, and a critical Froude number of 1.7 serves as the boundary between jumps with breaking waves, including strong jumps, steady jumps, oscillating jumps, weak jumps, and undular jumps without breaking waves [10,11,12]. This classification of jump forms based on the Froude number has also been applied to hydraulic bores classification, including propagation celerity [13], in which breaking bores occur under the conditions of F > 1.7, and undular bores with soliton fission occur under F < 1.2 [14, 15]. Experiments on jumps on flat riverbeds have been conducted downstream of a sluice gate that controls the upstream hydraulic conditions. Moreover, experimental studies on jumps with wave breaking have focused on air entrainment characteristics and velocity distribution in the jump region [16, 17]. In the study of undular jumps without wave breaking, the critical Froude number depends not only on the Froude number of the supercritical flow just upstream of the jump, but also on the degree of the development condition of the boundary layer [18].

Several studies on the jets downstream of negative steps have primarily focused on submerged jets with sufficiently large drop-offs [19]. However, in jumps downstream of a river-crossing structure with a negative step, the critical flow is generated just upstream of the step, resulting in a wave jump and submerged jets with wave breaking [2, 3, 5]. The wave jump (Fig. 1a) occurs when the downstream water level is relatively high, whereas the submerged jet (Fig. 1b) occurs when the downstream water level is low and the difference from the upstream water level is greater than a certain degree. Unlike the case of flatbed jumps, it is known that there are conditions where both forms can co-exist depending on the initial conditions. Suzuki et al. [2, 3] experimentally investigated the mixing scale and velocity distribution in wave jumps and submerged jets downstream of a relatively low-negative step in a uniform-width channel and proposed a transition condition formula based on their experimental results. Ohtsu and Yasuda [4] conducted a systematic experimental investigation of various flow conditions at various relative step heights and aspect ratios and classified the jump conditions. Fujita [20] used particle image velocimetry (PIV) to investigate the spatial distribution of the mean velocity and turbulence statistics in an open channel flow at a negative step with a trench and investigated the relationship between the periodical flow pattern and conditions of the depth of the trench and the Froude number. Although studies have focused on hydraulic jumps in abrupt width expansion [21], research on the interaction between vortices induced by the negative step and abrupt width expansion is severely limited. In many cases, rivers contain negative steps of relatively small scale with side edges. Generally, when a negative step generates strong transverse vorticity and induces a change in the horizontal flow conditions, a complex three-dimensional (3D) vortex structure emerges [22, 23]. Therefore, revealing the phenomenon of hydraulic jumps under the interaction of strong separation vortices in two directions is crucial.

Fig. 1
figure 1

A wave jump and submerged jet downstream from a relatively low negative step for the same hydraulic conditions of discharge and tailwater depth at a co-existing condition

Full size image

In recent years, numerical models have been utilized to investigate open-channel flow dynamics in hydraulic jumps. In this regard, Bayon et al. [11] and Macián-Pérez et al. [24] performed 3D calculations with the Reynolds-averaged Navier–Stokes (RANS) equations with Flow-3D and OpenFOAM using the renormalization group (RNG) k-ε model for high-Froude-number hydraulic jumps with wave breaking, and both models showed good results for the water surface profiles, velocity, and pressure distribution in the jump. Biswas et al. [25] performed vertical two-dimensional (2-D) RANS equation calculations for an undular jump using the k-ω shear stress transport (SST) model, and the wave height was well reproduced using a power-law velocity distribution at the upstream end boundary condition. Ma et al. [26] performed numerical simulations of a hydraulic jump with wave breaking using RANS and detached eddy simulation (DES). They revealed that RANS yields a steady water surface in the wave-breaking region, whereas DES yields an unsteady water surface, accurately evaluating the air entrainment rate. Jesudhas et al. [27] applied the DES to a jump with high Froude numbers and showed that the DES is effective in revealing not only the water surface shape but also the turbulent structure in the breaking wave. Thus, the average flow and turbulent structures for various forms of hydraulic jumps were predicted in straight channels. Uchida [5] analyzed the flows downstream of the negative step using an advanced depth-integrated model with the ability to calculate non-equilibrium velocity and pressure vertical distributions [28]; they found that jumps with wave breaking are characterized by discontinuous water-surface velocity and the process of recovery of the velocity distribution with energy dissipation, whereas the non-hydrostatic pressure distribution is essential for wave jumps. However, the causal factors for hydraulic jumps remain uncharacterized, wherein water flow undergoes spontaneous morphological transformations based on the hydraulic conditions preceding and following the step.

To clarify why and how the flow is able to take the appropriate jump form for given boundary conditions, this study investigates the transition and formation mechanisms of wave jumps and submerged jets with wave breaking downstream of a negative step with abrupt width expansion through physical experiments and numerical simulations. The transition limits of these jumps and jets are discussed and formulated in relation to the critical condition of the undular jump on a flatbed, considering energy loss. Furthermore, the mechanical causes of transition limits are examined.

2 Experimental setup

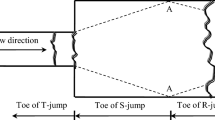
In the experiment, a rectangular straight channel 24 m in length and 0.8 m in width, with a gradient of 1/1000, was utilized. Figure 2 illustrates the installation of a smooth-surfaced vinyl chloride side wall in the channel. The channel width, B1, is set to 0.2 m for a distance of 2.0 m upstream from the negative step, which had a height w of 0.1 m. The channel width, B2, was changed to 0.2, 0.4, and 0.6 m (resulting in width expansions at the negative step, ΔB, of 0, 0.2, and 0.4 m, respectively) for a distance of 3.0 m downstream from the step.

Fig. 2
figure 2

Experimental channel (unit: m)

Full size image

The dimensional analysis is often used to represent complex phenomena such as hydraulic jumps [6, 29]. For the dimension analysis without referring to the momentum equations, mechanical considerations and investigations based on experiments or numerical simulations are indispensable in interpreting the results [29]. In this study, the energy loss downstream of the step is examined through the momentum equation, considering that the form of the hydraulic jump is decided by the difference in the total energy between upstream and downstream conditions, which is the reason for the occurrence of weak jumps or bores with wave breaking when F > 1.7. The hydraulic variables around the negative step governing the flow dynamics are defined as shown in Fig. 3, where q is the unit width discharge, w is the condition of the step, ΔH = H0 – Ht is head loss (H0 and Ht are the total heads upstream and downstream of the step, respectively). For hydraulic boundary conditions, q is the unit width discharge and ht is the tailwater depth downstream of the step. Here, hc is critical depth, indicating that the upstream of the step is subcritical flow except in the vicinity of the step, which means that no boundary condition other than flow rate q is required at the upstream end. Note that the shear stress at the bottom is negligible compared to the energy loss with the jump and the viscosity and surface tension [30] are excluded from the discussion. The wave jump is considered to be relatively unaffected by scale effects, whereas air entrainment caused by wave breaking with large energy loss is considered to be greatly affected by scale. There are still some issues to be solved regarding scale effects, but the Froude number can be considered to be the primary parameter that dominates the jump pattern, as seen in jumps and bores in flat river beds [10, 13, 29]. The transition conditions from submerged jet to wave jump (SW) were measured by gradually increasing the tailwater depth, ht, from the submerged jet conditions, whereas the transition conditions from wave jump to submerged jet (WS) were induced by gradually decreasing the tailwater depth, ht, from the wave jump conditions. Water levels were measured at three points on the section located 3.0 m downstream from the step using a point gauge. Experimental conditions for the jump-type transitions of the SW and WS are listed in Table 1. Six different channel width-expansion ratios, and the transition conditions were investigated at variable flow rates of 5, 10, 15, 20, 25, and 30 l/s.

Fig. 3
figure 3

Hydraulic variables downstream of the negative step

Full size image
Table 1 Experimental conditions
Full size table

Table 2 lists the hydraulic conditions used in the experiments and numerical simulations to investigate the flow structures downstream of the negative step with several expansion ratios for a flow rate of 20 l/s. Water surface profiles were measured using a servo-type wave height meter. The tailwater depth ht downstream end condition is regulated by a weir placed at the downstream end of the channel.

Table 2 Hydraulic conditions to investigate flow structures in submerged jet and wave jump
Full size table

3 Jump-type transition conditions required for energy loss

3.1 Jumps downstream of a negative step in a straight channel

Before discussing the effects of the abrupt width expansion at the negative step on the transition condition of the jump pattern, we present the factors that control the transition condition of the jump pattern for a straight channel of uniform width.

Figure 4 illustrates the transition conditions of SW and WS for cases where the channel width is uniform, specifically B1 = 0.2 and 0.4 m. The wave jump and submerged jet occur in the upper and lower zones from the gradient lines plotted in Fig. 4, respectively, whereas both jump types can be observed between the two lines, where the jump type depends on the history of the flow condition (Fig. 1). As reported in the existing literature [2, 3], the wave jump, submerged jet, and co-existing zones are defined by two lines of SW and WS transition conditions characterized by two non-dimensional parameters, ht/hc and w/hc (hc: critical depth), which are not sensitive to the variation in the channel width, B, for the conditional range of a vertical two-dimensional flow unaffected by shear forces on the sidewalls. Both transition relative depths, ht/hc, increase with the relative step height, w/hc. In the range shown in Fig. 4, the relationship between ht/hc and w/hc appears to be linear for both the SW and WS transitions.

Fig. 4
figure 4

The transition conditions of SW and WS downstream of a negative step in straight channels. SW submerged jet to wave jump, WS wave jump to submerged jet

Full size image

Let us derive the transition conditions of the jump types, considering that the type is determined by the required energy loss of the jump. Based on the definitions of the variables in Fig. 3, the energy loss in the hydraulic head upstream and downstream of the negative step ΔH can be expressed using Eq. (1).

$$\Delta H = H_{0} - H_{t} = \frac{3}{2}h_{c} + w - h_{t} - \frac{{q^{2} }}{{2gh_{t}^{2} }}$$
(1)

The experimental result presented in Fig. 4 clearly demonstrates that a submerged jet with breaking waves causes a greater energy loss than that caused by a wave jump. Therefore, a submerged jet can be considered to occur when the energy loss between the upstream and downstream flows is greater than ΔHWS (i.e., ΔH > ΔHWS). By dividing both sides of Eq. (1) by hc, we obtain Eq. (2) to represent the transition condition of the energy loss to the submerged jet from the wave jump.

$$\frac{\Delta H}{{h_{c} }} = \frac{3}{2} + \frac{w}{{h_{c} }} - \frac{{h_{t} }}{{h_{c} }} - \frac{1}{2}\left( {\frac{{h_{c} }}{{h_{t} }}} \right)^{2} > \frac{{\Delta H_{WS} }}{{h_{c} }}$$
(2)

The wave jump and submerged jet formed downstream of the negative step were considered analogous to the undular jump and weak jump on a flat riverbed, respectively, in terms of the presence or absence of wave breaking. The transition conditions from an undular jump to a weak jump with breaking the undular wave and from the weak jump to an undular jump are induced for an almost constant Froude number, F1 = 1.7 (F1: Froude number for the flow upstream from the jump) [10]. Notably, in an experiment conducted in the same channel as the present experiment by the authors (channel width of 0.2 m with a smooth flatbed) with a unit flow rate q = 0.05–0.15 l/s, the transition from the undular jump to the weak jump (UW) and from the weak jump to the undular jump (WU) occurred at F1 values of 1.70 ± 0.08 and 1.65 ± 0.03, respectively. The energy loss of the upstream and downstream flows at the hydraulic jump on the flatbed ΔHflat is given by Eq. (3), which is based on the depths, h1 and h2, of the upstream and downstream flows from the jump, respectively [10].

$$\frac{{\Delta H_{flat} }}{{h_{c} }} = \frac{{(h_{2} /h_{1} - 1)^{3} }}{{4h_{2} /h_{1} }}\frac{{h_{1} }}{{h_{c} }}$$
(3)

Equation (3) can be rewritten using the Froude number upstream of the jumping water F1 as

$$\frac{{h_{2} }}{{h_{1} }} = \frac{1}{2}\left( {\sqrt {1 + 8F_{1}^{2} } - 1} \right),\quad \frac{{h_{1} }}{{h_{c} }} = F_{1}^{ - 2/3}$$
(4)

Substituting F1 = 1.7 into Eq. (4) as the transition limit between the weak and undular jumps for h2/h1 and h1/hc, Eq. (3) yields ΔHflat/hc = 0.078. With a ΔHflat/hc value of 0.078, Eq. (1) yields the transition condition for the energy loss between undular and weak jumps on the flatbed.

$$\frac{{h_{t} }}{{h_{c} }} + \frac{1}{2}\left( {\frac{{h_{c} }}{{h_{t} }}} \right)^{2} < \frac{w}{{h_{c} }} + \frac{3}{2} - \frac{{\Delta H_{flat} }}{{h_{c} }} \approx \frac{w}{{h_{c} }} + 1.42$$
(5)

The transition limit from Eq. (5) is shown in Fig. 4. The dashed line neglects the second term on the left-hand side of Eq. (5); however, the effect of the second term is limited to the region where w/hc is extremely small, indicating that the transition limit can be expressed as a straight line. A comparison of the experimental results with the transition limit of Eq. (5) indicates that the SW and WS transitions downstream of the negative step are more likely to transition to the wave jump without wave breaking at lower tailwater depths, ht, than the jump on the flatbed. This can be attributed to the energy loss behind the negative step, which delayed the transition to a jump with wave breaking. With increasing w/hc, the energy dissipation within the separation zone behind the step increases. This implies that ht/hc increases with increasing w/hc for a relatively small step height. Considering that the energy loss behind the negative step is proportional to the step height w, the transition of the SW and WS behind the step is given by Eq. (6), with the coefficient a for the additional energy loss term from Eq. (5).

$$\frac{{h_{t} }}{{h_{c} }} = (1 - a)\left( {\frac{w}{{h_{c} }}} \right) + 1.42$$
(6)

Figure 4 validates that the transitions between the submerged jet and wave jump are well explained by Eq. (6) with ht/hc and w/hc for a relatively small step height w/hc < 10 by using the appropriate values of a and neglecting the second term on the left side of Eq. (5). To minimize the root-mean-square error (RMSE) of Eq. (6) to the experimental results in Fig. 4, we obtain aSW = 0.14 and aWS = 0.21 for the transition conditions from the submerged jet to wave jump (SW) and the wave jump to the submerged jet (WS), respectively. Thus, the energy loss increased by the presence of the negative step aw/hc in Eq. (6) is considerably larger than the amount that can be lost by the undular jump in a flat riverbed, ΔHflat/hc = 0.078, except for the condition of an extremely small step height (w/hc < 1). This is because the separation behind the negative step generates eddies with a mean flow scale size and dissipates energy through turbulence, indicating that the negative step plays an important role in energy dissipation, thereby determining the hydraulic jumping pattern downstream from the step. Moreover, the coefficient for the WS transition aWS = 0.21 is larger than the coefficient for the SW transition aSW = 0.14, which indicates that the wave jump causes a larger energy loss owing to the larger separation area behind the negative step for the transition condition. This is an important aspect for the co-existence regime between the two transition lines in Fig. 4, where both the wave jump and submerged jet can exist stably depending on the initial conditions (Fig. 1). Essentially, the additional energy loss induced by the step is greater for the wave jump than that for the submerged jet, resulting in the co-existence regime of both jumps downstream of the negative step.

3.2 Jump downstream of the step with an abrupt width expansion

Figure 5 plots the transition of SW and WS downstream of the step with an abrupt width expansion. The larger the abrupt width expansion to the channel width, the smaller the tailwater depths are required for both transitions of SW and WS, indicating that the wave jump can be maintained for larger energy loss conditions. This is because, in addition to the negative step, the energy dissipated with the abrupt width expansion compensates for the necessary energy loss to connect the flow conditions upstream and downstream of the step. Therefore, Eq. (6) is modified by adding the loss at the abrupt width expansion of the channel to derive the transition-limit condition. As in the case of a negative step in a straight channel, where the parameter w/hc = wB/Bhc is introduced to express the additional energy loss with the step in Eq. (6), we assume that the ratio of the increase in the cross-sectional area, htΔB/Bhc, is proportional to the additional energy loss induced by the abrupt width expansion for a relatively small ratio.

Fig. 5
figure 5

Comparison of transition conditions of SW and WS downstream of a negative step between straight and abrupt width expansion channels

Full size image

Considering the cross term for the loss with the negative step, Eq. (6) is revised by introducing two coefficients, b and c, as follows:

$$\frac{{h_{t} }}{{h_{c} }} = (1 - a)\left( {\frac{w}{{h_{c} }}} \right) + 1.42 - b\left( {\frac{{h_{t} \Delta B}}{{Bh_{c} }}} \right)\left\{ {1 + c\left( {\frac{w}{{h_{c} }}} \right)} \right\}$$
(7)

The coefficients representing the SW and WS transitions in Table 3 were obtained to minimize the difference between the experimental results and Eq. (7). Based on these coefficients, Eq. (7) can reproduce the transition pattern of the jump formed downstream of the negative step with an abrupt width expansion, as illustrated in Fig. 6. In Table 3, as in the case of the negative step in aWS = 0.21 and aSW = 0.14, the coefficient for the abrupt width expansion, b, was larger for WS than that for SW as bWS = 0.45 and bSW = 0.30. Notably, b is greater than twice a, indicating that the energy loss caused by the abrupt width increase is much larger than that for the negative step. This trend is attributed to be the vertical axis separation vortex created by the abrupt width expansion is rotated by the vertical velocity distribution formed by the hydraulic jump and negative step, creating 3D vortex motions, which effectively convert the energy of the larger mean flow scale vortex into the turbulent energy of smaller-scale eddies (Fig. 7). In particular, the rotation of the horizontal vorticity in the wave jump case is considered to produce a strong secondary flow [21] at the boundary of the abrupt width expansion, which triggers the momentum exchange in the transverse direction and results in large energy losses. Moreover, the coefficient c of the cross term between the abrupt width expansion and the negative step was negative. This implies that the energy loss owing to the negative step is smaller than that for the straight channel because the energy loss in the mean flow is lost owing to the energy loss at the abrupt width expansion. Presumably, the case with an abrupt width expansion makes the flow 3D, and thus, more prone to wave breaking, as described hereafter.

Table 3 Analysis of energy loss based on Eq. (7) for the transition of SW and WS
Full size table
Fig. 6
figure 6

Comparison of transition conditions of SW and WS between measurement and estimated by Eq. (7)

Full size image
Fig. 7
figure 7

Three-dimensional vortex motion generated by channel expansion at a negative step. The red vortex tubes generated by flow separation enhance momentum exchange and energy loss

Full size image

4 Numerical investigation of flow structures and energy loss with turbulence kinetic energy (TKE) distribution

In Sect. 3, we presented an energy-based approach to understanding why the transition occurs between wave jump and submerged jet with wave breaking by examining the energy loss contributions from the negative step and abrupt width expansion. In this section, to clarify how the transition occurs, we delve into the specifics of the energy loss mechanism and the factors influencing the transition of hydraulic jumps and wave breaking using numerical simulation results.

4.1 Numerical method and validation of the transition mechanism

In this study, we used interFoam [31], a two-phase flow solver for air–water flows, with the one-fluid model in OpenFOAM. The governing equations were the RANS equations, and the VOF method [31] was used for free-surface analysis. The k-ω SST model [32, 33] was chosen as the turbulence model. In this model, the k-ω model [34], which has been validated for evaluating velocity profiles in the low-Re region, was used near the wall, whereas the standard k-ε model was used in the region away from the wall. The RNG k-ε model [35] is generally used in numerical simulations of hydraulic jumps with wave breaking, such as weak jumps and submerged jets. However, no significant difference occurred in the water surface profile calculations among the turbulence models (k-ε, k-ω SST, and RNG k-ε models) reported by Bayon-Barrachina and Lopez-Jimenez [32]. Given the importance of accurately reproducing wave breaking induced by waveform gradient increases to calculate the transition from wave jumping to diving jets, we employed the k-ω SST model for numerical investigations after our preliminary calculations with k-ε, k-ω SST, and RNG k-ε models and comparisons with the experiment. The channel configurations used in the numerical investigation are as follows: hc = 0.10 (m), w/hc = 0.99, and B1/hc = 1.99 for both channels; ΔB = 0.2 m for the abrupt width expansion channel.

Figure 8 compares the temporal averaged water surface profiles for (a) submerged jet and (b) wave jump conditions in a straight channel. Herein, the downstream water depth is ht/hc = 1.91 for the submerged jet and ht/hc = 2.07 for the wave-jump condition. In a submerged jet, the water surface curvature changes abruptly at the junction of the free jet overflowing the step and the hydraulic jump of submerged jet zone downstream of the step. The calculated value was lower than the experimental value at the junction. This discrepancy arises from the complex two-phase air–liquid flow caused by a large amount of air entrainment at the junction point and the ambiguity in the definition of the water surface (in the analysis, the water surface is defined as the point where the liquid phase ratio is 0.5). However, in the jump section downstream of the junction point, the calculation results successfully reproduced the change in the curvature of the water surface. This result is similar to the results reported in the previous studies conducted with the k-ω SST model [36]. The convex curvature of the submerged jet is attributed to the attenuation of the velocity head of the vertical velocity profile due to momentum mixing [5], indicating that the numerical results can adequately evaluate the form and extent of energy loss in the jump. However, the wave jump connected the free jet smoothly to the downstream flow condition over a relatively longer distance compared to the submerged jet, with the wave height decaying in the downstream direction. As the water surface curvature reverses in a wavy jump, a non-hydrostatic pressure component is also generated alternately, resulting in wave generation [5]. Comparing the calculation and experimental results, the minima and first wave heights related to the water jump were optimally reproduced; however, the wavelengths were slightly shorter in the experimental results. Biswas et al. [25] also reproduced the vertical two dimensional calculations with different mesh size using k-ω SST model, which presented the over-estimation of wavelength, reproducing wave heights of the undular jumps. Our preliminary calculations comparing k-ε, k-ω SST, and RNG k-ε models indicated the different wave amplitudes, but no significant differences in the first wavelength among the calculations. The discrepancy in the wavelength may be attributed to the proximity of the wave jump to the transition condition for the submerged jet, causing some waves to break and resulting in unstable experimental results. Further studies are required to more accurately reproduce the experimental results, including refining the evaluation method of the computational mesh, turbulence model, and air–water phase model to capture the water surface.

Fig. 8
figure 8

Comparisons of water surface profiles for submerged jet and wave jump downstream of a negative step between calculations and measurements

Full size image

Figure 9 illustrates a comparison of the transition conditions between the numerical results and the transition formula (7). Similar to the experiments, the numerical calculations for the transition conditions were performed by gradually increasing the downstream water depth from the lower downstream end-depth for the SW transition and by gradually decreasing the water depth from the higher downstream depth for the WS transition. The transition conditions were defined as the water depth at which the jump pattern transformed and stabilized. The calculated transition condition depths were slightly lower than the estimated results of the line given by Eq. (7) for the straight channel; nevertheless, they were still within the range of variation of the experimental data scattered around the line. The calculation results also effectively reproduced the experimental results for the transition conditions of the step with abrupt width expansion. To comprehensively examine the transition mechanism of the jump forms, SW and WS, and to gain insights into the effects of negative steps and rapid width expansion, further careful discussions are needed to determine the local flow microstructure and turbulence structures. The calculation results are considered appropriate in this regard.

Fig. 9
figure 9

Comparisons of transition conditions of SW and WS downstream of a step between calculations and measurements for straight and abrupt width expansion channels

Full size image

4.2 Energy loss in the jumps and the transition conditions

The energy loss patterns in the wave jump and submerged jet downstream of the negative step were investigated using numerical simulations. Figure 10 presents the longitudinal distribution of the dimensionless depth-integrated turbulence kinetic energy (TKE) relative to the kinetic energy of the critical flow in a straight channel. In a submerged jet, the TKE is intensively generated at the plunging point of the free jet into the flow downstream of the step, where the kinetic energy of the mean flow is converted to the TKE through vortex action, resulting in a significant energy loss over a short distance. Because of the large energy loss at the plunging jet point, if the difference in the energy head between the flows upstream and downstream of the step is small, the energy loss required to maintain the submerged jet conditions cannot be rendered by the mean flow, and the submerged jet must transform into a wave jump. The minimum energy loss to sustain the submerged jet is considered to be aSW = 0.14, as calculated through Eq. (7). In contrast, a wave jump generates TKE over a longer distance without rapid decay, resembling a submerged jet. However, the TKE value in the first wave is considerably smaller than that in a submerged jet, indicating a limit to turbulence energy generation in wave jumps and the amount of kinetic energy that can be dissipated in a wave jump condition. If the energy loss required in the upstream and downstream flows exceeds the available amount, the wave jump transforms into a submerged jet, inducing wave breaking. The maximum energy loss associated with a wave jump is represented by aWS = 0.21 in Eq. (7).

Fig. 10
figure 10

Longitudinal distribution of depth integrated TKE in the submerged jet (Red) and wave jump (Blue) downstream of the negative step in a straight channel by the numerical results

Full size image

Figure 11 showcases the planar distribution of the dimensionless depth-integrated TKE relative to the kinetic energy of the critical flow downstream of a negative step with an abrupt width expansion. Here, ht/hc values of 1.62 and 1.99 are given as the downstream boundary conditions for the wave jump and the submerged jet, respectively. Figure 12 shows the calculated water surface profiles and surface velocity distributions for submerged jet and wave jump. The phenomenon of backflow vortices in the expansion region induces energy losses as they circulate into the mainstream flow just downstream of the jet plunge. In submerged jets, the flow from the expansion region is dominant, whereas, in wave jumps, the surface flow from the main channel is stronger, leading to a rapid recovery of surface flow velocity in the expansion region over a short distance. In terms of turbulent energy, the TKE was produced in the abrupt-width expansion area downstream of x/hc = 2 In both cases, t. In a submerged jet, the peak position of the TKE spreads as the water flows downstream, migrating from the expanded area toward the main flow direction. This phenomenon arises from fluid mixing between the stagnant zone of the expanded channel and the backwaters near the water surface of the submerged jet in the main channel. In contrast, in wave jumps, the large TKE generated in the abrupt width expansion area gradually spreads downstream, curving into the expanded channel. This behavior results from fluid mixing between the high flow near the water surface of the wave jump in the main channel and the stagnant water in the expanded channel.

Fig. 11
figure 11

Planar distribution of depth integrated TKE in the submerged jet and wave jump downstream of the negative step with abrupt width expansion according to the numerical results

Full size image
Fig. 12
figure 12

Calculated water surface profiles and velocity for submerged jet and wave jump

Full size image

In both types of jets, the vertical-axis vortex generated on the boundary between the main channel and the expanded channel downstream from the jet plunging point is bent by the vertical velocity distribution induced by the jet with a horizontal vortex behind the negative step (Fig. 7). This creates a large 3D vortex structure, resulting in rapid energy conversion from the mean flow to turbulent flow. With the addition of these large energy losses resulting from the abrupt width expansion, the minimum energy loss required to maintain the submerged jet and the maximum energy loss of the wave jump becomes larger, resulting in the water depth decreases by bSW = 0.30 and bWS = 0.45, as calculated through Eq. (7), respectively. Moreover, the regime of the wave jump condition (Fig. 5) becomes more prominent. In particular, the area of high TKE is extended for the wave jump condition, indicating that the energy loss due to the abrupt width expansion is large. The minimum energy loss required to maintain the submerged jet in the case of a straight channel, as well as in the case of abrupt width expansion, is greater than the maximum energy loss for the wave jump. Consequently, the coefficients of the WS transition are greater than those of the SW transition, aSW < aWS, bSW < bWS. This difference represents the co-existence region of the submerged jet and wave jump, as previously mentioned. Surprisingly, a well-designed hydraulic jump system naturally changes to a more energy-loss jump form, generating a large TKE as the difference between the energy heads of the flows upstream and downstream of the step increases. When these transitions were reversed, that is, aSW > aWS and bSW > bWS, neither jump form existed near the transition condition. For example, this condition represents the alternating repetition of two jump forms for a negative step with a trench [20]. In particular, such cyclic jumps also occur in moving bed phenomena downstream of a negative step [2, 6]. Alternatively, different forms of water jumps may potentially occur. Notably, the jump downstream of a negative step with an abrupt width expansion represents a 3D jump form with a change in the flow field in the transverse direction, which is not as easy to classify into two forms as in the case of a straight channel.

As previously discussed, the transition conditions of the jump downstream of a negative step with an abrupt width expansion were explained from the viewpoint of energy loss, particularly in terms of the minimum energy loss for the submerged jet and the maximum energy loss for the wave jump. However, the energy loss only describes the flow condition of each jumping form and does not explain the mode of jump transition. Therefore, a numerical model was used to investigate the flow wherein the transition occurs.

4.3 Transition mechanism

Figure 13 depicts the variations in the temporal averaged water surface profiles downstream of a negative step in the straight channel, specifically highlighting (a) the SW transition with increasing downstream water depth and (b) the WS transition with decreasing downstream water depth. The flow over the step causes critical flow, which transitions into supercritical flow. However, the flow conditions downstream of the negative step propagate upstream of the step because of the non-hydrostatic pressure distribution caused by the water surface curvature and separation [5]. As the downstream water depth increases, the pressure behind the step increases, and the water surface curvature decreases, resulting in an increase in the depth of flow over the step and a decrease in the angle of the plunging jet. In this numerical simulation, when the water surface angle (θ) yields tanθ < 0.18, the submerged jet state could not be maintained, and the flow transformed into a wave jump. However, the height of the wave jump increased as the downstream water depth decreased during the WS transition. Increasing the wave height in the wave jump enhances the energy loss. Furthermore, as the downstream water depth decreases, the wave steepness surpasses the critical gradient to maintain the wave jump and causes wave breaking, resulting in a transition into a submerged jet. As shown in Fig. 13b, wave breaking occurs in the second wave at Ht = 0.197 m, which propagates upstream and transitions into a submerged jet. The water depth at the downstream end of the wave steepness gradient, beyond the wave-breaking limit for the WS transition, is lower than that for the SW transition. Therefore, the plunging jet angle for the WS transition is larger than the SW transition limit, which maintains the submerged jet. This trend indicates that the minimum energy loss for a submerged jet is determined by the angle of the plunging jet required to sustain it, while the maximum energy loss for a wave jump is determined by the critical wave steepness required to prevent wave breaking.

Fig. 13
figure 13

Temporal averaged water surface profiles and critical angle of plunging jet at the (a) SW and (b) WS transition conditions downstream of the negative step in the straight channel

Full size image

The impact of abrupt width expansion on the transition condition is further examined in Fig. 14, which compares the water surface profiles for both channels along the centerline of the main channel and the expanded channel under co-existence conditions of the submerged jet and wave jump in a straight channel with ht = 0.202 m. In the abrupt-width expansion channel, the water surface at the center of the main channel exhibits a wave jump, albeit with a lower wave height compared to that in the straight channel. This discrepancy arises due to the propagation of the high water level in the upstream direction through the stagnant water region in the expanded channel. Consequently, the pressure behind the negative step increases, the overflow curvature decreases, and the water depth increases, resulting in a significant reduction in the angle of the plunging jet, preventing its transition into a submerged jet.

Fig. 14
figure 14

Comparison of water surface profile between straight and abrupt width-expansion channels under the co-existence condition for straight channel step

Full size image

Figure 15 presents the water surface profiles of the submerged jet and wave jump conditions along the center of the main channel (Y = 0.1 m) and right bank (Y = 0.02 m) under the co-existence condition of ht = 0.176 m for the abrupt-width expansion channel. The water surface angle of the jets is larger than that in the straight channel under identical co-existing conditions (tan θ = 0.18 in Fig. 14). Notably, due to the different downstream water-level conditions, comparing the water surface angles of only one side of the jet boundary as representatives of the critical plunging jet angle is not appropriate. However, the wave height of the wave jump at the center of the main channel is lower than that of the straight channel, whereas the wave height along the right bank is almost identical to that of the co-existing area in the straight channel. The lower transition condition of the water depth in a channel with an abrupt width expansion can be attributed to the lower wave height resulting from the propagation of higher water depths downstream to the back of the negative step, which increases the pressure. Consequently, both the minimum energy loss for the submerged jet condition and the maximum energy loss for the wave jump increased.

Fig. 15
figure 15

Comparison of water surface profiles between submerged and wave jump under the co-existence condition for abrupt width-expansion channel

Full size image

5 Conclusions

In this study, we conducted experimental and numerical investigations to explore the transition mechanism of the downstream jump pattern in a negative step with an abrupt width expansion, where critical flow occurs above the step. The key findings of this study can be summarized as follows.

The transition between the submerged jet and the wave jump downstream of a negative step was explained as the minimum energy loss for the submerged jet and the maximum energy loss for the wave jump. The transition condition encompassed the sum of the energy losses at the transition condition between the weak jump and the undular jump on the flatbed, as well as the energy loss behind the step. The co-existence region was manifested because the additional energy loss induced by the negative step was larger for the wave jump compared to the submerged jet.

The existence of an abrupt width expansion at the negative step decreases the transition depth between the submerged jet and wave jump by the additional energy loss. By incorporating this energy loss, we successfully formulated the transition condition between the wave jump and the submerged jet with/without abrupt width expansion in a unified manner. This formulation encompassed the case of a flat riverbed for the undular and weak jumps.

Numerical analysis using a 3D RANS model revealed that a submerged jet produces turbulent kinetic energy more rapidly than a wave jump, primarily owing to the presence of large vortices near the plunging jet point. Moreover, the energy dissipated at a shorter distance than that in a wave jet. Furthermore, in the case of a step with an abrupt width expansion, the vertical vortex generated by the separation of the expanded channel boundary was rotated by the vertical velocity distribution caused by the jets and the separation behind the step, resulting in a larger energy dissipation with a higher TKE production through the 3D vortex motion.

The transition between the wave jump and submerged jet is determined by the angle of the plunging jet and the wave breaking caused by the increase in the wave height during the wave jump. Our findings demonstrate that the presence of an abrupt width expansion leads to the propagation of high downstream pressure through the stagnant water zone in the expanded channel. This, in turn, increases the pressure behind the step, reduces the plunging jet angle and wave height, and ultimately decreases the critical depth condition for the transition in the case of a step with abrupt width expansion.