1 Introduction

Natural convection in sloping water bodies (lakes, reservoirs, wetlands) can occur when surface waters are heated or cooled with the same rate [1,2,3,4,5].

The natural convection induced by diurnal heating and cooling in a sloping water body has been investigated by few researchers [6,7,8]. Field observations [9,10,11] have shown that the circulation in the littoral region of a lake is not in phase with the thermal forcing, while Farrow and Patterson [6] confirmed the lag of the flow response to the thermal forcing and indicated that such a lag can be up to 12 h. Lei and Patterson [7], based on numerical simulations, found out that there is a distinct time lag in the overflow response to the switches of the thermal forcing and this lag depends on the Grashof number. Dittko et al. [8] used LES to model two lake sidearms which are part of Lake Audrey, NJ USA and Lake Alexandria, SA, Australia. They concluded that the average and maximum volumetric flow rates have a linear relationship with the cubic root of the Rayleigh number for both heating and cooling phases in the two side arms.

The vegetation presence in the shallow nearshore region of sloping water bodies and its effect on natural convection induced by cooling or heating have been studied by few researchers [12,13,14,15,16,17]. The vegetation effects on diurnal heating and cooling have been investigated numerically by Lin and Wu [18] and Ji et al. [19] in a water body of simple triangular cross section. Using asymptotic solutions, they determined the effect of vegetation shading (blockage), during daytime heating and nighttime cooling, on the exchange flow rates and the general circulation in a sloping water body with a very small slope (equal to 10−5). The asymptotic solutions were able to provide reasonable estimates of horizontal velocity and exchange flow rates, however they ignored the non-linear terms of the governing equations, excluded the flow instabilities, and limited the vegetation density.

In this work a 2D water body model is used, which consists of a compound cross section. One region with a slope So and length Ls and another region with horizontal bottom (deep region) and length Ld is considered. The vegetation, with porosity φ (the ratio of volume occupied by water to the total volume), is present in the sloping region with length Lv equal to Ls and its effect on the periodic solar radiation and surface cooling is investigated numerically for the first time. A 2D simulation can adequately reproduce the nature of a flow that is approximately 2D in nature. It cannot capture 3D aspects of the flow. More details about the validity of 2D simulations in such studies are discussed by Lei and Patterson [1]. The unsteady 2D Volume-Averaged Navier-Stokes (VANS) equations are solved in conjunction with the unsteady 2D Volume-Averaged equation in the vegetated region, using the Boussinesq approach used by Papaioannou and Prinos [20]. The averaging of the Navier-Stokes equation and the energy equation is based on the method of Volume Averaging according to Whitaker [21]. In the non-vegetated region these equations are simplified to the classical NS and Energy equations.

Initially, the non-vegetated sloping water body is considered for validation purposes since numerical results of Lei and Patterson [7] are available. Also, it is used for comparing the results with those of the vegetated cases and identifying the vegetation effects. The water body with vegetation in the sloping region is considered next. During the daytime heating due to solar radiation, a time-dependent thermal forcing is applied at the top free surface with a peak flux Io in the deep region and Iv, equal to φIo, in the vegetated region (the top of the emergent vegetation blocks 15% of the incoming radiation). During the nighttime cooling, heat loss through the free surface occurs with peak flux Io in the deep region and Iv, equal to φIo, in the vegetated region. Also, for investigating the effect of the vegetation shading, the case with complete blocking of incoming heating and cooling by the top of vegetation is considered (Iv = 0.0). This is an extreme case, however, in the field, Lövstedt & Bengtsson [15] found that Phragmites australis vegetation, with vertical straws and horizontal leafs, was able to reduce the heating 85% in comparison with that in the open lake.

Special emphasis is given to the vegetation effects (a) on the exchange flow rates during heating and cooling for water bodies with shallow waters (h is less than the penetration depth of the solar radiation (h < η-1), (b) on the time lag of the flow response to the switch between daytime radiative heating and nighttime surface cooling. Also, the effect of vegetation shading on the flow response during heating and cooling is considered.

2 Model specification and numerical procedure

2.1 Model specification

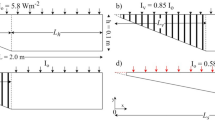
A two-dimensional (2D) model of the sloping water body is considered (Fig. 1). Its cross section is compound with two distinct regions, (1) a sloping region with length Ls = 1.0 m, maximum flow depth h = 0.1 m, slope So (= h/Ls) equal to 0.1 and vegetation length Lv equal to Ls, (2) a region of length Ld and uniform water depth (horizontal bottom) with no vegetation. The total length is L = 2.0 m. The model dimensions are those used by Lei and Patterson [7] for comparison purposes. The adopted Cartesian coordinate system starts at the left bottom point of the model (Fig. 1). The (a) geometry is the non-vegetated case with peak radiation flux Io equal to 50 W/m2. The absorption coefficient η is set equal to 6.2 m−1 (the dimensionless absorption coefficient, ηh, is equal to 0.62). The maximum water depth h is less that the penetration depth of the solar radiation (h < η−1) and hence shallow water body is considered. It is used in this work for validation purposes and computational results are compared against those of Lei and Patterson [7]. The vegetation porosity φ is equal to 0.85 and the peak flux Iv is either equal to 0.85 Io, or 0.0. The slope So is kept constant and equal to 0.1 which is considered as a large bottom slope. The Rayleigh number Ra, based on peak radiation flux Io and maximum flow depth h, is set equal to 1.21 × 108 (Ra = \(\frac{{g\beta {{\rm I}_o}{h^4}}}{{{\rho _o}{C_p}v{k^2}}}\), g = acceleration due to gravity, β = thermal expansion coefficient, ρο = initial water density, CP = specific heat of water, v = kinematic viscosity, k = thermal diffusivity). The same Ra number has been used by Lei &Patterson [7] for both experiments and numerical simulation.

Fig. 1
figure 1

Water body Geometry with and without vegetation

Full size image

Two types of thermal forcing are developed for simulating the diurnal cycle. They are represented by the sinusoidal function Isurf = Iosin(2πt/P) which is shown in Fig. 2.

Fig. 2
figure 2

Periodic thermal forcing at the free surface of the water body

Full size image

The flux at the water surface is Isurf, the peak flux is Io, t is the time and P is the period of the thermal forcing (14,000 s). During the first half of every forcing cycle (shaded areas of Fig. 2) solar radiation enters the water body from the free surface and hence Isurf is positive. It is absorbed by the water according to the Beer’s law and adopting a single-band model, the radiation flux I at a given distance from the free surface is given as I = Isurf ×e(h−y)η. During the second half of the forcing cycle there is a heat loss through the free surface and hence Isurf is negative. The present diurnal model ensures that the total heat absorbed by the water body during daytime is in balance with the total heat released by the water body during the night cooling. The parameters associated with the flow dynamics are (a) the Prandtl number Pr (= 7.07) and (b) the Rayleigh number Ra (= 1.21 × 108). Heat exchange between water and vegetation is neglected.

2.2 Governing equations

For the numerical simulation, the unsteady VANS equations are solved [Eqs. (1) and (2)] in conjunction with the unsteady VAE equation [Eq. (3)] in the vegetated region, using the Boussinesq approach. The derivation of these equations is based on the method of Volume Averaging used by Whitaker [21] and is presented in detail by [22,23,24,25], among others. In the non-vegetated region these equations are simplified to the classical NS and Energy equations. These equations are shown below:

$$\frac{{\partial {{\left\langle {{U_i}} \right\rangle }^f}}}{{\partial {x_i}}}=0$$
(1)
$$\frac{{\partial {{\left\langle {{U_i}} \right\rangle }^f}}}{{\partial t}}+{\left\langle {{U_j}} \right\rangle ^f}{\frac{{\partial \left\langle {{U_i}} \right\rangle }}{{\partial {x_j}}}^f}= - \frac{1}{{{\rho _o}}}{\frac{{\partial \left\langle p \right\rangle }}{{\partial {x_i}}}^f}+\frac{\partial }{{\partial {x_j}}}\left[ {v\left( {\frac{{\partial {{\left\langle {{U_i}} \right\rangle }^f}}}{{\partial {x_j}}}+{{\frac{{\partial \left\langle {{U_j}} \right\rangle }}{{\partial {x_i}}}}^f}} \right)} \right]+g\beta \left( {{{\left\langle T \right\rangle }^f} - {{\left\langle {{T_o}} \right\rangle }^f}} \right)+{F_i}$$
(2)
$${\frac{{\partial \left\langle T \right\rangle }}{{\partial t}}^f}+{\left\langle {{U_j}} \right\rangle ^f}{\frac{{\partial \left\langle T \right\rangle }}{{\partial {x_j}}}^f}=\frac{\partial }{{\partial {x_j}}}\left[ {k\left( {{{\frac{{\partial \left\langle T \right\rangle }}{{\partial {x_j}}}}^f}} \right)} \right]+<{S_h}{>^f}$$
(3)

where Ui = velocity in the direction i, p = pressure, T, To = fluid temperature and initial temperature respectively, Fi = resistance term due to vegetation and Sh = heat source term determining the absorption of the solar radiation by the water body during daytime heating (It is set to zero during nighttime cooling).

The symbols < > and < > f indicate the superficial and the intrinsic volume average of a parameter A (scalar, vector, or tensor) respectively which are defined as:

$$\left\langle A \right\rangle =\frac{1}{V}\int\limits_{{{V^f}}} {AdV} {\text{ and }}{\left\langle A \right\rangle ^f}=\frac{1}{{{V_f}}}\int\limits_{{{V^f}}} {AdV}$$
(4)

where Vf is the fluid volume contained in a volume V. The latter consists of a horizontal slab, extensive enough to eliminate plant-to-plant variations, but thin enough to preserve the characteristic variation of properties in the vertical dimension.

The term Fi, due to vegetation, is given by the Darcy-Forchheimer equation which includes linear and non-linear forces using porous media characteristics (e.g., vegetation permeability kp)

$${F_i}= - \varphi \frac{v}{{{k_p}}}{\left\langle {{U_i}} \right\rangle ^f} - {\varphi ^2}\frac{{{C_f}}}{{\sqrt {{k_p}} }}{\left\langle {{U_i}} \right\rangle ^f}\left| {{{\left\langle {{U_i}} \right\rangle }^f}} \right|$$
(5)

where φ = vegetation porosity, kp = vegetation permeability (m2) and Cf = dimensionless empirical coefficient. The permeability kp and the dimensionless coefficient Cf are determined by the following Eqs. (6) and (7) [26, 27].

$${k_p}=\frac{{d_{{50}}^{2}{\varphi ^3}}}{{{a_1}{{(1 - \varphi )}^2}}}$$
(6)
$${C_f}={b_1}\frac{{1 - \varphi }}{\varphi }\frac{{\sqrt {{k_p}} }}{{{d_{50}}}}$$
(7)

where d50 is the grain diameter, a1 and b1 are empirical coefficients. When the porous medium consists of cylinders then d50 is equal to 1.5 d (d is the diameter of the cylinders, Lowe et al. [26]). The empirical coefficients a1 and b1 take different values, depending on the type and the length scale of the porous medium. For example, Losada et al. [28] obtained values of a1 between 1000 and 2000 and b1 between 0.3 and 1.1. For φ = 0.85, d50 = 9.0 mm, α1 = 1000 and b1 = 1.1 the values for Cf and kp are calculated as: Cf = 0.484, kp = 5.04 × 10−6 m2.

The term Sh is given by the following:

$$S_{h} = \left\{ {\begin{array}{*{20}l} {I_{o} \sin \left( {\frac{{2\pi t}}{P}} \right)\eta e^{{ - \eta (h - y)}} ,} & {{\rm if}\,\sin \left( {\frac{{2\pi t}}{P}} \right) \ge 0} \\ {0,} & {{\rm if}\,\sin \left( {\frac{{2\pi t}}{P}} \right) < 0} \\ \end{array} } \right.$$
(8)

The boundary conditions are defined as follows:

  1. a)

    The left tip on Fig. 1 is cut off at x = 0.016 m for avoiding a singularity and the side wall is assumed to be rigid non-slip and adiabatic.

  2. b)

    The side wall in the deep region is also assumed to be rigid non-slip and adiabatic.

  3. c)

    The bottom of the water body is also rigid, non-slip and the following thermal flux is applied, assuming that the radiation absorbed by the boundary is conducted back into the fluid, Lei & Patterson [29].

    $$\frac{{\partial {\text{T}}}}{{\partial {\text{n}}}} = \left\{ {\begin{array}{*{20}l} { - \frac{1}{{{\text{k}}\rho _{o} {\text{C}}_{{\text{p}}} }}\varphi I_{o} \sin \left( {\frac{{2\pi t}}{{\text{P}}}} \right){\text{e}}^{{ - \eta (h - y)}} ,} & {{\text{if}}\,\sin \left( {\frac{{2\pi t}}{{\text{P}}}} \right) \ge 0} \\ {0,} & {{\text{if}}\,\sin \left( {\frac{{2\pi t}}{{\text{P}}}} \right) < 0} \\ \end{array} } \right.$$
    (9)

    where n is the direction normal to the bottom boundary.

  4. d)

    The water surface is assumed to be stress free and the applied thermal boundary condition is given by:

    $$\frac{{\partial {\text{T}}}}{{\partial {\text{y}}}} = \left\{ {\begin{array}{*{20}l} {0,} & {{\text{if}}\,\sin \left( {\frac{{2\pi t}}{{\text{P}}}} \right) \ge 0} \\ { - \frac{1}{{{\text{k}}\rho _{o} {\text{C}}_{{\text{p}}} }}\varphi {\text{I}}_{o} \sin \left( {\frac{{2\pi t}}{{\text{P}}}} \right),} & {{\text{if}}\,\sin \left( {\frac{{2\pi t}}{{\text{P}}}} \right) < 0} \\ \end{array} } \right.$$
    (10)

Initially, the water body has a temperature To = 293.15 K and is motionless.

2.3 Numerical scheme and mesh dependency tests

The Fluent 15.0.7 CFD code is applied for the numerical computations using a control volume technique. The extra source terms Fi and Sh are introduced to the initial equations using User Defined Functions (UDF) based on C + + code. The computational domain is divided into finite control volumes on which the governing equations are integrated. The Gambit program is used for the mesh generation. The segregated solution method is used and the velocity-pressure coupling is achieved with the SIMPLE algorithm. The PRESTO scheme is used for discretizing the pressure equation (continuity equation), while the QUICK scheme is used for the momentum and the energy equations [30]. The time step is set equal to 0.1 s. Such a time step is selected, in conjunction with the Δx (the grid size in the x direction) and the computed velocities, for satisfying the Courant-Friedrichs-Lewy (\(\text{C}\text{F}\text{L}=\text{u}{\Delta }\text{t}/{\Delta }\text{x}<1\)) criterion. The maximum CFL number in the simulations was 0.52. The total simulation time is 10P.

Three different grids were tested for examining the solution dependence on the grid spacing. The maximum number of grid points (in the x and y directions) was 1000 × 100 = 1 × 105, 4000 × 200 = 8 × 105 and 8000 × 400 = 3.2 × 106. The grid size in the y direction was smaller in the vicinity of the top and bottom boundaries while it was uniform in the x direction. The smallest cell dimensions (Δx × Δy), adjacent to the top and bottom boundary, were 1.0 mm × 0.16 mm, 0.5 mm × 0.08 and 0.25 mm × 0.04 mm for the three meshes while the biggest ones, in the deep section of h = 0.1 m, were 1.0 mm × 1.4 mm, 0.5 mm × 0.7 mm and 0.25 mm × 0.35 mm. The mesh with 3.2 × 106 was finally used which gave better structured plumes (more complete eddying motion in the plumes) in both the cooling and heating phases. Detailed results about the grid-sensitivity analysis are presented by Papaioannou and Prinos [17].

3 Analysis of results

Numerical results (temperatures, streamlines, exchange flow rates) for all cases are presented and analysed in the following paragraphs.

Initially the sloping water body with no vegetation is presented and analysed which is used for validation purposes as well as for comparison with the cases with vegetation. Figure 3 shows the temperature difference ΔΤ (= T − To), made dimensionless with Ioh/κ, at six characteristic times of the last forcing cycle. The first three (t/P = 0.0, 0.1 and 0.5) correspond to the daytime heating process while the last three (t/P = 0.7, 0.9 and 0.98) to the night cooling.

At the beginning of the last cycle (t/P = 0.0) the isotherms show that gravity currents, formed during the previous cooling phase, continue to flow downward along the sloping bottom and the horizontal bed. At t/P = 0.1 the temperature of the water body increases due to the absorption of radiation. The increase is higher in the shallow region of the water body and less in the deeper part.

Fig. 3
figure 3

Contours of (ΔT/(Ioh/κ)) at various stages for a diurnal thermal forcing (water body with no vegetation)

Full size image

The above findings are supported by the streamlines (ψ/ροLsk) shown in Fig. 4 at the same times (ψ is defined as mass discharge (kg/s)). Initially, at t/P = 0.0 the streamlines show a large-scale overturning circulation with multiple cores which has been developed during the preceding cooling phase as it can also be seen at t/P = 0.9 and 0.98 of the last cycle. At t/P = 0.1 a cellular flow structure is shown in the deep region of the waterbody which is due to the rising thermals while a large recirculation is observed in the sloping region of the water body, due to the development of a horizontal temperature difference between the shallow and the less shallow waters of the sloping region.

Fig. 4
figure 4

Streamlines (ψ/ροhk) at various stages for a diurnal thermal forcing (water body with no vegetation). The dashed and solid lines show clockwise and anticlockwise rotation respectively

Full size image

This large recirculation, with clockwise rotation, is further developed during the heating phase which extends through the whole water body (t/P = 0.5). During the cooling phase the growing thermal boundary layer at the free surface and the instabilities in the form of sinking plumes break the general circulation, developed previously, and at t/P = 0.7 a cellular flow structure is formed in the main part of the deep region. Also, the gravity currents, developed in the nearshore sloping region, result in a recirculation pattern which flushes the whole sloping region and part of the deep section. As the gravity currents continue to travel into the deep region this recirculation expands further covering the whole water body (t/P = 0.9 and 0.98). The above findings during the heating and cooling phase are in agreement with those found by Lei and Patterson [7] for shallow waters (Fig. 3 of Lei and Patterson [7]).

Τhe variation of the averaged exchange flow rate Q (made dimensionless with k) with time t/P is presented in Fig. 5 for the last five cycles in conjunction with the corresponding thermal forcing. Q is determined by integrating the flow rate Q(x), at a given x location, along the horizontal direction x. Hence,

$$Q=\frac{1}{L}\int\limits_{0}^{L} {Q(x)} dx{\text{ where }}Q(x)=\frac{1}{2}\int\limits_{0}^{h} {\left| u \right|} dy$$
(11)

Figure 5 shows that, in the beginning of the daytime heating, the thermal forcing increases continuously, however the Q/k decreases, due to the residual night time circulation from the preceding cooling phase. This decrease continues up to approximately t/P = 0.06 for each cycle. After t/P = 0.06, Q starts to increase in phase with the increasing thermal forcing.

Fluctuations of Q during the heating phase are apparent, especially around the heating peaks which are due to the instabilities associated with the bottom heating. When the radiative heating becomes sufficiently weak and the instabilities are weak Q decreases, even in the beginning of the cooling phase. There is also a time lag between the cooling increase and the exchange flow increase while thermal instabilities are present for most of the cooling phase.

After the time of maximum cooling (e.g. t/P = 0.75) the exchange flow rate continues to increase slightly and then starts to decrease. The strength of the circulation in the heating phase and the associated exchange flow rate is approximately of the same order as that in the cooling phase. Computed results are found in satisfactory agreement with those of Lei and Patterson [7]. The mean Q/k of the present simulations is 192.3 while that of Lei and Patterson [7] is 217.8 (11.7% difference).

In the following paragraphs the vegetation effects on the flow development and flow regimes are investigated for the water body with a vegetated sloping region.

Fig. 5
figure 5

Calculated horizontal exchange flow rate over one the last five cycles (Ra = 1.21 × 108)

Full size image

Figures 6 and 7 show the isotherms and the streamlines respectively for vegetation in the sloping region, with Iv = 0.85Io (the vegetation blocks 15% of the incoming heating and cooling). At t/P = 0.0 the isotherms show that the gravity currents, formed during the previous cooling phase (t/P = 0.98), move very slowly, due to the lower horizontal temperature gradient developed in this case, and remain in the sloping region even at t/P = 0.1. The rest of the water body is heated continuously with hot rising plumes developed at the bottom of the deep region (instabilities) due to the re-emission of energy from the bottom wall to the water. At t/P = 0.50 the shallow region is heated faster than the deep region but not as fast as the shallow non-vegetated region (Fig. 3), due to Iv = φΙο. In the cooling phase (t/P = 0.70) cold sinking plumes are developed along the top surface of the water body, however, the horizontal temperature gradient and the developed gravity currents are weak and move slowly in the sloping region for the whole cooling phase (t/P = 0.90 and 0.98) and for the subsequent heating phase. Most of the water body has mean temperatures above the initial ones (positive ΔT) for the full cycle.

Streamlines (Fig. 7) are in accordance with the temperature contours. At t/P = 0.0 the gravity currents have flushed a major part of the sloping vegetated region, after their formation late in the cooling phase, while at t/P = 0.1 the flushing covers the whole sloping region. A circulation is developed, at the scale of the sloping region, with anticlockwise rotation while, in the rest of the water body, a cellular flow structure is developed with adjacent cells of opposite rotation. At the time of minimum heating (t/P = 0.50) the circulation in the sloping region is of opposite rotation while in the deep region the flow structure observed previously remains active. In the cooling phase, the initial cooling and the cold plumes from the top surface contribute to the development of the cellular flow structure everywhere. This remains for the whole cooling phase without the development of large-scale circulation and the flushing of the whole water body as in the case with no vegetation in the sloping region (Fig. 4).

Fig. 6
figure 6

Contours of (ΔT/(Ioh/κ)) at various stages for a diurnal thermal forcing (Iv = φIo)

Full size image
Fig. 7
figure 7

Streamlines (ψ/ροhk) at various stages for a diurnal thermal forcing (Iv = φIo). The dashed and solid lines show clockwise and anticlockwise rotation respectively

Full size image

When the vegetation is such that blocks completely the incoming heating and cooling, the generated isotherms and streamlines (Figs. 8 and 9 respectively) are qualitatively different than those in the two previous cases. At t/P = 0.0 the isotherms show that two distinct regions, formed during the previous cooling phase (t/P = 0.98), are present in the water body, one with temperatures greater than To (the major part of the sloping vegetated region, due to Iv = 0.0) and another one with temperatures less that To, the deep section which is continuously heated and cooled. When heating continues (t/P = 0.10) the near surface heated water moves from the shallow to the deep region. The latter is heated continuously with hot rising plumes developed at the bottom of the deep region (instabilities) due to the re-emission of energy from the bottom wall to the water. At t/P = 0.50 the deep region has been heated more than the sloping region, a horizontal temperature gradient has been developed between the two regions and gravity currents appear along the bottom of deep region which flush the whole deep region and half of the vegetated sloping region. In the cooling phase (t/P = 0.70) cold sinking plumes are developed along the top surface of the deep region, however, the sloping region keeps high temperatures since it is not cooled. At t/P = 0.90 and 0.98 cooling of the deep region continues and the two distinct regions, observed at t/P = 0.0, start to develop with mean temperatures below the initial ones (negative ΔT) in the deep region and above the initial ones (positive ΔΤ) in the sloping region.

Fig. 8
figure 8

Contours of (ΔΤ/(Ioh/κ)) at various stages for a diurnal thermal forcing (Iv = 0)

Full size image

Streamlines (Fig. 9) are in accordance with the temperature contours. At t/P = 0.0 a circulation pattern, developed during the previous cooling phase, is still active, due to the temperature difference between the sloping region (not cooled) and the deep region (cooled). At t/P = 0.1 the instabilities at the bottom of the deep region result in a cellular flow structure which continues to develop and at the end of the heating period (t/P = 0.50) the circulation in the whole water body is of opposite rotation, due to the gravity currents developed at the bottom of the deep region. Such an overturning circulation is split in two major cellular patterns, of opposite rotation, in the deep region during the cooling phase (t/P = 0.70). At later stages of the cooling phase (t/P = 0.90 and 0.98) the cell with the clockwise rotation expands towards the side wall of the deep region, due to the increasing temperature difference between the sloping region and the deep one, and as a result a large circulation pattern, of clockwise rotation, is dominant until the beginning of the heating phase (t/P = 0.0).

Fig. 9
figure 9

Streamlines (ψ/ροhk) at various stages for a diurnal thermal forcing (Iv = 0). The dashed and solid lines show clockwise and anticlockwise rotation respectively

Full size image

The variation of the averaged exchange flow rate Q (made dimensionless with k) with time t/P is presented in Fig. 10 for all the abovementioned cases in conjunction with the corresponding thermal forcing. Computed results for the case with no vegetation are found in satisfactory agreement with those of Lei and Patterson [7], as discussed also in Fig. 5. In Fig. 10 the variation of the exchange flow rate (Q/k) with time is also shown for Iv = φIo and Iv = 0.0. For the former, the exchange flow rate Q/k is significantly lower than that of the non-vegetated sloping water body (42.2%), although the peak flux in the vegetated region is only 15% less than the one in the region with no vegetation. For Iv = 0.0 the exchange flow rate Q/k is also less than that of the non-vegetated water body (32% approximately) but higher than that for Iv = 0.85Io, however, the developed circulation patterns for the two cases are qualitatively different.

Fig. 10
figure 10

Calculated horizontal exchange flow rate during the last five cycles for a water body with and without vegetation

Full size image

The vegetation effect on the variation of ΔTmax (Tmax − To), ΔTmin and ΔTavg with time is shown in Fig. 11 (a, b and c respectively). The variation of ΔTmax, made dimensionless with Ioh/κ, is similar for the no-vegetation and vegetation with Iv = 0.85Io cases (Fig. 11a), however its highest value appears earlier in the former case (t/P = 0.32). For vegetation with Iv = 0.0, the highest value is small and does not vary within the cycle. The variation of ΔTmin is also similar for the first two cases (Fig. 11b). The lowest value appears earlier again, at t/P = 0.98, for the no vegetation case while it appears at t/P = 0.99 for the vegetation case (Iv = 0.85Io). Again, the variation of ΔTmin, for vegetation with Iv = 0.0, is not significant with the lowest value below zero at t/P = 0.98. The variation of ΔTavg is more significant for Iv = 0.85Io with maximum and minimum values to be higher and appear later than those of the no vegetation case (Fig. 11c).

Fig. 11
figure 11

Diurnal variation of (a) ΔTmax, (b) ΔTmin and (c) ΔΤavg for a waterbody with and without vegetation

Full size image

Finally, the diurnal variation of the dimensionless velocity u/(k/h), at two locations along the sloping region, x/h = 4.0 and 10.0 (x/Ls = 0.4 and 1.0), is shown in Fig. 12 (a and b respectively) for the three cases considered. At x/h = 4.0, for water body with no vegetation, the velocity u is positive near the bottom of the sloping region (up to the middle of the water depth) during the whole cooling phase as well as in the beginning of the heating phase (t/P = 0.0). This is due to the gravity currents moving along the bottom of the water body towards the side wall of the deep section. During the heating period (t/P = 0.1 and 0.5) the velocity, for y/h less than 0.82, is negative, towards the nearshore region, since the faster heating of the shallow region is responsible for a large-scale circulation which is of opposite rotation to that produced during the cooling period. For water body with vegetation and Iv = 0.85Io, the velocity is less than that for the non-vegetated sloping region, due to the drag resistance exerted by the vegetation. The u profiles are similar with those of the no vegetation case, however, appear with some delay within the cycle. Near-surface profiles (up to the middle of the water depth) are negative at t/P = 0.90 and 0.98 (cooling phase) and t/P = 0.0 and 0.10 (heating phase). They are positive at t/P = 0.5 and 0.7 indicating the significant time lag between the forcing and the flow response. Finally, for complete vegetation shading (Iv = 0.0) the velocities are further reduced (up to 100%) and the u profiles are similar qualitatively with those of the water body with no vegetation.

At x/h = 10.0 (interface between the sloping and the horizontal sections of the water body) the velocity profiles for the three cases are different both quantitively and qualitatively. For the no vegetation case the velocity profiles are similar with those at x/h = 4.0 since the gravity currents, during the night cooling, have travelled down to the deep section of the water body. For vegetated sloping region with Iv = 0.85 Io the velocity profiles are quite complex since this location corresponds to the interface between the vegetated sloping section and the deep section of the water body. A three-layer flow structure is evident during the cooling period while a four-layer flow structure is shown at t/P = 0.1, however the velocities are very low especially at the top half of the water depth. Such structures (either three- or four- layer) are due to the counter-rotating cells developed at this location which, in turn, are induced by either the sinking plumes during the night (cooling phase) or the rising plumes from the bottom during the day (heating phase).

For Iv = 0.0 a three-layer flow structure is only evident at t/P = 0.1 while at the other time instants the velocity profiles are in accordance with the differential cooling between the veg. and the non veg. sections of the water body. At the end of the heating period (t/P = 0.5) the velocity profile is also compatible with the differential heating between the two sections. The three-layer structure at t/P = 0.1 is due to the formation of local convective cells along the bed of the deep section, induced by the rising hot plumes. Some cells are of opposite rotation than that of the overlying water and as a result two layers, near the bed and the free surface, have positive velocities while a middle layer has a negative velocity.

Fig. 12
figure 12

Diurnal variation of velocity u/(k/h) at (a) x/h = 4.0, (b) x/h = 10.0, for a water body with and without vegetation

Full size image

4 Conclusions

The present work considers the natural convection induced by diurnal heating (due to solar radiation) and cooling in water bodies with aquatic vegetation. The latter is present in the sloping region of the water body and is able to block partially or fully the incoming heating and cooling. The following conclusions can be derived:

  1. (a)

    For the water body with no vegetation the cold gravity currents, appearing during most of the night, due to surface cooling, are still present at the start of the day. A large-scale anti-clockwise recirculation is observed during this period. During the day a thermal boundary layer along the sloping and flat bottom is grown with an upward flow along the slope which is dominated by topographic effects later. The large-scale anticlockwise recirculation breaks down and convective cells are generated which are developed later as a large-scale clockwise recirculation.

  2. (b)

    For the water body with a vegetation in the sloping region, which allows 85% of heating/cooling from the free surface, the cold gravity currents are rather weak, appear in the sloping region late at night and early in the morning, while three recirculation regions are observed. During the day, a thermal boundary layer appears in the deep region which becomes unstable later and convective cells are generated. In the sloping region the shallow area is heated faster than the deeper one and hence a clockwise recirculation is developed. During the night, various recirculation regions of opposite rotation are formed which are due to the instabilities of the thermal boundary layer at the free surface.

  3. (c)

    For the water body with a vegetation which completely blocks the surface heating and cooling the significant difference in radiation flux and temperature between the vegetated and the non-vegetated free surface results in alternate large-scale circulation patterns with night and early day (t/P = 0.90, 0.97 and 0.0) convective currents along the free surface and late day (t/P = 0.50) gravity currents along the bottom with a large- scale overturning circulation.

  4. (d)

    The variation of the exchange flow rate, the maximum, minimum and average temperature of the water body with vegetation in the sloping region indicates that the exchange flow rate is lower (42.2%) for a vegetated sloping region with Iv = φΙο than that with no vegetation while the variation of temperature (ΔTmax, ΔTmin and ΔTavg) is not significant for Iv = 0.0 in comparison with that of the other two cases.

  5. (e)

    The velocity profiles at two locations within the sloping region (x/h = 4.0 and 10.0) indicated the decrease of velocity due to vegetation resistance at x/h = 4.0, while, at the vegetated/non-vegetated interface (x/h = 10.0), profiles, of low velocities, with three- or four- layers are apparent due to the counter-rotating cells developed there.