Functional and variables selection in extreme value models for regional flood frequency analysis

Abstract

The problem of estimating return levels of river discharge, relevant in flood frequency analysis, is tackled by relying on the extreme value theory. The Generalized Extreme Value (GEV) distribution is assumed to model annual maxima values of river discharge registered at multiple gauging stations belonging to the same river basin. The specific features of the data from the Upper Danube basin drive the definition of the proposed statistical model. Firstly, Bayesian P-splines are considered to account for the non-linear effects of station-specific covariates on the GEV parameters. Secondly, the problem of functional and variable selection is addressed by imposing a grouped horseshoe prior to the coefficients to encourage the shrinkage of non-relevant components to zero. A cross-validation study is organized to compare the proposed modeling solution to other models, showing its potential to reduce the uncertainty of the ungauged predictions without affecting their calibration.

1 Introduction

An effective prediction of flood phenomena is crucial for protecting and managing territories. A rigorous hydrological approach to the problem can be profitably supported by flood frequency analysis, which is a data-based framework aimed at providing reliable estimates of expected return periods of a flood event characterized by a certain magnitude. When data from multiple gauging stations placed in a target catchment or area are included in the analysis, a regional flood frequency analysis is carried out (Hosking and Wallis 1997). The main advantage of this approach is the possibility to borrow strength from available stations to obtain calibrated and reliable estimates also for ungauged locations. This task represents one of the primary challenges within the field of hydrology, and the use of statistical tools can be a crucial asset in the integration of diverse information sources (Blöschl et al. 2013). In the framework of regional flood frequency analysis, a pioneering approach is the flood index by Dalrymple (1960). Such a method is characterized by a multi-step procedure, where the main stages can be summarised in (i) classifying stations in homogeneous regions; (ii) choosing a suitable frequency distribution for the locations included in a region; (iii) estimating the distribution parameters, commonly relying on the L-moments algorithm. For an overview of this approach, see Hosking and Wallis (1997).

An alternative strategy enabling the estimation of return levels, even for ungauged locations, relies on modeling the sequence of yearly maxima of river discharge (m³/s) through a suitable distribution. This can be done by assuming that the distribution parameters are dependent on covariates and other station-related factors. In flood frequency analysis, different distributions are suggested such as the Pearson III, the Log-Normal, or the Generalized Extreme Value (GEV) distributions (Millington et al. 2011). In this paper, the choice falls on the GEV distribution, which represents a cornerstone of extreme value theory as it is the limiting distribution of a sequence of scaled maxima (Coles 2001) and it is particularly general, embedding the Frechet, Gumbel, and Weibull distributions as special cases. The GEV distribution has already been exploited in regional flood frequency analysis, often adopting a Bayesian inferential approach. For example, Thorarinsdottir et al. (2018) use it to study floods in Norway, including in the analysis of some features of the stations and the related sub-catchments. A similar modeling strategy is also set by Jóhannesson et al. (2022), which propose a computationally efficient procedure for its estimation, exploiting the representation of the model as a generalized latent Gaussian model. They also include in the predictors spatially structured random effects, as done, among the others, by Dyrrdal et al. (2015) and Geirsson et al. (2015) in modeling precipitation extremes. This model architecture is also used, for example, by Huerta and Sansó (2007) to analyze Ozone concentration extremes, Lee et al. (2013) to model wind data, and Räty et al. (2022) for sea levels. A limitation of such a strategy is caused by the conditional independence assumption among stations: this allows only to predict marginal return levels. If multivariate return levels are needed, a max-stable modeling framework should be pursued (Asadi et al. 2015).

In flood frequency analysis, this class of GEV regression models generally assumes linearity among the covariates and parameters. This could represent an important restriction in the analysis of complex environmental processes that can be relaxed by defining flexible models based on spline regression. In this paper, the setting of Bayesian P-splines by Lang and Brezger (2004) is adopted. Its convenience is due to the parsimonious parameterization brought by the usage of basis functions and the automatic penalization for roughness induced by the use of smoothing priors for splines coefficients (Fahrmeir et al. 2010). Räty et al. (2022) proposed their usage in modeling sea level extremes. Other examples of extreme values models that include spline regressions can be found in Lee et al. (2013), which exploited Bayesian multivariate adaptive regression spline in modeling extreme loads in wind turbines and Yousfi and Adlouni (2017) which discuss and compare different penalization methods for B-splines. Lastly, it is worth mentioning the body of literature focusing on frequentist spline models, such as Chavez-Demoulin and Davison (2005), Padoan and Wand (2008) and Rohmer et al. (2021), for which interesting computational tools are also provided (e.g., the evgam package available for R, Youngman 2022).

In this paper, data from stations located in the Upper Danube River basin are analyzed with the aim of carrying out a regional flood frequency analysis. The exploratory analysis pointed out that the relationship between station-specific covariates and the GEV parameters is strongly non-linear, motivating the proposal of a GEV regression model with Bayesian P-splines. In this framework, another interesting problem is the selection of relevant regressors. For example, Dyrrdal et al. (2015) carry out this step through a Bayesian model averaging step in a regional flood frequency analysis model that assumes linearity. The use of P-splines poses an additional problem of function selection, in order to obtain a model with only relevant covariates showing a parsimonious representation of their effect, i.e., their impact on parameters. This task was tackled by Scheipl et al. (2012), which proposed a particular formulation of spike-and-slab prior that hierarchically performs both the selection steps at once. An interesting prior distribution that is able to mimic the behavior of the spike-and-slab prior is the horseshoe (HS, Carvalho et al. 2010 ), which does not introduce discrete latent variables and, for this reason, it is also implementable within the popular Stan probabilistic language (Carpenter et al. 2017). The HS prior can be extended to define a grouped HS prior (Xu et al. 2016) that is able to perform both variable and functional selection. Such a prior distribution is adopted for the coefficients involved in the GEV regression with P-splines and its effectiveness in improving the predictions of return levels for ungauged locations is discussed by means of a cross-validation study.

The rest of the paper is organized as follows. Section 2 contains an introduction to extreme value theory and the GEV distribution, setting also basic notations. The Danube data are introduced in Sect. 3, together with an exploratory analysis that motivates the development of the proposed modeling solutions, which are defined in Sect. 4. The empirical results coming from a cross-validation study and from the analysis of the whole dataset are shown in Sect. 5, whereas Sect. 6 offers some concluding remarks.

2 Basic concepts of extreme value theory

When the main interest of a statistical procedure is to describe a phenomenon through quantities strongly related to the tails of the distribution, then it is necessary to resort to the extreme value theory. In this branch of statistics, two main approaches can be pursued: block maxima and peak-over-threshold (Coles 2001; Beirlant et al. 2004). The first strategy considers the maxima of a time block sequence, which are used to estimate the parameters of the assumed distribution: the most common is the GEV distribution, but other proposals such as the Log-Normal, the Pearson III and the Log-Pearson III distribution are largely used in flood frequency analysis. The second procedure is constituted by two steps: i) a threshold above which observations are considered to be extremes is selected; ii) the threshold exceedances are used to estimate the parameters of a Generalized Pareto distribution, that can be shown to be connected with the GEV. In this framework, alternative strategies are available in the literature: among the others, Bačová-Mitková and Onderka (2010) proposed a Weibull distribution instead of the Generalized Pareto and many studies investigate the use of mixture models (see Pan et al. 2022, for a review).

In this paper, the block maxima approach is adopted, and the GEV distribution is used as a foundation for the proposed statistical procedure. According to the Fisher–Tippett–Gnedenko theorem, the GEV distribution arises as the limiting distribution of a sequence of normalized block maxima related to a stationary series, and, hence, plays a relevant role in this framework. Indeed, this probabilistic result is exploited in extreme value theory, assuming that a sequence of recorded maxima over T distinct temporal blocks (e.g. years or days), denoted by $y_t,\ t=1,\dots ,T$, is distributed as

$$\begin{aligned} y_t|\mu ,\sigma ,\xi {\mathop {\sim }\limits ^{ind}}GEV(\mu ,\sigma ,\xi ),\quad \forall t. \end{aligned}$$

(1)

Such a distribution is ruled by three parameters: $\mu \in {\mathbb {R}}$ controls the location, $\sigma \in {\mathbb {R}}^+$ the scale and $\xi \in {\mathbb {R}}$ the shape, affecting the behavior of the distribution tails and, consequently, its support. In particular, $\xi <0$ implies a short and finite right-tail ($y_t\in (-\infty ;\mu -\sigma /\xi ]$), $\xi =0$ a light right-tail ($y_t\in {\mathbb {R}}$) and $\xi >0$ a heavy right-tail ($y_t\in [\mu -\sigma /\xi ,+\infty )$). In the latter case, $\xi$ has an impact also on the existence of the distribution moments: the moment of order $\rho$ is finite if $\xi <1/\rho$. The GEV distribution is usually defined through its cumulative distribution function:

$$\begin{aligned} F(y;\mu ,\sigma ,\xi )=\left\{ \begin{array}{ll} \exp \left\{ -\left[ 1+\xi \left( \frac{y-\mu }{\sigma }\right) \right] _+^{-\frac{1}{\xi }}\right\} , &{} \xi \ne 0; \\ \exp \left\{ -\exp \left\{ -\frac{y-\mu }{\sigma }\right\} \right\} , &{} \xi =0; \end{array} \right. \end{aligned}$$

(2)

where $[g]_+=\max (g,0)$.

In the statistical analysis of extremes, the most typical output is the estimation of return levels associated with a return period R. It is defined as the quantile $Q_p$ that has a probability equal to $p=1/R$ of being exceeded in the chosen time block. In other words, the return level $Q_{1/R}$ is expected to be surpassed once every R time blocks and, under the assumption of stationarity over time, it is defined inverting the (2) as

$$\begin{aligned} Q_{1/R}=\left\{ \begin{array}{ll} \mu -\frac{\sigma }{\xi }\left[ 1+\log (1-1/R)^{-\xi }\right] , &{} \xi \ne 0; \\ \mu -\sigma \log \left[ -\log (1-1/R)\right] , &{} \xi =0. \end{array} \right. \end{aligned}$$

(3)

Once the probabilistic setting is defined, some remarks about the inferential side of the problem are worthy. In this paper, a Bayesian approach is adopted: it is becoming increasingly popular in extreme value statistics thanks to the possibility of eliciting prior information and the natural ability to estimate the model uncertainty, propagating it in distinct steps of the analysis (Coles and Powell 1996; Coles 2001). For example, making inference on return levels (3) requires combining the three distribution parameters that need to be estimated: if the Bayesian approach is chosen and Monte Carlo Markov Chain (MCMC) methods are exploited, then draws from the parameters posterior can be combined to obtain the whole posterior distribution of $Q_{1/R}$. Once the posterior distribution becomes available, several summary statistics can be computed, including the mean for point estimates, the standard deviation as a measure of dispersion, and quantiles to construct credible intervals. It is worth noting that analogous computations can be performed within a frequentist inferential framework using approximations, such as the Delta method, and computational tools like parametric and non-parametric bootstrap methods.

3 Data on Danube river basin

The proposed strategy targets the estimation of return levels for the discharge of rivers belonging to the Danube upper basin (i.e. the part located both in Germany and Austria). The analysis considers data that are freely available from different sources to propose a general procedure that can also be replicated in other river basins. In this section, the sources of information considered in the analysis are listed, together with some remarks about the data integration procedure.

Table 1 Station-specific covariates used in the analysis

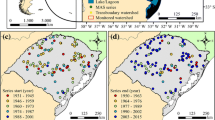
The response variable required for implementing a flood frequency analysis is the river discharge, usually measured in $m^3/s$. The time series with daily river discharge observations are retrieved from the GRDC portal (The Global Runoff Data Centre 1988), selecting all the gauging stations present in the area under study. To determine the final set of locations, some data quality and reliability checks are performed: by focusing on the period 1985–2017, only stations with a maximum of 2% daily missing observations in each year are selected. Furthermore, the coordinates of the gauges should correctly locate on the river network to avoid location inconsistencies and possible mismatches. The shapefiles with the network of main rivers in the basin are retrieved from the River Network Database (Copernicus Programme 2020). The final database is constituted by yearly maxima from $S=62$ stations that satisfied the aforementioned requirements (Fig. 1). The yearly maxima are denoted as $y_{st}$, referring to the gauging station $s=1,\dots ,62$ in the year $t=1,\dots ,33$. For brevity, ${\textbf{y}}_s$ indicates the vector of maxima related to a single station s.

Fig. 1

Gauging stations of the Danube upper basin included in the analysis

River discharge values are complemented by station-specific auxiliary variables, that are listed in Table 1. To carry out the proposed analysis, certain features of the catchment area, typically taken into account in flood frequency analysis, are incorporated into the study. These characteristics are chosen to encompass various factors that might influence the flooding process, and it is important to note that the list can be adapted to account for specific features of the basin, as briefly described in what follows. Most of the considered variables are derived from the EU Digital Elevation Model (EU-DEM, Copernicus Programme 2016), starting from the determination of stations sub-catchments through GIS-based tools within the whitebox R package (Lindsay 2016). The spatial location is accounted for by latitude and longitude, the sub-catchment area is an important measure directly related to the river discharge magnitude, whereas the features of the terrain characterizing the sub-catchment are computed by averaging indicators derived from the EU-DEM in the area (elevation, slope and aspect). In addition, the average rainfall (O’Donnell and Ignizio 2012) and the proportion of area covered by buildings (from CORINE land cover raster, Buchhorn et al. 2020 ) are considered. The final dataset is provided in the Supplementary material.

3.1 Exploratory analysis

This section presents the results of an exploratory analysis aimed at elucidating the primary motivations for the modeling strategies discussed in the paper. A two-step analysis is performed: firstly, a GEV distribution is fitted on the maxima sequences ${\textbf{y}}_s$ registered at each station s: $y_{st}{\mathop {\sim }\limits ^{ind}}GEV(\mu _s,\sigma _s,\xi _s),\ \forall t$. Then, the estimates of the GEV parameters are used as responses in Bayesian semi-parametric additive models, to investigate how they are influenced by the station-specific covariates.

In the first step, $S=62$ station-specific GEV models are fitted adopting the Bayesian approach. To retrieve the posterior distributions of the parameters, the model specification must be completed by choosing prior distributions. Given the exploratory purpose of this step, non-informative priors on the parameters are set; namely, zero mean Gaussian distributions with scale 10,000 for $\mu _s$ and $\log (\sigma _s)$, and a standard normal for the shape parameter $\xi _s$. Samples from the posterior distribution of the GEV parameters are drawn using an MCMC algorithm implemented in Stan (Carpenter et al. 2017) via its R interface, rstan (Stan Development Team 2023). As point estimates, the posterior means are then computed and are denoted as $({\hat{\mu _s}},{\hat{\sigma _s}},{\hat{\xi _s}}),\ \forall s$.

The first goal of this exploratory step is to assess whether the multivariate link function proposed in Jóhannesson et al. (2022) is reasonable for the discussed application. They propose to link the covariates to three transformations of the original set of GEV parameters, namely

$$\begin{aligned} g(\mu _s,\sigma _s,\xi _s)=\left( \psi _s = \log (\mu _s), \tau _s = \log (\sigma _s/\mu _s), \phi _s = h(\xi _s)\right) ^\top ,\ \forall s. \end{aligned}$$

(4)

The function applied to the shape parameter, denoted as $h(\xi _s)$, is characterized by the expression:

$$\begin{aligned} h(\xi _s)=a_\phi +b_\phi \log \left\{ -\log \left[ 1-(\xi +0.5)^{c_\phi }\right] \right\} , \end{aligned}$$

(5)

with specific coefficients $(a_\phi ,b_\phi ,c_\phi )=(0.062376,0.39563,0.8)$. The purpose of this transformation is to confine the range of $\xi _s$ within the interval $(-0.5,0.5)$ while maintaining an approximately linear relationship with $\xi _s$ around zero. This domain restriction ensures that the variance of the GEV distribution is finite (when $\xi _s<0.5$) and that the upper bound of the distribution remains greater than $\mu _s+2\sigma _s$ (when $\xi _s>-0.5$). Within this range, the regularity conditions required for the existence of maximum likelihood estimators are also met ($\xi _s>-0.5$). Importantly, this lower bound should not pose a limitation in flood frequency analysis, as negative values for the shape parameter are rarely observed in practice (Martins and Stedinger 2000). It is worth noting that while the shape parameter is typically directly linked to the predictor, its limited range of commonly assumed values suggests that appropriate link functions can not only highlight how covariates may influence it but also stabilize the estimates. Nevertheless, alternative transformations have been recently proposed, such as a logit function truncated to restrict the domain of $\xi _s$ to the interval $(-1,0.5)$ (mgcv package, Wood 2017). Lastly, it is important to emphasize that the subsequent developments discussed in this paper remain applicable even if a different link function is chosen.

Figure 2 reports the distributions of the estimated GEV parameters, which are contained in the following vectors: $\hat{\varvec{\mu }}=({\hat{\mu }}_1,\dots ,{\hat{\mu }}_S)^\top$, $\hat{\varvec{\sigma }}$, $\hat{\varvec{\xi }}$. We first note that all the MCMC draws from the posteriors of $\mu _s,\ \forall s$, are positive, and the distribution of $\hat{\varvec{\mu }}$ is markedly skewed. For this reason, modeling the logarithmic transformation of the location parameter might be useful to reduce the skewness, noting that the implied positivity assumption is not restrictive. Furthermore, Pearson’s linear correlation between $\log (\hat{\varvec{\mu }})$ and $\log (\hat{\varvec{\sigma }})$ is 0.987: consequently, modeling the functional $\tau _s=\log \left( \sigma _s/\mu _s\right)$ as dispersion parameter in place of $\sigma _s$ is convenient to reduce the dependency between model parameters. Lastly, the restricted interval for $\xi _s$ appears to be justifiable as only four stations show an estimate ${\hat{\xi }}_s$ higher than 0.5.

Fig. 2

Histograms of posterior means for the station-specific GEV parameters

In the second step of the analysis, the transformations of GEV parameters estimates, i.e. $\log (\hat{\varvec{\mu }})$, $\log (\hat{\varvec{\sigma }}/\hat{\varvec{\mu }})$ and $h(\hat{\varvec{\xi }})$, are used as responses in three distinct Bayesian Gaussian additive models implemented by the stan_gamm4() function of the rstanarm package (Goodrich et al. 2022). All the covariates summarized in Table 1, transformed according to the reported function, are included in the model as smooth terms through a Bayesian P-spline representation. This choice is motivated by the presence of non-linear relationships among the covariates and the target parameters (e.g., see Fig. 3). The exploration of the posterior results supports the choice of specifying smooth effects for the covariates. The residuals of the fitted additive models are studied in order to check if a residual spatial trend can be detected (Cooley et al. 2007). The variograms reported in Fig. 4 are related both to the model with all the covariates (Full) and the model without covariates (Null) and they do not point out a relevant residual spatial variation when the full model is considered.

Fig. 3

Effect of the logarithm of the elevation on the transformed parameters estimates $\log (\hat{\varvec{\mu }})$, $\log (\hat{\varvec{\sigma }}/\hat{\varvec{\mu }})$ and $h(\hat{\varvec{\xi }})$

For these reasons, our modeling proposal focuses mainly on the presence of non-linear relationships among the transformations of the GEV parameters and the covariates included in the analysis. On the other hand, the inclusion of spatially structured random effects is omitted to keep the model as simple as possible, pointing the attention on the implementation of Bayesian semi-parametric GEV models.

Fig. 4

Variograms for the residuals of the models fitted with (Full) or without (Null) covariates on the transformations of the GEV parameters

4 The proposed modeling framework

Let us consider that a collection of N maxima $y_{st}$ from $s=1,\dots ,S$ gauging stations are available for blocking times $t=1,\dots ,T$. It is assumed that, conditionally on site-specific parameters, the maxima are distributed as:

$$\begin{aligned} y_{st}|\mu _s,\sigma _s,\xi _s{\mathop {\sim }\limits ^{ind}}GEV(\mu _s,\sigma _s,\xi _s),\ \forall s, t. \end{aligned}$$

(6)

The assumption of conditional independence represents a simplification but it is a quite standard one in the extreme value literature when marginal return levels need to be estimated (Dyrrdal et al. 2015; Thorarinsdottir et al. 2018; Jóhannesson et al. 2022). Alternatively, max-stable spatial processes can be considered, even if the complexity of the modeling framework sensibly increases (Asadi et al. 2015). As already hinted in Sect. 3.1, the multivariate link function proposed in Jóhannesson et al. (2022) and reported in equation (4) is adopted, to obtain transformed parameters that are convenient to specify regression models for. To simplify the notation, the station-specific transformed parameters are stored in the following vectors: $\varvec{\psi }= (\psi _1,\dots ,\psi _S)^\top$, $\varvec{\tau }= (\tau _1,\dots ,\tau _S)^\top$ and $\varvec{\phi }= (\phi _1,\dots ,\phi _S)^\top$.

If a linear relationship between covariates and the parameters is assumed, the following latent regression models are specified:

$$\begin{aligned} \begin{aligned}&\varvec{\psi }= {\varvec{1}}_S\beta _{0\psi }+{\textbf{X}}\varvec{\beta }_{\psi }+{\textbf{u}}_\psi ;\\&\varvec{\tau }= {\varvec{1}}_S\beta _{0\tau }+{\textbf{X}}\varvec{\beta }_{\tau }+{\textbf{u}}_\tau ;\\&\varvec{\phi }= {\varvec{1}}_S\beta _{0\phi }+{\textbf{X}}\varvec{\beta }_{\phi }+{\textbf{u}}_\phi ; \end{aligned} \end{aligned}$$

(7)

where the design matrix ${\textbf{X}}=[{\textbf{x}}_{\bullet 1}\cdots {\textbf{x}}_{\bullet M}]\in {\mathbb {R}}^{S\times M}$ contains the standardized covariates ${\textbf{x}}_{\bullet m}\in {\mathbb {R}}^S,\ m=1,\dots ,M$. The standardization procedure is carried out without loss of generality in order to have zero mean and unit standard deviation. Each predictor, related to the generic parameters vector $\varvec{\theta }\in \{\varvec{\psi },\varvec{\tau },\varvec{\phi }\}$, is constituted by an overall intercept $\beta _{0\theta }$ and a linear regression with coefficients stored in $\varvec{\beta }_{\theta }\in {\mathbb {R}}^{M}$. A vector of station-specific unstructured random effects ${\textbf{u}}_\theta \in {\mathbb {R}}^S$ completes the equation, to account for possible residual variation. To keep the notation simple, all the model equations in (7) contain the same covariates, as will be the case in the application, but this assumption can be easily relaxed.

The model specification must be completed by setting prior distributions for the parameters. Firstly, weakly informative Gaussian priors are assumed for the coefficients. To account that the transformed GEV parameters have different magnitudes, they are calibrated by exploiting the results from the exploratory analysis of Sect. 3.1. More in detail, following the advices from the rstanarm package (Goodrich et al. 2022), the following prior is set for the intercepts:

$$\begin{aligned} \beta _{0\theta }\sim {\mathcal {N}}\left( m_{{\hat{\theta }}},2^2s^2_{{{\hat{\theta }}}}\right) , \end{aligned}$$

(8)

where $m_{{\hat{\theta }}}$ and $s^2_{{{\hat{\theta }}}}$ are the mean and the variance of the generic vector of fitted parameters $\hat{\varvec{\theta }}$. Recalling that the covariates are standardized, independent zero-mean Gaussian priors with equal scales are specified for the regression coefficients:

$$\begin{aligned} \beta _{\theta m }\sim {\mathcal {N}}\left( 0,2^2\right) ,\ m=1,\dots ,M. \end{aligned}$$

(9)

Lastly, focusing on the vector of unstructured random effects, a spherical multivariate Gaussian prior with scale parameter $\kappa _{\theta }$ is set:

$$\begin{aligned} {\textbf{u}}_{\theta }|\kappa _{\theta }\sim {\mathcal {N}}_S({\varvec{0}},\kappa _{\theta }^2{\textbf{I}}_S), \quad \kappa _{\theta }\sim {\mathcal {N}}^+(0,2^2), \quad \theta \in \{\psi ,\tau ,\phi \}; \end{aligned}$$

(10)

where ${\mathcal {N}}^+(\cdot , \cdot )$ indicates an half-Normal distribution. It is worth noting that the prior specification strategy described so far exclusively includes Gaussian priors for the predictor parameters, thereby defining a Generalized Latent Gaussian Model. This same assumption underpins the modeling formulations introduced in the subsequent paragraphs.

4.1 GEV regression with Bayesian P-splines

When the evidence of non-linear relationships between covariates and responses is pointed out, it is natural to extend the linear models in (7) by allowing for flexible regression terms. Among the possible strategies, the Bayesian P-splines method by Lang and Brezger (2004) is implemented:

$$\begin{aligned} \begin{aligned}&\varvec{\psi }= {\varvec{1}}_S\beta _{0\psi }+\sum _{m=1}^M{\textbf{B}}_{m}\varvec{\gamma }_{\psi ,m}+{\textbf{u}}_\psi ;\\&\varvec{\tau }= {\varvec{1}}_S\beta _{0\tau }+\sum _{m=1}^M{\textbf{B}}_{m}\varvec{\gamma }_{\tau ,m}+{\textbf{u}}_\tau ;\\&\varvec{\phi }= {\varvec{1}}_S\beta _{0\phi }+\sum _{m=1}^M{\textbf{B}}_{m}\varvec{\gamma }_{\phi ,m}+{\textbf{u}}_\phi . \end{aligned} \end{aligned}$$

(11)

The predictors are characterized by the sum of M flexible regression terms defined as the product of a matrix ${\textbf{B}}_{m}\in {\mathbb {R}}^{S\times K}$ of cubic B-spline basis functions evaluated at K knots, multiplied by a vector of associated coefficients $\varvec{\gamma }_{\theta m}\in {\mathbb {R}}^K$. In the P-splines approach, the smoothness of the fitted effect is encouraged by setting a second-order random walk prior on the splines coefficients:

$$\begin{aligned} \varvec{\gamma }_{\theta m}|\omega _{\theta m}\sim {\mathcal {N}}_K({\varvec{0}},\omega _{\theta m}^2{\textbf{K}}_\gamma ^-), \quad \omega _{\theta m}\sim {\mathcal {N}}^+(0,2^2), \quad \forall m;\ \theta \in \{\psi ,\tau ,\phi \}. \end{aligned}$$

(12)

The matrix ${\textbf{K}}_\gamma$ has rank $K-2$ and it is a precision matrix describing a second-order random walk, whereas $\omega _{\theta m}$ is a scaling parameter. Due to the rank deficiency of the precision matrix, the prior is improper and the specification of linear constraints might be required. To better understand the features of the P-splines setting, the representation of the (11) as a mixed model could be useful.

4.1.1 Mixed model representation

The linear predictors defined in (11) can be reparameterized by exploiting the spectral decomposition of ${\textbf{B}}_{m}{\textbf{K}}_\gamma ^-{\textbf{B}}_{m}^\top$, i.e. the covariance matrix of ${\textbf{B}}_{m}\varvec{\gamma }_{\theta m}$. The model representation defined in the following is particularly suitable to perform functional selection since the structured and improper prior on the spline coefficients in (12) is traced back to a proper spherical Gaussian prior on coefficients, associated with a matrix of orthonormal basis (Scheipl et al. 2012).

To set the notation, the spectral decomposition is defined as:

$$\begin{aligned} {\textbf{B}}_{m}{\textbf{K}}_\gamma ^-{\textbf{B}}_{m}^\top =\begin{bmatrix} {\textbf{U}}_+&{\textbf{U}}_0 \end{bmatrix}^\top \begin{bmatrix} \varvec{\Lambda }_+&{}{\varvec{0}}\\ {\varvec{0}} &{} {\varvec{0}} \\ \end{bmatrix} \begin{bmatrix} {\textbf{U}}_+&{\textbf{U}}_0 \end{bmatrix}={\textbf{U}}_+\varvec{\Lambda }_+{\textbf{U}}_+^\top , \end{aligned}$$

(13)

where $\varvec{\Lambda }_+\in {\mathbb {R}}^{(K-2)\times (K-2)}$ is a diagonal matrix containing the non-null eigenvalues, ${\textbf{U}}_+\in {\mathbb {R}}^{S\times (K-2)}$ is the orthogonal matrix with the associated eigenvectors and ${\textbf{U}}_0\in {\mathbb {R}}^{S\times (R-K+2)}$ contains the eigenvectors that span the null space of ${\textbf{B}}_{m}{\textbf{K}}_\gamma ^-{\textbf{B}}_{m}^\top$.

Combining the prior in (12) and the spectral decomposition (13), it is possible to split the generic flexible term ${\textbf{B}}_m\varvec{\gamma }_{\theta m}$ into a penalized component and an unpenalized one:

$$\begin{aligned} {\textbf{B}}_m\varvec{\gamma }_{\theta m} = {\textbf{x}}_{\bullet m}\beta _{\theta m}+\tilde{{\textbf{B}}}_{m}\varvec{{\tilde{\gamma }}}_{\theta m}. \end{aligned}$$

The unpenalized part is constituted by the term ${\textbf{x}}_{\bullet m}\beta _{\theta m}$ and it is strictly related to the null space of the structure matrix that defines the prior assumed for the splines coefficients. Indeed, under the considered second-order random walk, a polynomial of order one in the covariate is required, i.e. a constant term (already included in the overall intercept) and a linear trend on the covariate. Concerning the penalized component, $\tilde{{\textbf{B}}}_{m} = {\textbf{U}}_+\varvec{\Lambda }_+^{\frac{1}{2}}\in {\mathbb {R}}^{S\times (K-2)}$ determines a matrix of orthonormal basis and $\tilde{\varvec{\gamma }}_{\theta m}\in {\mathbb {R}}^{K-2}$ constitutes the vector of related splines coefficients. Due to the orthogonalization procedure, such vector of coefficients has a spherical prior: $\tilde{\varvec{\gamma }}_{\theta m}|\omega _{\theta m}\sim {\mathcal {N}}_{K-2}({\varvec{0}},\omega _{\theta m}^2{\textbf{I}}_{K-2})$. Hence, linear predictors in (11) can be expressed in the following way:

$$\begin{aligned} \varvec{\theta }= {\varvec{1}}_S\beta _{0\theta }+{\textbf{X}}\varvec{\beta }_\theta +\sum _{m=1}^M\tilde{{\textbf{B}}}_{m}\varvec{{\tilde{\gamma }}}_{\theta m}+{\textbf{u}}_\theta . \end{aligned}$$

(14)

The model specification can be completed by the already discussed priors (8), (9) and (10), whereas for the scaling parameter $\omega _{\theta m}$ the same prior of equation (12) can be set. In this way, a standard Bayesian P-splines model can be implemented, even if only proper priors are specified.

4.1.2 Variable selection: the grouped HS prior

When several covariates are available and their relationships with the modeled latent parameters are unknown, it can be useful to set a prior distribution that is able to shrink the non-relevant regressors to zero. Scheipl et al. (2012) proposed to use spike-and-slab priors for functional selection. The behavior of such priors is also mimicked by the HS priors, which have been proposed in a hierarchical version to deal with shrinkage of grouped regression terms (Xu et al. 2016). Since all the coefficients related to a covariate can be considered to form a group, a grouped HS prior appears suitable to be applied in this framework, rearranging the model in (14) to

$$\begin{aligned} \varvec{\theta }= {\varvec{1}}_S\beta _{0\theta }+\sum _{m=1}^M{\textbf{Z}}_{m}\varvec{\alpha }_{\theta m}+{\textbf{u}}_\theta , \end{aligned}$$

(15)

where ${\textbf{Z}}_{m} = [{\textbf{x}}_{\bullet m}\ \ \tilde{{\textbf{B}}}_{m}]\in {\mathbb {R}}^{S\times (K-1)}$ and $\varvec{\alpha }_{\theta m}=\left( \beta _{\theta m}, \tilde{\varvec{\gamma }}_{\theta m}\right) \in {\mathbb {R}}^{K-1}$. To implement the grouped HS prior, the following hierarchy is necessary:

$$\begin{aligned} \begin{aligned}&\varvec{\alpha }_{\theta m}|\varvec{\delta }_{\theta m},\lambda _{\theta m},\eta _\theta \sim {\mathcal {N}}_{K-1}({\varvec{0}},\eta _\theta ^2\lambda _{\theta m}^2\text {diag}[\varvec{\delta }_{\theta m}]),\ m=1,\dots M;\\&\delta _{\theta km}\sim {\mathcal {C}}^+(0,1),\ \ k=1,\dots ,K-1;\ \ m=1,\dots M; \\&\lambda _{\theta m}\sim {\mathcal {C}}^+(0,1),\ m=1,\dots M;\\&\eta _\theta \sim {\mathcal {C}}^+(0,s_{{{\hat{\theta }}}}); \end{aligned} \end{aligned}$$

(16)

where $\varvec{\delta }_{\theta m} = \left( \delta _{\theta 1\,m},\dots ,\delta _{\theta (K-1)m}\right) ^\top$ and ${\mathcal {C}}^+(\cdot ,\cdot )$ denotes an half-Cauchy distribution. The parameter $\eta _\theta$ represents the global scale of the regression coefficients. For this reason, its prior scale is set equal to the standard deviation of posterior estimates obtained from the station-specific exploratory GEV models, to account for the different magnitudes of the modeled quantities. The prior hierarchy is completed by a covariate-specific scale $\lambda _{\theta m}$ that controls the relevance of the whole effect and the coefficient-specific parameter $\delta _{\theta km}$.

4.2 Posterior inference and model comparison

As previously mentioned, an MCMC approach is adopted to draw B samples from the posterior distributions of the model parameters, by exploiting the Stan probabilistic language. In the Supplementary material, the code for implementing the discussed models is provided. After obtaining draws from the posteriors of the basic parameters, it is possible to consequently retrieve posterior distributions of other useful quantities. More in detail, it is possible to have the posterior for the generic GEV parameter related to station s: $\theta _s|{\textbf{y}}$. If the interest is on an out-of-sample location $s^\prime$, such quantity cannot be computed due to the presence of the station-specific random effect term. To propagate the uncertainty, it is possible to obtain a prediction of the GEV parameter defined as ${\tilde{\theta }}_{s^\prime }|{\textbf{y}}=\left( \beta _{0\theta }+f({\textbf{x}}_{s^\prime \bullet }^T)+{\tilde{u}}_{\theta }\right) |{\textbf{y}}$. The function of the covariates $f({\textbf{x}}_{s^\prime \bullet }^T)$ depends on the kind of model that is analyzed (linear or spline regression) and the b-th replicate of random effect term is generated as ${\tilde{u}}_{\theta }^{(b)}\sim {\mathcal {N}}\left( 0,{\kappa _\theta ^2}^{(b)}\right)$, where ${\kappa _\theta ^2}^{(b)}$ is the b-th draw from $\kappa _\theta ^2|{\textbf{y}}$. The samples from $\theta _s|{\textbf{y}}$ or ${\tilde{\theta }}_{s^\prime }|{\textbf{y}}$ can be combined by following the (3) to have posterior distributions of the return period denoted with $Q_{1/R,s}|{\textbf{y}}$ or $\tilde{Q}_{1/R,s^\prime }|{\textbf{y}}$ for the estimated and the predicted ones, respectively.

The posterior predictive distribution is another important quantity for making predictions and model assessments. It is possible to recover a random sample from it by exploiting the MCMC posterior samples of GEV parameters. In particular, the b-th replicate from the posterior predictive $y_{st}^{rep}|{\textbf{y}},\forall s,t,$ is obtained generating from: ${y_{st}^{rep}}^{(b)}\sim GEV(\mu _s^{(b)},\sigma _s^{(b)},\xi _s^{(b)})$. Similarly, the posterior predictive distributions for out-of-sample stations, denoted as ${{\tilde{y}}}_{s^\prime t}^{rep}|{\textbf{y}},\forall s^\prime ,t$, can be drawn relying on the posteriors ${\tilde{\theta }}_{s^\prime }|{\textbf{y}}$.

The posterior predictive distribution constitutes the pillar of several model performance evaluation tools that are listed hereafter. In particular, as shown in the next section, a cross-validation study is carried out to assess and compare the performances of the models. The quantities that are introduced in the following are computed by relying on the posterior predictive ${{\tilde{y}}}_{s t}^{rep}|{\textbf{y}}_{-s}$, i.e., obtained after fitting a model without observations from station s.

To evaluate the calibration of predictions produced by Bayesian models, the probability integral transforms (PIT) are widely used (Dawid 1984). In particular, they are defined as

$$\begin{aligned} PIT_{st}={\mathbb {P}}\left[ {{\tilde{y}}}_{s t}^{rep}<y_{st}|{\textbf{y}}_{-s}\right] , \end{aligned}$$

(17)

i.e. the cumulative probability of the posterior predictive distribution up to the observed value $y_{st}$. If the model predictions are calibrated, PIT values follow a uniform distribution. Bayesian p-values constitute another useful posterior predictive check. They can be flexibly defined, depending on the inferential goal characterizing the procedure. In extreme value estimation, GEV quantiles represent an important target quantity, since they determine return levels. For this reason, station-specific Bayesian p-values are defined for a given return period R:

$$\begin{aligned} \text {P-val}_{R,s} = {\mathbb {P}}\left[ \tilde{Q}_{1/R,s}<q_{1/R}({\textbf{y}}_s)|{\textbf{y}}_{-s}\right] , \end{aligned}$$

(18)

where $q_{1/R}({\textbf{y}}_s)$ is the sample quantile of the maxima of station s (computed using Definition 6 from Hyndman and Fan 1996). In this case, good model performances are underlined by values of $\text {P-val}_{s}$ nearby 0.5.

Lastly, the continuous ranked probability score (CRPS) is largely used to evaluate the probabilistic predictions under continuous densities, even in the extreme values literature (Friederichs and Thorarinsdottir 2012). It is a score computed specifically for each observation $y_{st}$ and it is indicated with $\text {CRPS}(y_{st})$, and the R package scoringRules can be exploited to evaluate it (Jordan et al. 2019). Note that the model showing lower scores is preferable in terms of calibration and sharpness of the predictions.

5 Application

The modeling strategies described in Sect. 4 are applied to the Danube basin data introduced in Sect. 3. In particular, results about three different Bayesian models are compared: the one assuming linear effects for the covariates, labeled as Linear and defined by equations in (7), the basic P-spline model of (11), labeled as Splines, and its extension to automatically perform model selection through grouped HS priors (labeled as Splines-HS).

To assess the performances of the considered models, results from a folded cross-validation study are reported in Sect. 5.1, whereas the outcomes from the analysis carried out on the full dataset are discussed in Sect. 5.2.

5.1 Cross-validation study

The whole set of $S=62$ stations is randomly partitioned into $G=31$ groups constituted by a couple of stations each. A folded cross-validation study is executed, by repeatedly fitting the 3 compared models and excluding a couple of stations at each iteration. The quantities introduced in Sect. 4.2, particularly PIT and CRPS, are evaluated for the out-of-sample stations.

A first indication from the folded cross-validation study concerns the stability of the estimates with respect to the removal of stations. Given that the models are characterized by different parameterizations, the intercepts $\beta _{0\theta }$ are taken into consideration for this aspect. Figure 5 compares the distributions of the posterior means obtained in the 31 runs (via box-plots) to the estimates of the intercepts in the models fitted considering all the stations (red dotted lines). The estimation of such parameters seems to be stable: the estimates obtained using the full dataset are often close to the median of the distribution and, in general, are included within the boxes. The only exception concerns the $\varvec{\phi }$ parameter under Linear, remaking that such parameter is also characterized by evident differences in the estimates across the models. This could be expected due to the difficulties in identifying the shape parameter.

Fig. 5

Box-plots of the $G=31$ posterior means from the cross-validation compared to the estimate obtained in the model fitted with all the stations (red dotted lines)

The calibration of the predictions produced by the compared models is firstly evaluated by exploring the distribution of $PIT_{st}$, recalling that a uniform distribution is required for a calibrated model. The kernel densities are shown in Fig. 6, compared with the expected uniform distribution. In the models including flexible regression terms (Splines and Splines-HS), PIT distributions are more compliant with the uniform when compared to the Linear model, where the excess of values far from 0 or 1 is more evident. The visual interpretation is supported by the outcomes of the Kolmogorov-Smirnov test, which assesses the null hypothesis that the set of PIT values conforms to a Uniform distribution. Indeed, considering a significance level of 0.05, the null hypothesis is not rejected for Splines and Splines-HS models (p-values equal to 0.07 and 0.20, respectively) and it is rejected under the Linear model (p-value of 0.01). Another indication about the calibration of predictions can be deduced from the Bayesian p-values $\text {P-val}_{R,s}$. To summarise them, $\text {P-val}_{R}^*$ denotes the proportion of Bayesian p-values far from the extremes, i.e. included in the interval (0.05, 0.95). Selecting $R=$20, $\text {P-val}_{R}^*$ is equal to 0.84 for Splines, 0.84 for Splines-HS and 0.85 for Linear; concerning $R=$30, a value of 0.87 is observed for Splines, and 0.92 for Linear and Splines-HS. In summary, all three models demonstrate good prediction calibration, with the Linear model showing slight deviations in PIT.

Fig. 6

Kernel densities of the distribution of $PIT_{st},\ \forall s,t$, density of the Uniform distribution as dashed line

Lastly, further evaluations of the reliability and the sharpness of predictions are discussed. The average CRPS (ACRPS) is computed to have a station-specific summary: $\text {ACRPS}_s=T^{-1}\sum _t\text {CRPS}(y_{st})$, and their distributions across the stations are depicted in Fig. 7. To set the proposed Splines-HS model as a benchmark, the values are relativized by dividing them for the corresponding ACRPS observed under this model. The median of the distributions of relative ACRPS is above 1 for both the Linear and Splines models. Specifically, 60% of stations have higher ACRPS than under the Splines-HS model for the Linear model, and 61% for the Splines model. Note that the $61\%$ of stations have higher ACRPS under Linear model if compared to the Splines one, pointing out the merits of introducing flexible effects in the model. Another indication about the sharpness of prediction can be deduced from the width of the 90% credible intervals of the posterior of quantiles ${\tilde{Q}}_{1/R,s}|{\textbf{y}}_{-s}$, for $R=\{20,30\}$. Also in this case, Fig. 7 reports the distribution of the station-specific widths divided by those obtained under the Splines-HS model. It is interesting to stress how the Splines-HS model has intervals in median the 26.6% and 42.6% narrower than the intervals retrieved with Splines and Linear models, respectively.

Table 2 Posterior estimates related to the random effects scale parameters

5.2 Results

According to the results of the folded cross-validation study presented in the previous section, allowing for non-linear relationships among covariates and GEV parameters leads to some gains in terms of predictive ability. These improvements are even more noticeable when a prior able to automatically execute the variables selection step is assumed. Similar conclusions can also be detected by comparing the models fitted relying on the whole dataset. As an overall measure of goodness of fit, the leave-one-out information criterion (LOOIC, Vehtari et al. 2017) is considered. Models incorporating spline terms exhibit similar LOOIC values, with Splines-HS at 22219.5 and Splines at 22222.1. In contrast, the Linear model shows inferior performance with a LOOIC of 22245.7.

Fig. 7

Left-hand-side plot: box-plot of ACRPS$_s$. Right-hand-side: box-plot of the widths of 90% credible intervals for ${\tilde{Q}}_{1/R,s}|{\textbf{y}}_{-s}$. In both cases, the values are divided by the corresponding ones obtained under the Splines-HS model (benchmark). Values higher than one (dashed line) indicate that the ACRPS or CI widths are higher if compared to the benchmark

A first insight to understand the benefits led by the models with Bayesian P-splines can be deduced from Table 2, reporting the posterior summaries about the random effects scale parameters $\kappa _{\theta }$. Such quantities can be considered as measures of the amount of signal captured by the covariates in the regression models: the higher the values, the lower the variability explained by the covariates. The Linear model registers noticeably higher scales, especially for the random effects related to parameters $\varvec{\psi }$ and $\varvec{\tau }$. Despite such differences, it is interesting to remark that the in-sample estimates of the stations-specific GEV parameters $\mu _s$ and $\sigma _s$ are similar across the considered models, whereas differences can be observed for the shape parameter $\xi _s$, for which the models induce different levels of shrinkage. These results are depicted by the box-plots in the first row of Fig. 8, where also the estimates obtained under the station-specific models are added for benchmarking purposes. As a consequence, the inflation of the scales $\kappa _\theta$ might lead to over-dispersed out-of-sample predictions: such behavior is captured by the PIT distribution previously reported in Fig. 6 and the general increase of the width of the credible intervals (Fig. 7).

Fig. 8

Box-plots of GEV parameters posterior means under the considered models (first row). Comparison between estimates (second row) and out-of-sample predictions (third row) from the Splines-HS model and the station-specific ones. The red triangles indicate the stations considered for return levels of Fig. 10

To have a comprehensive understanding of the relationships between covariates and the transformed GEV parameters across the three compared models, Tables 3 and 4 are produced. The mixed model representation of Bayesian P-splines, as described in Sect. 4.1.1, allows us to explore the relevance of the linear trend in all models. In pursuit of this goal, Table 3 highlights the variables that exhibit a linear impact on the parameters. These relationships are labeled as relevant when it holds that $\max \left\{ {\mathbb {P}}[\beta _{\theta m}>0|{\textbf{y}}],{\mathbb {P}}[\beta _{\theta m}<0|{\textbf{y}}]\right\}$ exceed 0.8. Notable distinctions become apparent when comparing the Linear model with models incorporating spline terms, especially in the modeling of the location parameter. Moreover, the effect of the grouped HS prior is evident, as the relevant coefficients under the Splines-HS model constitute a subset of those considered relevant under the Splines model. Subsequently, to ascertain the presence of evidence for non-linear relationships, Table 4 reports the count of relevant splines coefficients, i.e. $\sum _{k=1}^{7}{\varvec{1}}\left( \max \left\{ {\mathbb {P}}[{\tilde{\gamma }}_{\theta m k}>0|{\textbf{y}}],{\mathbb {P}}[{\tilde{\gamma }}_{\theta m k}<0|{\textbf{y}}]\right\} >0.8\right)$, where ${\varvec{1}}(A)$ is an indicator function assuming value one if the event A is observed and zero otherwise. Once again, the Splines-HS model stands out for its parsimony, resulting in a lower number of relevant coefficients. However, there is an exception in the case of the relationship between longitude and the location parameter, where this model identifies a notably non-linear function. In summary, these findings suggest that non-linear relationships are indeed observable in the case study under consideration.

Table 3 Relevance of the coefficients related to the linear terms

Table 4 For each variable and transformed GEV parameters, the number of relevant splines coefficients is reported, comparing model Splines and Splines-HS

Let us shift the focus to the comparison between the two models that include flexible regression terms, in order to better understand how the grouped HS prior works. Figure 9 shows how three selected covariates (area, elevation and slope) impact on the transformations of GEV parameters. The trends detected by the two models are similar but the impact of the grouped HS prior for the splines coefficients emerges. The shrinkage towards zero for negligible effects is evident under the Splines-HS model, especially when modeling $\varvec{\phi }$, i.e. the function of the shape parameter. In this case, the Splines model identifies trends endowed with considerably higher uncertainty, producing intervals that include the 0 value almost everywhere. The decrease in the effect uncertainty is also detectable when modeling parameters $\varvec{\psi }$ and $\varvec{\tau }$, even if less pronouncedly. When observing the effect of area on the location parameter $\varvec{\psi }$, it becomes evident that the grouped HS prior effectively constrains the flexible effect back to the linearity assumption.

Fig. 9

Covariate effects estimated for three selected covariates under models Splines and Splines-HS for the three functionals of GEV parameters. Shaded areas depict the 90% credible intervals

The results concerning covariate effects can be put in relationship with those about the random effects scales shown in Table 2. Indeed, the combination of these outputs allows to motivate the lower dispersion of the station-specific estimates of the shape parameters $\xi _s$ under the Splines-HS model, already noticed in box-plots of the first row in Fig. 8. On the other hand, the Splines model produces scattered estimates. Considering the substantial shrinkage imposed by the grouped HS priors, the variability in estimates may not be well supported by the data, potentially resulting in issues of instability. In fact, it is widely known that the identification of the shape parameter of the GEV distribution is a tricky task (see, e.g., Jóhannesson et al. 2022), and the grouped HS prior can help in avoiding over-fitting in this framework. In consideration of these findings suggesting a potentially limited impact of modeling the shape parameter, the three discussed models are also fitted with a shared shape parameter for all monitoring stations to explore whether a more streamlined configuration would yield significant improvements. While detailed results are omitted here for conciseness, it is worth noting that the estimates remained largely similar, with only slight increases in the LOOIC values observed for these simplified models.

The second and the third rows of Fig. 8 allow us to delve deeper into the connections between parameters estimates obtained with the Splines-HS model and the GEV distribution fitted on the single stations. The results related to the in-sample estimates confirm that no relevant differences are detected in estimating $\mu _s$ and $\sigma _s$, whereas they provide further evidence of the strong shrinking process affecting the estimates of $\xi _s$, which are gathered around 0.25 (Pearson’s correlation equal to 0.60). It is also interesting to explore how the GEV parameters are predicted when data related to the station are excluded from the fitting sample, taking the outcome of the folded cross-validation study (third row). As expected, the predictions concerning $\mu _s$ and $\sigma _s$ are more scattered with respect to the estimates from the single-station models, even if the correlation between estimates and predictions is strong. From these diagnostic plots, three stations, whose points are embedded in a red triangle, are selected to investigate the inference on return levels through the different modeling strategies. To this aim, the distances between predictions and single-station model estimates are considered, focusing on the stations having maximum (#6242530), median (#6243240) and minimum (#6342610) distances, noting that such stations are also representative of different values of the shape parameter according to the single-station models.

To complete the analysis of the results, a brief discussion on the estimates and the out-of-sample predictions of river discharge return levels is carried out (outcomes reported in Fig. 10). As expected, the in-sample estimates are generally characterized by lower levels of uncertainty than predictions, whose variability is inflated by the presence of random effects generated from the prior, as described in Sect. 4.2. Another general trend to point out is that the single-station models produce estimates with larger credible intervals, mainly due to the issues in estimating the shape parameters. Conversely, the models fitted on the overall basin allow borrowing strength across the stations, reducing such variability through the aforementioned shrinkage process on $\xi _s$. Besides, as already pointed out in Sect. 5.1, the Splines-HS model is also able to produce return level estimates with lower uncertainty levels than the other strategies, by combining lower variability in effects identification (Fig. 9) and lower random effects scale parameters (Table 2). Despite the narrower bands, the points representing the observed values are included in the credible intervals, with the exception of predictions for station #6242530, i.e. the one characterized by the maximum distance between predicted and estimated parameters.

Fig. 10

Return levels of river discharge (in $m^3/s$) estimated with the whole sample (left column) and excluding the observation available from the station (right column). The shaded areas indicate the 90% credible interval. The points represent the ordered observations

6 Concluding remarks

This paper aims at illustrating the potential of Bayesian models in introducing flexibility in extreme value analysis. In particular, the linearity assumption, often restrictive in dealing with complex phenomena such as environmental ones, is relaxed proposing non-linear functional relationships. Furthermore, a suitable regularizing prior is introduced, allowing the incorporation of variables and functional selection steps within the model. While it is true that the introduction of such a shrinkage prior noticeably complicates the model specification, the Stan code provided in the Supplementary material can assist practitioners in utilizing this more sophisticated technique. Interestingly, it could streamline the analysis process since when working with these types of models, selecting relevant covariates and determining the appropriate functional forms can often be challenging. It is worth remarking that the proposed method automatically addresses this task, eliminating the need for additional steps.

The performances of the models considered in the paper are compared by means of a cross-validation study that evaluates their ability in predicting return levels at ungauged locations. In doing so, the advantages brought by the use of splines regression tied with a regularizing prior can be highlighted. Indeed, its use allows us to sensibly reduce the uncertainty of the predictions without affecting model calibration if compared to other considered model specifications.

The results obtained by applying GEV regression models with these flexible specifications to the discussed case study also provide insights into common assumptions in regional flood frequency analysis. Firstly, as discussed throughout this paper, it can be noted that the estimation of the shape parameter seems to be minimally influenced by the covariates, aligning with previous findings in the literature (e.g., see Lima et al. 2016). Furthermore, the adoption of the multivariate link proposed by (Jóhannesson et al. 2022) allows us to model a dispersion parameter that has been adjusted for the location effect ($\tau _s$ can be seen as the logarithm of a kind of coefficient of variation). This approach is consistent with the index flood method, which estimates return periods by scaling data relative to the index flood (Hosking and Wallis 1997).

Despite that the application tackles extreme value analysis from the block-maxima perspective, by adopting the typical GEV distribution, the underlying idea of setting a semi-parametric regression with regularizing priors can also be extended to other distributional assumptions and approaches of extreme value theory. Among the others, we mention the Blended-GEV by Castro-Camilo et al. (2022), which solves the GEV problem of having a finite lower tail when the shape parameter is positive, or the widespread peak-over-threshold approach. In the latter framework, the proposed strategy might help in both in determining a non-stationary threshold (e.g. through quantile regression, as in Northrop and Jonathan 2011) and in the analysis of the exceedances through the Generalized Pareto distribution.

Lastly, it is worth stressing that the principle behind the use of a prior encouraging a grouped variable selection can also be extended to other low-rank structure matrices such as tensors, useful to model a spatially structured effect jointly modeling latitude and longitude, interactions and also categorical variables (Scheipl et al. 2012).