Distortions in Investment Timing and Quantity in Real Options with Asymmetric Information

Abstract

We analyze real options investment under asymmetric information on investment costs, where decisions not only involve investment timing, but also investment quantity. A principal, the regulator, offers a menu of contracts to the agent (the regulated firm). The regulated firm has better information on costs than the regulator, and the optimal regulation trades off distortions in investment decisions and informational rents left to the firm. In a non-dynamic situation, it is well known that optimal contracts involve downward distortions on investment quantity. In the dynamic, real options situation, distortions also occur in investment timing: a high-cost firm’s investment will be delayed beyond the optimal time, until revenues reach a higher investment threshold. We explore the effect on investment quantity in this real option regulation under various assumptions on the stochastic process for revenues. On the one hand, the higher investment threshold tends to increase investment quantities, whereas screening of high-cost firms would favour reducing their investment quantity. We find a simple sufficient condition for the latter, quantity-reducing, effect to dominate, and show that it is satisfied for a wide range of commonly used stochastic processes.

1 Introduction

Firm investment decisions are often taken by decision makers who are not the ultimate beneficiaries of those investments. This is clear in regulated environments, such as the energy sector, where many of the large investments needed for the energy transition are made by monopolists who get their income from regulated access tariffs. And it is also evident in corporate finance situations, where executive boards decide on capacity investments on behalf of the owners of the firm. In either of those situations, the decision makers will act as agents for a principal, and these agents will be responsive to incentives given to them in contracts (be it regulatory contracts, or employment and remuneration contracts) through which these principals have delegated those decision rights.

In the presence of asymmetries of information, these incentives typically result in investment decisions that are distorted away from those that maximize the principal’s welfare. In the seminal work on regulation under asymmetric information on costs by Baron and Myerson (1982), optimal regulation of a monopolist balances rents that need to be left to the agent against distortions in quantity. The result is that high-cost agents invest in inefficiently low quantities. In a dynamic corporate finance application of real option investments by a manager, Grenadier and Wang (2005) study distortions in the timing of real-option exercise. They find that, to incentivize the agent-manager, a principal-owner should excessively delay investments for agents of high-cost firms, compared to the optimal investment delay well-known in real options from McDonald and Siegel (1986).

In many real-option investment problems, decisions involve both timing of investment and the size of the investment, and one may expect optimal contracts to involve both distortions in timing and in quantity. However, whereas in the static, Baron and Myerson (1982) context, the principal reduces quantities in order to screen high-cost from low-cost agents, the timing delays in real options lead to increased threshold prices. These higher prices upon investment in turn lead to upward pressure on quantities for the high-cost agent, compared to first-best levels. The reason is that the higher demand, resulting from the postponed investment, warrants higher investments in capacity by the agent.

In this paper, we explore which effect dominates choice of investment size for the principal in a real-option situation when there is asymmetric information on variable cost of investment. Does the principal reduce investment quantity for higher cost agents in order to reduce informational rents, as in the Baron and Myerson (1982) model of investment regulation? Or will quantity increase as a result of the delay of investment timing (as in Grenadier and Wang, 2005), and the associated higher value of marginal investment because of higher prices at investment?

We explore this question in a real option model of investment under uncertainty, where both investment timing and quantity must be chosen. There is asymmetric information on variable costs of investment between the agent and a principal. In the optimal contract, there will be delays in investment timing, but also distortions in investment quantity. We study the effect on quantity under general uncertain price processes, making extensive use of a formulation due to Dixit et al. (1999) to express optimality conditions in terms of the elasticity of the expected stochastic discount factor, $E\left( e^{-rT}\right)$. This allows us to study the problem beyond the usual geometric Brownian motion process that is ubiquitous in the real-options literature.

We find, firstly, that the direction of the distortion in investment quantity depends on this elasticity, $\beta (X)$, of the discount factor with respect to (stochastic) demand size X: as long as this elasticity is non-decreasing in the investment demand size threshold X, the quantity reduction effect as in the static Baron–Myerson model dominates. This condition holds for often-used stochastic processes such as geometric Brownian motion (which has constant elasticity), arithmetic Brownian motion and various processes with mean reversion.

Second, on a methodological note, we explore in some detail the connection between elasticity $\beta (X)$, the expected discount factor, and stochastic (Ito) processes that exhibit those functional forms of elasticities and expected discount factors. We use a generalization of what is known as the ‘fundamental quadratic’ (Dixit and Pindyck, 1994) to derive a one-parameter family of stochastic processes that include geometric Brownian motion and arithmetic Brownian motion as examples.

Finally, we explore, as a (counter)example, the investment model under a stochastic process that is designed to have decreasing elasticity, and where asymmetric information may actually increase investment quantity relative to the symmetric information situation. The scope for this decrease in elasticity is limited by the model having to satisfy the second-order conditions on the investment threshold X, to make sure that delaying investment in response to asymmetric information is indeed optimal.

Real options involving not only investment timing but also investment size have been studied since Bar-Ilan and Strange (1999) and Dangl (1999), and more recently in works such as Hagspiel et al. (2016) (who focus on the effects of flexible use of the invested capacity), All these papers exclusively focus on geometrical Brownian motion. Our focus, using the elasticity approach of the discount factor following Dixit et al. (1999), allows us to explore the robustness of results to this assumption on the stochastic process.

Earlier studies on asymmetric information in a real-option framework, following Grenadier and Wang (2005), include Shibata (2009), Morellec and Schürhoff (2011), Grenadier and Malenko (2011) in various corporate finance contexts. Real options in (price-cap) regulation have been studied by Dobbs (2004), Guthrie (2006), Moretto et al. (2008), and Evans and Guthrie (2012) where the latter authors also focus on effects of investment size. An approach focussing on optimal contracting under asymmetric information in a regulation context was taken by Broer and Zwart (2013), who focus on timing distortions only. Willems and Zwart (2018) study the problem in an environment of continuous expansion of size. A recent related paper to ours is Cui and Shibata (2017), who look at timing and quantity in a situation where information asymmetry is on fixed costs, rather than marginal investment costs as in our model. In their model, under geometric Brownian motion, the information asymmetry leads to expansion of size in response to the asymmetric information, in line with the difference between asymmetric information on marginal versus fixed costs in static models of regulation (Armstrong and Sappington, 2007). In this paper, we explore the effect of asymmetric information on variable costs, and moreover verify how that effect may be sensitive to the choice of stochastic process.

2 The Model

We consider an investment project of variable scale, q, that will be undertaken by an agent on behalf of a principal. The principal’s pay-off of the investment will be dependent on the investment quantity q according to a constant elasticity demand curve,

$$\begin{aligned} \text{ pay-off }= P(q) q = x q^{1-\gamma } \end{aligned}$$

and is modeled as a one-off benefit to the principal at the moment of investment. Here $P(q)= x q^{-\gamma }$ is the principal’s benefit (‘price’) per unit, $0<\gamma <1$ is the inverse elasticity of demand, and x is a stochastic quantity measuring demand intensity. x will satisfy an autonomous stochastic (Ito) process of the form

$$\begin{aligned} \frac{dx}{x}=\mu (x) dt +\sigma (x) dz \end{aligned}$$

with dz a Wiener increment. (For $\mu (x), \sigma (x)$ constants, this would be geometrical Brownian motion, but we allow for more general well-behaved processes.)

The principal will discount its pay-off by a constant discount rate, r, so that the present value of its pay-off will be $E\left( e^{-rT}P(q)q \right)$. We will consider stopping times that can be described as the time when demand intensity x for the first time exceeds a threshold, X, so that $x(T)=X$.

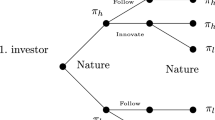
The agent will be the party carrying out the investment. The agent’s cost of investing has a fixed component F, and variable costs, cq. The agent’s present value of investing an amount q at time T then is $-E\left( e^{-rT}(c q + F) \right)$. The fixed cost, F, is common knowledge among principal and agent. On the other hand, the variable cost parameter, c, is not. c can be either low, $\underline{c}$, or high, $\bar{c}$. While the agent knows his cost c, the principal only knows c is low with probability $\phi$, or high with probability $1-\phi$. It is this asymmetry of information that will be at the root of the inefficiency in this investment problem.

The principal now contracts with the agent on investment time, T (defined in terms of the observable x crossing the threshold X), and investment quantity q. This contract will specify a remuneration w, to be paid by the principal to the agent at time T, in return for the specified investment q at time T. For a given set of w, X and q, the principal’s total net present value will be

$$\begin{aligned} NPV= E\left( e^{-rT}\right) \left( Xq^{1-\gamma }-w\right) \equiv D(x,X)\left( Xq^{1-\gamma }-w\right) \end{aligned}$$

with $D(x,X)=E\left( e^{-rT}\right)$ the expected discount factor, given current demand intensity x and threshold X.¹

2.1 Optimal Contracting with Asymmetric Information

In response to the asymmetric information, the principal will optimally offer a menu of two contracts, which is designed to make sure that each type of agent (low-cost or high-cost) self-selects, out of this menu, the contract intended for its type (the incentive compatibility constraint), provided the agent will at least get its cost reimbursed under that contract (the participation constraint). In our model, such a contract consists of the offer of the agent’s remuneration w upon investment, the intended investment threshold, X, and the investment quantity, q, one such triple for each type.

The incentive compatibility conditions now become

$$\begin{aligned} D(x,\bar{X})\left( \bar{w}-\bar{c}\bar{q}-F\right)&\ge D(x,\underline{X})\left( \underline{w}-\bar{c}\underline{q}-F\right) \qquad \qquad \qquad \qquad \qquad ({\overline{IC}}) \end{aligned}$$

$$\begin{aligned} D(x,\underline{X})\left( \underline{w}-\underline{c}\underline{q}-F\right)&\ge D(x,\bar{X})\left( \bar{w}-\underline{c}\bar{q}-F\right) \qquad \qquad \qquad \qquad \qquad ({\underline{IC}}) \end{aligned}$$

for the high, $\bar{c}$, and the low, $\underline{c}$, cost types, respectively. From the first condition, $\overline{IC}$, the high type will prefer accepting its contract (payment $\bar{w}$ for investing at threshold $\bar{X}$ a quantity $\bar{q}$) rather than pretending to be low cost, but having to invest the amount $\underline{q}$ (at threshold $\underline{X}$) at its (privately known) cost level $\bar{c}$. And conversely, a low-cost agent will opt for $\underline{w}, \underline{X},\underline{q}$, instead of getting remuneration intended for the high-cost type at the intended timing and quantity for the high-cost type.

Participation constraints in turn make sure that neither type of firm makes negative profit when it accepts its intended contract:

$$\begin{aligned} D(x,\bar{X})\left( \bar{w}-\bar{c}\bar{q}-F\right)&\ge 0 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad ({\overline{PC}}) \end{aligned}$$

$$\begin{aligned} D(x,\underline{X})\left( \underline{w}-\underline{c}\underline{q}-F\right)&\ge 0 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad ({\underline{PC}}) \end{aligned}$$

The principal will now design its contract offers, $(\bar{w},\bar{X},\bar{q})$ and $(\underline{w},\underline{X},\underline{q})$, to maximize its expected pay-off:

$$\begin{aligned} W=\phi D(x,\underline{X})\left( \underline{X}\underline{q}^{1-\gamma }-\underline{w}\right) +(1-\phi ) D(x,\bar{X})\left( \bar{X}\bar{q}^{1-\gamma }-\bar{w}\right) , \end{aligned}$$

subject to the four constraints.

The analysis of this optimization leads, as is standard (Laffont and Martimort, see e.g. 2002), to the conclusion that there will be two binding constraints, $\overline{PC}$ and $\underline{IC}$ (with the other two being slack)²: high-cost types make zero profits (while low-cost ones will end up earning an informational rent), and it will be those with low cost $\underline{c}$ who will have to be dissuaded from accepting the high-cost contract (which promises to remunerate the high investment costs to high-cost agents). Using those two constraints that hold with equality to substitute for $\bar{w}$ and $\underline{w}$ leads to a rewritten optimization problem

$$\begin{aligned} W=\phi D(x,\underline{X})\left( \underline{X}\underline{q}^{1-\gamma }- \underline{c}\underline{q}-F\right) +(1-\phi ) D(x,\bar{X})\left( \bar{X}\bar{q}^{1-\gamma }- \tilde{c}\bar{q}-F\right) , \end{aligned}$$

where $\tilde{c}$ equals

$$\begin{aligned} \tilde{c}=\bar{c}+\frac{\phi }{1-\phi }\Delta c. \end{aligned}$$

In other words, the effect of asymmetric information is that, optimally, the principal chooses timing X and quantity q consistent with total surplus optimization, but as if actual costs for the high-cost agent is inflated to the higher virtual cost level $\tilde{c}$.

2.2 The Static, Baron–Myerson, Case

In case initial price parameter x is large, it will be optimal to invest immediately, and there is no option value in delaying, $D(x,X)=1$. In that situation, we are in a static principal-agent situation that was analyzed by Baron and Myerson (1982), where only a distortion in quantity q is used to distinguish the low and the high cost types. The optimum contracts then allow an efficient, low-cost firm, to invest first-best quantities and earn an informational rent over and above its investment cost. A high-cost firm, instead, will get a contract that only remunerates its costs, $\bar{w}=\bar{c}\bar{q}+F$, but will be required to invest a quantity $\bar{q}$ that lies below its first-best level, so as to reduce the rents that need to be paid to low-cost agents in order to dissuade them from pretending to be high-cost.

Quantities in this Baron–Myerson case optimize virtual surplus

$$\begin{aligned} W^{BM}=\phi \left( x\underline{q}^{1-\gamma }-\underline{c}\underline{q}-F\right) +(1-\phi ) \left( x\bar{q}^{1-\gamma }-\tilde{c}\bar{q}-F\right) , \end{aligned}$$

leading to

$$\begin{aligned} {(\underline{q}_{BM})}^\gamma =(1-\gamma )\frac{x}{\underline{c}},\quad {(\bar{q}_{BM})}^\gamma =(1-\gamma )\frac{x}{\tilde{c}} \end{aligned}$$

(where $\bar{q}_{BM}$ is below its efficient level, because $\tilde{c}>\bar{c}$).

The intuition for the effect is that low-cost, $\underline{c}$, agents, are tempted to take contracts offered to high-cost agents and pocket the higher remuneration of costs $\bar{w}$. Reducing quantity $\bar{q}$ lowers that remuneration and hence makes it cheaper for the principal to keep low-cost agents from posing as high-cost ones.

In the static case, only this downward distortion in quantity $\bar{q}$ is used to screen agents. In contrast, when demand x is low, and there is option value in waiting before investing, there is an additional tool: the principal can also distort investment timing, delaying investment for the high-cost agents to occur at a higher demand size X. As a result of the additional discounting, this reduces the benefit for low-cost agents to taking high-costs’ contracts.

Since, all else equal, price $P(q)=xq^{-\gamma }$ is proportional to x, such a longer delay increases price P(q) at which investment takes place for the high-cost agent. This price increase makes quantity $\bar{q}$ more profitable, driving up that quantity, and thus working against the Baron–Myerson reduction in quantity to screen high-cost agents. We next analyze whether the resulting effect can be an increase in quantity $\bar{q}$.

3 Real-Option Analysis

We now turn to the real-option analysis where waiting to invest is valuable. We consider the Ito process governing the demand-level, x,

$$\begin{aligned} \frac{dx}{x}=\mu (x)dt+\sigma (x)dz. \end{aligned}$$

This stochastic process enters the analysis through the expected discount factor, $D(x,X) =E(e^{-rT})$ for demand-level x’s first crossing of the threshold price level X. As an example, for geometric Brownian motion, which has $\mu (x)=\mu$ and $\sigma (x)=\sigma$ constant, we have the well-known expression

$$\begin{aligned} D(x,X)=\left( \frac{x}{X}\right) ^\beta \end{aligned}$$

(as long as $x<X$). Here, $\beta$ is the positive root of the characteristic quadratic equation

$$\begin{aligned} r=\mu \beta +{\textstyle {\frac{1}{2}}}\sigma ^2 \beta (\beta -1). \end{aligned}$$

(1)

As we have seen, the principal chooses contracts involving X and q for each cost type to maximize, for each type of agent separately, the virtual surplus W, which in our two-type case is computed with cost $c=\tilde{c}$ instead of $\bar{c}$ for the high-cost type, and with actual cost $c=\underline{c}$ for the low cost type:

$$\begin{aligned} W(X,q)= D(x,X)\left( Xq^{1-\gamma }- c q - F\right) . \end{aligned}$$

For quantity, q, in this optimum we retain the relation

$$\begin{aligned} q^{\gamma }=(1-\gamma )\frac{X}{c}. \end{aligned}$$

Substituting the optimal q, we obtain an expression in terms of X. It turns out helpful to use notation

$$\begin{aligned} \pi (X)=\max _q\left( Xq^{1-\gamma }- c q \right) = \gamma (1-\gamma )^{\frac{1}{\gamma }-1}c\left( \frac{X}{c}\right) ^{\frac{1}{\gamma }} \end{aligned}$$

(2)

for the X-dependent benefits of investing F with the optimal quantity q. Also, what will play a crucial role in the analysis is the elasticity of the expected discount factor (see Dixit, Pindyck and Sødal, 1999)³

$$\begin{aligned} \beta (X) = -\frac{\partial \log D(x,X)}{\partial \log X}. \end{aligned}$$

For the familiar example of geometric Brownian motion (GBM), we have $\beta (X)=\beta$, the constant, positive root of the characteristic quadratic equation as highlighted above. In this sense, one may view GBM as the constant elasticity version of stochastic processes. For alternative processes, $\beta (X)$ will vary with X, and the way in which it does will turn out important for our question. We will look at the relation between $\beta (X)$ and various stochastic processes in more detail later.

In terms of $\pi (X)$ and $\beta (X)$, optimal investment can be described as follows.⁴

Proposition 1

Optimal investment for an agent of virtual costs c takes place at threshold level for demand-size X satisfying

$$\begin{aligned} \pi (X)=\frac{\gamma \beta (X)}{\gamma \beta (X)-1}F, \end{aligned}$$

(FOC)

where $\beta (X)$ is the elasticity of the expected discount factor. Second-order conditions require that

$$\begin{aligned} X\beta '(X)\ge -\frac{1}{\gamma ^2}\frac{\pi (X) F}{(\pi (X) - F)^2}. \end{aligned}$$

(SOC)

The formulation in terms of variable profits $\pi$ and elasticity $\beta (X)$ makes clear the relation with well-known real option results in simpler contexts. In its simplest form, for geometric Brownian motion ($\beta (X)=\beta$) and without any quantity effects so that pay-off is equal to (or directly proportional to) the stochastic variable X (i.e., $\gamma =1$), we would have a first-order condition

$$\begin{aligned} \pi (X)=\frac{\beta }{\beta -1}F, \end{aligned}$$

as in the standard McDonald and Siegel (1986) situation. For $\pi \sim X^{1/\gamma }$, one replaces $\beta$ by $\gamma \beta$ (see e.g. Dobbs, 2004, for an example of that involving continuous, gradual capacity expansion). Proposition 1 demonstrates that those well-known expressions can be extended for more general stochastic processes in terms of the X-dependent elasticity $\beta (X)$.⁵

Provided there is a solution of the first-order condition with $\gamma \beta (X)>1$, this first-order condition demonstrates that there is option value in waiting: variable benefits $\pi$, at the moment of investing T, are strictly larger than the fixed costs of investing F. The difference reflects the well-known opportunity costs of exercising the option to wait; these opportunity costs need to be added to actual fixed costs F to determine optimal investment.

As we saw before, in the presence of information asymmetry on variable costs c, the optimal contract that the principal writes with the agent will require maximizing virtual surplus, which involves a marginal cost parameter c that has been increased to reflect asymmetric information for all but the most efficient agents. For answering the question how the principal optimally distorts investment timing and quantities, we then need to consider how both X and q change as c is increased from its real value for a high-cost agent, $\bar{c}$, to its virtual value $\tilde{c}>\bar{c}$. This can again be conveniently phrased in terms of the elasticity $\beta (X)$, and its derivative $\beta '(X)$, as the following proposition shows.

Proposition 2

In the equilibrium, we have comparative statics

$$\begin{aligned} \frac{\partial \log X}{\partial \log c}=\frac{(1-\gamma )\frac{\pi (X) F}{\gamma ^2(\pi (X)-F)^2}}{X\beta '(X)+\frac{\pi (X) F}{\gamma ^2(\pi (X)-F)^2}}>0 \end{aligned}$$

and, secondly, the sign of the derivative of investment quantity q with respect to marginal cost c is given by the sign of

$$\begin{aligned} \frac{d\log q}{d\log c}&=\frac{1}{\gamma }\left( \frac{\partial \log X}{\partial \log c}-1 \right) \\&=\frac{1}{\gamma }\left( \frac{(1-\gamma )\frac{\pi (X) F}{\gamma ^2(\pi (X)-F)^2}}{X\beta '(X)+\frac{\pi (X) F}{\gamma ^2(\pi (X)-F)^2}}-1 \right) \end{aligned}$$

A sufficient condition for quantity q to decrease with increasing c is that $\beta '(X)\ge 0$.

The first comparative static, the effect of increasing costs c on X, the investment threshold, is always positive. This means that for any stochastic process, introducing asymmetric information will result in a delay of investment for the high-cost agent, as virtual costs will exceed actual costs for this type. The intuition for this is that, whatever the stochastic process, delay will make it less attractive for low-cost agents to grab the benefits of the larger remuneration handed out to the (genuinely) high-cost agent: this higher remuneration will be paid out later, and hence will have lower present value.

The second result relates to our main question. From the former result, the investment threshold X (and hence the value to the principal of increased quantity, P(q)) increase for the high-cost agent as a result of asymmetric information. This effect gives upward pressure on the optimal quantity q for this type. On the other hand, the higher virtual costs also make producing this higher q less attractive: this is the Baron–Myerson effect, which encapsulates the loss in principal’s welfare from low-cost types extracting informational rents. Which of these two effects dominates depends on the sign of the second expression. As long as $\beta '(X)\ge 0$, we see that it is the Baron–Myerson effect that is the most important, and $\bar{q}$ shrinks as informational asymmetries increase. (And for sufficiently small negatively sloped $\beta$, that remains the case.)

As we will see presently, $\beta (X)$ is indeed non-decreasing for a class of well-known stochastic processes, including geometrical Brownian motion (which has constant elasticity $\beta$) and arithmetic Brownian motion. In those cases, the Baron–Myerson effect, a downward distortion in quantities in response to asymmetric information, therefore dominates the increased threshold price at which investment takes place in the real option context.

As Proposition 2 also shows, there is some scope for quantities increasing with costs c. That would imply that asymmetric information causes the invested quantities to increase, rather than decrease: the larger marginal value of quantity from waiting longer (higher threshold X) in that case outweighs the Baron–Myerson effect that favours quantity reductions. In this case elasticity $\beta$ must be negatively sloped. The extent to which that is possible is limited by the second-order condition, which requires the denominator in the comparative statics expression in proposition 1 to be positive. We will present an example of such a process later. But first, we will study $\beta (X)$, its relation with the stochastic process, and its form in some often-used stochastic processes.

4 The Relation Between Elasticity $\beta (X)$ and the Stochastic Process

It is clear that, if we know the stochastic process, characterized by drift $\mu (x)$ and volatility $\sigma (x)$, we can compute, in principle, the discount rate D(x, X), and hence its elasticity $\beta (X)$. As remarked before, for example, for GBM, this discount rate equals $(x/X)^{\beta _1}$, leading to constant elasticity $\beta _1$, with $\beta _1$ the positive root of the characteristic quadratic equation (1).

Likewise, we can compute elasticity for other often used processes (Dixit et al., 1999), such as arithmetical Brownian motion, $dx=\mu dt+ \sigma dz$, which has

$$\begin{aligned} D(x,X)=e^{-\lambda (X-x)}, \text { and }\beta (X)=\lambda X, \end{aligned}$$

(where $\lambda$ is the positive solution of $r=\mu \lambda +{\textstyle {\frac{1}{2}}}\sigma ^2\lambda ^2$), for which clearly elasticity $\beta (X)$ is increasing in X.⁶

It is also instructive to work in the reverse direction and derive a stochastic process from the elasticity, $\beta (X)$. To do so, note that, by the definition

$$\begin{aligned} \beta (X)=-\frac{\partial \log D}{\partial \log X}, \end{aligned}$$

and the fact that $D(X,X)=1$, we can integrate to

$$\begin{aligned} D(x,X)=e^{-\int _{x}^{X}\beta (s)\frac{ds}{s}}. \end{aligned}$$

(3)

Moreover, note that D(x, X) should satisfy the Hamilton-Jacobi-Bellman equation,

$$\begin{aligned} rD=\mu (x) x D_x +{\textstyle {\frac{1}{2}}}\sigma ^2(x)x^2 D_{xx}, \end{aligned}$$

which in terms of the elasticity now reduces to the condition

$$\begin{aligned} r=\mu (x)\beta (x)+{\textstyle {\frac{1}{2}}}\sigma ^2(x)\left( \beta (x)^2-\beta (x)+x\beta '(x)\right) . \end{aligned}$$

(CQ)

This equation, CQ, generalizes the characteristic quadratic (1) from geometrical Brownian motion, which corresponds to the special case where $\beta (X)=\beta$ is constant, and $\mu (x)=\mu$ and $\sigma (x)=\sigma$. Similarly, one can substitute $\beta (X)=\lambda X$ and recover that arithmetic Brownian motion, with $\mu (x)=\mu /x$ and $\sigma (x)=\sigma /x$, is one solution to this case.

Looking at this generalized characteristic quadratic CQ, we may get more intuition for our result that increasing $\beta (X)$ matters for determining effects on investment size q as costs increase. If $\beta '(X)$ is negative, then CQ tells us that the drift rate $\mu (x)$ must grow faster as x grows: the larger x becomes, the larger x’s growth rate, all else equal. If this effect is large enough, the expected growth in prices as a result of higher investment threshold will then, at some point, overtake the reduction in quantities through the Baron–Myerson effect.

Apart from the pure cases of arithmetic and geometric Brownian motion, this formulation suggests considering a one-parameter family of stochastic processes, with $\beta (X)=\lambda X^\alpha$ ($\alpha \ge 0$), that incorporates geometric and arithmetic Brownian motions as special cases. By substituting this $\beta (X)$ into the generalized characteristic quadratic (CQ), we find that a simple stochastic process leading to this elasticity $\beta (X)$ is

$$\begin{aligned} dx=(\mu x^{1-\alpha }+(1-\alpha ){\textstyle {\frac{1}{2}}}\sigma ^2x^{1-2\alpha })dt + \sigma x^{1-\alpha }dz \end{aligned}$$

(with the constant $\lambda$ again satisfying $r=\mu \lambda +{\textstyle {\frac{1}{2}}}\sigma ^2\lambda ^2$). The discount functions associated to this one-parameter family can be evaluated by (3) to

$$\begin{aligned} D(x,X)=e^{-\frac{\lambda }{\alpha }(X^\alpha -x^\alpha )} \end{aligned}$$

for $\alpha >0$, and $D(x,X)=\left( \frac{x}{X}\right) ^\lambda$ for $\alpha =0$.

For $\alpha =0$ and $\alpha =1$ we recover the geometric and arithmetic Brownian motions, as mentioned. Also noteworthy is the case $\alpha ={\textstyle {\frac{1}{2}}}$, with

$$\begin{aligned} dx=\mu (\sqrt{x}+\frac{\sigma ^2}{4\mu })dt+\sigma \sqrt{x} dz, \end{aligned}$$

which for negative $\mu$ is a mean reverting process, tending to a mean $\bar{x}=\frac{\sigma ^4}{16\mu ^2}$. By construction, all these processes have increasing elasticity $\beta (X)$.

In the following, we will use this procedure of reverse engineering—if we are given the elasticity $\beta (X)$, what is the expected discount factor—to construct a stochastic process that will serve as a counterexample. The counterexample will be designed to feature a stochastic process where, in response to asymmetric information on variable costs c, investment will optimally be delayed for high-cost firms (as always), but investment quantity q for these firms will be higher, rather than lower, for these firms.

5 A Counter example

Recall the line of argument: if we introduce asymmetric information into variable investment costs c, then real option investment timing and quantity will optimally be distorted away from first-best timing and quantity. The optimal distortion will involve contracts that look like those occurring in a model without asymmetric information where all costs c have been replaced with their virtual counterparts $\tilde{c}$. For high-cost agents, these virtual costs are higher than their real costs.

As Proposition 2 demonstrated, replacing costs c with higher virtual costs $\tilde{c}$ always leads to delay in investment timing (first part of Proposition 2) compared to non-distorted costs. This will be true for any process for x. The situation is different, however, for investment quantity q. As the second part of Proposition 2 showed, quantity q often goes down (compared to its symmetric information counterpart) in response the rise in cost levels from actual to virtual. The exception is when the elasticity of the expected discount rate, $\beta (X)$ is sufficiently negatively sloped at its investment level.

To construct a (counter)example that illustrates this exception, and where quantity indeed increases in response to the introduction of asymmetric information, we now use the insights from the previous section. We will construct a suitable, negatively-sloped, elasticity $\beta (X)$, and reverse-engineer a stochastic process that indeed results in an expected discount rate that features quantity expansion, rather than contraction, in response to the introduction of asymmetric information. The rise in price (created by the higher threshold X) upon investment is then sufficiently large to outweigh the reducing effect on quantity created by the increase in costs from $\bar{c}$ to $\tilde{c}$.

To illustrate increasing quantity q, note that by Proposition 2, for such a increase to occur we need

$$\begin{aligned} -\frac{\pi (X) F}{\gamma ^2(\pi (X)-F)^2}< X\beta '(X)<-\gamma \frac{\pi (X) F}{\gamma ^2(\pi (X)-F)^2} \end{aligned}$$

to hold for all relevant c. Note, from equation (2) that the expressions defining those bounds depend on c through $\pi (X)\sim c\left( \frac{X}{c}\right) ^{\frac{1}{\gamma }}$. The first inequality is necessary for the second-order condition, making sure that there is real option value in delaying investment, while the second makes sure that $\beta '(X)$ is sufficiently negative to create an expansion of quantity q in response to increasing the high-cost agent’s marginal cost c from its actual level $\bar{c}$ to its virtual level $\tilde{c}$.

As an example of a function $\beta (X)$ that satisfies both these bounds, we consider the case

$$\begin{aligned} X\beta '(X)=-\alpha \frac{\bar{\pi }(X) F}{\gamma ^2(\bar{\pi }(X)-F)^2} \end{aligned}$$

for some parameter $\alpha$ satisfying $\gamma<\alpha <1$, and where $\bar{\pi }(X)$ equals $\pi (X)$ evaluated at $c=\bar{c}$,

$$\begin{aligned} \bar{\pi }(X)=\gamma (1-\gamma )^{\frac{1}{\gamma }-1}\bar{c}\left( \frac{X}{\bar{c}}\right) ^{\frac{1}{\gamma }}. \end{aligned}$$

This automatically ensures that $\beta '(X)$ is within these bounds at $c=\bar{c}, X=\bar{X}$, and by continuity extends to all $\underline{c}\le c \le \tilde{c}$ provided neither $\Delta c$ nor $\frac{\phi }{1-\phi }$ is too large. By integrating this expression for $\beta '(X)$, we then have

Proposition 3

An example for which investment quantity q increases as a result of asymmetric information is when $\beta (X)$ satisfies

$$\begin{aligned} \beta (X)= \alpha \frac{F}{\gamma (\bar{\pi }(X)-F)}+ (1-\alpha )\bar{\beta }+\alpha /\gamma , \end{aligned}$$

and

$$\begin{aligned} D(x,X)=\left( \frac{\bar{\pi }(x)-F}{\bar{\pi }(X)-F}\right) ^\alpha \left( \frac{\bar{\pi }(x)}{\bar{\pi }(X)}\right) ^{\gamma \bar{\beta }(1-\alpha )} \end{aligned}$$

where $\gamma<\alpha <1$, $\bar{\pi }(X)$ equals $\pi (X)$ evaluated at $\bar{c}$, and with integration constant $\bar{\beta }>\frac{1}{\gamma }$.

The integration constant is chosen such that at first-best investment for a firm with marginal costs $\bar{c}$, elasticity at investment equals $\bar{\beta }$. As discussed earlier, we need $\gamma \beta >1$ at investment.

The discount function expression in proposition 3 has been constructed so as to lead to the phenomenon of demand growth X near the investment threshold to ‘out-speed’ contraction by the increase of investment costs, from $\bar{c}$ to $\tilde{c}$, as a reflection of the information asymmetry.

To get further insight into the characteristic that makes demand growth outstrip the need to reduce quantity in this constructed example, it is instructive to look at the process that governs the evolution of x in this construction, and compare it with the benchmark of geometric brownian motion. To do so, we need to recognize that a given $\beta (x)$ (or equivalently, an expected discount function D(x, X)) is not associated with a unique stochastic process. For instance, for GBM, there is a family of $\mu ,\sigma$ pairs that all lead to the same $\beta _1$, and hence the same discount function. All that is needed is that drift $\mu$ and volatility $\sigma$ satisfy the characteristic quadratic, $r=\mu \beta _1+{\textstyle {\frac{1}{2}}}\sigma ^2 \beta _1(\beta _1-1)$.

Similar logic applies to other stochastic processes: given $\beta (x)$, for any choice of volatility $\sigma (x)$ we can back out a drift function $\mu (x)$ that solves the generalized characteristic quadratic CQ. In our case, one example might be taking $\sigma (x)=\sigma$ constant (as in the standard GBM model). In that concrete example, we are looking at a stochastic process

$$\begin{aligned} dx=\mu (x)xdt+\sigma x dz, \end{aligned}$$

with

$$\begin{aligned} \mu (x)=\frac{r-{\textstyle {\frac{1}{2}}}\sigma ^2\left( \beta (x)^2-\beta (x)+x\beta '(x)\right) }{\beta (x)} \end{aligned}$$

where $\beta (x)$ is given by proposition 3, and

$$\begin{aligned} x\beta '(x)=-\alpha \frac{\bar{\pi }(x) F}{\gamma ^2(\bar{\pi }(x)-F)^2}. \end{aligned}$$

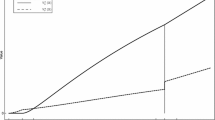
To give an impression of how these processes compare to GBM, Fig. 1 illustrates the path of demand x(t) in the deterministic variant, where $\sigma =0$, alongside a similar path for geometric Brownian motion. Clearly, in the constructed counter-example process, demand growth becomes progressively faster than the exponential growth exhibited by the regular GBM process. This faster demand expansion is then reflected in an expansion in invested capacity q as investment is delayed.

Fig. 1

Exponential growth (Geometrical Brownian Motion with zero volatility) compared with demand growth for the counter-example process in its deterministic limit

6 Conclusion

In this paper, we explore the nature of investment distortions that result from information asymmetries between providers of capital and management of firms in a real option setting. One may think of regulatory investment problems, where for example an energy network firm needs to sink capital, on behalf of a regulator, into network expansion or into new, green technology. Or of an industrial firm that invests in new production capacity on behalf of outside capital providers, such as shareholders or banks.

We focus here on those investments that have real option characteristics: pay-offs are stochastic, investments are irreversible. As is well known (Dixit and Pindyck, 1994), in that context investment timing is non-trivial, as there may be option value to delaying the investment. We further assume that there is information asymmetry on the marginal costs of those investments: the firm knows its marginal costs, the principal (regulator, shareholder) does not. In typical principal-agent models of this kind, investment sizes tend to be reduced compared to first-best size (Baron and Myerson, 1982). The reason is that the agent tends to overstate its costs, hoping to get a better deal. By reducing quantities, the principal diminishes the incentive for such cost exaggeration.

The main message of this paper is that there is a counterveiling effect to that quantity reduction if we also take into account investment timing. Postponing investments is another well-known strategy to induce truthful cost revelation. Since that strategy leads to higher demand for investment to occur, quantities may actually increase relative to the first-best. We characterize stochastic demand processes for which this effect outweighs the standard Baron–Myerson effect. As a by-product, we adapt a methodology for dealing with less standard stochastic processes in real-option analysis due to Dixit et al. (1999).

Appendix: Proofs

Proof of proposition 1

We have total profits upon investment equal to $\pi (X)-F$, where $\pi (X)$ is the variable part of profits,

$$\begin{aligned} \pi (X)=\max _q \left( X q^{1-\gamma }-cq\right) , \end{aligned}$$

with $0<\gamma <1$. Maximization over q occurs at

$$\begin{aligned} (1-\gamma )Xq^{-\gamma }=c, \end{aligned}$$

(provided $\pi (X)>F$ at that value), so that

$$\begin{aligned} \pi (X)=\gamma (1-\gamma )^{\frac{1}{\gamma }-1}\left( \frac{X}{c}\right) ^{\frac{1}{\gamma }}c \end{aligned}$$

from which it will be convenient to notice that $X\frac{\partial \pi }{\partial X}=\frac{\pi }{\gamma }$.

For the real option problem, we need to maximize

$$\begin{aligned} \max _X D(x,X)\left( \pi (X)-F\right) . \end{aligned}$$

For the first-order conditions, computationally, it is convenient to consider the logarithm of this expression, and take the derivative with respect to $\log X$ to find

$$\begin{aligned} -\beta (X)+\frac{\pi /\gamma }{\pi -F}=0 \end{aligned}$$

(4)

with $\beta (X)$ the elasticity of the discount factor,

$$\begin{aligned} \beta (X)=-\frac{\partial \log D}{\partial \log X}. \end{aligned}$$

The first-order condition can be rewritten in the more usual real-option investment rule

$$\begin{aligned} \pi (X)=\frac{\gamma \beta (X)}{\gamma \beta (X)-1}F. \end{aligned}$$

The second-order condition can straightforwardly be obtained from acting with $X\frac{d}{dX}$ on (4), again using the equality $X\frac{\partial \pi }{\partial X}=\frac{\pi }{\gamma }$. Demanding that our solution is a maximum then places a lower bound on $\beta '(X)$:

$$\begin{aligned} X\beta '(X)+\frac{\frac{\pi F}{\gamma ^2}}{(\pi -F)^2}>0. \end{aligned}$$

□

Proof of Proposition 2

We are interested in how both X and, ultimately, q, depend on c. From the first-order condition (4), by the implicit function theorem we have

$$\begin{aligned} \frac{\partial \log X}{\partial \log c}=\frac{(1-\gamma )\frac{\pi F}{\gamma ^2(\pi -F)^2}}{X\beta '(X)+\frac{\pi F}{\gamma ^2(\pi -F)^2}}>0 \end{aligned}$$

(where the sign follows from the second-order condition).

Since $q\sim \left( \frac{X}{c}\right) ^{1/\gamma }$ we then have

$$\begin{aligned} \frac{d\log q}{d\log c}&=\frac{1}{\gamma }\left( \frac{\partial \log X}{\partial \log c}-1 \right) \\&=\frac{1}{\gamma }\left( \frac{(1-\gamma )\frac{\pi F}{\gamma ^2(\pi -F)^2}}{X\beta '(X)+\frac{\pi F}{\gamma ^2(\pi -F)^2}}-1 \right) \end{aligned}$$

It is then clear that the sign of $\frac{dq}{dc}$ is certainly negative for $\beta '(X)>0$, and that the lower bound on $X\beta '(X)$ for that sign is

$$\begin{aligned} X\beta '(X)> -\gamma \frac{\pi F}{\gamma ^2(\pi -F)^2}. \end{aligned}$$

Since $\gamma <1$, there is a narrow scope for $X\beta '(X)$ to violate this condition while still satisfying the second-order condition, which we will exploit in the counterexample. □

Proof of Proposition 3

For the counterexample in which q rises as a result of asymmetric information, and the associated increase of high-type cost $\bar{c}$ to virtual cost level $\tilde{c}=\bar{c}+\frac{\phi }{1-\phi }\Delta c$, we need a sufficiently negatively sloped $\beta (X)$ in the relevant range, satisfying

$$\begin{aligned} -\frac{\pi (X) F}{\gamma ^2(\pi (X)-F)^2}<X\beta '(X)< -\gamma \frac{\pi (X) F}{\gamma ^2(\pi (X)-F)^2} \end{aligned}$$

(satisfied with $\pi$ evaluated at any c in the relevant range). The left-hand inequality is the second-order condition: we want there to be a positive option value of delay; the right-hand inequality makes sure that q is going to increase as we increase c from $\bar{c}$ to $\tilde{c}$.

To find a stochastic process, with a discount factor D(x, X), satisfying these conditions, let us pick a $\beta$ sloped in between those two values, and then integrate to find $\beta (X)$, and hence D(x, X). We will pick

$$\begin{aligned} X\beta '(X)=-\alpha \frac{\bar{\pi }(X) F}{\gamma ^2(\bar{\pi }(X)-F)^2} \end{aligned}$$

with $\gamma< \alpha < 1$, with $\bar{\pi }(X)$ equal to the profit function $\pi (X)$ evaluated for $c=\bar{c}$,

$$\begin{aligned} \bar{\pi }(X)=\gamma (1-\gamma )^{\frac{1}{\gamma }-1}\bar{c}\left( \frac{X}{\bar{c}}\right) ^{\frac{1}{\gamma }}. \end{aligned}$$

(E.g., $\alpha =\sqrt{\gamma }$, the geometric mean of 1 and $\gamma$, would do.) As long as asymmetric information is not too large, the relevant bounds will then continue to hold also for $c=\tilde{c}$.

We can now integrate $\beta '(X)$. It is convenient to change variables from X to $\bar{\pi }(X)\sim \left( \frac{X}{\bar{c}}\right) ^\frac{1}{\gamma }\bar{c}$, noting that $X\frac{d\pi }{dX}=\frac{\pi }{\gamma }$. We then have

$$\begin{aligned} \beta (X)= \alpha \frac{F}{\gamma (\bar{\pi }(X)-F)}+ \text {constant}. \end{aligned}$$

We will choose the integration constant to set the level $\beta (X)$ for efficient investment at costs $\bar{c}$ to some $\bar{\beta }$ that satisfies $\gamma \bar{\beta }>1$, as is necessary for delay to be optimal. That choice then fixes the threshold level $\bar{X}$ associated with costs $\bar{c}$ to satisfy the first-order condition

$$\begin{aligned} \bar{\pi }(\bar{X})=\frac{\gamma \bar{\beta }}{\gamma \bar{\beta }-1}F, \quad \text { or }\quad \gamma \bar{\beta }=\frac{\bar{\pi }(\bar{X})}{\bar{\pi }(\bar{X})-F} \end{aligned}$$

In order to achieve that, we need to choose the constant to equal

$$\begin{aligned} \text {constant}=(1-\alpha )\bar{\beta }+\alpha /\gamma . \end{aligned}$$

Next, integrating once again, we can find the discount function D(x, X):

$$\begin{aligned} \log D(x,X)&= - \int _x^X\beta (x)\frac{dx}{x}\\&=-\int _{\bar{\pi }(x)}^{\bar{\pi }(X)}\left( \frac{\alpha F}{\bar{\pi }(\bar{\pi }-F)}+\gamma \frac{\text {constant}}{\bar{\pi }}\right) d\bar{\pi }\end{aligned}$$

which then leads to

$$\begin{aligned} D(x,X)=\left( \frac{\bar{\pi }(x)-F}{\bar{\pi }(X)-F}\right) ^\alpha \left( \frac{\bar{\pi }(X)}{\bar{\pi }(x)}\right) ^\alpha \left( \frac{\bar{\pi }(x)}{\bar{\pi }(X)}\right) ^{\gamma \cdot \text {constant}} \end{aligned}$$

or

$$\begin{aligned} D(x,X)=\left( \frac{\bar{\pi }(x)-F}{\bar{\pi }(X)-F}\right) ^\alpha \left( \frac{\bar{\pi }(x)}{\bar{\pi }(X)}\right) ^{\gamma \bar{\beta }(1-\alpha )}. \end{aligned}$$

□