The Macroeconomic Effects of Longevity Risk Under Private and Public Insurance and Asymmetric Information

Abstract

We study the impact of a fully-funded social security system in an economy with heterogeneous consumers. The unobservability of individual health conditions leads to adverse selection in the private annuity market. Introducing social security—which is immune to adverse selection—affects capital accumulation and individual welfare depending on its size and on the pension benefit rule that is adopted. If this rule incorporates some implicit or explicit redistribution from healthy to unhealthy individuals then the latter types are better off as a result of the pension system. In the absence of redistribution the public pension system makes everybody worse off in the long run. Though attractive to distant generations, privatization of social security is not generally Pareto improving to all generations.

1 Introduction

More than half a century ago Yaari (1965) proved convincingly that private annuities are very attractive insurance instruments when non-altruistic individuals face longevity risk. Simply put, annuities are desirable because they insure such agents against the risk of outliving their assets. Yaari also proved a much stronger result: in the absence of an intentional bequest motive, rational utility-maximizing individuals should fully annuitize all of their savings. Yaari derives this result under the strong assumption that actuarially fair annuities are available. In a more recent paper, however, Davidoff et al. (2005) have demonstrated that the full annuitization result holds in a much more general setting than the one adopted by Yaari, for example when annuities are less than actuarially fair.

Despite the theoretical attractiveness of annuities, there is a vast body of empirical evidence showing that in reality people do not invest heavily in private annuity markets. The discrepancy between the theoretical predictions and the observable facts regarding annuity markets is know as the annuity puzzle. Of course there are many reasons why individuals may not choose to fully annuitize their wealth. Friedman and Warshawsky (1990, pp. 136–137), for example, argue that purchases of private annuities are low because (a) individuals may want to leave bequests to their offspring, (b) agents may already implicitly hold social annuities because they are participating in a system of mandatory public pensions, and (c) private annuities may be priced unattractively, for example because of transaction costs and taxes, excessive profits extracted by imperfectly competitive annuity firms, and adverse selection. Intuitively, under asymmetric information annuity companies cannot observe an individual’s health status. Adverse selection arises in such a setting because agents with above-average health are more likely to buy annuities. This implies that such “high-risk types” are overrepresented in the group of clients of annuity firms and that pricing of annuities cannot be based on the average health status of the population at large.

While recognizing their potential role in accounting for parts of the annuity puzzle, we ignore intentional bequest motives, administrative costs, and imperfect competition in this paper. Instead, we follow inter alia Abel (1986), Walliser (2000), Palmon and Spivak (2007), Sheshinski (2008) and Heijdra and Reijnders (2012) by focusing on the adverse selection channel. We approach the material sequentially by first demonstrating the adverse selection effect in an economy without public pensions. In the next step we introduce social annuities and study the general equilibrium interactions between private and public annuity markets under different pension benefit rules.

Our paper is most closely related to earlier work by Heijdra and Reijnders (2012). They study a discrete-time overlapping generations model in which non-altruistic agents differ in their innate health status, which is assumed to be private information. The private annuity market settles in a risk-pooling equilibrium in which the unhealthiest segment of the population experiences binding borrowing constraints (because they are unable to go short on annuities) and the other agents receive a common yield on their annuity purchases. They also show that the introduction of a mandatory public pension system—though immune to adverse selection by design—leads to a reduction in steady-state welfare, an aggravation of adverse selection in the private annuity market, and a reduction in the economy-wide capital intensity.

We extend the work by Heijdra and Reijnders (2012) by assuming that the individuals populating the economy differ by two dimensions of heterogeneity (health and ability) rather than just a single one (health). The introduction of heterogeneous abilities serves two purposes. First, as was shown by Walliser (2000, pp. 374–375) in a partial equilibrium setting, “(the simulations reveal that) between 40 and 60 percent of the measured adverse selection is due to the positive correlation between income and mortality...” By incorporating health-ability heterogeneity, and by assuming that there is a positive correlation between the two characteristics, we are able to capture this reputedly important source of adverse selection in the private annuity market. There is a second reason why heterogeneity matters which is related to the type of funded public pension system that is in place. Indeed, depending on the details regarding pension contributions and receipts, social security systems can have vastly different welfare implications for consumers with different health status and/or ability. In this paper we consider three different public pension schemes which differ in the degree to which they lead to (implicit or explicit) redistribution from healthy to unhealthy individuals.

Our main findings are as follows. Firstly, a plausibly calibrated version of the model reveals that, compared to the case with full information, asymmetric information on the part of annuity companies is important quantitatively in that it causes substantial reductions in steady-state output per efficiency unit of labour and the capital intensity. The general equilibrium effects are thus shown to matter a lot. Second, the introduction of a funded social security system reduces the capital intensity and output per efficiency unit even further, more so the larger is the system, i.e. the higher is the replacement rate it incorporates. These results are consistent with Palmon and Spivak (2007) and Heijdra and Reijnders (2012). Third, privatizing social security (by abolishing the public pension system) is not generally Pareto improving to all generations. Indeed, in our simulations we find that healthy agents born at the time of the shock would have been better off if the social security system had not been privatized. Just as for unfunded pensions, getting rid of a pre-existing funded system is not an easy task to accomplish.

The remainder of the paper is organized as follows. In Sect. 2 we set up the model and characterize the microeconomic choices and the resulting macroeconomic equilibrium under full information, i.e. the hypothetical case in which insurance companies can perfectly observe an individual’s characteristics. In Sect. 3 we introduce asymmetric information inhibiting insurance companies and show that it leads to a pooling equilibrium in the annuity market. In Sect. 4 we introduce a fully-funded social security system in which pension contributions are proportional to labour income during youth. We analyze three specific versions of this system which differ with respect to the pension receipts during old age. Section 5 considers the consequences of privatizing social security. The final section concludes. Some technical issues are dealt with in three brief appendices.

2 Model

2.1 Consumers

In each period the population in the closed economy under consideration features two overlapping generations of heterogeneous agents. Each person can live at most for two periods, namely ‘youth’ (superscript y) and ‘old age’ (superscript o). Individuals are heterogenous along two exogenously given dimensions. First, they differ by health status which we capture by the probability of surviving into old-age. Everyone faces lifetime uncertainty at the end of the first period, and the survival probability is denoted by $\mu$. This means that unhealthy people have a higher risk of dying and a shorter expected life span (which equals $1+\mu$ periods). Second, individuals differ in their working ability as proxied by innate labour productivity $\eta$.

We assume that consumer types are continuous and uniformly distributed on these two dimensions, i.e. $\mu \in [\mu _{L},\mu _{H}]$ (such that $0<\mu _{L}<\mu _{H}<1$) and $\eta \in [\eta _{L},\eta _{H}]$ (such that $0<\eta _{L}<\eta _{H}$). Furthermore, we postulate that $\mu$ and $\eta$ are positively correlated. Hence, a person in better health is more likely to possess higher working abilities, and vice versa. The bivariate uniform distribution used in this paper is characterized by the following probability density function:

$$\begin{aligned} h(\mu ,\eta )=\frac{1+\xi \,(\mu -{\bar{\mu }})(\eta -{\bar{\eta }})}{(\mu _{H}-\mu _{L})(\eta _{H}-\eta _{L})}, \end{aligned}$$

(1)

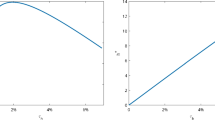
where $\xi$ is a parameter regulating the correlation between $\mu$ and $\eta$ (such that $\xi >0$), and ${\bar{\mu }}$ and ${\bar{\eta }}$ denote the unconditional means of $\mu$ and $\eta$, respectively. In Fig. 1 the distribution function is depicted in panel (a) whilst the probability density function is shown in panel (b). From the graph of the density function it is clear that there is a higher probability for healthier consumers to possess higher working abilities, and vice versa. For future reference we postulate Lemma 1 which summarizes some useful properties of the bivariate distribution that we employ.

Lemma 1

The distribution function for the survival probability$\mu$and labour productivity$\eta$is given by:

$$\begin{aligned} H(\mu ,\eta )=\frac{(\mu -\mu _{L})(\eta -\eta _{L})}{(\mu _{H}-\mu _{L})(\eta _{H}-\eta _{L})}\left[ 1+\frac{\xi }{4}\,(\mu _{H}-\mu )(\eta _{H}-\eta )\right] , \end{aligned}$$

where$\mu _{L}\le \mu \le \mu _{H}$and$\eta _{L}\le \eta \le \eta _{H}$. The density function is given in (1). Further properties of the distribution are: (i) the marginal density functions are$h_{\mu }(\mu )=1/(\mu _{H}-\mu _{L})$and$h_{\eta }(\mu )=1/(\eta _{H}-\eta _{L})$ ; (ii) the unconditional means are${\bar{\mu }}=(\mu _{L}+\mu _{H})/2$and${\bar{\eta }}=(\eta _{L}+\eta _{H})/2$; (iii) the unconditional variances are$\sigma _{\mu }^{2}=\left( \mu _{H}-\mu _{L}\right) ^{2}/12$and$\sigma _{\eta }^{2}=\left( \eta _{H}-\eta _{L}\right) ^{2}/12$; (iv) the covariance is${\mathrm{cov}}\left( \eta ,\mu \right) =\xi \sigma _{\eta }^{2}\sigma _{\mu }^{2}$and the correlation is${\mathrm{cor}}\left( \eta ,\mu \right) =\xi \sigma _{\eta }\sigma _{\mu }$; (v) the conditional probability density functions are:

$$\begin{aligned} h_{\mu |\eta }\left( \mu \right)&\equiv \frac{h\left( \eta ,\mu \right) }{ h_{\eta }\left( \eta \right) }=\frac{1+\xi \,(\mu -{\bar{\mu }})(\eta -\bar{\eta })}{\mu _{H}-\mu _{L}}, \\ h_{\eta |\mu }\left( \eta \right)&\equiv \frac{h\left( \eta ,\mu \right) }{ h_{\mu }\left( \mu \right) }=\frac{1+\xi \,(\mu -{\bar{\mu }})(\eta -{\bar{\eta }}) }{\eta _{H}-\eta _{L}}, \end{aligned}$$

and (vi) the conditional mean of$\eta$for a given$\mu$is:

$$\begin{aligned} \Gamma _{1}\left( \mu \right) \equiv \frac{\int _{\eta _{L}}^{\eta _{H}}\eta h\left( \eta ,\mu \right) d\eta }{\int _{\eta _{L}}^{\eta _{H}}h\left( \eta ,\mu \right) d\eta }=\frac{h_{\mu }(\mu )\int _{\eta _{L}}^{\eta _{H}}\eta h_{\eta |\mu }\left( \eta \right) d\eta }{h_{\mu }(\mu )}={\bar{\eta }}+\xi \sigma _{\eta }^{2}(\mu -{\bar{\mu }}). \end{aligned}$$

Proof

see Supplementary Material, Appendix A. $\square$

Fig. 1

Features of the distribution for $\mu$ and $\eta$. Health and innate ability are proxied by, respectively, the survival probability $\mu$ and the labour productvity parameter $\eta$. The two characteristics of an individual are positively correlated. The distribution $H(\mu ,\eta )$ is bivariate uniform. The marginal distributions of $\mu$ and $\eta$ are both uniform. See Supplementary Material (Appendix A) and Lemma 1 for further features of the distribution

From the perspective of birth, the expected lifetime utility of a person with health status $\mu$ and working ability $\eta$ is given by:

$$\begin{aligned} {\mathbb{E}}\Lambda _{t}(\mu ,\eta )\equiv U\left( {C_{t}^{y}(\mu ,\eta )} \right) +\mu \beta U\left( {C_{t+1}^{o}(\mu ,\eta )}\right) , \end{aligned}$$

(2)

where $C_{t}^{y}(\mu ,\eta )$ and $C_{t+1}^{o}(\mu ,\eta )$ are consumption during youth and old age, respectively, $\beta$ is the parameter capturing pure time preference ($0<\beta <1$), and U(C) is the felicity function:

$$\begin{aligned} U(C)\equiv {\left\{ \begin{array}{ll} \dfrac{C^{1-1/\sigma }-1}{1-1/\sigma },\quad &{} \text {for }\sigma \ne 1, \\ \ln C &{} \text {for }\sigma =1, \end{array}\right. } \end{aligned}$$

(3)

where $\sigma$ is the intertemporal elasticity of substitution ($\sigma >0$ ). Equation (2) incorporates the assumption that individuals do not have a bequest motive, i.e. utility solely depends on own consumption during one’s lifetime.

In this section we postulate the existence of perfect private annuities. Specifically, we adopt the following assumptions regarding the market for private annuities:

• (A0) Health status is public information.

• (A1) The annuity market is perfectly competitive. A large number of risk-neutral firms offer annuities to individuals, and annuity firms can freely enter or exit the market.

• (A2) Annuity firms do not use up any real resources.

As is explained by Heijdra and Reijnders (2012, pp. 322–323), in this Full Information case (abbreviated as FI) each health type receives its actuarially fair rate of return and achieves perfect insurance against longevity risk. If $A_{t}^{p}\left( \mu ,\eta \right)$ denotes the private annuity holdings of an agent of health type $\mu$ then the net rate of return on annuities will be equal to:

$$\begin{aligned} 1+r_{t+1}^{p}\left( \mu \right) =\frac{1+r_{t+1}}{\mu }, \end{aligned}$$

(4)

where $r_{t+1}$ is the net rate of return on physical capital (see also below). Since the survival rate is such that $0<\mu <1$, it follows from (4) that $r_{t+1}^{p}\left( \mu \right)$ exceeds $r_{t+1}$ so that all agents will completely annuitize their wealth. This classic result was first derived by Yaari (1965).

We assume that individuals work full time during youth and part time in old age as a result of a system of mandatory retirement. With full annuitization of assets the periodic budget identities are given by:

$$\begin{aligned} C_{t}^{y}(\mu ,\eta )+A_{t}^{p}(\mu ,\eta )&=w_{t}(\eta ), \end{aligned}$$

(5)

$$\begin{aligned} C_{t+1}^{o}(\mu ,\eta )&=\lambda w_{t+1}(\eta )+(1+r_{t+1}^{p}\left( \mu \right) )A_{t}^{p}(\mu ,\eta ), \end{aligned}$$

(6)

where $w_{t}(\eta )$ is the wage rate of an $\eta$ type in period t, $\lambda$ is the proportion of time that is devoted to work in old age ($0<\lambda <1$), and $1+r_{t+1}^{p}\left( \mu \right)$ is the rate of return on private annuities. The periodic budget identities can be combined to obtain the consolidated budget constraint:

$$\begin{aligned} C_{t}^{y}(\mu ,\eta )+\frac{C_{t+1}^{o}(\mu ,\eta )}{1+r_{t+1}^{p}\left( \mu \right) }=w_{t}(\eta )+\frac{\lambda w_{t+1}(\eta )}{1+r_{t+1}^{p}\left( \mu \right) }. \end{aligned}$$

(7)

The present value of lifetime consumption (left-hand side) equals the present value of lifetime income (right-hand side). That is, people consume their human wealth.

Consumers choose $C_{t}^{y}(\mu ,\eta )$ and $C_{t+1}^{o}(\mu ,\eta )$ in order to maximize expected lifetime utility (2) subject to the budget constraint (7). The optimal consumption plans and annuity demands are fully characterized by:

$$\begin{aligned} C_{t}^{y}(\mu ,\eta )&=\Phi \left( \mu ,\frac{1+r_{t+1}}{\mu }\right) \left[ w_{t}(\eta )+\frac{\lambda \mu w_{t+1}(\eta )}{1+r_{t+1}}\right] , \end{aligned}$$

(8)

$$\begin{aligned} \frac{\mu C_{t+1}^{o}(\mu ,\eta )}{1+r_{t+1}}&=\left[ 1-\Phi \left( \mu , \frac{1+r_{t+1}}{\mu }\right) \right] \left[ w_{t}(\eta )+\frac{\lambda \mu w_{t+1}(\eta )}{1+r_{t+1}}\right] , \end{aligned}$$

(9)

$$\begin{aligned} A_{t}^{p}(\mu ,\eta )&=\left[ 1-\Phi \left( \mu ,\frac{1+r_{t+1}}{\mu } \right) \right] w_{t}(\eta )-\Phi \left( \mu ,\frac{1+r_{t+1}}{\mu }\right) \frac{\lambda \mu w_{t+1}(\eta )}{1+r_{t+1}}, \end{aligned}$$

(10)

where we have substituted the expression for the actuarially fair annuity rate (4), and where $\Phi (\mu ,x)$ is the marginal propensity to consume out of lifetime income during youth:

$$\begin{aligned} \Phi (\mu ,x)\equiv \frac{1}{1+(\mu \beta )^{\sigma }x^{\sigma -1}}. \end{aligned}$$

(11)

From Eqs. (8) and (9) we find that consumption during youth and old-age are both proportional to human wealth. Furthermore, Eq. (10) shows that annuity demand depends positively on the wage income during youth and negatively on old-age labour income.

The optimal consumption choices of different types of consumers are illustrated in Fig. 2. To avoid cluttering the diagram we illustrate the choices made by the four extreme types, unhealthy and healthy lowest-skilled $(\mu _{L},\eta _{L})$ and $(\mu _{H},\eta _{L})$, and unhealthy and healthy highest-skilled $(\mu _{L},\eta _{H})$ and $(\mu _{H},\eta _{H})$. For a given working ability type $\eta _{i}$, the line labelled ${\mathrm{LBC}}(\mu _{L},\eta _{i})$ and ${\mathrm{LBC}}(\mu _{H},\eta _{i})$ are the lifetime budget constraints as given in (7). For skill type $\eta _{L}$ the income endowment point $(w_{t}(\eta ),\lambda w_{t+1}(\eta ))$ is located at point ${\mathrm{E}}_{{L}}$. With perfect annuities, ${\mathrm{LBC}}(\mu _{L},\eta _{i})$ is steeper than ${\mathrm{LBC}}(\mu _{H},\eta _{i})$ because the unhealthy get a much higher annuity rate than the healthy.

Fig. 2

Consumption-saving choices under full information. ${\mathrm{LBC}}(\mu _{i},\eta _{j})$ is the lifetime budget constraint for an individual with survival probability $\mu _{i}$ and productivity level $\eta _{j}$. IEL is the income endowment line and agents are located on the line segment ${\mathrm{E}}_L{\mathrm{E}}_H$. MRSC is the consumption Euler equation under perfect information with actuarially fair annuities at the individual level. Optimal consumption for individual $(\mu _{i},\eta _{j})$ is located at the intersection of MRSC and ${\mathrm{LBC}}(\mu _{i},\eta _{j})$. All individuals purchase annuities

In the presence of perfect annuities and under full annuitization, the consumption Euler equation is given by:

$$\begin{aligned} \frac{U^{\prime }(C_{t}^{y}\left( \mu ,\eta \right) )}{\beta U^{\prime }(C_{t+1}^{o}\left( \mu ,\eta \right) )}=\mu \left( 1+r_{t+1}^{p}\left( \mu \right) \right) =1+r_{t+1}, \end{aligned}$$

(12)

where we have used (4) to get from the first to the second equality. The crucial thing to note is that all agents equate the marginal rate of substitution between current and future consumption to the gross interest factor on capital. Intuitively, as was first pointed out by Yaari (1965), the mortality rate drops out of the expression characterizing the life-cycle profile of consumption because agents are fully insured against the unpleasant aspects of lifetime uncertainty. For the homothetic felicity function (3) it is easy to show that (12) is a ray from the origin—see the locus labelled MRSC in Fig. 2. Optimal choices are located at the intersection of MRSC and the relevant lifetime budget constraint. It follows that types $(\mu _{L},\eta _{L})$ and $(\mu _{H},\eta _{L})$ consume at points A and B respectively.

What about the choices made by the highest-ability types? Given the specification of technology adopted below, it follows that $w_{t}(\eta )=\eta w_{t}$ and $w_{t+1}(\eta )=\eta w_{t+1}$ so that income endowment points lie along the ray from the origin labelled IEL. Furthermore, it follows from (7) that ${\mathrm{LBC}}(\mu _{L},\eta _{H})$ is parallel to LBC $(\mu _{L},\eta _{L})$ whilst ${\mathrm{LBC}}(\mu _{H},\eta _{H})$ is parallel to ${\mathrm{LBC}} (\mu _{H},\eta _{L})$. Hence types $(\mu _{L},\eta _{H})$ and $(\mu _{H},\eta _{H})$ consume at points C and D respectively.

Several conclusions can be drawn from the microeconomic behaviour discussed in this subsection. First, in this closed economy featuring a positive capital stock (see below) all agents are net savers, i.e. everybody expresses a positive demand for private annuities, $A_{t}^{p}(\mu ,\eta )>0$ for all $\mu$ and $\eta$. This result follows readily from Fig. 2 because the MRSC line lies to the left of the IEL line. Second, for a given value of agent productivity $\eta$, the demand for annuities is increasing in the survival probability $\mu$, i.e. $\partial A_{t}^{p}(\mu ,\eta )/\partial \mu >0$. Intuitively, healthy people buy more annuities than do unhealthy people of the same skill category because they expect to live longer a priori. Again this result follows readily from Fig. 2 because ${\mathrm{LBC}}(\mu _{L},\eta _{i})$ is steeper than ${\mathrm{LBC}}(\mu _{H},\eta _{i})$. Third, the demand for annuities is increasing in the skill level, i.e. $\partial A_{t}^{p}(\mu ,\eta )/\partial \eta >0$. This can be see graphically in Fig. 2 and can be proved formally by noting that $A_{t}^{p}(\mu ,\eta )$ in (10) is linear in $\eta$.

2.2 Demography

Let $L_{t}$ denote the size of the population cohort born at time t. The density of consumers with health type $\mu$ and working ability $\eta$ is thus:

$$\begin{aligned} L_{t}(\mu ,\eta )\equiv h(\mu ,\eta )L_{t}, \end{aligned}$$

(13)

where the density function $h(\mu ,\eta )$ is stated in (1) above. The density of (young and old) consumers of type $\mu$ alive at time t is given by:

$$\begin{aligned} P_{t}(\mu )\equiv \mu \int _{\eta _{L}}^{\eta _{H}}L_{t-1}(\mu ,\eta )d\eta +\int _{\eta _{L}}^{\eta _{H}}L_{t}(\mu ,\eta )d\eta =\mu h_{\mu }(\mu )L_{t-1}+h_{\mu }(\mu )L_{t}, \end{aligned}$$

(14)

where $h_{\mu }(\mu )$ is the marginal distribution of $\mu$ [see Lemma 1(i)]. If newborn cohort sizes evolves according to $L_{t}=(1+n)L_{t-1}$ (with $n>-1$), the total population at time t is given by:

$$\begin{aligned} P_{t}\equiv \int _{\mu _{L}}^{\mu _{H}}P_{t}(\mu )d\mu =\frac{1+n+{\bar{\mu }}}{ 1+n}L_{t}, \end{aligned}$$

(15)

where ${\bar{\mu }}\equiv \int _{\mu _{L}}^{\mu _{H}}\mu h_{\mu }(\mu )d\mu$ is the average survival rate of a newborn cohort.

2.3 Production

We assume that perfect competition prevails in the goods market. The technology is represented by the following Cobb–Douglas production function:

$$\begin{aligned} Y_{t}=\Omega _{0}K_{t}^{\varepsilon }N_{t}^{1-\varepsilon }, \end{aligned}$$

(16)

where $Y_{t}$ is total production, $K_{t}$ is the aggregate capital stock, $\varepsilon$ is the efficiency parameter of capital ($0<\varepsilon <1$), $\Omega _{0}$ is total factor productivity (assumed to be constant), and $N_{t}$ is the effective labor force, which is defined as:

$$\begin{aligned} N_{t}\equiv \int _{\eta _{L}}^{\eta _{H}}\int _{\mu _{L}}^{\mu _{H}}\eta \left[ L_{t}(\mu ,\eta )+\lambda L_{t-1}(\mu ,\eta )\right] d\mu d\eta . \end{aligned}$$

(17)

Note that $N_{t}$ has the dimension of worker efficiency (denoted by $\eta$ ) times number of working hours. By using (13) in (17) and noting that $L_{t}=(1+n)L_{t-1}$ we find that $N_{t}/L_{t}$ can be written as:

$$\begin{aligned} \frac{N_{t}}{L_{t}}={\bar{\eta }}+\frac{\lambda }{1+n}\left[ {\bar{\eta }}{\bar{\mu }} +{\mathrm {cov}}\left( \eta ,\mu \right) \right] , \end{aligned}$$

(18)

where ${\mathrm{cov}}\left( \eta ,\mu \right) \equiv \xi \sigma _{\eta }^{2}\sigma _{\mu }^{2}$ is the (positive) covariance between $\mu$ and $\eta$ [see Lemma 1(iv)].

By defining $y_{t}\equiv Y_{t}/N_{t}$${\mathrm{and}}\ k_{t}\equiv K_{t}/N_{t}$, the intensive-form production function can be written as:

$$\begin{aligned} y_{t}=\Omega _{0}k_{t}^{\varepsilon }. \end{aligned}$$

(19)

Firms choose efficiency units of labour and the capital stock such that profits are maximized. This optimization problem gives the following factor demand equations:

$$\begin{aligned} r_{t}+\delta&=\varepsilon \Omega _{0}k_{t}^{\varepsilon -1}, \end{aligned}$$

(20)

$$\begin{aligned} w_{t}&=(1-\varepsilon )\Omega _{0}k_{t}^{\varepsilon }, \end{aligned}$$

(21)

$$\begin{aligned} w_{t}(\eta )&=\eta w_{t}, \end{aligned}$$

(22)

where $r_{t}$ is the net rate of return on physical capital, $\delta$ is the depreciation rate of capital ($0<\delta <1$), and $w_{t}$ is the rental rate on efficiency units of labour. With perfect substitutability of efficiency units of labour, the wage rate of a $\eta$ type worker, $w_{t}(\eta )$, is $\eta$ times the rental rate $w_{t}$ (as was asserted above).

2.4 Equilibrium

The model is completed by a description of the macroeconomic equilibrium. Since all annuity purchases are invested in the capital market we find that:

$$\begin{aligned} K_{t+1}=L_{t}\int _{\mu _{L}}^{\mu _{H}}\int _{\eta _{L}}^{\eta _{H}}A_{t}^{p}(\mu ,\eta )h(\mu ,\eta )d\eta d\mu , \end{aligned}$$

(23)

where $A_{t}^{p}(\mu ,\eta )$ is given in (10) above. Intuitively, Eq. (23) says that next period’s aggregate capital stock is equal to total savings in the current period (consisting of private annuities). By substituting the demand for annuities (10) and the wage equation (22) into (23) we obtain the fundamental difference equation for the capital intensity:

$$\begin{aligned} k_{t+1}=\frac{1}{1+n}\frac{L_{t}}{N_{t}}\left[ {\bar{\eta }}w_{t}-\int _{\mu _{L}}^{\mu _{H}}\Phi \left( \mu ,\frac{1+r_{t+1}}{\mu }\right) \left[ w_{t}+ \frac{\lambda \mu w_{t+1}}{1+r_{t+1}}\right] h_{\mu }(\mu )\Gamma _{1}(\mu )d\mu \right] , \end{aligned}$$

(24)

where $\Gamma _{1}(\mu )$ is the conditional mean of $\eta$ given $\mu$ [see Lemma 1(vi)]. In view of (20)–(21) $w_{t}$ and $r_{t+1}$ depend on, respectively, $k_{t}$ and $k_{t+1}$ so (24) is a non-linear implicit function relating $k_{t+1}$ to $k_{t}$ and the exogenous variables.

2.5 Parameterization and Visualization

In order to visualize the main features of the economy we parameterize the model by selecting plausible values for the structural parameters—see Table 1. We follow Heijdra and Reijnders (2012) in the parameterization procedure. First, we postulate plausible values for the intertemporal elasticity of substitution ($\sigma =0.7$), the efficiency parameter of capital ($\varepsilon =0.275$), the annual capital depreciation rate ($\delta _{a}=0.06$), the annual growth rate of the population ($n_{a}=0.01$) and the target annual steady-state interest rate (${\hat{r}} _{a}=0.05$). Using these parameters we can determine the steady-state (annual) capital-output ratio (${\hat{K}}/{\hat{Y}}=\varepsilon /({\hat{r}} _{a}+\delta _{a})=2.5$). Second, we set the length of each period to be 40 years and compute the values for n, $\delta$ and ${\hat{r}}$ (noting that $n=(1+n_{a})^{40}-1$, $\delta =1-(1-\delta _{a})^{40}$ and ${\hat{r}} =(1+r_{a})^{40}-1$). Third, we assume that the mandatory retirement age is 65 years so that $\lambda =25/40=0.625$. In the fourth step, we choose $\eta _{L}=0.5$, $\eta _{H}=1.5$, $\mu _{L}=0.05$, $\mu _{H}=0.95$, so that the average health status is ${\bar{\mu }}=0.5$, average working ability is $\bar{ \eta }=1$, and the variances are $\sigma _{\eta }^{2}=0.0833$ and $\sigma _{\eta }^{2}=0.0675$. By setting $\xi =4$ we ensure that there is a strong correlation between health and ability, i.e. ${\mathrm{cor}}(\mu ,\eta )=0.300$.¹ In the fifth step we choose $\Omega _{0}$ such that ${\hat{y}}=10$ in the initial steady state. This also pins down the steady state values for ${\hat{k}}$ and ${\hat{w}}$. In the final step the discount factor $\beta$ is used as a calibration parameter, i.e. it is set at the value such that the steady-state version of the fundamental difference equation (24) is satisfied. To interpret the value of $\beta$ in Table 1, note that the annual rate of time preference is $\rho _{a}=\beta ^{-1/40}-1=0.0204$ (a little over two percent per annum).

Table 1 Structural parameters

The main features of the steady-state FI equilibrium are reported in column (a) of Table 2. Consistent with the calibration procedure, output per efficiency unit of labour is equal to ten (${\hat{y}}=10$) whilst the steady-state interest rate is five percent on an annual basis (${\hat{r}} ^{a}=0.05$). The steady-state capital intensity equals ${\hat{k}}=0.395$. Ownership of the capital stock is highly uneven due to the fact that individuals differ in terms of labour productivity. Indeed, as is noted in the table, the first ability quartile of agents (averaged over all survival rates) owns 12.34% of the capital stock. In contrast, the top ability quartile owns 39.12% of the economy’s stock of capital.

Table 2 Allocation and welfare

Steady-state consumption (per efficiency unit of labour) by the young and surviving old are given by:

$$\begin{aligned} {\hat{c}}^{y}&\equiv \frac{L_{t}}{N_{t}}\int _{\eta _{L}}^{\eta _{H}}\int _{\mu _{L}}^{\mu _{H}}{\hat{C}}^{y}\left( \mu ,\eta \right) h(\mu ,\eta )d\mu d\eta , \end{aligned}$$

(25)

$$\begin{aligned} {\hat{c}}^{o}&\equiv \frac{1}{1+n}\frac{L_{t}}{N_{t}}\left[ \int _{\eta _{L}}^{\eta _{H}}\int _{\mu _{l}}^{\mu _{h}}\mu {\hat{C}}^{o}\left( \mu ,\eta \right) h(\mu ,\eta )d\mu d\eta \right] . \end{aligned}$$

(26)

Inequality due to heterogeneous productivity also shows up in the consumption levels during youth and old-age. The two lowest-ability quartiles enjoy a modest and declining share of total consumption over the life-cycle due to the positive correlation between health and ability. The opposite holds for the two highest-ability quartiles. Finally, Table 2 also reports some welfare indicators. Not surprisingly we find that expected lifetime utility is lowest for individuals with low ability and poor health ($\mu _{L},\eta _{L}$) and highest for those lucky ones with high ability and excellent health ($\mu _{H},\eta _{H}$).²

In Fig. 3 we depict the steady-state profiles for youth consumption, old-age consumption, annuity demand, and expected utility. These profiles have been averaged over $\eta$ values and are thus a function of the survival probability only:

$$\begin{aligned} {\hat{C}}^{y}(\mu )&\equiv \frac{\int _{\eta _{L}}^{\eta _{H}}{\hat{C}} ^{y}\left( \mu ,\eta \right) h(\mu ,\eta )d\eta }{\int _{\eta _{L}}^{\eta _{H}}h(\mu ,\eta )d\eta }=\Phi \left( \mu ,\frac{1+{\hat{r}}}{\mu }\right) \left[ 1+\frac{\lambda \mu }{1+{\hat{r}}}\right] {\hat{w}}\Gamma _{1}(\mu ), \end{aligned}$$

(27)

$$\begin{aligned} {\hat{C}}^{o}(\mu )&\equiv \frac{\int _{\eta _{L}}^{\eta _{H}}{\hat{C}} ^{o}\left( \mu ,\eta \right) h(\mu ,\eta )d\eta }{\int _{\eta _{L}}^{\eta _{H}}h(\mu ,\eta )d\eta }=\left[ 1-\Phi \left( \mu ,\frac{1+{\hat{r}}}{\mu } \right) \right] \left[ \frac{1+{\hat{r}}}{\mu }+\lambda \right] {\hat{w}}\Gamma _{1}(\mu ), \end{aligned}$$

(28)

$$\begin{aligned} {\hat{A}}^{p}(\mu )&\equiv \frac{\int _{\eta _{L}}^{\eta _{H}}{\hat{A}} ^{p}\left( \mu ,\eta \right) h(\mu ,\eta )d\eta }{\int _{\eta _{L}}^{\eta _{H}}h(\mu ,\eta )d\eta }=\left[ 1-\Phi \left( \mu ,\frac{1+{\hat{r}}}{\mu } \right) \left[ 1+\frac{\lambda \mu }{1+{\hat{r}}}\right] \right] {\hat{w}}\Gamma _{1}(\mu ), \end{aligned}$$

(29)

$$\begin{aligned} {\mathbb{E}}\Lambda (\mu )&\equiv \frac{\int _{\eta _{L}}^{\eta _{H}}{\mathbb{E}} \Lambda \left( \mu ,\eta \right) h(\mu ,\eta )d\eta }{\int _{\eta _{L}}^{\eta _{H}}h(\mu ,\eta )d\eta }. \end{aligned}$$

(30)

In panel (a) we find that ${\hat{C}}^{y}(\mu )$ is increasing in $\mu$. This result is the opposite of the findings reported by Heijdra and Reijnders (2012, p. 321) who assume that all individuals have the same labour productivity (i.e., $\sigma _{\eta }^{2}=0$ in their model). In our model, for a given productivity level $\eta$, youth consumption is decreasing in the survival probability (see Fig. 2). But as a result of the positive correlation between $\eta$ and $\mu$, healthy agents also tend to be wealthy agents who consume more in youth as a result. Referring to equation (27), the term $\Phi \left( \mu ,\frac{1+{\hat{r}}}{\mu }\right) \left[ 1+\frac{\lambda \mu }{1+{\hat{r}}}\right]$ is decreasing in $\mu$ but the $\Gamma _{1}(\mu )$ term is increasing in $\mu$ [see Lemma 1(vi)]. Due to the strong correlation between $\mu$ and $\eta$ the latter effect dominates the former, thus ensuring that ${\hat{C}}^{y}(\mu )$ is increasing in the survival probability.

Fig. 3

Steady-state profiles. The solid lines depict the steady-state profiles for the full information (FI) case featuring perfect annuities. The dashed lines visualize the profiles for the asymmetric information (AI) case in which adverse selection results in a single pooling rate of interest on annuities, ${\bar{r}}_{t+1}^{p}$. In the AI case agents with poor health face binding borrowing constraints regardless of their productivity in the labour market

As panel (b) shows, the profile for old-age consumption ${\hat{C}}^{o}(\mu )$ is also increasing in $\mu$. Again this result is reversed if all agents feature the same labour productivity, as can be easily verified with the aid of Fig. 2. In panel (c) we find that ${\hat{A}}^{p}(\mu )$ is increasing in $\mu$. This result even holds if $\sigma _{\eta }^{2}=0$ (so that $\Gamma _{1}(\mu )$ is a constant) because $1-\Phi \left( \mu ,\frac{1+ {\hat{r}}}{\mu }\right) \left[ 1+\frac{\lambda \mu }{1+{\hat{r}}}\right]$ is increasing in $\mu$. Finally, as panel (d) illustrates, ${\mathbb{E}}\hat{ \Lambda }(\mu )$ is increasing in the survival probability. Intuitively, for a given productivity level $\eta$ individual lifetime utility is increasing in $\mu$ (people like surviving into old-age). Furthermore, $\mu$ and $\eta$ are positively correlated thus strengthening the positive link between utility and health.

3 Informational Asymmetry in the Private Annuity Market

In the previous section we have studied the steady state of an economy populated by heterogeneous individuals facing longevity risk and differing in terms of their innate labour productivity. With full information about the health status of individuals, annuity firms can effectively segment the market for private annuities and offer these insurance products at a price that is actuarially fair for all individuals. In this section we study the less pristine—and arguably much more realistic—scenario under which information regarding a person’s health is not perfectly observable by insurance firms. Indeed, from here on we drop Assumption (A0) and replace it by the following alternative assumptions:

• (A3) Health status and productivity are private information of the annuitant. The distribution of health and productivity types in the population, $H(\mu ,\eta )$, is common knowledge.

• (A4) Annuitants can buy multiple annuities for different amounts and from different annuity firms. Individual annuity firms cannot monitor their clients’ wage income or annuity holdings with other firms.

As is explained by Heijdra and Reijnders (2012, pp. 325–326), in this Asymmetric Information case (abbreviated as AI) the market for private annuities is characterized by a pooling equilibrium. In this equilibrium there is a single pooled annuity rate, ${\bar{r}}_{t+1}^{p}$, which applies to all purchasers of private annuities. Lacking information about an individual’s health and productivity, the annuity company cannot obtain full information revelation by setting both price and quantity. As a result, Pauly’s (1974) linear pricing concept is the relevant one.³ A second feature of the pooling equilibrium is that there typically are unhealthy agents who drop out of the annuity market altogether and face binding borrowing constraints. Indeed, since an individual’s human wealth is proportional to his/her labour productivity, and individual consumption is decreasing in the survival rate, there may exist a cut-off survival probability, $\mu _{t}^{bc}$, below which individuals would like to go short on annuities. But this is impossible because in doing so they would reveal their poor health status and obtain an offer they cannot possibly accept from annuity firms (more on this below).⁴

The pooled annuity rate, ${\bar{r}}_{t+1}^{p}$, is determined as follows. We assume that the cut-off health type is $\mu _{t}^{bc}$ such that consumers with health type $\mu _{L}\le \mu <\mu _{t}^{bc}$ purchase no annuities. Net savers feature a survival probability such that $\mu _{t}^{bc}\le$$\mu \le \mu _{H}$ and purchase annuities. The zero-profit condition for the private annuity market is given by:

$$\begin{aligned} (1+r_{t+1})\int _{\eta _{L}}^{\eta _{H}}\int _{\mu _{t}^{bc}}^{\mu _{H}}L_{t}(\mu ,\eta )A_{t}^{p}(\mu ,\eta )d\mu d\eta =(1+{\bar{r}} _{t+1}^{p})\int _{\eta _{L}}^{\eta _{H}}\int _{\mu _{t}^{bc}}^{\mu _{H}}\mu L_{t}(\mu ,\eta )A_{t}^{p}(\mu ,\eta )d\mu d\eta , \end{aligned}$$

(31)

where $1+r_{t+1}$ is the gross rate of return on physical capital, $1+{\bar{r}} _{t+1}^{p}$ is the gross rate of return on private annuities, $L_{t}(\mu ,\eta )$ is the density of type $(\mu ,\eta )$ consumers in period t, and $A_{t}^{p}(\mu ,\eta )$ is the density of private annuities that is purchased by such agents. The gross returns from the annuity savings of all annuitants in period t (left-hand side of (31)) are redistributed to the surviving annuitants in the form of insurance claims in period $t+1$ (right-hand side of (31)). It follows that the pooling rate equals:

$$\begin{aligned} 1+{\bar{r}}_{t+1}^{p}=\frac{1+r_{t+1}}{{\bar{\mu }}_{t}^{p}}, \end{aligned}$$

(32)

where ${\bar{\mu }}_{t}^{p}$ denotes the asset-weighted average survival rate of annuity purchasers:

$$\begin{aligned} {\bar{\mu }}_{t}^{p}\equiv \int _{\mu _{t}^{bc}}^{\mu _{H}}\mu \omega _{t}(\mu )d\mu ,\quad \omega _{t}(\mu )\equiv \frac{\int _{\eta _{L}}^{\eta _{H}}A_{t}^{p}(\mu ,\eta )h(\mu ,\eta )d\eta }{\int _{\eta _{L}}^{\eta _{H}}\int _{\mu _{t}^{bc}}^{\mu _{H}}A_{t}^{p}(\mu ,\eta )h(\mu ,\eta )d\mu d\eta }. \end{aligned}$$

(33)

In view of the fact that the asset-weighted survival rate is such that $\mu _{t}^{bc}<{\bar{\mu }}_{t}^{p}<\mu _{H}<1$, it follows from (32) that ${\bar{r}}_{t+1}^{p}$ exceeds $r_{t+1}$ so that all net savers will completely annuitize their wealth. Hence, Yaari’s (1965) classic result also holds in the pooled annuity market.

The pooling rate (32) is demographically unfair because it is based on the asset-weighted survival rate ${\bar{\mu }}_{t}^{p}$ rather than on the average survival rate in the population ${\bar{\mu }}$. The demographically fair pooling rate is given by:

$$\begin{aligned} 1+{\bar{r}}_{t+1}^{{ df }}=\frac{1+r_{t+1}}{{\bar{\mu }}}, \end{aligned}$$

(34)

and, since ${\bar{\mu }}<{\bar{\mu }}_{t}^{p}$ (see Supplementary Material, Appendix B), it follows readily from the comparison of (32) and (34) that $\bar{ r}_{t+1}^{p}<{\bar{r}}_{t+1}^{{ df }}$. In our numerical exercise we follow Walliser (2000, p. 380) by constructing an adverse selection index ${ AS }_{t}$ (or ‘load factor’) which shows by how much the asking price of an annuity insurance company exceeds the demographically fair price:

$$\begin{aligned} { AS }_{t}\equiv \frac{1/(1+{\bar{r}}_{t+1}^{p})}{1/(1+{\bar{r}}_{t+1}^{ { df }})}=\frac{{\bar{\mu }}_{t}^{p}}{{\bar{\mu }}}. \end{aligned}$$

(35)

As a result of adverse selection in the private annuity market, ${ AS } _{t}$ exceeds unity. Furthermore, the larger is ${ AS }_{t}$, the more severe is the adverse selection problem.

Under the maintained assumption that $\mu _{L}<\mu _{t}^{bc}<\mu _{H}$, there are two types of agents in the economy. Individuals with a relatively low survival probability ($\mu _{L}\le \mu <\mu _{t}^{bc}$) will face a binding borrowing constraint, whilst healthier individuals ($\mu _{t}^{bc}\le \mu \le \mu _{H}$) will be net savers. It follows that constrained individuals simply consume their endowment incomes in the two periods:

$$\begin{aligned} C_{t}^{y}(\mu ,\eta )&=w_{t}(\eta ), \end{aligned}$$

(36)

$$\begin{aligned} C_{t+1}^{o}(\mu ,\eta )&=\lambda w_{t+1}(\eta ). \end{aligned}$$

(37)

For unconstrained individuals the consolidated budget constraint in a pooled annuity market is given by:

$$\begin{aligned} C_{t}^{y}(\mu ,\eta )+\frac{C_{t+1}^{o}(\mu ,\eta )}{1+{\bar{r}}_{t+1}^{p}} =w_{t}(\eta )+\frac{\lambda w_{t+1}(\eta )}{1+{\bar{r}}_{t+1}^{p}}, \end{aligned}$$

(38)

where ${\bar{r}}_{t+1}^{p}$ is the pooling rate of interest. Such consumers choose $C_{t}^{y}(\mu ,\eta )$ and $C_{t+1}^{o}(\mu ,\eta )$ in order to maximize expected lifetime utility (2) subject to the budget constraint (38). The optimal consumption plans and annuity demand are fully characterized by:

$$\begin{aligned} C_{t}^{y}(\mu ,\eta )&=\Phi \left( \mu ,\frac{1+r_{t+1}}{{\bar{\mu }}_{t}^{p}} \right) \left[ w_{t}(\eta )+\frac{\lambda {\bar{\mu }}_{t}^{p}w_{t+1}(\eta )}{ 1+r_{t+1}}\right] , \end{aligned}$$

(39)

$$\begin{aligned} \frac{{\bar{\mu }}_{t}^{p}C_{t+1}^{o}(\mu ,\eta )}{1+r_{t+1}}&=\left[ 1-\Phi \left( \mu ,\frac{1+r_{t+1}}{{\bar{\mu }}_{t}^{p}}\right) \right] \left[ w_{t}(\eta )+\frac{\lambda {\bar{\mu }}_{t}^{p}w_{t+1}(\eta )}{1+r_{t+1}}\right] , \end{aligned}$$

(40)

$$\begin{aligned} A_{t}^{p}(\mu ,\eta )&=\left[ 1-\Phi \left( \mu ,\frac{1+r_{t+1}}{{\bar{\mu }} _{t}^{p}}\right) \right] w_{t}(\eta )-\Phi \left( \mu ,\frac{1+r_{t+1}}{\bar{ \mu }_{t}^{p}}\right) \frac{\lambda {\bar{\mu }}_{t}^{p}w_{t+1}(\eta )}{1+r_{t+1} }, \end{aligned}$$

(41)

where we have used the expression for the pooled annuity rate as given in (32).

Fig. 4

Consumption-saving choices under asymmetric information. ${\mathrm{LBC}}(\eta _{j})$ is the lifetime budget constraint for an individual with productivity $\eta _{j}$. IEL is the income endowment line and agents are located on the line segment ${\mathrm{E}}_L{\mathrm{E}}_H$. ${\mathrm{MRSC}}(\mu _{i}$) is the consumption Euler equation for an individual with survival rate $\mu _{i}$ facing a pooled annuity rate of interest ${\bar{r}} _{t+1}^{p}$. For individuals with $\mu _{t}^{bc}\le \mu \le \mu _{H}$ optimal consumption is located at the intersection of ${\mathrm{MRSC}}(\mu _{i}$) and ${\mathrm{LBC}}(\eta _{j}$). All other individuals face borrowing constraints and consume along ${\mathrm{E}}_L{\mathrm{E}}_H$

The optimal consumption choices of different types of consumers are illustrated in Fig. 4. Just as for the FI case we only illustrate the choices made by the four extreme types, unhealthy and healthy lowest-skilled $(\mu _{L},\eta _{L})$ and $(\mu _{H},\eta _{L})$, and unhealthy and healthy highest-skilled $(\mu _{L},\eta _{H})$ and $(\mu _{H},\eta _{H})$. In view of (38) the location of an individual’s lifetime budget constraint only depends on the person’s productivity level, so that ${\mathrm{LBC}}(\eta _{L})$ and ${\mathrm{LBC}}(\eta _{H})$ are parallel. As before the income endowment line is given by IEL, so that the two relevant endowment points are given by, respectively, points ${\mathrm{E}}_{{L}}$ and ${\mathrm{E}}_{{H}}$. The consumption Euler equation for unconstrained consumers operating in a pooled annuity market is given by:

$$\begin{aligned} \frac{U^{\prime }(C_{t}^{y}\left( \mu ,\eta \right) )}{\beta U^{\prime }(C_{t+1}^{o}\left( \mu ,\eta \right) )}=\mu \left( 1+{\bar{r}} _{t+1}^{p}\right) =\frac{\mu }{{\bar{\mu }}_{t}^{p}}(1+r_{t+1}), \end{aligned}$$

(42)

where we have used (32) to get from the first to the second equality. Using the CRRA felicity function stated in (3), we easily find that the Euler equation is a straight line from the origin with a slope that depends positively on $\mu$. In Fig. 4 we have drawn the Euler equations as ${\mathrm{MRSC}}(\mu _{H})$ and ${\mathrm{MRSC}}(\mu _{L})$. Since ${\mathrm{MRSC}}(\mu _{H})$ lies to the left of IEL, points B and D denote the optimal (unconstrained) consumption points for, respectively, the lowest-skilled and highest-skilled consumers. In contrast, since ${\mathrm{MRSC}}(\mu _{L})$ lies to the right of IEL, points A and C are infeasible as they would involve going short on annuities. It follows that all lowest-health individuals face borrowing constraints. Furthermore, the Euler equation (42) that coincides with the IEL, ${\mathrm{MRSC}}(\mu _{t}^{bc})$, determines the cut-off health type $\mu _{t}^{bc}$:

$$\begin{aligned} \mu _{t}^{bc}=\frac{{\bar{\mu }}_{t}^{p}U^{\prime }(w_{t}(\eta ))}{ (1+r_{t+1})\beta U^{\prime }(\lambda w_{t+1}(\eta ))}. \end{aligned}$$

(43)

Unconstrained consumers are located in the area ${\mathrm{E}}_{{L}}{\mathrm{BDE}}_{{H}}$ whilst constrained individuals are bunched on the line segment ${\mathrm{E}}_{{L}}{\mathrm{E}}_{{H}}$. It is worth noting that $\mu _{t}^{bc}$ depends on the current and future capital intensity in the economy via factor prices. Given the specification of preferences and technology, however, $\mu _{t}^{bc}$ does not depend on $\eta$ itself.

In the presence of binding borrowing constraints, the capital accumulation identity (23) is augmented to:

$$\begin{aligned} K_{t+1}=L_{t}\int _{\eta _{L}}^{\eta _{H}}\int _{\mu _{t}^{bc}}^{\mu _{H}}A_{t}^{p}(\mu ,\eta )h(\mu ,\eta )d\eta d\mu . \end{aligned}$$

(44)

By substituting the demand for annuities (41) into (44 ) we obtain the fundamental difference equation for the capital intensity:

$$\begin{aligned} k_{t+1}=\frac{1}{1+n}\frac{L_{t}}{N_{t}}\left[ \int _{\mu _{t}^{bc}}^{\mu _{H}}\left[ w_{t}-\Phi \left( \mu ,\frac{1+r_{t+1}}{{\bar{\mu }}_{t}^{p}} \right) \left[ w_{t}+\frac{\lambda {\bar{\mu }}_{t}^{p}w_{t+1}}{1+r_{t+1}} \right] \right] h_{\mu }(\mu )\Gamma _{1}(\mu )d\mu \right] , \end{aligned}$$

(45)

where $\Gamma _{1}(\mu )$ is the conditional mean of $\eta$ [defined in Lemma 1(vi) above], and the factor prices follow from (20)–(21).

The main features of the steady-state AI equilibrium are reported in column (b) of Table 2. As a result of asymmetric information in the annuity market, output per efficiency unit of labour drops by 1.60% (${\hat{y}}=9.840$) whilst the steady-state capital intensity falls by 5.71% (${\hat{k}}=0.373$). The decrease in the capital intensity causes the annual interest rate to rise by 12 basis points (${\hat{r}}^{a}=5.11\%$) and the wage rate to fall by 1.60%. So despite the fact that only 5.83% of young individuals face binding borrowing constraints (see ${\widehat{BC}}$), the macroeconomic effects of information asymmetry are far from trivial in size. The adverse selection index, as defined in (35) above, equals ${\widehat{AS}}=1.31$ and the asset-weighted average survival rate of annuitants equals $\hat{{\bar{\mu }}}^{p}=0.66$. Finally, as the welfare indicators at the bottom of Table 2 reveal, under asymmetric information unhealthy individuals are worse off while their healthy cohort members are better off than under the FI case. The information asymmetry redistributes resources from unhealthy to healthy agents.

In Fig. 3 we depict with dashed lines the steady-state profiles for youth consumption, old-age consumption, annuity demand, and expected utility. Just as for the FI case these profiles have been averaged over $\eta$:

$$\begin{aligned} {\hat{C}}^{y}(\mu )&=\left[ 1-{\mathbb{I}}_{AI}(\mu )+{\mathbb{I}}_{AI}(\mu )\Phi \left( \mu ,\frac{1+{\hat{r}}}{\hat{{\bar{\mu }}}^{p}}\right) \left[ 1+\frac{ \lambda \hat{{\bar{\mu }}}^{p}}{1+{\hat{r}}}\right] \right] {\hat{w}}\Gamma _{1}(\mu ), \end{aligned}$$

(46)

$$\begin{aligned} {\hat{C}}^{o}(\mu )&=\left[ [1-{\mathbb{I}}_{AI}(\mu )]\lambda +{\mathbb{I}} _{AI}(\mu )\left[ 1-\Phi \left( \mu ,\frac{1+{\hat{r}}}{\hat{{\bar{\mu }}}^{p}} \right) \right] \left[ \frac{1+{\hat{r}}}{\hat{{\bar{\mu }}}^{p}}+\lambda \right] \right] {\hat{w}}\Gamma _{1}(\mu ), \end{aligned}$$

(47)

$$\begin{aligned} {\hat{A}}^{p}(\mu )&={\mathbb{I}}_{AI}(\mu )\left[ 1-\Phi \left( \mu ,\frac{1+ {\hat{r}}}{\hat{{\bar{\mu }}}^{p}}\right) \left[ 1+\frac{\lambda \hat{{\bar{\mu }}} ^{p}}{1+{\hat{r}}}\right] \right] {\hat{w}}\Gamma _{1}(\mu ), \end{aligned}$$

(48)

where ${\mathbb{I}}_{AI}(\mu )=0$ for $\mu _{L}\le \mu <{\hat{\mu }}^{bc}$ and ${\mathbb{I}}_{AI}(\mu )=1$ for ${\hat{\mu }}^{bc}\le \mu \le \mu _{H}$. In panel (a) we find that youth consumption ${\hat{C}}^{y}(\mu )$ is increasing in $\mu$. Interestingly, for $\mu$ close to ${\hat{\mu }}^{bc}$ youth consumption is higher under AI than for the FI case. Young individuals facing borrowing constraints are unable to smooth consumption in the AI case and just consume their endowment income. Net savers featuring a survival probability close to ${\hat{\mu }}^{bc}$ purchase virtually no annuities at all as the pooling rate is unattractive to them—see panel (c). For higher levels of $\mu$ annuity demands are higher and saving for old-age increases. In panel (b) we show that the healthiest agents consume more during old-age under AI compared to FI. In panel (d) we find that the healthiest individuals are actually better off under AI than under FI. The information asymmetry benefits such individuals.

4 Public Annuities to the Rescue?

In the adverse selection economy studied in the previous section relatively unhealthy annuitants face a disadvantageous pooling rate of interest on their annuities. In essence such individuals are subsidizing their healthy cohort members through the annuity market. Following Abel (1987) we now extend our model by introducing a fully-funded mandatory social security system that is run by the government.⁵ Such a system is immune to adverse selection because all individuals are forced to participate in it—the government possesses the power to tax. In particular, every individual pays a social security tax $\theta$ (such that $0<\theta <1$) and receives a retirement pension upon surviving into old-age. We assume that the pension contribution is proportional to wage income. Like the private sector, the government cannot observe an individual’s health status though it can measure a person’s income. It follows that the pension contribution can be written as $A_{t}^{s}(\eta )=\theta w_{t}(\eta )$. Total pension contributions amount to $A_{t}^{s}=\theta {\bar{\eta }}w_{t}L_{t}$ and are invested in the capital market earning a gross rate of return equal to $1+r_{t+1}$. In the next period the returns $R_{t+1}=(1+r_{t+1})A_{t}^{s}$ are paid out to surviving agents. Under this funded pension system redistribution takes place between agents of the same birth cohort (from those who die to survivors). Hence, social security plays the role of public annuities. In this section we consider three prototypical types of pension systems. The difference lies in the method in which the returns are distributed to surviving individuals.

• Pension system A pension receipts during old-age are proportional to contributions made during youth.

• Pension system B pension contributions of $\eta$ types are distributed during old-age to surviving $\eta$ types.

• Pension system C pension receipts are the same in absolute value for all surviving agents.

4.1 Pension System A

Under system A pension receipts are given by:

$$\begin{aligned} R_{t+1}^{s}(\eta )=\zeta \theta w_{t}(\eta ), \end{aligned}$$

(49)

where $\zeta$ is a parameter to be determined below. The clearing condition for the public annuity system is given in this case by:

$$\begin{aligned} (1+r_{t+1})A_{t}^{s}=\int _{\eta _{L}}^{\eta _{H}}\int _{\mu _{L}}^{\mu _{H}}\mu R_{t+1}^{s}(\eta )L_{t}(\mu ,\eta )d\mu d\eta . \end{aligned}$$

(50)

The left-hand side of this expression is the total amount to be distributed to survivors and the right-hand side represents total pension payments. By substituting (49) into (50) and noting that $w_{t}(\eta )=\eta w_{t}$ and $L_{t}(\mu ,\eta )=L_{t}h(\mu ,\eta )$ we find the balanced-budget solution for $\zeta$:

$$\begin{aligned} \zeta =\zeta _{A}\ \frac{1+r_{t+1}}{{\bar{\mu }}},\qquad \zeta _{A}\equiv \frac{ {\bar{\eta }}{\bar{\mu }}}{{\mathrm{cov}}\left( \eta ,\mu \right) +{\bar{\eta }}\bar{\mu }}, \end{aligned}$$

(51)

where ${\bar{\mu }}$ is the average survival rate of the population and $\zeta _{A}$ is a constant (featuring $0<\zeta _{A}<1$ because ${\mathrm{cov}}\left( \eta ,\mu \right)$ is positive). It follows from (51) that under pension system A the rate of return on social annuities falls short of the demographically fair social annuity yield, $(1+r_{t+1})/{\bar{\mu }}$, because health and productivity are positively correlated. Intuitively, the high contributors (featuring a high $\eta$) tend to live longer than average.

Just as in the adverse selection economy studied in the previous section individuals can buy private annuities in the pooled annuity market but some agents will face borrowing constraint. Constrained individuals simply consume their endowment incomes in the two periods:

$$\begin{aligned} C_{t}^{y}(\mu ,\eta )&=(1-\theta )w_{t}(\eta ), \end{aligned}$$

(52)

$$\begin{aligned} C_{t+1}^{o}(\mu ,\eta )&=\lambda w_{t+1}(\eta )+R_{t+1}^{s}(\eta ). \end{aligned}$$

(53)

For unconstrained individuals the consolidated budget constraint in the presence of a pooled annuity market is given by:

$$\begin{aligned} C_{t}^{y}(\mu ,\eta )+\frac{C_{t+1}^{o}(\mu ,\eta )}{1+{\bar{r}}_{t+1}^{p}} =(1-\theta )w_{t}(\eta )+\frac{\lambda w_{t+1}(\eta )+R_{t+1}^{s}(\eta )}{1+ {\bar{r}}_{t+1}^{p}}, \end{aligned}$$

(54)

where ${\bar{r}}_{t+1}^{p}$ is the pooling rate of interest. The pension system reduces current wage income but increases future income. Consumers choose $C_{t}^{y}(\mu ,\eta )$ and $C_{t+1}^{o}(\mu ,\eta )$ in order to maximize expected lifetime utility (2) subject to the budget constraint (54). The optimal consumption plans and annuity demands are fully characterized by:

$$\begin{aligned} C_{t}^{y}(\mu ,\eta )&=\Phi \left( \mu ,\frac{1+r_{t+1}}{{\bar{\mu }}_{t}^{p}} \right) \left[ (1-\theta )w_{t}(\eta )+\theta \zeta _{A}w_{t}(\eta )\frac{\ {\bar{\mu }}_{t}^{p}}{{\bar{\mu }}}+\frac{\lambda {\bar{\mu }}_{t}^{p}w_{t+1}(\eta )}{ 1+r_{t+1}}\right] , \end{aligned}$$

(55)

$$\begin{aligned} \frac{{\bar{\mu }}_{t}^{p}C_{t+1}^{o}(\mu ,\eta )}{1+r_{t+1}}&=\left[ 1-\Phi \left( \mu ,\frac{1+r_{t+1}}{{\bar{\mu }}_{t}^{p}}\right) \right] \left[ (1-\theta )w_{t}(\eta )+\theta \zeta _{A}w_{t}(\eta )\frac{\ {\bar{\mu }} _{t}^{p}}{{\bar{\mu }}} \right. \nonumber \\&\quad \left. +\frac{\lambda {\bar{\mu }}_{t}^{p}w_{t+1}(\eta )}{1+r_{t+1}}\right] , \end{aligned}$$

(56)

$$\begin{aligned} A_{t}^{p}(\mu ,\eta )&=\left[ 1-\Phi \left( \mu ,\frac{1+r_{t+1}}{{\bar{\mu }} _{t}^{p}}\right) \right] (1-\theta )w_{t}(\eta ) \nonumber \\&\quad -\Phi \left( \mu ,\frac{1+r_{t+1}}{{\bar{\mu }}_{t}^{p}}\right) \left[ \theta \zeta _{A}w_{t}(\eta )\frac{\ {\bar{\mu }}_{t}^{p}}{{\bar{\mu }}}+\frac{ \lambda {\bar{\mu }}_{t}^{p}w_{t+1}(\eta )}{1+r_{t+1}}\right] , \end{aligned}$$

(57)

where we have used the expression for the pooled annuity rate as given in (32). The social annuity system affects an individual’s human wealth at birth [the term in square brackets on the right-hand side of (55)] but it is not a priori clear in which direction. Indeed, the effective pension contribution rate is:

$$\begin{aligned} \theta _{t}^{n}\equiv \theta \left( 1-\zeta _{A}\frac{\ {\bar{\mu }}_{t}^{p}}{ {\bar{\mu }}}\right) . \end{aligned}$$

(58)

On the one hand, with a positive correlation between health and ability $\zeta _{A}$ is such that $0<\zeta _{A}<1$. On the other hand, the survival rate of private annuitants exceeds the population-wide average survival rate, i.e. ${\bar{\mu }}_{t}^{p}/{\bar{\mu }}>1$. It thus follows that $\theta _{t}^{n}$ is ambiguous in sign. In this paper we focus on the case for which $\theta _{t}^{n}$ is negative so that, ceteris paribus factor prices and the pooled survival rate, human wealth is increased as a result of the public pension system.⁶

Fig. 5

Consumption-saving choices under pension system A. ${\mathrm{LBC}}(\eta _{j})$ is the lifetime budget constraint for an individual with productivity $\eta _{j}$. IEL is the income endowment line and agents are located on the line segment ${\mathrm{E}}_L{\mathrm{E}}_H$. ${\mathrm{MRSC}}(\mu _{i}$) is the consumption Euler equation for an individual with survival rate $\mu _{i}$ facing a pooled annuity rate of interest ${\bar{r}} _{t+1}^{p}$. For individuals with $\mu _{t}^{bc}\le \mu \le \mu _{H}$ optimal consumption is located at the intersection of ${\mathrm{MRSC}}(\mu _{i}$) and ${\mathrm{LBC}}(\eta _{j}$). All other individuals face borrowing constraints and consume along ${\mathrm{E}}_L{\mathrm{E}}_H$. The dashed lines visualize the corresponding schedules for the AI case. Factor prices are held the same for SA and AI to facilitate the comparison

The optimal consumption choices can be explained with the aid of Fig. 5. To facilitate the comparison with the AI case we keep factor prices and the pooled survival rate at the levels for that case. Hence the diagram shows the partial equilibrium effects on individual choices of the introduction of a pension system. The dashed lines correspond to the AI case. As a result of the public pension system the lifetime budget constraints shift outward (because $\theta _{t}^{n}<0$), more so the higher is $\eta$. The income endowment line rotates in a counter-clockwise fashion. Unconstrained individuals increase consumption during youth and old-age. In contrast, constrained individuals are forced to consume less during youth. Such agents are bunched along the line segment ${\mathrm{E}}_{{L}}{\mathrm{E}}_{{H}}$. Just as for the AI case there is a single cut-off value for the survival probability below which agents are facing borrowing constraints:

$$\begin{aligned} \mu _{t}^{bc}=\frac{{\bar{\mu }}_{t}^{p}U^{\prime }((1-\theta )w_{t}(\eta ))}{ (1+r_{t+1})\beta U^{\prime }\left( \lambda w_{t+1}(\eta )+\theta \zeta _{A}\ \frac{1+r_{t+1}}{{\bar{\mu }}}w_{t}(\eta )\right) }. \end{aligned}$$

(59)

Because wages and pension receipts are proportional to $\eta$ and the felicity function is homothetic, it follows from (59) that $\mu _{t}^{bc}$ does not depend on $\eta$. As is clear from the diagram, the introduction of public pensions will increase the population fraction of people facing borrowing constraints.

In order to glean the general equilibrium effects of introducing a public pension system we must formulate the capital accumulation identity. Since public and private annuities are invested in the capital markets, the accumulation equation takes the following format:

$$\begin{aligned} K_{t+1}=L_{t}\left[ A_{t}^{s}+\int _{\eta _{L}}^{\eta _{H}}\int _{\mu _{t}^{bc}}^{\mu _{H}}A_{t}^{p}(\mu ,\eta )h(\mu ,\eta )d\eta d\mu \right] . \end{aligned}$$

(60)

By substituting the demand for annuities (57) into (60 ) we obtain the fundamental difference equation for the capital intensity:

$$\begin{aligned} k_{t+1}&=\frac{1}{1+n}\frac{L_{t}}{N_{t}}\left[ \theta {\bar{\eta }} w_{t}+\int _{\mu _{t}^{bc}}^{\mu _{H}}\left( (1-\theta )w_{t}-\Phi \left( \mu ,\frac{1+r_{t+1}}{{\bar{\mu }}_{t}^{p}}\right) \right. \right. \nonumber \\&\quad \left. \left. \cdot \left[ (1-\theta )w_{t}+\theta \zeta _{A}w_{t}\frac{\ {\bar{\mu }} _{t}^{p}}{{\bar{\mu }}}+\frac{\lambda {\bar{\mu }}_{t}^{p}w_{t+1}}{1+r_{t+1}}\right] \right) h_{\mu }(\mu )\Gamma _{1}(\mu )d\mu \right] , \end{aligned}$$

(61)

where $\Gamma _{1}(\mu )$ is the conditional mean of $\eta$ [defined in Lemma 1(vi) above], and the factor prices follow from (20)–(21).

The main features of the steady-state equilibrium with pension system A (labeled SA) are reported in columns (c)–(d) of Table 2. In column (c) the contribution rate equals $\theta =0.010$ which means that the system is relatively small as the income replacement rate during retirement, $\xi _{SA}\equiv \theta \zeta _{A}(1+{\hat{r}})/[(1-\lambda )\bar{ \mu }]$, is only about 0.3812. In column (d) the contribution rate equals $\theta =0.025$ which results in a large pension system, i.e. $\xi _{SA}=0.9776$. Comparing columns (b) and (d) we find that output per efficiency unit of labour drops by 1.62% (${\hat{y}}=9.680$) whilst the steady-state capital intensity falls by 5.76% (${\hat{k}}=0.351$). As a result of the decrease in the capital intensity, the annual interest rate rises by 11 basis points (${\hat{r}}^{a}=5.22\%$) whilst the wage rate falls by 1.6%. The proportion of constrained individual rises from 5.83 to 17.66%. The adverse selection index, as defined in (35) above, increases to ${\widehat{AS}}=1.39$ and the asset-weighted average survival rate of annuitants rises to $\hat{{\bar{\mu }}}^{p}=0.70$. Despite the fact that the rate of return on capital increases, the return on private annuities decreases slightly because the pooled survival rate $\hat{{\bar{\mu }} }^{p}$ increases by more. Finally, as the welfare indicators at the bottom of Table 2 reveal, under pension system A all individuals are worse off compared to the AI case. The pension system crowds out capital and exacerbates the adverse selection problem in the market for private annuities.

Fig. 6

Steady-state profiles under pension system A. The solid lines depict the steady-state profiles under pension system A (SA), and the dashed lines visualize the profiles for the asymmetric information (AI) case without pensions. In both cases adverse selection results in a single pooling rate of interest on annuities, ${\bar{r}} _{t+1}^{p}$, and agents with poor health face binding borrowing constraints. The SA case has been drawn for a large system featuring $\theta =0.025$

In Fig. 6 we use solid lines to depict the profiles for youth and old-age consumption, annuity demand, and utility (averaged over $\eta$) for the SA case. These are given by:

$$\begin{aligned} \frac{{\hat{C}}^{y}(\mu )}{{\hat{w}}}&=\left[ 1-{\mathbb{I}}_{SA}(\mu )+{\mathbb{I}} _{SA}(\mu )\Phi \left( \mu ,\frac{1+{\hat{r}}}{\hat{{\bar{\mu }}}^{p}}\right) \left[ 1-\theta +\theta \zeta _{A}\frac{\hat{{\bar{\mu }}}^{p}}{{\bar{\mu }}}+ \frac{\lambda \hat{{\bar{\mu }}}^{p}}{1+{\hat{r}}}\right] \right] \Gamma _{1}(\mu ), \end{aligned}$$

(62)

$$\begin{aligned} \frac{{\hat{C}}^{o}(\mu )}{{\hat{w}}}&=[1-{\mathbb{I}}_{SA}(\mu )]\left[ \lambda +\theta \zeta _{A}\frac{1+{\hat{r}}}{{\bar{\mu }}}\right] \Gamma _{1}(\mu )+ {\mathbb{I}}_{SA}(\mu )\left[ 1-\Phi \left( \mu ,\frac{1+{\hat{r}}}{\hat{\bar{\mu }}^{p}}\right) \right] \nonumber \\&\quad \cdot \left[ \left( 1-\theta +\theta \zeta _{A}\frac{\hat{{\bar{\mu }}} ^{p}}{{\bar{\mu }}}\right) \frac{1+{\hat{r}}}{\hat{{\bar{\mu }}}^{p}}+\lambda \right] \Gamma _{1}(\mu ), \end{aligned}$$

(63)

$$\begin{aligned} \frac{{\hat{A}}^{p}(\mu )}{{\hat{w}}}&={\mathbb{I}}_{SA}(\mu )\left[ 1-\theta -\Phi \left( \mu ,\frac{1+{\hat{r}}}{\hat{{\bar{\mu }}}^{p}}\right) \left[ 1-\theta +\theta \zeta _{A}\frac{\hat{{\bar{\mu }}}^{p}}{{\bar{\mu }}}+\frac{ \lambda \hat{{\bar{\mu }}}^{p}}{1+{\hat{r}}}\right] \right] \Gamma _{1}(\mu ), \end{aligned}$$

(64)

where ${\mathbb{I}}_{SA}(\mu )=0$ for $\mu _{L}\le \mu <{\hat{\mu }}^{bc}$ and ${\mathbb{I}}_{AI}(\mu )=1$ for ${\hat{\mu }}^{bc}\le \mu \le \mu _{H}$. The dashed lines in Fig. 6 correspond to the profiles for the AI case. Youth consumption, annuity demand, and lifetime utility are all lower under SA than under AI. Old-age consumption is higher under AI for most borrowing constrained individuals.

4.2 Pension System B

Under pension system B the government uses information on a person’s wage income to deduce that individual’s innate ability. It uses its knowledge of $\eta$ by setting pension receipts according to the following rule:

$$\begin{aligned} R_{t+1}^{s}(\eta )=\zeta (\eta )\theta w_{t}(\eta ), \end{aligned}$$

(65)

where $\zeta (\eta )$ is a function to be determined below. For each ability level $\eta$, the budget constraint for the public pension system is given by:

$$\begin{aligned} (1+r_{t+1})\theta w_{t}(\eta )\int _{\mu _{L}}^{\mu _{H}}L_{t}(\mu ,\eta )d\mu =\int _{\mu _{L}}^{\mu _{H}}\mu R_{t+1}^{s}(\eta )L_{t}(\mu ,\eta )d\mu . \end{aligned}$$

(66)

The left-hand side of this expression is the total amount to be distributed to type $\eta$ survivors whilst the right-hand side represents total pension payments to such individuals. Under this system public annuities are such that longevity risk is shared among individuals of the same productivity type. By substituting (65) into (66) and noting that $w_{t}(\eta )=\eta w_{t}$ and $L_{t}(\mu ,\eta )=L_{t}h(\mu ,\eta )$ we find the balanced-budget solution for $\zeta (\eta )$:

$$\begin{aligned} \zeta (\eta )=\zeta _{B}(\eta )\ \frac{1+r_{t+1}}{{\bar{\mu }}},\qquad \zeta _{B}(\eta )\equiv \frac{{\bar{\mu }}}{{\bar{\mu }}+\xi \sigma _{\mu }^{2}(\eta - {\bar{\eta }})}. \end{aligned}$$

(67)

For relatively productive individuals (featuring $\eta >{\bar{\eta }}$) the rate of return on social annuities falls short of the actuarially fair social annuity yield, $(1+r_{t+1})/{\bar{\mu }}$, because such people tend to have a relatively high survival rate. In contrast, for relatively unproductive individuals (with $\eta <{\bar{\eta }}$) the rate of return on social annuities is better than the actuarially fair social annuity yield because such people tend to have a relatively low survival rate.

Individuals facing a binding borrowing constraint consume according to (52), (53) with $R_{t+1}^{s}(\eta )$ as stated in (65) and (67). For unconstrained individuals the optimal consumption plans and annuity demands are fully characterized by:

$$\begin{aligned} C_{t}^{y}(\mu ,\eta )&=\Phi \left( \mu ,\frac{1+r_{t+1}}{{\bar{\mu }}_{t}^{p}} \right) \left[ (1-\theta )w_{t}+\theta \zeta _{B}(\eta )w_{t}\frac{\ \bar{\mu }_{t}^{p}}{{\bar{\mu }}}+\frac{\lambda {\bar{\mu }}_{t}^{p}w_{t+1}}{1+r_{t+1}} \right] \eta , \end{aligned}$$

(68)

$$\begin{aligned} \frac{{\bar{\mu }}_{t}^{p}C_{t+1}^{o}(\mu ,\eta )}{1+r_{t+1}}&=\left[ 1-\Phi \left( \mu ,\frac{1+r_{t+1}}{{\bar{\mu }}_{t}^{p}}\right) \right] \left[ (1-\theta )w_{t}+\theta \zeta _{B}(\eta )w_{t}\frac{\ {\bar{\mu }}_{t}^{p}}{ {\bar{\mu }}}\right. \nonumber \\&\quad \left. +\frac{\lambda {\bar{\mu }}_{t}^{p}w_{t+1}}{1+r_{t+1}}\right] \eta , \end{aligned}$$

(69)

$$\begin{aligned} A_{t}^{p}(\mu ,\eta )&=\left[ 1-\Phi \left( \mu ,\frac{1+r_{t+1}}{{\bar{\mu }} _{t}^{p}}\right) \right] (1-\theta )\eta w_{t} \nonumber \\&\quad -\Phi \left( \mu ,\frac{1+r_{t+1}}{{\bar{\mu }}_{t}^{p}}\right) \left[ \theta \zeta _{B}(\eta )w_{t}\frac{\ {\bar{\mu }}_{t}^{p}}{{\bar{\mu }}}+\frac{ \lambda {\bar{\mu }}_{t}^{p}w_{t+1}}{1+r_{t+1}}\right] \eta , \end{aligned}$$

(70)

where we have substituted $w_{t}(\eta )=\eta w_{t}$ and used the expression for the pooled annuity rate as given in (32).

Fig. 7

Consumption-saving choices under pension system B. ${\mathrm{LBC}}(\eta _{j})$ is the lifetime budget constraint for an individual with productivity $\eta _{j}$. IEL is the income endowment line and agents are located on the line segment ${\mathrm{E}}_L{\mathrm{E}}_H$. ${\mathrm{MRSC}}(\mu _{i}$) is the consumption Euler equation for an individual with survival rate $\mu _{i}$ facing a pooled annuity rate of interest ${\bar{r}} _{t+1}^{p}$. The dashed and dotted lines visualize the corresponding schedules for the AI and SA cases respectively. Factor prices are held the same for SB and AI to facilitate the comparison. An individual with productivity $\eta _{j}$ faces borrowing constraints if $\mu <\mu _{t}^{bc}( \eta _{j})$ and is unconstrained otherwise

The optimal consumption choices can be explained with the aid of Fig. 7. Just as before we focus on the four extreme types. The solid lines depict the situation under pension system B. For purposes of reference the dashed lines in the diagram represent the AI case (without pensions) whilst the thin dotted lines represent the SA case. We keep factor prices constant at their AI levels. Under pension system B the IEL pivots around some point C on the old IEL line for the SA case. Intuitively this is because system B incorporates explicit redistribution from high-ability to low-ability individuals and, as a result of the positive correlation between ability and health, implicit redistribution from healthy to unhealthy individuals. With asymmetric information in the private annuity market the pooling equilibrium causes a redistribution of resources from unhealthy to healthy individuals, i.e. from people who tend to be poor to individuals who tend to be rich. Pension system A does nothing to redress this phenomenon. In contrast, under system B the high-skilled get a lower return on social annuities than the low-skilled do, so there is some redistribution from healthy to unhealthy individuals via that channel.

As is marked in the diagram, lowest-ability types experience borrowing constraint for $\mu <\mu _{t}^{bc}(\eta _{L})$ whilst highest-ability individuals experience such constraints for $\mu <\mu _{t}^{bc}(\eta _{H})$, where $\mu _{t}^{bc}(\eta _{H})<\mu _{t}^{bc}(\eta _{L})$. Mathematically, an individual with productivity $\eta$ experiences a binding borrowing constraint if his/her survival probability falls short of $\mu _{t}^{bc}(\eta )$:

$$\begin{aligned} \mu _{t}^{bc}(\eta )=\frac{{\bar{\mu }}_{t}^{p}U^{\prime }((1-\theta )\eta w_{t})}{(1+r_{t+1})\beta U^{\prime }\left( \lambda \eta w_{t+1}+\theta \eta \zeta _{B}(\eta )\ \frac{1+r_{t+1}}{{\bar{\mu }}}w_{t}\right) } \end{aligned}$$

(71)

Despite the fact that the felicity function is homothetic and wages are proportional to $\eta$, $\mu _{t}^{bc}$ depends on $\eta$ because productivity features nonlinearly in $\zeta _{B}(\eta )$.

Fig. 8

Ability and borrowing constraints. Under pension systems B and C the critical level of the survival rate below which borrowing constraints become active, $\mu _{t}^{bc}(\eta )$, depends negatively on the individual’s productivity $\eta$. In Fig. 7 the income endowment points no longer lie along a ray from the origin

In Fig. 8 we illustrate the relationship between ability $\eta$ and the critical survival rate $\mu _{t}^{bc}(\eta )$. The thin solid line represents the AI case for which ${\hat{\mu }}^{bc}=0.1028$ and $5.83\%$ of agents are constrained. The dashed line depicts the situation for the SA case (with $\theta =0.025$) for which ${\hat{\mu }}^{bc}=0.2090$ and $17.66\%$ of agents are constrained. Finally, the thick solid line in Fig. 8 illustrates the SB case. As is predicted by the theory there is a downward sloping relationship between $\eta$ and ${\hat{\mu }}^{bc}$. For the lowest-ability types the cut-off value equals 0.2590 whereas it is equal to 0.1902 for the highest-ability individuals. So by engaging in redistribution from high-ability to low-ability individuals the policy maker worsens the incidence of borrowing constraints to the latter types.

Fig. 9

Comparing pension systems. The fair-rate share $\zeta _{i}(\eta )$ measures the individual’s gross yield on social annuities under pension system i expressed as a share of the actuarially fair yield, $(1+{\bar{r}}_{t+1}^{p})/ {\bar{\mu }}$. A negative value for the effective pension contribution rate $\theta _{t}^{n}(\eta )$ implies that the pension system makes individuals wealthier in a partial equilibrium sense

In Fig. 9 we compare some features of pension systems A and B. Panel (a) depicts the fair-rates shares $\zeta _{A}$ (a constant) and $\zeta _{B}(\eta )$ (downward sloping because of redistribution). Panel (b) shows that pensions receipts are increasing in ability for both systems. In panel (c) we depict the effective pension contribution rate $\theta _{t}^{n}(\eta )$. Under system A this is a negative constant, but under system B the effective rate is increasing in ability:

$$\begin{aligned} \theta _{t}^{n}(\eta )\equiv \theta \left( 1-\zeta _{B}(\eta )\frac{\ \bar{ \mu }_{t}^{p}}{{\bar{\mu }}}\right) . \end{aligned}$$

(72)

For our parameterization $\theta _{t}^{n}(\eta )$ remains negative for all ability levels, although barely so for the highest-ability types.

Under pension system B the capital accumulation identity is given by:

$$\begin{aligned} K_{t+1}=L_{t}\left[ A_{t}^{s}+\int _{\eta _{L}}^{\eta _{H}}\int _{\mu _{t}^{bc}(\eta )}^{\mu _{H}}A_{t}^{p}(\mu ,\eta )h(\mu ,\eta )d\eta d\mu \right] , \end{aligned}$$

(73)

where $\mu _{t}^{bc}(\eta )$ is determined in (71) and is illustrated in Fig. 8. By substituting the demand for annuities (70) into (73) we obtain the fundamental difference equation for the capital intensity:

$$\begin{aligned} k_{t+1}&=\frac{1}{1+n}\frac{L_{t}}{N_{t}}\left[ \theta {\bar{\eta }} w_{t}+\int _{\eta _{L}}^{\eta _{H}}\int _{\mu _{t}^{bc}(\eta )}^{\mu _{H}} \left( (1-\theta )w_{t}-\Phi \left( \mu ,\frac{1+r_{t+1}}{{\bar{\mu }}_{t}^{p}} \right) \right. \right. \nonumber \\&\quad \left. \left. \cdot \left[ (1-\theta )w_{t}+\theta \zeta _{B}(\eta )w_{t}\frac{\ {\bar{\mu }}_{t}^{p}}{{\bar{\mu }}}+\frac{\lambda {\bar{\mu }}_{t}^{p}w_{t+1}}{ 1+r_{t+1}}\right] \right) \eta h(\mu ,\eta )d\mu d\eta \right] . \end{aligned}$$

(74)

The main features of the steady-state equilibrium with a small and large pension system B (labeled SB) are reported in, respectively, columns (e) and (f) of Table 2. We focus attention at the large pension system featuring $\theta =0.025$. Comparing columns (b) and (f) we find that output per efficiency unit of labour drops by 1.74% (${\hat{y}}=9.668$) whilst the steady-state capital intensity falls by 6.19% (${\hat{k}}=0.350$). As a result of the decrease in the capital intensity, the annual interest rate rises by 12 basis points (${\hat{r}}^{a}=5.23\%$) whilst the wage rate falls by 1.74%. The proportion of constrained individual rises from 5.83% to 19.33%. The adverse selection index, as defined in (35) above, increases to ${\widehat{AS}}=1.40$, the asset-weighted average survival rate of annuitants rises to $\hat{{\bar{\mu }}}^{p}=0.70$, and the return on private annuities decreases slightly to $\hat{{\bar{r}}}^{p}=9.98$. Finally, as the welfare indicators at the bottom of Table 2 reveal, under pension system B poor-health individuals are better off compared to the AI case as a result of the redistributionary feature of system B. The opposite holds for the healthy agents. Even though the policy maker cannot observe an individual’s health status, by including a redistributionary component in the public pension system, the unhealthiest in society are aided somewhat.

Fig. 10

Steady-state profiles under pension system B. The solid lines depict the steady-state profiles under pension system B (SB), and the dashed lines visualize the profiles for the asymmetric information (AI) case without pensions. In both cases adverse selection results in a single pooling rate of interest on annuities, ${\bar{r}} _{t+1}^{p}$, and agents with poor health face binding borrowing constraints. The SB case has been drawn for a large system featuring $\theta =0.025$

In Fig. 10 we present the $\eta$-averaged profiles for consumption during youth and old-age, annuity demand, and lifetime utility. These profiles are defined as:

$$\begin{aligned} \frac{{\hat{C}}^{y}(\mu )}{{\hat{w}}}&=(1-\theta )\int _{\eta _{L}}^{\eta _{H}} \left[ 1-{\mathbb{I}}_{SB}(\mu ,\eta )\right] \frac{\eta h(\mu ,\eta )}{h_{\mu }(\mu )}d\eta \nonumber \\&\quad +\left( 1-\theta +\frac{\lambda \hat{{\bar{\mu }}}^{p}}{1+{\hat{r}}} \right) \int _{\eta _{L}}^{\eta _{H}}\Phi \left( \mu ,\frac{1+{\hat{r}}}{\hat{ {\bar{\mu }}}^{p}}\right) {\mathbb{I}}_{SB}(\mu ,\eta )\frac{\eta h(\mu ,\eta )}{ h_{\mu }(\mu )}d\eta \nonumber \\&\quad +\theta \frac{\hat{{\bar{\mu }}}^{p}}{{\bar{\mu }}}\int _{\eta _{L}}^{\eta _{H}}\Phi \left( \mu ,\frac{1+{\hat{r}}}{\hat{{\bar{\mu }}}^{p}}\right) \zeta _{B}(\eta ){\mathbb{I}}_{SB}(\mu ,\eta )\frac{\eta h(\mu ,\eta )}{h_{\mu }(\mu )}d\eta , \end{aligned}$$

(75)

$$\begin{aligned} \frac{{\hat{C}}^{o}(\mu )}{{\hat{w}}}&=\int _{\eta _{L}}^{\eta _{H}}\left( \lambda +\theta \zeta _{B}(\eta )\frac{1+{\hat{r}}}{{\bar{\mu }}}\right) \left[ 1- {\mathbb{I}}_{SB}(\mu ,\eta )\right] \frac{\eta h(\mu ,\eta )}{h_{\mu }(\mu )} d\eta \nonumber \\&\quad +\left( (1-\theta )\frac{1+{\hat{r}}}{\hat{{\bar{\mu }}}^{p}}+\lambda \right) \int _{\eta _{L}}^{\eta _{H}}\left[ 1-\Phi \left( \mu ,\frac{1+{\hat{r}} }{\hat{{\bar{\mu }}}^{p}}\right) \right] {\mathbb{I}}_{SB}(\mu ,\eta )\frac{\eta h(\mu ,\eta )}{h_{\mu }(\mu )}d\eta \nonumber \\&\quad +\theta \frac{1+{\hat{r}}}{{\bar{\mu }}}\int _{\eta _{L}}^{\eta _{H}} \left[ 1-\Phi \left( \mu ,\frac{1+{\hat{r}}}{\hat{{\bar{\mu }}}^{p}}\right) \right] \zeta _{B}(\eta ){\mathbb{I}}_{SB}(\mu ,\eta )\frac{\eta h(\mu ,\eta ) }{h_{\mu }(\mu )}d\eta , \end{aligned}$$

(76)

$$\begin{aligned} \frac{{\hat{A}}^{p}(\mu )}{{\hat{w}}}&=(1-\theta )\int _{\eta _{L}}^{\eta _{H}} {\mathbb{I}}_{SB}(\mu ,\eta )\frac{\eta h(\mu ,\eta )}{h_{\mu }(\mu )}d\eta \nonumber \\&\quad -\left( 1-\theta +\frac{\lambda \hat{{\bar{\mu }}}^{p}}{1+{\hat{r}}} \right) \int _{\eta _{L}}^{\eta _{H}}\Phi \left( \mu ,\frac{1+{\hat{r}}}{\hat{ {\bar{\mu }}}^{p}}\right) {\mathbb{I}}_{SB}(\mu ,\eta )\frac{\eta h(\mu ,\eta )}{ h_{\mu }(\mu )}d\eta \nonumber \\&\quad -\theta \frac{\hat{{\bar{\mu }}}^{p}}{{\bar{\mu }}}\int _{\eta _{L}}^{\eta _{H}}\Phi \left( \mu ,\frac{1+{\hat{r}}}{\hat{{\bar{\mu }}}^{p}}\right) \zeta _{B}(\eta ){\mathbb{I}}_{SB}(\mu ,\eta )\frac{\eta h(\mu ,\eta )}{h_{\mu }(\mu )}d\eta , \end{aligned}$$

(77)

where ${\mathbb{I}}_{SB}(\mu ,\eta )=0$ if ${\hat{A}}^{p}(\mu ,\eta )<0$ and ${\mathbb{I}}_{SB}(\mu ,\eta )=1$ if ${\hat{A}}^{p}(\mu ,\eta )\ge 0$.⁷ The profiles for SB and SA (in Fig. 6) are very similar.

4.3 Pension System C

The final case we consider is pension system C under which the government engages in more extreme redistribution from the rich to the poor (than under system B) by providing every surviving individual with the same pension payment:

$$\begin{aligned} R_{t+1}^{s}(\eta )={\bar{R}}_{t+1}^{s}, \end{aligned}$$

(78)

where ${\bar{R}}_{t+1}^{s}$ is to be determined below. The clearing condition for the public pension system is given in this case by:

$$\begin{aligned} (1+r_{t+1})\theta {\bar{\eta }}w_{t}L_{t}=L_{t}\int _{\mu _{L}}^{\mu _{H}}\int _{\eta _{L}}^{\eta _{H}}\mu {\bar{R}}_{t+1}^{s}h(\mu ,\eta )d\eta d\mu , \end{aligned}$$

(79)

so that ${\bar{R}}_{t+1}^{s}$ is given by:

$$\begin{aligned} {\bar{R}}_{t+1}^{s}=\theta {\bar{\eta }}w_{t}\frac{1+r_{t+1}}{{\bar{\mu }}}. \end{aligned}$$

(80)

Expressing the pension receipt in terms of the contribution made during youth we find for a person of type $\eta$ that $R_{t+1}^{s}(\eta )=\zeta (\eta )\theta w_{t}(\eta )$ where $\zeta (\eta )$ is given by:

$$\begin{aligned} \zeta (\eta )=\zeta _{C}(\eta )\ \frac{1+r_{t+1}}{{\bar{\mu }}},\qquad \zeta _{C}(\eta )\equiv \frac{{\bar{\eta }}}{\eta }. \end{aligned}$$

(81)

See Fig. 9 for features of pension system C. It follows from (81) that for individuals with above-average productivity, $\eta > {\bar{\eta }}$, the rate of return on social annuities falls short of the actuarially fair social annuity yield, $(1+r_{t+1})/{\bar{\mu }}$. In contrast, below-average individuals get a better-than actuarially fair rate on the pension contributions. Intuitively these results follow from the fact that the pension system redistributes resources from productive to less productive agents.

Fig. 11

Steady-state profiles under pension system C. The solid lines depict the steady-state profiles under pension system C (SC), and the dashed lines visualize the profiles for the asymmetric information (AI) case without pensions. In both cases adverse selection results in a single pooling rate of interest on annuities, ${\bar{r}} _{t+1}^{p}$, and agents with poor health face binding borrowing constraints. The SC case has been drawn for a large system featuring $\theta =0.025$

Qualitatively system C is very similar to system B (in that both feature redistribution for healthy to unhealthy agents) and the key expressions characterizing system C can be obtained by replacing $\zeta _{B}(\eta )$ with $\zeta _{C}(\eta )$ in Eqs. (68)–(77). The main features of system C are the following. First, the comparison of columns (b) and (g) in Table 2 reveals that output and wages fall by 1.83% (${\hat{y}}=9.660$) and the capital intensity drops by 6.49% (${\hat{k}}=0.349$). Out of the three pension systems considered, system C features the largest macroeconomic effects. Redistribution is macroeconomically costly. Second, from Fig. 9 it is clear that pension system C indeed features the highest degree of redistribution from healthy to unhealthy individuals. Indeed, as can be observed in panel (c) the effective contribution rate $\theta _{t}^{n}(\eta )$ becomes positive for the most healthy individuals. Such individuals experience the pension system as a tax burden. Third, as is shown in Fig. 8 low-ability types are affected most severely by borrowing constraints under pension system C. Finally, the individual $\eta$-averaged profiles for consumption, annuity demands, and utility are depicted in Fig. 11. These profiles are very similar to the ones we found for system B.

5 Privatizing Social Security

The key message of the previous section is loud and clear. The mandatory funded pension systems that we have studied are immune to adverse selection by design but they exacerbate the adverse selection problem in the market for private annuities, increase the fraction of borrowing-constrained (‘over-annuitized’) individuals in the population, and lead to long-run crowding out of capital and substantial output losses. This begs the following question: is it better to privatize social security altogether and to allow individuals to insure against longevity risk in the private annuity market even though this market is not perfect? Referring to Table 2 we find that abolishing the large pension system A (featuring $\theta =0.025$) would increase output by 1.65% in the long run. In addition, it would increase steady-state welfare of all corner types in the economy, cf. the information contained in columns (d) and (b). At least in the long run, privatization is a ‘win-win’ scenario.

Of course, comparing steady states gives only part of the answer. What matters is whether or not is possible to abolish the funded pension system in a Pareto improving manner, i.e. is it a ‘win-win’ scenario to all generations? To answer this question we now study the transitional dynamic effects of abolishing pension system A. The economy is in the steady state for the SA system with $\theta =0.025$ and the capital intensity is equal to ${\hat{k}}_{SA}=0.351$. At shock-time $t=0$, the pension system is abolished so that young individuals do not pay the pension contribution anymore, i.e. wage income from $t=0$ onward equals $w_{t}(\eta )$ and pensions receipts from period $t=1$ onward are equal to zero, $R_{t}^{s}(\eta )=0$. Of course the old survivors at the time of the shock receive the pension they saved for, i.e. $R_{0}^{s}(\eta )>0$.

Fig. 12

Abolishing pension system A. At time $t=0$ pension system A with a contribution rate of $\theta =0.025$ is abolished permanently. The system is initially in the steady state featuring a capital intensity ${\hat{k}} _{SA}=0.351$. a Over time the economy converges monotonically to the steady-state for the AI case with ${\hat{k}}_{AI}=0.373$. b, c Show the percentage change in, respectively, youth and old-age consumption for an individual of type $(\mu _{i},\eta _{L})$. d Depicts the percentage change in annuity demand of a person of type $(\mu _{H},\eta _{L})$ . See also Table 2

Figure 12 depicts some of the key features of the transition process. Panel (a) shows that the capital intensity is predetermined at impact but thereafter rises monotonically to settle at the new steady-state level associated with the AI equilibrium, ${\hat{k}} _{AI}=0.373$. Panel (b) show the percentage change in youth-consumption for healthy and unhealthy individuals with the lowest skill level. Interestingly, the healthy individuals decrease their consumption whilst the unhealthy increase it. The response of the latter group of people is easy to understand: these individuals were facing severe borrowing constraints in the SA system (and will continue to do so to a lesser degree in the AI equilibrium). Because the pension system is abolished (and $\theta =0$) they can increase their consumption during youth and reduce the degree of overannuitization. Note that in panel (c) the overannuitization faced by the unhealthy is illustrated by the dramatic fall in old-age consumption for period $t=1$ (when the surviving shock-time young are old) and beyond. Finally, in panel (d) we show that there is a strong increase in the demand for private annuities by the healthy agents.⁸ There is virtually no transitional dynamics in $\mu _{t}^{bc}$ which falls from ${\hat{\mu }}^{bc}=0.2090$ to $\mu _{0}^{bc}=0.1026$ and thereafter settles at ${\hat{\mu }}^{bc}=0.1025$. It follows that all agents featuring $\mu <0.1025$ face borrowing constraints during youth no matter when they are born.

Fig. 13

Lifetime utility of corner types. The solid lines depict the steady-state lifetime utility levels attained by the different corner types under pension system A (SA) with $\theta =0.025$. The abolishment of the pension system occurs at time $t=0$ and affects lifetime utility of different types over time. Unhealthy agents benefit from the policy initiative no matter when they are born. Healthy individuals born at the time of the shock are worse off as a result of it

In Fig. 13 we illustrate the effects on lifetime welfare for the four corner types in the economy, i.e. $(\mu _{L},\eta _{L})$ , $(\mu _{L},\eta _{H})$, $(\mu _{H},\eta _{L})$, and $(\mu _{H},\eta _{H})$ . Regardless of when they are born and irrespective of their productivity level, the unhealthiest individuals are better off as a result of the pension abolishment. Expected lifetime utility rises over time so for all corner types the gain is higher the later they are born. Interestingly, healthy agents born at the time of the shock are worse off than they would have been under the SA system. Privatizing social security is not a ‘win-win’ scenario to all generations.

6 Conclusion

In our paper we have developed an overlapping generations model which features adverse selection in the private annuity market and endogenously determined borrowing constraints in the capital market. Consumers are assumed to be heterogeneous in two dimensions—working ability and health status—which in the absence of perfect information leads to adverse selection in the private annuity market. Furthermore, they are restricted from borrowing against their anticipated future wage income due to the borrowing constraints. We demonstrate numerically that the informational asymmetry matters quantitatively in that, compared to the world with perfect information, it causes first-order reductions in output per efficiency unit of labour and the capital intensity. Starting from the benchmark model with adverse selection we introduce a fully-funded social security system and study its impact on capital accumulation and individual welfare under three different pension benefit rules.

We find that the social security system affects both capital accumulation and the proportion of individuals that are facing borrowing constraints. Capital crowding out increases and borrowing constraints become more prevalent the larger is the pension system. Intuitively a social security system causes more consumers to be over-annuitized and to face borrowing constraints. They cannot undo the effects of social security by transacting in their private accounts because any attempt to go short on annuities (demanding life-insured loans) would reveal their health status to the insurance companies in a world with asymmetric information.

The welfare effects of social security depend both on the pension recipient’s type and on the specific form of the pension benefit rule. Provided the rule incorporates some implicit or explicit redistribution from healthy to unhealthy individuals, the latter group will actually benefit from the existence of the social security system in the steady state. In contrast, if pension benefits are proportional to an individual’s contributions during youth and the proportionality factor is the same for everybody then the pension system makes everybody worse off in the long run.

A comparison of steady-state equilibria is not a guarantee that the privatization of social security is Pareto improving for all generations. For example, the simulations have shown that the abolition of a public pension system featuring a proportional benefit rule will harm shock-time healthy individuals. Even though all other generations and types are better off as a result, the privatization does not constitute a ‘win-win’ scenario.

In this paper we have intentionally ignored the role of an intentional bequest motive and its effect on capital accumulation. Of course, the intention to leave bequests to one’s offspring does affect an individual’s attitude toward private annuities. Indeed, with an operative bequest motive, the rational individual will no longer fully annuitize his/her assets. Despite the high return on private annuities the individual will put aside a certain amount of unannuitized savings to pass on to their offspring upon death. In future work we intend to generalize the heterogeneous-agent model developed here by including an intentional bequest motive and to study the effects of social security with this extended framework.