Introduction

Atlantic salmon (Salmo salar) is important economically and culturally for Canadians and First Nations communities alike and is targeted by conservation efforts (Smialek et al. 2021; Gillis et al. 2023) due to the steady decline of populations over the past decades (ICES 2023). The juvenile life stage of salmonids is of particular concern, given the increasing frequency of thermal stress events in freshwater habitat due to climate change (Woodward et al. 2010; Breau et al. 2011; Dugdale et al. 2016; Morash et al. 2021; Smialek et al. 2021; Gallagher et al. 2022; Gillis et al. 2023). Furthermore, the juvenile life stage is critical for salmonids as they typically exhibit strong population regulation during their first summer of life (Elliott 1994; Nislow et al. 2004; Imre et al. 2005; Smialek et al. 2021; Lobon-Cervia 2022), and small reductions in body size can have long-term effects on population productivity (Koenings et al. 1993; Ulaski et al. 2022). Given the important role that somatic growth plays in salmon ecology and survival, monitoring this key parameter is essential for comprehending the potential effects and outcomes of climate change on populations.

Forecasting the effects of climate change on fitness is critical for conservation and management of Atlantic salmon (Ulaski et al. 2022; Gillis et al. 2023). A recent meta-analysis by Gallagher et al. (2022) quantified important spatial and temporal variation in salmonid productivity related to the impact of climate change on a variety of complex biological processes. However, they also underscored that the important influence of methodological and statistical techniques was challenging to ascertain in a meta-analytical framework due to substantial variation in study designs, unbalanced replication, and geographical biases. Similarly, other studies have found an important effect of study design on salmonid growth (i.e. Laplanche et al. 2019; Matte et al. 2020a), but such effects are often concomitant with potential biases induced by spatial and temporal scales (Bal et al. 2011; Gregory et al. 2017; Charron et al. 2019; Laplanche et al. 2019), and which metric/s of growth (Lugert et al. 2016) and water temperatures (Ouellet-Proulx et al. 2023) are used. Therefore, it is challenging to disentangle the potential impacts of analytical and methodological designs on reported growth-temperature relationships from other processes but warrants further investigation.

Differences in study design typically lead to different analyses due to the nature of the data collected. More specifically, investigating the effects of global climate change on salmonid growth relies on both long-term observational datasets to quantify temporal trends (Parra et al. 2009; Bal et al. 2011; Kanno et al. 2015; Laplanche et al. 2019) and short-term studies, which often include repeated measurement throughout the growth season, to investigate finer growth mechanisms and the effects of climactic extremes (e.g. Strothotte et al. 2005; Breau et al. 2011; Corey et al. 2017; Frechette et al. 2018). Both approaches provide complementary insights, but are often analyzed with different metrics of growth, and thus follow different assumptions (Lugert et al. 2016). For instance, long-term surveys without individual growth data assume that fish are sedentary, and that size-selective mortality is minimal between sampling events (Bal et al. 2011). In addition, long-term surveys conducted over larger spatial and temporal scales often rely on size-at-age data to construct seasonal growth trajectories (Parra et al. 2009; Laplanche et al. 2019; Burbank et al. 2023), usually from functions such as the von Bertalanffy Growth Function (VBGF).

Increasingly, size-at-age datasets are analysed with hierarchical modelling (e.g., when units of analysis are drawn from clusters within a population) to account for variation occurring over large spatial and temporal resolution (He and Bence 2007; Bal et al. 2011; Parent et al. 2013; Cafarelli et al. 2017; Laplanche et al. 2019). Nevertheless, an important issue is that VBGF typically models fish growth at an annual rate, even though within-season fluctuations in temperatures have a well-known influence on behavior and growth (Mallet et al. 1999; Breau et al. 2007; Dzul et al. 2017). This issue is not specific to temperature, other factors important for growth such as food availability, water discharge, or conspecific density (Heggenes 1990; Imre et al. 2005; Matte et al. 2020b) are also difficult to account for in observational designs. Consequently, the effects of temperature on growth may be more challenging to detect at a seasonal scale using VBGF models than at finer temporal resolutions.

Conversely, short-term studies on growth rates of fish that involve repeated measurement throughout the growth season are better suited to detect growth-temperature relationships (e.g. Flodmark et al. 2004; Meeuwig et al. 2004; Strothotte et al. 2005; Eldridge et al. 2015; Matte et al. 2020b). This is likely because the finer temporal resolution at which the data are collected aligns more closely with the biological processes. However, instantaneous growth rates derived from these experiments cannot be extrapolated over longer periods of time and are often calculated using the first and last measurements only, ignoring any intermediate growth measurements (Lugert et al. 2016). Furthermore, collecting growth data at time scales shorter than those required for annual size-at-age relationships is costly, labor-intensive, and often impractical (Bentley and Schindler 2013). Consequently, instantaneous growth rates are advantageous for investigating mechanisms, but pose challenges when attempting to convert them into meaningful metrics for management and conservation purposes, such as size at the end of the growing season. Despite the highlighted differences between size-at-age and instantaneous growth rates methods and their underlying assumptions, the extent to which temperature-growth relationships differ between these approaches has not received attention in the literature.

The metrics used for incorporating temperature in growth models are equally important. Historically, the effect of temperature on growth was modelled with measures of central tendency, either for air or water temperatures (Ouellet-Proulx et al. 2023). To improve these models, cumulative degree-days have also widely been used to explicitly incorporate thermal variability within a season (e.g. Strotthotte et al. 2005; Venturelli et al. 2010; Chezik et al. 2014). However, several studies failed to detect an effect of degree-days on growth (e.g. Strotthotte et al. 2005; Ouellet-Proulx et al. 2023), perhaps because the using of degree-days is equivalent to assuming a linear relationship between temperature and growth. This assumption is contradicted by experimental work on salmonids, where the relationship between growth and temperature follows a bell-shaped curve between 6 and 28 °C, with maximum growth around 16–18 °C depending on the population (Elliott et al. 1995; Mallet et al. 1999). Accordingly, Mallet et al. (1999) developed a mathematical relationship relating growth coefficients to daily temperature to estimate daily growth potential, accounting for the range of temperature at which growth occurs (hereafter referred to as growth potential in the text and subsequent analyses). The use of this growth potential metric allowed Bal et al. (2011) to detect an effect of temperature on the growth parameter K in the VBGF. To account for variation in growth season duration, Ouellet-Proulx et al. (2023) introduced the potential growth thermal index (PGTI) wherein growth potential is summed over the growth season. Studies comparing the performance of multiple temperature metrics often found that their performance is context-dependent (e.g. Charron et al. 2019; Ouellet-Proulx et al. 2023). Consequently, it is plausible that some of the idiosyncratic results reported among studies, beyond biological processes, may be related to the choice of temperature metric(s).

In the present study, we use a juvenile Atlantic salmon growth dataset collected in two eastern Canadian rivers (Margaree and Miramichi rivers) from 2000 to 2002 as a case study to investigate the potential effects of analytical and modelling decisions on the detectability of climate change effects on salmonid performance. This dataset has enough body size measurements throughout the growth season to analyze both seasonal growth trajectories and instantaneous growth rates. This approach complements recent meta-analyses (Gallagher et al. 2022) and reviews (Smialek et al. 2021; Gillis et al. 2023) as it provides an opportunity to isolate the potential effects of modelling and study designs from the important spatial and temporal biases present amongst studies, as well as providing a better understanding of the complex biological processes operating differently amongst natural systems. Using this approach, we investigate: (1) whether seasonal growth trajectories built from size-at-age data (similarly to how long-term data is analysed) differ from those derived from instantaneous growth rates while accounting for hierarchical structure at varying spatial scales (sites, populations); (2) whether these different approach influence our ability to derive temperature-growth relationships; and (3) whether combining these approaches can yield valuable insight from a management standpoint, such as predicting the size at the end of the growing season. Using our case study dataset, we test the following predictions: (1) size-at-age data will be best quantified with a VBGF using a nested spatial hierarchy (sites within populations), with a weak correlation between temperature and growth parameter K given that the former is averaged over the entire growing season; (2) temperature will be a strong driver of instantaneous growth rates, given the shorter timescale matches biological processes more closely; (3) size at the end of the growing season will be best predicted by combining insights from both size-at-age and instantaneous growth models.

Methods

Study area

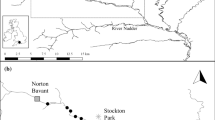
The study was conducted in two Atlantic salmon populations from eastern Canada: the Margaree River, on the western side of Cape Breton, Nova Scotia, and the Miramichi River, in New Brunswick (Fig. 1). The Margaree River drains a watershed area of 1100 km2, whereas that of the Miramichi River is approximately 12 000 km2 (Marshall 1982; Amiro 1983).

Fig. 1
figure 1

Location of sampling sites in the Miramichi and Margaree rivers, in eastern Canada

Full size image

Fish Sampling methodology

Both the Margaree and Miramichi rivers were sampled using single pass backpack electrofishing following the same methodology (Strothotte et al. 2005; Dauphin et al. 2019) than the one used in the Fisheries and Oceans Canada long term monitoring program. The main discrepancy with the monitoring program being that in this study more emphasis was put in capturing a reasonable amount of fish during each sampling event to acpture the variability in size of each age category, sometimes resulting in higher effort. Sampling occurred across the stream from bank to bank in successive upstream transects. Fish were caught with hand held dip-nets and with a 1 m wide seine (1 mm mesh) downstream of each sweep (Strothotte et al. 2005). A total of 12 sites (n = 4 for Margaree River and n = 8 for Miramichi River) were repeatedly sampled (n = 5–12) throughout the growing season (Julian dates between 131 and 309, corresponding to May 10th – November 5th ) (see Table 1 for details). The Margaree River was not sampled in 2002 due to logistical constraints, but this is not expected to induce an influence on the analyses given that the year-level variation is modest (see Results). Sampling events were approximately 3 weeks apart, on average, in both populations (18.8 and 21.4 days for Margaree and Miramichi rivers, respectively). A total of 1252 and 6631 young-of-the-year (0+) salmon were caught in the Margaree and Miramichi rivers, respectively. Fork length of captured fish was measured, and age of fish was determined by visually inspecting length-frequency distributions (Sethi et al. 2017). In this analysis, only growth pattern of 0 + were investigated as they constitute the most abundant age class (42.0% of all samples) and are the only age consistently estimated across datasets (i.e., when aging juveniles based on length frequency, the overlap in size is larger between 1 + and 2 + than between 0 + and 1+). Further, the effect of environmental conditions is assumed to be more important for 0 + than older parr (Parra et al. 2012).

Table 1 Sampling design for 0 + Atlantic salmon from the Miramichi (2000–2002) and Margaree (2000–2001) rivers
Full size table

Temperature metrics

Water temperature was monitored using VEMCO data loggers installed at each site, which recorded data hourly (± 0.1 °C). Missing data were estimated with a Generalized Additive model relating observed water temperature averaged daily to daily air temperature data, while accounting for seasonality with Julian date using a cyclical cubic spline given the cyclical nature of seasonal data (Caissie 2006), and a site-specific random effect (RMSE: 1.07 °C and 1.47 °C for Margaree and Miramichi rivers, respectively). Daily air temperature estimates were obtained from the ERA5 reanalysis database with a 0.25 × 0.25-degree grid resolution (Hersbach et al. 2020), which were then assigned to sampling sites based on latitude and longitude.

Using predicted daily water temperatures, growth potential was calculated as in Mallet et al. (1999). Briefly, growth potential \(\mathrm{f(}{\mathrm{T}}_{\mathrm{i}}\mathrm{)}\) is a metric ranging from 0 to 1, representing no growth and maximal growth, respectively:

$$f\left(T_i\right)=\frac{\sum\varphi_i\left(T_{i,d}\right)}{t_2-t_1}\\$$
(1)

where t1 and t2 represent the start and end dates, respectively, and \({\phi }_{i}\left({T}_{i,d}\right)\) represents the growth potential for a given day at an observed average daily water temperature.

Growth potential, \({\phi }_{i}\left({T}_{i,d}\right),\) is defined as:

$$\varphi_i\left(T_{i,d}\right)=\frac{\left(T_{i,d}-Tmin\right)\left(T_{i,d}-Tmax\right)}{\left(T_{i,d}-Tmin\right)\left(T_{i,d}-Tmax\right)-\left(T_{i,d}-Topt\right)^2}$$
(2)

where \({T}_{i,d}\) is the observed average daily water temperature, \(\mathrm{Tmin}\), \(\mathrm{Tmax}\), and \(\mathrm{Topt}\) are the minimum, maximum, and optimal temperature for growth, respectively. Cases where \({T}_{i,d}\)is above the maximum or below the minimum for growth are assigned a growth potential of zero (\(\mathrm{f(}{\mathrm{T}}_{\mathrm{i}}\mathrm{)}\mathrm{=0}\)). \(\mathrm{Tmin}\), \(\mathrm{Tmax}\), and \(\mathrm{Topt}\) were set at 6, 27, and 18 °C, respectively, as these values match those proposed in other studies including fish from the Miramichi River population (Breau et al. 2011; Ouellet-Proulx et al. 2023).

The potential growth thermal index (PGTI) was also calculated as in Ouellet-Proulx et al. (2023) – the key difference with the growth potential from Mallet et al. (1999) being that daily growth potentials were summed over the growth season rather than averaged, to account for changes in the number of days suitable for growth:

$${\mathrm{f(T}}_\mathrm{i}\mathrm{)}=\sum\phi_i\left(T_{i,d}\right)$$
(3)

  

Lastly, cumulative degree days were calculated as the cumulative sum of daily Celsius degrees above 0, as in Strottotte et al. (2005). These four temperature metrics (air temperature, growth potential, PGTI, and degree days) were chosen because they correlate well with salmonid growth (Ouellet-Proulx et al. 2023). Additionally, they can be applied at both the seasonal scale and at a finer temporal resolution for instantaneous growth rates (e.g. weeks).

Size-at-age (during the growing season)

Hypotheses were tested by implementing nonlinear hierarchical modelling under a Bayesian framework. First, hierarchical models without temperature metrics were defined; potential drivers were then added to increase complexity of models with varying levels of hierarchy. Performance of competing models was compared using the Watanabe-Akaike information criterion, which is a more generalized metric compared to the Bayesian information criterion (WAIC, Gelman et al. 2014).

2.4.1 Parametrization of hierarchical structure

The fork lengths L of fish i from site j in river l and in year m were assumed to be normally distributed as:

$$L_{ijlm}\left|\mu_{ijlm}^L,\right.\sigma_l^L\sim N(\mu_{ijlm}^L,\sigma_l^L)$$
(4)

where \({\sigma }_{l}^{L}\) is the standard deviation associated with the VBGF and assumed to vary across rivers, and \({\mu }_{ijlm}^{L}\) is the average predicted fork length of fish i from site j in river l and year m according to the standard parametrization of the VBGF:

$$L_{ijlm}=L\infty_{jlm}\left(1-e^{-K_{jlm}\left(t_{ijlm}-T0_{jlm}\right)}\right)$$
(5)

where L ∞ jlm represents the asymptotic fork length for a 0 + at the end of the growth season, Kjlm is the growth rate, and T0jlm is the first day of growth at site j in river l and year m.

Due to the nature of the data used in this study, a hierarchical structure was implemented for the various parameters of the VBGF reflects the belief that these processes should be similar from one site/river to another (He and Bence 2007; Bal et al. 2011; Parent et al. 2013; Cafarelli et al. 2017; Laplanche et al. 2019). Therefore, the asymptotic fork length and first day of growth parameters are drawn from Gamma distributions with river-specific mean (\({\mu }_{l}^{L\infty }\) and \({\mu }_{l}^{T0}\), respectively) and standard deviation (\({\sigma }_{l}^{L\infty }\) and \({\sigma }_{l}^{T0}\), respectively) parameters to reflect potential difference across rivers as follows:

$$L\infty_{jlm}\left|\mu_l^{L\infty},\right.\sigma_l^{L\infty}\sim Gamma(\mu_l^{L\infty},\sigma_l^{L\infty})$$
(6)

  

$${T0}_{jlm}\left|\mu_l^{T0},\right.\sigma_l^{T0}\sim Gamma(\mu_l^{T0},\sigma_l^{T0})$$
(7)

For estimated parameter Kjlm, a beta distribution was chosen as the value of this parameter is likely bound between 0 and 1:

$$K_{jlm}\left|\mu_l^K,\right.\sigma_l^K\sim{Beta(\mu_l^K,\sigma_l^K)}$$
(8)

where \({\mu }_{l}^{K}\) and \({\sigma }_{l}^{K}\) are the mean and standard deviation of growth rate in catchment l.

2.4.2 Incorporation of temperature metrics to the VBGF

Water temperature was added to the VBGF by relating the growth rate Kjlm to temperature metrics using a linear mixed model, taking advantage of the expected relationship between growth rate Kjlm and temperature as in previous work (Taylor 1960; Fontora and Agostino 1996; Mallet et al. 1999), Eq. 8 becomes:

$$\mu_{jlm}^K=\alpha_l\cdot T_{jlm}+Z_l\\$$
(9)
$$K_{jlm}\left|\mu_{jlm}^K,\right.\sigma_{jlm}^K\sim{Normal(\mu_{jlm}^K,\sigma_{jlm}^K)}$$
(10)

where al and Zl are catchment-level slope and intercept parameters, respectively. \({T}_{jlm}\) is the observed temperature metric of interest for site j in catchment l and year m (i.e., growth potential, PGTI, or degree days), and \({\mu }_{jlm}^{K}\) and \({\sigma }_{jlm}^{K}\) are the mean and associated standard deviation of growth rate. Linear mixed models were used given that the nonlinearity of the growth-temperature relationship was explicitly included in the growth potential metric (Mallet et al. 1999) and PGTI (Ouellet-Proulx et al. 2023).

Instantaneous growth rates

Using the average size of fish during each sampling event, instantaneous growth rates were calculated between consecutive sampling events within a given site separated by at least 10 days to minimize the potential effects of measurement errors, given that fish were not individually marked. Instantaneous growth rates for any given sites displayed strong non-linear patterns and were therefore analysed using Generalized additive models (GAMs). Temperature metrics for these analyses were calculated over the same time interval used to calculate instantaneous growth rates within a given site (e.g., growth rate calculated between June 1st -20th were paired with temperature metrics also calculated between June 1st -20th within that site).

Size at the end of the growing season

Sizes at the end of the growing season (October 1st ) were estimated using the best size-at-age model, given that size in October is important for later life stages (Bal et al. 2011). These extrapolations were then related to temperature metrics with GAMs using the same hierarchical structures (i.e., catchment, site, year) as those used in the instantaneous growth rates models. For these analyses, temperature metrics were calculated over the entire growing season (May-October), given that the objective was to predict the size at the end of the growing season.

Bayesian modelling

Bayesian inference for the size-at-age models was conducted with the package nimble (v. 0.13.1) in R (v. 4.2.2), given the flexibility required to build the size-at-age models with the VBGF framework as described above (i.e., these analyses could not easily be replicated with the brms package as described below). All parameters were given weakly informative priors (Table 2) except for \({\mu }_{l}^{L\infty }\) and \({\mu }_{l}^{T0}\) which were given uniform priors ranging from 40 to 120 (mm) and 75 to 165 (Julian day), respectively, to reflect our knowledge about the date of Atlantic salmon fry emergence and the maximum size 0+ can reach (Randall 1982; Swansburg et al. 2002). All parameters were estimated using 2 parallel Markov-Chain-Monte-Carlo (MCMC) chains, with 105 iterations, a burn-in of 104, and a thinning rate of 10. Convergence of nimble models was assessed with potential scale reduction factor (Brooks and Gelman 1998, Ȓ< 1.05) and confirmed visually with caterpillar plots. Model comparison was conducted using the Watanabe-Akaike information criterion (WAIC), for which lower values indicate a better fit to the data. More parsimonious models were selected when WAIC was similar (∆WAIC < 2).

Table 2 Priors for parameters of von Bertalanffy models for 0 + Atlantic salmon from the Miramichi and Margaree rivers in 2000–2002
Full size table

Relationships between both instantaneous growth rates and size at the end of the growing season, and temperature metrics, were strongly nonlinear and, thus, were best analysed with GAM models. The brms package (a high-level interface for Stan; Carpenter et al. 2017) was used, given that the framework to build GAMs in a Bayesian framework is already implemented. All parameters of these models were estimated from a single chain with 104 iterations (including a warmup of 1000), a thinning rate of 10 resulting in 900 values retained, as is standard with brms (Bürkner 2017). Model comparison was conducted with leave-one-out cross-validation information criterion (LOOIC), and convergence of these models were also assessed with Ȓ, as provided by Stan (Vehtari et al. 2021).

The structure of all models (Table S1) and the associated diagnostic plots (Fig. S1-S12) are available in supplementary information.

Results

Overview of temperature and growth potential among rivers

Average summer water temperatures were significantly colder in the Margaree River (11.27 ± 4.98 °C) than in the Miramichi River (13.10 ± 5.93 °C, p < 0.001) from April 1st to October 1st. Similarly, air temperature was marginally colder for the Margaree River (12.43 ± 6.12 °C) than in the Miramichi River (12.79 ± 6.40 °C; p = 0.07). These differences in water temperature led to marginally smaller growth potential in the Margaree River (Growth potential = 69.15 ± 8.8%; PGTI = 105.80 ± 13.51) than the Miramichi River (Growth potential = 76.91 ± 6.01%; PGTI = 117.67 ± 9.20; p = 0.08). Daily water temperatures followed a Gaussian curve governed by three parameters: a, the maximum temperature; b, a measure of the duration of the warm period (i.e., > 0 °C), and c the Julian date at which this maximum occurs (Daigle et al. 2019). The Miramichi River exhibited a higher peak water temperature (a = 20.20 ± 1.97 °C) occurring earlier in the season (c = 206.70 ± 6.12), but a shorter growing season (b = 57.60 ± 6.15 days) than for the Margaree River (a = 16.58 ± 2.28 °C; b = 66.07 ± 1.64, c = 217.37 ± 2.18 days; all p < 0.001). No significant differences in water temperature were detected among the three years during which the studies were conducted (p = 0.21).

VBGF model

Out of the eleven models tested, the best model (based on WAIC score and parsimony of parameters) was M2 (Table 3) and did not support the hypothesis that size-at-age is best quantified with a nested spatial hierarchy and a linear relationship between temperature and parameter growth K. More specifically, model comparison from size-at-age data revealed that the most appropriate hierarchical structure included random variation among sites and years (Fig. 2; Table 3; all Ȓ < 1.001), but no systematic differences between the two rivers’ populations (Table 3; \({\mu }^{K}\) = 0.013 mm day−1, CI: 0.011–0.015; \({\mu }^{L\infty }\) = 67.2 mm, CI: 62.5–72.7; \({\mu }^{T0}\) = 119.97, CI: 111.35–128.76). VBGF models with the same hierarchical structure were also not improved by the inclusion of any temperature metrics (M4,5,6,7 ∆WAIC < 0.1; Table 3). Furthermore, the slopes of the linear regression for growth potential (M4, 0.008, CI: -0.018–0.035), degree days (M5, 2.4e-06, CI: -3.9e-06–8.5e-06), PGTI (M6, 5.7e-05, CI: -1.2e-04–2.27e-04), and air temperature (M7, 0.0011, CI: 0.0001–0.0032) were estimated at or close to 0 for all three models (Table 3), and the standard deviation in growth rate \({\sigma }_{l}^{K}\) was slightly larger with the inclusion of temperature metrics than without (\({\sigma }_{l}^{K}\)= 0.005 and 0.004, respectively). Incorporating a nested random effect of site within river (M8, M9, M10, M11) did not improve model performance (∆WAIC > 1.5, Table 3).

Table 3 Parameterization of von Bertalanffy models (hierarchical structure and temperature metrics used), parameters estimates (mean and standard deviation) and WAIC of size-at-age models for 0 + Atlantic salmon from the Miramichi and Margaree rivers in 2000–2002. The model in bold is the best model (lowest WAIC; or the most parsimonious if the difference in WAIC is inferior to 2)
Full size table
Fig. 2
figure 2

Mean fork length of Atlantic salmon young of the year (0+) sampled at Miramichi and Margaree rivers. Each colour indicates a specific year, the size of the dots is proportional to the number of 0 + sampled at a particular sampling event date. Lines corresponds to the average VBGF curves (most parsimonious model, M2), and error bar is the standard deviation of fork length within a sampling event

Full size image

Residuals of the most parsimonious VBGF model (M2) were unrelated to any temperature metrics, quantified either cumulatively from the start of the season to the sampling date or calculated over the entire summer season (Fig. 3). Taken together, these results suggest important site-level variation in size-at-age (Table 4), but no detectable relationship between temperature metrics and the growth parameter K of the VBGF model in these populations.

Fig. 3
figure 3

Residuals of the most parsimonious size-at-age model (M2) in relation to temperature metrics (A, E: Potential  Growth Thermal Index (PGTI); B, F: growth potential; C,G: Degree days); D, H: Air temperature (°C), quantified either  cumulatively from the start of the season to the sampling date (A - D) or seasonally (E-H). Average residual is 0.00027

Full size image
Table 4 Site-specific parameter estimates (mean and standard deviation) from the best size at age model (VBGF, M2)
Full size table

Instantaneous growth rates model

The models investigated in this study support our prediction that temperature is a strong driver of instantaneous growth rates, as the short timescale aligns more closely aligns with biological processes. The best model for growth rate (M12, ∆LOOIC < 3.3; Table 5) described a nonlinear relationship with Julian day in which the highest growth rate occurred in mid-July (Ȓ < 1.001; Fig. 4a), and a positive relationship with growth potential (Ȓ < 1.001; Fig. 4b). Accounting for potential hierarchical structure did not improve the model – no systematic differences were found among sites, populations, or sites nested within populations (M15, M16, M17, M18, ∆ LOOIC < -3.3; Table 5). The gradient of instantaneous growth rate ranged from − 0.001 (95% CI: -0.008-0.0065) to 0.011 mm.day−1 (95% CI: 0.005–0.018), from the lowest (10%) and highest (99.8%) growth potential, respectively.

Table 5 Model selection for instantaneous growth rate of 0 + Atlantic salmon in Margaree and Miramichi rivers in 2000–2002. The model in bold is the best model (Lowest LOOIC; or the most parsimonious if the difference in LOOIC is inferior to 2)
Full size table
Fig. 4
figure 4

Effect of (A) growth potential and (B) Julian day on instantaneous growth rates (M10 fit) of 0 + Atlantic salmon in two populations (blue: Margaree River; red: Miramichi River; dot size is proportionate to the number of days between sampling events at a given site). Note: in some case the instantaneous growth rate is negative and reflects sampling variation at a particular site this likely does not reflect a negative growth of individuals

Full size image

Size at the end of the growing season

The model investigated in this study also supports our hypothesis that size at the end of the growing season will be best predicted by combining insights from both size-at-age and instantaneous growth rates models. Size at the end of the growing season as estimated by the best hierarchical VBGF model (M2) was not different among populations (Margaree River: 57.3 ± 7.5 mm; Miramichi River: 53.6 ± 5.4 mm; p = 0.30) or across years (p = 0.36). Instead, size at the end of the growing season was positively related to air temperature (M29, Table 6; Fig. 5a, LOOIC = 143.54), PGTI (M33; Table 6; Fig. 5c; ΔLOOIC < 1), and growth potential (M34; Table 6; Fig. 5b; ΔLOOIC < 1). Size at the end of the growing season increased from 47.6 mm (CI: 32.6–63.0) at 13.5 ◦C to 56.3 mm at 15.3 ◦C (M28; Fig. 5). Similarly, M33 predicted a 3.7 mm increase in size from 53.5 mm (CI: 39.7–68.0) to 57.2 mm (CI: 41.6–73.0), approximately 7.0% of fork length across the gradient of seasonal growth potential due to temperature (62–91%; Fig. 5). Models incorporating differences among rivers (M28, M30, M31, M35) performed equally well, but were less parsimonious (ΔLOOIC < -2). Conversely, models with degree days (M37; Fig. 5d) worse than the ones using other temperature metrics (ΔLOOIC > 2) and showed no clear relationship. These results suggest that the relationship between size at the end of the growing season and temperature was not different among rivers.

Table 6 Model selection for size at the end of the growing season of 0 + Atlantic salmon in Margaree and Miramichi rivers in 2000–2002. The model in bold is the best model (Lowest LOOIC; or the most parsimonious if the difference in LOOIC is inferior to 2)
Full size table
Fig. 5
figure 5

Effect of (A) Air temperature (◦C), (B) growth potential, (C) potential growth thermal index,

and D) degree days on size-at-age (mm) of 0 + Atlantic salmon on October 1st (estimated from M2)

Full size image

Discussion

Modelling mechanisms underpinning the effects of climate change on juvenile salmonid growth is challenging given the large range of spatiotemporal scales, metrics of temperature and growth, and statistical analyses investigated across studies. Here, size-at-age data analysed seasonally with the VBGF framework failed to detect an influence of temperature on growth parameters or residuals. Conversely, instantaneous growth rates between sampling dates derived from the same dataset were strongly related to growth potential, PGTI, air temperature, and even degree days to a lesser extent. However, the instantaneous growth rates models have a poor predictive capacity which limits their relevancy for population management purposes. Size at the end of the growing season was best predicted from the VBGF model accounting for random variation among sites and years and were strongly related to temperature metrics (air temperature, growth potential, PGTI) such as instantaneous growth rate models.

Here, we show that combining these two approaches (i.e., size-at-age and instantaneous growth rates modelling) can circumvent their intrinsic drawbacks and reveal essential patterns for population management that may otherwise remain undetected if only one approach was used. Further, in cases where instantaneous growth rates are not available to investigate finer patterns, relating size-at-age predicted from hierarchical VBGF can provide an interesting alternative, even if the VBGF parameters or its residuals are unrelated to temperature metrics.

Relationship between growth parameter K and temperature

The lack of relationship between the VBGF growth parameter K and temperature metrics contrasts with previous work in which such relationships are evident (Taylor 1960; Fontoura and Agostinho 1996; Mallet et al. 1999; Bal et al. 2011). An important difference is that the current study was conducted in the summer whereas Mallet et al. (1999) was conducted throughout the year, resulting in a larger gradient of temperatures and growth rates in the latter. Nevertheless, the range of growth potential among sites (62–91%) in this study was larger than in Bal et al. (2011; 72–83%), in which a small effect of temperature on growth parameter K was detected, in part due to strong density effects. Thus, it appears unlikely that our range of growth potential was too small to detect the expected relationship.

The most likely explanation is that the VBGF is not sensitive enough to detect statistically significant relationships. More specifically, VBGF parameters were usually correlated, especially growth K and asymptotic length L∞, as is common for VBGF models (Pauly 1980). Thus, small changes in growth parameter K due to temperature fluctuations are likely compensated by the other parameters (L∞, T0) during parameter estimation, exacerbating the difficulty in detecting these relationships. Taken together, results suggest that relating growth parameter K to temperature metrics may fail to detect subtle underlying growth-temperature relationship.

Relationship between instantaneous growth rates and temperature

In contrast, instantaneous growth rates calculated from the same dataset were strongly related to temperature metrics, as commonly observed in salmonids (Jensen 2003; Jonsson and Jonsson 2009). Interestingly, growth potential performed better than PGTI for instantaneous growth models. One likely explanation is that PGTI, which is summed over a given time interval, is less appropriate to quantify an average growth rate from variable time intervals compared to growth potential, which is also averaged over the time interval. The nonlinear relationship between instantaneous growth rate and Julian date peaked in early summer, which is also quite common in salmonids (e.g., Rossi et al. 2022). The two negative outliers (Fig. 4a) are likely caused by sampling variation occurring early in the season. These results differ from the VBGF model which did not detect an effect of temperature on growth rate, supporting the assertion that growth quantified at a finer temporal resolution better reflect biological processes (Mallet et al. 1999; Dzul et al. 2017).

Results also differ from a previous analysis of the same dataset for the Margaree River, which found no relationship between growth rates and temperature in 0 + juveniles (Strothotte et al. 2005). The key difference with the analysis published in Strothotte et al. (2005) is the inclusion of growth potential and PGTI, which are metrics that are more biologically relevant than degree days to quantify growth (Mallet et al. 1999).

Size at the end of the growing season

Size at the end of the growing season, as predicted by the best VBGF model (M2), was strongly related to air temperature, growth potential and PGTI, suggesting that the influence of temperature was easier to detect as a cumulative effect of daily variation over the entire growing season, after accounting for site-level variation, than through its influence on the VBGF growth parameter K. This is similar to Bal et al. (2011), which found a subtle but significant effect of temperature on the fork length reached by 0 + in October. Conversely, using degree days as a temperature metric did not find a clear relationship.

The gradient in size at the end of the growing season for 0 + in both rivers attributable to air temperature and growth potential, calculated as the maximum minus minimum size on October 1st across the range of values of the temperature metric, was 8.7 mm and 3.4 mm, respectively. These reductions are comparable to long-term studies on the impact of climate change on juvenile Atlantic salmon. Ryan et al. (2023) found a ~ 5 mm fork length reduction in 1 + parr (~ 4% of total length) in East Macchias and Sheepscot populations (air temperature: 15.7–19.7 °C), whereas Bal et al. (2011) described a slightly larger size variation of 0 + juveniles (~ 11 mm, 12% of total length) in a Normandy population (water temperature: 13.6–16.3 °C).

Hierarchical structure

When fitting fork length data to VBGF models, the most parsimonious structure only accounted for random variation among sites and years, without systematic differences among populations. This suggests important spatial heterogeneity within population, likely related to important site-level variation in terms of temperature patterns across different branches (Swansburg et al. 2002), fish density (Imre et al. 2005), and/or habitat productivity. However, no consistent differences were detected between populations, either in growth trajectories or size at the end of the growing season. One possible explanation is that the differences in thermal regime detected among rivers (e.g. peak daily water temperature averages: Margaree River, 16.58 ± 2.28 °C; Miramichi River, 20.20 ± 1.97 °C) occurred on either side of the optimal growth temperature (~ 18 °C degrees: Breau et al. 2007; Ouellet-Proulx et al. 2023). Ultimately, these differences in temperatures led to comparable growth potential among rivers (Margaree River, 69.15 ± 8.8%; Miramichi River, 76.91 ± 6.01%), possibly explaining the similar growth trajectories among populations. Similarly, no difference was detected in air temperature among populations (Margaree River, 12.43 ± 6.3◦C; Miramichi River, 12.79 ± 6.4◦C, p > 0.05).

In contrast, instantaneous growth rates were not explained by spatiotemporal hierarchy, suggesting that fish from different sites, rivers, or years, would exhibit comparable changes in growth rates given similar temperature fluctuations on a given Julian date. Taken together, these results suggests that seasonal growth trajectories are mostly linked to local site-level characteristics, but that fish growth rates respond similarly to daily temperature fluctuations across sites within these two populations and over the period considered (2000–2002).

Caveats

The models described in this study rely on several key assumptions. First, growth is estimated by leveraging multiple sampling events, without individually marking fish. This assumes that (1) fish have high site fidelity between sampling events, (2) size-selective mortality does not occur between sampling events (Bal et al. 2011) and (3) all fish have the same proability of capture througout the duration of the study. It is likely that these assumptions are met in the current study. Atlantic salmon can drift downstream over a significant distance post-emergence (Eisenhauer et al. 2021), but they are mostly territorial during the first summer of life (Steingrimsson and Grant 2008). Furthermore, evidence for size-selective mortality in juvenile Atlantic salmon suggests that it is either weak, or variable across seasons or years (Einum and Fleming 2000; Good et al. 2001; Letcher and Horton 2008). For example, size-selective mortality in the first summer of life can occur under extreme climactic events such as droughts or floods (Good et al. 2001), but to the authors knowledge no such event occurred in the current study. Additionally, it is worth noting that juvenile Atlantic salmon can disperse during high temperature events (Corey et al. 2023) but this behavior has only been observed for older juveniles (1 + and 2+) and 0 + do not seem to exhibit this behavior (Breau et al. 2007). Furthermore, there is evidence that the probability of capture may vary with the date of sampling depending on the age of the juvenile (e.g., 0 + have lower probabilities of capture earlier in the year, see Dauphin et al. 2019), this may due to differential response to the electric field and/or different habitat use: young 0 + closer to the riverbed might get stuck in the gravel when entering electronarcosis making them more difficult to net. However, this bias should be systematic across sites and affecting mainly the sampling events early in the growth season and should be compensated by the large number of sampling event occurring for any given site. Finally, factors important for growth beyond temperature, such as food availability, water discharge, or conspecific density (Heggenes 1990; Imre et al. 2005; Matte et al. 2020b) are currently modelled indirectly within year- and site-level variation. Data associated with these factors were not available for the current study and could not be explicitly accounted for. When available, the inclusion of such data could provide additional insight, and may improve our ability to detect temperature-growth relationship.

The relationships between temperature metrics and growth identified in this study are quantified from among-site variation over only three years, rather than long-term temporal trends. Nevertheless, the magnitude of temperature fluctuations among sites were comparable to those in long-term climate change studies. Rates of warming in eastern Canadian rivers is approximately 1.3 °C over the past 50 years (Swansburg et al. 2002), whereas our dataset exhibited about 4 °C difference in peak temperature across rivers, and a standard deviation of ~ 2 °C across measurements within rivers. While this work focused on a finer spatial and temporal resolution, future work should incorporate broader spatiotemporal scales, and incorporate other important drivers of growth beyond temperature (Heggenes 1990; Imre et al. 2005). Furthermore, growth measurement at an individual level obtained (e.g., through scales and/or otoliths; Wright et al. 1990) by collecting fish at the end of the summer/growing season may provide additional insight.

Management implications

The VBGF is amongst the most widely used model in stock assessments providing science advice to inform fisheries management. Despite consideration of potential hierarchical structure, the VBGF model relating growth parameter K to temperature failed to detect the expected growth-temperature relationship. The influence of temperature on growth was detected with instantaneous growth rate, but the use of instantaneous growth rates to inform fisheries management is difficult because growth rates cannot be used for predictions (Lugert et al. 2016). In the present study, we show that taking advantage of the hierarchical VBGF’s predictive power to estimate size at the end of the growing season and combining these predictions to temperature metrics can detect the expected growth-temperature relationships. This methodology is particularly useful in long-term monitoring programs with size-at-age data, and/or for monitoring data-poor fisheries.

Specifically, identifying changes in size-at-age in 0 + salmonids could be a tool to monitor demographic changes occurring at a population scale. In Atlantic salmon, freshwater age is mainly determined by the duration of the growth season and will affect the age at smoltification (Thorpe 1986; Metcalfe 1998; Jonsson and Jonsson 2007) and furthermore, maturation (developmental, physiological, morphological, and behavioral processes leading to reproductive capacity) takes place over the entire lifecycle of Atlantic salmon (Mobley et al. 2021). In some populations, there is evidence of evolutionary trade-offs for parr choosing to stay in freshwater to mature early versus migrating to sea (Buoro et al. 2012). The age at smoltification has consequences on returning adults since salmon smoltifying at an earlier age tend to have a higher reproductive fitness (Mobley et al. 2020) but are exposed to higher predation (McCormick et al. 1998).

Applying this method to the Miramichi and Margaree rivers over the 2000–2002 period showed no consistent differences in growth trajectories among populations, despite significantly different temperature regimes. Instead, we found important site-level variation in fish size linked to growth potential. These results differ from previously published analyses on the same dataset that showed no effect of degree days on growth in 0+, highlighting the importance of incorporating more biologically relevant predictors such as growth potential (Mallet et al. 1999) and PGTI (Ouellet-Proulx et al. 2023).