A Bioeconomic Model of Non-profit and For-profit National Parks Integrating Locals in Biodiversity Conservation

Abstract

To achieve the conservation goals of national parks, involving locals in park operations provides a win/win approach for local development and wildlife management. However, while some bioeconomic studies examine the effectiveness of biodiversity conservation projects that employ locals, most ignore the direct involvement of local workers in national park operations. Moreover, the existing literature tends to assume that national parks are for-profit organizations, whereas they are generally non-profit entities. In this study, we develop a bioeconomic model to investigate the extent to which involving locals in tourism in a national park managed under two different styles of management (i.e., non-profit and for-profit agencies) influences wildlife conservation. We find certain conditions under which involving locals in national park operations can conserve wildlife. Under these conditions, if wildlife conservation does not reduce agricultural productivity, non-profit agencies raise the utility of locals and promote wildlife conservation more than for-profit agencies. Otherwise, non-profit agencies do not necessarily increase the utility of locals or improve conservation compared with for-profit agencies. In addition, we compare the equilibria under both types of agencies and show that they do not generally achieve the social optimum.

1 Introduction

National parks have long played a significant role in protecting biodiversity.¹ However, involving locals in the operations of national parks has recently become a park management decision (Dudley 2008). In contrast to traditional national park management, which disregards locals’ interest and does not encourage their participation, including local communities in natural resource management provides a win/win solution by linking local development with biodiversity conservation (Wells et al. 1992). Natural resource management projects that involve locals in national park operations are sometimes called integrated conservation development projects (ICDPs) or community-based natural resource management (CBNRM).

Tourism, as one of the primary objectives of national park management, provides opportunities to involve locals in park operations. Tourism is a vital source of income for national parks and the local economy, as it creates jobs and encourages infrastructure development (Twining-Ward et al. 2018). According to Chidakel et al. (2021) and World Bank (2021), tourism accounts for 40% of locals’ household income and 30% of locals’ jobs around South Luangwa National Park in Zambia. In Batang Ai National Park in Malaysia, locals work, for example, as general park staff, tourist guides, and restaurant servers, and the earnings that they receive owing to park tourism are substantial (Svadlenak-Gomez et al. 2007). Similarly, in Namibia, employment in tourism improves locals’ livelihoods in rural areas (Spenceley et al. 2019). In addition to the economic advantages, such a participatory approach under which local communities benefit from park tourism can alter their attitudes toward national parks and biodiversity conservation (Tosun 2006). Moreover, involving locals in park tourism can raise their ecological knowledge, which is considered to be essential to ecosystem conservation in national parks (Milupi et al. 2017).

However, the conservation outcomes of tourism projects involving locals remain ambiguous. Although tourism can foster local development, it can also harm the environment (Kiss 2004).² The model proposed in this study analyzes the effectiveness of the involvement of locals as well as captures the negative impact of tourism on the wildlife population.

The bioeconomic literature has studied the extent to which the involvement of locals in tourism and wildlife resource management affects conservation. Skonhoft (1998) introduces a national park that promotes tourism, including hunting, and examines the conflicts between locals and wildlife. His study shows that when the national park agency involves locals in wildlife conservation by sharing the profit from tourism with them, the wildlife population decreases in the long run.

In addition, Johannesen and Skonhoft (2005) explore the effect of a wildlife conservation project in which a national park transfers a proportion of revenue to locals. They conclude that the impacts of such a project on the wildlife population and social welfare are ambiguous. Similarly, Winkler (2011) considers an ecotourism enterprise that distributes a proportion of tourism revenue to local communities. He proves that the social optimum of the wildlife population cannot be achieved under the revenue distribution scheme; hence, this scheme is failing to achieve its goals. Furthermore, Fischer et al. (2010) analyze the participation of a local community in wildlife conservation by receiving a share of the revenue from selling hunting licenses and ecotourism. They discuss the anti-poaching behavior of a local community under different management regimes and benefit-sharing schemes. The authors conclude that a benefit-sharing scheme does not necessarily guarantee an increase in the wildlife population; in particular, the scheme’s effect is ambiguous when the park agency is profit-maximizing.

However, these previous studies are limited in two aspects. First, all four studies ignore the aspect of people’s direct participation in national park tourism. On the one hand, the first three only discuss the allocation of local labor to private production activities such as agricultural production, hunting, and raising livestock. On the other hand, Fischer et al. (2010) target the benefits shared with locals gained from wildlife use on communal land to incentivize them to voluntarily engage in anti-poaching behavior, which differs from the direct inclusion of locals in national park tourism.

Second, these studies assume that the national park agency maximizes its profit, namely, the difference between the revenue from tourism and sales of hunting licenses and operating costs. Profit maximization can be justified in privately owned protected areas (Dudley 2008). However, as indicated by the aims of national parks, the principle of profit maximization does not always apply to park management. Thus, it could be replaced with a non-profit goal, such as raising the wildlife population to evaluate the role of national parks in biodiversity conservation.³

To bridge this gap in the body of knowledge, this study constructs a bioeconomic model to explore the effect of involving locals in national park tourism on biodiversity conservation, with the supposition that a national park can be either a non-profit or for-profit organization. According to Dudley (2008), the primary objective of a national park is to preserve natural biodiversity, including its underlying ecological structure, while promoting education and recreation. However, budget constraints, particularly if a park consistently operates at a deficit, can hinder its sustainability in terms of biodiversity conservation and fulfillment of its primary objectives. Therefore, this paper assumes that a national park operates as a non-profit entity, that is, it does not strive to maximize profit but instead aims to avoid running a deficit in order to sustain its operations while fulfilling its purpose. In other words, we consider a non-profit park that focuses on wildlife conservation by maximizing the wildlife population within the constraint of costs not exceeding revenue. This supposition, though in a different context, shares similarities with the behavior of non-profit agencies discussed by Newhouse (1970); he proposed that a non-profit hospital agency maximizes the provision of healthcare services while ensuring that costs remain lower than revenue.

Meanwhile, local people determine how much labor is employed by the park and in agricultural production. Here, agricultural production is positively, neutrally, or negatively influenced by the wildlife population (i.e., the wildlife population has a positive, zero, or negative externality).⁴ To consider locals’ decision to work in a national park, we assume that the local labor market determines the extent to which they work in tourism. Here, the labor market reflects the opportunity cost of locals participating in park tourism and the revenue potential of the park from hiring locals. The national park agency hires locals directly through the labor market, whose equilibrium endogenously determines the wage rate.

In this study, we first investigate the necessary conditions for involving locals in national park operations to enhance biodiversity conservation. Then, we examine how non-profit and for-profit agencies impact the wildlife population, the utility of locals, and social welfare. We show the wildlife population for which the park should involve locals in tourism operations, as indicated by the functions of our bioeconomic model.

Second, we show that the impacts on the wildlife population and utility of locals crucially depend on how the wildlife population affects agricultural production. If it does not reduce agricultural production, then the wildlife population and utility of locals are both higher under a non-profit park agency. However, contrary to our intuition, we find that if the wildlife population is a pest, a for-profit park agency can increase either the wildlife population or the utility of locals compared with a non-profit park agency. Third, if the wildlife population is not a pest, social welfare under the for-profit agency is always lower than the social optimum, while its position compared with the social optimum under the non-profit agency is ambiguous.

The rest of this paper is organized as follows. Section 2 defines the dynamic and steady-state level of the wildlife population. Section 3 presents the labor market equilibrium for the two types of agencies and the results for the wildlife population and utility of locals. Section 4 analyzes the results of the social optimum, and Sect. 5 provides a numerical simulation. Finally, Sect. 6 concludes.

2 The Bioeconomic Model

Let us consider a national park agency that manages biodiversity and conducts tourism based on that biodiversity. The park is a habitat of wildlife that characterizes the biodiversity of the park and attracts tourists.

The park agency gains revenue from the entry fee paid by tourists. Subsequently, a proportion of the revenue is invested in purchasing the equipment or building the facilities needed to conserve wildlife. We call the amount of equipment and facilities the “conservation capital stock (CCS),” which is expressed by C. We assume that CCS is central to park management. Here, park management refers to the set of conservation activities, including preserving the natural habitat, preventing poaching, and controlling introduced species, which will result in a higher bio-growth rate.

The park agency launches a project that includes locals in tourism operations. We assume that the number of tourists rises as a result of the involvement of locals.⁵ Although increasing tourism generates higher revenue, it also increases the negative impact on the wildlife population. Extensive literature has pointed out that tourism harms biodiversity and the natural habitat.⁶ Researchers have also found evidence that animals used to human presence are more likely to be killed by predators (for more details, see Kasereka et al. 2006; Geffroy et al. 2015).

Based on the above assumptions, in our model, the wildlife population in the national park is determined by the bio-growth rate of the wildlife population, CCS, and negative impact of tourism. We express the bio-growth function by F(X, C), where X is the wildlife population in the park with $F_X\gtreqless 0$ and $F_{C}>0$ (the bio-growth rate under higher CCS is higher). We assume that F is a logistic function, with $F_{X}>0$ up to some $X_{MSY}$ and $F_{X}<0$ for $X >X_{MSY}$ with $F_{X_{MSY}}=0$ for a given C. Thus, the rate of change in the wildlife population is given by

$$\begin{aligned} \frac{dX}{dt}=F(X,C)-\alpha V(\tau ,E,X), \end{aligned}$$

(1)

where $\alpha V(\tau ,E,X)$ expresses the negative impact of tourism on the wildlife population as a function of the number of tourists $V(\tau ,E,X)$. The number of tourists depends on the entry fee $\tau$, involvement of locals in tourism E, and X. We assume that $V_{\tau }<0$ (i.e., a higher entry fee decreases the number of tourists), $V_{E}>0$, and $V_{X}>0$ (i.e., a greater involvement of locals or a rise in the wildlife population increases the number of tourists).

Since our analysis is developed at the equilibrium level, the steady-state level of the wildlife population is determined by $dX/dt=0$ in (1) as

$$\begin{aligned} F(X,C)= \alpha V(\tau ,E,X) \end{aligned}$$

(2)

from which the steady-state X with the involvement of locals in tourism is expressed by $X(E, C, \tau )$ as a function of C, $\tau$, and E, while $X(0, C, \tau )$ denotes the wildlife population before the involvement of locals. We state that the involvement of locals in tourism enhances the wildlife population under labor supply $\bar{E}$ with the given $(C,\tau )$ if it holds at $\bar{E}$ that

$$\begin{aligned} X(\bar{E}, C,\tau )- X(0, C,\tau )=\int _{0}^{\bar{E}}\frac{dX(E, C,\tau )}{dE}dE>0. \end{aligned}$$

(3)

That is, after the national park starts to involve local labor, the steady-state wildlife population is always greater than $X(0, C,\tau )$ if we ensure $dX/dE>0$. Therefore, in this study, $dX/dE>0$ for each E is regarded as the condition for involving locals in tourism to achieve success (i.e., to improve wildlife conservation).

Recalling that the park management uses a proportion of the revenue from tourism in CCS, we suppose that C has the following form:

$$\begin{aligned} \begin{aligned}&\frac{dC}{dt} =I-\delta C, \\ I&=(1-\gamma )\tau V(\tau ,E,X), \end{aligned} \end{aligned}$$

(4)

where $\delta$ is the depreciation rate of CCS. Investment I is determined by the revenue of the park $\tau V(\tau ,E,X)$ at the investment rate $1-\gamma$. Since we focus on the steady state, I must be equivalent to the replacement of depreciated CCS. That is, CCS at the steady state is determined by

$$\begin{aligned} C =\frac{(1-\gamma )\tau V(\tau ,E,X)}{\delta }. \end{aligned}$$

(5)

(5) implies that steady-state C is a function of $\gamma$, $\tau$, and $V(\tau ,E,X)$. Substituting (5) into (2) yields that the steady-state equilibrium X can be solved as a function of $\gamma$, $\tau$, and E; that is, $X(C,E,\tau )$ can be expressed by $X(E,\gamma ,\tau )$.

We then explore the condition for $X_{E} \equiv dX/dE>0$. Differentiating $X(E,\gamma ,\tau )$ with respect to E yields

$$\begin{aligned} X_E\equiv \frac{dX}{dE}=\frac{V_E[\alpha - \frac{1}{\delta } (1-\gamma )\tau F_C ]}{ F_X+ V_X\left[ \frac{1}{\delta } (1-\gamma )\tau F_C - \alpha \right] }. \end{aligned}$$

(6)

Hereafter, we assume that the steady state is locally stable, which means

$$\begin{aligned} F_X+ V_X\left[ \frac{1}{\delta } (1-\gamma )\tau F_C - \alpha \right] <0. \end{aligned}$$

(7)

See “Appendix 1”. Equations (6) and (7) imply that $X_E>0$ if $\frac{1}{\delta } (1-\gamma )\tau F_C >\alpha$. Therefore, in view of (6) and (7), we have the following proposition:

Proposition 1

Suppose that the steady state is locally stable, that is, (7) holds. Then, $X_E >0$ holds if and only if $\frac{1}{\delta } (1-\gamma )\tau F_C >\alpha$.

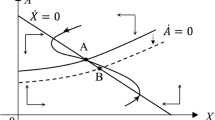
Proposition 1 states that the effects of the change in the number of tourists and marginal bio-growth rate determine the success of the involvement of locals. Once the national park starts to involve local labor, CCS increases by $\frac{1}{\delta }(1-\gamma )\tau V_{E}$, which raises the bio-growth rate by $\frac{1}{\delta } (1-\gamma )\tau V_{E} F_{C}$. By contrast, increasing the number of tourists lowers $\alpha V_{E}$. As long as the increase in the wildlife population brought about by increasing CCS and the involvement of local labor dominates the increased environmental damage from tourism, including locals in park operations enhances conservation. Figure 1 depicts the successful and unsuccessful cases under local stability.

Fig. 1

The effect of increasing the involvement of local labor on the steady-state biodiversity level

In Fig. 1, the inverse U-shaped curve expresses F(X, C), while the upward sloping line shows $\alpha V$. Here, A is the original equilibrium of the park before locals are involved in park operations. That is, at A, $X=X(0,\gamma ,\tau )$ and $V=V(\tau ,0,X)$, while after locals are involved, $X=X(E,\gamma ,\tau )$ and $V=V(\tau ,E,X)$ with $E>0$. Recall that when the national park involves locals, it increases the number of tourists and thus revenue, but inevitably harms the wildlife population to a greater degree. Thus, $\alpha V$ then rotates to the left and the F(X, C) curve moves upward. The figure shows two possible locations for the new steady state, B and D. At B, involving locals increases the wildlife population ($\frac{1}{\delta } (1-\gamma )\tau F_C >\alpha$), that is, $X^B>X^A$. However, at D, $\frac{1}{\delta } (1-\gamma )\tau F_C <\alpha$, that is, $X^A>X^D$. In this case, implementing this project leads to a lower wildlife population, which shows that involving locals in tourism operations leads to less conservation.

Additionally, we derive the effects of changing $\tau$ and $\gamma$ on the steady-state wildlife population under the conditions of stability and $X_E >0$. Differentiating $X(E, \gamma ,\tau )$ with respect to $\gamma$ and $\tau$, we obtain

$$\begin{aligned} X_\tau \equiv \frac{dX}{d\tau }&=\frac{V_\tau \left[ \alpha -\frac{1}{\delta } (1-\gamma )\tau F_C\right] -\frac{1}{\delta } (1-\gamma )V F_C}{ F_X+ V_X\left[ \frac{1}{\delta } (1-\gamma )\tau F_C -\frac{1}{\delta } (1-\gamma )\tau \alpha \right] }, \end{aligned}$$

(8)

$$\begin{aligned} X_\gamma \equiv \frac{dX}{d\gamma }&=\frac{\frac{1}{\delta } \tau V F_C }{ F_X+ V_X\left[ \frac{1}{\delta } (1-\gamma )\tau F_C - \alpha \right] }. \end{aligned}$$

(9)

We rewrite the numerator of (8) as

$$\begin{aligned} \alpha V_\tau + \frac{1}{\delta }(1-\gamma ) V F_C (\varepsilon _\tau -1), \end{aligned}$$

(10)

where $\varepsilon _\tau \equiv -\frac{\tau V_\tau }{V}$ is the entry fee elasticity of tourism demand. If $\varepsilon _\tau \le 1$, $X_\tau >0$; otherwise, $X_\tau \lessgtr 0$. In addition, the relationship between $\tau$ and revenue depends on $\varepsilon _\tau$. When tourism is inelastic or unit elastic (i.e., $\varepsilon _\tau \le 1$), the increase in $\tau$ raises the revenue of the national park despite the decrease in the number of tourists since $d(\tau V)/d\tau =V(1-\varepsilon _\tau )$. That is, there is more revenue to invest in conservation, which mitigates the negative impact of tourism and eventually increases the wildlife population. Moreover, it holds that $X_\gamma <0$ from (9) because increasing $\gamma$ reduces CCS investment,⁷ which results in a lower bio-growth rate. Table 1 lists the variables and functions used in the model, including those that will be mentioned in subsequent sections ahead.

Table 1 Variables and functions used in the model

3 Management of National Parks

So far, we have focused on the effectiveness of the involvement of locals in tourism conducted by the national park agency. However, only when $X_E>0$ should the national park agency hire local workers.⁸ Therefore, our argument is now developed under the conditions ensuring $X_E >0$.

We assume that a national park is operated under either of two management styles: non-profit and for-profit. Under the non-profit management style, the main objective of a national park is to advance its conservation goal under budget constraints.

In our model, X is the target variable, which is positively dependent solely on E. Therefore, each type of national park maximizes its objective by determining E, while $\tau$ and $\gamma$ are exogenously given for the park agencies.⁹ We first analyze the optimal solution for the non-profit agency and then examine that for the for-profit agency. The difference between the solutions under the labor market equilibrium is shown in the last subsection.

3.1 Non-profit National Park Agency

When the national park agency adopts a non-profit style, it aims to maximize the wildlife population subject to its budget constraints. As the steady-state wildlife population is expressed by $X(E; \gamma ,\tau )$, the problem for the non-profit agency is

$$\begin{aligned} \underset{E}{\text {max}}{} &\quad {} X(E) \\\text {s.t.}{} &\quad {} \tau V(E,X;\tau )\ge wE+I.\\ \end{aligned}$$

(11)

From (4), the budget constraint can be rewritten as $\gamma \tau V(E,X;\tau )\ge wE$.

Since we are investigating when the involvement of locals in tourism is beneficial for conservation (i.e., the objective function X(E) is an upward sloping curve), the non-profit agency employs as much labor as possible considering its budget constraints. $E^{NP}$ (here, the superscript “NP” stands for the optimal solution of the non-profit agency) solves the budget constraint:

$$\begin{aligned} \tau \gamma V(E^{NP},X;\tau )=wE^{NP}. \end{aligned}$$

(12)

Under the non-profit agency, we show that the following property holds:

Lemma 1

For the non-profit national park agency, $w> \tau \gamma (V_E + V_X X_E)$ at $E^{NP}$.

Proof

The Lagrangian function of (11) is

$$\begin{aligned} \mathscr {L}= X(E) +\lambda (\gamma \tau V(E,X;\tau )- wE), \end{aligned}$$

(13)

where $\lambda$ is the Lagrange multiplier. The first-order condition for the maximum is

$$\begin{aligned} X_E=\lambda [w-\gamma \tau (V_E+ V_XX_E)], \end{aligned}$$

(14)

which implies that $\lambda \ne 0$ and $\gamma \tau (V_E+ V_XX_E) \ne w$ at $E^{NP}$ because $X_E>0$. Note that $V_E+ V_XX_E \equiv \frac{dV}{dE}$. If $\gamma \tau \frac{dV}{dE}>w$ at $E^{NP}$, then, for a sufficiently small $dE>0$, it holds that $\tau \gamma \frac{dV}{dE} dE> wdE$, which means that increasing E by $dE>0$ to increase X more at $E^{NP}$ is feasible because $X_E>0$. As this contradicts that $E^{NP}$ maximizes X, we obtain $w >\tau \gamma \frac{dV}{dE}$ at $E^{NP}$. $\square$

3.2 For-profit National Park Agency

Let us now analyze the optimality of the for-profit agency. The objective of this type of agency is to maximize profits, as formalized below:

$$\begin{aligned} \begin{aligned}&\underset{E }{\text {max}}{} & {} \pi = \tau V(E,X; \tau )-(wE+I). \\ \end{aligned} \end{aligned}$$

(15)

The first-order condition for this problem is

$$\begin{aligned}&w = \tau \gamma (V_E + V_X X_E). \end{aligned}$$

(16)

Equation (16) implies that $E^{FP}$ (here, the superscript “FP” denotes the optimal solution of the for-profit agency) is determined to satisfy that the net marginal cost of labor w equals marginal revenue $\tau \gamma (V_E+ V_X X_E)$. Based on (14) and (16), we make the following remark.

Remark 1

The non-profit park agency demands more labor than the for-profit one.

Proof

Contrarily, assume that $E^{FP}\ge E^{NP}$. First, assume that $E^{FP}=E^{NP}$. Then, $dV(E^{FP})/dE=dV(E^{NP})/dE$, which contradicts Lemma 1 and (16). Next, assume that $E^{FP}> E^{NP}$. However, this means that $E> E^{NP}$ satisfies $wE=\gamma \tau V(E,X; \tau )$, which leads to $X(E)>X(E^{NP})$ because $X_E>0$. This contradicts that X is maximized by $E^{NP}$. Thus, we obtain $E^{FP}<E^{NP}$. $\square$

Here, we remark that when w is fixed (i.e., the wage rate is exogenously given for the two types of agencies), then $E^{NP}>E^{FP}$ and $X^{NP}>X^{FP}$ always hold.

3.3 Labor Market Equilibrium

In this study, we consider that locals decide whether to work at a national park and assume a local labor market in which demand for labor in national parks and the supply of local labor are adjusted by the wage rate. Labor demand is determined by (14) and (16). We clarify the labor supply below.

Following the assumptions of previous bioeconomic research (Johannesen 2007; Rondeau and Bulte 2007), people who live near protected areas generally work in agriculture. We assume that a representative individual is endowed with H units of labor and that they allocate labor for agriculture and for the national park under the time endowment constraint:

$$\begin{aligned} H=L+E, \end{aligned}$$

where L is the labor input for agricultural production.

This representative individual maximizes their utility, which is defined as

$$\begin{aligned} u(M),\ \ M=wE+pQ(L,X). \end{aligned}$$

Here, M represents total income, which is the sum of the payments from the national park and income from agriculture. The price of agricultural products is fixed at p. Agricultural production Q(L, X) is determined by agricultural labor and the wildlife population because wildlife may decrease agricultural production (i.e., as pests). Meanwhile, agricultural production could increase if the wildlife population is positively associated with biodiversity (i.e., pollinators such as bees). The positive effect of the wildlife population on agriculture is expressed by $Q_{LX} > 0.$¹⁰ We assume that $Q_L>0$ and $Q_{LL}<0$ (i.e., $\partial Q_L/\partial E>0$).

The wildlife population X is exogenous for individuals; therefore, it becomes an exogenous variable in the agricultural production function. By maximizing the instantaneous utility function, the individual decides L as follows:

$$\begin{aligned} \frac{w}{p}=Q_L. \end{aligned}$$

(17)

This condition denotes that the optimal agricultural labor input is determined when the real wage rate (marginal opportunity cost of agriculture) equals the marginal agricultural production of labor (marginal benefit). The supply of $E=H-L$ is determined simultaneously.

Recalling demand for labor in (12) and (16), together with (17), the market equilibria (here, the subscript “m” stands for the market equilibrium) are determined by

$$\begin{aligned}&w^{NP}_m=pQ_L(E^{NP}_m,X^{NP}_m)=f(E^{NP}_m)+\frac{X_E(E^{NP}_m)}{\lambda }, \end{aligned}$$

(18)

$$\begin{aligned}&w^{FP}_m=pQ_L(E^{FP}_m,X^{FP}_m)=f(E^{FP}_m), \end{aligned}$$

(19)

where we define

$$\begin{aligned} f(E)\equiv \tau \gamma (V_E+V_XX_E), \end{aligned}$$

(20)

with $df/dE<0.$¹¹ We have the following lemma.

Lemma 2

At the market equilibrium, it holds that $E^{NP}_m \ne E^{FP}_m$.

Proof

Contrarily, suppose that $E^{NP}_m = E^{FP}_m$. However, (18) and (19) produce $\frac{X_E(E^{NP}_m)}{\lambda }=0$, which contradicts our assumption $X_{E}>0$. Therefore, we prove the claim of the lemma. $\square$

We propose the following:

Proposition 2

If the wildlife population does not decrease marginal agricultural production, that is, $Q_{LX}\ge 0$, then employment, the wage rate, and the utility of locals as well as the wildlife population at the market equilibrium are higher under the non-profit park agency than under the for-profit park agency, that is, $E^{NP}_m>E^{FP}_m, w^{NP}_m>w^{FP}_m, u^{NP}_m>u^{FP}_m$ and $X^{NP}_m>X^{FP}_m$.

Proof

See “Appendix 2”. $\square$

The next proposition deals with the case of $Q_{LX}<0$, for which we define the function g(E) as

$$\begin{aligned} g(E)\equiv Q_{L}(H-E, X(E)), \end{aligned}$$

(21)

where $g'(E)=-Q_{LL}+Q_{LX}X_E\gtreqless 0$ when $Q_{LX}<0$.

Proposition 3

Suppose that the wildlife population decreases marginal agricultural production, that is, $Q_{LX}< 0$. If $g'(E)<0$ and $X_E$ is sufficiently small, then it holds that $E^{FP}_m> E^{NP}_m$, $X^{FP}_m> X^{NP}_m$, but $w^{NP}_m>w^{FP}_m$ and $u^{NP}_m>u^{FP}_m$. If $g'(E)\ge 0$ or $g'(E)<0$ with a slightly larger $X_E$, then $E^{NP}_m>E^{FP}_m$, $X^{NP}_m> X^{FP}_m$, but $w^{NP}_m\gtrless w^{FP}_m$ and $u^{NP}_m \gtrless u^{FP}_m$.

Proof

See “Appendix 2”. $\square$

Proposition 3 suggests that although the non-profit agency always demands more labor than the for-profit agency, it does not always result in the employment of more labor under the labor market equilibrium if $g'(E)<0$ and $X_E$ is small. This unanticipated finding suggests that there is a special case in which the non-profit agency does not lead to a higher wildlife population at the market equilibrium, which we refer to as Case A. By contrast, we call the case in which $E^{NP}_m> E^{FP}_m$ holds, that is, when $g'(E)\ge 0$ or $g'(E)<0$ with a slightly larger $X_{E}$, Case B. Therefore, the marginal effect of wildlife on agricultural production determines whether the for-profit agency can increase the wildlife population more than the non-profit agency. Table 2 summarizes Propositions 2 and 3.

Table 2 Summary of the results

Before ending this section, we would like to mention the assumptions about the labor market. This study assumes that the labor market is perfectly competitive. However, it may be more realistic to assume that the agency is a monopsonist because there is only one labor-demanding entity (i.e., the national park). Even if we assume that the labor market is monopsonistic, we confirm that all the conclusions are valid if certain conditions are satisfied.¹²

4 Social Optimum

We have thus far compared the equilibria under the non-profit and for-profit agencies. However, these equilibria do not reflect the livelihood of locals. In particular, if the wildlife population damages agricultural products, ignoring locals’ well-being would lead to equilibria considered as undesirable solutions for the local community. In this sense, it is worthwhile comparing the two equilibria with the social optimum.

Consider a social planner, who aims to maximize the social benefits of the wildlife population and the utility of locals. Accordingly, we define the social welfare function as $W=\eta ( X)+u(M)$, where $\eta ( X)$, with $\eta '>0$, reflects the existence value of wildlife. This value is positively related to the wildlife population.

The local social planner optimizes the resource allocation by determining the levels of E provided by locals and T, which is the transfer of income from the park to locals. Thus, the problem for the social planner is

$$\begin{aligned} \underset{T,E }{\text {max}}{} &\quad {} \eta ( X(E))+u(T+pQ(L,X(E))) \\\text {s.t.}{} &\quad {} \tau V(E,X;\tau )\ge T+I,\\ \end{aligned}$$

(22)

where $I=(1-\gamma )V$. The Lagrangian function is $\mathscr {L}= \eta ( X(E))+u(T+pQ(L,X(E))) +\mu (\gamma \tau V(E,X;\tau )- T)$, where $\mu$ is the Lagrange multiplier. The first-order conditions for the social planner are

$$\begin{aligned}&u'=\mu , \end{aligned}$$

(23)

$$\begin{aligned}&u'p(Q_{L}- Q_X X_E) =\mu \gamma \tau (V_E+ V_X X_E)+ \eta ' X_E. \end{aligned}$$

(24)

(24) shows that $E^s$ (here, the superscript “s” stands for the social optimum) is determined at the level at which the marginal effects of labor on agricultural production (left-hand side) equal the sum of the marginal revenue of the park and the marginal value of the wildlife population (right-hand side).

We then compare the local social optimum with the market equilibria based on the following equations:

$$\begin{aligned}&pQ_{L}(E^s, X^{s}) = \gamma \tau (V_E+ V_X X_E)+ \left( \frac{\eta '}{u'} + pQ_X\right) X_E(E^s), \end{aligned}$$

(25)

$$\begin{aligned}&pQ_L(E^{NP}_m,X^{NP}_m)= \tau \gamma (V_E+V_XX_E)+\frac{X_E(E^{NP}_m)}{\lambda }, \end{aligned}$$

(26)

$$\begin{aligned}&pQ_L(E^{FP}_m,X^{FP}_m)= \tau \gamma (V_E+V_XX_E). \end{aligned}$$

(27)

Note that all the above equations contain different terms on the right-hand side, which causes the difference between the social optimum and non-profit or for-profit equilibrium.

That is, the market solutions may fail to achieve the social optimum, as the marginal social welfare of wildlife, $(\eta ' + u' pQ_X)X_E$, is ignored by park agency. However, there are various cases where the social optimum, non-profit and for-profit equilibria do not coincide. Table 3 summarizes these results, showing that the magnitude of the relationship between the market equilibria and social optimum depends critically on certain conditions. “Appendix 3” explains the details of the results.

Table 3 Comparison of the market equilibria and social optimum

Nevertheless, the social optimum can be reached by setting a tax or subsidy on the wage rate depending on the management style of the agency (non-profit or for-profit) under which each equilibrium achieves the social optimum. For example, the social planner may introduce a subsidy or tax t on wage rate w such that the labor supply of locals becomes

$$\begin{aligned} w+t=pQ_{L} \end{aligned}$$

(28)

where t is subsidy (tax) if $t>(<)0$.

In case of a for-profit agency, on the one hand, if the social planner specifies t as $t^{FP}$ such that

$$\begin{aligned} t^{FP}=X_E^{s}\left( pQ_X^{s}+\frac{\eta '}{u'}\right) , \end{aligned}$$

(29)

where $X_{E}^{s}$, $Q_{X}^{s}$, and $\eta '/u'$ are evaluated at $E^{s}$, the market equilibrium achieves the social optimum. In case of a non-profit agency, on the other hand, the following $t^{NP}$ implements the social optimum:

$$\begin{aligned} t^{NP}=\gamma \tau \left[ (V_E^s+ V_X^s X_E^s)-\frac{V^s}{E^s}\right] + X_E^{s}\left( pQ_X^{s}+\frac{\eta '}{u'}\right) . \end{aligned}$$

(30)

The calculation process is provided in “Appendix 3”. $t^{FP}$ is a subsidy when $Q_{X} \ge 0$, while it can be a tax otherwise, depending on the magnitude of the relationship between $Q_{X}$ and $\frac{\eta '}{u'}$. However, whether $t^{NP}$ is positive or negative is rather complicated.

5 Numerical Simulation

In this section, we numerically show the transition dynamics of the wildlife population and CCS. To simplify the simulation, we use a discrete-time model instead of a continuous one under the specifications of our functions.¹³ Recall that the following two equations form the dynamic system:

$$\begin{aligned}&X_{t+1}-X_t=F(X_t,C_t)-\alpha V(E_t,X_t;\tau ) \end{aligned}$$

(31)

$$\begin{aligned}&C_{t+1}-C_t=(1-\gamma )\tau V(E_t,X_t;\tau )-\delta C_t, \end{aligned}$$

(32)

where the initial values of $X_0$ and $C_0$ are given. The functional forms used to describe the dynamic system are presented in “Appendix 4”.

Using the given parameter values, we can now numerically solve the time paths and steady states for the system, where we assume that the non-profit agency at time t maximizes $E_{t}$ subject to $X_t$ and $C_t$. Similarly, the for-profit agency maximizes its profit under the same condition following the optimization behaviors at each steady state. Table 4 summarizes the baseline values of the parameters used in the numerical simulation as well as the steady-state values. These parameter values are selected for illustrative purposes. We then use MATLAB to conduct all the computations.

Table 4  Summary of the parameter values and results

Figure 2 shows the time paths of $X_t$, $C_t$, and $E_t$ under the non-profit and for-profit agencies. Recall that we consider that involving more local labor attracts more visitors, but also increases the negative impact of tourism on the wildlife population. Consequently, as illustrated in Fig. 2a, c, although the difference between $E^{NP}_t$ and $E^{FP}_t$ is remarkably large over time, the difference between $X^{NP}_t$ and $X^{FP}_t$ could be relatively small. We also observe that the $X_t$, $C_t$, and $E_t$ paths are monotonically increasing and converging to the steady states when $X_0=15$ and $C_0=2$.

Fig. 2

Time series of wildlife population, CCS, and local labor under two parks, $X_0=15$ and $C_0=2$

However, if the initial value of the wildlife population $X_0$ is higher, then the time paths of $X_t$ and $E_t$ do not monotonically increase. Figure 3 shows the time paths under $X_0=28$ and $C_0=2$. When the initial value of the wildlife population is high and close to the steady-state value, a larger negative effect of tourism arises by attracting more tourists. During this period, it is thus optimal for the park agency to reduce the involvement of locals to mitigate this negative impact (Fig. 3c). However, the decline ceases and the wildlife population quickly starts to increase because of the accumulation of CCS. A higher value of initial CCS can mitigate this negative effect of tourists. For example, even in the case of $X_0=28$, if the value of $C_0$ increases from 2 to 5, then the time paths of $X_t$ and $E_t$ monotonically increase under both agencies, as illustrated in Fig. 4.

Fig. 3

Time series of wildlife population, CCS, and local labor under two parks, $X_0=28$ and $C_0=2$

Fig. 4

Time series of wildlife population, CCS, and local labor under two parks, $X_0=28$ and $C_0=5$

Furthermore, it is possible that $X^{NP}_t<X^{FP}_t$ in the time paths, even though the steady state of the non-profit agency exceeds that of the for-profit one (i.e., $X^{NP}_m>X^{FP}_m$). Figures 2a, 3a and 4a all show that during the early periods, the wildlife population under the for-profit agency exceeds that under the non-profit agency because the latter maximizes E. Hence, it boosts tourism more than under the for-profit agency. This initially leads to a larger negative effect of tourism, with the higher rate of the accumulation of CCS offsetting this negative effect in the short run. The time paths of CCS monotonically increase in all the above cases.

We also demonstrate the welfare of locals on the time path under the baseline parameter values. Figure 5a, b show that the non-profit agency always raises local welfare more than the for-profit one. Moreover, the welfare of locals decreases monotonically over time because the wildlife population increases and thus its negative impact on agricultural production also increases, which leads to a continuous decrease in the agricultural income of locals. Contrarily, if we consider the case in which the wildlife population increases agricultural production, then the time paths of the welfare of locals increase monotonically, as shown in Fig. 5b.

Fig. 5

Time series of local’s utility under two parks, $X_0=15$ and $C_0=2$

Finally, as discussed in the previous section, the relationship between the social optimum and market equilibria critically depends on the parameter values in $\eta (X)$ and u(M). Figures 2a, 3a and 4a demonstrate the case in which $X^{NP}_m>X^{s}>X^{FP}_m$. If we increase the weight of the social benefits of wildlife in the social welfare function by changing the value of the parameter $a_4$, then the value of $X^s$ increases beyond $X^{NP}_m$ (and vice versa).

6 Discussion and Concluding Remarks

Biodiversity conservation projects that consider locals’ interests are designed to conserve the ecosystem and advance local development by including the local population in the operations of national parks and by transferring the benefits received from the creation of such parks to local communities. However, the existing economics literature on such conservation projects largely ignores the direct inclusion of locals by assuming that monetary transfers are provided to them without their employment in such projects. The exception is Fischer et al. (2010), although they still ignore the involvement of locals in tourism as well as the negative effects of tourism on biodiversity. To overcome this limitation, this study assumes that a national park implements a conservation project that incorporates locals into its tourism operations, where tourism is assumed to harm the wildlife population. Moreover, considering that national parks are not always for-profit entities, this study compares the effectiveness of this conservation attempt under a non-profit agency with that under a for-profit agency.

When aiming to conserve biodiversity by establishing protected areas, who runs and manages these areas can be a crucial question. One might expect a non-profit park agency to better conserve biodiversity than a for-profit one since the former places biodiversity conservation as its highest priority. However, the results of this study suggest that this is only true when the wildlife population is not a pest for locals. In this case, the non-profit agency enhances not only the wildlife population, but also the utility of locals as well as social welfare.

By contrast, if the wildlife population is a pest, the for-profit agency could better conserve biodiversity than the non-profit one. However, in this case, we show that the utility of locals is always higher under the non-profit agency than under the for-profit one (Case A in Table 2). Meanwhile, a case also exists in which the wildlife population is higher under the non-profit agency, whereas the utility of locals is lower (Case B in Table 2). Therefore, a trade-off exists between conservation and improving the utility of locals. In each case, however, the evaluation for social welfare is ambiguous; it could be higher, equivalent, or lower under the non-profit agency depending on the functions of the existing value of wildlife and utility of locals. That is, each equilibrium tends to differ from the social optimum unless certain conditions are all met.

Agricultural damage by wildlife, which significantly decreases agricultural production around protected areas, is a principal cause of the conflicts between locals and wildlife (McShane and Wells 2004).¹⁴ Therefore, the case in which wildlife has a negative externality seems closer to the reality of protected areas. In this sense, deploying a for-profit management style could improve both conservation outcome and the well-being of locals considerably, while these two objectives are not achieved simultaneously under the above-stated trade-off.

Our results crucially depend on the rational behavior of locals. When the park hires non-locals instead of locals, the results may be simplified if the opportunity cost of non-locals participating in the park’s operations is the prevailing wage rate outside the park, say, $\bar{w}$. In this case, the equilibrium wage rate for park operations is also $\bar{w}$. Hence, the labor demand of the park solely determines employment at the wage rate $\bar{w}$. Since this leads to the result only for $Q_{LX}=0$, employment and the wildlife population under the non-profit agency are always higher than those under the for-profit one.

Although this study focuses on the effect of involving locals in national park tourism on biodiversity conservation, we provide the following implications. First, since our model revealed the various cases in which a non-profit national park agency performs better, our results might imply that as long as there is no budget deficit, governments should not attach too much importance to the revenue or profit of national parks when evaluating their performance. Second, although tourism can raise local development by generating income for local communities through job creation, ecotourism may not benefit local communities or conservation because of the low wages (Zacarias and Loyola 2017). Our model suggests that if locals make their own decisions with regard to working in national parks, the inclusion of locals in tourism could improve their utility.

Furthermore, in the real world, the objective function of a non-profit national park may not necessarily differ from that of a social planner. In other words, the national park agency might also take local development into consideration. Nevertheless, in the context of traditional national parks, the interests of locals have often been ignored from park management before the implementation of ICDPs or CBNRM initiatives (Wells et al. 1992). This implies that the objective function of a non-profit park agency can be formulated differently compared to that of a social planner who considers the well-being of the local community, as reflected in the study.

Some future research avenues are worth noting. First, a quantitative analysis of the role played by a national park in employing local people could be important. However, such an analysis would only be possible by collecting real-world empirical data, which are not currently available to the best of our knowledge. Second, the present study ignored the impact of agriculture outside the park on biodiversity within the park. Using natural resources such as water in agricultural production may conflict with the needs of the wildlife population. Including this aspect may thus change the results by altering the bio-growth function.

Third, although we assumed that the national park is financially self-dependent, many national parks receive budgets from governments. Therefore, the size of the budget could influence the goals of the park and including this aspect would change the budget constraint and derived results. Finally, poaching is regarded as a serious threat to biodiversity conservation in protected areas (Skonhoft and Solstad 1996). Although we implicitly considered the existence of poaching in relation to CCS, we did not explicitly include the behavior of poachers in the model. As a national park may hire more workers to prevent poaching, it may thus be interesting to study biodiversity conservation projects by considering the aspect of poaching in two types of labor markets (i.e., tourism and anti-poaching efforts).

Appendices

Appendix 1: Local Stability

Consider the dynamic system in (1) and (4) for a given E. Let $(\bar{X},\bar{C})$ represent the steady state. The conditions for local stability are

$$\begin{aligned} \textrm{Tr}A&= F_{X}-\alpha V_X-\delta <0 \end{aligned}$$

(A1)

$$\begin{aligned} |A|&= -\delta (F_{X}-\alpha V_X)-F_{C} (1-\gamma )\tau V_{X}>0, \end{aligned}$$

(A2)

where

$$\begin{aligned} A= \left( \begin{array}{cc} F_{X}-\alpha V_X &{} F_{C} \\ (1-\gamma )\tau V_{X} &{} -\delta \\ \end{array} \right) \end{aligned}$$

(A3)

Appendix 2: Comparison of $E^{NP}_m$ and $E^{FP}_m$

Proof of Proposition 2

Since we have Lemma 2, to suppose the contrary leads to $E^{FP}_m>E^{NP}_m$ so that $X^{FP}_m>X^{NP}_m$ for $Q_{LX}\ge 0$. This supposition implies that

$$\begin{aligned} pQ_L(E^{FP}_m,X^{FP}_m)\ge pQ_L(E^{FP}_m,X^{NP}_m)>pQ_L(E^{NP}_m,X^{NP}_m). \end{aligned}$$

(A4)

However, if $E^{FP}_m>E^{NP}_m$, owing to $f'(E)<0$, we obtain

$$\begin{aligned} f(E^{NP}_m)=pQ_L(E^{NP}_m,X^{NP}_m)- \frac{X_E(E^{NP}_m)}{\lambda }>pQ_L(E^{FP}_m,X^{FP}_m)=f(E^{FP}_m), \end{aligned}$$

(A5)

which contradicts (A4). Hence, it must be $E^{NP}_m>E^{FP}_m$ so that $X^{NP}_m>X^{FP}_m$ by $X_{E}>0$. Based on this result, we have $pQ_L(E^{NP}_m,X^{NP}_m)>pQ_L(E^{FP}_m,X^{FP}_m)$, and thus $w^{NP}_m> w^{FP}_m$. The total income of locals under the non-profit agency is

$$\begin{aligned} \begin{aligned} M^{NP}_m&= w^{NP}_m E^{NP}_m+\int _{E^{FP}_m}^{H}pQ_L(E, X^{NP}_m)dE\\&= w^{NP}_m E^{FP}_m+\int _{E^{FP}_m}^{E^{NP}_m}pQ_L(E^{NP}_m, X^{NP}_m)dE+\int _{E^{NP}_m}^{H}pQ_L(E, X^{NP}_m)dE. \end{aligned} \end{aligned}$$

(A6)

The total income under the for-profit agency is

$$\begin{aligned} \begin{aligned} M^{FP}_m&= w^{FP}_m E^{FP}_m +\int _{E^{FP}_m}^{H}pQ_L(E, X^{FP}_m)dE\\&= w^{FP}_m E^{FP}_m +\int _{E^{FP}_m}^{E^{NP}_m}pQ_L(E, X^{FP}_m)dE +\int _{E^{NP}_m}^{H}pQ_L(E, X^{FP}_m)dE. \end{aligned} \end{aligned}$$

(A7)

Since $\partial Q_L/\partial E=-Q_{LL}>0$, $\int _{E^{FP}_m}^{E^{NP}_m}pQ_L(E^{NP}_m, X^{NP}_m)dE >\int _{E^{FP}_m}^{E^{NP}_m}pQ_L(E, X^{FP}_m)dE$, so $u^{NP}_m> u^{FP}_m$ because $M^{NP}_m> M^{FP}_m$. $\square$

Proof of Proposition 3

First, suppose that $E^{FP}_m>E^{NP}_m$ so that $X^{FP}_m>X^{NP}_m$. When $g'(E)\ge 0$, it implies $pQ_L(E^{FP}_m,X^{FP}_m)\ge pQ_L(E^{NP}_m,X^{NP}_m)$. However, this means that

$$\begin{aligned} pQ_L(E^{FP}_m,X^{FP}_m)>pQ_L(E^{NP}_m,X^{NP}_m)-\frac{X_E(E^{NP}_m)}{\lambda }. \end{aligned}$$

(A8)

Hence, $f(E^{FP}_m)> f(E^{NP}_m)$ must hold, which implies that $E^{NP}_m> E^{FP}_m$ because of $f'(E)<0$. However, this contradicts our earlier supposition. Therefore, $E^{NP}_m>E^{FP}_m$ must hold under $g'(E)\ge 0$.

Second, suppose that $E^{FP}_m>E^{NP}_m$, but under $g'(E)<0$. Then, we have $pQ_L(E^{FP}_m,X^{FP}_m)<pQ_L(E^{NP}_m,X^{NP}_m)$ from $g'(E)<0$. This supposition is feasible only when $\frac{X_E(E^{NP}_m)}{\lambda }$ is sufficiently small such that the following holds:

$$\begin{aligned} pQ_L(E^{FP}_m,X^{FP}_m)<pQ_L(E^{NP}_m,X^{NP}_m)-\frac{X_E(E^{NP}_m)}{\lambda }. \end{aligned}$$

(A9)

Otherwise, we obtain a contradiction similar to (A8), meaning that $E^{FP}_m<E^{NP}_m$ holds.

With respect to the market-clearing wage rate, when $E^{FP}_m> E^{NP}_m$ holds, (18) and (19) with $g'(E)<0$ imply that $w^{NP}_m>w^{FP}_m$. Meanwhile, if $E^{NP}_m> E^{FP}_m$, then $w^{NP}_m\gtrless w^{FP}_m$. Based on this observation, we can discuss $M^{NP}_m$ and $M^{FP}_m$ in three cases.

Case 1: When $E^{FP}_m> E^{NP}_m$ and $w^{NP}_m>w^{FP}_m$, income under the non-profit agency is

$$\begin{aligned} \begin{aligned} M^{NP}_m= w^{NP}_m E^{NP}_m+\int _{E^{NP}_m}^{E^{FP}_m}pQ_L(E, X^{NP}_m)dE+\int _{E^{FP}_m}^{H}pQ_L(E, X^{NP}_m)dE. \end{aligned} \end{aligned}$$

(A10)

Under the for-profit agency, income is

$$\begin{aligned} \begin{aligned} M^{FP}_m= w^{FP}_m E^{NP}_m +\int _{E^{NP}_m}^{E^{FP}_m}pQ_L(E^{FP}_m, X^{FP}_m)dE +\int _{E^{FP}_m}^{H}pQ_L(E, X^{FP}_m)dE. \end{aligned} \end{aligned}$$

(A11)

Since $\partial Q_L/\partial E>0$, we have $\int _{E^{NP}_m}^{E^{FP}_m}pQ_L(E, X^{NP}_m)dE>\int _{E^{NP}_m}^{E^{FP}_m}pQ_L(E^{NP}_m, X^{NP}_m)dE$. Then, from $w^{NP}_m>w^{FP}_m$, that is, $\int _{E^{NP}_m}^{E^{FP}_m}pQ_L(E^{NP}_m, X^{NP}_m)dE =w^{NP}(E^{FP}-E^{NP}) > w^{FP}(E^{FP}-E^{NP}) = \int _{E^{NP}_m}^{E^{FP}_m}pQ_L(E^{FP}_m, X^{FP}_m)dE$, we conclude that $M^{NP}_m> M^{FP}_m$.

When $E^{NP}_m> E^{FP}_m$, we have $w^{FP}_m>w^{NP}_m$ when $g'(E)<0$ and $w^{NP}_m\ge w^{FP}_m$ when $g'(E)\ge 0$. In both cases, $M^{NP}_m$ and $M^{FP}_m$ have the same expression as in (A6) and (A7).

Case 2: When $E^{NP}_m> E^{FP}_m$ under $g'(E)<0$, then $w^{FP}_m> w^{NP}_m$ holds. (A6) and (A7) lead to $M^{FP}_m> M^{NP}_m$ since $\int _{E^{FP}_m}^{E^{NP}_m}pQ_L(E, X^{FP}_m)dE> \int _{E^{FP}_m}^{E^{NP}_m}pQ_L(E^{FP}_m, X^{FP}_m)dE =w^{FP}(E^{NP}-E^{FP})>w^{NP}(E^{NP}-E^{FP})=\int _{E^{FP}_m}^{E^{NP}_m}pQ_L(E^{NP}_m, X^{NP}_m)dE$.

Case 3: When $E^{NP}_m> E^{FP}_m$ under $g'(E)\ge 0$, we have $w^{NP}_m\ge w^{FP}_m$. Although $w^{NP}_m E^{FP}_m \ge w^{FP}_m E^{FP}_m$, we have $\int _{E^{NP}_m}^{H}pQ_L(E, X^{NP}_m)dE<\int _{E^{NP}_m}^{H}pQ_L(E, X^{FP}_m)dE$ but $\int _{E^{FP}_m}^{E^{NP}_m}pQ_L(E^{NP}_m, X^{NP}_m)dE\gtrless \int _{E^{FP}_m}^{E^{NP}_m}pQ_L(E, X^{FP}_m)dE$ because of $Q_{LX}<0$. Therefore, the magnitude of the relationship between $M^{NP}_m$ and $M^{FP}_m$ (i.e., $u^{NP}_m$ and $u^{FP}_m$) is ambiguous. $\square$

Appendix 3: Social Optimum and the Tax/Subsidy

If $Q_{LX} \ge 0$ or $Q_{LX} <0$ with a sufficiently small $X_{E}$, so that $g'(E) \ge 0$ in (21), $E^s>E^{FP}_m$ holds. The magnitude of the relationship between $E^{s}$ and $E^{NP}$, however, depends on that between $\frac{X_E(E^{NP}_m)}{\lambda }$ and $\left( \frac{\eta '}{u'}+ pQ_X\right) X_E(E^s)$. It holds if $\frac{\eta ' }{u'}+ pQ_X \gtreqless \frac{1}{\lambda }$ , then, $E^s\gtreqless E^{NP}_m$.

Meanwhile, when $g'(E) < 0$, which holds when $Q_{LX} <0$ with a large $X_{E}$, the relationship becomes more complicated, as shown by the argument on page 17 about the magnitude of the relationship between $E^{NP}_m$ and $E^{FP}_m$.

We then show the determination of a tax/subsidy scheme. Recall that if the social planner introduces a subsidy or tax on wage rate w, the labor supply of locals becomes

$$\begin{aligned} w^{}+t=pQ_{L}^{}, \end{aligned}$$

(A12)

The market equilibrium under government intervention is expressed by (16) and (A12), as

$$\begin{aligned} pQ_L-t= \gamma \tau (V_E+ V_X X_E). \end{aligned}$$

(A13)

Let us define t as

$$\begin{aligned} t=X_E\left( pQ_X+\frac{\eta }{u'}\right) , \end{aligned}$$

(A14)

then (A13) leads to

$$\begin{aligned}&pQ_L-X_E\left( pQ_X+\frac{\eta }{u'}\right) = \gamma \tau V_E+ \gamma \tau V_X X_E, \end{aligned}$$

(A15)

$$\begin{aligned}&\quad \Leftrightarrow X_E(\eta +u'pQ_X+u'\gamma \tau V_X) =u'pQ_{L}-u' \gamma \tau V_E. \end{aligned}$$

(A16)

This means that if the social planner specifies t as $t^{FP}$ such that

$$\begin{aligned} t^{FP}=X_E^{s}\left( pQ_X^{s}+\frac{\eta '}{u'}\right) , \end{aligned}$$

(A17)

where $X_{E}^{s}$ and $Q_{X}^{s}$ are evaluated at $E^{s}$, the market equilibrium achieves the social optimum because we observe that (A16) is the same as (24).

To implement the social optimum in the case of a non-profit national park, let us introduce a tax/subsidy $t^{NP}$ such that

$$\begin{aligned} t^{NP}=\gamma \tau \left[ (V_E^s+ V_X^s X_E^s)-\frac{V^s}{E^s}\right] + X_E^s\left( pQ_X^s+\frac{\eta ' }{u'}\right) . \end{aligned}$$

(A18)

Under this scheme, the market equilibrium under a non-profit park agency is

$$\begin{aligned} pQ_L=\frac{\gamma \tau V}{E}+t^{NP}. \end{aligned}$$

(A19)

Therefore, the labor market achieves the social optimum $\left( {pQ_{L} = \gamma \tau \left( {V_{E} + V_{X} X_{E} } \right) + X_{E} \left( {pQ_{X} + \frac{{\eta \prime }}{{u\prime }}} \right)} \right)$.

Appendix 4: Functional Forms for Simulation

We specify the functions F, V, Q, $\eta (X(E))$, and u(M) as

$$\begin{aligned}&F(X_t,C_t)=rX_t(1-X_t/K)-hX_tC_t^\theta \end{aligned}$$

(A20)

$$\begin{aligned}&V(E_t,X_t;\tau )=AE_t^{a_1}X_t^{a_2}(1+\tau )^{a_3} \end{aligned}$$

(A21)

$$\begin{aligned}&Q(L_t,X_t)=(1-dX_t)(H-E_t)^\beta \end{aligned}$$

(A22)

$$\begin{aligned}&\eta (X(E))=a_4\ln (1+X(E)) \end{aligned}$$

(A23)

$$\begin{aligned}&u(M)=a_5M^{a_6}. \end{aligned}$$

(A24)

All the assumptions about F, V, Q, $\eta (X(E))$, and u(M) are satisfied in the specified functions.