Abstract
This paper addresses the verification of non-blockingness for modular discrete-event systems, i.e., discrete-event systems that are composed from component models. For such systems, the explicit construction of a monolithic representation turns out intractable for relevant applications, since such a construction in general is of exponential cost w.r.t. the number of components. One well established approach to circumvent the need for a monolithic representation for the verification task at hand is to alternate (a) the substitution of individual components by abstractions and (b) the composition of only a small number of strategically chosen components at a time. When successful, one ends up with a single moderately sized automaton which does not represent the overall behaviour in any detail but which does block if and only if the original modular system fails to be non-conflicting. This approach is referred to as compositional verification and originates from the field of process algebra with more recent adaptations to finite automata models. The main contribution of the present study is the development of a number of abstraction rules valid for compositional verification of non-conflictingness in the presence of global event priorities, i.e., where high priority events from one component possibly preempt events with lower priority of all components.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Considering discrete-event systems that are representable as finite automata, a well studied liveness property is non-blockingness, i.e., the ability of the system to attain an accepted configuration from any reachable state. For example, in the context of supervisory control theory (Ramadge and Wonham 1987), where marked states are used to represent task-completion, non-blockingness is a desired closed-loop property.
For a moderately sized single automaton, non-blockingness can be verified by a straightforward enumeration-based reachability analysis. In principle, this approach is also applicable to modular systems consisting of a number of component models since the overall behaviour can again be represented as a single automaton. The construction of such a monolithic representation for the purpose of verification, however, does not scale well with the number of components, and, for relevant applications tends to turn out infeasible. The situation for off-line analysis contrasts that for implementing the overall behaviour by computer software and hardware, e.g. by a programmable logic controller (PLC) in an industrial automation context: the latter does not require a monolithic representation; see e.g. Moor (2022). This motivates the interest in methods for the verification of non-blockingness for modular discrete-event systems that likewise circumvent an explicit monolithic representation.
One well established approach to address this situation is referred to as compositional verification. Inspired by the testing theory (Nicola and Hennessy 1984), compositional non-blockingness verification attempts to abstract each component model while preserving non-blockingness when composed with any arbitrary other test-automaton. This of course includes the special case of the test-automaton to match the composition of the remaining component models. Such an abstraction is called conflict equivalent. Specifically for automata representations of component models and their synchronous composition, various qualifying abstraction rules have been proposed in the literature; see e.g. Flordal and Malik (2009); Su et al. (2010); Ware and Malik (2012); Pilbrow and Malik (2015); Mohajerani et al. (2016). Once abstraction rules have been applied to the component models, one strategically chooses a small number of components and substitutes them with their actual synchronous composition. While this increases the state count, it also potentially decreases the number of shared events. In turn, a subsequent substitution via conflict equivalent abstractions is expected to again decrease the state count. The two forms of substitutions are then alternated until only one automaton is left. The latter automaton is tested for non-blockingness. By using only conflict-preserving abstractions, the result carries over to the original modular system. Clearly, one does not expect to beat computational complexity and the overall procedure may need to be aborted due to exceeding available computational resources. However, the literature cited above demonstrates by a number of practical case studies the applicability to relevant large scale systems with an impressive computational performance.
In the present paper, we consider the situation where, besides the synchronous composition of all automata, the global behaviour of the system is additionally affected by event priorities (Lúttgen 1998; Cleaveland et al. 2007). In this scenario, each event is associated with an integer attribute to represent its priority. At any global state, events with higher priority preempt those with lower priority; i.e., events become disabled whenever events with higher priority are enabled. In particular, this includes the case where the preempting event is private to some other module. Our main technical contribution are a number of abstraction rules which turn out conflict equivalent and, hence, can be used for compositional verification with event priorities.
We envisage two main use cases for our findings. First, consider the verification of a control algorithm that is implemented by a PLC. A common approach here is to preprocess the PLC code to obtain a more formal representation. Inspecting the semantics of sequential function charts (SFCs) as specified in IEC 61131-3, we observe distinguished classes of events with different priorities to preempt each other, e.g. reading from line levels, execution of activity code, reconfiguration of tokens, writing to line levels; see also (Blech and Ould Biha 2011) for formal SFC semantics. For a second use case, consider the scenario where a modular discrete-event system has been synthesised by formal methods to enforce a language inclusion specification next to a non-blocking closed loop. Here, we may after the fact want to introduce priorities to achieve a consistent and repeatable behaviour, which relates to the command selection problem in Malik (2003). When introducing priorities after synthesis one needs to verify whether the non-blockingness from the original design is maintaned. This is of particular interest when implementing a modular supervisor by converting the component models to executable PLC code using a code generator which explicitly or implicitly assigns priorities; see e.g. Moor (2022); Fabian and Hellgren (1998); Qamsane et al. (2016); Verbakel et al. (2022).
This paper is an extended version of our earlier conference contribution (Tang and Moor 2022) in that we now (i) include relevant technical lemmata to formally establish our main results and (ii) generalise the acceptance condition of automata to a multitasking setup, i.e., instead of having one set of accepted configurations (Flordal and Malik 2009), we now consider multiple sets of accepted configurations, all of which required to be reachable from any reachable state (Hering de Queiroz et al. 2005; Schmidt et al. 2007). The organisation is as follows. In Section 2, we formally introduce event priorities and derive a suitable form of synchronous composition by shaping the overall behaviour. This discussion leads to an adapted notion of conflict equivalence w.r.t. prioritised events. In Section 3, we derive conflict-preserving abstractions as our main technical contribution. For this, we essentially adapt the abstraction rules proposed by the literature to account for prioritised events; see also Flordal and Malik (2009); Su et al. (2010); Ware and Malik (2012); Pilbrow and Malik (2015). Specifically, we derive a partial variant of the shaping operator which preserves conflicts; we discuss how to treat silent live-locks; we make use of a prioritised variant of weak bisimulation Lúttgen (1998) which in turn leads to the redundant silent step rule; and we propose a prioritised variant of incoming equivalence which in turn leads to the active event rule, the silent continuation rule, the only silent incoming/outgoing rules and finally adapt the certain conflicts rule. In Section 4, we evaluate our results by a scalable example of concatenated conveyor belts.
2 Preliminaries
We introduce some basic notation in order to address discrete-event systems with prioritised events. We then discuss synchronous composition for modular systems up to the point where we are in the position to formally characterise conflict-preserving abstractions. The identification of such abstractions then becomes the technical problem to be addressed in the subsequent section.
2.1 Basic notation
Events and strings Consider a universe of symbols \(\mathfrak {A}\) also referred to as events, which are the basic elements to represent discrete-event dynamics. All events throughout this paper are considered elements of \(\mathfrak {A}\). A string s is either a finite sequence of events or the empty string \(\epsilon \notin \mathfrak {U}\). The concatenation of two strings s and t is denoted st, specifically, we have \(\epsilon s = s= s\epsilon \) for any string s. For two strings s and r, s is considered a prefix of r if there exists some string t such that \(st=r\); this is denoted \(s\leqslant r\). The Kleene closure of a set of events \(A\subseteq \mathfrak {U}\) is denoted \(A^*\) and amounts to the set of all strings constructed from events in A, including the empty string \(\epsilon \). By convention we have \(\emptyset ^*=\{\epsilon \}\) and we write \(A^+\) to exclude the empty string; i.e., \(A^+:=A^*-\{\epsilon \}\). Except that we beforehand declare the universe of all symbols \(\mathfrak {A}\), our notation so far is in line with the textbook (Cassandras and Lafortune 2008).
Priorities We assign a priority to each event from \(\mathfrak {A}\). This is a means of refining execution semantics. When confronting a choice of executing one of multiple enabled transition labeled with events of different priority, preference is given to the highest priority. Technically, we refer to the priority assignment function
as a global entity and priorities are read as ordinal numbers, i.e., \(1\in \mathbb {N}\) is considered the first priority, \(2\in \mathbb {N}\) the second priority, etc. As a greater ordinal number denotes a lower priority, 1 is the unique highest priority. Thus, when writing e.g. \(\textsf{prio}(\sigma )<\textsf{prio}(\rho )\), we indicate that the priority of \(\sigma \) is higher than that of \(\rho \). For convenience, the following notations are used for any event set \(A\subseteq \mathfrak {U}\):
-
events with priority higher (or not lower) than \(n\in \mathbb {N}\) within A\(A^{<n}:=\{\,\alpha \in A\,\vert \, \textsf{prio}(\alpha )<n\,\}\); \(A^{\le n}:=\{\,\alpha \in A\,\vert \, \textsf{prio}(\alpha )\le n\,\}\);
-
events with priority higher (or not lower) than \(\textsf{prio}(\alpha )\) for \(\alpha \in \mathfrak {U}\) within A\(A^{<\alpha }:= A^{<\textsf{prio}(\alpha )}\); \(A^{\le \alpha }:= A^{\le \textsf{prio}(\alpha )}\);
-
the lowest priority value within A\(\textsf{lo}(A):= \left\{ \,\begin{array}{lll} \textsf{max}\{\,\textsf{prio}(\alpha )\,\vert \,\alpha \in A\,\} &{} &{} \text { if } A\ne \emptyset ;\\ 1 &{} &{} \text { if } A=\emptyset . \end{array}\right. \)
Silent events For modular systems, a dedicated representation of behaviour which is internal to an individual module and, hence, irrelevant for synchronisation with the remaining modules, is of a particular interest. Technically, we represent such internal behaviour by distinguished silent events \(\tau \in \Upsilon \subset \mathfrak {U}\). The remaining events \(\sigma \in \mathfrak {U}-\Upsilon \) are considered regular. We use the terminology alphabet to refer to any finite set \(\Sigma \) of regular events, i.e., \(\Sigma \subseteq \mathfrak {U}-\Upsilon \). Only regular events are shown explicitly to the external environment for the purpose of synchronisation. Regarding the priority assignment, it suffices to let \(\Upsilon \) be such that each priority value \(n\in \mathbb {N}\) is bijectively mapped to one event in \(\Upsilon \). We hence use the symbolic representation \(\tau _{(n)}\) for the unique silent event with priority \(n\in \mathbb {N}\) and we then have
Most prominently, our set-up guarantees that each regular event has a unique counterpart silent event with the same priority. Formally, the hiding map \(\textsf{hide}:(\mathfrak {U}-\Upsilon )\rightarrow \Upsilon \) is defined by
for each \(\sigma \in \mathfrak {U}-\Upsilon \). This construct is also utilised in Lúttgen (1998) and constitutes an extension of the more common single distinguished silent event \(\Upsilon =\{\tau \}\) when no priorities are to be considered; see e.g. Milner (1989); Flordal and Malik (2009). In this regard, we utilise natural projection \(\textsf{p}: \mathfrak {U}^*\rightarrow (\mathfrak {U}-\Upsilon )^*\) to remove all silent events from any string \(s\in \mathfrak {U}^*\) Cassandras and Lafortune (2008). Formally, \(\textsf{p}\) is iteratively defined by
2.2 Finite automata
Throughout this paper, we consider discrete-event systems represented by non-deterministic automata, defined as follows.
Definition 2.2.1
A finite automaton is a tuple \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) where
-
Q is the finite state set;
-
\(\Sigma \) is the alphabet;
-
\(\rightarrow \,\subseteq Q\times (\Sigma \cup \Upsilon )\times Q\) is the transition relation;
-
\(Q^\circ \subseteq Q\) is the set of initial states;
-
\(M\subseteq 2^\Sigma \) is the marking set.
Recall that, by convention, \(\Sigma \subseteq \mathfrak {U}-\Upsilon \), i.e. the alphabet consists of regular events only.
Our definition diverges in two aspects when compared e.g. to the textbook (Cassandras and Lafortune 2008). First, we formally declare the alphabet \(\Sigma \) to consist of regular events only while the transition relation also accounts for silent events. This is cosmetic and simplifies the subsequent formal discussion of conflict-preserving abstractions. Second, rather than to have a set of marked states as an acceptance condition we have a set M of sets of terminal events \(\Omega \subseteq \Sigma \). In order to discuss the intended semantics of this construct, we need to introduce adequate notions of reachability and co-reachability. For notational convenience, we write \(x\xrightarrow {\alpha }y\) for \((x,\alpha ,y)\in \, \rightarrow \) and this infix notation is iteratively extended to string-valued labels; namely, (i) for all \(x\in Q\) let \(x\xrightarrow {\epsilon }x\) and (ii) for all \(x,\,z\in Q\), \(s\in \mathfrak {A}^*\) and \(\alpha \in \mathfrak {A}\) such that \(x\xrightarrow {s}y\) and \(y\xrightarrow {\alpha }z\) for some \(y\in Q\) let \(x\xrightarrow {s\alpha }z\). Moreover, we write \(x\xrightarrow {s}\) as a short form for \(x\xrightarrow {s}y\) for some \(y\in Q\).
Definition 2.2.2
Given an automaton \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \), let \(A=\Upsilon \cup \Sigma \). A state \(x\in Q\) is reachable if there exists \(s\in A^*\) such that \(Q^{\circ }\xrightarrow {s}x\). A state \(x\in Q\) is co-reachable if for all \(\Omega \in M\), there exists \(t\in A^*\) and \(\omega \in \Omega \) such that \(x\xrightarrow {t\omega }\). The automaton G is non-blocking if all its reachable states are co-reachable.
Example 1
Consider the automaton \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) given in Fig. 1 with \(\Sigma =\{\sigma ,\rho ,\omega \}\). Clearly, both states are reachable. Two alternative marking sets M are discussed: with \(M=\{\{\sigma ,\omega \},\{\rho ,\omega \}\}\), then G is non-blocking; on the other hand, with \(M=\{\{\sigma ,\omega \},\{\rho \}\}\), G turns out blocking since \(\rho \) cannot be executed any more once state \(\textrm{II}\) is attained.
The definition of non-blockingness in the current paper is a variation of the so-called coloured marking proposed in the context of multitasking supervisory control (Hering de Queiroz et al. 2005; Schmidt et al. 2007). For each \(\Omega \in M\), we require the possibility of executing some \(\omega \in \Omega \). Thus, for the case in Example 1, if we have \(M=\{\{\sigma ,\omega \},\{\rho ,\omega \}\}\), then any state being able to execute \(\omega \) is clearly co-reachable since \(\omega \) appears in both event sets in M. For the special case of \(M=\{\{\omega \}\}\), where \(\omega \in \Sigma \subseteq \mathfrak {A}-\Upsilon \), we have a unique termination event \(\omega \) which matches the more common setting used e.g. in Flordal and Malik (2009). Note that by definition any terminal event in M is required to be regular (non silent).
In support of the subsequent discussion, we introduce some more convenient notation referring to a given automaton \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \).
-
Let \(A_G:=\Sigma \cup \Upsilon \) denote the alphabet of G plus all silent events. The subscript \((\cdot )_G\) is omitted when G is clear from the context.
-
We write \(X\xrightarrow {s}Y\) with \(X,Y\subseteq Q\), \(s\in A^*\), whenever there exist \(x\in X\) and \(y \in Y\) so that \(x\xrightarrow {s}y\).
-
We write
 with \(X,Y\subseteq Q\), \(s\in A^*\), to indicate that \((x,s,y)\not \in \,\rightarrow \) for all \(x\in X\) and \(y\in Y\).
with \(X,Y\subseteq Q\), \(s\in A^*\), to indicate that \((x,s,y)\not \in \,\rightarrow \) for all \(x\in X\) and \(y\in Y\). -
We use short forms \(X\xrightarrow {s}\) and \(G\xrightarrow {s}\) for \(X\xrightarrow {s}Q\) and \(Q^\circ \xrightarrow {s}Q\), respectively.
-
A trace is a sequence of alternating states and events, i.e.
$$\begin{aligned} x_0\xrightarrow {\alpha _1}x_1\xrightarrow {\alpha _2} \cdots \xrightarrow {\alpha _k}x_k. \end{aligned}$$(6) -
The abstract transition relation \(\mathrel {{{\Rightarrow }^{}}{}}\ \subseteq Q\times \Sigma ^*\times Q\) is defined for \(x,y\in Q\), \(s\in \Sigma ^*\) with \(x\mathrel {{{\Rightarrow }^{s}}{}}y\) if and only if there exists \(s'\in A^*\) such that \(\textsf{p}(s')=s\) and \(x\mathrel {{\xrightarrow []{s'}}{}}y\). Regarding reachability, Definition 2.2.2, note that when substituting \(\mathrel {{\xrightarrow []{(\,\cdot \,)}}{}}\) by \(\mathrel {{{\Rightarrow }^{(\,\cdot \,)}}{}}\) and when quantifying over strings from \(\Sigma ^*\) as opposed to \(A^*\), we obtain the same reachable states. Likewise for co-reachability.
-
When concatenating transitions, we may omit the intermediate state, i.e., we write \(x\mathrel {{\xrightarrow []{s}}{}}\mathrel {{{\Rightarrow }^{s'}}{}}y\) if and only if there exists z such that \(x\mathrel {{\xrightarrow []{s}}{}}z\mathrel {{{\Rightarrow }^{s'}}{}}y\).
-
The set of active events in state \(x\in Q\) is given by
$$\begin{aligned} G(x):=\{\,\alpha \in A\,\vert \,x\xrightarrow {\alpha }\,\}. \end{aligned}$$(7) -
The set of active events in state \(x\in Q\) with priority higher (or not lower) than \(n\in \mathbb {N}\) are denoted \(G^{<n}(x):=\{\alpha \in G(x)\,\vert \, \textsf{prio}(\alpha )<n\}\); \(G^{\le n}(x):=\{\alpha \in G(x)\,\vert \, \textsf{prio}(\alpha )\le n\}\).
-
The silent active events in state \(x\in Q\) (with priority higher or not lower than \(n\in \mathbb {N}\)) are denoted \(G_\textrm{slnt}(x):=G(x)\cap \Upsilon \); \(G_\textrm{slnt}^{<n}(x):=G^{<n}(x)\cap \Upsilon \); \(G_\textrm{slnt}^{\le n}(x):=G^{\le n}(x)\cap \Upsilon \);
-
The regular active events in state \(x\in Q\) (with priority higher or not lower than \(n\in \mathbb {N}\)) are denoted \(G_\textrm{rglr}(x):=G(x) - \Upsilon \); \(G_\textrm{rglr}^{<n}(x):=G^{<n}(x) - \Upsilon \); \(G_\textrm{rglr}^{\le n}(x):=G^{\le n}(x) - \Upsilon \);
To formally address the effect of event priorities to the behaviour associated with an automaton, we introduce the following shaping operator. Effectively, it removes all transitions that will be preempted by a transition labeled with a higher-priority event. Although this appears a trivial exercise for a single automaton, it becomes more involved when considering modular systems.
Definition 2.2.3
Given an automaton \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \), the shaping operator \(\mathcal {S}(\cdot )\) is defined as such that \(\mathcal {S}(G) := \langle Q,\Sigma ,\rightarrow ^\mathcal {S},Q^\circ ,M\rangle \) where
Throughout this paper, we concisely write \((\,\cdot \,)^{<\alpha }\) with \(\alpha \in \mathfrak {U}\) as an abreviation for \((\,\cdot \,)^{<\textsf{prio}(\alpha )}\).
Note that after shaping an automaton, some states may become unreachable and that such can be removed.Footnote 1 Specifically, a blocking automaton can become non-blocking after shaping and vice-versa.
Example 2
Consider again the automaton \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) given in Fig. 1 and recall that G is blocking for the marking \(M=\{\{\sigma ,\omega \},\{\rho \}\}\). If either \(\rho \) or \(\sigma \) are assigned a higher priority than \(\omega \), i.e. if \(\textsf{prio}(\rho )<\textsf{prio}(\omega )\) or \(\textsf{prio}(\sigma )<\textsf{prio}(\omega )\), then state \(\textrm{II}\) becomes unreachable and, hence, \(\mathcal {S}(G)\) turns out non-blocking.
2.3 Synchronous composition and non-conflictingness
Turning to modular systems consisting of multiple modules each represented by an automaton, the overall behaviour is commonly defined by the synchronisation of shared events. I.e., any individual module at any time can only take a transition labeled with an event shared with some other modules if all modules that share this event take a respective transition simultaneously. The below definition for the synchronous composition of two modules is a variation of Cassandras and Lafortune (2008) that takes into account our specific setting with distinguished silent events \(\Upsilon \), which on purpose and in contrast to regular events are not subject to synchronisation; see also Milner (1989).
Definition 2.3.1
Given two automata \(G_i=\langle Q_{i},\Sigma _{i}, \rightarrow _{i}, Q^\circ _{i}, M_{i}\rangle \), \(i\in \{1,2\}\), their synchronous composition is defined by \(G_1\parallel G_2:=G:=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) where \(Q:=Q_1\times Q_2\), \(\Sigma :=\Sigma _1\cup \Sigma _2\), \(\rightarrow \,\subseteq Q\times (\Sigma \cup \Upsilon )\times Q\), \(Q^\circ :=Q_1^\circ \times Q_2^\circ \), \(M:=M_1\cup M_2\), with \((x_1,x_2)\xrightarrow {\alpha }(y_1,y_2)\) if and only if either of the below conditions hold:
A transition \((x_1,x_2)\mathrel {{\xrightarrow []{\alpha }}{}}(y_1,y_2)\) is driven by \(G_1\) if \(x_1\mathrel {{\xrightarrow []{\alpha }}{}_{1}}y_1\); likewise, it is driven by \(G_2\) if \(x_2\mathrel {{\xrightarrow []{\alpha }}{}_{2}}y_2\). The events \(\Sigma _1\cap \Sigma _2\) are referred to as shared events, all other events are private events.
Up to trivial renaming of states, the synchronous composition is associative and commutative; see Milner (1989). Given a modular system consisting of k modules represented by the automata \(G_1,\dots ,G_k\), for the purpose of the present paper the overall behaviour is given by \(\mathcal {S}(G_1\parallel \cdots \parallel G_k)\); i.e., event preemption by prioritisation is meant to have a global effect on the overall behaviour. Specifically, the shaping operator \(\mathcal {S}\) does not distribute over synchronous compositions. The terminology of a modular system to be non-conflicting is then introduced as a synonym for the associated overall behaviour to be non-nonblocking.
Definition 2.3.2
A family \((G_i)_{1\le i \le k}\) of automata is non-conflicting w.r.t. prioritised events if and only if \(\mathcal {S}(G_1\parallel G_2\parallel \cdots \parallel G_k)\) is non-blocking.
Non-conflictingness of a modular system neither implies nor is implied by non-blockingness of each individual module. Thus, the conventional way to check non-conflictingness is to explicitly construct a monolithic representation and then to test for non-blockingness. This approach greatly suffers from the fact that the overall state count grows exponentially with the number of modules. This problem can be decently addressed by compositional verification, in which we seek for abstractions of individual modules such that non-conflictingness is preserved. Given a modular system
let’s choose \(G:=G_1\) as the automaton we are about to abstract, and denote H the remaining part consisting of the synchronous composition of all modules except for G. Since synchronous composition is commutative and associative, our choice of \(G:=G_1\) is not restrictive and we can repeat the subsequent argument for the abstraction of any other module. An abstraction \(G'\) of G qualifies for our purposes if
An elementary abstraction that suits our needs is referred to as hiding, and technically amounts to relabelling transitions with specific regular events by their silent counterpart of the same priority.
Definition 2.3.3
Let \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) be an automaton. Hiding \(\Delta \subseteq \Sigma \) in G results in an automaton \(G/_\Delta =\langle Q, \Sigma , \rightarrow _\Delta , Q^\circ , M\rangle \) where \(x\xrightarrow {\alpha }_\Delta y\) if and only if either of the following conditions is satisfied:
When synchronising an automaton G with the remaining part H, we can hide all private events in G which are not utilised in the marking set while preserving any conflicts. Formally, we make the following observation.
Observation 2.3.4
Let \(G=\langle Q_{G},\Sigma _{G}, \rightarrow _{G}, Q^\circ _{G}, M_{G}\rangle \) and \(H=\langle Q_{H},\Sigma _{H}, \rightarrow _{H}, Q^\circ _{H}, M_{H}\rangle \) be two automata. Let \(\Delta \subseteq \Sigma _G-\Sigma _H\) be such that for all \(\Omega _G\in M_G\), \(\Delta \cap \Omega _G=\emptyset \). Then \(G':= G/_\Delta \) satisfies Eq. 13.
For practical purposes, a qualifying abstraction scheme only makes sense, if it avoids an explicit reference to the remaining part H; i.e., there shall be no need to compute a monolithic representation of H in order to compute the abstraction \(G'\). This is indeed true for hiding as defined above. To this end, the literature proposes the notion of conflict equivalence. There, non-blockingness is required to be preserved for the composition not only with one specific remaining part H but with any automaton T, the latter then being referred to as test automaton; see e.g. Malik et al. (2004). For the situation of prioritised events, one obtains the following formal definition.
Definition 2.3.5
Two automata \(G'\) and G are conflict equivalent w.r.t. prioritised events, denoted \(G'\simeq ^{\mathcal {S}}G\), if for any automaton T, it holds that
Clearly, conflict-equivalence w.r.t. prioritised events implies Eq. 13. Moreover, the above definition avoids any reference to a specific remaining part H. Since the shaping operator does not distribute over synchronous composition, abstraction schemes from the literature that are known to be conflict equivalent may in general fail to also be conflict equivalent w.r.t. prioritised events. For the remainder of this paper, we use conflict equivalence concisely for conflict equivalence w.r.t. prioritised events. In particular, an abstraction \(G'\) of G is a conflict-preserving abstraction of G if \(G'\simeq ^{\mathcal {S}}G\).
3 Conflict-preserving abstractions
It has been demonstrated by example that given an automaton there in general is no unique state minimal conflict-preserving abstraction; see Flordal and Malik (2006)Footnote 2. Hence the interest in a variety of individual rules that yield conflict-preserving abstractions and that can be utilised in an iterative fashion, e.g., until fixpoint is obtained. As our main technical contribution, we adapt the known abstraction rules from the literature to account for event priorities; see also Flordal and Malik (2009); Su et al. (2010); Ware and Malik (2012); Pilbrow and Malik (2015).
3.1 Partial shaping and quotient automata
When shaping an individual module locally before the overall synchronous composition is constructed, we miss out in that a shared high-priority event in one module may be deactivated by some other module. Specifically, \(G':=\mathcal {S}(G)\) in general fails to be a conflict-preserving abstraction of G. However, we may restrict the shaping operator to only affect transitions for which we know by G that they will be preempted by a local silent event.
Definition 3.1.1
Given an automaton \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \), the \(\Upsilon \)-shaping operator \(\mathcal {S}_\Upsilon (\cdot )\) is defined by \(\mathcal {S}_\Upsilon (G) := \langle Q,\Sigma ,\rightarrow ^{\mathcal {S}_\Upsilon },Q^\circ \rangle \) where
An automaton G is said to be \(\Upsilon \)-shaped if \(G=\mathcal {S}_\Upsilon (G)\).
Technically, for any \(\tau \in \Upsilon \) and \(\alpha \in A\) so that \(x\xrightarrow {\tau }\) and \(x\xrightarrow {\alpha }\) for some state x with \(\textsf{prio}(\tau )<\textsf{prio}(\alpha )\), the latter transition will never be executed once full shaping will eventually be applied. This leads to the following observation, which renders \(G':=\mathcal {S}_\Upsilon (G)\) a conflict-preserving abstraction of G.
Observation 3.1.2
For any two automata G and T, it holds that
Remark 1
If the alphabet \(\Sigma _H\) of the remaining part in H is known, partial shaping can be applied more aggressively by also accounting for regular events which are private to G. ; i.e. using \(G^{<\alpha }(x)\cap (\Upsilon \cup (\,\Sigma _G - \Sigma _H)\,)=\emptyset \) in Eq. 16. We refer to this variant as private shaping \(\mathcal {S}_{\Pi }(\,\cdot \,)\). Similar to hiding, this yields an abstraction that satisfies Eq. 13 but technically fails to be conflict-preserving because it refers to \(\Sigma _H\).
In the absense of event priorities, an enabled silent event in the module G does not affect the transitions which the remaining part H can possibly take. This contrasts our setting in which a high-priority event in G, whether silent or not, preempts any event of lower priority in H. Specifically, if G can indefinitely generate silent events of a certain priority, it may trap the overall system into a live-lock. Technically, we consider the following situation.
Definition 3.1.3
Given a \(\Upsilon \)-shaped automaton \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \), an n-live-lock in G is a non-empty set of states \(X\subseteq Q\) where for all \(x\in X\)
-
(L1)
\(x\mathrel {{\xrightarrow []{\tau }}{}}y\) with \(\tau \in \Upsilon \) implies that \(y\in X\);
-
(L2)
for all \(x,y\in X\) there exists a trace \(x\mathrel {{\xrightarrow []{\alpha _1}}{}}x_1\mathrel {{\xrightarrow []{\alpha _2}}{}}x_2\mathrel {{\xrightarrow []{\alpha _3}}{}}\,\cdots \,x_k\mathrel {{\xrightarrow []{\alpha _k}}{}}y\), where \(x_i\in X\), \(\alpha _i\in \Upsilon \), for all \(i=1,\,2,\,\ldots \,k\); and
-
(L3)
\(\textsf{lo}(\cup _{x'\in X}G_\textrm{slnt}(x'))=n\).
We concisely write \(\alpha \)-live-lock to denote \(\textsf{prio}(\alpha )\)-live-lock where \(\alpha \in \mathfrak {A}\).
By (L1), X is invariant w.r.t. silent transitions; i.e., once in a state \(x\in X\), G can only exit X by a transition labeled with a regular event. By (L2), each pair of states in X is strongly connected w.r.t. silent transitions; i.e., when in a state \(x\in X\), any state \(y\in X\) can be reached by taking only silent transitions. By (L3), in a state \(x\in X\), all its active silent events have at least priority n. Thus, as intended, G may indefinitely trap H by preempting events with lower priority than n.
Example 3
Let G, \(G'\) and H be three automata as given in Fig. 2. In particular, \(\{\textrm{I},\textrm{II}\}\) is a 2-live-lock in G. When G and H are synchronised, the only transition in H, which is labelled by \(\tau _{(3)}\), can never be executed. On the other hand, \(\{\textrm{I}',\textrm{II}'\}\) does not form any live-lock in \(G'\) due to the invalidation of (L1). By reaching \(\textrm{III}'\), the trapping effect is released which allows H to proceed.
Note that (L1) in conjunction with (L2) implies maximality in the sense that for two n-live-locks X and Y with \(X\cap Y\ne \emptyset \) we must have \(X=Y\). Specifically, the computational detection of live-locks can be easily accomplished by seeking for Strongly Connected Components (SCCs) in a suitably preprocessed transition structure; see Aho et al. (1974).
A common technique for the reduction of the state count on an automation is to take the so called quotient w.r.t. an equivalence relation \(\sim \,\subseteq Q\times Q\) on the state set Q. This effectively merges sets of states form one equivalence class into one single state each; see also Flordal and Malik (2009).
Definition 3.1.4
Given an \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) and an equivalence relation \(\sim \,\subseteq Q \times Q\), denote the equivalence classes \([x]:=\{x'\in Q\,\vert \,(x,x')\in \ \sim \}\). The quotient automaton \(G{}{/\hspace{-1.0ex}\bullet \hspace{-.7ex}}\sim \) of G w.r.t. \(\sim \) is defined by \(G{/\hspace{-1.0ex}\bullet \hspace{-.7ex}}\sim \, :=\, \langle Q/{\sim }, A, \mathrel {{\xrightarrow []{}}{}_{{}_\sim }^\bullet }, \tilde{Q}^\circ , M \rangle \) where \(Q/{\sim }:={}\{\,[x]\,\vert \,x\in Q \,\}\), \(\tilde{Q}^\circ :={}\{\,[x^\circ ]\,\vert \,x^\circ \in Q^\circ \,\}\), and \(\mathrel {{\xrightarrow []{}}{}_{{}_\sim }^\bullet }:={}\{\,[x]\xrightarrow {\alpha }[y]\,\vert \,x\xrightarrow {\alpha }y\,\} \).
Clearly, if one seeks for a conflict-preserving abstraction, one will need to imply further requirements on \(\sim \), and we will do so in the following section. At this point, we want to show-case a potential issue when it comes to n-live-locks. Specifically, when two equivalent states \(x\sim y\) originally have a silent transition \(x\xrightarrow {\tau } y\), the quotient automaton \(G/{\sim }\) will contain a self-loop \([x]\xrightarrow {\tau }[x]\). Thus, taking quotients will potentially introduce n-live-locks. This situation can be conveniently fixed by post-processing the quotient automaton accordingly.
Definition 3.1.5
Given a \(\Upsilon \)-shaped automaton \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) and an equivalence relation \(\sim \,\subseteq Q \times Q\), the shaped quotient automaton
 of G w.r.t. \(\sim \) is defined as the ordinary quotient automaton
of G w.r.t. \(\sim \) is defined as the ordinary quotient automaton
 except that we now consider the transition relation
except that we now consider the transition relation

Example 4
Consider the automaton G given in Fig. 3. The state set \(\{\textrm{I},\textrm{II}\}\) is a 2-live-lock and merging it should result in a \(\tau _{(2)}\)-self-loop in order to preserve situations, in which G traps some test automaton T. By the ordinary quotient automaton \(G{/\hspace{-1.0ex}\bullet \hspace{-.7ex}}\sim \), we would additionally obtain a \(\tau _{(1)}\)-self-loop. Namely, \(G{/\hspace{-1.0ex}\bullet \hspace{-.7ex}}\sim \) will trap certain test cases, which the original automaton G would not trap. This is undesired. Likewise, the state set \(\{\textrm{III},\textrm{IV}\}\) is not a live-lock, and merging those two states shall not result in a silent self loop. In contrary, the trapping power of the original automaton is preserved in its shaped quotient automaton
 .
.
In the remainder of this article, since we are only interested in the shaped quotient of an automaton, we will consistently utilise notations \(G/{\sim }\) and \(\xrightarrow {}_{\sim }\) to denote
 and
and
 , respectively. In addition, we concisely utilise the terminology quotient for shaped quotient. We now consider several useful properties of quotient automata.
, respectively. In addition, we concisely utilise the terminology quotient for shaped quotient. We now consider several useful properties of quotient automata.
Lemma 3.1.6
Given a \(\Upsilon \)-shaped automaton \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) and an equivalence relation \(\sim \,\subseteq Q \times Q\), denote the shaped quotient \(G/{\sim }\, :=\, \langle Q/{\sim }, A, \mathrel {{\xrightarrow []{}}{}_{{}_\sim }}, \tilde{Q}^\circ , M \rangle \). Then
-
(i)
for any transition \([x]\mathrel {{\xrightarrow []{\alpha }}{}_{{}_\sim }}[y]\), there exist \(x'\in [x]\) and \(y'\in [y]\) so that \(x'\mathrel {{\xrightarrow []{\alpha }}{}}y'\); and
-
(ii)
if \(G/{\sim }_\textrm{slnt}^{<n}([x])=\emptyset \) for some \(x\in Q\) and \(n\in \mathbb {N}\), then there exists \(x'\in [x]\) so that \(G_\textrm{slnt}^{<n}(x')=\emptyset \).
Proof
Claim (i) is an immediate consequence of \(\mathrel {{\xrightarrow []{}}{}_{{}_\sim }}\subseteq {}\{\,[x]\xrightarrow {\alpha }[y]\,\vert \,x\xrightarrow {\alpha }y\,\} \). Regarding (ii), consider \(x\in Q\) with \(G/{\sim }_\textrm{slnt}^{<n}([x])=\emptyset \). Specifically, we have by Eq. 18 that \(x'\mathrel {{\xrightarrow []{\tau }}{}} y'\) with \(x'\in [x]\) and \(\tau \in \Upsilon ^{<n}\) implies \(y'\in [x]\). For a proof by contradiction, assume that \(G_\textrm{slnt}^{<n}(x')\ne \emptyset \) for all \(x'\in [x]\). Then, for each \(x'\in [x]\), there exists a transition \(x'\mathrel {{\xrightarrow []{\tau }}{}} y'\) with \(y'\in [x]\) and \(\tau \in \Upsilon ^{<n}\). This implies the existence of a silent SCC within [x] with priorities all above n, i.e., a subset \(X\subseteq [x]\) which qualifies for an m-live-lock, \(m<n\). By Eq. 18, \([x]\mathrel {{\xrightarrow []{\tau _{\mathrm {(m)}}}}{}}[x]\) is not removed from \(\rightarrow _\sim \), and this establishes a contradiction to \(G/{\sim }_\textrm{slnt}^{<n}([x])=\emptyset \) \(\square \)
Conventions Various statements and their proofs in the remainder of this chapter involve an automaton G to be abstracted and an arbitrary test-automaton T. In such cases, we take the following conventions for brevity:
-
Given G and an equivalence relation \(\sim \,\subseteq Q\times Q\), we always denote by \(G/{\sim }\) the shaped quotient given in Definition 3.1.5.
-
States in G are always indicated with a subscript \((\cdot )_G\), e.g. \(x_G,x'_G,y_G,\dots \), while states in T are always indicated with a subscript \((\cdot )_T\).
-
Subscripts \((\cdot )_G\) and \((\cdot )_T\) are omitted for transitions in G and T since they can be read from the states of the transition, e.g. \(x_G\mathrel {{\xrightarrow []{\alpha }}{}}y_G\) must be a transition in G.
-
Since T is arbitrary and its marking set can also contain private regular events, we may aggressively assume that none of the transitions in T is silent. In addition, the notation of \(\Sigma _{T\backslash G}:=\Sigma _T-\Sigma _G\) denotes the private event set of T where \(\Sigma _G\) and \(\Sigma _T\) are the alphabets of G and T, respectively. Notations
$$\begin{aligned} T_\textrm{prvt}(x_T):={}&\{\,\tau \in \Sigma _{T\backslash G}\,\vert \,x_T\mathrel {{\xrightarrow []{\tau }}{}}\,\};\\ T_\textrm{prvt}^{<n}(x_T):={}&\{\,\tau \in T_\textrm{prvt}(x_T)\,\vert \,\textsf{prio}(\tau )<n\,\} \end{aligned}$$are utilised to denote active private events (with priority higher than n) in state \(x_T\), respectively. Furthermore, a trace is considered asynchronous if all event labels within this trace are from \(\Upsilon \cup \Sigma _{T\backslash G}\).
3.2 Prioritised weak bisimulation
In the absence of event priorities, taking quotient automata w.r.t. weak bisimulations (also known as observation equivalences) is a well studied method of abstraction. Historically, the concept originates from process algebra, where we specifically refer to the Calculus of Communicating Systems (CCS) (Milner 1989). It has been shown by Malik et al. (2004) that weak bisimulations yield conflict quivalent abstractions. To account for event priorities, we mimic the same line of thought, however, now referring to the variant process algebra CCSch (Lúttgen 1998). The latter refers to operational semantics with event priorities and proposes the notion of prioritised weak bisimulation (PWB). Our conjecture here is that quotient automata w.r.t. PWB are conflict equivalent w.r.t. prioritised events. In this section, we provide a self-contained proof of this conjecture. As in Lúttgen (1998), we distinguish three classes of transitions.
Definition 3.2.1
Given a \(\Upsilon \)-shaped automaton \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \), define the following extended transition relations:
-
(T1)
\(\xrightarrow [\Delta :n]{}\,\subseteq Q\times A\times Q\): \(x\xrightarrow [\Delta :n]{\alpha }y\) if \(x\xrightarrow {\alpha }y\) and \(G_\textrm{rglr}^{<n}(x)\subseteq \Delta \);
-
(T2)
\({\Rightarrow }^{}\,\subseteq Q\times \{\epsilon \}\times Q\): \(x{\Rightarrow }^{\epsilon }y\) if \(x\xrightarrow [\Delta :n]{\tau _1}\xrightarrow [\Delta :n]{\tau _2}\cdots \xrightarrow [\Delta :n]{\tau _k}y\), \(k\ge 0\) and \(\tau _1\cdots \tau _k\in (\Upsilon ^{\le n})^*\);
-
(T3)
\({\Rightarrow }^{}\,\subseteq Q\times \{\epsilon \}\times Q\): \(x{\Rightarrow }^{\epsilon }y\) if \(x\xrightarrow {\tau _1}\xrightarrow {\tau _2}\cdots \xrightarrow {\tau _k}y\), \(k\ge 0\) and \(\tau _1\cdots \tau _k\in (\Upsilon ^{\le n})^*\).
For brevity, we use \(\mathrel {{\xrightarrow [\Delta :\alpha ]{}}{}}\), \(\mathrel {{{\Rightarrow }^{}}{}}\) and \(\mathrel {{{\Rightarrow }^{}_{\alpha }}{}}\) with \(\alpha \in A\) to refer to \(\mathrel {{\xrightarrow [\Delta :\textsf{prio}(\alpha )]{}}{}}\), \(\mathrel {{{\Rightarrow }^{}}{}}\) and \(\mathrel {{{\Rightarrow }^{}}{}}\), respectively.
Transition relations (T1) and (T2) are in general harder to preempt – when being synchronised with another automaton, we wish that preemption caused by shared high-priority events shall not take place before the target state is reached. Thus, in (T1) and (T2), the set of active regular high-priority events is restricted in respective states. Also note that \(x{\Rightarrow }^{\epsilon }y\) implies \(x{\Rightarrow }^{\epsilon }y\) for any \(\Delta \subseteq \mathfrak {U}\). Furthermore, although (T1) in general can not be extended to string-valued labels, we still stipulate that \(x\xrightarrow [\Delta :n]{\epsilon }x\), \(x\mathrel {{{\Rightarrow }^{\epsilon }}{}}x\) and \(x\mathrel {{{\Rightarrow }^{\epsilon }}{}}x\) hold for any state x, any event set \(\Delta \) and any priority value n. It is worth mentioning that in these cases, there is in fact no restriction on the active event set in x. In addition, by writing \(\mathrel {{{\Rightarrow }^{}}{}}\), we intend to describe a sequence of \(\tau _{(1)}\) events. The execution of such a sequence cannot be disturbed through preemption.
We are now in the position to formally define prioritised weak bisimulation (PWB).
Definition 3.2.2
Let \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) be an \(\Upsilon \)-shaped automaton. A symmetric relation \(\approx \,\subseteq Q\times Q\) is a prioritised weak bisimulation on G (PWB) if for any \(x, x'\in Q\) so that \(x\approx x'\), the following hold:
-
(P1)
If \(G^{<n}_{\textrm{slnt}}(x)=\emptyset \) for some \(n\ge 0\), then there exists \(y'\) so that \(x\approx y'\), \(G^{<n}_{\textrm{slnt}}(y')=\emptyset \), \(G^{<n}_{\textrm{rglr}}(y')\subseteq \Delta \) and \(x'\mathrel {{{\Rightarrow }^{\epsilon }}{}} y'\) where \(\Delta =G^{<n}_{\textrm{rglr}}(x)\);
-
(P2)
If \(x\mathrel {{\xrightarrow []{\alpha }}{}}y\), then there exists \(y'\) so that \(y\approx y'\) and \(x'\mathrel {{{\Rightarrow }^{\epsilon }}{}}\mathrel {{\xrightarrow [\Delta :\alpha ]{\textsf{p}(\alpha )}}{}}\mathrel {{{\Rightarrow }^{\epsilon }}{}}y'\) where \(\Delta =G_{\textrm{rglr}}^{<\alpha }(x)\).
In support of proving our conjecture, we make the following technical observation.
Proposition 3.2.3
Let \(G=\langle Q_{G},\Sigma _{G}, \rightarrow _{G}, Q^\circ _{G}, M_{G}\rangle \) an \(\Upsilon \)-shaped automaton with a PWB \(\approx \ \subseteq Q_G\times Q_G\) on G. The following two statements hold for any automaton \(T=\langle Q_{T},\Sigma _{T}, \rightarrow _{T}, Q^\circ _{T}, M_{T}\rangle \), any \(x_G,y_G\in Q_G\), any \(\alpha \in A\) and any \(x_T,y_T\in Q_T\):
-
(C1)
if \(([x_G],x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}([y_G],y_T)\) in \(\mathcal {S}(G/{\approx }\parallel T)\), then for all \(x'_G\in [x_G]\), there exists some \(y'_G\in [y_G]\) so that \((x_G,x_T)\mathrel {{{\Rightarrow }^{\textsf{p}(\alpha )}}{}^{\mathcal {S}}}(y_G,y_T)\) in \(\mathcal {S}(G_{}\parallel T)\).
-
(C2)
if \((x_G,x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}(y_G,y_T)\) in \(\mathcal {S}(G_{}\parallel T)\), then \(([x_G],x_T)\mathrel {{\xrightarrow []{\textsf{p}(\alpha )}}{}^{\mathcal {S}}}([y_G],y_T)\) in \(\mathcal {S}(G/{\approx }\parallel T)\).
Proof
(C1): There are two cases:
-
(Case 1)
If \(([x_G],x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}([y_G],y_T)\) is driven by \(G/{\approx }\), then from (P2), for all \(x'_G\in [x_G]\), there exists some \(\bar{x}_G\in Q_G\), \(\bar{y}_G\in Q_G\) and \(y'_G\in [y_G]\) so that \(x'_G\mathrel {{{\Rightarrow }^{\epsilon }}{}}\bar{x}_G\mathrel {{\xrightarrow [\Delta :\alpha ]{\textsf{p}(\alpha )}}{}}\bar{y}_G\mathrel {{{\Rightarrow }^{\epsilon }}{}}y'_G\) where \(\Delta =G_{\textrm{rglr}}^{<\alpha }(x_G)\). Note that \(\Delta \subseteq G/{\approx }_\textrm{rglr}^{<\alpha }([x_G])\). This enables a sequence of transitions \((x'_G,x_T)\mathrel {{{\Rightarrow }^{\epsilon }}{}^{\mathcal {S}}}(\bar{x}_G,x_T)\mathrel {{\xrightarrow [\Delta :\alpha ]{\textsf{p}(\alpha )}}{}^{\mathcal {S}}}(\bar{y}_G,y_T)\mathrel {{{\Rightarrow }^{\epsilon }}{}^{\mathcal {S}}}(y'_G,y_T)\) in \(\mathcal {S}(G_{}\parallel T)\).
-
(Case 2)
Otherwise, \(([x_G],x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}([y_G],y_T)\) is not driven by \(G/{\approx }\). This implies that \([x_G]=[y_G]\), \(\alpha \in \Upsilon \) and \(G/{\approx }_\textrm{slnt}^{<\alpha }([x_G])=\emptyset \). Then from (P1), for all \(x'_G\in [x_G]\), there exists \(y'_G\in [y_G]=[x_G]\) so that \(G^{<\alpha }_{\textrm{slnt}}(y'_G)=\emptyset \), \(G^{<\alpha }_{\textrm{rglr}}(y'_G)\subseteq \Delta \) and \(x'_G\mathrel {{{\Rightarrow }^{\epsilon }}{}} y'_G\) where \(\Delta =G^{<\alpha }_{\textrm{rglr}}(x_G)\). This enables a sequence of transitions \((x'_G,x_T)\mathrel {{{\Rightarrow }^{\epsilon }}{}^{\mathcal {S}}}(y'_G,x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}(y'_G,y_T)\) in \(\mathcal {S}(G_{}\parallel T)\)
(C2): There are two cases:
-
(Case 1)
Let \((x_G,x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}(y_G,y_T)\) be driven by G. In this case, if \(x_G\approx y_G\) and \(\alpha \in \Upsilon \), then we have a transition \((x_G,x_T)\mathrel {{\xrightarrow []{\epsilon }}{}^{\mathcal {S}}}(y_G,y_T)=(x_G,x_T)\) in \(\mathcal {S}(G_{}\parallel T)\). Otherwise, suppose
 in \(\mathcal {S}(G_{}\parallel T)\) and we prove by contradiction. In this case, there must exist some \(\alpha '\in A\) so that \(([x_G],x_T)\mathrel {{\xrightarrow []{\alpha '}}{}^{\mathcal {S}}}\) in \(\mathcal {S}(G/{\approx }\parallel T)\) and \(\textsf{prio}(\alpha ')<\textsf{prio}(\alpha )\). Clearly, \(([x_G],x_T)\mathrel {{\xrightarrow []{\alpha '}}{}^{\mathcal {S}}}\) cannot be driven by T from \((x_G,x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}(y_G,y_T)\). There are two further sub-cases:
in \(\mathcal {S}(G_{}\parallel T)\) and we prove by contradiction. In this case, there must exist some \(\alpha '\in A\) so that \(([x_G],x_T)\mathrel {{\xrightarrow []{\alpha '}}{}^{\mathcal {S}}}\) in \(\mathcal {S}(G/{\approx }\parallel T)\) and \(\textsf{prio}(\alpha ')<\textsf{prio}(\alpha )\). Clearly, \(([x_G],x_T)\mathrel {{\xrightarrow []{\alpha '}}{}^{\mathcal {S}}}\) cannot be driven by T from \((x_G,x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}(y_G,y_T)\). There are two further sub-cases: -
(i)
\(\alpha '\in \Upsilon \). Note that in this case, \(\alpha '\) cannot appear as a self-loop over \([x_G]\) in \(G/{\approx }\). If so, then \([x_G]\) contains some \(\alpha '\)-live-lock in G. Note that \(G_\textrm{slnt}^{<\alpha }(x_G)=\emptyset \) must hold from the \(\Upsilon \)-shapedness. Then from (P1), \([x_G]\) cannot contain such \(\alpha '\)-live-locks. Thus, there exists some \(x'_G\in [x_G]\) and \(z_G\in Q_G - [x_G]\) so that \(x'_G\mathrel {{\xrightarrow []{\alpha '}}{}}z_G\). From (P2), it implies the existence of some \(\tau \in G_\textrm{slnt}(x_G)\) so that \(\textsf{prio}(\tau )\le \textsf{prio}(\alpha ')\), which contradicts \((x_G,x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}(y_G,y_T)\).
-
(ii)
If \(\alpha '\in \Sigma \), then similar to (i), either \(\alpha '\in G(x_G)\) or some \(\tau \in G^{\le \alpha '}(x_G)\). Both contradict \((x_G,x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}(y_G,y_T)\).
-
(i)
-
(Case 2)
Otherwise, \((x_G,x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}(y_G,y_T)\) is not driven by G. This case can be reasoned from (i) and (ii) as in Case 1 of C2 directly.\(\square \)
By performing a simple induction on the result of the above proposition, we establish that quotients w.r.t. PWS are indeed conflict equivalent w.r.t. prioritised events.
Theorem 3.2.4
Let \(G=\langle Q_{G},\Sigma _{G}, \rightarrow _{G}, Q^\circ _{G}, M_{G}\rangle \) be an \(\Upsilon \)-shaped automata with an PWB \(\approx \ \subseteq Q\times Q\). It then holds that \(G\simeq ^{\mathcal {S}}(G/{\approx })\).
Proof
Let \(T=\langle Q_{T},\Sigma _{T}, \rightarrow _{T}, Q^\circ _{T}, M_{T}\rangle \) be any automaton. Suppose \(\mathcal {S}(G_{}\parallel T)\) is non-blocking, we shall attempt to prove that \(\mathcal {S}(G/{\approx }\parallel T)\) must be non-blocking (The proof for the conversed case is similar). Pick any \(y_G\in Q_G\) so that \(([x^\circ _G],x^\circ _T)\mathrel {{{\Rightarrow }^{s}}{}^{\mathcal {S}}}([y_G],y_T)\) for some \(s\in \Sigma ^*\), \(x^\circ _G\in Q^\circ _G\), \(x^\circ _T\in Q_T^\circ \) and \(y_T\in Q_T\). Note that \([x_G^\circ ]\in \tilde{Q}_G\) must hold. By Proposition 3.2.3.(C1), it follows from induction on concatenated transitions of any trace in \(([x^\circ _G],x^\circ _T)\mathrel {{{\Rightarrow }^{s}}{}^{\mathcal {S}}}([y_G],y_T)\) that there exists \(y'_G\in [y_G]\) so that \((x^\circ _G,x^\circ _T)\mathrel {{{\Rightarrow }^{s}}{}^{\mathcal {S}}}(y'_G,y_T)\) in \(\mathcal {S}(G_{}\parallel T)\), i.e. \(\mathcal {S}(G_{}\parallel T)\mathrel {{{\Rightarrow }^{s}}{}^{\mathcal {S}}}(y'_G,y_T)\). Moreover, since \(\mathcal {S}(G_{}\parallel T)\) is non-blocking, \((y'_G,y_T)\mathrel {{{\Rightarrow }^{t\omega }}{}^{\mathcal {S}}}\) in \(\mathcal {S}(G_{}\parallel T)\) for some \(t\in \Sigma ^*\) must hold. Again from Proposition 3.2.3.(C2), we can conclude through induction that \(([y'_G],y_T)=([y_G],y_T)\mathrel {{{\Rightarrow }^{t\omega }}{}^{\mathcal {S}}}\) in \(\mathcal {S}(G/{\approx }\parallel T)\). The proof is indeed closed since \(y_G\) is arbitrarily picked.\(\square \)
From Definition 3.2.2, we note that PWB is defined as such that if a regular event \(\sigma \) is to execute at some state, then an equivalent state must be able to execute \(\sigma \) either directly or after a delay of several silent steps with priority not lower than \(\sigma \). The reason of this restriction can be seen from the following example. For brevity of examples in the remainder, we take the convention that, if not explicitly specified, the marking set of any automaton is \(\{\{\omega \}\}\) with \(\textsf{prio}(\omega )=1\).
Example 5
Consider the automaton G given in Fig. 4. It follows from (P1) directly that
 . If \(\textrm{I}\) and \(\textrm{II}\) are merged through some equivalence relation \(\sim \) which generates \(G/{\sim }\), a counterexample T can be constructed as given in Fig. 4 to witness that
. If \(\textrm{I}\) and \(\textrm{II}\) are merged through some equivalence relation \(\sim \) which generates \(G/{\sim }\), a counterexample T can be constructed as given in Fig. 4 to witness that
 , since \(\mathcal {S}(G_{}\parallel T)\) is blocking while \(\mathcal {S}(G/{\sim }\parallel T)\) is not.
, since \(\mathcal {S}(G_{}\parallel T)\) is blocking while \(\mathcal {S}(G/{\sim }\parallel T)\) is not.
Consider the automaton G given in Fig. 4 again. The failure of the abstraction is in fact caused by the reachable state \((\textrm{I},\textrm{i})\) in \(\mathcal {S}(G_{}\parallel T)\), since \(\tau _{(2)}\) in \(\textrm{i}\) will not be preempted by the shared event \(\sigma \), whose priority is higher than \(\tau _{(2)}\). However, this preemption indeed will happen in \(([\textrm{I}],\textrm{i})\) in \(\mathcal {S}(G/{\sim }\parallel T)\) due to the state merging. In this regard, our idea to ensure conflict equivalence is to add further restriction on the automaton so that such “bad” states will always be unreachable. As for G in Fig. 4, consider adding a new state \(\textrm{IV}\) with a new transition \(\textrm{IV}\mathrel {{\xrightarrow []{\tau _{(3)}}}{}}\textrm{I}\). Furthermore, let \(\textrm{IV}\) be the only new initial state. For such an automaton \(G'\) as given in Fig. 5, merging \(\textrm{I}\) and \(\textrm{II}\) does yield a conflict-preserving abstraction. The intuition behind this modification is that, in order to visit \(\textrm{II}\) under synchronisation, \(\textrm{IV}\) must be visited at first. However, when \((\textrm{IV},x_T)\mathrel {{\xrightarrow []{\tau _{(3)}}}{}^{\mathcal {S}}}(\textrm{I},x_T)\) is executed for some \(x_T\), the next step must be \((\textrm{I},x_T)\mathrel {{\xrightarrow []{\tau _{(2)}}}{}^{\mathcal {S}}}(\textrm{II},x_T)\) since \(\textrm{I}\) cannot execute any synchronised event and \(x_T\) cannot execute any private event with priority higher than 3 either. This observation motivates the definition of redundant silent step and it is shown in the following that merging a redundant silent step, which is referred to as the redundant silent step rule, is a conflict-preserving abstraction.
Definition 3.2.5
Let \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) be a \(\Upsilon \)-shaped automaton. A transition \(x\mathrel {{\xrightarrow []{\tau }}{}}x'\) with \(x,x'\in Q\) and \(\tau \in \Upsilon \) is a redundant silent step if this is the only transition outgoing from x, \(x\notin Q^\circ \) and \(y\mathrel {{\xrightarrow []{\alpha }}{}}x\) for any \(y\in Q\) implies \(\alpha \in \Upsilon \) and \(\textsf{prio}(\alpha )>\textsf{prio}(\tau )\). An equivalence \(\sim \,\subseteq Q\times Q\) on G is induced by the transition \(x\mathrel {{\xrightarrow []{\alpha }}{}}x'\) if \(x\sim x'\) and for all \(y\in Q-\{x,x'\}\), [y] is a singleton class.
From Definition 3.2.5, we note that a silent self-loop can never be a redundant silent step. In addition, the definition of redundant silent step does not specifically handle the existence of live-locks. The reason is that the active event set of the target state of a redundant silent step can be completely preserved in the quotient automaton. This is stated by the following lemma.
Lemma 3.2.6
Let \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) be a \(\Upsilon \)-shaped automaton and the equivalence \(\sim \,\subseteq Q\times Q\) is induced by the redundant silent step \(x\mathrel {{\xrightarrow []{\tau }}{}}x'\). It holds that \(G(x')=G/{\sim }([x])\)
Proof
It suffices to consider the case that \([x]\mathrel {{\xrightarrow []{\tau '}}{}_{{}_\sim }}[x]\) in \(G/{\sim }\) for some \(\tau '\in \Upsilon \). In this case, [x] contains a \(\tau '\)-live-lock from G which is formed either by \(\{x,x'\}\) or solely by \(\{x'\}\) (solely by \(\{x\}\) is clearly impossible). The case of solely by \(\{x'\}\) is rather trivial, while when \(\{x,x'\}\) is a \(\tau '\)-live-lock, we must have \(x'\mathrel {{\xrightarrow []{\tau '}}{}}x\) since from the definition of redundant silent step, \(\textsf{prio}(\tau ')>\textsf{prio}(\tau )\) must hold.\(\square \)
Consider a redundant silent step \(x_G\mathrel {{\xrightarrow []{\tau }}{}}x'_G\) in a \(\Upsilon \)-shaped automaton G with some regular event \(\sigma \) so that \(\textsf{prio}(\sigma )<\textsf{prio}(\tau )\), \(\sigma \notin G(x_G)\) and \(\sigma \in G(x'_G)\), we can assert that \(x_G\) and \(x'_G\) are never equivalent w.r.t. any PWB. Intuitively, this invalidates the property given in Proposition 3.2.3 if it is assumed that the resulting quotient automaton and the original one are “equivalent”. More precisely, for some state \(x_T\) in a test automaton T, if \(x_T\mathrel {{\xrightarrow []{\tau '}}{}}\) for some \(\tau '\in \Sigma _{T\backslash G}\) where \(\textsf{prio}(\tau ')\le \textsf{prio}(\tau )\), we must have \((x_G, x_T)\mathrel {{\xrightarrow []{\tau '}}{}^{\mathcal {S}}}\) in \(\mathcal {S}(G_{}\parallel T)\), while \(([x_G],x_T)\mathrel {{\xrightarrow []{\tau '}}{}^{\mathcal {S}}}\) may not hold in \(\mathcal {S}(G/{\sim }\parallel T)\) when \(\sigma \in T(x_T)\) and \(\textsf{prio}(\sigma )<\textsf{prio}(\tau ')\). Interestingly, such \((x_G,x_T)\) is never reachable in \(\mathcal {S}(G_{}\parallel T)\).
Proposition 3.2.7
Let \(G=\langle Q_{G},\Sigma _{G}, \rightarrow _{G}, Q^\circ _{G}, M_{G}\rangle \) be a \(\Upsilon \)-shaped automaton and the equivalence \(\sim \,\subseteq Q_G\times Q_G\) is induced by the redundant silent step \(\bar{x}_G\mathrel {{\xrightarrow []{\tau }}{}}\bar{x}'_G\). Let \(T=\langle Q_{T},\Sigma _{T}, \rightarrow _{T}, Q^\circ _{T}, M_{T}\rangle \) be any automaton. For all \(\bar{x}_T\in Q_T\) so that \(T_\textrm{prvt}^{\le \tau }(\bar{x}_T)\ne \emptyset \), \((\bar{x}_G,\bar{x}_T)\) is not reachable in \(\mathcal {S}(G_{}\parallel T)\).
Proof
We prove by contradiction. Pick any \(\bar{x}_T\in Q_T\) so that \(T_\textrm{prvt}^{\le \tau }(\bar{x}_T)\ne \emptyset \). Note that \((\bar{x}_G,\bar{x}_T)\) can never be initial. Thus, to reach \((\bar{x}_G,\bar{x}_T)\), one shall first reach some \((y_G,y_T)\) where \(y_G\in Q_G\), \(y_T\in Q_T\) so that \(y_G\mathrel {{\xrightarrow []{\tau '}}{}}\bar{x}_G\) with some \(\tau '\in \Upsilon \). From Definition 3.2.5, it is clear that \(\textsf{prio}(\tau ')> \textsf{prio}(\tau )\). This implies that
 . With this observation, we continue the proof by attempting to construct a trace from \((y_G,y_T)\) to \((\bar{x}_G,\bar{x}_T)\), which must fail. Consider the following cases:
. With this observation, we continue the proof by attempting to construct a trace from \((y_G,y_T)\) to \((\bar{x}_G,\bar{x}_T)\), which must fail. Consider the following cases:
-
(Case 1)
\(T_\textrm{prvt}^{\le \tau }(y_T)\ne \emptyset \). Let \(y_T\mathrel {{\xrightarrow []{\tau ''}}{}}\bar{y}_T\) for some \(\bar{y}_T\in Q_T\) and \(\tau ''\in T_\textrm{prvt}^{\le \tau }(y_T)\). Clearly, \(\textsf{prio}(\tau '')<\textsf{prio}(\tau ')\), and we concatenate \((y_G,y_T)\mathrel {{\xrightarrow []{\tau ''}}{}^{\mathcal {S}}}(y_G,\bar{y}_T)\) (without losing generality, we can assume that \(T_\textrm{prvt}^{<\tau ''}(y_T)=\emptyset \)). If \(T_\textrm{prvt}^{\le \tau }(\bar{y}_T)\ne \emptyset \) always holds for such concatenation, then the construction is trapped in Case 1 and \(\bar{x}_G\) can never be visited. Otherwise, let \(T_\textrm{prvt}^{\le \tau }(\bar{y}_T)=\emptyset \), which leads to Case 2.
-
(Case 2)
\(T_\textrm{prvt}^{\le \tau }(y_T)=\emptyset \). From \((y_G,y_T)\), since only private events can be executed, consider the possibility of concatenating \((y_G,y_T)\mathrel {{\xrightarrow []{\tau '}}{}^{\mathcal {S}}}(\bar{x}_G,y_T)\) in \(\mathcal {S}(G_{}\parallel T)\), since executing a private transition in T indeed rolls the construction back to the beginning of either Case 1 or 2. However, if \((y_G,y_T)\mathrel {{\xrightarrow []{\tau '}}{}^{\mathcal {S}}}(\bar{x}_G,y_T)\), it implies that the next transition which can be concatenated must be \((\bar{x}_G,y_T)\mathrel {{\xrightarrow []{\tau }}{}^{\mathcal {S}}}(\bar{x}'_G,y_T)\) since \(\textsf{prio}(\tau )<\textsf{prio}(\tau ')\) and executing any shared event with priority higher than \(\tau \) in \((\bar{x}_G,y_T)\) is not possible. Recall that \(y_T\ne \bar{x}_T\) due to \(T_\textrm{prvt}^{\le \tau }(\bar{x}_T)\ne \emptyset \), i.e. for any \(z_T\in Q_T\) so that \((\bar{x}_G,z_T)\) is reachable in \(\mathcal {S}(G_{}\parallel T)\), \(T_\textrm{prvt}^{\le \tau }(\bar{z}_T)=\emptyset \) must hold. This indeed closes the proof.\(\square \)
When merging a redundant silent step, states characterised in Proposition 3.2.7 are exactly the “bad” states which potentially invalidate conflict equivalence. With this observation, the following proposition is derived which is similar to Proposition 3.2.3.
Proposition 3.2.8
Let \(G=\langle Q_{G},\Sigma _{G}, \rightarrow _{G}, Q^\circ _{G}, M_{G}\rangle \) be a \(\Upsilon \)-shaped automaton and the equivalence \(\sim \,\subseteq Q_G\times Q_G\) is induced by the redundant silent step \(\bar{x}_G\mathrel {{\xrightarrow []{\tau }}{}}\bar{x}'_G\). Let \(T=\langle Q_{T},\Sigma _{T}, \rightarrow _{T}, Q^\circ _{T}, M_{T}\rangle \) be any automaton.
-
(i)
For any transition \(([x_G],x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}([y_G],y_T)\) in \(\mathcal {S}(G/{\sim }\parallel T)\), at least one of the following two statements is true for any \(x'_G\in [x_G]\):
-
a)
There exists \(y'_G\in [y_G]\) so that \((x'_G,x_T)\mathrel {{{\Rightarrow }^{\textsf{p}(\alpha )}}{}^{\mathcal {S}}}(y'_G,y_T)\) in \(\mathcal {S}(G_{}\parallel T)\), or
-
b)
\((x'_G,x_T)\) is not reachable in \(\mathcal {S}(G_{}\parallel T)\).
-
a)
-
(ii)
For any transition \((x_G,x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}(y_G,y_T)\) in \(\mathcal {S}(G_{}\parallel T)\), at least one of the following two statements is true:
-
a)
\(([x_G],x_T)\mathrel {{\xrightarrow []{\textsf{p}(\alpha )}}{}^{\mathcal {S}}}([y_G],y_T)\) in \(\mathcal {S}(G/{\sim }\parallel T)\), or
-
b)
\((x_G,x_T)\) is not reachable in \(\mathcal {S}(G_{}\parallel T)\).
-
a)
Proof
Ad(i). If \([x_G]\) is a singleton, then statement a) holds trivially. Thus, we let \([x_G]=[\bar{x}_G]\). In this case, note that if \(([x_G],x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}([y_G],y_T)\) is not driven by G, then statement a) must be true as well since either \((\bar{x}_G,x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}(\bar{x}_G,y_T)\) or \((\bar{x}_G,x_T)\mathrel {{\xrightarrow []{\tau }}{}^{\mathcal {S}}}(\bar{x}'_G,x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}(\bar{x}'_G,y_T)\) holds in \(\mathcal {S}(G_{}\parallel T)\) from Lemma 3.2.6. Thus, let \(([x_G],x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}([y_G],y_T)\) be driven by G. This implies \(\alpha \in G(\bar{x}'_G)\) due to Lemma 3.2.6 and we pick \(x'_G\in [x_G]\). There are two cases:
-
(Case 1)
\(x'_G=\bar{x}'_G\). We shall note that \(G(\bar{x}'_G)=G/{\sim }([\bar{x}'_G])\) from Lemma 3.2.6. Thus, in this case, statement a) must hold.
-
(Case 2)
\(x'_G=\bar{x}_G\). We directly suppose that statement a) is not true, i.e.
 in \(\mathcal {S}(G_{}\parallel T)\) for any \(y'_G\in [y_G]\). This implies that \(T_\textrm{prvt}^{<\tau }(x_T)\ne \emptyset \), since otherwise, we must be able to execute \((\bar{x}_G,x_T)\mathrel {{\xrightarrow []{\tau }}{}^{\mathcal {S}}}(\bar{x}'_G,x_T)\), which leads to Case 1. Note that \(T_\textrm{prvt}^{<\tau }(x_T)\ne \emptyset \) implies \(T_\textrm{prvt}^{\le \tau }(x_T)\ne \emptyset \). Thus, in this case, statement b) must hold from Proposition 3.2.7.
in \(\mathcal {S}(G_{}\parallel T)\) for any \(y'_G\in [y_G]\). This implies that \(T_\textrm{prvt}^{<\tau }(x_T)\ne \emptyset \), since otherwise, we must be able to execute \((\bar{x}_G,x_T)\mathrel {{\xrightarrow []{\tau }}{}^{\mathcal {S}}}(\bar{x}'_G,x_T)\), which leads to Case 1. Note that \(T_\textrm{prvt}^{<\tau }(x_T)\ne \emptyset \) implies \(T_\textrm{prvt}^{\le \tau }(x_T)\ne \emptyset \). Thus, in this case, statement b) must hold from Proposition 3.2.7.
Ad (ii). Note that statement a) must hold if \([x_G]\) is a singleton. In addition, statement a) holds for \(x_G=\bar{x}'_G\) as well from Lemma 3.2.6. Let \(x_G=\bar{x}_G\). If \((x_G,x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}(y_G,y_T)\) is driven by G, then \(y_G=\bar{x}'_G\) and statement a) holds from a transition \(([x_G],x_T)\mathrel {{\xrightarrow []{\epsilon }}{}}([y_G],x_T)\). Let \((x_G,x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}(y_G,y_T)\) be not driven by G. In this case, statement b) must hold from Proposition 3.2.7 since \(\textsf{prio}(\alpha )\le \textsf{prio}(\tau )\), i.e. \(\alpha \in T_\textrm{prvt}^{\le \tau }(x_T)\).\(\square \)
In Proposition 3.2.8, both statements (i.a) and (ii.a) are synonymous to Proposition 3.2.3. We are now in the position to state the redundant silent step rule as follows.
Theorem 3.2.9
[redundant silent step rule] Let \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) be a \(\Upsilon \)-shaped automaton and the equivalence \(\sim \,\subseteq Q\times Q\) is induced by some redundant silent step. It holds that \(G\simeq ^{\mathcal {S}}(G/{\sim })\).
Proof
The proof is literally the same as the proof of Theorem 3.2.4 up to uniform substitution of the equivalence relation. Note that for all states reached by the induction, statements (i.a) and (ii.a) of Proposition 3.2.8 must hold.\(\square \)
3.3 Abstraction rules based on incoming equivalence
In the ordinary context without prioritised events, Flordal and Malik (2009) introduced several abstraction rules based on incoming equivalence. Thist section adapts these rules for prioritised events.
The motivation of introducing incoming equivalence is to pre-partition states that can be reached in the same way; namely, when a state can be reached under synchronisation with some test, an incoming equivalent state must be reachable under the synchronisation with the same test as well. Incoming equivalence does not necessarily imply (ordinary) conflict equivalence, but serves as a filter to enable two conflict-preserving abstraction rules, i.e. the active events rule and the silent continuation rule. The key property of incoming equivalence in the ordinary context is, all states in the same class can be reached from the same state with a regular event, possibly with some silent events before or after the regular event. Since this property is rather cumbersome to achieve when considering prioritised events, a formal definition of this property is first given and named as redirectability.
Definition 3.3.1
Let \(G=\langle Q_{G},\Sigma _{G}, \rightarrow _{G}, Q^\circ _{G}, M_{G}\rangle \) be a \(\Upsilon \)-shaped automaton. An equivalence \(\sim \,\subseteq Q_G\times Q_G\) is redirectable if and only if for any automaton \(T=\langle Q_{T},\Sigma _{T}, \rightarrow _{T}, Q^\circ _{T}, M_{T}\rangle \), \(y_G\in Q_G\), \(y_T\in Q_T\) and \(s_T\in \Sigma _{T\backslash G}^*\), the following two statements hold:
-
(R1)
\((x_G,x_T)\mathrel {{\xrightarrow []{\sigma }}{}^{\mathcal {S}}}\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}(y_G,y_T)\) in \(\mathcal {S}(G_{}\parallel T)\) for any \(x_G\in Q_G\), \(x_T\in Q_T\) and \(\sigma \in \Sigma _G\) implies that for all \(y'_G\in [y_G]\), \((x_G,x_T)\mathrel {{{\Rightarrow }^{\sigma s_T}}{}^{\mathcal {S}}}(y'_G,y_T)\) in \(\mathcal {S}(G_{}\parallel T)\);
-
(R2)
\(\mathcal {S}(G_{}\parallel T)\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}(y_G,y_T)\) implies that for all \(y'_G\sim y_G\), \(\mathcal {S}(G_{}\parallel T)\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}(y'_G,y_T)\).
It is to observe from Definition 3.3.1 that, for a redirectable equivalence relation, the synchronised behaviour can choose any state in a class to proceed if at least one state in the class can be reached by a regular event followed by some private events (or the synchronised behaviour is currently in the initial state). From this observation, redirectability can commonly be utilised in such scenarios where a transition need to be redirected to a successor, in which desired future behaviour is guaranteed. This feature is especially useful when reasoning about the original behaviour from the abstracted behaviour. In this regard, we review Lemma 3.1.6.(i), which is a general property for any arbitrary equivalence stating that a transition in the original behaviour can always be reconstructed from the abstracted behaviour. Note that the existence statement “there exists \(y'\in [y]\)...” in Lemma 3.1.6 does not allow concatenating multiple reconstructed transitions, i.e. we can not guarantee that e.g. \(([x_G],x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}([y_G],y_T)\mathrel {{\xrightarrow []{\alpha '}}{}^{\mathcal {S}}}([z_G],z_T)\) implies the existence of \(x'_G\in [x_G]\), \(y'_G\in [y_G]\) and \(z'_G\in [z_G]\) so that \((x'_G,x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}(y'_G,y_T)\mathrel {{\xrightarrow []{\alpha '}}{}^{\mathcal {S}}}(z'_G,z_T)\). Nevertheless, this problem can be solved by requiring redirectability on an equivalence if a trace begins with a regular event from G. This is stated by the following proposition which is inspired by (Flordal and Malik 2009, Lemma 2).
Proposition 3.3.2
Let \(G=\langle Q_{G},\Sigma _{G}, \rightarrow _{G}, Q^\circ _{G}, M_{G}\rangle \) be a \(\Upsilon \)-shaped automaton with a redirectable equivalence \(\sim \,\subseteq Q\times Q\) on G. For any automaton \(T=\langle Q_{T},\Sigma _{T}, \rightarrow _{T}, Q^\circ _{T}, M_{T}\rangle \), the following two statements hold:
-
(i)
For any trace
$$\begin{aligned} ([x_{G0}],x_{T0})\mathrel {{\xrightarrow []{\alpha _1}}{}^{\mathcal {S}}}([x_{G1}],x_{T1})\mathrel {{\xrightarrow []{\alpha _2}}{}^{\mathcal {S}}}\cdots \mathrel {{\xrightarrow []{\alpha _k}}{}^{\mathcal {S}}}([x_{Gk}],x_{Tk}) \end{aligned}$$(19)in \(\mathcal {S}(G/{\sim }\parallel T)\) where \(k\ge 1\), \(\alpha _1\in \Sigma _G\) and \(\alpha _i\in A_G\cup A_T\) for all \(i\in \{2,\cdots ,k\}\), there exist \(x'_{G0}\in [x_{G0}]\) and \(x'_{Gk}\in [x_{Gk}]\) so that \((x'_{G0},x_{T0})\mathrel {{{\Rightarrow }^{\textsf{p}(\alpha _1\cdots \alpha _k)}}{}^{\mathcal {S}}}(x'_{Gk},x_{Tk})\) in \(\mathcal {S}(G_{}\parallel T)\);
-
(ii)
If \(\mathcal {S}(G/{\sim }\parallel T)\mathrel {{{\Rightarrow }^{s}}{}^{\mathcal {S}}}([x_G],x_T)\) for some \(s\in (\Sigma _G\cup \Sigma _T)^*\), then there exists \(x'_G\in [x_G]\) so that \(\mathcal {S}(G_{}\parallel T)\mathrel {{{\Rightarrow }^{s}}{}^{\mathcal {S}}}(x'_G,x_T)\).
Proof
(i) We prove by induction:
(Base case) For \(k=1\), it holds immediately that there exists \(x'_{G0}\in [x_{G0}]\) and \(x'_{G1}\in [x_{G1}]\) so that \((x'_{G0}, x_{T0})\mathrel {{\xrightarrow []{\alpha _1}}{}^{\mathcal {S}}}(x'_{G1},x_{T1})\) in \(\mathcal {S}(G_{}\parallel T)\) from Lemma 3.1.6.(i) since \(\alpha _1\in \Sigma _G\).
(Inductive step) Suppose the proposition holds for some \(k\ge 1\), i.e. for some trace
in \(\mathcal {S}(G/{\sim }\parallel T)\) where \(\alpha _1\in \Sigma _G\) and \(\alpha _i\in A_G\cup A_T\) for all \(i\in \{2,\dots ,k\}\), there exist \(x'_{G0}\in [x_{G0}]\) and \(x'_{Gk}\in [x_{Gk}]\) so that
in \(\mathcal {S}(G_{}\parallel T)\). From this hypothesis, we show that the proposition holds for \(k+1\) as well. Consider any successive transition
of trace Eq. 20. This indeed implies the existence of \(x''_{Gk}\in [x_{Gk}]\) and \(x'_{Gk+1}\in [x_{Gk+1}]\) so that \((x''_{Gk},x_{Tk})\mathrel {{\xrightarrow []{\alpha _{k+1}}}{}^{\mathcal {S}}}(x'_{Gk+1},x_{Tk+1})\) in \(\mathcal {S}(G_{}\parallel T)\) due to either Lemma 3.1.6.(i) (if Eq. 22 is driven by G) or Lemma 3.1.6.(ii) (if Eq. 22 is not driven by G). Now if \([x_{Gk}]\) is a singleton, the proof closes directly since \(x'_{Gk}=x''_{Gk}\). Otherwise, from trace Eq. 20, we shall find the last regular transition driven by G, i.e. we consider the trace fragment
from Eq. 20 where \(\alpha _i\in \Sigma _G\) and \(\alpha _{i+1}\cdots \alpha _k\in (\Sigma _{T\backslash G}\cup \Upsilon )^*\). Let \(s_T=\textsf{p}(\alpha _{i+1}\cdots \alpha _k)\). From this and due to the inductive hypothesis, we can extract the fragment
from Eq. 21 for some \(\bar{x}_G\in Q_G\) and \(\bar{x}_T\in Q_T\). Since \(\sim \) is redirectable, we have
from (R1), which can be concatenated by \((x''_{Gk},x_{Tk})\mathrel {{\xrightarrow []{\alpha _{k+1}}}{}^{\mathcal {S}}}(x'_{Gk+1},x_{Tk+1})\). (ii) We separate the proof into two cases:
-
(Case 1)
\(s\in \Sigma _{T\backslash G}^*\). This case holds directly from (R2). Note that we have proven an even more general version of the current statement, i.e. the statement holds for all states in \([x_G]\) instead of the existence of some state in \([x_G]\), which will be utilised in the proof for the next case.
-
(Case 2)
\(s\notin \Sigma _{T\backslash G}^*\). Then let
$$\begin{aligned} \mathcal {S}(G/{\sim }\parallel T)\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}([y_G],y_T)\mathrel {{\xrightarrow []{\sigma }}{}^{\mathcal {S}}}([z_G],z_T)\mathrel {{{\Rightarrow }^{t}}{}^{\mathcal {S}}}([x_G],x_T) \end{aligned}$$(26)where \(s_T\in \Sigma _{T\backslash G}^*\), \(\sigma \in \Sigma _G\) and \(t\in (\Sigma _G\cup \Sigma _T)^*\) so that \(s_T\sigma t=s\). From Case 1, for all \(y'_G\in [y_G]\), \(\mathcal {S}(G_{}\parallel T)\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}(y'_G,y_T)\). From statement (i), there exists \(y''_G\in [y_G]\) and \(x'_G\in [x_G]\) so that \((y''_G,y_T)\mathrel {{{\Rightarrow }^{\sigma t}}{}^{\mathcal {S}}}(x'_G,x_T)\), which closes the proof.\(\square \)
In order to achieve redirectability, we are going to define incoming equivalence for prioritised events by adapting the ordinary version introduced in (Flordal and Malik 2009, Definition 7). From the notion of PWB, intuitively, the transition sequence \(\mathrel {{{\Rightarrow }^{\epsilon }}{}}\mathrel {{\xrightarrow [\Delta :\alpha ]{\textsf{p}(\alpha )}}{}}\mathrel {{{\Rightarrow }^{\epsilon }}{}}\) is tolerant against preemption and can possibly be utilised for the definition of incoming equivalence w.r.t. prioritised events. In particular, the execution of \(\mathrel {{{\Rightarrow }^{\epsilon }}{}}\) cannot be disturbed by any remaining part due to preemption. In fact, this requirement can be relaxed when considering redirectability. Consider some new transition relations as follows.
Definition 3.3.3
Given a \(\Upsilon \)-shaped automaton \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \), define the following extended transition relations:
-
(T4)
\(\xrightarrow [!]{}\,\subseteq Q\times \Upsilon \times Q\): \(x\xrightarrow [!]{\tau }y\) if \(x\xrightarrow {\tau }y\) and \(G_\textrm{rglr}^{<\tau }(x)=\emptyset \).
-
(T5)
 :
:
 if either of the following holds:
if either of the following holds: -
(i)
\(n=1\) and \(x\mathrel {{{\Rightarrow }^{\epsilon }}{}}y\), or
-
(ii)
\(n\ge 2\), \(x\xrightarrow [!]{\tau _1}\xrightarrow [!]{\tau _2}\cdots \xrightarrow [!]{\tau _k}y\), \(k\ge 1\) and \(\textsf{lo}(\{\tau _1\cdots \tau _k\}) = n\).
-
(i)
Transition relations introduced in Definition 3.3.3 are generally more restrictive than those in Definition 3.2.1 in that preemption through regular events shall never take place on a \(\hookrightarrow \)-transition before the last state. Note that the new transition symbol “\(\hookrightarrow \)” is utilised intentionally to differ from \(\rightarrow \) and \(\Rightarrow \) since when \(n\ge 2\),
 generally does not hold for an arbitrary state x, because at least one \(\tau _{(n)}\) transition must exist within
generally does not hold for an arbitrary state x, because at least one \(\tau _{(n)}\) transition must exist within
 . Based on Definition 3.3.3, the adapted definition of incoming equivalence is presented as follows.
. Based on Definition 3.3.3, the adapted definition of incoming equivalence is presented as follows.
Definition 3.3.4
Let \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) be a \(\Upsilon \)-shaped automaton. An equivalence \(\sim _\text {inc}\,\subseteq Q\times Q\) on G is an incoming equivalence if and only if for any \(x,x'\in Q\) so that \(x\sim _\text {inc}x'\), all the following statements hold:
-
(I1)
For any \(\sigma \in \Sigma \), \(n\in \mathbb {N}\) and \(y\in Q\),
 where \(\Delta =G_\textrm{rglr}^{<\sigma }(y)\);
where \(\Delta =G_\textrm{rglr}^{<\sigma }(y)\); -
(I2)
For any \(n\in \mathbb {N}\),
 ;
; -
(I3)
If \(x\ne x'\), then for any \(y\in Q\) and \(\tau \in \Upsilon \), \(y\mathrel {{\xrightarrow []{\tau }}{}}\mathrel {{{\Rightarrow }^{\epsilon }}{}}x\) or \(y\mathrel {{\xrightarrow []{\tau }}{}}\mathrel {{{\Rightarrow }^{\epsilon }}{}}x'\) implies \(G_\textrm{rglr}^{<\tau }(y)=\emptyset \).
Incoming equivalence distributes over arbitrary union. Hence, it is legit to utilise \(\sim _\text {inc}\) to denote the coarsest incoming equivalence of an automaton. In addition, any equivalence finer than an incoming equivalence is an incoming equivalence as well. Thus, the notation of \(\sim \,\subseteq \,\sim _\text {inc}\) is often utilised to indicate that \(\sim \) is an incoming equivalence. Similar to the ordinary version in Flordal and Malik (2009), Definition 3.3.4 attempts to equalise states which can be reached in the same way, i.e. only the past of a state is considered and its future behaviour is totally ignored. However, such intuition is inadequate when prioritised events are taken into consideration, since redirectability requires that the same state \(y_T\) from some test T should be reached before and after abstraction. If no restrictions over the future behaviour of incoming equivalent states are given, redirectability can be easily invalidated if two equivalent states have different preemptive power. In addition, we notice that when abstracting an automaton through quotient automaton construction, it is almost always required that the quotient automaton of a \(\Upsilon \)-shaped automaton shall be \(\Upsilon \)-shaped as well, which can not be guaranteed solely by incoming equivalence. To this end, we first introduce our definitions of active-event equivalence and silent-continuation equivalence.
Definition 3.3.5
Let \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) be a \(\Upsilon \)-shaped automaton. An equivalence \(\sim _\text {ae}\,\subseteq Q\times Q\) on G is an active-event equivalence if for any \(x,x'\in Q\) so that \(x\sim _\text {ae}x'\) and \(x\ne x'\), the following two statements hold:
-
(AE1)
\(G_\textrm{slnt}(x)=G_\textrm{slnt}(x')=\emptyset \);
-
(AE2)
\(G_\textrm{rglr}(x)=G_\textrm{rglr}(x')\).
Definition 3.3.6
Let \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) be a \(\Upsilon \)-shaped automaton. An equivalence \(\sim _\text {sc}\,\subseteq Q\times Q\) on G is a silent-continuation equivalence if for any \(x,x'\in Q\) so that \(x\sim _\text {sc}x'\) and \(x\ne x'\), all the following statements hold for some \(\tau \in \Upsilon \):
-
(SC1)
\(\tau \in G(x)\cap G(x')\);
-
(SC2)
\(G_\textrm{rglr}^{<\tau }(x)=G_\textrm{rglr}^{<\tau }(x')=\emptyset \);
-
(SC3)
Neither x nor \(x'\) is in any live-lock.
Similar to \(\sim _\text {inc}\), we utilise \(\sim _\text {ae}\), \(\sim _\text {sc}\) to denote the coarsest active-event equivalence and silent-continuation equivalence and write \(\sim \,\subseteq \,\sim _\text {ae}\) or \(\sim \,\subseteq \,\sim _\text {sc}\) to denote that \(\sim \) is an equivalence of the corresponding type, respectively. By combining \(\sim _\text {inc}\) with either \(\sim _\text {ae}\) or \(\sim _\text {sc}\), the redirectability can be achieved.
Proposition 3.3.7
Let \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) be a \(\Upsilon \)-shaped automaton with an equivalence \(\sim \,\subseteq Q\times Q\) on G be such that either \(\sim \,\subseteq \,\sim _\text {inc}\!\cap \!\sim _\text {ae}\) or \(\sim \,\subseteq \,\sim _\text {inc}\!\cap \!\sim _\text {sc}\). It holds that \(\sim \) is redirectable.
Before proceeding to prove Proposition 3.3.7, note that \(\sim _\text {ae}\) imposes a relatively strong restriction on equivalent states that silent events are never active on any state in a non-singleton class. Readers familiar with Flordal and Malik (2009) may be curious about the possibility of relaxing Definition 3.3.5 to equate states with regular active events delayed by \(\mathrel {{{\Rightarrow }^{\epsilon }}{}}\), i.e., by defining \(\Delta _\textrm{ae}(x):=\{\sigma \in \Sigma \,\vert \, x\mathrel {{{\Rightarrow }^{\epsilon }}{}}\mathrel {{\xrightarrow []{\sigma }}{}}\}\), one may expect that \(x\sim x'\) when \(\Delta _\textrm{ae}(x)=\Delta _\textrm{ae}(x')\). However, combining such a “relaxed” active-event equivalence with incoming equivalence does not guarantee conflict equivalence. Consider the following example:
Example 6
Consider automata G and T given in Fig. 6. Note that G is \(\Upsilon \)-shaped and \(\textrm{I}\sim _\text {inc}\textrm{III}\) clearly holds since state \(\textrm{III}\) can be reached from the initial state through \(\tau _{(1)}^*\). Furthermore, from \(\Delta _\textrm{ae}(x)=\Delta _\textrm{ae}(x')\), we equate \(\textrm{I}\) and \(\textrm{III}\) from the “relaxed” active-event equivalence, which results in \(G/{\sim }\). In this case, although \(([\textrm{II}],\textrm{ii})\) is reachable in \(\mathcal {S}(G/{\sim }\parallel T)\), \((\textrm{II},\textrm{ii})\) is not reachable in \(\mathcal {S}(G_{}\parallel T)\) since \(\textrm{i}\mathrel {{\xrightarrow []{\tau _{(2)}}}{}}\textrm{ii}\) cannot happen before \(\textrm{I}\mathrel {{\xrightarrow []{\tau _{(1)}}}{}}\textrm{III}\) and the transition \(\textrm{I}\mathrel {{\xrightarrow []{\sigma }}{}}\textrm{II}\) is labelled by a shared event \(\sigma \). One observes that in this example, \(\textrm{I}\mathrel {{\xrightarrow []{\tau _{(1)}}}{}}\textrm{III}\) somewhat “disables” \(\textrm{I}\mathrel {{\xrightarrow []{\sigma }}{}}\textrm{II}\) although both events are with the same priority. In this case, equating \(\textrm{I}\) and \(\textrm{III}\) does not guarantee conflict equivalence, especially when both states have different future behaviour, e.g. one leads to a non-blocking future while another blocks. Finally, it is also worth noting that “preserving” \(\textrm{I}\mathrel {{\xrightarrow []{\tau _{(1)}}}{}}\textrm{III}\) into a \(\tau _{(1)}\)-self-loop (which is against the quotient automaton construction) in \(G/{\sim }\) does not solve the issue, since a 1-live-lock will be formed in the quotient automaton which was not existent in G.
As a counterexample, Example 6 shows that for two incoming equivalent states, additionally requiring them to have the same preemptive power is essential to achieve redirectability. Otherwise, private transitions in T may be inconsistently preempted. This can be guaranteed by \(\sim _\text {ae}\) or \(\sim _\text {sc}\), as being stated in the following lemma.
Lemma 3.3.8
Let \(G=\langle Q_{G},\Sigma _{G}, \rightarrow _{G}, Q^\circ _{G}, M_{G}\rangle \) be a \(\Upsilon \)-shaped automaton. Let \(\sim \,\subseteq Q\times Q\) be an equivalence on G so that either \(\sim \,\subseteq \,\sim _\text {ae}\) or \(\sim \,\subseteq \,\sim _\text {sc}\) holds. For any automaton \(T=\langle Q_{T},\Sigma _{T}, \rightarrow _{T}, Q^\circ _{T}, M_{T}\rangle \) and any trace
in \(\mathcal {S}(G_{}\parallel T)\) where \(k\ge 0\) and \(\tau _i\in \Sigma _{T\backslash G}\) for all \(i\in \{1,\dots ,k\}\), it holds that for any \(x'_G\in [x_G]\), a trace
exists in \(\mathcal {S}(G_{}\parallel T)\) as well.
Proof
The claim is trivially true from (AE1), (AE2), (SC1) and (SC2).\(\square \)
At the current stage, the fundamental components for achieving redirectability have indeed been collected. In fact, we can temporarily define a “strengthened incoming equivalence”, denoted by \(\sim _{\textrm{inc}}^!\), by strengthening Definition 3.3.4 as such that
-
all \(\hookrightarrow \)-transitions are uniformly replaced by \(\mathrel {{{\Rightarrow }^{\epsilon }}{}}\) (strengthens (I1) and (I2)) and
-
“implies \(G_\textrm{rglr}^{<\tau }(y)=\emptyset \)” in (I3) is uniformly replaced by “implies \(\tau =\tau _{(1)}\)” (strengthens (I3)).
Within this definition, redirectability could be easily achieved by either \(\sim _{\textrm{inc}}^!\cap \sim _\text {ae}\) or \(\sim _{\textrm{inc}}^!\cap \sim _\text {sc}\), i.e. a slightly strengthened version of Proposition 3.3.7 (which can be obtained by uniformly substituting \(\sim _\text {inc}\) with \(\sim _{\textrm{inc}}^!\)) can be easily shown to be true. Instead of proving it formally, we consider the following example, in which we utilise a test T to give us some intuition of why substituting \(\sim _\text {inc}\) with \(\sim _{\textrm{inc}}^!\) in Proposition 3.3.7 yields a statement that obviously holds. The observations from this example will be generalised later on, to support the proof of Proposition 3.3.7.
Example 7
Consider automata G and T given in Fig. 7. Note that in G, states are partitioned by the equivalence \(\sim \) so that \((\textrm{II},\textrm{IV})\in \ \sim \ \subseteq \ \sim _\textrm{inc}^!\cap \sim _\text {ae}\). In this case, \(\sim \) is redirectable. We consider synchronising G with an automaton T. In particular, since state \((\textrm{II},\textrm{ii})\) is reachable, the reachability of state \((\textrm{IV},\textrm{ii})\) should be guaranteed as well to achieve redirectability since \(\textrm{II}\sim \textrm{IV}\). This must hold since the only silent predecessor of \(\textrm{IV}\), i.e. \(\textrm{III}\), reaches \(\textrm{IV}\) via \(\tau _{(1)}\). Thus, regardless the priority of successive transition in T, G can always execute all its \(\tau _{(1)}\)-transitions first, then T executes its private transitions. However, this is not the case if we replace the transition label of \(\textrm{III}\mathrel {{\xrightarrow []{\tau _{(1)}}}{}}\textrm{IV}\) by e.g. \(\tau _{(2)}\), which results in \(G'\). The resulting equivalence relation \(\sim '\) is no longer redirectable, since \((\textrm{IV}',\textrm{ii})\) is rendered unreachable.
Despite the awareness that the strengthened incoming equivalence contributes to achieve redirectability, we are interested in a more relaxed definition, i.e. utilising the original Definition 3.3.4. By reviewing Example 7, the statement “G can always execute all its \(\tau _{(1)}\)-transitions first, then T executes its private transitions” can be relaxed by \(\hookrightarrow \)-transitions while still preserving redirectability. In the following, we consider the properties of \(\hookrightarrow \)-transitions by mainly focusing on traces under synchronisation with only private events. Such traces are referred to as asynchronous traces. Recall that from Definition 3.3.3, the execution of a \(\hookrightarrow \)-transition cannot be preempted by regular events. This is then reflected by (I3) in that, for some state x that is incoming equivalent to another state \(x'\), we require that each incoming silent transition sequence to x is indeed a \(\hookrightarrow \)-transition. This ensures that reaching x indeed always utilises some transition sequence from a \(\hookrightarrow \)-transition preceding to x. Note that temporarily in Lemma 3.3.9 and Proposition 3.3.10, we do not require either automaton to be \(\Upsilon \)-shaped since the discussed properties are stated for traces instead of for automata. This benefits some proofs in that two traces from their corresponding automata can be freely swapped.
Lemma 3.3.9
Let \(G=\langle Q_{G},\Sigma _{G}, \rightarrow _{G}, Q^\circ _{G}, M_{G}\rangle \) and \(T=\langle Q_{T},\Sigma _{T}, \rightarrow _{T}, Q^\circ _{T}, M_{T}\rangle \) be two arbitrary automata and
be an asynchronous trace in \(\mathcal {S}(G_{}\parallel T)\) so that \(k\ge 0\) and for all \(i\in \{1,\cdots ,k\}\), \((x_G,x_{Ti-1})\mathrel {{\xrightarrow []{\tau _j}}{}^{\mathcal {S}}}(x_G,x_{Tj})\) is driven by T and \((x_G,x_{Tk})\mathrel {{\xrightarrow []{\tau _{k+1}}}{}^{\mathcal {S}}}(y_G,x_{Tk})\) is driven by G. It holds that \(\textsf{prio}(\tau _{k+1})\ge \textsf{lo}(\{\tau _1,\cdots ,\tau _k\})\).
Proof
Note that for all \(i\in \{1,\cdots ,k\}\), \((x_G,x_{Ti})\mathrel {{\xrightarrow []{\tau _{k+1}}}{}}\) in \(G_{}\parallel T\). Thus, the current statement must hold as the trace is in a shaped automaton \(\mathcal {S}(G_{}\parallel T)\).\(\square \)
The statement of Lemma 3.3.9 may seem verbose at first glance. Nevertheless, it induces an interesting property of asynchronous traces in shaped synchronous compositions: each time when the “transition-driving” automaton alternates, the priority of the silent event on the next transition cannot elevate. Consider the sketch in Fig. 8, where an asynchronous trace under shaped synchronous composition is given in grid. Points on the horizontal axis correspond to states in \(Q_G\), while those on the vertical axis correspond to states in \(Q_T\). Consider those states at which the driving automaton alternates, i.e. the “direction” of the trace changes. We conclude from Lemma 3.3.9 that \(m\le n\le r\) must hold. More importantly, if the trace ends with a transition driven by G (this is indeed the case in Fig. 8), it can be immediately concluded that the last “T-state” of the last state (\(x_{Tk}\) in Fig. 8) cannot execute any private events whose priority is higher than any transition in the trace. At the same time, the lowest priority of all transitions driven by G cannot be higher than the lowest priority of any transition driven by T. These properties are formalised by the following proposition.
Proposition 3.3.10
Let \(G=\langle Q_{G},\Sigma _{G}, \rightarrow _{G}, Q^\circ _{G}, M_{G}\rangle \) and \(T=\langle Q_{T},\Sigma _{T}, \rightarrow _{T}, Q^\circ _{T}, M_{T}\rangle \) be two arbitrary automata and
be an asynchronous trace in \(\mathcal {S}(G_{}\parallel T)\) where \(k\ge 1\) and the last transition \((x_{Gk-1},x_{Tk-1})\mathrel {{\xrightarrow []{\tau _k}}{}^{\mathcal {S}}}(x_{Gk},x_{Tk})\) is driven by G.
-
(i)
Let \(n=\textsf{lo}(\{\tau _1,\cdots ,\tau _k\})\). It holds that \(T_\textrm{prvt}^{<n}(x_{Tk})=\emptyset \);
-
(ii)
If at least one transition in Eq. 30 is driven by T ,then \(n_G\ge n_T\) where
$$\begin{aligned} n_G=&{}\textsf{lo}(\{\tau _i\,\vert \, (x_{Gi-1},x_{Ti-1})\mathrel {{\xrightarrow []{\tau _i}}{}^{\mathcal {S}}}(x_{Gi},x_{Ti}) \text { is driven by } G\});\end{aligned}$$(31)$$\begin{aligned} n_T=&{} \textsf{lo}(\{\tau _i\,\vert \, (x_{Gi-1},x_{Ti-1}) \mathrel {{\xrightarrow []{\tau _i}}{}^{\mathcal {S}}}(x_{Gi},x_{Ti}) \text { is driven by } T\}). \end{aligned}$$(32)
Proof
Note that both statements hold trivially if all transitions in Eq. 30 are driven by G. Thus, we assume that there exists at least one transition driven by T in Eq. 30.
(i) Let \(\tau \in T_\textrm{prvt}(x_{Tk})\) and consider the trace fragment
where \(0\le i<j<k\) and all transitions before \((x_{Gj},x_{Tj})\) are driven by T while all transitions after \((x_{Gj},x_{Tj})\) are driven by G. It follows immediately that \(\textsf{prio}(\tau )\ge \textsf{lo}\{\tau _{j+1},\cdots ,\tau _k\}\ge \textsf{prio}(\tau _{j+1})\). Furthermore, from Lemma 3.3.9, we have \(\textsf{prio}(\tau _{j+1})\ge \textsf{lo}\{\tau _{i+1},\cdots ,\tau _j\}\ge \textsf{prio}(\tau _{i+1})\). This is sufficient for an induction to reason the entire trace.
(ii) Consider the trace fragment \((x_{Gi},x_{Ti})\mathrel {{\xrightarrow []{\tau _{i+1}}}{}^{\mathcal {S}}}\cdots \mathrel {{\xrightarrow []{\tau _{k}}}{}^{\mathcal {S}}}(x_{Gk},x_{Tk})\) where \(0<i<k\) and all transitions are driven by G but \((x_{Gi-1},x_{Ti-1})\mathrel {{\xrightarrow []{\tau _i}}{}^{\mathcal {S}}}(x_{Gi},x_{Ti})\) is driven by T. The current statement is clearly true since \(\textsf{prio}(\tau _{i+1})\ge n_T\) from statement (i) by swapping G and T, and \(n_G\ge \textsf{prio}(\tau _{i+1})\) must hold as well.\(\square \)
Combining Proposition 3.3.10 and Lemma 3.3.8, we are now in the position to conclude the following Proposition 3.3.11. Specifically, part (ii) of the proposition will be the key property to establish Proposition 3.3.7. Note that the Example 7 is a special case of 3.3.11.(ii) and we suggest the reader to first consider this statement. For the case that either all transitions in Eq. 34 are driven by G or by T, the proof of 3.3.11.(ii) is straight forward. For the general case, Proposition 3.3.11.(ii) is established via the iterative construction in 3.3.11.(i). Also note that we again require G to be \(\Upsilon \)-shaped from now on.
Proposition 3.3.11
Let \(G=\langle Q_{G},\Sigma _{G}, \rightarrow _{G}, Q^\circ _{G}, M_{G}\rangle \) be a \(\Upsilon \)-shaped automaton and
be an asynchronous trace in \(\mathcal {S}(G_{}\parallel T)\) where \(k\ge 0\). Let \(n=\textsf{lo}(\{\tau _i\,\vert \, (x_{Gi-1},x_{Ti-1})\mathrel {{\xrightarrow []{\tau _i}}{}}(x_{Gi},x_{Ti}) \text { is driven by } G\})\) and
with \(k'\) \(\ge 0\) be a trace in G so that all events on this trace are silent, \(\textsf{lo}(\{\tau '_1,\cdots ,\tau '_{k'}\})=n\) and for all \(i'\in \{1,\cdots ,k'\}\), \(G_\textrm{rglr}^{<\tau '_i}(x'_{Gi'-1})=\emptyset \).Footnote 3 The following two statements hold:
-
(i)
Let \(k\ge 1\), \(k'\ge 1\) and let the last transition \((x_{Gk-1},x_{Tk-1})\mathrel {{\xrightarrow []{\tau _k}}{}^{\mathcal {S}}}(x_{Gk},x_{Tk})\) in Eq. 34 be driven by G. Under these assumptions, we have \((x'_{G0},x_{T0})\mathrel {{{\Rightarrow }^{\textsf{p}(\tau _1\cdots \tau _k)}}{}^{\mathcal {S}}}(x'_{Gk'},x_{Tk})\) in \(\mathcal {S}(G_{}\parallel T)\) where the last transition is driven by G;
-
(ii)
Let \(\sim \,\subseteq Q_G\times Q_G\) be an equivalence on G so that either \(\sim \,\subseteq \,\sim _\text {ae}\) or \(\sim \,\subseteq \,\sim _\text {sc}\). If \(x_{Gk}\sim x'_{Gk'}\), then \((x'_{G0},x_{T0})\mathrel {{{\Rightarrow }^{\textsf{p}(\tau _1\cdots \tau _k)}}{}^{\mathcal {S}}}(x'_{Gk'},x_{Tk})\) in \(\mathcal {S}(G_{}\parallel T)\).
Proof
Note that the restriction \(G_\textrm{rglr}^{<\tau '_i}(x'_{Gi'-1})=\emptyset \) for \(i'\in \{1,\cdots ,k'\}\) excludes the possibility of preemption through regular events before reaching \(x'_{Gk'}\). For convenience, let \(n'= \textsf{lo}(\{\tau '_1,\cdots ,\tau '_{k'}\})\).
(i) It suffices to construct an asynchronous trace from \((x'_{G0},x_{T0})\) to \((x'_{Gk'},x_{Tk})\) which will not be influenced by shaping and the last transition is driven by G. Let \(i'=j=0\) and we start the construction from the first state \((x'_{Gi'},x_{Tj})=(x'_{G0},x_{T0})\). Note that due to Case 2 of Step 2 in the following, it is not possible to reach \(x'_{Gk'}\) before \(x_{Tk}\) is reached.
-
(Step 1)
Consider two possible cases:
-
(Case 1)
Only \(j=k\) holds, i.e. \(x_{Tk}\) is reached. Consider the trace given in Eq. 34 and from Proposition 3.3.10.(i), it follows that \(T_\textrm{prvt}^{<n}(x_{Tk})=\emptyset \). Since \(n=n'\) is required, we are able to directly complete the construction by concatenating the remaining transitions driven by G to reach \(x'_{Gk'}\), i.e. we must have \((x'_{Gi'},x_{Tk})\mathrel {{{\Rightarrow }^{\epsilon }}{}^{\mathcal {S}}}(x'_{Gk'},x_{Tk})\) where all transitions are driven by G in \(\mathcal {S}(G_{}\parallel T)\), since priority of all remaining transitions driven by G cannot be lower than any \(\tau \in T_\textrm{prvt}(x_{Tk})\) and preemption through shared events is impossible. This terminates the construction.
-
(Case 2)
Neither \(i'=k'\) nor \(j=k\) holds. Proceed to Step 2.
-
(Case 1)
-
(Step 2)
Since preemption through shared prioritised events is not possible, we can proceed from \((x'_{Gi'},x_{Tj})\) with either one transition driven by G or one driven by T, or both. Consider the two possible cases:
-
(Case 1)
\(\textsf{prio}(\tau '_{Gi'+1})\ne n'\). Then concatenate either \((x'_{Gi'},x_{Tj})\mathrel {{\xrightarrow []{\tau '_{i'+1}}}{}^{\mathcal {S}}}(x'_{Gi'+1},x_{Tj})\) or \((x'_{Gi'},x_{Tj})\mathrel {{\xrightarrow []{\tau _{j+1}}}{}^{\mathcal {S}}}(x'_{Gi'},x_{Tj+1})\) according to their priority and update either \(i':=i'+1\) or \(j:=j+1\), respectively. Note that each time when the current case is met, we must have not reached \(x'_{Gk'}\) yet since the transition with the lowest priority in Eq. 35 has not been reached yet. Go back to Step 1.
-
(Case 2)
\(\textsf{prio}(\tau '_{Gi'+1}) = n'\). Since \(n=n'\) was required, from Proposition 3.3.10.(ii), it follows that \(\textsf{prio}(\tau '_{Gi'+1}) \!=\! n \!\ge \! \textsf{lo}(\{\tau _i\,\vert \, \!(x_{Gi-1},x_{Ti-1})\mathrel {{\xrightarrow []{\tau _i}}{}^{\mathcal {S}}}(x_{Gi},x_{Ti})\, \text {is driven by} T\})\). Thus, we are able to concatenate the remaining transitions driven by T to reach \(x_{Tk}\), i.e. we have \((x'_{Gi'},x_{Tj})\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}(x'_{Gi'},x_{Tk})\) where all transitions are driven by T in \(\mathcal {S}(G_{}\parallel T)\) and \(s_T\in T_\textrm{prvt}^*\) is the remaining private event sequence in T. Update \(j:=k\) and go to Step 1. We will be in Case 1 of Step 1.
-
(Case 1)
(ii) The current statement holds trivially if all transitions in Eq. 34 are driven by G. In addition, the current statement holds directly if all transitions in Eq. 34 are driven by T from Lemma 3.3.8. Thus, it suffices to consider Eq. 34 as such that it includes at least one transition driven by G and one transition driven by T. In this case, if the last transition in Eq. 34 is driven by G, the current statement holds directly as well from statement (i). The only remaining case is that Eq. 34 ends with such a trace fragment \((x_{Gi},x_{Ti})\mathrel {{\xrightarrow []{\tau _{i+1}}}{}^{\mathcal {S}}}\cdots \mathrel {{\xrightarrow []{\tau _k}}{}^{\mathcal {S}}}(x_{Gk},x_{Tk})\) with \(i\in \{1,\cdots ,k-1\}\) where all transitions are driven by T (i.e. \(x_{Gi}=x_{Gk}\)) and \((x_{Gi-1},x_{Ti-1})\mathrel {{\xrightarrow []{\tau _i}}{}^{\mathcal {S}}}(x_{Gi},x_{Ti})\) is driven by G. From statement (i), \((x'_{G0},x_{T0})\mathrel {{{\Rightarrow }^{\textsf{p}(\tau _1\cdots \tau _i)}}{}^{\mathcal {S}}}(x'_{Gk'},x_{Ti})\) in \(\mathcal {S}(G_{}\parallel T)\) holds. Furthermore, due to Lemma 3.3.8, we must be able to concatenate the remaining transitions driven by T to reach \(x_{Tk}\), i.e. \((x'_{Gk'},x_{Ti})\mathrel {{{\Rightarrow }^{\textsf{p}(\tau _{i+1}\cdots \tau _k)}}{}^{\mathcal {S}}}(x'_{Gk'},x_{Tk})\).\(\square \)
Proposition 3.3.11.(ii) shows us an important property between asynchronous traces when preemption through shared events is excluded: for two traces with the same lowest priority and both final states are equivalent w.r.t. either \(\sim _\text {ae}\) or \(\sim _\text {sc}\), they can be utilised to synchronise the same private-event trace. This matches the definition of \(\hookrightarrow \)-transition which is utilised in Definition 3.3.4. With all the preparation, we are now ready to prove that Proposition 3.3.7 is true.
Proof (Proof of Proposition 3.3.7)
[Proof of Proposition 3.3.7] We establish (R1) as follows. Given any sequence of transitions \((x_G,x_T)\mathrel {{\xrightarrow []{\sigma }}{}^{\mathcal {S}}}\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}(y_G,y_T)\) in \(\mathcal {S}(G_{}\parallel T)\) with \(\sigma \in \Sigma _G\), we pick any arbitrary \(y'_G\in [y_G]\). If \(y'_G=y_G\), we directly obtain \((x_G,x_T)\mathrel {{{\Rightarrow }^{\sigma s_T}}{}^{\mathcal {S}}}(y'_G,y_T)\), which settles the trivial case. We now assume \(y'_G\ne y_G\) and pick \(\bar{x}_G\in Q_G\) and \(\bar{x}_T\in Q_T\) so that \((x_G,x_T)\mathrel {{\xrightarrow []{\sigma }}{}^{\mathcal {S}}}(\bar{x}_G,\bar{x}_T)\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}(y_G,y_T)\) in \(\mathcal {S}(G_{}\parallel T)\). For the fragment \((\bar{x}_G,\bar{x}_T)\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}(y_G,y_T)\), there must exist a silent transition sequence that connects \(\bar{x}_G\) and \(y_G\) in G, and by (I3), this silent transition sequence must be able to be written in the form of
 with some \(n\in \mathbb {N}\). From (I1), for each \(y'_G\), we must have some \(\bar{x}'_G\in Q_G\) so that
with some \(n\in \mathbb {N}\). From (I1), for each \(y'_G\), we must have some \(\bar{x}'_G\in Q_G\) so that
 where \(\Delta = G_\textrm{rglr}^{<\sigma }(x_G)\). Clearly, we directly have \((x_G,x_T)\mathrel {{{\Rightarrow }^{\sigma }}{}^{\mathcal {S}}}(\bar{x}'_G,\bar{x}_T)\). In addition, since we are having both
where \(\Delta = G_\textrm{rglr}^{<\sigma }(x_G)\). Clearly, we directly have \((x_G,x_T)\mathrel {{{\Rightarrow }^{\sigma }}{}^{\mathcal {S}}}(\bar{x}'_G,\bar{x}_T)\). In addition, since we are having both
 and
and
 , \((\bar{x}'_G,\bar{x}_T)\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}(y'_G,y_T)\) can also be guaranteed from Proposition 3.3.11.(ii) or directly from Lemma 3.3.8. This indeed shows that (R1) of Definition 3.3.1 is fulfilled. The proof for (R2) is similar by only considering \((\bar{x}_G,\bar{x}_T)\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}(y_G,y_T)\) and letting \((\bar{x}_G,\bar{x}_T)\) be any initial state in \(\mathcal {S}(G_{}\parallel T)\).\(\square \)
, \((\bar{x}'_G,\bar{x}_T)\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}(y'_G,y_T)\) can also be guaranteed from Proposition 3.3.11.(ii) or directly from Lemma 3.3.8. This indeed shows that (R1) of Definition 3.3.1 is fulfilled. The proof for (R2) is similar by only considering \((\bar{x}_G,\bar{x}_T)\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}(y_G,y_T)\) and letting \((\bar{x}_G,\bar{x}_T)\) be any initial state in \(\mathcal {S}(G_{}\parallel T)\).\(\square \)
With Proposition 3.3.7 proved, the conjunction of \(\sim _\text {inc}\) with either \(\sim _\text {ae}\) or \(\sim _\text {sc}\) guarantees that a trace in the original behaviour can be reconstructed from a trace after abstraction. To imply conflict-equivalence (which is an if-and-only-if statement), a similar property in the converse direction is to clarify as well.
Proposition 3.3.12
Let \(G=\langle Q_{G},\Sigma _{G}, \rightarrow _{G}, Q^\circ _{G}, M_{G}\rangle \) be a \(\Upsilon \)-shaped automaton with an equivalence \(\sim \,\subseteq Q_G\times Q_G\) on G so that either \(\sim \,\subseteq \,\sim _\text {ae}\) or \(\sim \,\subseteq \,\sim _\text {sc}\) holds. For any automaton \(T=\langle Q_{T},\Sigma _{T}, \rightarrow _{T}, Q^\circ _{T}, M_{T}\rangle \) and any transition \((x_G,x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}(y_G,y_T)\) in \(\mathcal {S}(G_{}\parallel T)\), it holds that \(([x_G],x_T)\mathrel {{\xrightarrow []{\textsf{p}(\alpha )}}{}^{\mathcal {S}}}([y_G],y_T)\) in \(\mathcal {S}(G/{\sim }\parallel T)\).
Proof
If \(x_G\sim y_G\), \(\alpha \in \Upsilon \) and \((x_G,x_T)\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}(y_G,y_T)\) is driven by G, we will have a transition \(([x_G],x_T)\mathrel {{\xrightarrow []{\epsilon }}{}^{\mathcal {S}}}([y_G],y_T)=([x_G],x_T)\) in \(\mathcal {S}(G/{\sim }\parallel T)\). Otherwise, \(([x_G],x_T)\xrightarrow {\alpha }([y_G],y_T)\) in \(G/{\sim }\parallel T\). This transition will clearly not be shaped due to the definition of \(\sim _\text {ae}\) and \(\sim _\text {sc}\).\(\square \)
We are now in the position to state two conflict-preserving abstraction rules, i.e. the active events rule and the silent continuation rule, in Theorems 3.3.14 and 3.3.15. For the active events rule, the following lemma is given to simplify the proof.
Lemma 3.3.13
Let \(G=\langle Q_{G},\Sigma _{G}, \rightarrow _{G}, Q^\circ _{G}, M_{G}\rangle \) be a \(\Upsilon \)-shaped automaton with an equivalence \(\sim \,\subseteq \,\sim _\text {ae}\). For any automaton \(T=\langle Q_{T},\Sigma _{T}, \rightarrow _{T}, Q^\circ _{T}, M_{T}\rangle \), if \(([x_G],x_T)\mathrel {{{\Rightarrow }^{s_T\textsf{p}(\alpha )}}{}^{\mathcal {S}}}\) in \(\mathcal {S}(G/{\sim }\parallel T)\) for some \(x_G\in Q_G\), \(x_T\in Q_T\), \(s_T\in \Sigma _{T\backslash G}^*\) and \(\alpha \in A_G\), then for all \(x'_G\in [x_G]\), \((x'_G,x_T)\mathrel {{{\Rightarrow }^{s_T \textsf{p}(\alpha )}}{}^{\mathcal {S}}}\) in \(\mathcal {S}(G_{}\parallel T)\).
Proof
Recall that for any non-singleton class \([x_G]\), \(G_\textrm{slnt}(x_G)=\emptyset \) must hold. Consider two cases:
-
(Case 1)
\(\alpha \in \Upsilon \). If there is some trace in \(([x_G],x_T)\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}\) where all transitions are not driven by G, the current statement is directly true due to Lemma 3.3.8. Otherwise, let
$$\begin{aligned} ([x_G],x_T)\mathrel {{{\Rightarrow }^{t_T}}{}^{\mathcal {S}}}([\bar{x}_G],y_T)\mathrel {{\xrightarrow []{\tau }}{}^{\mathcal {S}}}([y_G],y_T)\mathrel {{{\Rightarrow }^{u_T}}{}^{\mathcal {S}}} \end{aligned}$$(36)in \(\mathcal {S}(G/{\sim }\parallel T)\) for some \(\tau \in \Upsilon \), \(\bar{x}_G,y_G\in Q_G\), \(y_T\in Q_T\), \(t_Tu_T=s_T\), \(([\bar{x}_G],y_T)\mathrel {{\xrightarrow []{\tau }}{}^{\mathcal {S}}}([y_G],y_T)\) is driven by G and all transitions in the fragment \(([y_G],y_T)\mathrel {{{\Rightarrow }^{u_T}}{}^{\mathcal {S}}}\) are not driven by G. Note that all states on \([x_G]\mathrel {{{\Rightarrow }^{\epsilon }}{}_{{}_\sim }}[\bar{x}_G]\) in \(G/{\sim }\) are singletons. Thus, there must exist \(y'_G\in [y_G]\) so that \((x_G,x_T)\mathrel {{{\Rightarrow }^{t_T}}{}^{\mathcal {S}}}(\bar{x}_G,y_T)\mathrel {{\xrightarrow []{\tau }}{}^{\mathcal {S}}}(y'_G,y_T)\) in \(\mathcal {S}(G_{}\parallel T)\). In addition, \((y'_G,y_T)\mathrel {{{\Rightarrow }^{u_T}}{}}\) in \(\mathcal {S}(G/{\sim }\parallel T)\) must hold due to Lemma 3.3.8.
-
(Case 2)
\(\alpha \in \Sigma _G\), i.e. \(\textsf{p}(\alpha )=\alpha \) and we have \(([x_G],x_T)\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}\) in \(\mathcal {S}(G/{\sim }\parallel T)\). Following Case 1, if there exists a trace on the fragment \(([x_G],x_T)\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}\) where all transitions are not driven by G, then the current statement holds directly in that for all \(x'_G\in [x_G]\), \(\alpha \in G(x'_G)\) holds. Otherwise, consider concatenating an \(\alpha \) transition at the end of Eq. 36, i.e.
$$\begin{aligned} ([x_G],x_T)\mathrel {{{\Rightarrow }^{t_T}}{}^{\mathcal {S}}}([\bar{x}_G],y_T)\mathrel {{\xrightarrow []{\tau }}{}^{\mathcal {S}}}([y_G],y_T)\mathrel {{{\Rightarrow }^{u_T}}{}^{\mathcal {S}}}\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}. \end{aligned}$$(37)Recall that all transitions on the fragment \(([y_G],y_T)\mathrel {{{\Rightarrow }^{u_T}}{}^{\mathcal {S}}}\) are not driven by G, i.e. before executing the final \(\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}\)-transition, \([y_G]\) will not execute any transition. Thus, from Lemma 3.3.8, \((x_G,x_T)\mathrel {{{\Rightarrow }^{t_T}}{}^{\mathcal {S}}}(\bar{x}_G,y_T)\mathrel {{\xrightarrow []{\tau }}{}^{\mathcal {S}}}(y'_G,y_T)\mathrel {{{\Rightarrow }^{u_T}}{}^{\mathcal {S}}}\mathrel {{\xrightarrow []{\alpha }}{}^{\mathcal {S}}}\) for some \(y'_G\in [y_G]\) must hold.\(\square \)
Theorem 3.3.14
[active events rule] Let \(G=\langle Q_{G},\Sigma _{G}, \rightarrow _{G}, Q^\circ _{G}, M_{G}\rangle \) be a \(\Upsilon \)-shaped automaton with an equivalence \(\sim \,\subseteq \,\sim _\text {ae}\cap \sim _\text {inc}\) on G. It holds \(G\simeq _\mathcal {S} (G/{\sim })\).
Proof
Let \(T=\langle Q_{T},\Sigma _{T}, \rightarrow _{T}, Q^\circ _{T}, M_{T}\rangle \) be any automaton:
(\(\Rightarrow \)) Suppose \(\mathcal {S}(G_{}\parallel T)\) is non-blocking. Pick \(x_G\in Q_G\), \(x_T\in Q_T\) and \(s\in (\Sigma _G\cup \Sigma _T)^*\) so that \(\mathcal {S}(G/{\sim }\parallel T)\mathrel {{{\Rightarrow }^{s}}{}^{\mathcal {S}}}([x_G],x_T)\). By Proposition 3.3.2.(ii), there exists \(x'_G\in [x_G]\) so that \(\mathcal {S}(G_{}\parallel T)\mathrel {{{\Rightarrow }^{s}}{}^{\mathcal {S}}}(x'_G,x_T)\) and due to the non-blockingness of \(\mathcal {S}(G_{}\parallel T)\), for each \(\Omega \in M_G\cup M_T\), there exists \(\omega \in \Omega \) so that \((x'_G,x_T)\mathrel {{{\Rightarrow }^{t\omega }}{}^{\mathcal {S}}}\) in \(\mathcal {S}(G_{}\parallel T)\) for some \(t\in (\Sigma _G\cup \Sigma _T)^*\). By Proposition 3.3.12, it holds that \(([x_G],x_T)\mathrel {{{\Rightarrow }^{t\omega }}{}^{\mathcal {S}}}\).
(\(\Leftarrow \)) Suppose \(\mathcal {S}(G/{\sim }\parallel T)\) is non-blocking and pick \(x_G\in Q_G\), \(x_T\in Q_T\) and \(s\in (\Sigma _G\cup \Sigma _T)^*\) so that \(\mathcal {S}(G_{}\parallel T)\mathrel {{{\Rightarrow }^{s}}{}^{\mathcal {S}}}(x_G,x_T)\). From Proposition 3.3.12 and the non-blockingness of \(\mathcal {S}(G/{\sim }\parallel T)\), for each \(\Omega \in M_G\cup M_T\), there exists \(\omega \in \Omega \) and \(t\in (\Sigma _G\cup \Sigma _T)^*\) so that \(\mathcal {S}(G/{\sim }\parallel T)\mathrel {{{\Rightarrow }^{s}}{}^{\mathcal {S}}}([x_G],x_T)\mathrel {{{\Rightarrow }^{t\omega }}{}^{\mathcal {S}}}\). There are two cases:
-
(Case 1)
\(t\in \Sigma _{T\backslash G}^*\). This case holds directly from Lemma 3.3.13. Note that the sub-case of \(\omega \in \Sigma _{T\backslash G}\) holds as well.
-
(Case 2)
For any t, Case 1 does not hold. Then we must first have \(([x_G],x_T)\mathrel {{{\Rightarrow }^{s_T}}{}}\mathrel {{\xrightarrow []{\sigma }}{}}\) for some \(\sigma \in \Sigma _G-\Omega \) and \(s_T\in \Sigma _{T\backslash G}^*\). By applying Lemma 3.3.13, we have
$$\begin{aligned} (x_G,x_T)\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}(\bar{x}_G,\bar{x}_T)\mathrel {{\xrightarrow []{\sigma }}{}^{\mathcal {S}}}(y_G,y_T) \end{aligned}$$(38)in \(\mathcal {S}(G_{}\parallel T)\) for some \(\bar{x}_G,y_G\in Q_G\) and \(\bar{x}_T,y_T\in Q_T\) so that \(s_T\sigma \leqslant t\). From Proposition 3.3.12 and the non-blockingness of \(\mathcal {S}(G/{\sim }\parallel T)\), \(([y_G],y_T)\mathrel {{{\Rightarrow }^{t'\omega '}}{}^{\mathcal {S}}}\) must hold for some \(t'\in (\Sigma _G\cup \Sigma _T)^*\) and \(\omega '\in \Omega \). Consider the following two sub-cases (which are comparable with Case 1 and Case 2), i.e. either
-
(i)
\(t'\omega '\in \Sigma _{T\backslash G}^+\). From Lemma 3.3.13, we directly have \((y_G,y_T)\mathrel {{{\Rightarrow }^{t'\omega '}}{}^{\mathcal {S}}}\).
-
(ii)
Case 2.(i) does not hold for any \(t'\omega '\). By applying Proposition 3.3.12 and then Lemma 3.3.13 again, we have altogether
$$\begin{aligned} (x_G,x_T)\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}(\bar{x}_G,\bar{x}_T)\mathrel {{\xrightarrow []{\sigma }}{}^{\mathcal {S}}}\mathrel {{{\Rightarrow }^{t_T}}{}^{\mathcal {S}}}(\bar{y}_G,\bar{y}_T)\mathrel {{\xrightarrow []{\sigma '}}{}^{\mathcal {S}}} \end{aligned}$$(39)in \(\mathcal {S}(G_{}\parallel T)\) for some \(\bar{y}_G\in Q_G\), \(\bar{y}_T\in Q_T\), \(t_T\in \Sigma _{T\backslash G}^*\) and \(\sigma '\in \Sigma _G\). From Proposition 3.3.12, Proposition 3.3.2.(i) and the non-blockingness of \(\mathcal {S}(G/{\sim }\parallel T)\), there exists \(\bar{y}'_G\in [\bar{y}_G]\), \(\omega ''\in \Omega \) and \(u\in (\Sigma _G\cup \Sigma _T)^*\) so that \((\bar{y}'_G,\bar{y}_T)\mathrel {{{\Rightarrow }^{u\omega ''}}{}^{\mathcal {S}}}\) and \(\sigma '\leqslant u\omega ''\). Note that \((\bar{x}_G,\bar{x}_T)\mathrel {{\xrightarrow []{\sigma }}{}^{\mathcal {S}}}\mathrel {{{\Rightarrow }^{t_T}}{}^{\mathcal {S}}}(\bar{y}_G,\bar{y}_T)\). From Proposition 3.3.7, \(\sim \) is redirectable and we thus have \((\bar{x}_G,\bar{x}_T)\mathrel {{{\Rightarrow }^{\sigma t_T}}{}^{\mathcal {S}}}(\bar{y}'_G,\bar{y}_T)\mathrel {{{\Rightarrow }^{u\omega ''}}{}^{\mathcal {S}}}\).\(\square \)
-
(i)
Example 8
Consider the automaton G given in Fig. 9. \(\textrm{I}\sim _\text {inc}\textrm{III}\) must hold since they both are initial states and can be reached from \(\textrm{IV}\) via \(\rho \). Besides, since they cannot execute silent events and they have the same set of active regular events, \(\textrm{I}\sim _\text {ae}\textrm{III}\) holds. Thus, \(\textrm{I}\) and \(\textrm{III}\) can be merged through the active events rule which results in the conflict equivalent \(G/{\sim }\).
Theorem 3.3.15
[silent continuation rule] Let \(G=\langle Q_{G},\Sigma _{G}, \rightarrow _{G}, Q^\circ _{G}, M_{G}\rangle \) be a \(\Upsilon \)-shaped automaton with an equivalence \(\sim \,\subseteq \,\sim _\text {inc}\cap \sim _\text {sc}\). It holds \(G\simeq _\mathcal {S} (G/{\sim })\).
Proof
Let \(T=\langle Q_{T},\Sigma _{T}, \rightarrow _{T}, Q^\circ _{T}, M_{T}\rangle \) be any automaton:
(\(\Rightarrow \)) Same as the proof of Theorem 3.3.14
(\(\Leftarrow \)) Suppose \(\mathcal {S}(G/{\sim }\parallel T)\) is non-blocking. Pick \(x_G\in Q_G\) and \(x_T\in Q_T\) so that \(\mathcal {S}(G_{}\parallel T)\mathrel {{{\Rightarrow }^{s}}{}^{\mathcal {S}}}(x_G,x_T)\) for some \(s\in (\Sigma _G\cup \Sigma _T)^*\). From Proposition 3.3.12 and the non-blockingness of \(\mathcal {S}(G/{\sim }\parallel T)\), for all \(\Omega \in M_G\cup M_T\), there exists \(t\in (\Sigma _G\cup \Sigma _T)^*\) and \(\omega \in \Omega \) so that \(\mathcal {S}(G/{\sim }\parallel T)\mathrel {{{\Rightarrow }^{s}}{}^{\mathcal {S}}}([x_G],x_T)\mathrel {{{\Rightarrow }^{t\omega }}{}^{\mathcal {S}}}\). Consider three cases:
-
(Case 1)
\([x_G]\) is a singleton and there exists some trace in \(([x_G],x_T)\mathrel {{{\Rightarrow }^{t\omega }}{}^{\mathcal {S}}}\) which begins with \(([x_G],x_T)\mathrel {{\xrightarrow []{\sigma }}{}^{\mathcal {S}}}\) for some \(\sigma \in \Sigma _G\). From Propositions 3.3.7, \(\sim \) is redirectable. Thus, this case is directly true from Proposition 3.3.2.(i).
-
(Case 2)
\([x_G]\) is not a singleton. Since \(x_G\) is not in any live-lock but there exists \(\tau \in G_\textrm{slnt}(x_G)\), there must exist some \(y_G\in Q_G\) so that \(x_G\mathrel {{{\Rightarrow }^{\epsilon }}{}}y_G\) and \(G_\textrm{slnt}(y_G)=\emptyset \) in G. There are two further possibilities:
-
(i)
There exists some \(s_T\in \Sigma _{T\backslash G}^*\), \(y_T\in Q_T\) and \(\sigma \in \Sigma _G\) so that \((x_G,x_T)\mathrel {{{\Rightarrow }^{s_T}}{}^{\mathcal {S}}}(y_G,y_T)\mathrel {{\xrightarrow []{\sigma }}{}^{\mathcal {S}}}\) in \(\mathcal {S}(G_{}\parallel T)\). Note that \(([y_G],y_T)\) must be co-reachable since from Proposition 3.3.12, \(([y_G],y_T)\) is reachable in \(\mathcal {S}(G/{\sim }\parallel T)\) which is non-blocking. In addition, since \(G_\textrm{slnt}(y_G)=\emptyset \), \([y_G]\) must be a singleton. Thus we have reached a Case 1 situation.
-
(ii)
If Case 2.(i) does not hold, then there exist \(z_G\in Q_G- \{y_G\}\), \(z_T\in Q_T\) and \(t_T\in \Sigma _{T\backslash G}^*\) so that \((x_G,x_T)\mathrel {{{\Rightarrow }^{t_T}}{}^{\mathcal {S}}}(z_G,z_T)\) and \(z_G\mathrel {{\xrightarrow []{\tau '}}{}}\mathrel {{{\Rightarrow }^{\epsilon }}{}}y_G\) for some \(\tau '\in \Upsilon \). In addition, the execution of \(z_G\mathrel {{\xrightarrow []{\tau '}}{}^{\mathcal {S}}}\) in \((z_G,z_T)\) is disallowed. This could be caused by
-
a)
\((z_G,z_T)\mathrel {{\xrightarrow []{\sigma }}{}^{\mathcal {S}}}\) in \(\mathcal {S}(G_{}\parallel T)\) for some \(\sigma \in \Sigma _G\) so that \(\textsf{prio}(\sigma )<\textsf{prio}(\tau ')\). This again implies that \([z_G]\) is a singleton state from (SC1) and (SC2), i.e. a Case 1 situation is reached; or
-
b)
\(z_T\) is in some n-live-lockFootnote 4 in T with \(n<\textsf{prio}(\tau ')\). Note that \(([z_G],z_T)\) must be co-reachable since from Proposition 3.3.12, \(([z_G],z_T)\) is reachable in \(\mathcal {S}(G/{\sim }\parallel T)\) which is non-blocking. In this situation, \([z_G]\) cannot execute any transition driven by G in \(\mathcal {S}(G/{\sim }\parallel T)\) as well (this is clear if \([z_G]\) is a singleton; otherwise \([z_G]\) is not a singleton, then from (SC2), all its active events are not executable due to the n-live-lock in T, which includes \(z_T\)). This implies \(M_G=\emptyset \). In addition, \(([z_G],z_T)\) is co-reachable in \(\mathcal {S}(G/{\sim }\parallel T)\) implies that \((z_G,z_T)\) is co-reachable in \(\mathcal {S}(G_{}\parallel T)\).
Note that we do not need to take special care to the situation where the execution of \(z_G\mathrel {{\xrightarrow []{\tau '}}{}^{\mathcal {S}}}\) in \((z_G,z_T)\) is preempted by a private active event in \(z_T\) whose priority is higher than \(\tau '\). This situation must lead to either (i), (ii).a) or (ii).b) in the current case.
-
a)
-
(i)
-
(Case 3)
\([x_G]\) is a singleton and all traces in \(([x_G],x_T)\mathrel {{{\Rightarrow }^{t\omega }}{}^{\mathcal {S}}}\) begin with an event \(\alpha \notin \Sigma _G\). If there exists some trace in \(([x_G],x_T)\mathrel {{{\Rightarrow }^{t\omega }}{}^{\mathcal {S}}}\) where each state consists of a singleton state from \(Q_G/{\sim }\), the current statement is trivially true. Otherwise, let
$$\begin{aligned} ([x_G],x_T)=([x_{G0}],x_{T0})&\mathrel {{\xrightarrow []{\alpha _1}}{}^{\mathcal {S}}}([x_{G1}],x_{T1})\mathrel {{\xrightarrow []{\alpha _2}}{}^{\mathcal {S}}}\cdots \nonumber \\&\cdots \mathrel {{\xrightarrow []{\alpha _k}}{}^{\mathcal {S}}}([x_{Gk}],x_{Tk})\mathrel {{\xrightarrow []{\alpha _{k+1}}}{}^{\mathcal {S}}}([x_{Gk+1}],x_{Tk+1})\mathrel {{\xrightarrow []{\alpha _{k+2}}}{}^{\mathcal {S}}}\cdots \end{aligned}$$(40)be a trace in \(([x_G],x_T)\mathrel {{{\Rightarrow }^{t\omega }}{}^{\mathcal {S}}}\) where \(k\ge 0\), \([x_{Gk+1}]\) is not a singleton and all \([x_{Gi}]\) with \(i\in \{0,\dots ,k\}\) are singletons. Clearly, \(([x_{Gk}],x_{Tk})\mathrel {{\xrightarrow []{\alpha _{k+1}}}{}^{\mathcal {S}}}([x_{Gk+1}],x_{Tk+1})\) is driven by \(G/{\sim }\) since \([x_{Gk}]\) is a singleton while \([x_{Gk+1}]\) is not. Clearly, there exists \(x'_{Gk+1}\in [x_{Gk+1}]\) so that \((x_{Gk},x_{Tk})\mathrel {{\xrightarrow []{\alpha _{k+1}}}{}^{\mathcal {S}}}(x'_{Gk+1},x_{Tk+1})\) in \(\mathcal {S}(G_{}\parallel T)\). This indicates that Case 3 always reaches a Case 2 situation if at least one non-singleton state is visited in \(([x_G],x_T)\mathrel {{{\Rightarrow }^{t\omega }}{}^{\mathcal {S}}}\).\(\square \)
Example 9
Consider the automaton G given in Fig. 10. Clearly, \(\textrm{II}\sim _\text {inc}\textrm{III}\) holds. In addition, \(\tau _{(2)}\in G_\textrm{slnt}(\textrm{II})\cap G_\textrm{slnt}(\textrm{III})\) while \(G_\textrm{rglr}^{<2}(\textrm{II})=G_\textrm{rglr}^{<2}(\textrm{III})=\emptyset \). This implies that \(\textrm{II}\sim _\text {sc}\textrm{III}\) and merging \(\textrm{II}\) and \(\textrm{III}\) yields a conflict-preserving abstraction.
At the end of the current section, we briefly introduce the adjustment of three further abstraction rules introduced in Flordal and Malik (2009). The adjustment of these rules follows immediately from the intuition in Flordal and Malik (2009). The first two rules are the only silent incoming rule and the only silent outgoing rule. Both rules can be adjusted in a straightforward manner by combining PWB and the silent continuation rule.
Theorem 3.3.16
[only silent incoming rule] Let \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) be a \(\Upsilon \)-shaped automaton and let \(\bar{x}\in Q\) be such that \(\bar{x}\) is not in any live-lock, \(\tau _{(1)}\in G(\bar{x})\) and \(y\mathrel {{\xrightarrow []{\alpha }}{}}\bar{x}\) implies \(\alpha =\tau _{(1)}\). For the automaton \(G'=\langle Q, \Sigma , \rightarrow ', Q^\circ , M\rangle \) with
it holds that \(G\simeq ^{\mathcal {S}}G'\).
Theorem 3.3.17
[only silent outgoing rule] Let \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) be a \(\Upsilon \)-shaped automaton and let \(\bar{x}\in Q\) be such that \(\bar{x}\) is not in any live-lock, \(G(\bar{x})=\{\tau _{(1)}\}\) and \(z\mathrel {{\xrightarrow []{\alpha '}}{}}\bar{x}\) implies \(\alpha '\notin \Upsilon \). Let \(\bar{Q}:=\{y\in Q\,\vert \,\bar{x}\mathrel {{\xrightarrow []{\tau _{(1)}}}{}}y\}\) and \(G'=\langle Q-\{\bar{x}\}, \Sigma , \rightarrow ', {Q^{\circ \prime }}, M\rangle \) with
It holds that \(G\simeq ^{\mathcal {S}}G'\).
Finally, the certain conflicts rule can be adjusted immediately as well. Generally, for non-blockingness verification, we can merge all blocking states into a single blocking state. In fact, Flordal and Malik (2009) showed several cases that the blocking behaviour in the future cannot be avoided even upon reaching some co-reachable state. These states are handled by the certain conflicts rule, which removes outgoing transitions from these states. Since the transition removal may potentially render co-reachable states blocking, the set of blocking states can be enlarged. For a more detailed discussion of the certain conflicts rule, see (Flordal and Malik 2009, Example 3) and Malik (2004).
Theorem 3.3.18
[certain conflicts rule] Let \(G=\langle Q_{},\Sigma _{}, \rightarrow _{}, Q^\circ _{}, M_{}\rangle \) be a \(\Upsilon \)-shaped automaton. Let \(Q_\textrm{c}\subseteq Q\) be the set of co-reachable states in G and \(Q_\textrm{uc}:=Q-Q_\textrm{c}\) the set of non-co-reachable states in G. Define two transition sets as
and let \(G'=\langle Q, \Sigma , \rightarrow -\,(\rightarrow _1\cup \rightarrow _2), Q^\circ , M\rangle \). It holds that \(G\simeq ^{\mathcal {S}}G'\).
3.4 Outline of the overall verification algorithm
With the abstraction rules developed above, we are now in the position to perform compositional non-blockingness verification w.r.t. prioritised events. Recall that given a family of automata \((G_i)_{1\le i \le k}\), the global behaviour amounts to \(G:=\mathcal {S}(G_1\parallel G_2\parallel \cdots \parallel G_k)\). Here each individual module \(G_i\) is subject to abstraction and any pair of modules can be substituted by its synchronous composition. Except that we shall apply abstraction rules that account for event priorities, the overall verification procedure as given in Algorithm 1 is essentially the same as (Pilbrow and Malik 2015, Algorithm 1).
The main function IsNonConflicting takes a family of automata \(\mathfrak {G}=\{G_1,\dots ,G_k\}\), \(k\ge 2\), which is to be tested for non-conflictingness. For the preprocessing, we refer to Observation 2.3.4 (hiding) and Remark 1 (shaping w.r.t. all private events). Note that hiding preserves \(\Upsilon \)-shapedness. Hence, we can apply all abstraction rules developed in this section. This is implemented by invoking the function ConflictPreservingAbstraction; Line 19.Footnote 5 After each individual automaton has been processed, the while-loop in Line 8 is entered. In each iteration, we pick a pair of two modules \(G_i\) and \(G_j\) for composition. There are various heuristics by which to take the specific choice; see Flordal and Malik (2009). The result \(H=G_i\parallel G_j\) is then processed in the same manner in the initial for-loop. Finally, H is used to replace \(G_i\) and \(G_j\) in the family \(\mathfrak {G}\). Overall, the while-loop in Line 8 reduces the size of \(\mathfrak {G}\) by one automaton per iteration. The loop is terminated if only one automaton G is left. For the latter, non-blockingness is tested e.g. via enumeration based methods to obtain the final result.
4 Example
To evaluate the performance of our compositional non-blockingness verification method with prioritised events, consider the concatenated conveyor belts \(\textsf{CB}_1\) to \(\textsf{CB}_k\) shown in Fig. 11. In this scenario, workpieces are to be transported from the source on the left to the sink on the right. Each of the components is equipped with a sensor to indicate the presence of a workpiece. Besides, each conveyor belt is equipped with a motor which drives the belt. The components are controlled in a modular fashion, with the respective automata given in Fig. 12; see also Table 1 for a listing of all referenced events. Specifically, each conveyor belt \(\textsf{CB}_i\) is modelled as a local closed loop
with the special cases \(F_0\) and \(F_{k+1}\) for source and sink, and with successive components \(F_i\) and \(F_{i+1}\) coupled by the automaton \(C_i\). The overall model so far is given by
i.e., for a conveyor belt system with k conveyor belts, we have in total \(2k+3\) automata. Let \(M_{F_i}\), \(M_{C_i}\) and \(M_{F_{k+1}}\) be the marking set of each \(F_i\), \(C_i\) and \(F_{k+1}\), respectively, where \(0\le i\le k\). These marking sets are given correspondingly by
This definition indicates that at any state, each conveyor belt must be able to receive a new workpiece in the future.
For a physcal implementation of the controller, we effectively implement the behaviour of F with specific execution preferences. Actuators \({on}_i\) and \({off}_i\) are assigned a higher priority than the sensor events \({ar}_i\) and \({lv}_i\); i.e., when in a state where the controller could either wait for a sensor event to occur or execute an actuator event at some point in time, the physical implementation of the controller will do the latter immediately. Likewise, the events \({sd}_i\) for inter-module communication are preferred over actuator events. Only when in a state where exclusively sensor events are enabled, the physical implementation will wait until one such event is generated by the plant. Although intuitive from a technological perspective, this scheme of execution preferences may render the overall model blocking even it was non-blocking before introducing priorities. Hence our interest in the verification of \(\mathcal {S}(F)\).
The performance of a prototypical software implementation of the abstraction rules discussed in our study is given in Table 2. The first column shows the number of conveyor belts. The second and third column show the state count of the monolithic representation and the final state count after applying compositional verification. In this example, the latter matches the maximal state count experienced during the entire verification procedure. The fourth and fifth column show the elapsed time for verification with or without applying compositional verification. All computations are performed on a standard 2022 desktop computer (Intel Core i7-10510U 2.30 GHz CPU with 16GB RAM; however, memory is not a limiting factor for this example). Through comparing the fourth and fifth column, a substantial performance improvement becomes evident.
5 Conclusion
In this paper, we address the verification of non-conflictingness for modular systems, where each module is represented by a finite automaton. For this task, the literature proposes the method of compositional verification, in which conflict equivalent abstractions and module composition are alternated until only one module is left. This approach is well established and gains significant computational benefits; see Flordal and Malik (2009); Su et al. (2010); Ware and Malik (2012); Pilbrow and Malik (2015). Our main technical contribution is an extension to account for event priorities. The latter is technically represented by a shaping operator \(\mathcal {S}(\,\cdot \,)\) which removes transitions that are preempted by higher-priority events. Since \(\mathcal {S}(\,\cdot \,)\) does not commute with synchronous composition \((\,\cdot \,)\parallel (\,\cdot \,)\), the consideration of event priorities requires an adaptation of the established abstraction rules. To this end, we introduce a shaped quotient to account for silent live-locks and recover a variant of weak bisimulation and related equivalences as basis for abstractions, that turn out conflict equivalent w.r.t. prioritised events.
If compositional verification yields a negative result, it is of great practical interest to resolve the present conflicts. For the situation without priorities, Malik and Ware (2020) proposed how to extract a counter-example as diagnostic information; i.e., a path that leads to a blocking state. Such diagnostic information may guide the programmer to accommodate the situation for manually written PLC programs. At the current stage, we have an experimental adaptation of the results in Malik and Ware (2020) with a specific focus on composed systems with event priorities that model SFCs. A more sophisticated strategy to address conflicts is the systematic design of a supervisor that further restricts the overall system to avoid blocking configurations. Addressing extended finite automata (EFA) as base models, Goorden et al. (2021) proposed a likewise compositional procedure to synthesise a so-called coordinator. The composition of the coordinator with the original system is by construction non-conflicting. For a future direction of research, one may investigate whether and how the techniques proposed by Goorden et al. (2021) can be adapted to address prioritised events.
Notes
Throughout this paper, we will always assume that unreachable states are removed after shaping.
Allthough the cited literature does not account for event priorities, the case carries through to our setting here in that we may design the same priority uniformly to all events.
Here, \(x'_{Gi'-1}\) denotes the previous state of \(x'_{Gi'}\) in Eq. 35. This style of notation is utilised later on as well.
Here, we slightly abuse the definition of live-lock in T in that we uniformly substitute all \(G_\textrm{slnt}\) with \(T_\textrm{prvt}\) in Definition 3.1.3.
As being discussed in Pilbrow and Malik (2015), the order of the abstraction rules in ConflictPreservingAbstraction may influence the algorithm efficiency. In fact, the observation in Pilbrow and Malik (2015) fits our use-case as well – we shall prefer putting abstraction rules with higher complexity to the later stage of ConflictPreservingAbstraction, i.e. the abstractions through PWB and both rules based on incoming equivalences. Both rules need high-order polynomial time computation time to perform state partition iteratively. In comparison, the other three rules appearing in ConflictPreservingAbstraction are generally less time-consuming since they can be performed on a per-state basis.
References
Aho AV, Hopcroft JE, Ullman JD (1974) The Design and Analysis of Computer Algorithms. Addison-Wesley Publishing Company, Massachusetts, USA
Blech JO, Ould Biha S (2011) Verification of PLC properties based on formal semantics in coq. In: Software engineering and formal methods, pp 58–73
Cassandras CG, Lafortune S (2008) Introduction to Discrete Event Systems, 2nd edn. Springer, New York, USA
Cleaveland R, Lüttgen G, Natarajan V (2007) Priority and abstraction in process algebra. Inform Comput 205(9):1426–1458
Fabian M, Hellgren A (1998) PLC-based implementation of supervisory control for discrete event systems. Proceedings of the 37th IEEE Conference on Decision and Control 3, 3305–3310
Flordal H, Malik R (2009) Compositional verification in supervisory control. SIAM J Control Optim 48:1914–1938
Flordal H, Malik R (2006) Modular nonblocking verification using conflict equivalence. In: 2006 8th International workshop on discrete event systems, pp 100–106
Goorden M, Fabian M, van de Mortel-Fronczak J, Reniers M, Fokkink W, Rooda J (2021) Compositional coordinator synthesis of extended finite automata. Discrete Event Dynamic Syst 31:1–32
Hering de Queiroz M, Cury J, Wonham W (2005) Multitasking supervisory control of discrete-event systems. Discrete Event Dynamic Syst 15:375–395
Lúttgen G (1998) Pre-emptive modeling of concurrent and distributed systems. PhD thesis, Universität Passau
Malik P (2003) From supervisory control to nonblocking controllers for discrete event systems. PhD thesis, Universität Kaiserslautern
Malik R (2004) On the set of certain conflicts of a given language. IFAC Proceedings Volumes 37(18), 267–272. 7th International Workshop on Discrete Event Systems (WODES’04), Reims, France, September 22-24 2004
Malik R, Ware S (2020) On the computation of counterexamples in compositional nonblocking verification. Discrete Event Dynamic Syst 30:301–334
Malik R, Streader D, Reeves S (2004) Fair testing revisited: a process-algebraic characterisation of conflicts. In: Automated technology for verification and analysis, pp 120–134
Milner R (1989) Communication and Concurrency. Prentice-Hall Inc, USA
Mohajerani S, Malik R, Fabian M (2016) A framework for compositional nonblocking verification of extended finite-state machines. Discrete Event Dynamic Syst 26:33–84
Moor T (2022) CompileDES: executable-code generation from synchronised libFAUDES automata. https://fgdes.tf.fau.de/compiledes, Accessed 27 Jun 2022
Nicola RD, Hennessy MCB (1984) Testing equivalences for processes. Theoret Comput Sci 34(1):83–133
Pilbrow C, Malik R (2015) An algorithm for compositional nonblocking verification using special events. Sci Comput Program 113:119–148
Qamsane Y, Abdelouahed T, Philippot A (2016) A synthesis approach to distributed supervisory control design for manufacturing systems with Grafcet implementation. Int J Prod Res 55:1–21
Ramadge P, Wonham W (1987) Supervisory control of a class of discrete event systems. SIAM J Control Optim 25:206–230
Schmidt K, de Queiroz MH, Cury JER (2007) Hierarchical and decentralized multitasking control of discrete event systems. In: 2007 46th IEEE conference on decision and control, pp 5936–5941
Su R, van Schuppen JH, Rooda JE, Hofkamp AT (2010) Nonconflict check by using sequential automaton abstractions based on weak observation equivalence. Automatica 46(6):968–978
Tang Y, Moor T (2022) Compositional verification of non-blockingness with prioritised events. 16th IFAC Workshop on Discrete Event Systems (WODES) 55(28), 236–243
Verbakel JJ, Vos de Wael MEW, van de Mortel-Fronczak JM, Fokkink WJ, Rooda JE (2022) Supervisory control of roadside units. IFAC-PapersOnLine 55(28), 79–86. 16th IFAC Workshop on Discrete Event Systems WODES 2022
Ware S, Malik R (2012) Conflict-preserving abstraction of discrete event systems using annotated automata. Discrete Event Dynamic Systems 22:451–477
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tang, Y., Moor, T. Compositional non-blockingness verification of finite automata with prioritised events. Discrete Event Dyn Syst 34, 125–161 (2024). https://doi.org/10.1007/s10626-024-00394-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10626-024-00394-2



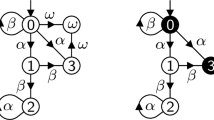


 with
with 

 in
in 

 in
in  :
:
 if either of the following holds:
if either of the following holds:  where
where  ;
;






