Abstract
In this paper, the intelligent traffic management within a smart city environment is addressed by developing an ad-hoc model predictive control strategy based on an event-driven formulation. To this end, a constrained hybrid system description is considered for safety verification purposes and a low-demanding receding horizon controller is then derived by exploiting set-theoretic arguments. Simulations are performed on the train-gate benchmark system to show the effectiveness and benefits of the proposed methodology.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Nowadays urban areas offer economic, social, and political significant opportunities as well as potential for greater environmental sustainability. However, it is necessary to find new ways to manage complexity, to increase efficiency, to reduce expenses, and to improve quality of life. In other words, cities need to get smarter (Cassandras 2016).
Progress means an accurate view across urban infrastructure, the right level of intelligence to optimize resources, and the capability to merge information from all departments to predict and to cope with events. Smart city transformation relies on exploiting powerful analytical techniques to extract insights from real-world events in order to improve urban business processes. Creating and applying a unified information framework gives the possibility to obtain a more complete picture of urban activities, see Chourabi et al. (2012) and Morrissett and Abdelwahed (2018) and references therein.
Besides, smart cities need intelligent transport services which means proper movement of people, goods and services improving growth and development of a region. Transportation is indeed a human-oriented field with ample and distinct highly demanding problems requiring proper and efficient solutions. Features and performance of transport systems, services, costs, infrastructures, vehicles and control systems are usually defined on the basis of quantitative evaluation of their main effects. Most of the transport decisions take place under imprecision, uncertainty and partial truth. Some objectives and constraints are often difficult to be measured by precise values (Hoogendoorn and Bovy 2001).
Basically, Smart Cities whereas Intelligent Transportation Systems are large-scale event-driven systems involving humans, information technology, and physical infrastructures, all interacting in complex ways. The dynamic behavior is usually and obviously affected by both uncertainty and nonlinearities, and significantly sensitive to perturbations. Such a complex infrastructure requires a set of applications related to newly decision support systems designed for emergency warning systems, public safety and many other human activities. Nonetheless a significant number of instances related to technical, economic, political, social aspects and so on, while determining a decision, must be taken into consideration. This is mainly due to inherent obstacles when collecting relevant, reliable and complete information (Dotoli and Fanti 2006; Di Febbraro et al. 2016).
From a methodological point of view, an adequate framework to formalize the description of the above event-driven phenomena relies on the use of the well-known hybrid system paradigm that characterizes plants involving both discrete and continuous dynamic behaviors (Antsaklis 2000). In the last two decades, hybrid systems analysis and control problems have grown in interest amongst the researchers mainly because the related theoretical tools require the intersection between mainstream engineering control theory methodologies and computer science verification techniques (Branicky et al. 1998; Tomlin et al. 1998; Balluchi et al. 2000; Engell et al. 2000). Hence, in order to understand the dynamical behaviour, to simulate first and to design then better performing control strategies, theoretical advances and numerical tools have assumed an increasing relevance. This essentially leads to the concept of formal verification that translates in solving reachability problems, see e.g. Alur et al. (1995). On the other hand such a problem is undecidable and, therefore, it is necessary to define modelling formalisms capable to be used so that related algorithms can be efficiently used. Along these lines, theoretical issues on hybrid automata have been formally discussed in Henzinger et al. (1998) where it has been proved that even slight generalizations of rectangular automata lead to undecidable reachability problems.
Following this reasoning, the Mixed Logical Dynamical (MLD) formalism (Di Cairano et al. 2009) is capable to specify the evolution of continuous variables through linear dynamic equations of discrete variables using propositional logic statements and automata. A relevant tool capable of building MLD models is HYSDEL (Hybrid System DEscription Language) developed in Torrisi and Bemporad (2004). Such toolbox is capable of modelling, in a human-readable fashion, the class of hybrid systems described by the interconnections of linear dynamic systems, automata, if-then-else statements and propositional logic rules. Moreover, any HYSDEL system can be formally and analytically translated into a MLD model for analysis and design purposes. Furthermore, since every well-posed MLD has been proved to have an equivalent Piecewise Affine (PWA) system representation (Heemels et al. 2001), any HYSDEL model can also be recast into a PWA characterized by a collection of affine system descriptions where each dynamics is defined over a polyhedral set (Bemporad et al. 2000).
From the control perspective, Model Predictive Control (MPC) provides the means to tackle some of the previously described Smart City/Intelligent Transportation Systems challenges, since it allows to directly take in to account constraints, preview information, as well as physical world models (Roncoli et al. 2015; Kamal et al. 2013, 2014; Papamichail et al. 2019).
As it is well known for hybrid linear systems, the MPC framework falls in the class of mixed integer linear programming (MILP) problems if the objective function is a linear function or in the class of mixed integer quadratic programming (MIQP) problems when the objective function is quadratic. Both MILP or MIQP problems are difficult to solve and some interesting properties like convexity are lost. Moreover, the complexity is NP-hard and, since no optimality conditions there exist, it is not possible to certificate the nature of a feasible solution.
As outlined in literature, see Lin and Antsaklis (2014) and references therein, the most common robust strategy to address such a class of optimization problems is Branch and Bound (Conforti et al. 2014; Fletcher and Leyffer 1998). In fact, in spite of poor control performance when an admissible optimization is considered, the algorithm is capable to achieve a global optimum or to asses its infesibility. On the other hand, Branch and Bound techniques solve an MIQP by constructing a search tree and at each node a Quadratic Program (QP) is solved to bound the objective function over a subset of the search space. This gives rise to non-trivial computational difficulties that essentially make such methods less appealing when plant dimensions increase.
Alternative approaches have been proposed to design MPC controllers. In particular, logic constraints have been addressed by exploiting constraint satisfaction problems in Bemporad and Giorgetti (2006). Whereas sub-optimal solutions have been derived by means of heuristic techniques: genetic algorithms (Cortés et al. 2010; Duzinkiewicz et al. 2009) and ant colony schemes (Sandou and Olaru 2007). have been used.
Due these unavoidable computational difficulties, the idea was to compute off-line the optimal control as done in e.g. Oberdieck and Pistikopoulos (2015). However, the application of these explicit methods is typically limited to low-dimensional systems, with very few discrete variables. The attempts to find explicit solutions for hybrid MPC controllers have been more successful when a PWA model is considered (Bemporad et al. 2002b; Wittmann-Hohlbein and Pistikopoulos 2014; Axehill et al. 2014). Unfortunately, it is obvious that the biggest drawback of this class of algorithms is the computational burden that grows exponentially as the prediction horizon increases: in fact by exploiting multi-parametric MILP approaches, the off-line complexity could become prohibitive for large-scale systems and real-time scenarios (Barić et al. 2008; Habibi et al. 2016).
Finally, it is important to recall that applications of hybrid MPC can be found in different fields. In automotive systems, hybrid MPC has been applied to traction control systems (Borrelli et al. 2006), adaptive cruise control (Corona et al. 2006), power systems to cogeneration plants (Ferrari-Trecate et al. 2004) or current converter control (Geyer et al. 2008), real-time optimization of public transport systems operations (Cortés et al. 2010), modeling and control of production-inventory systems (Nandola and Rivera 2011).
Starting from these considerations, in this paper we develop a set-theoretic receding horizon control strategy for the class of constrained PWA models capable to capture the dynamics of transportation systems for intelligent traffic management purposes. Accordingly, the main aim is to provide a solution capable to mitigate the computational obstacles arising when approximate explicit solutions are pursued. In fact from one hand the explicit framework is capable to reduce on-line computational burdens, on the other hand it gives rise to an off-line phase that could be computational intractable. Such an hitch is here tackled by exploiting controllability/reachability concepts combined with the polyhedral set description to move off-line most of computations. The advantage of such an approach is that off-line computational loads are also significantly weakened because it is not required to determine a feasible controller for each partition of the admissible state space region.
In the sequel, a formal verification of the underlying hybrid system is first presented and then the controller is designed by using reachability sets computations (Blanchini and Miani 2008). Essentially, the main contributions can be summarized as follows:
-
(Analysis) Forward and backward reachability concepts are used to address safety verification queries;
-
(Design) A real-time affordable MPC control scheme capable of regulating the plant state trajectory to a desired configuration, while prescribed safety requirements are fulfilled, is achieved.
Roughly speaking, the resulting control algorithm lies at the intersection of explicit (completely off-line) and MIP (completely on-line and based on MIP optimizations) strategies. In particular, most of the required computations are off-line moved while the on-line phase requires the solution of a simple and real-time affordable quadratic programming (QP) optimization problem, (Angeli et al. 2008; Lucia et al. 2017).
Finally, the simulation section is devoted to show the applicability of the proposed strategy to the train-gate system that is well-known in the timed automata verification literature, see e.g. Lygeros et al. (1996). Here, the traffic regulation management problem is of interest because it perfectly adapts to the proposed framework and MPC solution: since a train control system (see Baouya et al. 2019) has to be capable of
-
merging computer-based and network-based technologies for monitoring and controlling trains in a specific geographical area,
-
meeting safety requirements,
the resulting hard constrains on the system variables can be efficiently addressed via receding horizon control arguments.
The paper is organized as follows. In Section 3 safety and regulation problems are formally stated; Section 4 describes algorithmic solutions to safety verification queries addressing reachability properties. In Section 5, the proposed set-theoretic receding horizon controller is presented, while Section 6 validates the effectiveness by means of numerical simulations carried on the train-gate benchmark system.
2 Preliminaries
Definition 1
(Polyhedron) A polyhedron is the intersection of a finite number of closed and/or open halfspaces. A polygon is the union of a finite number of polyhedra.
Definition 2
(Polyhedral partition) Let \(\mathcal {P}\) be a polygon. A collection of polyhedra \(\{\mathcal {P}_{1}, \ldots ,\mathcal {P}_{l}\} \) is a polyhedral partition of \(\mathcal {P}\) if \(\mathcal {P}:=\left \{\bigcup _{i\in \mathcal {I}}\mathcal {P}_{i}\right \}\) and \(\mathcal {P}_{i}\cap \mathcal {P}_{j}=\emptyset \) ∀i≠j.
Let us consider the discrete-time nonlinear plant description
where  and
and  denote the state and input vectors, respectively, and
denote the state and input vectors, respectively, and  . Without loss of generality, it is supposed that f is continuous in its arguments and f(0n,0m) = 0n. Moreover, the following constraints are prescribed
. Without loss of generality, it is supposed that f is continuous in its arguments and f(0n,0m) = 0n. Moreover, the following constraints are prescribed

with \(\mathcal {X}\) and \(\mathcal {U}\) compact polyhedra.
Definition 3
(Backward Reachability) Given a set \(\mathcal {T}\subseteq \mathcal {X},\) the predecessor set of \(\mathcal {T},\) denoted as \(Pre(\mathcal {T}),\) is the set of states for which there exists an input \(u(k)\in \mathcal {U}\) such that \(x(k+1) \in \mathcal {T},\) i.e.
Definition 4
(Forward Reachability) Given a compact set \(\mathcal {T}\subseteq \mathcal {X}\), the successor set of \(\mathcal {T},\) denoted as \(Post(\mathcal {T}),\) is the set of states reachable in one step from \(\mathcal {T}\) by using an admissible input \(u\in \mathcal {U},\) i.e.

Definition 5
(Projection operator) Given a compact set  , the projection of \(\mathcal {Z}\) onto \(\mathcal {X}\), denoted as \(Proj_{\mathcal {X}}\{\mathcal {Z}\},\) is
, the projection of \(\mathcal {Z}\) onto \(\mathcal {X}\), denoted as \(Proj_{\mathcal {X}}\{\mathcal {Z}\},\) is
3 Problem formulation
Let us consider the following controlled switching hybrid model
where \(x(t)\triangleq [z(t)^{T} w(t)^{T}]^{T}\) is state vector with  , and \(w(t)\in \mathcal {W}=\)
, and \(w(t)\in \mathcal {W}=\)  denotes the continuous dynamics,
denotes the continuous dynamics,  the finite dynamics and w+ the successor of w, i.e an event-driven signal. See Branicky et al. (1998) for technical details.
the finite dynamics and w+ the successor of w, i.e an event-driven signal. See Branicky et al. (1998) for technical details.
Moreover, the following assumptions are made:
-
1.
switching input constraints are prescribed:
$$ u(t)\in \mathcal{U}(z(t),w(t)) $$(7)with \(\mathcal {U}(z(t),w(t))\) a convex and compact set;
-
2.
a subset of the system state space, namely
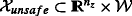 , is unsafe and, starting from any admissible initial condition, the system trajectory never enters inside, i.e.
$$ x(t) \notin \mathcal{X}_{unsafe}, \forall t. $$(8)
, is unsafe and, starting from any admissible initial condition, the system trajectory never enters inside, i.e.
$$ x(t) \notin \mathcal{X}_{unsafe}, \forall t. $$(8)
The following verification and control problems are considered:
Verification and Control of Hybrid Systems Under Safety Requirements (VCHSSR) -
Given the constrained hybrid model (6)-(8) and a target set 
-
(P1) - Hybrid System Verification: provide a formal solution to the following queries:
-
(Query 1) Let
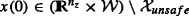 be an initial state condition and \(N<\infty \) a finite prediction horizon. There exists an input sequence u[0,N− 1) := {u(0),…,u(N − 1)} such that \(x(N) \in \mathcal {X}_{unsafe}\)?
be an initial state condition and \(N<\infty \) a finite prediction horizon. There exists an input sequence u[0,N− 1) := {u(0),…,u(N − 1)} such that \(x(N) \in \mathcal {X}_{unsafe}\)? -
(Query 2) Let \(\bar {x}\in \mathcal {X}_{unsafe}\) be a critical condition and \(N<\infty \) a finite prediction horizon. Determine the set of initial conditions
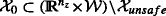 for which there exists an input sequence u[0,N− 1) := {u(0),…,u(N − 1)} such that \(x(N) \equiv \bar {x};\)
for which there exists an input sequence u[0,N− 1) := {u(0),…,u(N − 1)} such that \(x(N) \equiv \bar {x};\) -
(Query 3) Let \(N<\infty \) be a finite a finite prediction horizon. Determine the set of initial state conditions
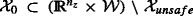 for which it is guaranteed the existence of an input sequence u[0,N− 1) capable to steer the state trajectory within Ξ, i.e. x(N) ∈Ξ.
for which it is guaranteed the existence of an input sequence u[0,N− 1) capable to steer the state trajectory within Ξ, i.e. x(N) ∈Ξ.
-
-
(P2) - Constrained Regulation: design a state-feedback control law
$$ u(\cdot)=g(x(\cdot),{\varXi}) $$capable to drive the state trajectory of Eq. 6 into Ξ in a finite number of steps while preserving the prescribed constraints (7)-(8).
In the sequel, these problems will be addressed by recasting the class of hybrid systems (6)-(7) as a discrete-time constrained PWA model.
For the sake of clarity, it is worth noticing that the plant (6)-(7) can be described as a discrete-time MLD or event-driven MLD (eMLD) system, see e.g. (Torrisi and Bemporad 2004). Then, each well-posed MLD model can be recast into an equivalent PWA representation and vice-versa (Heemels et al. 2001).
Therefore, the following state space description is achieved:
where  is the index set accounting for all convex polyhedra \(\mathcal {P}_{i}, i \in \mathcal {I},\) and \(\mathcal {P}\) a polyhedral partition. Moreover, the safety constraint (8) is characterized by the following polyhedral region
is the index set accounting for all convex polyhedra \(\mathcal {P}_{i}, i \in \mathcal {I},\) and \(\mathcal {P}\) a polyhedral partition. Moreover, the safety constraint (8) is characterized by the following polyhedral region
which leads to an additional non-convex state constraint on the plant model (9):

with  .
.
Finally, it is important to remark that the required time instant \(\bar {t}\) is in turn bounded, i.e there exists a finite time instant, say Tmax, such that \(0<\bar {t}<T_{max}<\infty .\)
4 Verification of constrained PWA systems
In this section, forward and backward reachability concepts are adapted to the constrained PWA plant description (9)-(10) with the aim to provide algorithmic answers to Queries 1-3 of the proposed VCHSSR-(P1) problem. Specifically, the following results come out.
Proposition 1
Let a polygon \(\mathcal {T}=\bigcup _{j\in \mathcal {J}}\mathcal {T}_{j} \subset Proj_{x}\{\mathcal {P}\},\) with \(\{\mathcal {T}_{j}\}_{j\in \mathcal {J}}\) convex sets, be given. Then, the predecessor set \(Pre(\mathcal {T})\) is
Proof
- The proof directly follows from the backward reachability Definition 3. According to the PWA description (9), the predecessor set \(Pre(\mathcal {T})\) is the union of all admissible sets of states arising from the the polyhedral partition \(\mathcal {P}.\) In fact for any element \(\mathcal {P}_{i}\) of \(\mathcal {P},\) one obtains the regions \(\mathcal {X}_{i,j}\subseteq Proj_{x}\{\mathcal {P}_{i}\}\) compatible with Eq. 3. As a consequence, the set \(Pre(\mathcal {T})\) is a polygon built as the union of \(\mathcal {X}_{i,j}, \forall i\in \mathcal {I}, \forall j\in \mathcal {J}.\)□
Proposition 2
Let a polygon \(\mathcal {T}=\bigcup _{j\in \mathcal {J}}\mathcal {T}_{j} \subset Proj_{x}\{\mathcal {P}\},\) with \(\{\mathcal {T}_{j}\}_{j\in \mathcal {J}}\) convex sets, be given. Then, the successor set \(Post(\mathcal {T})\) is

Proof
- By resorting to Definition 4, similar arguments of Proposition 1 apply. □
4.1 Query 1
Proposition 3
Let an initial state condition \(x(0)\in (\mathcal {X}_{safe}\cap Proj_{x}\{P\})\) and a positive integer N (prediction horizon) be given. Then, the following AQ-1 algorithm provides a solution to Query 1:

Proof
- Since the proof follows by construction, the graphical description of the AQ-1 algorithm in Fig. 1 will be hereafter considered for the sake of comprehension. Starting from the initial condition x(0) (the red star) and according to the following recursions:
a family \(\{\mathcal {T}^{r}\}_{r=1}^{N}\) of successor sets (green polyhedra) is computed via Steps 1-3. Then, the set \(\mathcal {X}_{intersect} := \{\mathcal {T}^{r}\}_{r=1}^{N} \cap \mathcal {X}_{unsafe}\) is obtained by means of Step 5, where \(\mathcal {X}_{unsafe}\) (the red polyhedron) is the unsafe region. Finally, Steps 7-8 provide the answer. □
4.2 Query 2
Proposition 4
Let the unsafe region \(\mathcal {X}_{unsafe}\) and a positive integer N (prediction horizon)
be given. Then, the following AQ-2 algorithm provides a solution to Query 2:

Proof
- Starting from \(\mathcal {T}^{0}:=\mathcal {X}_{unsafe},\) the predecessor sets sequence \(\{\mathcal {T}^{r}\}_{r=1}^{N}\) (see green polyhedra of Fig. 2) is computed according to the following recursions:
via Steps 1-3. Hence the set of states, characterizing the admissible initial conditions (??) is computed (Step 5) under the requirement that the state trajectory enters \(\mathcal {X}_{unsafe}\) in at most N steps. □
4.3 Query 3
Proposition 5
Let a target set Ξ and a positive integer N (prediction horizon)
be given. Then, the following AQ-3 algorithm provides a solution to Query 3:

Proof
- The proof follows similar lines of Proposition 4 under the following customizations:
-
recursion (17) origins from the target set Ξ (green polyhedra in Fig. 3);
-
the predecessor set computation exploits the set-difference operator in order to rule out any state belonging to \(\mathcal {X}_{unsafe}:\)
$$ \begin{array}{c} \mathcal{T}^{0}:={\varXi}, \mathcal{T}^{r}:=Pre(\mathcal{T}^{r-1})\setminus \mathcal{X}_{unsafe}, r=1,\ldots, N \end{array} $$(19)
□
Remark 1
The difference between the polygon \(Pre{(\mathcal {T}^{r-1})}\) and the polyhedron \(\mathcal {X}_{unsafe}\) (Step 1 of AQ-3) is a set-difference for each polyhedron \(\mathcal {X}_{i,j}\) belonging to \(Pre{(\mathcal {T}^{r-1})}\)
This, in principle, could give rise to a non convex set \(\hat {\mathcal {X}}_{i,j}.\)
Then, in order to overcome such a drawback and to ensure that \(\mathcal {T}^{r}\) is given by the union of convex polyhedra, the idea is to consider any non convex polyhedral set \(\hat {\mathcal {X}}_{i,j}\) as the union of a finite number (\(p<\infty \)) convex polyhedra (see Fig. 4), i.e.
5 A receding horizon control scheme for PWA system
In this section, the constrained regulation problem VCHSSR-(P2) will be addressed via a low-demanding MPC strategy. The key idea is to off-line compute a family of predecessor sets \(\{\mathcal {T}_{r}\}_{r=1}^{N}\) to be used during the on-line operations in a receding horizon fashion for determining sequences of control inputs {u(k)} compatible with the prescribed constraints. Specifically, the on-line phase has the following abstract structure:
where \(\underline {i}\in \mathcal {I}\) denotes the index of the so-called active PWA model and J(x(k),u) a pre-assigned convex cost function. In other words, the optimization (21)-(22) will force the one-step state evolution x(k + 1) to belong to the successor of the current controllable set, i.e.
Note that the off-line computations required for \(\{\mathcal {T}_{r}\}_{r=1}^{N}\) match those of AQ-3. A key question concerns with the pertinence of this scheme to the proposed PWA model framework because (as pointed out in Remark 1) each predecessor set \(\mathcal {T}^{r}\) is the union of convex polyhedra (Rakovic et al. 2006) and, therefore, Eqs. 21-22 is a non-convex optimization. An admissible, though not optimal, method to overcome such a drawback consists in verifying if, for which polyhedron \(\mathcal {X}^{r-1}_{i,j} \subset \mathcal {T}^{r-1},\) the following convex optimization admits a solution:
Once a candidate polyhedron \(\underline {\mathcal {X}}^{r-1}_{i,j}\subset \mathcal {T}^{r-1}\) has been identified, then the optimization (21)-(22) can be recast as a convex QP problem:
The above developments allow to write down the following computable algorithm, hereafter denoted as PWA - RHC.

Proposition 6
Let the family of predecessor sets \(\{\mathcal {T}^{r}\}_{r=0}^{N}\) be non-empty and
Then, the PWA - RHC algorithm always satisfies the prescribed constraints and ensures that x(k) ∈Ξ for some k ≤ N.
Proof
It is sufficient to prove that Steps 3-4 of the PWA-RHC algorithm admit a solution at each time instant. Since the family of predecessor sets \(\{\mathcal {T}^{r}\}_{r=0}^{N}\) defines the domain of attraction (DoA) of the resulting receding horizon controller then, for any initial condition \(x(0)\in \bigcup _{r=0}^{N}\left \{\mathcal {T}^{r}\right \},\) there exists a finite sequence of control moves capable to drive the state trajectory to Ξ, see Proposition 5. As a consequence, there always exists a polyhedral region \({\underline {\mathcal {X}}}_{i,j} \subset \mathcal {T}^{r-1}\) satisfying (23) and the optimization (24) has a feasible solution u(k) such that
Hence, by induction, the state trajectory x(k) enters \(\mathcal {T}^{0}\equiv {\varXi }\) in at most N steps. □
6 Case study
In this section, a benchmark road traffic model is used to show the effectiveness of the proposed methodology. The first part introduces the mathematical plant description and constraints that have to be considered. Then, the receding horizon feedback controller results are detailed and presented. All the simulations are carried out on a laptop equipped with Intel Core i7-4810MQ, 32 GB DDR3L Notice that forward and backward reachability sets have been obtained by resorting to the computation capability of the MPT3 toolbox (Herceg et al. 2013).
6.1 Train gate model and constraints
The train-gate system detailed in Henzinger et al. (1997) and Di Cairano et al. (2009) is here considered. The system dynamics is modelled by means of the following continuous-time state space description
where xT and xG account for train positions and gate opening status (open if xG ≥ 0.95 and closed if xG ≤ 0.05), respectively; uT and uG are the control inputs and fi an exogenous input. Then, the gate automaton depicted in Fig. 5 describes the finite dynamics (w), while the switching input constraints are collected in Table 1.
Such a model falls under the class of systems (6) by exploiting the following arguments. First, an HYSDEL model description can be obtained by resorting to the event-driven model (Torrisi and Bemporad 2004) (see also the HYSDEL 2.0.6 description of Eq. 27 available at the web link: https://goo.gl/tDyH8n)
where the state t(k) and input q(k) = t(k + 1) − t(k) have been added in order to avoid any mode mismatch after the discretization of Eq. 26, see e.g. Júlvez et al. (2014). Note that q(k) accounts for the time interval between two consecutive events while t the elapsed time.
Moreover, the additional input constraint
is imposed to force a maximum and minimum time interval between two consecutive control actions. This is required to avoid the system stays in a open-loop condition for too long or high frequency chatterings and Zeno behaviors (Zhang et al. 2000).
6.2 Simulation results
The HYSDEL model described in the previous subsection has been translated into an equivalent MLD formulation by resorting to the algorithm developed in Bemporad (2002a). Finally, by resorting to the built-in developed in Bemporad (2003), the MLD has been converted into an equivalent PWA model whose state and input vectors are
where ΔxT(k) = uT(k)q(k) and ΔxG(k) = uG(k)q(k) denote train and gate position displacements within q(k), while C,Cl,O,Op refer to the gate automaton states of Fig. 5. Moreover, a polyhedral state space partition has been achieved as the union of 31 polyhedral regions \(\mathcal {P}_{i}.\)
Finally, the \(\mathcal {X}_{unsafe}\) has been defined by taking care of the dangerous scenario: train crossing and gate not closed, i.e. − 10 ≤ xT ≤ 10,xG ≥ 0.05. Therefore, the following region comes out
6.2.1 Risk analysis
The simulation first considers the following operating scenario:
Starting from an initial condition characterized as follows:
-
the train is far away from the gate:
$$ x_{g}<-20 $$(29) -
the gate is in any status:
$$ 0\leq x_{G} \leq 1 $$(30)
provide an answer to the question: is the unsafe region Xunsafe reachable within N = 100 steps?
In order to deal with such a request, a family of 100 successor sets \(\{\mathcal {T}^{r}\}_{r=1}^{100}\) has been computed via the AQ-1 procedure, see Fig. 6 (blue square region). A straightforward analysis shows that the reachable set covers \(\mathcal {X}_{unsafe}\) (the violet square region).
Train-gate forward reachability analysis. The blue regions are the reachable sets projected along XT and XG. The violet square region characterize the unsafe region (28)
Then, this requires the design of a controller module capable to avoid the unsafe region (28) while the train is crossing.
6.2.2 Train-gate traffic regulation management
According to the prescriptions of the PWA-RHC algorithm, a family of one-step state ahead controllable sets has been computed by using the procedure AQ-3 with Ξ, defined by Eqs. 29–30, as the initial condition. The resulting DoA is depicted in Fig. 7. As it clearly results, DoA ∩ Xunsafe = ∅ and, as a consequence, the system state trajectory is confined within the admissible state space region \(Proj_{x}\{\mathcal {P}\}\setminus \mathcal {X}_{unsafe}.\)
Numerical results are collected in Figs. 8, 9, and 10. As expected all the prescribed constraints are always satisfied, see Fig. 8. Then, the evolution of the gate automaton binary variables is depicted in Fig. 10, where the resulting mutually exclusive behaviour is complying with the prescriptions of the automaton of Fig. 5. In Fig. 9 where train and gate position dynamical evolutions are reported, the capability of the proposed strategy to guarantee a safe and intelligent management of the train-gate system is explicitly outlined: during the time interval [20 60]sec. (the green zone) while the train is crossing (− 10 ≤ xT(t) ≤ 10 in the upper sub-graph), the algorithm recognizes such an event and autonomously maintains closed the gate (xG(t) ≤ 0.05 in the lower sub-graph). Finally for the sake of completeness, Fig. 11 shows the set-membership signal r(t), exploited in the On-line phase of the PWA-RHC algorithm. It is important to remark that the dynamical behaviour of r(t) testifies that the train-gate state trajectory monotonically converges to the target region \({\varXi }\equiv \mathcal {T}^{0}\) by evolving within the state trajectories tube defined through the sequence of predecessor sets \(\left \{\mathcal {T}^{r}\right \}_{r=0}^{100}.\)
7 Conclusions
In this paper, a model predictive control strategy has been developed with the aim to formally address traffic control issues within a smart city framework. By first rephrasing a class of transportation systems as constrained PWA state space models, forward and backward reachability concepts have been exploited in order to efficiently answer safety verification queries. Then, a constrained regulation control problem has been presented and solved by means of a low-demanding MPC scheme based on the computation of reachability sets sequences. In order to challenge the proposed approach, a well-known case study in the intelligent transportation filed has been considered for simulation purposes. The numerical results are encouraging in terms of the capability to efficiently prevent critical scenarios.
Future studies will focus on the occurrence of unknown events giving rise to time-varying unsafe regions. In principle, this will allow of enlarging the domain of applicability of the proposed approach at the expense of increasing computational loads.
References
Alur R, Courcoubetis C, Halbwachs N, Henzinger T A, Ho P-H, Nicollin X, Olivero A, Sifakis J, Yovine S (1995) The algorithmic analysis of hybrid systems. Theor Comput Sci 138(1):3–34
Angeli D, Casavola A, Franzè G, Mosca E (2008) An ellipsoidal off-line mpc scheme for uncertain polytopic discrete-time systems. Automatica 44 (12):3113–3119
Antsaklis P J (2000) A brief introduction to the theory and applications of hybrid systems. In: Proceedings of IEEE, Special Issue on Hybrid Systems: Theory and Applications. Citeseer
Axehill D, Besselmann T, Raimondo D M, Morari M (2014) A parametric branch and bound approach to suboptimal explicit hybrid mpc. Automatica 50(1):240–246
Balluchi A, Benvenuti L, Di Benedetto M D, Pinello C, Sangiovanni-Vincentelli A L (2000) Automotive engine control and hybrid systems: Challenges and opportunities. Proc IEEE 88(7):888–912
Baouya A, Mohamed O A, Bennouar D, Ouchani S (2019) Safety analysis of train control system based on model-driven design methodology. Comput Ind 105:1–16
Barić M, Grieder P, Baotić M, Morari M (2008) An efficient algorithm for optimal control of pwa systems with polyhedral performance indices. Automatica 44(1):296–301
Bemporad A, Torrisi F D, Morari M (2000) Optimization-based verification and stability characterization of piecewise affine and hybrid systems. In: International Workshop on Hybrid Systems: Computation and Control, vol 2000. Springer, pp 45–58
Bemporad A (2002a) An efficient technique for translating mixed logical dynamical systems into piecewise affine systems. In: 2002, Proceedings of the 41st IEEE Conference on Decision and Control, vol 2. IEEE. pp 1970–1975
Bemporad A, Morari M, Dua V, Pistikopoulos E N (2002b) The explicit linear quadratic regulator for constrained systems. Automatica 38(1):3–20
Bemporad A (2003) Hybrid toolbox-user’s guide, http://cse.lab.imtlucca.it/~bemporad/hybrid/toolbox
Bemporad A, Giorgetti N (2006) Logic-based solution methods for optimal control of hybrid systems. IEEE Trans Autom Control 51(6):963–976
Blanchini F, Miani S (2008) Set-theoretic methods in control. Springer
Borrelli F, Bemporad A, Fodor M, Hrovat D (2006) An mpc/hybrid system approach to traction control. IEEE Trans Control Syst Technol 14 (3):541–552
Branicky M S, Borkar V S, Mitter S K (1998) A unified framework for hybrid control: Model and optimal control theory. IEEE Trans Autom Control 43(1):31–45
Cassandras C G (2016) Smart cities as cyber-physical social systems. Engineering 2(2):156–158
Chourabi H, Nam T, Walker S, Gil-Garcia J R, Mellouli S, Nahon K, Pardo T A, Scholl H J (2012) Understanding smart cities: An integrative framework. In: 2012 45th Hawaii International Conference on System Sciences, pp 2289–2297
Conforti M, Cornuéjols G, Zambelli G, et al. (2014) Integer programming, vol 271. Springer
Corona D, Lazar M, De Schutter B, Heemels M (2006) A hybrid mpc approach to the design of a smart adaptive cruise controller. In: 2006 IEEE Conference on Computer Aided Control System Design, 2006 IEEE International Conference on Control Applications, 2006 IEEE International Symposium on Intelligent Control. IEEE, pp 231–236
Cortés C E, Sáez D, Milla F, Núñez A, Riquelme M (2010) Hybrid predictive control for real-time optimization of public transport systems’ operations based on evolutionary multi-objective optimization. Transp Res Part C: Emerg Technol 18(5):757–769
Di Cairano S, Bemporad A, Júlvez J (2009) Event-driven optimization-based control of hybrid systems with integral continuous-time dynamics. Automatica 45(5):1243–1251
Di Febbraro A, Giglio D, Sacco N (2016) A deterministic and stochastic petri net model for traffic-responsive signaling control in urban areas. IEEE Trans Intell Transp Syst 17(2):510–524. https://doi.org/10.1109/TITS.2015.2478602
Dotoli M, Fanti M P (2006) An urban traffic network model via coloured timed petri nets. Control Eng Pract 14(10):1213–1229
Duzinkiewicz K, Brdys M A, Kurek W, Piotrowski R (2009) Genetic hybrid predictive controller for optimized dissolved-oxygen tracking at lower control level. IEEE Trans Control Syst Technol 17(5):1183–1192
Engell S, Kowalewski S, Schulz C, Stursberg O (2000) Continuous-discrete interactions in chemical processing plants. Proc IEEE 88(7):1050–1068
Ferrari-Trecate G, Gallestey E, Letizia P, Spedicato M, Morari M, Antoine M (2004) Modeling and control of co-generation power plants: A hybrid system approach. IEEE Trans Control Syst Technol 12(5):694–705
Fletcher R, Leyffer S (1998) Numerical experience with lower bounds for miqp branch-and-bound. SIAM J Optim 8(2):604–616
Geyer T, Papafotiou G, Morari M (2008) Hybrid model predictive control of the step-down dc–dc converter. IEEE Trans Control Syst Technol 16 (6):1112–1124
Habibi J, Moshiri B, Sedigh A K, Morari M (2016) Low-complexity control of hybrid systems using approximate multi-parametric milp. Automatica 63:292–301
Heemels Wilhemus PMH, De Schutter B, Bemporad A (2001) Equivalence of hybrid dynamical models. Automatica 37(7):1085–1091
Henzinger T A, Ho P-H, Wong-Toi H (1997) Hytech: A model checker for hybrid systems. In: International Conference on Computer Aided Verification. Springer, pp 460–463
Henzinger T A, Kopke P W, Puri A, Varaiya P (1998) What’s decidable about hybrid automata?. J Comput Syst Sci 57:94–124
Herceg M, Kvasnica M, Jones C N, Morari M (2013) Multi-parametric toolbox 3.0. In: Control Conference (ECC), 2013 European. IEEE, pp 502–510
Hoogendoorn S, Bovy P (2001) State-of-the-art of vehicular traffic flow modeling. J Syst Cont Eng 215:283–303. https://doi.org/10.1243/0959651011541120
Júlvez J, Di Cairano S, Bemporad A, Mahulea C (2014) Event-driven model predictive control of timed hybrid petri nets. Int J Robust Nonlinear Control 24(12):1724–1742
Kamal M A S, Mukai M, Murata J, Kawabe T (2013) Model predictive control of vehicles on urban roads for improved fuel economy. IEEE Trans Control Syst Technol 21(3):831–841. https://doi.org/10.1109/TCST.2012.2198478
Kamal M A S, Imura J, Hayakawa T, Ohata A, Aihara K (2014) Smart driving of a vehicle using model predictive control for improving traffic flow. IEEE Trans Intell Transp Syst 15(2):878–888. https://doi.org/10.1109/TITS.2013.2292500
Lin H, Antsaklis P J (2014) Hybrid dynamical systems: An introduction to control and verification. Found Trends Syst Control 1(1):1–172
Lucia W, Famularo D, Franze G (2017) A set-theoretic reconfiguration feedback control scheme against simultaneous stuck actuators. IEEE Trans Autom Control 63(8):2558–2565
Lygeros J, Godbole D N, Sastry S (1996) Multiagent hybrid system design using game theory and optimal control. In: Proceedings of 35th IEEE Conference on Decision and Control, vol 2. IEEE, pp 1190–1195
Morrissett A, Abdelwahed S (2018) A physical testbed for smart city research. In: 2018 IEEE/ACS 15th International Conference on Computer Systems and Applications (AICCSA), pp 1–2
Nandola N N, Rivera D E (2011) An improved formulation of hybrid model predictive control with application to production-inventory systems. IEEE Trans Control Syst Technol 21(1):121–135
Oberdieck R, Pistikopoulos E N (2015) Explicit hybrid model-predictive control: The exact solution. Automatica 58:152–159
Papamichail I, Bekiaris-Liberis N, Delis A I, Manolis D, Mountakis K , Nikolos I K, Roncoli C, Papageorgiou M (2019) Motorway traffic flow modelling, estimation and control with vehicle automation and communication systems. Annu Rev Control 48:325–346. https://www.scopus.com
Rakovic S V, Kerrigan E C, Mayne D Q, Lygeros J (2006) Reachability analysis of discrete-time systems with disturbances. IEEE Trans Autom Control 51(4):546–561
Roncoli C, Papamichail I, Papageorgiou M (2015) Model predictive control for motorway traffic with mixed manual and vacs-equipped vehicles. In: Transportation Research Procedia, vol 10, pp 452–461. www.scopus.com. Cited By :7
Sandou G, Olaru S (2007) Ant colony and genetic algorithm for constrained predictive control of power systems. In: International Workshop on Hybrid Systems: Computation and Control. Springer, pp 501–514
Tomlin C, Pappas G J, Sastry S (1998) Conflict resolution for air traffic management: A study in multiagent hybrid systems. IEEE Trans Autom Control 43(4):509–521
Torrisi F D, Bemporad A (2004) Hysdel-a tool for generating computational hybrid models for analysis and synthesis problems. IEEE Trans Control Syst Technol 12(2):235–249
Wittmann-Hohlbein M, Pistikopoulos E N (2014) Approximate solution of mp-milp problems using piecewise affine relaxation of bilinear terms. Comput Chem Eng 61:136–155
Zhang J, Johansson K H, Lygeros J, Sastry S (2000) Dynamical systems revisited: Hybrid systems with zeno executions. In: International Workshop on Hybrid Systems: Computation and Control, vol 1790. Springer, pp 451–464
Funding
Open access funding provided by Università della Calabria within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article belongs to the Topical Collection: Smart Cities Guest Editors: (Samuel) Qing-Shan Jia, Mariagrazia Dotoli, and Qian-chuan Zhao
The work of W. Lucia was supported in part by the Natural Science and Engineering Council of Canada under Grant RGPIN-2018-06713 and in part by the Fonds Qué bécois de la Recherche sur la Nature et les Technologies under Grant 2020-NC-268119.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lucia, W., Franzè, G. & Famularo, D. A receding horizon event-driven control strategy for intelligent traffic management. Discrete Event Dyn Syst 31, 469–488 (2021). https://doi.org/10.1007/s10626-020-00337-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10626-020-00337-7





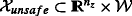 , is unsafe and, starting from any admissible initial condition, the system trajectory never enters inside, i.e.
, is unsafe and, starting from any admissible initial condition, the system trajectory never enters inside, i.e.
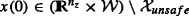 be an initial state condition and
be an initial state condition and 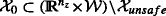 for which there exists an input sequence u[0,N− 1) := {u(0),…,u(N − 1)} such that
for which there exists an input sequence u[0,N− 1) := {u(0),…,u(N − 1)} such that 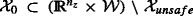 for which it is guaranteed the existence of an input sequence u[0,N− 1) capable to steer the state trajectory within Ξ, i.e. x(N) ∈Ξ.
for which it is guaranteed the existence of an input sequence u[0,N− 1) capable to steer the state trajectory within Ξ, i.e. x(N) ∈Ξ.









