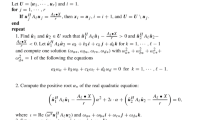New families of quaternionic Hadamard matrices

Abstract

A quaternionic Hadamard matrix (QHM) of order n is an $n\times n$ matrix H with non-zero entries in the quaternions such that $HH^*=nI_n$, where $I_n$ and $H^*$ denote the identity matrix and the conjugate-transpose of H, respectively. A QHM is dephased if all the entries in its first row and first column are 1, and it is non-commutative if its entries generate a non-commutative group. The aim of our work is to provide new constructions of infinitely many (non-commutative dephased) QHMs; such matrices are used by Farkas et al. (IEEE Trans Inform Theory 69(6):3814–3824, 2023) to produce mutually unbiased measurements.

1 Introduction

A Hadamard matrix (HM) of order n is an $n\times n$ matrix H with entries from $\{-1,1\}$ such that $HH^\intercal =nI_n$ where $H^\intercal$ is the transpose of H and $I_n$ is the identity matrix of order n. HMs are of interest, both for their applications (see below) and for the captivating simplicity of the Hadamard Conjecture, which asserts that a HM of order 4n exists for every positive integer n. There are several constructions of infinite families of HMs, however, as of 2023, no method is known to produce a HM for every order 4n; the smallest order for which the existence of a HM is unknown is 668.

Properties of HMs such as invertibility, balanced number of matches and miss-matches between entries of distinct rows, and zero cross-correlation of distinct rows, have enabled these matrices to have applications in the areas of digital signal processing, error-correcting codes, experimental designs, and cryptography (see [13, Chapter 3]). Motivated by these applications, HMs have been generalised in multiple ways, depending on the type of property one seeks to retain. In 1962, Butson [5] introduced HMs with entries from the n-th roots of unity; such matrices are known as Butson Hadamard matrices (BHMs). These matrices belong to a larger class of matrices called complex Hadamard matrices (CHMs) which are defined by the unimodularity of their entries and row orthogonality property. CHMs have received special attention in the last decades due to their connection to Mutually Unbiased Bases (MUBs), which are relevant in quantum information theory, see [22] and the references therein. Research in this area has primarily focused on the construction, classification and enumeration of such matrices, as well as the development of methods to convert CHMs to real HMs, see [7, 9] for more details.

In 1952, Rutledge [19] studied the structure of square matrices with entries from a 16-element subset of the double-tetrahedron group $\mathcal {Q}_{24}$ satisfying the row orthogonality condition. He called such matrices Quaternionic Hadamard matrices (QHMs), and described a canonical form for QHMs of square-free order. In 1944, Williamson [25] introduced a plug-in method for finding HMs with real entries, using the standard matrix representation of the quaternion group; such matrices are known as Williamson Hadamard matrices (WHMs), but they produce matrices with entries in $\{\pm 1\}$. Williamson’s approach has proliferated into various plug-in techniques, see for example [20, Sect. 4]. In 2008, Chterental and Djokovich [8] introduced HMs over the quaternion algebra $\mathbb {H}$ within the study of qustochastic and bistochastic matrices; they also called such matrices QHMs. Moreover, they introduced the notion of quaternionic MUBs in quaternionic Hilbert spaces, and determined all QHMs of order $n\leqslant 4$. Recent work of Farkas et al. (2023) showed that QHMs are relevant in quantum information theory, by proving that such QHMs lead to mutually unbiased measurements (MUMs). They also showed that non-commutative dephased QHMs yield a class of MUMs which are not direct sums of mutually unbiased bases (MUBs); recall that a QHM is dephased if all the entries in its first row and first column are 1, and it is non-commutative if its entries generate a non-commutative group. We also mention the related work of Kharaghani et al. [15] which discusses the more general concept of orthogonal designs over quaternions and relations to QHMs.

Our main results are new constructions for infinitely many (non-commutative dephased) QHMs, see Sect. 3. Our constructions yield the following.

Theorem 1

There exists a non-commutative dephased QHM of order d for every d that is a product of numbers e as listed below. Let $L=\{$5,6,7,9,10,11,13,14,15,17, 18,19,20,21,22,23,25,26,27,28,29,30,31,33,34,35, 36,37,38,39,41,42,43,44,45,46,49,50$\}$.

• (i) $e=\ell m$ where $\ell \in L$ and m is the order of any HM;

• (ii) $e=\Pi _{\ell \in L}\ell ^{r_\ell }$, where each $r_\ell \geqslant 0$ is an integer (not all 0);

• (iii) $e=(q_1+1)\dots (q_t+1)$ where each $q_i\equiv 1\bmod 4$ is a prime power and $t\ge 1$ an integer;

• (iv) $e=q+1$ where $q\equiv 1\bmod 4$ is a prime power;

• (v) $e=4m+2$ where m satisfies one of the following: m is a prime, or $2m+1$ is a prime power congruent 3 modulo 4, or $m=2^k-1$ with $k\geqslant 2$, or $m=p(p + 2)$ where p and $p + 2$ are primes.

To the best of our knowledge, Theorem 1 includes infinitely many new orders d for QHMs. We note that MUMs, and therefore QHMs, are related to so-called super-dense coding protocols, see [10, Definition 3.1 and Theorem 3.3]. However, it is already known that constructions involving CHMs produce super-dense coding protocols for all dimensions, see [24, Sect. 4].

2 Preliminaries

We provide some background information and introduce the required notation. Throughout, for an integer $n>0$, let $I_n$ and $J_n$ be the identity matrix and the all-1s matrix, respectively. For a prime power q, the field with q elements is $\text {GF}(q)$. The quaternion algebra $\mathbb {H}$ has $\mathbb {R}$-basis $\{1,\text {i},\text {j},\text {k}\}$ and multiplicative identity 1; its multiplication is $\mathbb {R}$-linear and non-commutative and defined by $\text {i}^2=\text {j}^2=\text {k}^2=\text {i}\text {j}\text {k}=-1$. Its $\mathbb {R}$-linear complex conjugation is defined by $1^*=1$ and $x^*=-x$ for $x\in \{\text {i},\text {j},\text {k}\}$. We write $\mathcal {Q}_8$ and $\mathcal {Q}_{24}$ for the multiplicative groups generated by $\{\text {i},\text {j}\}$ and $\{\text {i},\text {j},\textrm{q}\}$, respectively, where $\textrm{q}=(1+\text {i}+\text {j}+\text {k})/2$; they have order 8 and 24, respectively. In particular, $\mathcal {Q}_{24}=\mathcal {Q}_8\cup \textrm{q}\mathcal {Q}_8\cup \textrm{q}^*\mathcal {Q}_8$.

2.1 QHMs

For an $n\times n$ matrix H over $\mathbb {H}$, we denote by $H^\intercal$ and $H^*$ the transpose and conjugate-transpose of H, respectively. The matrix H is a quaternionic Hadamard matrix (QHM) if $HH^*=nI_n$. Examples are the matrices $H_3,\ldots ,H_6$ (with $H_i$ of order i) defined as below.

3 Constructions of QHMs

We generalise classical constructions of HMs to produce infinite families of non-commutative dephased QHMs. We also use existing infinite families of perfect quaternionic sequences to establish infinitely many non-commutative dephased QHMs.

3.1 QHMs from Kronecker products

Let $A = [a_{ij}]$ and $B = [b_{kl}]$ be $m \times m$ and $n \times n$ matrices, respectively. The (left) Kronecker product of A and B is the $mn \times mn$ matrix $A \otimes B = [a_{ij}B]$; the right Kronecker product is the $mn\times mn$ matrix $A \hat{\otimes } B = [Ab_{kl}]$. If B is an $mn\times mn$ matrix, then B is naturally partitioned in $n\times n$ submatrices, and for $i,j\in \{1,\ldots ,m\}$, the (i, j; n)-block of B is the $n\times n$ submatrix starting in row $(i-1)n+1$ and column $(j-1)n+1$. For example, if $B=[b_{ij}C_{ij}]$ is an $mn\times mn$ block matrix where each $C_{ij}$ is $n\times n$, then the (i, j; n)-block of B of is $b_{ij}C_{ij}$ and the (i, j; n)-block of $B^*$ is $C_{ji}^*b_{ji}^*$. If $D=[d_{ij}E_{ij}]$ is defined analogously, then BD is a block matrix whose (i, j; n)-block is $\sum _{s=1}^m b_{is}C_{is}d_{sj}E_{sj}$.

Proposition 2

If A and B are (dephased / non-commutative) QHMs, then so are $-A$, $A^*$, and $A \otimes B$; in particular, the t-fold Kronecker product $\otimes ^t A$ is a (dephased/non-commutative) QHM for every $t>0$.

Proof

The first two claims are obvious; the last one follows from a general observation: If A and B are $m\times m$ and $n\times n$ matrices over $\mathbb {H}$, then $(A \otimes B)^*= B^*\hat{\otimes } A^*$, and the (i, k; n)-th block of $(A\otimes B)(B^* \hat{\otimes } A^*)$ is $\sum _{s=1}^m a_{is}BB^*a_{ks}^*$; note that the entry in row s and column j of $A^*$ is $a_{js}^*$. $\square$

3.2 Plug-in techniques for QHMs

Standard HM plug-in techniques apply to QHMs; they are useful in later sections for constructing non-commutative dephased QHMs. A direct calculation confirms the following.

Proposition 3

Let D, E, F be diagonal matrices such that their diagonal elements are unit quaternions and their top left entry is  1, and let W, X, Y, Z be (non-commutative / dephased) QHMs of order n. Then

$$\begin{aligned} \begin{bmatrix} X &{}\quad DY \\ X &{}\quad -DY \end{bmatrix},\quad \begin{bmatrix} X &{}\quad X \\ Y &{}\quad -Y \end{bmatrix},\quad \text {and}\quad \begin{bmatrix} W &{}\quad DX &{}\quad EY &{}\quad FZ\\ W &{}\quad -DX &{}\quad EY &{}\quad -FZ\\ W &{}\quad DX &{}\quad -EY &{}\quad -FZ\\ W &{}\quad -DX &{}\quad -EY &{}\quad FZ \end{bmatrix} \end{aligned}$$

are a (non-commutative/dephased) QHMs of order 2n, 2n, and 4n, respectively.

Similar methods for doubling the size of a QHMs can be obtained. For example, Tadej and Życzkowski [22, Sect. 4.5] presented a generalisation of the Kronecker product of complex HMs. A quick calculation shows that this construction generalises to QHMs, which is summarised as follows.

Proposition 4

For $r=2,\dots ,m$, let $D_r$ be a diagonal matrix such that their diagonal elements are unit quaternions and their top left entry is   1. If $A=[a_{ij}]$ and $B_1,\dots , B_m$ are (non-commutative / dephased) QHMs, with A of order m and each $B_i$ of order n, then

$$\begin{aligned} \begin{bmatrix} a_{11}B_1 &{}\quad a_{12}D_2B_2 &{}\quad \dots &{}\quad a_{1m}D_mB_m \\ \vdots &{}\quad \vdots &{}\quad &{}\quad \vdots \\ a_{m1}B_1 &{}\quad a_{m2}D_2B_2 &{}\quad \dots &{}\quad a_{mm}D_mB_m \end{bmatrix} \end{aligned}$$

is a (non-commutative/dephased) QHM of order mn.

3.3 QHMs from Paley matrices

We now generalise the construction of Paley I and Paley II HMs (see [13, Lemma 2.4]) to QHMs over the alphabet $\mathcal {Q}_8$. We start by recalling some required definitions.

The quadratic character $\chi _{q}:\text {GF}(q) \rightarrow \{-1,0,1\}$ for q an odd prime power is defined by $\chi _q(0)=0$, $\chi _q(x)=1$ if $x\in \text {GF}(q)^\times$ is a square, and $\chi _q(x)=-1$ otherwise. Recall that $G_q=\text {GF}(q)^\times$ is cyclic of order $q-1$, say with generator $\gamma$, and let $\omega _q:G_q \rightarrow G_q$, $x\mapsto x^{(q-1)/2}$, which is a group homomorphism. If $x\in G_q$, then $\omega _q(x)^2=x^{q-1}=1$, which implies that $\omega _q(x)$ has order dividing 2, hence $\omega _q(x)\in \{\pm 1\}$. If particular, $x\in G_q$ satisfies $\omega _q(x)=1$ if and only if x lies in the unique subgroup of $G_q$ of order $(q-1)/2$. The latter subgroup is generated by $\gamma ^2$, which implies that $\chi _q(x)=\omega _q(x)$ for all $x\in G_q$; in particular, $\chi _q$ is indeed a homomorphism on $G_q$. Note that $-1\in G_q$ is a square if and only if $q\equiv 1\bmod 4$. Since $a-b=(-1)(b-a)$ for $a,b\in G$, this implies that

$$\begin{aligned} \chi _q(a-b)={\left\{ \begin{array}{ll}\hspace{8pt}\chi _q(b-a)&{} (q\equiv 1\bmod 4)\\ -\chi _q(b-a) &{} (q\equiv 3\bmod 4). \end{array}\right. } \end{aligned}$$

Let $f_0,\ldots ,f_{q-1}$ with $f_0=0$ be the elements of $\text {GF}(q)$ and define $Q_q$ to be the real $q\times q$ matrix

$$\begin{aligned} Q_q=[\chi _q(f_i-f_j)]. \end{aligned}$$

By what is said above, $Q_q$ is (skew-)symmetric if $q\equiv 1\bmod 4$ (if $q\equiv 3\bmod 4$). Since the kernel of $\omega _q$ has index 2 in $G_q$, we have $\sum _{i=1}^{q-1}\chi _q(f_i)=0$, and therefore $\sum _{i=0}^{q-1}\chi _q(f_i-f_j)=0$ for all j, hence $Q_qJ_q = J_qQ_q=0$ is the all-0s matrix. Another direct calculation (see [12, Lemma 7.10]) shows that

$$\begin{aligned} Q_qQ_q^\intercal = qI_q - J_q.\end{aligned}$$

(1)

In the matrices below, for a quaternion $a \in \mathbb {H}$, we denote by $\varvec{a}$ a suitable row vector $(a,\ldots ,a)$ of appropriate length.

Proposition 5

Let q be an odd prime power and let a, b, c, d, e be unit quaternions. The $(q+1)\times (q+1)$ matrix

$$\begin{aligned} M_{a,b,c,d,e}= \begin{bmatrix}a &{}\quad \varvec{b} \\ \varvec{c}^\intercal &{}\quad dQ_q + e I_q\end{bmatrix}\end{aligned}$$

is a QHM if and only if $ac^*+be^*=0$, and if $q\equiv 1\bmod 4$ then $ed^*+de^*=0$, otherwise $ed^*-de^*=0$.

Proof

We need to show that $K=(q+1)I_{q+1}$ for

$$\begin{aligned} K = \begin{bmatrix}a &{}\quad \varvec{b} \\ \varvec{c}^\intercal &{}\quad d Q_q + e I_q\end{bmatrix} \begin{bmatrix}a^* &{}\quad \varvec{c^*} \\ (\varvec{b^*})^\intercal &{}\quad d^* Q_q^* +e^* I_q\end{bmatrix}. \end{aligned}$$

We consider each of the four blocks of this matrix. The top left $1\times 1$ block of K is $aa^*+q(bb^*)=1+q$. Since $\varvec{x}Q_q=x\varvec{1}Q_q=x\varvec{0}=\varvec{0}$ for every x (and similarly for $Q_q^*$), the top right $1\times q$ block of K is $a\varvec{c^*}+\varvec{b}e^*=\varvec{0}$ if and only if $ac^*+be^*=0$. Analogously, the bottom right $q\times 1$ block of K is $\varvec{c}^\intercal a^*+eI_q(\varvec{b^*})^\intercal =\varvec{0}^\intercal$ if and only if $ca^*=-eb^*$, which is equivalent to the previous condition on a, b, c, e. Lastly, using (1), the bottom right $q\times q$ block of K is

$$\begin{aligned} \varvec{c}^\intercal \varvec{c^*}+\left( dQ_q+e I_q\right) \left( d^* Q_q^*+e^* I_q\right) =J_q+Q_qQ_q^*+I_q+de^*Q_q+ed^*Q_q^*, \end{aligned}$$

which equals $(1+q)I_q$ if and only if $de^*Q_q+ed^*Q_q^*$ is the zero matrix. If $q\equiv 1\bmod 4$ then $Q_q^*=Q_q$; if $q\equiv 3\bmod 4$, then $Q_q^*=-Q_q$.$\square$

Now we focus on $a,b,c,d,e\in \mathcal {Q}_8$. If $M_{a,b,c,d,e}$ is a QHM, then also $M_{\alpha (a),\alpha (b),\alpha (c),\alpha (d),\alpha (e)}$ for every automorphism $\alpha$ of $\mathcal {Q}_8$. Modulo this action of the automorphism group of $\mathcal {Q}_8$, a direct calculation shows the following: For $q\equiv 1\bmod 4$, there are 176 different 5-tuples in $\mathcal {Q}_8$ that produce QHMs (of which 112 are non-commutative), and there is a unique class (under the action induced by the automorphism group of $\mathcal {Q}_8$) of dephased QHMs, namely, $M_{1,1,1,\text {i},-1}$. For $q\equiv 3\bmod 4$, there are 100 different 5-tuples on $\mathcal {Q}_8$ that produce QHMs (of which 28 are non-commutative); there is a unique class (under the action induced by the automorphism group of $\mathcal {Q}_8$) of dephased QHMs, with representative $M_{1,1,1,1,-1}$.

Next, we consider analogs of the Paley II HMs.

Proposition 6

Let $q\equiv 1\bmod 4$ be an odd prime power. Let a, b, c, d, x, y be unit quaternions such that $x^*=-x$, and $y^*=-y$. Let

$$\begin{aligned} P_{a,b,c,d,x,y}=\begin{bmatrix}a(S+I_{q+1}S) &{}\quad b (S - I_{q+1}) \\ c (S - I_{q+1})&{}\quad d (-S -I_{q+1})\end{bmatrix}\quad \text {where}\quad S=\begin{bmatrix}0&{}\quad \varvec{x}\\ \varvec{x}^\intercal &{}\quad yQ_q\end{bmatrix}. \end{aligned}$$

With these assumptions on x and y, the matrix $P_{a,b,c,d,x,y}$ is a QHM if and only if $ac^*=bd^*$ and $azc^*=-bzd^*$ for both $z\in \{x,y\}$. For example, $P_{-\text {j}, \text {i}, \text {k}, 1, \text {i}, (\text {i}+\text {j})/\sqrt{2}}$ yields the dephased QHM

$$\begin{aligned} \begin{bmatrix} 1 &{}\quad \varvec{1} &{}\quad 1 &{}\quad \varvec{1} \\ \varvec{1}^\intercal &{}\quad (-\text {i}+\text {j})/\sqrt{2} (Q_q-I_q) &{}\quad -\varvec{1}^\intercal &{}\quad (-\text {i}+\text {j})/\sqrt{2} (Q_q-I_q)\\ 1 &{}\quad -\varvec{1} &{}\quad 1 &{}\quad \varvec{1} \\ \varvec{1}^\intercal &{}\quad (-\text {i}+\text {j})/\sqrt{2} (Q_q+I_q) &{}\quad -\varvec{1}^\intercal &{}\quad (\text {i}-\text {j})/\sqrt{2} (Q_q-I_q) \end{bmatrix}. \end{aligned}$$

(2)

Proof

Since $Q_q$ is real, $Q_qQ_q^*=Q_qQ_q^\intercal =qI_q-J_q$ by (1), and a short calculation shows that $SS^*=qI_{q+1}$. Recall that $Q_q$ is symmetric for $q\equiv 1\bmod 4$, so our choices of x and y imply that $S+S^*$ is the zero matrix. This already implies that the top left and bottom right $(q+1)\times (q+1)$ blocks of $P_{a,b,c,d,x,y} P_{a,b,c,d,x,y}^*$ equal $(2q+2)I_{q+1}$. Another calculation shows that the top right $(q+1)\times (q+1)$ block of $P_{a,b,c,d,x,y} P_{a,b,c,d,x,y}^*$ equals $(ac^*-bd^*)(q-1)I_q-2aSc^*-2bSd^*$; and this is zero if and only if $ac^*=bd^*$ and $azc^*=-bzd^*$ for $z\in \{x,y\}$. A similar argument applies for the bottom left $(q+1)\times (q+1)$ block. The last claim follows from a direct calculation with $P_{-\text {j}, \text {i}, \text {k}, 1, \text {i}, (\text {i}+\text {j})/\sqrt{2}}$. $\square$

Proposition 7

Let $q\equiv 3\bmod 4$ be an odd prime power. Let a, b, c, d, x, y be unit quaternions such that $x^*=-x$, and $y^*=y$. Let

$$\begin{aligned} R_{a,b,c,d,x,y}=\begin{bmatrix}a(S+I_{q+1}) &{}\quad b (S + I_{q+1}) \\ c (S + I_{q+1})&{}\quad d (S + I_{q+1})\end{bmatrix}\quad \text {where}\quad S=\begin{bmatrix}0&{}\quad \varvec{x}\\ \varvec{x}^\intercal &{}\quad yQ_q\end{bmatrix}. \end{aligned}$$

The matrix $R_{a,b,c,d,x,y}$ is a QHM if and only if $ac^*+bd^*=0$. For example, $R_{-\textrm{q}^* \text {j}, \text {j}, \text {i}, \textrm{q}, (\text {i}-\text {j})/\sqrt{2}, 1}$ yields the dephased QHM

(3)

Proof

As in the previous proof, $Q_qQ_q^*=Q_qQ_q^\intercal =qI_q-J_q$, and $S+S^*$ is the zero matrix, and so the top left and bottom right $(q+1)\times (q+1)$ blocks of $R_{a,b,c,d,x,y} R_{a,b,c,d,x,y}^*$ equal $(2q+2)I_{q+1}$. The top right $(q+1)\times (q+1)$ block of $R_{a,b,c,d,x,y} R_{a,b,c,d,x,y}^*$ equals $(ac^*+bd^*)(q-1)I_q$, and this is zero if and only if $ac^*+bzd^*=0$. A similar argument applies for the bottom left block. The last claim is again a direct calculation. $\square$

Applying Proposition 3 to the previous results yields the following.

Corollary 8

Let q be a prime power, let $s=(\text {i}+\text {j})/\sqrt{2}$, and $t=(-\text {i}+\text {j})/\sqrt{2}$. The matrices $M_{1,1,1,\text {i},-1}$, $P_{-\text {j}, \text {i}, \text {k}, 1, \text {i}, s}$ and $R_{-\textrm{q}^* \text {j}, \text {j}, \text {i}, \textrm{q}, t^*, 1}$ yield the following non-commutative dephased QHMs of order $2(q+1)$ for $q\equiv 1\bmod 4$, of order $4(q+1)$ for $q\equiv 1\bmod 4$, and of order $4(q+1)$ for $q\equiv 3\bmod 4$, respectively:

$$\begin{aligned} \begin{bmatrix} 1 &{}\quad \varvec{1} &{}\quad 1 &{}\quad \varvec{1} \\ \varvec{1}^\intercal &{}\quad \text {i}Q_q + I_q &{}\quad \varvec{\text {j}}^\intercal &{}\quad -\text {k}Q_q + \text {j}I_q \\ 1 &{}\quad \varvec{1} &{}\quad -1 &{}\quad -\varvec{1} \\ \varvec{1}^\intercal &{}\quad \text {i}Q_q + I_q &{}\quad -\varvec{\text {j}}^\intercal &{}\quad \text {k}Q_q - \text {j}I_q \end{bmatrix} \end{aligned}$$

$$\begin{aligned} \begin{bmatrix} 1 &{}\quad \varvec{1} &{}\quad 1 &{}\quad \varvec{1} &{}\quad 1 &{}\quad \varvec{1} &{}\quad 1 &{}\quad \varvec{1} \\ \varvec{1}^\intercal &{}\quad t (Q_q-I_q) &{}\quad -\varvec{1}^\intercal &{}\quad t (Q_q-I_q) &{}\quad \varvec{1}^\intercal &{}\quad t (Q_q-I_q) &{}\quad -\varvec{1}^\intercal &{}\quad t (Q_q-I_q)\\ 1 &{}\quad -\varvec{1} &{}\quad 1 &{}\quad \varvec{1} &{}\quad \text {k}&{}\quad -\varvec{\text {k}} &{}\quad k &{}\quad \varvec{\text {k}} \\ \varvec{1}^\intercal &{}\quad t (Q_q+I_q) &{}\quad -\varvec{1}^\intercal &{}\quad -t (Q_q-I_q) &{} \quad \varvec{1}^\intercal &{}\quad t (Q_q+I_q) &{}\quad -\varvec{1}^\intercal &{}\quad -t (Q_q-I_q)\\ 1 &{}\quad \varvec{1} &{}\quad 1 &{}\quad \varvec{1} &{}\quad -1 &{}\quad -\varvec{1} &{}\quad -1 &{}\quad -\varvec{1} \\ \varvec{1}^\intercal &{}\quad t (Q_q-I_q) &{}\quad -\varvec{1}^\intercal &{}\quad t (Q_q-I_q) &{}\quad -\varvec{1}^\intercal &{}\quad -t (Q_q-I_q) &{}\quad \varvec{1}^\intercal &{}\quad -t (Q_q-I_q)\\ 1 &{}\quad -\varvec{1} &{}\quad 1 &{}\quad \varvec{1} &{}\quad -\text {k}&{}\quad \varvec{\text {k}} &{}\quad -k &{}\quad -\varvec{\text {k}} \\ \varvec{1}^\intercal &{}\quad t (Q_q+I_q) &{}\quad -\varvec{1}^\intercal &{}\quad -t (Q_q-I_q) &{}\quad -\varvec{1}^\intercal &{}\quad -t (Q_q+I_q) &{}\quad \varvec{1}^\intercal &{}\quad t (Q_q-I_q) \end{bmatrix} \end{aligned}$$

Iterated Kronecker products (introduced in Sect. 3.1) of the dephased matrices of $M_{1,1,1,\text {i},-1}$,$P_{-\text {j}, \text {i}, \text {k}, 1, \text {i}, (\text {i}+\text {j})/\sqrt{2}}$ and $R_{-\textrm{q}^* \text {j}, \text {j}, \text {i}, \textrm{q}, (\text {i}-\text {j})/\sqrt{2}, 1}$ with $H_4,H_5,H_6$ (as defined in Sect. 2.1) yield non-commutative dephased QHMs. Note that each of $M_{1,1,1,\text {i},-1}$, $P_{-\text {j}, \text {i}, \text {k}, 1, \text {i}, (\text {i}+\text {j})/\sqrt{2}}$ depends on the underlying prime power q, hence these matrices describe in fact infinite families of QHMs.

3.4 QHMs from two-circulant-core matrices

A two-circulant core (TCC) HM is a HM of order $n=2m+2$ of the form

$$\begin{aligned} \begin{bmatrix} 1 &{}\quad 1 &{}\quad \varvec{1} &{}\quad \varvec{1}\\ 1 &{}\quad -1 &{}\quad \varvec{1} &{}\quad -\varvec{1}\\ \varvec{1}^\intercal &{}\quad \varvec{1}^\intercal &{}\quad A &{}\quad B\\ \varvec{1}^\intercal &{}\quad -\varvec{1}^\intercal &{}\quad B^\intercal &{}\quad -A^\intercal \end{bmatrix} \end{aligned}$$

(4)

where A and B are circulant matrices of order m, see [11]. Lists of orders for TCC HM are given in [4, Sect. 1], and TCC HMs are known for orders $4m+2$ where m satisfies the following: m is a prime, or $2m+1$ is a prime power congruent 3 modulo 4, or $m=2^k-1$ with $k\geqslant 2$, or $m=p(p + 2)$ where p and $p + 2$ are both primes. The next result follows from a direct calculation and the orthogonality properties of a TCC HM.

Proposition 9

If x is a unit quaternion, and A and B are the blocks of a TCC HM of order $2m+2$, then the following is a dephased QHM:

$$\begin{aligned} M_x=\begin{bmatrix} 1 &{}\quad 1 &{}\quad \varvec{1} &{}\quad \varvec{1}\\ 1 &{}\quad -1 &{}\quad -\varvec{x} &{}\quad \varvec{x}\\ \varvec{1}^\intercal &{}\quad -\varvec{1}^\intercal &{}\quad -\varvec{x} A &{}\quad \varvec{x}B\\ \varvec{1}^\intercal &{}\quad -\varvec{1}^\intercal &{}\quad -\varvec{x} B^\intercal &{}\quad \varvec{x} A^\intercal \end{bmatrix}. \end{aligned}$$

Proposition 3 with $X=Y=M_{\text {i}}$ and D the diagonal matrix with entries $1,\text {j},\ldots ,\text {j}$ shows the following.

Corollary 10

The matrix

$$\begin{aligned} \begin{bmatrix} 1 &{}\quad 1 &{}\quad \varvec{1} &{}\quad \varvec{1} &{}\quad 1 &{}\quad 1 &{}\quad \varvec{1} &{}\quad \varvec{1}\\ 1 &{}\quad -1 &{}\quad -\varvec{\text {i}} &{}\quad \varvec{\text {i}} &{}\quad \text {j}&{}\quad -\text {j}&{}\quad -\varvec{\text {k}} &{}\quad \varvec{\text {k}} \\ \varvec{1}^\intercal &{}\quad -\varvec{1}^\intercal &{}\quad -\varvec{\text {i}} A &{}\quad \varvec{\text {i}}B &{}\quad \varvec{\text {j}}^\intercal &{}\quad -\varvec{\text {j}}^\intercal &{}\quad \varvec{\text {k}} A &{}\quad -\varvec{\text {k}}B\\ \varvec{1}^\intercal &{}\quad -\varvec{1}^\intercal &{}\quad -\varvec{\text {i}} B^\intercal &{}\quad \varvec{\text {i}} A^\intercal &{}\quad \varvec{\text {j}}^\intercal &{}\quad -\varvec{\text {j}}^\intercal &{}\quad \varvec{\text {k}} B^\intercal &{}\quad -\varvec{\text {k}} A^\intercal \\ 1 &{}\quad 1 &{}\quad \varvec{1} &{}\quad \varvec{1} &{}\quad -1 &{}\quad -1 &{}\quad -\varvec{1} &{}\quad -\varvec{1}\\ 1 &{}\quad -1 &{}\quad -\varvec{\text {i}} &{}\quad \varvec{\text {i}} &{}\quad -\text {j}&{}\quad \text {j}&{}\quad \varvec{\text {k}} &{}\quad -\varvec{\text {k}} \\ \varvec{1}^\intercal &{}\quad -\varvec{1}^\intercal &{}\quad -\varvec{\text {i}} A &{}\quad \varvec{\text {i}}B &{}\quad -\varvec{\text {j}}^\intercal &{}\quad \varvec{\text {j}}^\intercal &{}\quad -\varvec{\text {k}} A &{}\quad \varvec{\text {k}}B\\ \varvec{1}^\intercal &{}\quad -\varvec{1}^\intercal &{}\quad -\varvec{\text {i}} B^\intercal &{}\quad -\varvec{\text {i}} A^\intercal &{}\quad \varvec{\text {j}}^\intercal &{}\quad \varvec{\text {j}}^\intercal &{}\quad -\varvec{\text {k}} B^\intercal &{}\quad \varvec{\text {k}} A^\intercal \end{bmatrix} \end{aligned}$$

is a non-commutative dephased QHM of order $4m+4$.

Some TCC type QHMs that follow a different pattern are determined as follows; again, the correctness follows from a direct calculation.

Proposition 11

If A and B are the blocks of a TCC HM of order $2m+2$, then the following are QHMs:

$$\begin{aligned} \begin{array}{ccc} \begin{bmatrix} 1 &{} 1 &{} -\varvec{\text {i}} &{} -\varvec{\text {i}}\\ 1 &{} -1 &{} -\varvec{\text {i}} &{} \varvec{\text {i}}\\ \varvec{\text {i}}^\intercal &{} \varvec{\text {i}}^\intercal &{} A &{} B\\ \varvec{\text {i}}^\intercal &{} -\varvec{\text {i}}^\intercal &{} B^\intercal &{} -A^\intercal \end{bmatrix} &{} \begin{bmatrix} \text {i}&{} \text {i}&{} -\varvec{\text {j}} &{} \varvec{\text {j}}\\ \text {i}&{} -\text {i}&{} -\varvec{\text {j}} &{} -\varvec{\text {j}}\\ \varvec{\text {k}}^\intercal &{} \varvec{\text {k}}^\intercal &{} \text {k}A &{} \text {k}B\\ \varvec{\text {k}}^\intercal &{} -\varvec{\text {k}}^\intercal &{} \text {k}B^\intercal &{} -\text {k}A^\intercal \end{bmatrix}&{} \begin{bmatrix} \text {j}&{} \text {j}&{} \varvec{\text {k}} &{} \varvec{\text {k}}\\ \text {j}&{} -\text {j}&{} \varvec{\text {k}} &{} -\varvec{\text {k}}\\ \varvec{\text {i}}^\intercal &{} \varvec{\text {i}}^\intercal &{} A &{} B\\ \varvec{\text {i}}^\intercal &{} \varvec{\text {i}}^\intercal &{} B^\intercal &{} A^\intercal \end{bmatrix}\\ \\ \begin{bmatrix} 1 &{} 1 &{} -\varvec{\text {i}} &{} -\varvec{\text {i}}\\ 1 &{} -1 &{} -\varvec{\text {i}} &{} \varvec{\text {i}}\\ \varvec{\text {j}}^\intercal &{} \varvec{\text {j}}^\intercal &{} \text {k}A &{} \text {k}B\\ \varvec{\text {j}}^\intercal &{} -\varvec{\text {j}}^\intercal &{} \text {k}B^\intercal &{} -\text {k}A^\intercal \end{bmatrix} &{} \begin{bmatrix} 1 &{} 1 &{} -\varvec{\text {i}} &{} \varvec{\text {j}}\\ 1 &{} -1 &{} -\varvec{\text {i}} &{} -\varvec{\text {j}}\\ \varvec{\text {j}}^\intercal &{} \varvec{\text {j}}^\intercal &{} \text {k}A &{} -B\\ \varvec{\text {j}}^\intercal &{} -\varvec{\text {j}}^\intercal &{} \text {k}B^\intercal &{} A^\intercal \end{bmatrix} &{} \begin{bmatrix} 1 &{} \text {i}&{} \varvec{\text {j}} &{} \varvec{\text {k}}\\ 1 &{} -\text {i}&{} \varvec{\text {j}} &{} -\varvec{\text {k}}\\ \varvec{1}^\intercal &{} \varvec{\text {i}}^\intercal &{} \text {j}A &{} \text {k}B\\ \varvec{1}^\intercal &{} \varvec{\text {i}}^\intercal &{} \text {j}B^\intercal &{} \text {k}A^\intercal \end{bmatrix}. \end{array} \end{aligned}$$

3.5 QHMs from Williamson and Ito matrices

HMs of order 4n and of the form

$$\begin{aligned} \begin{bmatrix} A &{}\quad B &{}\quad C &{}\quad D\\ -B &{}\quad A &{}\quad -D &{}\quad C\\ -C &{}\quad D &{}\quad A &{}\quad -B\\ -D &{}\quad -C &{}\quad B &{}\quad A \end{bmatrix}\quad \text {and}\quad \begin{bmatrix} A &{}\quad B &{}\quad C &{}\quad D\\ -B &{}\quad A &{}\quad -D &{}\quad C\\ -C^\intercal &{}\quad D^\intercal &{}\quad A^\intercal &{}\quad -B^\intercal \\ -D^\intercal &{}\quad -C^\intercal &{}\quad B^\intercal &{}\quad A^\intercal \end{bmatrix} \end{aligned}$$

are Williamson HMs (WHM, left) and Ito HMs (IHMs, right), where A, B, C, D are $n\times n$ block matrices. It is sometimes required that the blocks A, B, C, D are circulant. We refer to [2] for more details and a historic overview of the development of WHMs, and to [13, Sect. 2.3.2] for more details on IHMs. The following can be proved by a short direct computation.

Proposition 12

If A, B, C, D are the blocks of a WHM or IHM, then

$$\begin{aligned} \begin{bmatrix} A &{}\quad \text {i}B &{}\quad \text {j}C &{}\quad \text {k}D\\ \text {i}B &{}\quad A &{}\quad \text {k}D &{}\quad \text {j}C\\ \text {j}C &{}\quad \text {k}D &{}\quad A &{}\quad \text {i}B\\ \text {k}D &{}\quad \text {j}C &{}\quad \text {i}B &{}\quad A \end{bmatrix}\quad {and}\quad \begin{bmatrix} A &{}\quad \text {i}B &{}\quad \text {j}C &{}\quad \text {k}D\\ \text {i}B &{}\quad A &{}\quad \text {k}D &{}\quad \text {j}C\\ \text {j}C^\intercal &{}\quad \text {k}D^\intercal &{}\quad A^\intercal &{}\quad \text {i}B^\intercal \\ \text {k}D^\intercal &{}\quad \text {j}C^\intercal &{}\quad \text {i}B^\intercal &{}\quad A^\intercal \end{bmatrix} \end{aligned}$$

is a a QHM for WHM (left) and IHM (right).

Known orders of WHMs are summarised in [2, Appendix A], and it follows that for each of these orders there exists a QHM of the same order; similarly, for known orders of IHMs. For example, [21, Corollary 3.6] implies that if $n>0$ is an integer such that n is odd, or $2n-1$ or $4n-1$ is a prime power, then there is an IHM of order 4m for every $m=2^a\cdot 10^b\cdot 26^c\cdot n$, with $a,b,c\geqslant 0$.

3.6 QHMs from complex HMs

A QHM whose entries lie in the subalgebra of $\mathbb {H}$ generated by $\{1,\text {i}\}$ is called a complex HM (CHMs). These matrices are abundant and are known to exist for all orders, for example using the Discrete Fourier Transform. For a recount on this topic see [13, Chapter 4] and [22]. By applying an automorphism of $\mathbb {H}$ to a CHM with entries of the form $a+b\text {i}$, for $a,b\in \mathbb {R}$, one obtains a matrix with entries in $\{a\pm b\text {j}\}$ or in $\{a\pm b\text {k}\}$ that satisfies the same orthogonality properties. This simple observation proves useful when constructing non-commutative dephased QHMs.

Proposition 13

Let H be a CHM of order n; if the entries of H are not all real, then H can be used to create a non-commutative dephased QHM of size 2n.

Proof

Let $\alpha$ an $\mathbb {R}$-linear automorphism of $\mathbb {H}$ that maps $\text {i}$ into $\text {j}$. Let $H^\alpha$ be the matrix obtained from H by applying $\alpha$ to every entry of H. Now Proposition 3 with $X=H$, $Y=H^\alpha$, and $D=I_n$ yields the desired QHM. $\square$

For example, if $N_x$ for $x\in \mathbb {H}$ denotes the matrix

$$\begin{aligned} N_{x}= \begin{bmatrix} 1 &{}\quad 1 &{}\quad 1 &{}\quad 1\\ 1 &{}\quad x &{}\quad -1 &{}\quad -x \\ 1 &{}\quad -1 &{}\quad 1 &{}\quad -1 \\ 1 &{}\quad -x &{}\quad -1 &{}\quad x \end{bmatrix}, \end{aligned}$$

then applying Proposition 3 to $X=N_{\text {i}}$, $Y=N_\text {j}$, and $D=I$, but also to $X=Y=N_\text {i}$ and $D=\text {diag}(1,-\text {k},1,-\text {k})$, yields the QHMs

$$\begin{aligned} \begin{bmatrix} 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} \text {i}&{} -1 &{} -\text {i}&{} 1 &{} \text {j}&{} -1 &{} -\text {j}\\ 1 &{} -1 &{} 1 &{} -1 &{} 1 &{} -1 &{} 1 &{} -1\\ 1 &{} -\text {i}&{} -1 &{} \text {i}&{} 1 &{} -\text {j}&{} -1 &{} \text {j}\\ 1 &{} 1 &{} 1 &{} 1 &{} -1 &{} -1 &{} -1 &{} -1 \\ 1 &{} \text {i}&{} -1 &{} -\text {i}&{} -1 &{} -\text {j}&{} 1 &{} \text {j}\\ 1 &{} -1 &{} 1 &{} -1 &{} -1 &{} 1 &{} -1 &{} 1\\ 1 &{} -\text {i}&{} -1 &{} \text {i}&{} -1 &{} \text {j}&{} 1 &{} -\text {j}\\ \end{bmatrix} \quad \text {and}\quad \begin{bmatrix} 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} \text {i}&{} -1 &{} -\text {i}&{} -\text {k}&{} \text {j}&{} \text {k}&{} -\text {j}\\ 1 &{} -1 &{} 1 &{} -1 &{} 1 &{} -1 &{} 1 &{} -1\\ 1 &{} -\text {i}&{} -1 &{} \text {i}&{} -\text {k}&{} -\text {j}&{} \text {k}&{} \text {j}\\ 1 &{} 1 &{} 1 &{} 1 &{} -1 &{} -1 &{} -1 &{} -1 \\ 1 &{} \text {i}&{} -1 &{} -\text {i}&{} \text {k}&{} -\text {j}&{} -\text {k}&{} \text {j}\\ 1 &{} -1 &{} 1 &{} -1 &{} -1 &{} 1 &{} -1 &{} 1\\ 1 &{} -\text {i}&{} -1 &{} \text {i}&{} \text {k}&{} \text {j}&{} -\text {k}&{} -\text {j}\\ \end{bmatrix}. \end{aligned}$$

Observe that there is no $\mathbb {R}$-linear automorphism of $\mathbb {H}$ that can map the first matrix to the second one, even thought the initial matrices have this property. A similar application of Proposition 3 yields the following.

Corollary 14

Let $M_\text {i}$ be the matrix in Proposition 9. Then the matrix

$$\begin{aligned} \begin{bmatrix} M_\text {i}&{} M_\text {j}\\ M_\text {i}&{} -M_\text {j}\end{bmatrix} \end{aligned}$$

is a non-commutative dephased QHM. Similar results apply to the matrices $M_{1,1,1,\text {i},-1}$, $P_{-\text {j}, \text {i}, \text {k}, 1, \text {i}, s}$ and $R_{-\textrm{q}^* \text {j}, \text {j}, \text {i}, \textrm{q}, t^*, 1}$ in Propositions 5, 6 and 7, for $s=(\text {i}+\text {j})/\sqrt{2}$ and $t=(-\text {i}+\text {j})/\sqrt{2}$.

The following result shows that non-commutative dephased QHMs are abundant if any unit quaternion entries are allowed.

Proposition 15

There are uncountably many non-commutative dephased QHMs.

Proof

It is shown in [13, Sect. 4.2.2] that there are uncountably many (inequivalent) CHMs of the form

$$\begin{aligned} M_{\text {i},a}= \begin{bmatrix} 1 &{}\quad 1 &{}\quad 1 &{}\quad 1\\ 1 &{}\quad \text {i}\exp ({\text {i}a}) &{}\quad -1 &{}\quad -\text {i}\exp ({\text {i}a}) \\ 1 &{}\quad -1 &{}\quad 1 &{}\quad -1 \\ 1 &{}\quad -\text {i}\exp ({\text {i}a}) &{}\quad -1 &{}\quad \text {i}\exp (\text {i}a) \end{bmatrix},\quad \text {with}\quad a\in [0,\pi ). \end{aligned}$$

The claim follows from applying Proposition 3 to the matrices $X=M_{\text {i},a}$, $Y=M_{\text {j},a}$, and $D=I$. $\square$

3.7 QHMs from perfect quaternionic sequences

Let $S=(s_0,\ldots ,s_{n-1})$ be a (periodic) sequence over a quaternion alphabet $\mathcal {A}\subseteq \mathbb {H}$, that is, we use the convention that $s_z=s_{z\bmod n}$ for all $z\in \mathbb {Z}$. For $t\in \mathbb {Z}$, the right periodic t-autocorrelation value of S is

$$\begin{aligned} {{\mathrm{{AC}}}}^\textrm{R}_S(t)=\sum \limits _{r=0}^{n-1}s_rs_{r+t}^{*}, \end{aligned}$$

and S is perfect if ${{\mathrm{{AC}}}}^\textrm{R}(S)=({{\mathrm{{AC}}}}^\textrm{R}_S(0),\ldots ,{{\mathrm{{AC}}}}^\textrm{R}_S(n-1))=(x,0,\ldots ,0)$ for some non-zero entry x. The non-commutativity of $\mathbb {H}$ also admits the concept of left periodic autocorrelations, however, perfection does not depend on this choice, see [16, Lemma 1]; we refer to [1, 3, 16, 17] for a detailed discussion of these sequences.

Proposition 16

Arranging the cyclic shifts of a quaternionic perfect sequence of length n as the rows of a matrix of order n yields a QHM of order n. If $q \equiv 1\bmod 4$ is a prime power, then there are QHMs over $\mathcal {Q}_8$ and $\mathcal {Q}_{24}$ of order n, where $n=2^t$ with $t\ge 1$, $n=q+1$, and $n=2^t(q+1)/2$ with $t\ge 0$.

Proof

The first claim is obvious. Perfect sequences of the required lengths are established in [6, Theorem 7], [3, Theorem 6], [2, Proposition 3.2], and [2, Lemma 2.1 & Proposition 3.2]. $\square$

Proposition 17

Let $m>0$ be an integer and $s \in \{1,11,17,23,29,33,39,43\}$. There exist infinitely many coprime $u_1,\ldots ,u_m$ in the set $T=\{(q+1)/2: q \equiv 1 \bmod 4 \ \text {a prime power}\}$ such that there are QHMs of the following orders n:

• $n = 2u_1u_2$ and $n = 2su_1$ for any $t \ge 0$, over $\mathcal {Q}_{8}\cup \textrm{q}\mathcal {Q}_8$.

• $n = 2^tu_1 \dots u_m$ and $n = 2^t su_1 \dots u_m$ for any $t \ge 0$, over $\mathcal {Q}_{24}$.

Proof

Perfect sequences of lengths $2u_1$, with $u_1\in T$, over $\mathcal {Q}_8$ are reported in [3, Theorem 6]; perfect sequences of lengths $u_1,u_2,\dots u_r\in T$ over $\mathcal {Q}_8\cup \textrm{q}\mathcal {Q}_8$ are reported in [2, Lemma 3.4 and Proposition 3.5]; perfect sequences of lengths 1, 11, 17, 23, 29, 33, 39, 43 are reported in [2, Proposition 3.6]; finally, perfect sequences of lengths $2^t$ for $t\geqslant 1$ over $\mathcal {Q}_8$ are reported [6, Theorem 7]. The result follows from the composition of perfect sequences of co-prime lengths described in [2, Sect. 2]. The existence of infinitely many coprime $u_1,\ldots ,u_m$, as stated in the lemma, is proved in [2, Lemma 3.4]. $\square$

Proposition 18

The perfect sequences in Table 1 yield non-commutative dephased QHMs of orders 5, 6, 7,  $9,10,11,13,14,15,17,18,19,20,21,22,23,25,26,27,28,29,30,31,33,34,35,36,37,38$,39, 41, 42,43, 44, 45, 46, 49, 50. Moreover, there is a non-commutative dephased QHM of order n for every $n=(q+1)/2$ with $q\equiv 1\bmod 4$ a prime power.

Table 1 Perfect sequences for Proposition 18 and their lengths (left column)

Proof

The sequences in Table 1 have been obtained from exhaustive searches or from the classification of Turyn type Williamson Matrices (WMs) in [18]. We now consider the second claim. Perfect sequences of length n over the alphabet $\mathcal {Q}_8\cup \textrm{q}\mathcal {Q}_8$ are into one to one correspondence with WMs of order 4n having circulant (but not necessarily symmetric) components [2, Theorem 2.4]; we recall a few details from this correspondence that are required here. If $S=(s_0,\dots ,s_{n-1})$ is a perfect sequence over $\mathcal {Q}_8\cup \textrm{q}\mathcal {Q}_8$, then the mapping presented in [2, Table 1] yields the entries of a matrix

$$\begin{aligned} \text {R}(S)=\left( {\begin{matrix} a_0 &{}\quad a_1 &{}\quad \ldots &{}\quad a_{n-1} \\ b_0 &{}\quad b_1 &{}\quad \ldots &{}\quad b_{n-1} \\ c_0 &{}\quad c_1 &{}\quad \ldots &{}\quad c_{n-1} \\ d_0 &{}\quad d_1 &{}\quad \ldots &{}\quad d_{n-1} \end{matrix}}\right) ; \end{aligned}$$

for example, if $s_r=\text {i}$, then $(a_r,b_r,c_r,d_r)=(1,-1,-1,1)$. The WM matrix $\text {WM}(S)$ corresponding to S has circulant blocks whose first rows are the rows a, b, c, d of $\text {R}(S)$. Conversely, for a WM M of order 4n let $\text {R}(M)$ be the $4\times n$ matrix consisting of the first rows of the circulant blocks of M. Via [2, Table 1], The r-th column of $\text {R}(M)$ now corresponds to an element $s_r\in \mathcal {Q}_8\cup \textrm{q}\mathcal {Q}_8$, and the sequence $\text {PS}(M)=(s_0,\ldots ,s_{n-1})$ is perfect.

The existence of perfect sequences of length $\ell =(q+1)/2$ of the form

$$\begin{aligned} S=(\textrm{q}, s_1,\dots ,s_r,s_r,\dots ,s_1) \end{aligned}$$

with each $s_t\in \{\pm 1,\pm \text {j}\}$ are reported in [2, Proposition 3.2], so let S be one such sequence. Under the aforementioned correspondence (the mapping defined by [2, Table 1]), these sequences are into one-to-one correspondence with WMs of order $4\ell$ having circulant symmetric components A, B, C, D such that A and B differ only in the main diagonal and $C=D$. Specifically, the diagonal entries of A are all 1, whereas B has diagonal entries $-1$. Now it follows from a result of Turyn (see [23, p. 319]) that such a WM is equivalent the complex HM

$$\begin{aligned} K=\begin{bmatrix} (A-I_\ell )+\text {i}I_\ell &{}\quad C \\ -C &{}\quad (A-I_\ell )-\text {i}I_\ell \end{bmatrix}. \end{aligned}$$

We now show that S has at least one entry $\text {j}$ or $-\text {j}$. Suppose, for a contradiction, that this is not the case, that is, each $a_i\in \{\pm 1\}$. This implies that $B=C=D$. Let $a=(1,a_1,\dots ,a_r,a_r,\dots ,a_1)$ be first row of the matrix A. Since K is a HM, we have $KK^*=2\ell {I_{2\ell }}$, which implies that $(A-I)^2+I+B^2=2\ell I_{\ell }$; solving $A^2+3B^2=4\ell {I_\ell }$ for $B^2$ and substituting this in the previous equation now yields $A^2-3A=(\ell - 3)I_\ell$. This implies that the non-trivial autocorrelation values $\text {AC}_i(a)$ of the binary sequence a are given by $\text {AC}_i(a)=3a_i$ for $i=1\dots , \ell -1$. Note that there exist $1\leqslant i,j\leqslant \ell -1$ such that $a_ia_j=-1$, since otherwise the sequences S would take the form $(\textrm{q}, 1,\dots , 1,1, \dots , 1)$ or $(\textrm{q}, -1,\dots , -1,-1, \dots , -1)$, which is not perfect. Without loss of generality, suppose $a_i=1$ and $a_j=-1$. It is shown in [14, Corollary 1.2] that a periodic autocorrelation of a binary sequence s of length v satisfies $\text {AC}_k(s)\equiv v\bmod 4$ for all k. Applying this to our situation, we obtain the conditions $3=\text {AC}_i(a)\equiv \ell \bmod 4$ and $-3=\text {AC}_j(a)\equiv \ell \bmod 4$, so $\ell \equiv 0\bmod 4$. This is a contradiction to $\ell =(q+1)/2$ since we have $q\equiv 1\bmod 4$. Thus, S hat at least one entry $\text {j}$ or $-\text {j}$.

Next, we show that S has at least one entry 1 or $-1$. Again, suppose for a contradiction, that this is not the case, that is $a_i\in \{\pm \text {j}\}$. This implies that $C=-A$. It follows from $KK^*=2\ell I_{\ell }$ that $(A-I)^2+I_\ell +A^2=2\ell I_\ell$; which in turn implies $2(A^2-A)={(2\ell -1)I_\ell }$ yielding a contradiction. Thus, S hat at least one entry 1 or $-1$.

Lastly, we consider cyclically shift S to obtain the perfect sequence $S'=(s_1,\dots ,s_r,s_r,\dots ,s_1,\textrm{q})$, and let H be the QHM obtained by applying Proposition 16 to $S'$. Due to the symmetry of $S'$, there exists an entry $s_i=\pm 1$ with $s_{i+1}=\pm \text {j}$. After dephasing H, if $s_1=\pm 1$ then the second row of Hhas entries $\pm \textrm{q}^* \text {j}^*$ and $\pm \textrm{q}^* \textrm{q}^*$ which do not commute. Otherwise, the second row has entries $\pm \text {j}\textrm{q}^*\text {j}^*$ and $\pm \text {j}\textrm{q}^*\text {j}\textrm{q}^*$, which do not commute either. Thus, H is non-commutative, as claimed. $\square$

3.8 Proof of Theorem 1

Proposition 1 follows from Proposition 2, together with our constructions presented in Sect. 3.