Analysis of the single-permutation encrypted Davies–Meyer construction

Abstract

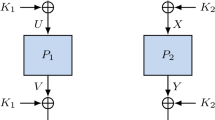
We consider the so-called Encrypted Davies–Meyer (EDM) construction, which turns a permutation P on $\{0,1\}^n$ into a function from $\{0,1\}^n$ to $\{0,1\}^n$ defined as $P(P(x)\oplus x)$. A similar construction using two independent permutations, namely $P'(P(x)\oplus x)$, was previously analyzed by Cogliati and Seurin (Advances in cryptology—CRYPTO 2016 (Proceedings, Part I). LNCS, vol 9814, pp. 121–149, 2016) who showed that when P and $P'$ are secret and random, then any black-box adversary needs at least roughly $2^{2n/3}$ queries to distinguish the construction from a uniformly random function from $\{0,1\}^n$ to $\{0,1\}^n$. In this paper, we focus on the single-permutation variant of the construction. Our main result is that the PRF-security of the single-permutation EDM construction is also (at least) roughly $2^{2n/3}$, in the sense that any black-box adversary needs at least this number of queries to distinguish the construction from a uniformly random function. This yields the first PRP-to-PRF conversion method which uses a single permutation, does not shrink the original domain nor range of the permutation, and provides security beyond the birthday bound.

Appendix: Basics of discrete Fourier analysis

We recall some classical results on Fourier analysis over the abelian group $\mathbb {Z}_2^n$, taken from [8]. In the following, given a subset $S\subset \{0,1\}^n$, we denote $\mathbb {1}_S:\{0,1\}^n\rightarrow \{0,1\}$ the characteristic functions of S, namely $\mathbb {1}_S(x)=1$ if $x\in S$ and $\mathbb {1}_S(x)=0$ if $x\notin S$. Given two functions $f,g:\{0,1\}^n\rightarrow \mathbb {R}$, we denote

$$\begin{aligned} \langle f,g\rangle =\mathbb {E}[fg]=\frac{1}{2^n}\sum _{x\in \{0,1\}^n}f(x)g(x) \end{aligned}$$

the inner product of f and g, and, for all $x\in \{0,1\}^n$, we denote

$$\begin{aligned} (f *g)(x)=\sum _{y\in \{0,1\}^n}f(y)g(x\oplus y) \end{aligned}$$

the convolution of f and g. Given $\alpha \in \{0,1\}^n$, we denote $\chi _{\alpha }:\{0,1\}^n \rightarrow \{\pm 1\}$ the character associated with $\alpha$ defined as

$$\begin{aligned} \chi _{\alpha }(x)=(-1)^{\alpha \cdot x}. \end{aligned}$$

The all-one character $\chi _0$ is called the principal character. All other characters $\chi \ne 1$ corresponding to $\alpha \ne 0$ are called non-principal characters. The set of all characters forms a group for the pointwise product operation $(\chi _{\alpha }\chi _{\beta })(x)=\chi _{\alpha }(x)\chi _{\beta }(x)$ and one has $\chi _{\alpha }\chi _{\beta }=\chi _{\alpha \oplus \beta }$.

Given a function $f:\{0,1\}^n\rightarrow \mathbb {R}$ and $\alpha \in \{0,1\}^n$, the Fourier coefficient of f corresponding to $\alpha$ is

$$\begin{aligned} {\widehat{f}}(\alpha )\mathrel {\mathop =^\mathrm{def}}\langle f,\chi _{\alpha } \rangle =\frac{1}{2^n}\sum _{x\in \{0,1\}^n}f(x)(-1)^{\alpha \cdot x}. \end{aligned}$$

The coefficient corresponding to $\alpha =0$ is called the principal Fourier coefficient, all the other ones are called non-principal Fourier coefficients. Note that for a set $S\subseteq \{0,1\}^n$ one has

$$\begin{aligned} \widehat{\mathbb {1}_S}(0)=\frac{|S|}{2^n}, \end{aligned}$$

namely the principal Fourier coefficient of $\mathbb {1}_S$ is equal to the relative size of the set. We will also use the following three classical results, holding for any functions $f,g,:\{0,1\}^n\rightarrow \mathbb {R}$, any $\alpha \in \{0,1\}^n$, and any $S\subseteq \{0,1\}^n$:

$$\begin{aligned} \sum _{x\in \{0,1\}^n}f(x)g(x)&=2^n\sum _{\alpha \in \{0,1\}^n}{\widehat{f}}(\alpha ){\widehat{g}}(\alpha ) \end{aligned}$$

(21)

$$\begin{aligned} {\widehat{(f*g)}}(\alpha )&=2^n{\widehat{f}}(\alpha ){\widehat{g}}(\alpha ) \end{aligned}$$

(22)

$$\begin{aligned} \sum _{\alpha \in \{0,1\}^n}|\widehat{\mathbb {1}_S}(\alpha )|^2&=\frac{|S|}{2^n}. \end{aligned}$$

(23)