Improving Cointegration-Based Pairs Trading Strategy with Asymptotic Analyses and Convergence Rate Filters

Abstract

A pairs trading strategy (PTS) constructs a mean-reverting portfolio whose logarithmic value moves back and forth around a mean price level. It makes profits by longing (or shorting) the portfolio when it is underpriced (overpriced) and closing the portfolio when its value converges to the mean price level. The cointegration-based PTS literature uses the historical sample mean and variance to establish their open/close thresholds, which results in bias thresholds and less converged trades. We derive the asymptotic mean around which the portfolio value oscillates. Revised open/close thresholds determined by our asymptotic mean and standard derivations significantly improve PTS performance. The derivations of asymptotic means can be extended to construct a convergence rate filter mechanism to remove stock pairs that are unlikely to be profitable from trading to further reduce trading risks. Moreover, the PTS literature oversimplifies the joint problem of examining a stock pair’s cointegration property and selecting the fittest vector error correction model (VECM). We propose a two-step model selection procedure to determine the cointegration rank and the fittest VECM via the trace and likelihood ratio tests. We also derive an approximate simple integral trading volume ratio to meet no-odd-lot trading constraints. Experiments from Yuanta/P-shares Taiwan Top 50 Exchange Traded Fund and Yuanta/P-shares Taiwan Mid-Cap 100 Exchange Traded Fund constituent stock tick-by-tick backtesting during 2015–2018 show remarkable improvements by adopting our approaches.

1 Introduction

The pairs trading strategy (PTS), a well-known market-neutral strategy that originated on Wall Street in the 1980s, has become increasingly prevalent, as it is difficult to determine whether a stock is over or underpriced (Chang et al., 2020). Instead of guessing at unpredictable market tendencies, the PTS forms a portfolio by longing one stock and shorting another at a specific ratio to eliminate this risk. The specific linear combination of logarithmic values of these two stocks, referred to as the "spread," moves back and forth around a particular level and thus exhibits mean reversion. When the spread process deviates excessively, an investor can buy the undervalued stock and short the overvalued stock; the investor can close the portfolio to make a profit when the spread reverts to its mean-reverting level.

Among the various techniques used to construct a PTS suggested in Krauss (2017), our paper focuses on the Johansen cointegration approach, which is shown to outperform other methods, as described in Do and Faff (2010, 2012), Huck and Afawubo (2015), and Rad et al. (2016). Engle and Granger (1987) represent the cointegration relationship by a vector error correction model (VECM), and Vidyamurthy (2004) presents the theoretical framework of cointegration-based PTS in terms of a VECM. Although a PTS can also be implemented by the Engle and Granger cointegration test, as stated in Lin et al. (2006), this test is characterized by the asymmetry problem, which argues which stock price should be treated as either the explanatory or the response variable. This paper proposes an improved method based on the Johansen cointegration test to calibrate the price processes of a pair of assets eligible for a PTS, and we conduct comprehensive experiments to demonstrate the superiority of our approach.

Appropriate selection of proper VECM models has been studied by Johansen (1995). However, the cointegrated-based PTS literature either selects models heuristically (see Li et al. (2014) and Rad et al. (2016)) or even ignores this issue. In addition, we find that Johansen’s model selection begins from the narrowest VECM and may excessively eliminate eligible stock pairs for the PTS that belong to more comprehensive models. To address this issue, we will propose a two-step model selection method that employs the trace test in the first stage to calibrate the logarithmic stock price processes of each stock pair to identify eligible VECMs possessing cointegration properties. Then, we select the fittest model from the candidates identified in the first stage with the likelihood ratio test in the second stage.¹ Experiments suggest that adopting our model selection significantly improves trading performance.

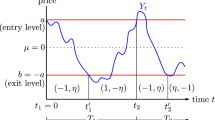
Vidyamurthy (2004) uses the sample mean and standard deviation of a spread to estimate the mean-reverting level and the open threshold for a PTS. This approach is widely adopted in the PTS literature, such as Huck and Afawubo (2015), Huck (2010), and Rad et al. (2016). Rad et al. (2016) find that a large portion of spread processes fail to converge to sample means,² which significantly erodes profits. Indeed, we also discover that the intraday spread process generally oscillates around the asymptotic mean (derived in Sect. 3.2) rather than the sample mean, as illustrated in Fig. 1. This is because heavy stock price fluctuations and high trading volumes typically occur at the beginning of each trading day, reflecting the impact of overnight information such as breaking news during market closed periods, as suggested in Tian (2007). Therefore, these price fluctuations significantly bias sample means and standard deviations of spread processes, frequently resulting in the above-mentioned failure to converge. By rewriting a VECM with higher lag orders into a companion form with lag order 1 as in Hansen (2000), this paper explores the asymptotic behavior of the spread mean (as illustrated by the green line in Fig. 1). Then we derive the asymptotic limit of the spread mean (the orange line) and its standard deviation by taking advantage of the recursive relation of the VECM selected by the aforementioned two-step method. Numerical results suggest that determining the mean-reverting level and the open threshold with our asymptotic results outperforms the naive adoption of sample means and standard deviations.

Fig. 1

Sample Illustration of Stock Price Processes, Spread Process, Sample Mean, Asymptotic Mean, and Convergence Mean. The spread process is constructed by a linear combination of intra-day price processes of stocks with tick symbols 1319 and 1477 on Jan 5th, 2016. The asymptotic mean is constructed by calibrating Model 1 defined in Sect. 3.3 with parameters $\alpha ={\left(- 0.02, 0.02\right)}^{\prime},\boldsymbol{ }\beta ={\left(1, -0.68\right)}^{\prime}$, and M = 0 as derived in Sect. 3.2. The convergence rate measures how fast the convergence mean converges to the asymptotic mean described in Sect. 3.4. (Color figure online)

Indeed, rapid market change may break the cointegration relationship due to the occurrence of structural breaks, which results in significant loss (Huang et al. 2020). Sarmento and Horta (2020) and Lu et al. (2022) reduce PTS trading risks by using machine learning models to filter out unprofitable stock pairs. However, these black-box models are not interpretable. To avoid the risk of overnight structural breaks occurring during the market closed period, we follow Stübinger (2019), Endres and Stübinger (2019), and Liu et al. (2017) by considering a high-frequency intraday PTS that limits the duration of our PTS to within a day. Costs are also suppressed since the Taiwan Stock Exchange provides a 50% discount on transaction costs on intra-day trading. To address structural breaks that occur during trading, we take advantage of the derivation of the asymptotic mean to measure the convergence rate of the spread (proxied by the convergence mean in Fig. 1) to its mean-reverting level (denoted by the asymptotic mean); this rate reflects the likelihood for a spread to return to the asymptotic mean and make a profit. Thus, we filter less profitable stock pairs by removing corresponding spreads with low convergence rates to improve win rates and the Sharpe ratio, as confirmed in our backtesting. Note that the ratio for shorting one stock and longing another derived by calibrating VECM parameters could be a non-simple irreducible ratio.³ In practice, however, the number of traded stocks cannot be infinitely divided, and intraday trading of odd lots is not allowed. Arbitrarily amplifying this trading ratio would erode PTS profits since a large trading volume could significantly influence stock prices and cause slippage. To our knowledge, this PTS study is the first to address this problem by adjusting the ratio to a nearby simple integer ratio with small magnitudes; thus, we reasonably trade indivisible stocks under the constraint of limited liquidity. To prevent such adjustment from weakening the stationary property of the spread and hence deteriorating PTS performance, we remove stock pairs whose adjusted spread processes fail to reject the null hypothesis (the presence of unit roots) of the augmented Dickey–Fuller (ADF) test. Experiments show that these proposed adjustments also yield profitable results.

The rest of this paper is organized as follows. Section 2 details the required background knowledge of PTS. Section 3 describes the derivations of asymptotic means and standard derivation used to build the open/close thresholds. These derivations can be further extended to remove spread processes with low convergence rates to reduce trading risks. Then we describe the two-step model selection method and adjustments to the trading ratio to meet the no-odd-lot and liquidity constraints without significantly sacrificing profitability. In Sect. 4, to confirm the superiority of our model, we analyze the tick-by-tick backtesting on the 0050.TW and 0051.TW constituent stocks, which were the top companies with the largest market capitalization from 2015 to 2018.⁴ We conclude in Sect. 5.

2 Preliminaries

In this section, we first survey the relevant PTS literature. Then we introduce the key properties of a vector autoregressive (VAR) model and a VECM required to implement our PTS improvements, after which we express the cointegration property under the VECM model.

2.1 Literature Review

Statistical and time series analyses are increasingly used in economic and financial applications. For instance, Xu and Ye (2023) optimize investments using value at risk measures, whereas Tsionas et al. (2023) apply Bayesian methods to examine decision making under uncertainty. Maiti et al. (2023) forecast India's post-COVID GDP with a factor-augmented error correction model, Liu et al. (2023) predict stock returns using a vector-based clustering ensemble, He et al. (2023) implement online portfolio selection with an aggregating algorithm, and Sapna and Mohan (2023) predict the implied volatility of Ethereum options. Bampinas and Panagiotidis (2015, 2016) explore the use of cointegration to hedge against inflation with gold, silver, and stock prices. This paper focuses on the application of statistical and time series analyses in pairs trading. We follow Krauss (2017) in dividing and surveying PTS techniques according to the five following groups. First, the distance method (abbreviated as DM) adopted in Bowen (2010), Do and Faff (2010, 2012), and Gatev et al. (2006) calculates the Euclidean distance of two stock price processes to measure their co-movements; they then apply PTS on stock pairs with close co-movements. Second, Engle and Granger (1987) and Johansen (1988) develop a cointegration test to determine the existence of a linear combination of stock prices that makes a stock portfolio's value a stationary process. Since the mean of the stationary process does not change with time, an investor can buy (sell) the portfolio when its value is below (above) the mean and close the position to make a profit when the value converges back. Vidyamurthy (2004), Lin et al. (2006), Li et al. (2014), Rad et al. (2016), Malkidis and Fountas (2020), and Lin and Tan (2023) apply the aforementioned cointegration tests to construct PTS-eligible stock pairs. Yan et al. (2020) find that the path-dependent cointegration model can further improve PTS performance. Third, Elliott et al. (2005) and Cummins and Bucca (2012) find optimal trading rules for PTS-eligible stock pairs under different time series models, such as the autoregressive moving average model, the generalized autoregressive conditional heteroscedasticity model, and the Ornstein–Uhlenbeck model. On the same premises, the fourth approach uses stochastic control theory to determine the best asset allocations for a PTS (see Do and Faff (2010)). The fifth category denotes other techniques, such as the principal component analysis method proposed by Avellaneda and Lee (2010), Krauss and Stübinger (2017), and Ferreira (2008), who reduce the dimension of the stock return vectors to find co-moving stock pairs. In addition, the copula method analyzed in Liew and Wu (2013), Rad et al. (2016), and Stander et al. (2013) estimates the joint distribution of the time series of stock returns to determine the overvalue or undervalue likelihoods, whereas Huck (2009) and Huck (2010) use multi-criteria decision techniques to rank and detect under- and over-valued stocks for PTS. This paper focuses on improving PTS construction based on the Johansen cointegration test, which outperforms other methods as studied in the following literature. Specifically, Do and Faff (2010, 2012) find that the DM performance declines over time and is generally not profitable when transaction costs are taken into account. Huck and Afawubo (2015) perform large-scale empirical tests on S&P 500 to show that the cointegration approach outperforms DM. Rad et al. (2016) also show that the cointegration approach exhibits better after-transaction-cost performance than the copula method on the entire US equity market from 1962 to 2014.

There are three different models (excluding trend-stationary models) with different determinist terms studied in Johansen (1995). A proper cointegration model selection method could more feasibly capture the characteristics of stock price processes and hence improve the PTS performance. However, the model selection issue is simplified or overlooked in the cointegration-based PTS literature. For example, Li et al. (2014) directly select the most generalized type (Model 3 defined in Sect. 3.3). Rad et al. (2016) directly use the simplest type (Model 1). Other papers even ignore this issue. On the other hand, Johansen (1995) suggests that the conventional method of model selection focuses on the existence of deterministic terms and begins the trace test from the narrowest model, Model 1, and then extends to broader models. However, this approach may excessively eliminate eligible stock pairs for PTS that belong to broader models. To mitigate this issue, we apply the trace test from the widest model, Model 3, and then extend this to Model 1. Additionally, if the price process of a stock pair cannot be rejected from belonging to more than one model, we enhance the model fitness by employing the likelihood ratio test, as discussed in Sect. 3.3. Additionally, Otero et al. (2022) demonstrate that the power of the Johansen cointegration test is influenced by the duration of the sample period and the number of observations. We align our study with this finding by adjusting both the length and frequency of the sample period. Subsequently, we evaluate the test's effectiveness in terms of trading performance.

Much of the literature improves PTS performance using machine learning techniques, such as Kim and Kim (2019), Sarmento and Horta (2020), Kuo et al. (2021), Lu et al. (2022), and Kuo et al. (2022). Although these approaches involve the use of deep or reinforcement learning techniques to determine optimal open/stop-loss thresholds or detect structural breaks, statistical methods such as the cointegration approach are still needed to identify stock pairs that are eligible for the PTS and to determine feasible investment capital ratios and mean-reverting levels. Thus, improving the quality of cointegrated-based PTS is important.

2.2 Required Properties for VAR and VECM

Başcı and Karaca (2013) suggest that a multivariate time series can be modeled by a VAR model, a multivariate generalization of an autoregressive model (AR). Let I(d) denote that the order of integration of a time series is d. A k-dimensional I(1) process ${X}_{t}$ following a VAR model of order p, or VAR(p) for short, can be expressed as

$$ X_{t} = c_{t} + \prod_{1} X_{t - 1} + \ldots + \prod_{p} X_{t - p} + u_{t} , t = 1, \ldots ,T {\text{ and }}p > 0 $$

(1)

where ${c}_{t}$ is a k-dimensional deterministic vector, ${\Pi }_{i}$ is a k × k matrix for 1 ≤ i ≤ p, and ${u}_{t}$ is a k-dimensional independent and identically distributed Gaussian white noise with mean zero and a positive definite covariance matrix Σ, i.e., ${u}_{t}\genfrac{}{}{0pt}{}{{\text{iid}}}{\sim }{\text{MVND}}\left(0,\Sigma \right).$ The VAR(p) process in Eq. (1) can be rewritten in terms of a VECM as

$$\Delta {X}_{t}={c}_{t}+\Pi {X}_{t-1}+{\sum }_{i=1}^{p-1}{\Gamma }_{i}\Delta {X}_{t-i}+{u}_{t}={c}_{t}+\alpha {\beta }^{\prime}{X}_{t-1}+{\sum }_{i=1}^{p-1}{\Gamma }_{i}\Delta {X}_{t-i}+{u}_{t}$$

(2)

where $\Delta {X}_{t}={X}_{t}-{X}_{t-1}$, $\Pi =-I+{\sum }_{i=1}^{p}{\Pi }_{i}$, and ${\Gamma }_{i}=-{\sum }_{j=i+1}^{p}{\Pi }_{j}$. If the rank of Π is a constant r larger than 0 and there exist two k × r matrices α and β such that $\Pi$ = $\alpha {\beta }^{\prime}$ and Rank (α) = Rank (β) = r, then ${X}_{t}$ is cointegrated with r linearly independent cointegrating vectors, as stated in Theorem 4.2 of Johansen (1995). Based on the above, Hansen (2000) deduces the following lemma about the companion form of matrices.

Lemma 1.

Let ${\widetilde{X}}_{t}={\left({X}_{t}^{\prime},{X}_{t-1}^{\prime},\dots ,{X}_{t-p+1}^{\prime}\right)}^{\prime}$ and the orthogonal complement of a matrix M be ${{\text{M}}}_{\perp }$ Then VECM(p) defined in Eq. (2) can be transferred to a companion form.

$$ \begin{aligned} \Delta \tilde{X}_{t} = & \tilde{\Pi }\tilde{X}_{t - 1} + \tilde{c}_{t} + \tilde{u}_{t} \\ = & \tilde{\alpha }\tilde{\beta }^{\prime} \tilde{X}_{t - 1} + \tilde{c}_{t} + \tilde{u}_{t} \\ \end{aligned} $$

where

$$\Delta {\widetilde{X}}_{t}={\left(\Delta {X}_{t}^{\prime},\Delta {X}_{t-1}^{\prime},\dots ,\Delta {X}_{t-p+1}^{\prime}\right)}^{\prime}$$

$$ \tilde{\prod } = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\alpha \beta^{\prime } + \Gamma_{1} } & {\Gamma_{2} - \Gamma_{1} } \\ I & { - I} \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\Gamma_{3} - \Gamma_{2} } & \cdots \\ \end{array} } \\ {\begin{array}{*{20}c} { 0 } & { \cdots } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\Gamma_{p - 1} - \Gamma_{p - 2} } & { - \Gamma_{p - 1} } \\ 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} {0 } & { I} \\ {0 } & { 0} \\ \end{array} } & {\begin{array}{*{20}c} { - I} & \\ { I} & { \ddots } \\ \end{array} } & {\begin{array}{*{20}c} & { \vdots } \\ \end{array} } \\ {\begin{array}{*{20}c} { \vdots } & { \vdots } \\ {0 } & { 0} \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} & \\ \end{array} } \\ \cdots \\ \end{array} } & {\begin{array}{*{20}c} { - I } & { 0} \\ {I } & { - I} \\ \end{array} } \\ \end{array} } \right] $$

$$\widetilde{\alpha }=\left[\begin{array}{ccc}\begin{array}{cc}\alpha & {\Gamma }_{1}\\ 0& I\end{array}& \begin{array}{c}\cdots \\ \end{array}& \begin{array}{c}{\Gamma }_{p-1}\\ 0\end{array}\\ \begin{array}{cc}\vdots & \end{array}& \ddots & \\ \begin{array}{cc}0& \end{array}& & I\end{array}\right]$$

$$\widetilde{\beta }=\left[\begin{array}{ccc}\begin{array}{cc}\beta & I\\ 0& -I\end{array}& \begin{array}{cc}0& \cdots \\ I& \end{array}& \begin{array}{c}0\\ \end{array}\\ \begin{array}{cc}\vdots & \end{array}& \begin{array}{cc}-I& \ddots \\ & \ddots \end{array}& \begin{array}{c} \\ I\end{array}\\ \begin{array}{cc}0& \end{array}& & -I\end{array}\right]$$

$$ \tilde{c}_{t} = \left( {c_{t}^{\prime} ,0_{{\left\{ {p - 1} \right\}}} } \right)^{\prime} $$

$$ \tilde{u}_{t} = \left( {u_{t}^{\prime} ,0_{{\left\{ {p - 1} \right\}}} } \right)^{\prime} $$

$${\widetilde{\alpha }}_{\perp }=\left[\begin{array}{c}\begin{array}{c}{\alpha }_{\perp }\\ -{\Gamma }_{1}^{\prime}{\alpha }_{\perp }\end{array}\\ \begin{array}{c}\vdots \\ -{\Gamma }_{p-1}^{\prime}{\alpha }_{\perp }\end{array}\end{array}\right]$$

and

$${\widetilde{\beta }}_{\perp }=\left[\begin{array}{c}\begin{array}{c}{\beta }_{\perp }\\ {\beta }_{\perp }\end{array}\\ \begin{array}{c}\vdots \\ {\beta }_{\perp }\end{array}\end{array}\right]$$

2.3 Cointegrated VECM for PTS

The cointegration property of a collection of time series with integration order m denotes that the existence of a linear combination of series from this collection has an integration order less than m. This useful property can be used to construct a linear combination of log-stock prices, referred to as the "spread," following a stationary process (i.e., an I(0) process) given that the log-stock price processes are non-stationary. The mean-reverting property of the stationary process allows us to apply a PTS to the stock portfolio to make profits. For convenience, define two logarithmic processes $\left\{{X}_{1t}\right\}$ and $\left\{{X}_{2t}\right\}$ by ${X}_{1t}={{\text{ln}} (X}_{1,t})$ and ${X}_{2t}={{\text{ln}} (X}_{2,t})$, where $\left\{{X}_{1,t}\right\}$ and $\left\{{X}_{2,t}\right\}$ denote the price processes of two arbitrary stocks. The stock portfolio is constructed by applying the Johansen cointegration test on the vector of time ${X}_{t}\equiv \left({X}_{1t},{X}_{2t}\right)$. The cointegration property entails that linear combination(s) ${\beta }^{\mathbf{^{\prime}}}{X}_{t}$ are stationary processes, where each column of β (defined in Eq. (2)) denotes a cointegrating vector. Here we combine the proof results in Hansen (2000) that will be used later as follows.

Lemma 2.

(Hansen, 2000) Let $\Gamma ={\text{I}}-{\sum }_{i=1}^{p-1}{\Gamma }_{i}.$ $\left|{\alpha }_{\perp }^{\prime}\Gamma {\beta }_{\perp }\right|\ne 0$ if and only if the absolute value of the eigenvalues of $\left(I+{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)$ are less than 1 for any VECM model.

In our backtest experiments, to ensure the $\left|{\alpha }_{\perp }^{\prime}\Gamma {\beta }_{\perp }\right|\ne 0$ property holds in our PTS model, we calibrate the price processes of each stock pair by Eq. (2) and exclude stock pairs whose estimated determinants of ${\alpha }_{\perp }^{\prime}\Gamma {\beta }_{\perp }$ are sufficiently small.

The property of "less-than-one" eigenvalues entails that ${\left({\text{I}}+{\widetilde{\beta }}^{\mathrm{^{\prime}}}\widetilde{\alpha }\right)}^{t}$ decays exponentially with increments in t. This result is useful to derive the asymptotic mean and variance of the spread process ${\beta }^{\mathrm{^{\prime}}}{X}_{t}$ as in Sect. 3.

3 Model Development

This section begins by detailing how we preprocess the transaction data and by outlining the structure of our PTS in Sect. 3.1. Following this, we highlight our major contributions towards enhancing PTS performance. The sample mean/variance used to build trading thresholds in the literature is replaced by the asymptotic mean/variance derived in Sect. 3.2. Section 3.3 selects the fittest VECM models that possess the cointegration property based on the two-step method which makes use of the trace test and the likelihood ratio test. Section 3.4 proposes the convergence rate filter based on the asymptotic mean/variance analyzed in Sect. 3.2 to filter out stock pairs that are unlikely to be profitable. Section 3.5 converts the non-integer trading ratio from the cointegrating vector into the approximated irreducible integer ratio to reasonably trade indivisible stocks with limited liquidity or to account for no-odd-lot trading limitations. Finally, Sect. 3.6 describes how we construct trading thresholds (i.e., open and close thresholds) and the execution process of the PTS.

3.1 Data Preprocessing and Structure of the PTS

Given that transaction expenses and price slippage heavily influence PTS profitability, in our later experiments we conduct intraday pairs trading using the constituent stocks of the 0050 TT YUANTA/P-SHRS TW and 0051 TT YUANTA/P-SHRS TW MID-CAP 100 ETFs listed on the Taiwan Stock Exchange without holding positions overnight. This is because these stocks have better liquidity (i.e., lower price slippage), and the Taiwan Stock Exchange grants 50% discounts for intraday trading.⁵ This reduction of slippage and cost significantly increases both win rates and profits. In addition, intraday trading also prevents investment losses caused by the ineffectiveness of the cointegration property due to changing market conditions and breaking news during market closed periods. On each trading day, the Taiwan Stock Exchange begins at 9:00 a.m. and closes at 1:30 p.m.; we use the first 150 min (i.e., the formation period) to find PTS-eligible stock pairs with the cointegration test and trade these pairs during the rest of the day. The t-th minute average stock price of the i-th stock, ${X}_{i,t}$, during the formation period is calculated as the volume-weighted average stock price that occurs at that minute and the log stock price series {${X}_{it}$} with length 150 is constructed by taking the logarithm on the minute-average price of the i-th stock. Otero et al. (2022) find that the power of a cointegration test is affected by the duration of the sample period—here referred to as the formation period—and the number of observations. To test their findings, in our later experiments we reduce the formation period from 150 to 100 min and change the sampling frequencies to assess the impact on PTS performance.

After this data preprocessing, we construct PTS-eligible stock pairs as illustrated in Fig. 2. We first filter all {${X}_{it}$} without unit root(s) via the ADF test proposed in Kwiatkowski et al. (1992) to ensure that all the log-stock price processes {${X}_{it}$} adopted for PTS are non-stationary⁶ (i.e., the ADF test stage). Next, we pick two different log-stock price processes to form a log-stock-price vector ${X}_{t}\equiv \left({X}_{1t},{X}_{2t}\right)$ and then calibrate it with the VAR defined in Eq. (2).⁷ The order of the VAR, denoted as p, under a given deterministic term ${c}_{t}$, can be estimated by the Bayesian information criterion (BIC), as described in Stoica and Selen (2004) (i.e., the order specification stage in Fig. 2). The BIC is formulated as ${\text{ln}}\left({\text{Max}}\left(\Sigma , p\right)\right)+\frac{{\text{ln}}(T)}{T}p{k}^{2}$, where Max(Σ, p) denotes the determinant of the maximum likelihood estimate of Σ for a VAR(p) model, T denotes the number of samples, and $k$ denotes the dimension of the VAR model as introduced in Sect. 2.2. To check whether the VAR(p) feasibly models the log-stock-price vector ${X}_{t}$, the third step estimates the residual vector ${a}_{t}$ and then applies the Jarque–Bera test and the portmanteau test to test the normality and the autocorrelation of ${u}_{t}$ (i.e., the model-checking stage).

Fig. 2

Flowchart for Finding Eligible Stock Pairs and Constructing Trading Strategies

To select the most suitable VECM model among those studied in Johansen (1995), we propose a two-step model selection process in Sect. 3.3. This process involves simultaneously determining eligible stock pairs for PTS and their corresponding models (i.e., the two-step model selection stage). We then use the selected model and its parameters to derive the asymptotic mean and variance for each stationary process (i.e., the asymptotic analysis stage), as detailed in Sect. 3.2. Next, we develop a convergence rate filter to remove unlikely profitable stock pairs that have low convergence rates (the pair filtering stage), as described in Sect. 3.4. The final stage converts the non-integer trading ratio of the stock pair into an integer one as in Sect. 3.5 to meet the no-odd-lot trading constraint.

Having completed the PTS settings using these procedures, we then calculate the trading thresholds (i.e., open and close thresholds) based on the asymptotic mean and variance. These thresholds are used to execute trades for each stock pair using the stock price tick data during the trading period, as discussed in Sect. 3.6.

3.2 Deriving Asymptotic Convergence Mean/Variance for the Spread

Based on the discussion in Sect. 2, we derive the values of the asymptotic mean and variance of the spread sequence ${\beta }^{\mathrm{^{\prime}}}{X}_{t}$ used to determine the thresholds for opening and closing the portfolio in our PTS by the following theorems and lemmas. First, we introduce Lemma 3 derived by Hansen (2000) to analyze the convergence property of VECM(p). To evaluate the asymptotic convergent mean and the variance of ${\beta }^{\mathrm{^{\prime}}}{X}_{t}$ with good readability, we first rewrite the stationary proofs of ${\beta }^{\mathrm{^{\prime}}}{X}_{t}$ in Theorem 4.2 of Johansen (1995) with our notation in the former part of Theorem 1. The rewritten formulae are used to derive the mean/variance and to define the convergence rate filter in Sect. 3.4.

Lemma 3.

(Hansen, 2000) If $\left|{\alpha }_{\perp }^{\prime}\Gamma {\beta }_{\perp }\right|\ne 0$, then $\widetilde{\alpha }$ and $\widetilde{\beta }$ defined in Lemma 1 have the following properties: For the eigenvalue λ of the matrix $I+{\widetilde{\beta }}^{\prime}\widetilde{\alpha }$, |λ|< 1, the matrix $I+{\widetilde{\beta }}^{\prime}\widetilde{\alpha }$ has no simple root and ${\left(I+{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)}^{t}$ converges exponentially to 0 as t increases.

The property $\left|{\alpha }_{\perp }^{\mathrm{^{\prime}}}\Gamma {\beta }_{\perp }\right|\ne 0$ in our experiment is ensured by excluding stock pairs whose estimated determinants of ${\alpha }_{\perp }^{\prime}\Gamma {\beta }_{\perp }$ are sufficiently small when calibrating the price processes of each stock pair by Eq. (2).

Theorem 1.

For any VECM(p) which is written as.

$$ \Delta X_{t} = \prod X_{t - 1} + \mathop \sum \limits_{i = 1}^{p - 1} \Gamma_{i} \Delta X_{t - i} + c_{t} + u_{t} $$

we assume $\left|{\alpha }_{\perp }^{\prime}\Gamma {\beta }_{\perp }\right|\ne 0$ and rewrite the stationary proof of ${\beta }{\prime}{X}_{t}$ proposed in Johansen (1995) using our notation to improve readability. Next, we show that the conditional mean E(${{\beta }^{\prime}X}_{t}|{X}_{0},{X}_{-1},\dots ,{X}_{-p+1}$) converges to a constant $J\left({\left(-{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)}^{-1}-I\right){\widetilde{\beta }}^{\prime}\widetilde{c}$. The variance converges to ${\left(J\left({\left(-{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)}^{-1}-I\right){\widetilde{\beta }}^{\prime}\right)}^{\prime}\widetilde{\Omega }J\left({\left(-{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)}^{-1}-I\right){\widetilde{\beta }}^{\prime}$. Here, ${X}_{0},{X}_{-1},\dots$ denotes the stock price data before time 0 used to calibrate the VECM.

Proof:

By Lemma 1, we transform VECM(p) into.

$$ \begin{aligned} \Delta \tilde{X}_{t} &= \tilde{\prod }\tilde{X}_{t - 1} + \tilde{c}_{t} + \tilde{u}_{t} \\ &= \tilde{\alpha }\tilde{\beta }^{\prime} \tilde{X}_{t - 1} + \tilde{c}_{t} + \tilde{u}_{t} \\ \end{aligned} $$

(3)

Since $\Delta {\widetilde{X}}_{t}={\widetilde{X}}_{t}-{\widetilde{X}}_{t-1}$, Eq. (3) can be converted to

$${\widetilde{X}}_{t}=\left(I+\widetilde{\alpha }{\widetilde{\beta }}^{\mathrm{^{\prime}}}\right){\widetilde{X}}_{t-1}+{\widetilde{c}}_{t}+{\widetilde{u}}_{t}$$

(4)

Multiplying Eq. (4) by β' gives

$$ \begin{aligned} \tilde{\beta }^{\prime} \tilde{X}_{t} = & \tilde{\beta }^{\prime} \left( {I + \tilde{\alpha }\tilde{\beta }^{\prime} } \right)\tilde{X}_{t - 1} + \tilde{\beta }^{\prime} \tilde{c}_{t} + \tilde{\beta }^{\prime} \tilde{u}_{t} \\ = & \left( {\tilde{\beta }^{\prime} + \tilde{\beta }^{\prime} \tilde{\alpha }\tilde{\beta }^{\prime} } \right)\tilde{X}_{t - 1} + \tilde{\beta }^{\prime} \tilde{c}_{t} + \tilde{\beta }^{\prime} \tilde{u}_{t} \\ = & \left( {I + \tilde{\beta }^{\prime} \tilde{\alpha }} \right)\tilde{\beta }^{\prime} \tilde{X}_{t - 1} + \tilde{\beta }^{\prime} \tilde{c}_{t} + \tilde{\beta }^{\prime} \tilde{u}_{t} \\ = & \left( {I + \tilde{\beta }^{\prime} \tilde{\alpha }} \right)^{t} \tilde{\beta }^{\prime} \tilde{X}_{0} + \mathop \sum \limits_{i = 1}^{t} \left( {I + \tilde{\beta }^{\prime} \tilde{\alpha }} \right)^{t - i} \tilde{\beta }^{\prime} \left( {\tilde{u}_{i} + \tilde{c}_{i} } \right) \\ \end{aligned} $$

(5)

where ${\widetilde{X}}_{0}$ is the realized value. Under the premise that $\left|{\mathrm{\alpha }}_{\perp }^{\mathrm{^{\prime}}}\Gamma {\beta }_{\perp }\right|\ne 0$, matrix ${\left(I+{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)}^{t}$ converges to 0 as stated in Lemma 3. Therefore, Eq. (5) is equal to $\sum_{i=1}^{t}{\left(I+{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)}^{t-i}{\widetilde{\beta }}^{\prime}({\widetilde{u}}_{i}+{\widetilde{c}}_{i})$ and is thus stationary. Now we retrieve ${\beta }^{\prime}{X}_{t}$ by defining a (K × Kp)-dimensional matrix $J=({I}_{K},\mathrm{0,0},\dots ,0)$ such that

$${\beta }^{\prime}{X}_{t}=J{\widetilde{\beta }}^{\prime}{\widetilde{X}}_{t}=J{\left(I+{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)}^{t}{\widetilde{\beta }}^{\prime}{\widetilde{X}}_{0}+J\sum_{i=1}^{t}{\left(I+{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)}^{t-i}{\widetilde{\beta }}^{\prime}({\widetilde{u}}_{i}+{\widetilde{c}}_{i}) \stackrel{t\to \infty }{\to }J\sum_{i=1}^{t}{\left(I+{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)}^{t-i}{\widetilde{\beta }}^{\prime}\left({\widetilde{u}}_{i}+{\widetilde{c}}_{i}\right)$$

(6)

We can assume ${\widetilde{c}}_{t}={\widetilde{c}}_{t-1}=\dots =\widetilde{c}$, because we can determine the value of ${c}_{t}$ for all t. Then, the expected value of $J\sum_{i=1}^{t}{\left(I+{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)}^{t-i}{\widetilde{\beta }}^{\prime}({\widetilde{u}}_{i}+{\widetilde{c}}_{i})$ is equal to.

$$J\sum_{i=1}^{t}{\left(I+{\widetilde{\beta }}^{\mathrm{^{\prime}}}\widetilde{\alpha }\right)}^{t-i}{\widetilde{\beta }}^{\mathrm{^{\prime}}}\widetilde{c}\stackrel{t\to \infty }{\to }J\left({\left(I-\left(I+{\widetilde{\beta }}^{\mathrm{^{\prime}}}\widetilde{\alpha }\right)\right)}^{-1}-I\right){\widetilde{\beta }}^{\mathrm{^{\prime}}}\widetilde{c}=J\left({\left(-{\widetilde{\beta }}^{\mathrm{^{\prime}}}\widetilde{\alpha }\right)}^{-1}-I\right){\widetilde{\beta }}^{\mathrm{^{\prime}}}\widetilde{c}$$

(7)

Next, since ${\widetilde{u}}_{t}$ is independently and identically distributed, we can assume.

$$Var\left({\widetilde{u}}_{t}\right)=E\left({\widetilde{u}}_{t}^{\mathrm{^{\prime}}}{\widetilde{u}}_{t}\right)=E\left(\begin{array}{ccc}\begin{array}{cc}{u}_{t}^{\mathrm{^{\prime}}}{u}_{t}& 0\\ 0& 0\end{array}& \cdots & 0\\ \vdots & \ddots & \\ 0& & 0\end{array}\right)=\left(\begin{array}{ccc}\begin{array}{cc}\Omega & 0\\ 0& 0\end{array}& \cdots & 0\\ \vdots & \ddots & \\ 0& & 0\end{array}\right)=\widetilde{\Omega }$$

So, the variance of $J\sum_{i=1}^{t}{\left(I+{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)}^{t-i}{\widetilde{\beta }}^{\prime}({\widetilde{u}}_{i}+{\widetilde{c}}_{i})$ is deduced to be

$$Var\left(J\sum_{i=1}^{t}{\left(I+{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)}^{t-i}{\widetilde{\beta }}^{\prime}\left({\widetilde{u}}_{i}+{\widetilde{c}}_{i}\right)\right)=Var\left(J\sum_{i=1}^{t}{\left(I+{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)}^{t-i}{\widetilde{\beta }}^{\prime}{\widetilde{u}}_{i}\right)={\left(J\sum_{i=1}^{t}{\left(I+{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)}^{t-i}{\widetilde{\beta }}^{\prime}\right)}^{\prime}\widetilde{\Omega }J\sum_{i=1}^{t}{\left(I+{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)}^{t-i}{\widetilde{\beta }}^{\prime}\stackrel{t\to \infty }{\to }{\left(J\left({\left(-{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)}^{-1}-I\right){\widetilde{\beta }}^{\prime}\right)}^{\prime}\widetilde{\Omega }J\left({\left(-{\widetilde{\beta }}^{\prime}\widetilde{\alpha }\right)}^{-1}-I\right){\widetilde{\beta }}^{\prime}$$

Note that the expected value or the variance are both independent with respect to the time variable t and the initial value ${X}_{0}$. This fact again confirms the stationarity.

3.3 Two-Step Model Selection

By excluding the two trend-stationary models, the remaining VECM models in Eq. (2) can be expressed in three different models (see Johansen (1995)): Model 1—no constant scenario,⁸ i.e., ${c}_{t}=0$; Model 2—restricted constant scenario, i.e., ${c}_{t}=\alpha {c}_{0}$; Model 3—unrestricted constant scenario, i.e., ${c}_{t}={\mu }_{0}$. The cointegration-based pairs trading literature either naively calibrates Model 3 or overlooks the model selection problem. However, the model selection proposed by Johansen (1995) begins the trace test⁹ from the narrowest model (Model 1) to broader models and may excessively eliminate eligible stock pairs for PTS that belong to broader models. To address this problem, we propose a two-step model selection method that uses the trace test and the likelihood ratio test¹⁰ (LRT) proposed in Johansen (1995) to determine the cointegration rank and the fittest deterministic term ${c}_{t}$ of the VECM defined as above. The flowchart of our two-step procedure is shown in Fig. 3. In the first stage, we test for the existence of a cointegration relationship for each stock pair from the most generalized model (Model 3) down to the most restrictive one (Model 1) by estimating the rank of Π in Eq. (2) with the trace test. In the second stage, we use LRT to select the fittest VECM from the eligible models identified in the first stage. Note that the cointegration relationship exists if the rank of Π in Eq. (2) is larger than 0. If the rank obtained from calibrating Model 3 is greater than 0, a cointegration relationship exists. Thus, we exclude stock pairs whose rank is 0 because they do not possess the cointegration property under the more constrained Model 2 or Model 1. For the remaining pairs, we estimate the rank by calibrating Model 2. If the rank is 0, we consider Model 3 to be the best fitting model. Otherwise, we check the rank using Model 1. If the rank is 0, only Models 3 and 2 are suitable for describing the spread's cointegration property. In such cases, our second-stage procedure utilizes the LRT¹¹ to select the best-fitting model between Models 2 and 3. However, if the rank is not 0 for Model 1, all three models are suitable, and the LRT selects the best-fitting one among them.

Fig. 3

Two-Step Model Selection. The first stage (in the red rectangle) uses the trace test to examine whether a VECM possesses the cointegration property. The second stage (the blue rectangle) uses the LRT to select the fittest one from the VECMs with the cointegration property determined in the first stage. (Color figure online)

Model selection and parameter calibration examples are given in Figs. 1 and 4. Note that the deterministic term ${c}_{t}$ in Model 1 is 0; hence the asymptotic mean M is also 0 as in Fig. 1. The asymptotic means of both Model 2 and 3 are non-zeros. Unlike Model 2, the unrestricted deterministic term ${c}_{t}$ of Model 3 is not a multiple of the vector α; therefore, the stock prices and the corresponding spread patterns of these two models are distinct, as shown in panels (a) and (b) of Fig. 4.

Fig. 4

Example of Model Selection and Calibration. The selected model, the ticker symbols, and the trading day are listed above each subfigure. Panel a calibrates Model 2 with parameters $\alpha ={\left(-0.018, 0.052\right)}{\prime}, \beta ={\left(1,-5.993\right)}^{\prime}$, ${c}_{t}={\left(0.017, -0.05\right)}^{\prime}$, and $M=-0.956$. Panel b calibrates Model 3 with parameters $\alpha = {\left(0.001, 0.038\right)}^{\prime}, \beta = {\left(1,-2.957\right)}^{\prime}$, ${c}_{t}={\left(-0.003, -0.078\right)}^{\prime}$, and $M=-2.038$. (Color figure online)

3.4 Convergence Rate Filter

A spread with a high convergence rate to its asymptotic mean is more likely to close the position to make profits before the end of the trading day. This convergence rate can be approximated by measuring how the expected value of the spread defined in Eq. (6), that is,

$$ {\text{E}}\left[ {\beta^{\prime}x_{t} } \right] = {\text{J}}\left( {I + \tilde{\beta }^{\prime} \tilde{\alpha }} \right)^{t} \tilde{\beta }^{\prime} \tilde{x}_{0}^{{}} + \mathop \sum \limits_{i = 0}^{t - 1} \left( {I + \tilde{\beta }^{\prime} \tilde{\alpha }} \right)^{i} {\tilde{\beta }}\left( {\tilde{c}_{t - i} } \right) $$

(8)

converges to its asymptotic mean defined in Eq. (7). We denote Eq. (8) as the convergence mean since it starts from the initial value ${\beta }^{\mathrm{^{\prime}}}{x}_{0}$ and converges to the asymptotic mean M with the increment of time t, as illustrated in the right panel of Fig. 1. Since a spread process with a slow convergence rate has a lower chance to close the position with positive profit, we build a convergence rate filter to filter out spreads with slow convergence rates from trading. The convergence rate is measured by how much time ${t}_{c}$ is required for the convergence mean to approach the asymptotic mean within a tolerance error ε defined as

$$ t_{c} : = {\text{arg}}\mathop {\min }\limits_{t} \left| {{\text{E}}\left[ {\beta^{\prime}x_{t} } \right] - M} \right| < \varepsilon $$

(9)

where ${\text{E}}\left[{\beta }^{\mathrm{^{\prime}}}{x}_{t}\right]$ is defined in Eq. (8), and the asymptotic mean M is defined in Eq. (7). Our convergence rate filter excludes spreads with a higher ${t}_{c}$ (i.e., slow convergence rate) from trading. Our later experiments show how this filtering mechanism improves the win rate and the Sharpe ratio.

3.5 Adjustment to Approximated Simple Integer Trading Ratio

Note that we cannot buy fractions of shares since traded stocks cannot be infinitely divided, and odd lot orders are not allowed during intraday trading. However, the cointegrating vector ${\beta }^{\prime}=\left[1,-{\beta }_{1}\right]$ determined in Eq. (2) denotes the weight of capital invested in stocks ${X}_{1}$ and ${X}_{2}$; thus the ratio of the number of shares for longing or shorting ${X}_{1}$ and ${X}_{2}$ at time t is a non-simple irreducible ratio vector.

$${{\varvec{\gamma}}}^{\mathbf{^{\prime}}}=(\frac{1}{{X}_{1t}}, \frac{-{\beta }_{1}}{{X}_{2t}})$$

where the denominators denote the prices of the two stocks at time t. In addition, we cannot amplify ${\gamma }^{\prime}$ since a large trading volume could significantly influence the stocks' prices and erode the PTS profits. To convert ${\gamma }^{\prime}$ into the closest simple integer ratio${\widetilde{\gamma }}^{\prime}$, we find a grid point on a two-dimensional Cartesian coordinate system whose y-coordinate: x-coordinate ratio is closest to ${\gamma }^{\prime}$ by comparing the included angles using the arctangent method. To prevent large trading volumes from impacting stock prices and thereby eroding profits, we limit the maximum number of shares traded for each stock to five lots in our subsequent experiments, with one lot representing 1000 shares.${\widetilde{\gamma }}^{\prime}\equiv \left(\widetilde{{\gamma }_{1}},-\widetilde{{\gamma }_{2}}\right)$ becomes the integer number of lots for longing/shorting the stocks in the proposed PTS.

3.6 Trading Threshold Constructions and PTS Execution

On each trading day, we retrieve the price processes of all stocks from the formation period. Then we find the PTS-eligible stock pairs and obtain the corresponding ratio of the number of stock lots by the procedure in Fig. 2, after which we trade these eligible pairs during the trading period. We follow Vidyamurthy (2004) by opening the position if the spread deviates by $1.5\sqrt{{\Gamma }_{0}}$ from its the mean-reverting level M and close the position when the spread converges back to M. Specifically, we long (short) $\widetilde{{\gamma }_{1}}$ lots of stock 1 and short (long) $\widetilde{{\gamma }_{2}}$ lots of stock 2 at time t if ${x}_{1t}-{\beta }_{1}{x}_{2t}\le M-1.5\sqrt{{\Gamma }_{0}}$ (${x}_{1t}-{\beta }_{1}{x}_{2t}\ge M+1.5\sqrt{{\Gamma }_{0}}$) and close the position at time t + i if ${x}_{1, t+i}-{\beta }_{1}{x}_{2, t+i}\ge M ({x}_{1, t+i}-{\beta }_{1}{x}_{2, t+i}\le M)$. Finally, the positions may still be open at the end of the trading day. We force-close the positions to avoid the risks of cross-day portfolios. Keeping all positions closed in one trading day (i.e., intra-day trading) also decreases the Taiwan Stock Exchange's transaction cost from 0.3 to 0.15%.

We demonstrate our trading strategies in Fig. 5. The stock price processes of 1319 and 1477 during the formation period (i.e., the first 150 min) are used to examine the cointegration property and to construct a stationary spread process (denoted by the blue curve) as the trading signal for the trading period. We open the position when the spread reaches the upper threshold denoted by the green line. We observe that the sample mean tends to underestimate the mean-reverting level of the spread, resulting in positions being forcibly closed at the end of the trading day, as depicted in the upper panel. In contrast, the spread oscillates around the asymptotic mean, enabling the closure of positions for profit, as shown in the lower panel. The experiments in the following section demonstrate the superiority of using the asymptotic mean proposed in Sect. 3.2.

Fig. 5

Graphical Representation of PTS. The blue curve denotes the spread process by longing 3 lots of the Tong Yang Group's stock (with ticker symbol 1319) and 2 lots of Makalot Industrial Ltd. (with ticker symbol 1477) on Jan 5, 2016. The orange line denotes the mean-reverting level M estimated by the sample mean in the upper panel and the asymptotic mean in the lower panel. The green and red lines indicate the upper threshold ($M+1.5\sqrt{{\Gamma }_{0}}$) and lower threshold ($M-1.5\sqrt{{\Gamma }_{0}})$ for opening the positions. The blue vertical dash line divides a trading day into the first 150 min (formation period) and the remaining 120 min (trading period). (Color figure online)

4 Empirical Results

To augment our contribution vis-à-vis established estimators, we first calibrate a VECM model using the historical prices that exhibit cointegration. We simulate stock price processes using this calibrated model and then employ these simulated processes to generate a pairs trading strategy based on the cointegration property. As illustrated by the orange curves in the upper panel of Fig. 6, we utilize the stock price processes with tick numbers 6176 and 2385 from January 3, 2018. We use the data between the purple and the light blue dashed lines (i.e., the formation period) for calibration. Data to the left of the purple line are excluded from calibration to prevent excessive volatility during the market opening from impairing the calibration quality. Conversely, the data to the right of the light blue dashed line are used for implementing the PTS (i.e., the trading period). The calibration of VECM Eq. (2) yields the parameters: $=\left[-0.283,-0.717\right],$ $\beta =\left[\mathrm{0.472,0.528}\right], {c}_{t}=\left[\mathrm{20.59,52.22}\right], {\Gamma }_{i}=\left[\left[-0.188 0.092\right], \left[0.336 -0.237\right]\right], {u}_{t}\sim N=\left(0,\left[\left[0.044 0\right],\left[0.019 0.118\right]\right]\right)$. Using these parameters, we simulate the stock price processes, represented by the blue curves. Calibrating these blue curves with Eq. (2) results in $\alpha =\left[-0.292, -0.708\right]$, $\beta =\left[0.483, 0.517\right], {c}_{t}=\left[21.24, 51.50\right], {\Gamma }_{i}=\left[\left[-0.236 0.094\right], \left[0.477 -0.350\right]\right]$, ${u}_{t}\sim N=\left(0,\left[0.0419 0\right], \left[0.0222 0.119\right]\right)$.

Fig. 6

The upper left and right panels display the stock prices with tick numbers 6176 and 2385, respectively. In these panels, the simulated and real prices are depicted by the blue and orange curves, respectively. The formation period is indicated between the purple and light blue vertical dashed lines, with the area to the right of the light blue line representing the trading period. The simulated and real spread processes used for PTS trading are shown in the lower left and right panels, respectively. The green, yellow, and red horizontal lines in these panels denote the upper open threshold, the mean-reverting level, and the lower open threshold, respectively. (Color figure online)

Now, we compare our trading simulations using models calibrated with both real and simulated prices to verify the robustness of our model. Both scenarios demonstrate similar trading ratios ${\gamma }^{\prime}$ for executing PTS, underscoring the model's consistency. In the real price scenario, the spread process crosses below the lower opening threshold in the 180th minute and returns above the mean in the 181st minute. Based on the capital weights (0.472, 0.528) divided by the opening prices (69.7, 75.3), we obtain ${\gamma }^{\prime}$ as (0.491, 0.509). Considering the maximum profit potential and limits on the number of shares traded, we long 5 lots (i.e., 5000 shares) of the paired stock at a cost of NTD 725,000 and close the position at NTD 727,166.5, yielding a profit of NTD 2,166.5. The total transaction costs, including the Securities Transaction Tax at 0.15%, are NTD 1,090.75. Thus, the net profit for this scenario is NTD 1,075.75 (= NTD 2,166.5-1,090.75).

For the simulated price scenario, the spread crosses above the open threshold in the 170th minute and returns below the mean in the 171st minute. Using capital weights (0.483, 0.517) divided by the opening prices (70.3705, 75.3117), we obtain ${\gamma }^{\prime}$ as (0.5001, 0.4999). We short 5 lots of the paired stock in the 170th minute for NTD 728,411 and close the position in the 171st minute at NTD 726,407, resulting in a profit of NTD 2,004. The total transaction costs are NTD 1,092.617, leading to a net profit of NTD 911.383 (= NTD 2,004-1,092.617).

Our experiments illustrate the trading performance improvements by adopting the proposed asymptotic mean method in Table 1, the two-step model selection in Table 2, the convergence rate filter method in Table 3, and the white noise test for residuals in Table 4. Finally, we examine the influence of changing the sample period duration and the number of observations on the power of the Johansen cointegration test, as discussed in Otero et al. (2022), with the results presented in Table 5. Here we first suggest quantitative indicators by which to compare the performance of different trading strategies through experiments. "Avg. PNL (profit and loss) per trade" denotes the average profit and loss for each trade in thousand New Taiwan dollars, "Win rate" denotes the percentage of trades with positive profits, "Normal close rate" denotes the ratio of spreads that converge back to the mean-reverting level before the close of the trading day, "Sharpe ratio" indicates the ratio of average trading return per trade divided by the standard deviation of the trade return, and "Total trades" denotes the number of trades over the period.

Table 1 Trading performance using asymptotic and sample means

Table 2 We evaluate the investment performance under different model selections

Table 3 Trading performance with/without using convergence rate filter under different model selection

Table 4 Trading performance with/without white noise test

Table 5 Analysis of impact of formation period duration and sampling frequency on power of Johansen cointegration test

Table 1 illustrates that adopting the asymptotic mean (Asy) derived in Eq. (7) as the mean-reverting level outperforms adopting the sample mean (Sam). Specifically, the former approach has a higher average PNL per trade, win rate, normal close rate, and Sharpe ratio than the latter approach in every year of 2015–2018. However, the much larger total trades and lower normal close rates imply that the sample mean estimates a biased spread mean-reverting level and hence employs more infeasible stock pairs for PTS.

The PTS literature either ignores the cointegration model selection problem or uses the most general model, Model 3, defined in Sect. 3.3, to describe all price processes of cointegrated stock pairs. Table 2 compares the investment performance for selecting the fittest VECM using our two-step model selection described in Sect. 3.3, Johansen (1995)’s model selection, or directly calibrating Model 3 (M3). It can be observed that in each year from 2015 to 2018, our two-step model exhibits the best performance in terms of Avg. PNL per trade, win rate, normal close rate, and Sharpe ratio. By selecting appropriate cointegration models, our two-step method provides a better VECM fit, resulting in the trading of fewer infeasible pairs with higher win rates. This also explains why our model selection significantly improves investment performance.

Recall that the convergence rate of a spread process to its mean-reverting level can be approximated by how fast its convergence mean defined in Eq. (8) approaches the asymptotic mean by time ${t}_{c}$ defined in Eq. (9). Removing slow convergence spread processes from trading reduces the likelihood that spreads do not converge back to mean-reverting levels and are forced to close positions at the end of the trading day, potentially resulting in significant losses. A fast convergence rate implies that a divergent spread converges to the mean-reverting level more quickly and prevents structural breaks from ruining PTS benefits (see Huang et al. 2020). Indeed, our experiments in Table 3 demonstrate that trading risk decreases after removing spreads with slow convergence rates. Here "Convergence filter" denotes that we remove stock pairs whose ${t}_{c}$ is larger than the convergence time threshold of 6 from trading; "No filter" denotes that we trade all cointegrated stock pairs without filtering. Note that filtering out slow convergence spreads significantly increases win rates and Sharpe ratios regardless of which kind of model selection is used.

In Fig. 7, we graph the impacts of varying convergence time thresholds on the average PNL per trade and the normal close rate in 2017. As a strict (i.e., lower) threshold filters out more spreads with slow convergence rates, the above two investment performance metrics also increase. In the experiments illustrated in Table 3, 6 is chosen as the convergence time threshold because these performance metrics decline significantly around 6 in Fig. 7.

Fig. 7

Impact of Varying Convergence Time Threshold on Average PNL per Trade and Normal Close Rate

The effectiveness of the VECM calibrations can be assessed by checking the quality of the residual vectors ${a}_{t}$ by the Jarque–Bera and portmanteau tests (see Demiroglu and Kilian (2000)). If the model assumptions fit the stock prices data well, ${a}_{t}$ should follow an independent and identically normal distribution. Otherwise, the data is inadequate for the selected VECM and might not exhibit the cointegration property. In Table 4, "Test" denotes that we remove stock pairs that fail the above two tests, and "No test" indicates that we trade all stock pairs. Although applying white noise tests significantly reduces the number of trades, it substantially increases trading quality, as seen in the increments of the average PNL per trade, the win rate, and the Sharpe ratio. It also reduces the risk, as seen in the decrements in the maximum draw down (abbreviated as MDD). Since the cointegration property is critical in PTS, we must test for white noise to ensure that the model assumptions hold.

Figure 8 displays the monthly Sharpe ratios for different PTS settings from 2015 to 2018. In the upper panel, adopting the asymptotic mean (yellow curve) as the mean-reverting level is clearly better than adopting the sampling mean (red curve). Incorporating convergence rate filters (purple curve) also improves the Sharpe ratio. Now we compare the performance of different model selections with asymptotic mean and convergence rate filters, as in the lower panel. Our two-step model selection method (purple curve) outperforms Model 3 (blue curve) and Johansen’s method (green curve) in almost every month, which also confirms the robustness of our contributions.

Fig. 8

4-year Monthly Sharpe Ratios. M3 denotes direct calibration of stock prices by Model 3 without model selection. J denotes Johansen’s model selection. Asy and Sam_mean denote adoption of the asymptotic or sample mean as the mean-reverting level for the spread. Filter indicates adoption of the convergence rate filter. (Color figure online)

Table 5 examines the impact of varying formation period durations and sampling frequencies on the power of the Johansen cointegration test, as reflected in trading performance metrics. The benchmark adopts the above experimental settings: a 150-min formation period with a one-minute sampling frequency. Numerical results indicate the differential in trading performance between the adjusted PTS and this benchmark. The left panel shows that reducing the formation period from 150 to 100 min diminishes the test's power, as indicated by the lower Avg. PNL and Sharpe ratios. However, this reduction extends the trading period, which reduces the likelihood of forced closures at day's end and might hence increase the win rate and normal close rate. In the right panel, a decrease in sampling frequency from one minute to two minutes similarly lessens the test's power, reflected in lowered metrics across all trading performance indicators. These findings align broadly with those reported by Otero et al. (2022).

5 Conclusion

This paper analyzes the convergence properties of the spread process constructed by Johansen cointegration tests to improve PTS performance. First, we derive and use the asymptotic mean as the mean-reverting level instead of the spread's sample mean used in the literature. Our experiments show that adopting the sample mean misplaces the open and close thresholds as shown in Fig. 5, which degrades the trading performance. Second, the process during the above derivation is helpful to obtain the convergence mean used to approximate the convergence rate of a spread to its mean-reverting level. Filtering out unlikely profitable stock pairs with slow convergence rates also improves trading performance. Third, to address the joint problem of examining a stock pair's cointegration property and selecting the fittest VECM, we propose two-step model selection that makes use of the trace test and likelihood ratio test. Experiments show that this approach generates higher win rates and average profits than the Johansen cointegration approach, which is extensively used in the literature, and directly adopting the most generalized model (Model 3), which is the most general model. Removing invalid model calibrations by checking the normality of residuals also reduces trading risks. Furthermore, this paper uses the high frequency trading data of the 0050.TW and 0051.TW constituent stocks from 2015 to 2018 to examine the superiority of the proposed PTS. Unlike most studies, which execute inter-day PTS using the close price of each trading day and require sufficiently long trading (and hence backtesting) periods, our high-frequency PTS limits the portfolio holding to within one trading day to avoid overnight holding risk. Even with a limited backtesting period due to the limited availability of tick data, our high-frequency PTS still yields approximately 3000 trading opportunities per year for comparison and analysis. Also, to satisfy the constraints of no-odd-lot trading and liquidity, we convert the trading ratios of stock pairs into a nearby simple integer ratio with small magnitudes, which significantly enhances the applicability of our work for real trading.

Appendix A

We adopt the LRT proposed in Johansen (1995) to select the fittest VECM in our second-stage model selection as illustrated in Fig. 3. We test the null hypothesis Model 2 versus the alternative hypothesis Model 3 with the LRT statistic:

$$ {\text{LR}}_{{23}} = T\sum\nolimits_{{i = r + 1~}}^{k} {\log } \left( {\frac{{1 - ~\lambda _{i}^{3} }}{{1 - \lambda _{i}^{2} }}} \right) $$

(10)

where ${\lambda }_{i}^{2}$ and ${\lambda }_{i}^{3}$ are generalized eigenvalues corresponding to Model 2 and Model 3 generated by maximum likelihood estimation. The asymptotic distribution of Eq. (10) is ${\chi }^{2}\left(k-r\right)$, as illustrated in Corollary 11.2 in Johansen (1995). We choose Model 3 if the p-value is less than 0.05. If Model 1 is also an eligible candidate, we proceed to test the null hypothesis Model 1 versus the alternative Model 2 with the LRT statistic:

$${{\text{LR}}}_{12}=T{\sum }_{i=1 }^{r}{\text{log}}\left(\frac{1- {\lambda }_{i}^{1}}{1-{\lambda }_{i}^{2}}\right)$$

(11)

where ${\lambda }_{i}^{1}$ is the generalized eigenvalue of Model 1. The asymptotic distribution of Eq. (11) is ${\chi }^{2}\left(r\right)$, as stated in Theorem 11.3 in Johansen (1995). We adopt Model 2 if the test's null hypothesis is rejected at the 0.05 significance level; otherwise we select Model 1.