Complementarity Modeling of a Ramsey-Type Equilibrium Problem with Heterogeneous Agents

Abstract

We contribute to the field of Ramsey-type equilibrium models with heterogeneous agents. To this end, we state such a model in a time-continuous and time-discrete form, which in the latter case leads to a finite-dimensional mixed complementarity problem. We prove the existence of solutions of the latter problem using the theory of variational inequalities and present further properties of its solutions. Finally, we compute the growth dynamics in a calibrated model in which households differ with respect to their relative risk aversion, their discount factors, their initial wealth, and with respect to their interest rates on savings.

1 Introduction

People are interested in future economic growth both in terms of national income but equally—or even more importantly—in terms of personal income. The acceptance of the free-market system will ultimately depend on the resulting long-run distribution of income and wealth rather than on allocative efficiency. This paper presents numerical experiments on the dynamics of income and wealth distribution in Germany. Moreover, it describes a computational approach to analyze this issue more flexibly compared to what is current practice in applied macroeconomics.

The natural starting point for the analysis of income dynamics is the well-understood Ramsey-type growth model. In this model, a representative agent chooses a welfare-maximizing consumption path, given initial endowments and technology. The optimal consumption path coincides with a decentralized perfect-foresight competitive-market equilibrium as long as markets are complete. Aggregation is no issue in this setting. Heterogeneity comes into play when it is assumed that there are many agents that differ in their initial endowments and preferences. The decentralized market outcome of such an economy cannot be identified simply by solving an optimal control problem with a given objective function, as it is the case in the model with a single representative agent. Agents must forecast future prices to base their decisions on. However, their decisions in turn jointly determine future prices. It is this coherence-loop in aggregation that makes these models complicated.

A broad literature addresses the heterogeneous agent growth model, following different methodological strategies. Most authors make assumptions so that aggregated variables still evolve as if a representative agent would act as the decision maker. An example is the seminal work by Caselli and Ventura (2000) and its slightly simplified textbook version; see Barro and Sala-i-Martin (1995), p. 120. Caselli and Ventura have shown that this aggregation is feasible as long as agents share CIES (constant inter-temporal elasticity of substitution) preferences with identical discount rates and a constant substitution rate between private and public consumption. Based on this, the authors follow a three-step procedure to deal with heterogeneity, see Caselli and Ventura (2000), p. 910: (1) solve the aggregated dynamics by constructing an adequate representative-agent model, (2) assume distributions on preference parameters and initial endowments, and (3) derive testable hypotheses. A similar approach is chosen by Turnovsky and García-Peñalosa (2008, 2013), who allow for heterogeneity in capital assets and labor productivity.

Another strategy to solve the heterogeneous agent model is based on an approach by Krussel and Smith; see Krusell et al. (1998) and the overview by Heathcote and co-authors in Heathcote et al. (2009). Krussel and Smith use an approximate aggregation for which the mean of the wealth distribution is all what the agents need to predict future prices. As before, the distribution of assets does not matter for aggregated outcomes. Their approach is particularly suited for stochastic growth models. Heathcote applied a related methodology to analyze Ricardian equivalence in a heterogeneous agent model; see Heathcote (2005). He identifies a saving rule, which does not depend on distributional parameters but on aggregated variables only.

In this paper, we follow a direct computational strategy, i.e., without analytical or approximate aggregation. This is different from what is done in the literature as it is both a ready-to-use and precise approach to model wealth distribution dynamics. As a consequence, we can cope with situations in which the distribution of assets does matter for aggregated outcomes. We use mixed complementarity problems (MCPs) as the main modeling tool to show that heterogeneous agents that cannot be easily solved analytically can be modeled effectively. Moreover, we achieve the ability to capture severe heterogeneity in the utility function and individual dynamics, which are far from the average. Even highly nonlinear functions do not impede our approach. The equilibrium model is obtained by the optimization problems of the heterogeneous households as well as by those of the production sector, which are coupled using suitably chosen equilibrating conditions for interest and wage rates.

Table 1 Functions and constants used in the model

The resulting equilibrium model in time-continuous and discretized form is presented in Sect. 2 as an MCP. The relation between MCPs and variational inequalities (VIs) is then used in Sect. 3 to prove existence of equilibria by exploiting the classic theory of VIs. In Sect. 4, we apply our modeling in a setting similar to the one used by Caselli and Ventura (2000). In particular, we compute the income dynamics on a model calibrated on data for Germany. Based on this, we investigate the impact of a highly stylized form of capital market imperfection, where the returns on investment depend on initial wealth, assuming that poor agents have higher costs to generate returns then richer ones. To show the versatility of our approach, we then implement a policy intervention, where agents must choose an investment path such that their final wealth distribution meets a given policy target. Finally, we demonstrate a two-data-point calibration of preference parameters. The model then replicates two given base years, which we consider a substantial improvement in numerical modeling. The paper ends with some concluding remarks in Sect. 5.

2 Continuous Modeling and Discretization

2.1 A Time-Continuous Model

We consider an equilibrium version of a Ramsey-type growth model with households $i \in {\mathcal {H}}= \{1, \dotsc , I\}$. First, we are interested in a time-continuous Ramsey model. Thus, we consider a time interval [0, T] with $T \in {\mathbb {R}}_{\ge 0}$. In the following, $c_i(t), a_i(t): [0,T] \rightarrow {\mathbb {R}}_{\ge 0}$ model consumption and capital asset of household $i \in {\mathcal {H}}$. The optimization problem of a household $i \in {\mathcal {H}}$ is given by

$$\begin{aligned} \max _{c_i(\cdot ),a_i(\cdot )} &{} \quad \int _0^Tu_i(c_i(t))e^{-\gamma _i t} \,\mathrm {d}t\\ \text {s.t.} &{} \quad \frac{ \,\mathrm {d}}{ \,\mathrm {d}t} a_i(t) = w(t)l_i(t) + (r(t) -\delta )a_i(t) - c_i(t), \quad t \in [0,T],\\ &{} \quad a_i(t) \ge 0, \quad c_i(t) \ge 0, \quad t \in [0,T],\\ &{} \quad a_i(0) = a_i^0, \quad a_i(T) \ge a_i^T, \end{aligned}$$

(1)

where $u_i$ is an isoelastic utility function with a positive degree of relative risk aversion, $\gamma _i \in (0,1)$ is a utility discount rate, $\delta \in (0,1)$ is the depreciation rate, $a_i^0$ is the initial capital asset, and $a_i^T$ is the minimum final capital stock. In the following, we assume $\sum _{i\in {\mathcal {H}}}a_i^0 > 0$, $\sum _{i\in {\mathcal {H}}}a_i^T > 0$, that labor $l_i(t)$ has a given wage rate w(t), and that capital asset $c_i(t)$ has a given interest rate r(t) for all $i \in {\mathcal {H}}$. Moreover, individual labor endowment is strictly positive and exogenously given, i.e., $l_i(t) > 0$ for all $t \in [0, T]$. Labor supply does not generate disutility by assumption. Hence, it does not enter $u_i$ and, consequently, is completely supplied to the labor market in a price-inelastic way.

In what follows, we assume that the utility functions $u_i$ of all households $i \in {\mathcal {H}}$ can be different but all satisfy the following standard assumptions, see, e.g., Chapter 8.1 in Acemoglu (2008): They are twice differentiable and it holds $u_i' > 0$, $u_i'' < 0$, i.e., $u_i$ are concave and strictly increasing. Moreover, we suppose that the so-called Inada conditions

$$\begin{aligned} \lim _{x \rightarrow \infty }u_i'(x) = 0 \quad \text {and} \quad \lim _{x \rightarrow 0}u_i'(x) = \infty \end{aligned}$$

hold.

In addition to the household model above, we consider a single firm, which maximizes its profit in each point of time, i.e.,

$$\begin{aligned} \max _{K(t),L(t) \ge 0} \ F({\mathcal {A}}(t),K(t),L(t)) - r(t)K(t) - w(t)L(t), \end{aligned}$$

(2)

for all $t \in [0,T]$, where ${\mathcal {A}}(t)$ is an exogenously given productivity factor, K(t) is the engaged capital at given price r(t), and L(t) is the engaged labor at given wage rate w(t), respectively. The production function is of Cobb–Douglas type, i.e.,

$$\begin{aligned} F({\mathcal {A}}(t),K(t),L(t)) = {\mathcal {A}}(t) K(t)^{\alpha } L(t)^{1-\alpha } \quad \text {for some}\quad \alpha \in (0,1). \end{aligned}$$

(3)

To obtain an equilibrium model, we need equilibrating conditions that the firm can use at most the households aggregated capital and at most their aggregated labor, i.e.,

$$\begin{aligned} 0 \le r(t) \perp \sum _{i\in {\mathcal {H}}}a_i(t) - K(t) \ge 0, \quad 0 \le w(t) \perp \sum _{i\in {\mathcal {H}}} l_i(t) - L(t) \ge 0 \end{aligned}$$

(4)

holds for all $t \in [0,T]$. In summary, the equilibrium problem in continuous time is given by

• households (1) for all$i \in {\mathcal {H}}$, firm (2), equilibrating conditions (4).

Au notation used in the model is given in Table 1.

2.2 Discretization

For a time discretization of the derived equilibrium problem we assume a finite termination time $T \in {\mathbb {R}}_{\ge 0}$. We discretize using n intervals given by $0 = t_0< t_1< \dots< t_{n-1} < t_n = T$ with interval lengths $\tau _k = t_{k+1} - t_k$ for all $k=0,\dots ,n-1$. Furthermore, we use the abbreviation $c_{i,k} =c_i(t_k)$ and the same abbreviation for the other discretized functions. Using the implicit Euler method leads to the finite-dimensional problem

$$\begin{aligned} \max _{c_i,a_i} &{} \,\, \sum _{k=1}^{n}u_i(c_{i,k})e^{-\gamma _i \sum _{m=1}^{k} \tau _m}\tau _k \\ \text {s.t.} &{} \,\, \frac{1}{\tau _k}(a_{i,k+1}-a_{i,k})=w_{k+1}l_{i,k+1} \\ &{}\quad \quad +(r_{k+1}-\delta )a_{i,k+1} - c_{i,k+1} ,\quad {k = 0, \dots , n-1}, \\ &{} \;\;c_{i,k} \ge 0 ,\quad {k = 1, \dots , n}, \\ &{} \;\; a_{i,0} = a_i^0, \quad a_{i,n} \ge a_i^T, \quad a_{i,k} \ge 0 ,\quad {k = 1, \dots , n-1}, \end{aligned}$$

(5)

for every household $i \in {\mathcal {H}}$. Here, $c_i$ and $a_i$ denote the vectors of all consumption and asset variables of household i. The Karush–Kuhn–Tucker (KKT) conditions of (5), already written in MCP form, are given by

$$\begin{aligned} 0&\le -u_i'(c_{i,k})e^{-\gamma _i \sum _{m=1}^{k} \tau _m}\tau _k + \lambda _{i,k-1} \perp c_{i,k} \ge 0 ,\quad {k=1, \dots ,n}, \end{aligned}$$

(6a)

$$\begin{aligned} 0&= a_{i,0} - a_i^0 \perp \frac{\lambda _{i,0}}{\tau _0} \text { free}, \end{aligned}$$

(6b)

$$\begin{aligned} 0&\le \lambda _{i,k-1}\left( \frac{1}{\tau _{k-1}} - (r_k-\delta )\right) - \frac{\lambda _{i,k}}{\tau _k} \perp a_{i,k} \ge 0 ,\quad {k=1,\dots ,n-1}, \end{aligned}$$

(6c)

$$\begin{aligned} 0&\le \lambda _{i,n-1}\left( \frac{1}{\tau _{n-1}}-(r_{n}-\delta )\right) \perp a_{i,n} - a_i^T \ge 0, \end{aligned}$$

(6d)

$$\begin{aligned} 0&= \frac{a_{i,k+1}-a_{i,k}}{\tau _k} - w_{k+1}l_{i,k+1}\nonumber \\&\quad - (r_{k+1}-\delta )a_{i,k+1} + c_{i,k+1} \perp \lambda _{i,k} \text { free} ,\quad {k=0,\dots ,n-1} \end{aligned}$$

(6e)

for all $i \in {\mathcal {H}}$. Note that these conditions are both necessary and sufficient in our setting.

The firm’s discretized optimization problem reads

$$\begin{aligned} \max _{K_k, L_k \ge 0} \quad F({\mathcal {A}}_k, K_k, L_k) - r_k K_k - w_k L_k ,\quad {k = 1, \dots , n}. \end{aligned}$$

(7)

Note that the baseline time period $k = 0$ could, in principle, also be added to replicate the benchmark parameters (see Sect. 4.1), which means that the firm absorbs $K_0$ and $L_0$ for the given initial interest rate $r_0$ and wage rate $w_0$ such that the baseline period data for K and L result from our model. However, for the ease of presentation, we omit this index in the following. The (again necessary and sufficient) KKT conditions of (7) in MCP form are given by

$$\begin{aligned}&0 \le\!{ -}F'_K({\mathcal {A}}_k, K_k, L_k)+r_k \,\perp K_k \ge 0 ,\quad {k = 1, \dots , n}, \nonumber \\&0 \le\! {-}F'_L({\mathcal {A}}_k, K_k, L_k)+w_k \perp L_k \ge 0 ,\quad {k = 1, \dots , n}, \end{aligned}$$

(8)

where $\kappa$ and $\phi$ are the dual variables of the inequality constraints in (7).

The discretized equilibrating conditions read

$$\begin{aligned} 0 \le r_k \perp \sum _{i\in {\mathcal {H}}}a_{i,k}-K_k \ge 0, \quad 0 \le w_k \perp \sum _{i \in {\mathcal {H}}} l_{i,k} - L_k \ge 0 ,\quad {k = 1,\dots ,n}. \end{aligned}$$

(9)

Putting everything together, the discretized Ramsey-like equilibrium problem is to find a solution of the MCP

• households (6) for all $i \in {\mathcal {H}}$, firm (8), equilibrating conditions (9). (10)

For the following section we finally need to discuss the domains of the parameters $K_k$ and $L_k$ of the Cobb–Douglas production function in (7). The partial derivatives are given by

$$\begin{aligned} F'_{K_k}({\mathcal {A}}_k, K_k, L_k) = \frac{\alpha }{K_k} F({\mathcal {A}}_k, K_k, L_k), \quad F'_{L_k}({\mathcal {A}}_k, K_k, L_k) = \frac{1-\alpha }{L_k} F({\mathcal {A}}_k, K_k, L_k). \end{aligned}$$

To ensure that the KKT conditions of (7) are well-defined and that production cannot reach infinity, we make the following standard assumption.

Assumption 1

There exist constants $m > 0$ and $M < \infty$ so that $K_k, L_k \ge m$ and $K_k, L_k \le M$ for all k.

3 Existence of Equilibria

In order to show existence of equilibria of (10), we use the classic theory of variational inequalities (VIs); see, e.g., Facchinei and Pang (2003). To this end, we re-state (10) as the VI

$$\begin{aligned} F(x)^\top (y - x) \ge 0 \quad \text {for all} \quad y \in X \end{aligned}$$

(11)

with

$$\begin{aligned}&X = {\mathbb {R}}_{\ge 0}^{|{\mathcal {H}}|n} \times X_2 \times {\mathbb {R}}^{|{\mathcal {H}}| n} \times {\mathbb {R}}_{\ge 0}^{n} \times {\mathbb {R}}_{\ge 0}^{n} \times {\mathbb {R}}_{\ge 0}^{n} \times {\mathbb {R}}_{\ge 0}^{n}, \\&X_2 = \prod _{i \in {\mathcal {H}}} \left( \{a_i^0\} \times {\mathbb {R}}_{\ge 0}^{n-1} \times {\mathbb {R}}_{\ge a_i^T} \right) , \\&F(x) = (F_j(x))_{j=1}^7 \text { with } x =(c^\top ,a^\top ,\lambda ^\top ,K^\top ,L^\top ,r^\top ,w^\top )^\top \end{aligned}$$

and

$$\begin{aligned} F_1(x)&= \left( -u_i'(c_{i,k})e^{-\gamma \sum _{m=1}^{k} \tau _m}\tau _k +\lambda _{i,k-1} \right) _{k = 1, \dotsc , n, \, i \in {\mathcal {H}}},\\ F_2(x)&= \left( \begin{array}{c} \frac{\lambda _{i,0}}{\tau _0}\\ \left( \lambda _{i,k-1}\left( \frac{1}{\tau _{k-1}}-(r_k-\delta )\right) -\frac{\lambda _{i,k}}{\tau _k}\right) _{k=1,\dotsc ,n-1}\\ \lambda _{i,n-1}\left( \frac{1}{\tau _{n-1}}-(r_{n}-\delta )\right) \end{array}\right) _{i \in {\mathcal {H}}},\\ F_3(x)&= \left( \frac{a_{i,k+1}-a_{i,k}}{\tau _{k}} - w_{k+1}l_{i,k+1} -(r_{k+1}-\delta )a_{i,k+1} + c_{i,k+1}\right) _{k = 0, \dotsc ,n-1, \, i \in {\mathcal {H}}},\\ F_4(x)&= \left( -F'_K({\mathcal {A}}_k,K_k,L_k)+r_k\right) _{k = 1, \dotsc , n},\\ F_5(x)&= \left( -F'_L({\mathcal {A}}_k,K_k,L_k)+w_k\right) _{k = 1, \dotsc , n},\\ F_6(x)&= \left( \sum _{i\in {\mathcal {H}}}a_{i,k}-K_k\right) _{k = 1, \dotsc , n}, \quad F_7(x) = \left( \sum _{i \in {\mathcal {H}}}l_{i,k}-L_k\right) _{k = 1, \dotsc , n}. \end{aligned}$$

It is easy to see that the Jacobian of F is not symmetric on X. For instance, $\frac{ \,\mathrm {d}}{ \,\mathrm {d}{K_k}}F_6(x)_k = -1 \ne 1 =\frac{ \,\mathrm {d}}{ \,\mathrm {d}{r_k}}F_4(x)_k$ holds. Thus, there is no function f with $\nabla f = F$, i.e., it is not possible to solve an optimization problem for solving the VI(F, X); see, e.g., Theorem 1.3.1 in Facchinei and Pang (2003).

We now first collect some general properties of the solutions of the VI with the overall goal to prove the existence of equilibria. First, we show that every household is consuming at every point in time.

Proposition 1

Suppose that $x^{*}$ is a solution of the VI (11). Then, $c^{*}_{i,k} > 0$ holds for all $i \in {\mathcal {H}}$ and all $k \in \{1, \dots , n\}$.

Proof

Assume there exists $i \in {\mathcal {H}}$ and $k \in \{1, \dotsc , n\}$ with $c^{*}_{i,k} \ge 0$ being arbitrarily small. The choice of the utility function implies $u_i'(c) \rightarrow \infty$ for $c \rightarrow 0$. Since $x^{*}$ is a solution, we have $F_1(x^{*}) \ge 0$, yielding that $\lambda ^{*}_{i,k}$ is getting arbitrarily large for $c^{*}_{i,k}$ getting arbitrarily small. Thus, $\lambda ^{*}_{i,k}$ would be unbounded, which cannot be a solution of the VI. $\square$

The next proposition states that for every point in time except for the last one, there is at least one household with strictly positive asset.

Proposition 2

Suppose that Assumption 1holds and that $x^{*}$ is a solution of the VI (11). Then, for each $k \in \{1, \dots , n-1\}$, there exists a household $i \in {\mathcal {H}}$ with $a^{*}_{i,k} > 0$.

Proof

Assumption 1 implies $F_4(x^{*}) = 0$ by complementarity. Because $K_k^{*}$ and $L_k^{*}$ are bounded above as well as bounded away by a constant from 0 and since $F'$ is continuous, we have that $r_k^{*}$ is bounded in the same way. Hence, $F_6(x) = 0$ holds by complementarity and $0 < K_k^{*} = \sum _{i \in {\mathcal {H}}} a^{*}_{i,k}$ holds, which proves the proposition. $\square$

Note that our numerical results in Sect. 4 show that there indeed are households with zero asset for some time periods.

By reasons of optimality, it is expected that the asset’s lower bound at the end of the time horizon is binding. However, this is only the case under certain assumptions on the discretization of the MCP, which leads to an a-priori criterion for the final time discretization being reasonable.

Proposition 3

Suppose that Assumption 1holds, that $x^{*}$ is a solution of the VI (11), and that $\tau _{n-1} < (\bar{r} -\delta )^{-1}$ holds with $\bar{r} :=F'_K({\mathcal {A}}_k,\sum _{i \in {\mathcal {H}}} a_i^T, \sum _{i\in {\mathcal {H}}}l_{i,n})$. Then, $a^{*}_{i,n} = a_i^T$ holds for all $i \in {\mathcal {H}}$, i.e., the households’ final asset constraint is binding.

Proof

It holds

$$\begin{aligned} r^{*}_n = F'_K\left( {\mathcal {A}}_k,\sum _{i \in {\mathcal {H}}} a^{*}_{i,n}, \sum _{i\in {\mathcal {H}}}l_{i,n} \right) \le F'_K\left( {\mathcal {A}}_k, \sum _{i \in {\mathcal {H}}} a_i^T, \sum _{i\in {\mathcal {H}}}l_{i,n} \right) = \bar{r}, \end{aligned}$$

since $\sum _{i \in {\mathcal {H}}} a^{*}_{i,n} \ge \sum _{i \in {\mathcal {H}}} a_i^T$. We prove the statement via contradiction. Hence, we assume that $a^{*}_{i,n} > a_i^T$ holds for a household $i \in {\mathcal {H}}$. From the complementarity condition it follows $\lambda ^{*}_{i,n-1}(1 / \tau _{n-1} - (r^{*}_n - \delta )) = 0$. Thus, either $\lambda ^{*}_{i,n-1} = 0$ holds, leading to

$$\begin{aligned} 0 = \lambda ^{*}_{i,n-1} \ge u_i'(c^{*}_{i,n})e^{-\gamma \sum _{m=1}^k\tau _m} \tau _n, \end{aligned}$$

which contradicts the properties of the chosen utility function, or $1 / \tau _{n-1} - (r^{*}_n - \delta ) = 0$ needs to hold, which yields

$$\begin{aligned} 0 = \frac{1}{\tau _{n-1}} + \delta - r^{*}_n> \frac{1}{\tau _{n-1}} + \delta - \bar{r}. \end{aligned}$$

However, since $\tau _{n-1}$ is chosen so that $1 / \tau _{n-1} +\delta - \bar{r} > 0$ holds, we also obtain a contradiction in this case as well. $\square$

In the numerical results discussed in Sect. 4 we thus choose an equidistant stepsize and ensure that this stepsize satisfies the condition in Proposition 3.

Next, we show an aggregation theorem that relates the VI for multiple but homogeneous households to a VI for a single but properly chosen household.

Theorem 1

Suppose that Assumption 1holds and that $\tau _{n-1}$ is chosen such that Proposition 3holds. Let $x^{*}=(c^{*}, a^{*}, \lambda ^{*}, K^{*}, L^{*}, r^{*}, w^{*})$ be a solution of the VI(F, X) in (11) with $|{\mathcal {H}}|$ households, initial capital stocks $a_i^0$, and minimum final capital stocks $a_i^T$ so that $a_i^0 = \beta a_i^T$ holds for all $i \in {\mathcal {H}}$ and some $\beta \in {\mathbb {R}}_{> 0}$, i.e., the capital distribution at time 0 is the same as at time T. Furthermore, let labor $l_{i,k}$ as well as the discount rate $\gamma _i = \gamma$ be given and suppose that the utility functions $u_i = u$ are the same and of CRRA (constant relative risk aversion) type. Finally, suppose that $a_{i,k}^{*} > 0$ holds for all $k \in \{1, \dots , n-1\}$ and $i \in {\mathcal {H}}$. Then, for $\tilde{{\mathcal {H}}}$, $|\tilde{{\mathcal {H}}}| =1$, the vector $\tilde{x}^{*} =(\tilde{c}^{*},\tilde{a}^{*}, \tilde{\lambda }^{*}, K^{*}, L^{*}, r^{*}, w^{*})$, with

$$\begin{aligned} \tilde{c}_{k}^{*} = \sum _{i \in {\mathcal {H}}} c_{i,k}^{*}, \quad \tilde{a}_{k}^{*} = \sum _{i \in {\mathcal {H}}} a_{i,k}^{*}, \quad \tilde{\lambda }_{k}^{*} = u'\left( \sum _{i \in {\mathcal {H}}} u'(\lambda _{i,k}^{*})^{-1} \right) , \end{aligned}$$

is a solution of the single-household VI$(\tilde{F}, \tilde{X})$ with initial capital stock $\tilde{a}^0 = \sum _{i \in {\mathcal {H}}}a_i^0$, minimum final capital stock $\tilde{a}^n = \sum _{i \in {\mathcal {H}}}a_i^T$, labor $\tilde{l}_k = \sum _{i \in {\mathcal {H}}}l_{i,k}$, as well as with the same utility function u and discount rate $\gamma$ as before.

The VIs depend on the initial parameters and the number of households. Thus, we denote with VI(F, X) the VI of the multi-household problem and with VI$(\tilde{F}, \tilde{X})$ the one corresponding to the aggregated, i.e., single-household, problem. Moreover, we omitted transposition of vectors for better reading.

Proof

Since $x^{*}$ solves VI(F, X), it holds $x^{*} \in X$. From the choice of $\tilde{c}^{*}$, $\tilde{a}^{*}$, and $\tilde{\lambda }^{*}$ it follows $\tilde{x}^{*} \in \tilde{X}$. We need to show that $\tilde{x}^{*}$ solves VI$(\tilde{F}, \tilde{X})$. From Proposition 1 it follows $c^{*} > 0$, hence $F_1(x^{*}) = 0$ holds due to complementarity. Next, we conclude

$$\begin{aligned} \tilde{\lambda }^{*}_{k-1}&= u'\left( \sum _{i \in {\mathcal {H}}} u'(\lambda _{i,{k-1}}^{*})^{-1} \right) = u'\left( \sum _{i \in {\mathcal {H}}} u' \left( u'(c_{i,k}^{*})e^{-\gamma \sum _{m=0}^{k}\tau _m}\tau _k\right) ^{-1} \right) \\&= u'\left( \sum _{i \in {\mathcal {H}}} u'\left( u'(c_{i,k}^{*})\right) ^{-1}u' \left( e^{-\gamma \sum _{m=0}^{k}\tau _m}\tau _k \right) ^{-1}\right) \\&= u'\left( \sum _{i \in {\mathcal {H}}} c_{i,k}^{*}\right) e^{-\gamma \sum _{m=0}^{k}\tau _m}\tau _k, \end{aligned}$$

by exploiting that CRRA utility functions satisfy $u'(gh) =u'(g)u'(h)$ and $u'(gh)^{-1} = u'(g)^{-1}u'(h)^{-1}$ for $g,h \in {\mathbb {R}}_{>0}$. This shows $\tilde{F}_1(\tilde{x}^{*}) = 0$.

Since $\tilde{a}^{*} > 0$, we need to show that $\tilde{F}_2(\tilde{x}^{*})_k = 0$ holds for all $k \in \{1, \dots , n-1\}$. Moreover, $c^{*} > 0$, $\tilde{c}^{*} > 0$, $F_1(x^{*}) =0$, and $\tilde{F}_1(\tilde{x}^{*}) = 0$ imply $\lambda ^{*} > 0$ and $\tilde{\lambda }^{*} > 0$. Exploiting that $F_2(x^{*})_{i,k} = 0$ holds for all $k \in \{1, \dots , n-1\}$ and $i \in {\mathcal {H}}$ yields that $\lambda _{i,k}^{*}/\lambda _{i,k-1}^{*} = R_k$ is the same for all $i \in {\mathcal {H}}$ by using that all households have the same utility function and time discount factor. Next, we conclude that

$$\begin{aligned} \frac{\tilde{\lambda }_k^{*}}{\tilde{\lambda }_{k-1}^{*}}&= \frac{u'\left( \sum _{i \in {\mathcal {H}}} u'(\lambda _{i,k}^{*})^{-1} \right) }{u'\left( \sum _{i \in {\mathcal {H}}} u'(\lambda _{i,k-1}^{*})^{-1}\right) } = u'\left( \frac{\sum _{i \in {\mathcal {H}}} u'(\lambda _{i,k}^{*})^{-1}}{\sum _{i \in {\mathcal {H}}} u'(\lambda _{i,k-1}^{*})^{-1}}\right) \\&= u'\left( \frac{\sum _{i \in {\mathcal {H}}}u'(R_k\lambda _{i,k-1}^{*})^{-1}}{\sum _{i \in {\mathcal {H}}} u'(\lambda _{i,k-1}^{*})^{-1}} \right) = u'\left( \frac{u'(R_k)^{-1}\sum _{i \in {\mathcal {H}}} u'(\lambda _{i,k-1}^{*})^{-1}}{\sum _{i \in {\mathcal {H}}}u'(\lambda _{i,k-1}^{*})^{-1}} \right) = R_k \end{aligned}$$

holds for all $k \in \{1, \dots , n-1\}$ by using the above mentioned properties of the utility function in the second and fourth equation and by exploiting the identity $\lambda _{i,k}^{*} =R_k\lambda _{i,k-1}$ in the third equation. Thus, $\tilde{F}_2(\tilde{x}^{*})_k = 0$ for all $k \in \{1, \dots , n-1\}$. Proposition 3 implies $a_{i,n}^{*} = a_i^T$, hence $\tilde{a}_n^{*} = \tilde{a}^n$, and $\tilde{F}_2(\tilde{x}^{*})_n \ge 0$ since $F_2(x^{*})_{i,n} \ge 0$ for all households $i \in {\mathcal {H}}$. Next, $\tilde{F}_3(\tilde{x}^{*})_k = \sum _{i \in {\mathcal {H}}} F_3(x^{*})_{i,k} = 0$ holds for all $k \in \{0, \dots , n-1\}$ because of $F_3(x^{*}) = 0$. Moreover, $\tilde{F}_4(\tilde{x}^{*}) = \tilde{F}_5(\tilde{x}^{*}) = 0$ is implied by $F_4(x^{*}) = F_5(x^{*}) = 0$. Finally, $\tilde{F}_6(\tilde{x}^{*}) = \tilde{F}_7(\tilde{x}^{*}) = 0$ holds because of $F_6(x^{*}) = F_7(x^{*}) = 0$, Assumption 1, $\tilde{a}_k^{*} = \sum _{i \in {\mathcal {H}}} a_{i,k}^{*}$, and $\tilde{l}_k = \sum _{i \in {\mathcal {H}}}l_{i,k}$. $\square$

This aggregation theorem shows that Gorman’s aggregation theorem, see, e.g., Acemoglu (2008), also holds for our model applied to homogeneous households. This allows us to compare our model later on with a standard numerical approach of solving Ramsey-like growth models.

Next, we prove the existence of solution by exploiting the following classical existence result for VIs.

Theorem 2

(Facchinei and Pang 2003, Corollary 2.2.5) Let $X \subseteq {\mathbb {R}}^n$ be a nonempty, convex, and compact set and let $F:X \rightarrow {\mathbb {R}}^n$ be a continuous function. Then, the VI(X, F) has a solution.

The VI function F is obviously continuous in our setting. However, the feasible set X is not compact but Assumption 1 can be used to show the existence of a compact and convex subset including all solutions of the original VI so that the last theorem can still be applied.

Theorem 3

Suppose that Assumption 1and $a_i^0 \ge a_i^T$ holds as well as that $\tau _k = \tau$ and $\delta$ are chosen sufficiently small. Then, there exists a convex and compact subset $\tilde{X} \subseteq X$ such that the solutions sets of VI(X, F) and VI$(\tilde{X},F)$ coincide.

Proof

Let $x^{*} = (c^{*}, a^{*}, \lambda ^{*}, K^{*}, L^{*}, r^{*}, w^{*})$ be a solution of the VI(F, X).¹ Assumption 1 implies that $r^- \le r_k^{*} \le r^+$ and $w^- \le w_k^{*} \le w^+$ holds for all $k \in \{1, \dotsc , n\}$ and some $r^-, r^+, w^-, w^+ \in {\mathbb {R}}_{> 0}$. Moreover, we have $F_4(x^{*}) = F_5(x^{*}) = 0$ due to Assumption 1. Since $r_k^{*} > 0$ is complementary to $F_6(x^{*})_k \ge 0$, and $w_k^{*}> 0$ to $F_7(x^{*})_k \ge 0$, this implies $\sum _i a_{i,k}^{*} = K_k^{*}$ and $\sum _{i \in {\mathcal {H}}}l_{i,k} = L_k$. Hence, $a_{j,k}^{*} \le \sum _{i \in {\mathcal {H}}} a_{i,k}^{*} = K_k^{*}$ is bounded by the upper bound of $K_k$ for all $j \in {\mathcal {H}}$. We also know that $c_{i,k}^{*}$ cannot get arbitrarily close to 0 for all i and k. Otherwise, for some $i \in {\mathcal {H}}$ and for all $k \in \{1,\dotsc ,n\}$ we would obtain $a_{i,k+1}^{*} > a_{i,k}^{*}$ due to $F_3(x^{*}) = 0$, which would yield $a_{i,n}^{*} > a_{i,0}^{*}$ and, thus, a contradiction to $a_{i}^T \le a_{i}^0$. For each household $i \in {\mathcal {H}}$ there is a $k \in \{0, \dots , n-1\}$ such that $a_{i,k+1}^{*} \le a_{i,k}^{*}$ holds. From $F_3(x^{*}) = 0$, it follows

$$\begin{aligned} c_{i,k+1}^{*} = w_{k+1}^{*}l_{i,k+1} + a_{i,k}^{*}\frac{1}{\tau _k} - a_{i,k+1}^{*}\left( \frac{1}{\tau _k} + \delta - r_{k+1}^{*}\right) \ge w_{k+1}^{*}l_{i,k+1} \ge w^-l_{i,k+1}, \end{aligned}$$

because $r_{k+1}^{*} > \delta$ is valid if $\delta$ is sufficiently small. Thus, we have a strictly positive lower bound on $c_{i,k+1}^{*}$. Consider now first the case $a_{i,k}^{*} = 0$. From $F_3(x^{*}) = 0$, it follows $c_{i,k}^{*} \ge w_{k+1}^{*} l_{i,k+1} \ge w^- l_{i,k+1}$. In the other case, i.e., $a_{i,k}^{*} > 0$, $c_{i,k}^{*}$ is implicitly given by

$$\begin{aligned} \frac{u'(c_{i,k+1}^{*})}{u'(c_{i,k}^{*})}e^{-\gamma \tau } = \tau \left( \frac{1}{\tau } - (r_k^{*}-\delta )\right) , \end{aligned}$$

which follows from $F_1(x^{*}) = 0$ and $F_2(x^{*}) = 0$. Hence, $c_{i,k}^{*}$ is bounded from below by a strictly positive constant and from above due to $F_3(x^{*}) = 0$ and the boundedness of a, r, and w. From $F_1(x^{*}) = 0$ and the continuity of $u'$, it follows that $\lambda _{i,k}^{*}$ is also bounded. $\square$

Note that, except for the proof of the aggregation Theorem 1, we considered the setting of heterogeneous households throughout this section. Thus, the utility functions of all households can be different and only have to satisfy the mild conditions stated in Sect. 2.1.

4 Numerical Results

We now present our numerical results. First, Sect. 4.1 presents a real-world calibration of the model outlined in Sect. 2. Afterward, we discuss the computational setup and a warmstarting strategy in Sect. 4.2. Finally, we discuss our numerical results in Sect. 4.3.

4.1 Calibration

The benchmark data are collected from various sources; see below and Bundesamt (2020). They refer to Germany in 2016 as the base period. Germany’s gross domestic product (GDP) was 3134 Bio. € in current prices and 38067 € in per capita terms. The Cobb–Douglas production function (3) is calibrated mainly based on the firm’s first-order optimality conditions for the base period $t=0$, i.e., 2016. From this it follows for (3) that $\alpha = r(0) K(0)/Y(0)$. We take the off-the-shelve value $\alpha = 0.3$, GDP is normed in baseline, and we set initial production $Y(0) = 100$, gross interest $r(0) = 0.08$, and wage rate index $w(0) = 1$. Hence, we obtain $L(0) = 70$ and $K(0) = 375$. Given these numbers, ${\mathcal {A}}(0) = 0.8634$ holds. We assume ${\mathcal {A}}(t) = {\mathcal {A}}(0)$ to be constant over time. To induce a reasonable economic initial growth rate, we increase the productivity factor by 20 %, i.e., we adapt ${\mathcal {A}}(t) \leftarrow 1.2{\mathcal {A}}(t)$.

In our numerical studies, we use the utility functions

$$ u_{i} (c_{i} ) = \left\{ {\begin{array}{*{20}l} {\frac{{c_{i}^{{1 - \eta _{i} }} - 1}}{{1 - \eta _{i} }},} \hfill & {\eta _{i} > 0{\text{, }}\eta _{i} \ne 1,} \hfill \\ {\log (c_{i} ),} \hfill & {\eta _{i} = 1,} \hfill \\ \end{array} } \right. $$

for $i \in {\mathcal {H}}$ with preferences $\eta _i$, which are of CRRA (constant relative risk aversion) type. Note that these specific choices for $u_i$ satisfy the standard assumptions mentioned in Sect. 2.1. The CRRA-specification of instantaneous utility is often used in applied economics, e.g., in dynamic stochastic general equilibrium modeling (Aruoba et al. 2003) or, more generally, in monetary economics. Usually, $\eta$ is referred to as the coefficient of relative risk aversion, which does not make sense in our risk-free setting. Here, $\eta$ is just a measure of inter-temporal elasticity of substitution or serves as the generational inequality aversion; see (Nordhaus 2018, p. 336). As proposed by Nordhaus in his DICE-13 model, we use $\eta = 1.45$ and set the discount factor $\gamma$ to be 0.03.

We consider $|{\mathcal {H}}| = 10$ households indexed by $i=1, \dotsc , 10$. They share the same endowment of labor $l_i(t) = l(t) = 7$ for all $t \in [0,T]$, $i \in {\mathcal {H}}$, but differ in initial capital asset holdings. As a proxy of initial asset holdings, we take the mean value of net wealth holdings as reported in (Bundesbank 2019, 31); see Table 2. Finally, a lower bound on the terminal capital stock $a_i^T$ of 5 % of the initial capital stock is used.

Table 2 Initial asset holding distribution for $|{\mathcal {H}}| = 10$

4.2 Numerical Setup and Warmstart Strategy

The numerical experiments have been carried out on a compute cluster with 755 GiB of memory and with an Intel(R) Xeon(R) CPU E5-2699 CPU. The operating system is Ubuntu 18.04.4. The instances are created by implementing Problem (10) as an MCP in GAMS 28.2.0 and are solved using PATH (version 5.0.00; see Dirkse and Ferris (1995)) with its default settings except for the parameter convergence_tolerance, which is set to $10^{-5}$.

To solve the instances more effectively, we use a grid refinement and warmstarting procedure in which we solve the problem with j discretization intervals and, for the next step, increase the number of intervals to 2j. For solving the new problem, we use the solution of the coarser problem as the initial point for the problem on the finer grid. Moreover, we use mean values for the new grid points between two old ones. We repeat this procedure until we reach the required grid size. For the initialization of the first problem to be solved we use

$$\begin{aligned}&a_{i,k} = a_{i}^0, \quad K_k = \sum _{i \in {\mathcal {H}}}a_{i,0}, \quad L_k = |{\mathcal {H}}|l_k = 70, \\&r_k = F'_K({\mathcal {A}}(0), K_0, L_0) = 0.096, \quad w_k = F'_L({\mathcal {A}}(0), K_0, L_0) = 1.2, \\&c_{i,k} = w_{k}l_{i,k}+(r_{k}-\delta )a_{i,k} = 8.4 + 0.046 a_{i}^0, \end{aligned}$$

for $k = 0, \dots , n$ and

$$\begin{aligned} \lambda _{i,k} = -u'_i(c_{i,1})e^{-\gamma \sum _{m=1}^{k+1}\tau _m}\tau _k, \end{aligned}$$

for $k=0, \dots , n-1$, which is the steady state that arises if $a_{i,k} = a_{i}^0$ is set for all $i \in {\mathcal {H}}$.

In our numerical experiments, the sketched grid refinement procedure leads to a significant speed-up. This is due to the fact that after the refinement step, the initial point generated for the next problem is of very good quality. Therefore, each refinement step takes the solver only a very small amount of iterations to converge. In contrast, solving the problem on the final grid from scratch takes rather long because the initial guess might be far away from being a solution. As a benchmark, we compare a problem with 10 households and 2000 discretization intervals. The MCP has about 68 000 rows and columns, about 240 000 non-zero entries, and takes 110 s to be solved. Compared to this, starting with 250 intervals results in a first MCP with about 8 500 rows and columns as well as about 30 000 non-zero entries. We refine the grid as stated above until we reach the final number of 2000 intervals. Here, the entire solution procedure takes only 10 s, which roughly corresponds to a speed-up factor of 11. Further tests confirmed this superior performance, which is why we use the grid refinement procedure for computing all numerical results discussed in the next section. Furthermore, we have chosen the number of equidistant grid points such that Proposition 3 is fulfilled in the final refinement step, i.e., the final capital stock constraints are binding.

4.3 Computational Experiments and Economic Discussion

The numerical experiments are economically interesting examples that are carried out on the fully specified and calibrated model as outlined before.

4.3.1 Baseline Replication

We start with a baseline replication experiment to show that our methodological approach works “in practice”. To this end, we compute a baseline in a setup that is almost exactly the same as in Turnovsky and García-Peñalosa (2009), i.e., agents differ only in their initial capital asset endowments. Turnovsky and García-Peñalosa (2009) show that inequality in asset holdings can both increase or decrease over time, depending on the chosen parameters. We replicate the results by using both our own methodology and the aggregation approach as outlined in Turnovsky and García-Peñalosa (2009).²

This double-check makes sense since the computational approach in Turnovsky and García-Peñalosa (2009) differs significantly from ours. They make use of Gorman’s aggregation theorem; see Gorman (1953). The theorem states that as long as welfare functions are homothetic and technologies are neoclassical, the economy can be modeled as if it would be represented by a single agent. This allows to solve the Ramsey model as a single nonlinear optimization problem (NLP). The MCP approach as outlined in this paper does not make use of this or other aggregation theorems. Hence, our approach is more flexible and can be applied to a much broader range of settings. On a time-scale of $T = 400$, we do not observe any significant differences between the NLP and MCP approach, neither in aggregated nor in individual asset holdings. This verifies that our approach can cope with the issues addressed in Turnovsky and García-Peñalosa (2009). Hence, it can complement or substitute aggregation-based techniques as used in the literature.

Fig. 1

Left: assets $a_i$ (dotted) and consumption $c_i$ (solid). Each color represents a different household. Right: Lorenz curves for $t \in \{0, 50, 100, 150, 200, 250, 300 \}$

Fig. 2

Firm’s capital in the three considered cases. (1) Homogeneous households (solid red), (2) policy maker (dashed green), (3) different capital market access (dotted yellow)

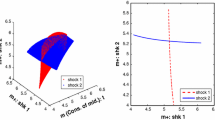
As an application, we calibrate our model on data for Germany in 2016 and implement production of Cobb–Douglas type. Figure 1 (left) shows the baseline results for consumption and capital assets of all 10 households. The solid red line in Fig. 2 shows aggregated capital as a result of the MCP approach, which coincides with the aggregated NLP approach. In both figures, the turnpike phenomenon is clearly visible. Moreover, we see that for the period in time during which the turnpike is visible w.r.t. the firm’s capital, it is also visible for the household’s consumption and asset holding. During these time periods, the economy is close to a steady state; see, e.g., Acemoglu (2008), Chapter 2.

The Lorenz curves in Fig. 1 (right) display the wealth dynamics.³ To hide finite time-horizon effects, the plots only show the results for $t \in \{0,50,100,150,200,250,300\}$. The wealth order is preserved over time, i.e., the ranking among the agents w.r.t. capital assets is preserved during the growth. Given the model’s specification and the choice of parameters, inequality decreases over time. Hence, according to our calibrated model, economic growth leads to less inequality among agents given that they differ only in their initial endowments.

4.3.2 Imperfect Capital Markets

An example, which clearly shows the advantage of our MCP-based modeling approach is the analysis of capital market imperfection. Access to the capital market can differ among agents, e.g., because of different capacities to process financial information. Likewise, some agents may be subject to unfavorable taxation of their financial transactions while others can trade without transaction costs. These asymmetries are reflected in our model by assuming small differences in the rate of return. To trigger these differences, we change the household’s discretized ODE by changing $r_k \leftarrow \kappa _i r_k$ for some $\kappa _i \in (0,1]$. We choose $\kappa _i = 1.0 - 0.2i / 10$ for $i \in {\mathcal {H}}$.

Figure 3 (left) shows the household’s consumption and asset holding. A comparison of these curves with the ones in Fig. 1 (left) shows a significant change in the turnpike behavior. The capital assets of most households are not entering a steady state. Aggregated capital (see Fig. 2), however, shows a turnpike behavior but the steady-state level of capital is significantly smaller than with a perfect capital market (dotted yellow line compared to the solid red line). Putting this in context with the baseline results and the following policy interventions scenario, we see that the small differences in the rate of return lead to a more uneven distribution of financial assets. Household 1 is increasing its financial assets just before the finite time horizon effect applies, whereas all other households are lowering their hold of financial assets. The Lorenz curves in Fig. 3 (right) illustrate this imbalance in capital distribution again. We see that the uneven distribution of capital is increasing. The implications of this asymmetry are remarkable. Only households 1 and 2 survive as “capitalists” while all other households decide to decrease or not to hold financial assets in the long run. We thus observe that imperfect capital markets strongly reinforce inequality in asset holdings.

Fig. 3

Left: assets $a_i$ (dotted) and consumption $c_i$ (solid) under the assumption of better capital market access for wealthy households. Right: corresponding Lorenz curves for $t \in \{0, 50, 100, 150, 200, 250, 300\}$

4.3.3 Policy Interventions

In this scenario, we assume that a policy maker targets the households minimum terminal capital stock. Household $i \in {\mathcal {H}}$ is equipped with a minimum final capital stock condition with lower bound $a_{10-i}^0/20$, which should induce a proper dynamics in asset holdings since the ordering of the households is reverted over time. Furthermore, we heterogenize the time discount factor of each household by setting it to $0.03+0.001i$. Figure 4 (left) shows the household’s consumption and asset holding. We see that due to the different final capital stock conditions and different time discount factors, the turnpike behavior is not as pronounced as in the baseline case. Moreover, the consumption patterns change compared to the numerical example discussed before. In Fig. 4 (left) we see the turnpike behavior in consumption and asset only for those households that are running out of money. Comparing this to Fig. 1 (left) shows significant changes in the turnpike pattern: Most households do not not reach a turnpike-like steady state or the time period of this state is significantly reduced. For example, household 1 (red) is increasing consumption over the time horizon. We also see some households with decreasing consumption (from $t=340$ to 380) just before they increase it again due to the considered finite time horizon. This is because the households run out of money and have to save to fulfill the final capital stock condition. The overall picture in Fig. 2 (dashed green line) is still comparable to the case discussed before (solid red line) but shows a narrow bend from $t=340$ to 380, which coincidences with the time period in which some households are lowering their consumption. The economy evolves towards a more uneven distribution of assets in the long run, hence inequality is strengthened. Figure 4 (right) shows the Lorenz curves, which also indicate increased inequality over time. Some households run out of assets completely. This is due to their higher impatience to consume as reflected by their higher discount rate. The latter, in particular, shows that even small differences in the discount rate really matter. Given their labor income, impatience to consume is too strong to overcome low interest rates on savings. This provocative result is known as the dominant consumer problem; see, e.g., Becker (2006) for an overview. It blames poor households (in terms of capital income) to be poor because of their preferences and not because of unfavorable initial capital holdings.

Fig. 4

Left: assets $a_i$ (dotted) and consumption $c_i$ (solid) under the assumption of a policy maker. Right: corresponding Lorenz curves for $t \in \{0, 50, 100, 150, 200, 250, 300\}$

4.3.4 Preference Heterogeneity Based on a Two-Data-Point Calibration

Our final experiment shows the strength of our modeling approach in the sense that we allow for heterogeneity in the utility discount rates $\gamma _i$ and in the preferences $\eta _i$ of the CRRA utility functions $u_i$; see Sect. 4.1. We use these parameters for a two-data-point calibration: we replicate the gross wealth dynamics of Germany based on the reference periods 2014 (corresponding to $t=0$) and 2017 ($t=5$) as described in Bundesbank (2019). To obtain the corresponding parameters $\gamma _i$, $\eta _i$, and ${\mathcal {A}}(0) = {\mathcal {A}}(t)$ for all t for given $a_i(0)$ and $a_i(5)$, see Table 3, we solve a modified complementarity problem for the respective fitting problem. In this modified problem, we consider $\gamma _i$, $\eta _i$, and ${\mathcal {A}}(0)$ as free variables and pair them with complementarity constraints that imply the given capital distribution and accumulation at time $t=5$. The fitted parameters then allow to get an insight of the further capital market development that is based on our model dynamics and that fits the respective data of 2014 and 2017. Here, we compute the wealth dynamics for the shorter time period $T=20$ to obtain economic results for a reasonable time horizon and we cut off the plot in Fig. 5 to visually cut off finite horizon effects. The initially wealthiest household behaves quite strange in this scenario. To replicate its behavior, it is the most patient one (lowest discount rate) but also displays the highest $\eta _i$. Other households evolve as expected. The Lorenz curve in Fig. 5 depicts a slowly changing asset distribution, pointing towards a more equal distribution.

Table 3 Parameters (top) and results (bottom) of the modified complementarity problem

Fig. 5

Left: assets $a_i$ (dotted) and consumption $c_i$ (solid) based on the fitted parameters of Table 3. Right: corresponding Lorenz curves for $t \in \{0, 2.5, 5, 7.5, 10, 12.5, 15\}$

5 Conclusion

In this paper, we discussed an MCP model of a time-discrete Ramsey-type equilibrium problem with heterogeneous agents, showed the existence of equilibria, and presented numerical results for a realistic calibration of the model. Our numerical approach does not make use of analytical or approximate aggregation and, hence, offers more flexibility in calibrating preferences of heterogeneous agents. This paves the way to consider equilibrium models of heterogeneous agents with additional complexity, e.g., by considering spatially dispersed households. Future work will focus on spatial processes in an optimal-control setting as in, e.g., Frerick et al. (2019a, 2019b), which we plan to generalize to an equilibrium setting in our future work.