Skip to main content
SpringerLink
Log in

Forecasting Inflation Uncertainty in the United States and Euro Area

  • Published:
Computational Economics Aims and scope Submit manuscript

Abstract

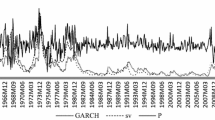
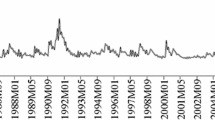
This study forecasts a particular type of economic uncertainty (inflation uncertainty) in the United States and Euro Area over 1997–2017. By using monthly data, we compute inflation uncertainty based on three models: symmetric and asymmetric generalized autoregressive conditional heteroscedasticity models and a stochastic volatility model. While the first two provide symmetric and asymmetric measures of inflation uncertainty, respectively, the third measure offers greater flexibility when measuring uncertainty. The analysis of the out-of-sample forecasts for inflation uncertainty shows the superiority of the stochastic volatility model for forecasting the dynamics of inflation uncertainty in both the short (1 year) and medium (4 years) terms. This finding is particularly interesting, as it allows researchers to better estimate the main inflation cost, namely inflation uncertainty, as well as its effect on the real economy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Notes

  1. Further, economic uncertainty, which is always unobserved (Charles et al. 2018), has always been challenging to measure and several proxies have been used: the VIX (Bloom et al. 2012), conditional variance models (Scotti 2012; Rossi and Sekhposyan 2017), the economic policy index (Baker et al. 2015), and perceived uncertainty from consumer surveys (Leduc and Sill 2013).

  2. It reached 1.5 and 2.96% in 2010 and 2011, respectively. It then changed to about 1.74% in 2012, 1.5% in 2013, 0.76% in 2014, 0.73% in 2015, and 2.07% in 2016.

  3. It decreased to 1.64 and 0.92% in 2008 and 2009, respectively before reaching 2.23, 2.75, and 2.22% in 2010, 2011, and 2012.

  4. p and q denote the lag order of the autoregressive and moving average parts, respectively. They are specified by using the information criteria and autocorrelation functions.

  5. The lags for a GARCH model might be specified by using information criteria, too. However, a GARCH(1,1) provides a suitable specification with which to capture the main volatility properties.

  6. Other methods of modelling stochastic volatility include Gaussian error models and heavy tails and serial dependence; however, the t-distribution is more appropriate (Chan 2013).

  7. For more details on the MDM statistic, see Harvey et al. (1997).

  8. The GARCH model is estimated by using the quasi-maximum likelihood technique of Bollerslev and Wooldridge (1992).

  9. To save space, we do not report the estimation results of the GARCH and GJR-GARCH specifications, but they are available upon request.

  10. For the medium term forecasting, the period of models estimation is from June 1997 to January 2013 for the case of US and from February 1997 to January 2013. The forecasting period is from February 2013 to January 2017.

  11. For the short-term forecast, the period of the model estimation runs from June 1997 to January 2016 for the United States and from February 1997 to January 2016 for the Euro Area. The forecasting period is therefore from February 2016 to January 2017.

References

  • Bachmann, R., Elstner, S., & Sims, S. (2013). Uncertainty and economic activity: Evidence from business survey data. American Economic Journal: Macroeconomics, 5, 217–249.

    Google Scholar 

  • Baker, S. R., Bloom, N., & Davis, S. J. (2015). Measuring economic policy uncertainty. National Bureau of Economic Research Working Paper 21633.

  • Bårdsen, G., Jansen, E. S., & Nymoen, R. (2002). Model specification and inflation forecast uncertainty. Annales d’Économie et de Statistique, 67(68), 495–517.

    Article  Google Scholar 

  • Bauer, C., & Neuenkirch, M. (2017). Forecast uncertainty and the Taylor rule. Journal of International Money and Finance, 77, 99–116.

    Article  Google Scholar 

  • Ben Nasr, A., Balcilar, M., Ajmi, A. N., Aye, G., Gupta, R., & Eyden, R. (2015). Causality between inflation and inflation uncertainty in South Africa: Evidence from a Markov-switching vector autoregressive model. Emerging Markets Review, 24, 46–68.

    Article  Google Scholar 

  • Berument, H., Yalcin, Y., & Yildirim, J. (2009). The effect of inflation uncertainty on inflation: Stochastic volatility in mean model within a dynamic framework. Economic Modelling, 26(6), 1201–1207.

    Article  Google Scholar 

  • Bloom, N., Bond, S. R., & Van Reenen, J. (2007). Uncertainty and investment dynamics. Review of Economic Studies, 74(2), 391–415.

    Article  Google Scholar 

  • Bloom, N., Floetotto, M., Jaimovich, N., Saporta-Eksten, I., & Terry, S.T. (2012). Really uncertain business cycles. National Bureau of Economic Research Working Paper 18245.

  • Bollerslev, T. (1986). Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics, 31, 307–327.

    Article  Google Scholar 

  • Bollerslev, T., & Wooldridge, J. (1992). Quasi-maximum likelihood estimation and inference in dynamic models with time-varying covariance. Econometric Review, 11, 143–172.

    Article  Google Scholar 

  • Chan, J. C. C. (2013). Moving average stochastic volatility models with application to inflation forecast. Journal of Econometrics, 176(2), 162–172.

    Article  Google Scholar 

  • Chan, J. C. C. (2017). The stochastic volatility in mean model with time-varying parameters: An application to inflation modelling. Journal of Business & Economics Statistics, 35(1), 17–28.

    Article  Google Scholar 

  • Charles, A., Darné, O., & Tripier, F. (2018). Uncertainty and the macroeconomy: Evidence from a composite uncertainty indicator. Applied Economics, 50(10), 1093–1107.

  • Diebold, F. X., & Mariano, R. S. (1995). Comparing predictive accuracy. Journal of Business and Economic Statistics, 13, 253–263.

    Google Scholar 

  • Engle, R. F. (1982). Autoregressive conditional heteroskedasticity with estimates of the variance of UK inflation. Econometrica, 50, 987–1008.

    Article  Google Scholar 

  • Glosten, L., Jagannathan, R., & Runkle, D. (1993). Relationship between the expected value and volatility of the nominal excess returns on stocks. Journal of Finance, 48, 1779–1802.

    Article  Google Scholar 

  • Golub, J. (1994). Does inflation uncertainty increase with inflation? Economic Review Federal Reserve Bank of Kansas City, 79, 27–38.

    Google Scholar 

  • Harvey, D. I., Leybourne, S. J., & Newbold, P. (1997). Testing the equality of prediction mean squared errors. International Journal of Forecasting, 13, 281–291.

    Article  Google Scholar 

  • Holland, S. (1993). Comment on inflation regimes and the sources of inflation uncertainty. Journal of Money Credit and Banking, 25, 514–520.

    Google Scholar 

  • Jurado, K., Ludvigson, S. C., & Ng, S. (2015). Measuring uncertainty. American Economic Review, 105, 1177–1216.

    Article  Google Scholar 

  • Koopman, S. J., & Hol Uspensky, E. (2002). The stochastic volatility in mean model: Empirical evidence from international stock markets. Journal of Applied Econometrics, 17(6), 667–689.

    Article  Google Scholar 

  • Lahiri, K., & Lui, F. (2006). Modelling multi-period inflation uncertainty using a panel of density forecasts. Journal of Applied Econometrics, 21, 1199–1219.

    Article  Google Scholar 

  • Leduc, S., & Sill, K. (2013). Uncertainty shocks are aggregate demand shocks. Journal of Monetary Economics, 82, 20–35.

    Article  Google Scholar 

  • Poon, S.-H., & Granger, C. W. J. (2003). Forecasting volatility in financial markets: A review. Journal of Economic Literature, 41(2), 478–539.

    Article  Google Scholar 

  • Rossi, B., & Sekhposyan, T. (2015). Macroeconomic uncertainty indices based on nowcast and forecast error distributions. American Economic Review, 105(5), 650–655.

    Article  Google Scholar 

  • Rossi, B., & Sekhposyan, T. (2017). Macroeconomic uncertainty indices for the Euro Area and its individual member countries. Empirical Economics, 53(1), 41–62.

    Article  Google Scholar 

  • Scotti, C. (2012). Surprise and uncertainty indexes: Real-time aggregation of real-activity macro surprises. Unpublished manuscript, Federal Reserve Board.

Download references

Author information

Authors and Affiliations

  1. EDC Paris Business School, OCRE-Lab, Paris, France

    Zied Ftiti

  2. High Institute of Management, ISGT, LR13ES01-GEF2A, University of Tunis, Le Bardo, Bouchoucha, 1002, Tunis, Tunisia

    Zied Ftiti

  3. University of Evry, 2, rue Facteur Cheval, 91025, Evry, France

    Fredj Jawadi

Authors
  1. Zied Ftiti
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fredj Jawadi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zied Ftiti.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ftiti, Z., Jawadi, F. Forecasting Inflation Uncertainty in the United States and Euro Area. Comput Econ 54, 455–476 (2019). https://doi.org/10.1007/s10614-018-9794-9

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10614-018-9794-9

Keywords

JEL Classification

Search

Navigation