Effect of mobility and convection-dominated flow on evaluation of reservoir dynamic performance by fast marching method

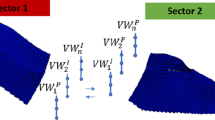
Abstract

The determination of optimum well locations and number of wells needed during green field development always comes with unprecedented challenges because of the geological uncertainty, and the non-linear relationship between the input and output variables associated with real reservoirs. These variables are key sources affecting the viability and validity of the results. Reservoir simulation is one of the least uncertain and most reliable prediction tools for dynamic performance of any reservoir. As field development progresses, more information becomes available, enabling us to continually update and, if needed, correct the reservoir description. The simulator can then be used to perform a variety of exercises or scenarios, with the goal of optimizing field development and operation strategies. Optimizing well numbers or locations under such geological uncertainty is achieved by using a reservoir simulator under several geological realizations, and these require multiple reservoir simulations to estimate the field performance for a given well configuration at a given location. Using reservoir simulation becomes impractical when dealing with real field cases incorporating multi-million cells because of the associated CPU demand constraints (Bouzarkouna et al. 2011). For instance, to determine the optimum well locations in a giant field that will result in the most efficient production rate scenario, one requires a large number of simulation runs for different realizations and well configurations. A large amount of runs is technically difficult to achieve even if we have access to super computers. The fast marching method (FMM), which is based on a solution of Eikonal equation, can be used to find the optimum well locations in a green oil field by tracking the pressure distribution in the reservoir. The FMM will enable us to calculate the radius of investigation or pressure front as a function of time without running any simulation and with a high degree of accuracy under primary depletion conditions. The main purpose of this paper is to study the effect of mobility on FMM and extend the investigation of its validity to include two-phase flow and convection-dominated flow and evaluate the ability of the methodology to predict the dynamic performance of the reservoir during pseudo-steady-state flow regime.

Appendices

Appendix 1. Solution of diffusivity equation in terms of Darcy flux

We approximate the transient flow as a series of pseudo-steady-state flows and use the approximation to derive the bottomhole flowing pressure equation, in which the drainage volumes are obtained from FMM.

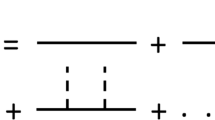
The general form of the governing diffusivity equation for radial flow is normally written as

$$ \frac{C_{1} }{r}\frac{\partial }{\partial r}\left( r\frac{k(r)}{\mu }\frac{\partial p}{\partial r}\right)=\varphi (r)c_{t} \frac{\partial p}{\partial t} $$

(13)

where pressure is the dependent variable. To obtain the Darcy flux expression, we change the dependent variable in Eq. 13 to rate instead of pressure. The rate at any point in the reservoir is, according to Darcy’s law

$$ q(r,t)=C_{1} hr\frac{k(r)}{\mu }\frac{\partial p(r,t)}{\partial r} $$

(14)

Rearranging Eq. 14 yields

$$ \frac{1}{C_{1} h}q(r,t)=r\frac{k(r)}{\mu }\frac{\partial p(r,t)}{\partial r} $$

(15)

Substituting Eq. 15 into Eq. 13 yields

$$ \frac{1}{r}\frac{\partial }{\partial r}\left( \frac{1}{h}q\right)=\varphi (r)c_{t} \frac{\partial p}{\partial t} $$

(16)

For a reservoir with constant thickness, Eq. 15 becomes

$$ \frac{1}{r\,h}\frac{\partial q}{\partial r}=\varphi (r)c_{t} \frac{\partial p}{\partial t} $$

(17)

Differentiating Eq. 17 with respect to r yields

$$ \frac{1}{h}\frac{\partial }{\partial r}\left( \frac{1}{r}\frac{\partial q}{\partial r}\right)=c_{t} \frac{\partial p}{\partial t}\frac{\partial \varphi (r)}{\partial r}+\varphi (r)c_{t} \frac{\partial^{2}p}{\partial t\partial r} $$

(18)

Rearranging Eq. 18 yields

$$ \frac{\partial p}{\partial t}=\frac{1}{r\,h\,\varphi (r)c_{t} }\frac{\partial q}{\partial r} $$

(19)

Differentiating Eq. 19 with respect to t yields

$$ \frac{\partial q}{\partial t}=C_{1} r\,h\frac{k(r)}{\mu }\frac{\partial^{2}p}{\partial t\,\partial r} $$

(20)

Rearranging Eq. 20 yields

$$ \frac{\partial^{2}p}{\partial t\,\partial r}=\frac{\partial q}{\partial t}\frac{\mu }{C_{1} r\,h\,k(r)} $$

(21)

Substituting Eqs. 19 and 21 into Eq. 18 yields

$$ \frac{\partial }{\partial r}\left( \frac{1}{r}\frac{\partial q}{\partial r}\right)=\frac{1}{r\,h\,\varphi (r)}\frac{\partial \varphi (r)}{\partial r}\frac{\partial q}{\partial r}+\frac{\varphi (r)\,\mu \,c_{t} }{C_{1} r\,h\,k(r)}\frac{\partial q}{\partial t} $$

(22)

For homogeneous reservoir, the porosity (φ) and permeability (k) are constant, and Eq. 22 simplifies to

$$ r\frac{\partial }{\partial r}\left( \frac{1}{r}\frac{\partial q}{\partial r}\right)=\frac{\varphi \,\mu \,c_{t} }{C_{1} \,h\,k}\frac{\partial q}{\partial t} $$

(23)

Expanding the LHS of Eq. 23 yields

$$ \frac{\partial^{2}q}{\partial r^{2}}-\frac{1}{r}\frac{\partial q}{\partial r}=\frac{\varphi \,\mu \,c_{t} }{C_{1} \,h\,k}\frac{\partial q}{\partial t} $$

(24)

We define the diffusivity constant as

$$ \alpha \text{=}\frac{\varphi \,\mu \,\mathrm{c}_{t} }{\mathrm{C}_{1} \,k} $$

(25)

Substituting Eq. 25 into Eq. 26 yields

$$ \frac{\partial^{2}q}{\partial r}-\frac{1}{r}\frac{\partial q}{\partial r}=\alpha \frac{\partial q}{\partial t} $$

(26)

Equation 26 may be solved using the following initial and boundary conditions:

$$ \left\{ {\begin{array}{l} \text{IC:}\,\,q\text{(}r\text{,}\,\,t\text{=}\,\text{0)}\,\text{=}\,\text{0} \\ \\ \text{IBC\thinspace 1:\thinspace }q\text{(}r_{\mathrm{e}} \text{,}t\text{)}\,\text{=}\,\text{0} \\ \\ \text{OBC\thinspace 2:\thinspace }q\text{(}r_{\mathrm{w}} \text{,}t\text{)}\,\text{=}\,q\text{} \end{array}} \right. $$

(27)

We define the following dimensionless variables

$$ \left\{ {\begin{array}{l} r_{D} =\frac{r}{r_{w} } \\ q_{D} =\frac{q}{q_{w} } \\ t_{D} =\frac{k\,t}{\varphi \,\mu \,c_{t} \,{r_{w}^{2}}}\text{} \end{array}} \right. $$

(28)

Rearranging and differentiating the above dimensionless variables yields

$$ \left\{ {\begin{array}{l} \partial r=r_{w} \partial \mathrm{r}_{D} \,\,\,\,\,\to \,\,\,\,\,\partial r^{2}=r_{w} \partial \mathrm{r}_{D}^{2} \\ \partial q=q_{w} \partial q_{D} \,\,\,\,\,\to \,\,\,\,\,\partial q^{2}=q_{w} \partial {q_{D}^{2}} \\ \partial t=\frac{\varphi \,\mu \,c_{t} \,{r_{w}^{2}}}{k}\partial t_{D} \text{} \end{array}} \right. $$

(29)

Substituting the derivative of the dimensionless variables into Eq. 26 yields

$$ \frac{\partial^{2}q_{D} }{\partial {r^{2}_{D}} }-\frac{1}{r_{D} }\frac{\partial q_{D} }{\partial r_{D} }=\frac{\partial q_{D} }{\partial t_{D} } $$

(30)

And the initial and boundary conditions become

$$ \left\{ {\begin{array}{l} \text{IC:}\,\,q_{D} \text{(}r_{D} \text{,}\,t_{D} \,\text{=}\,\text{0)}\,\text{=}\,\text{0} \\ \\ \text{OBC\thinspace 1:\thinspace }q_{D} \text{(}r_{D} \to \infty \,\text{,}t_{D} \text{)}\,\text{=}\,\text{0} \\ \\ \text{IBC\thinspace 2:\thinspace }q_{D} \text{(}r_{D} \to 0\,\text{,}t_{D} \text{)}\,\text{=}\,1\text{\thinspace } \end{array}} \right. $$

(31)

We use the following Boltzmann transform and utilize the dimensionless variables

$$ x=\frac{{r^{2}_{D}} }{4t_{D} } $$

(32)

$$ \left\{ {\begin{array}{l} t_{D} =\frac{k\,t}{\varphi \,\mu \,c_{t} \,{r_{w}^{2}}}\to \,x=\frac{\varphi \,\mu \,c_{t} \,{r_{w}^{2}}}{4k\,t}{r_{D}^{2}} \\ x=\frac{1}{4}\frac{\varphi \,\mu \,c_{t} }{k}\frac{\left( {r_{w} r_{D} } \right)^{2}}{t}=\frac{1}{4}\alpha \frac{\left( {r_{w} r_{D} } \right)^{2}}{t}\text{.} \end{array}} \right. $$

(33)

Differentiating the Boltzmann transform and using chain rule yields

$$ \left\{ {\begin{array}{l} \frac{\partial x}{\partial r_{D} }=\frac{r_{D} }{2\,t_{D} } \\ \frac{\partial x}{\partial t_{D} }=\frac{{r^{2}_{D}} }{4\,{t^{2}_{D}} } \\ \frac{\partial q_{D} }{\partial r_{D} }=\frac{\partial q_{D} }{\partial x}\frac{\partial x}{\partial r_{D} }=\frac{r_{D} }{2\,t_{D} }\frac{\partial q_{D} }{\partial x}\text{ \thinspace } \end{array}} \right. $$

(34)

$$ \left\{ {\begin{array}{l} \frac{\partial^{2}q_{D} }{\partial {r^{2}_{D}} }=\frac{\partial }{\partial r_{D} }\left( \frac{\partial q_{D} }{\partial r_{D} }\right)=\,\frac{\partial }{\partial x}\left( \frac{r_{D} }{2t_{D} }\frac{\partial q_{D} }{\partial x}\right)\frac{\partial x}{\partial r_{D} } \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,=\frac{\partial }{\partial x}\left( \frac{r_{D} }{2t_{D} }\frac{\partial q_{D} }{\partial x}\right)\frac{r_{D} }{2t_{D} } \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,=\frac{{r^{2}_{D}} }{2{t^{2}_{D}} }\frac{\partial^{2}q_{D} }{\partial^{2}x}+\frac{\partial q_{D} }{\partial x}\left( \frac{\partial }{\partial x}\left( \frac{\partial x}{\partial r_{D} }\right)\frac{\partial x}{\partial r_{D} }\right) \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,=\frac{{r^{2}_{D}} }{2{t^{2}_{D}} }\frac{\partial^{2}q_{D} }{\partial^{2}x}+\frac{\partial q_{D} }{\partial x}\left( \frac{\frac{\partial }{\partial r_{D} }\left( \frac{\partial x}{\partial r_{D} }\right)}{\frac{\partial x}{\partial r_{D} }}\frac{\partial x}{\partial r_{D} }\right) \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,=\frac{{r^{2}_{D}} }{2{t^{2}_{D}} }\frac{\partial^{2}q_{D} }{\partial^{2}x}+\frac{\partial q_{D} }{\partial x}\left( \frac{\partial }{\partial r_{D} }\left( \frac{\partial x}{\partial r_{D} }\right)\right) \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,=\frac{{r^{2}_{D}} }{2{t^{2}_{D}} }\frac{\partial^{2}q_{D} }{\partial^{2}x}+\frac{\partial q_{D} }{\partial x}\left( \frac{\partial }{\partial r_{D} }\left( \frac{r_{D} }{2t_{D} }\right)\right)\text{} \end{array}} \right. $$

(35)

From the equation set in Eq. 35, we get

$$ \frac{\partial^{2}q_{D} }{\partial {r^{2}_{D}} }\,=\frac{{r^{2}_{D}} }{2{t^{2}_{D}} }\frac{\partial^{2}q_{D} }{\partial^{2}x}+\frac{1}{2t_{D} }\frac{\partial q_{D} }{\partial x} $$

(36)

and

$$ \frac{\partial q_{D} }{\partial r_{D} }\,=\frac{\partial q_{D} }{\partial x}\frac{\partial x}{\partial t_{D} }=-\frac{{r^{2}_{D}} }{4{t^{2}_{D}} }\frac{\partial q_{D} }{\partial x} $$

(37)

Substituting Eqs. 37 and 38 into Eq. 30 yields

$$ \frac{{r^{2}_{D}} }{2{t^{2}_{D}} }\frac{\partial^{2}q_{D} }{\partial^{2}x}+\frac{1}{2t_{D} }\frac{\partial q_{D} }{\partial x}-\frac{1}{r_{D} }\frac{\partial q_{D} }{\partial r_{D} }=-\frac{{r^{2}_{D}} }{4{t^{2}_{D}} }\frac{\partial q_{D} }{\partial x} $$

(38)

Simplifying Eq. 38 yields

$$ \frac{\partial^{2}q_{D} }{\partial^{2}x}+\frac{\partial q_{D} }{\partial x}= 0 $$

(39)

The boundary conditions become

$$ \left\{ {\begin{array}{l} \text{OBC\thinspace 1:\thinspace }q_{D} \text{(}x\to \infty \,\text{,}t_{D} \text{)}\,\text{=}\,\text{0} \\ \\ \text{IBC\thinspace 2:\thinspace }q_{D} \text{(}x\to 0\,\text{,}t_{D} \text{)}\,\text{=}\,1\text{} \end{array}} \right. $$

(40)

The general solution of the homogenous Eq. 40 is

$$ q_{D} =c_{1} +c_{2} \,e^{-x} $$

(41)

Applying the boundary conditions to find c₁ and c₂ yields

$$ \left\{ {\begin{array}{l} 0=c_{1} +c_{2} \,e^{-\infty }\,\to \,c_{1} = 0 \\ 1=c_{2} \,e^{-0}\,\to \,c_{2} = 1\text{\thinspace \thinspace } \end{array}} \right. $$

(42)

and

$$ q_{D} =e^{-x} $$

(43)

Substituting $q_{D} =\frac {q}{q_{w} }$ into Eq. 43 yields

$$ q=q_{w} \,e^{-x} $$

(44)

Substituting $r_{D} =\frac {r}{r_{w} }$ into $\frac {1}{4}\alpha \frac {\left ({r_{w} r_{D} } \right )^{2}}{2}$ and simplifying it yield

$$ x=\frac{1}{4}\alpha \frac{r^{2}}{t} $$

(45)

Substituting Eq. 46 into Eq. 45 yields

$$ q=q_{w} \,e^{-\frac{1}{4}\alpha \frac{r^{2}}{t}} $$

(46)

From the definition of radius of investigation (r_inv)

$$ r=\sqrt {\frac{c\,t}{\alpha }} $$

(47)

By definition, the diffusive time of flight (τ) is

$$ \tau =\sqrt {c\,t} $$

(48)

where c = 4 for radial flow

Substituting Eq. 46 into Eq. 45 yields

$$ r=\frac{\tau }{\sqrt \alpha } $$

(49)

Substituting Eq. 49 into Eq. 47 yields

$$ q=q_{w} \,e^{-\frac{1}{4}\alpha \frac{\frac{\tau^{2}}{\alpha }}{t}} $$

(50)

Simplifying Eq. 51 yields

$$ q=q_{w} \,e^{-\frac{\tau^{2}}{4t}} $$

(51)

Using the following equation:

$$ c_{t} \frac{\partial p}{\partial t}=\frac{\partial q(V_{p} ,t)}{\partial V_{P} } $$

(52)

The approximation of transient flow to a pseudo-steadystate (PSS) flow leads to

$$ \frac{\partial p}{\partial t}\approx \overline {\frac{\partial p}{\partial t}} =-\frac{1}{c_{t} }\frac{q_{\text{well}} (t)}{V_{P} (t)} $$

(53)

Substituting Eq. 53 into Eq. 52 yields

$$ \frac{\partial q(V_{p} ,t)}{\partial V_{P} }=-\frac{q_{\text{well}} (t)}{V_{P} (t)} $$

(54)

From Eq. 54, we get

$$ \frac{\partial q(V_{p} ,t)}{\partial V_{P} (\tau )}=-\frac{q(t)}{V_{P} (t)} $$

(55)

Substituting Eq. 51 into Eq. 55 yields

$$ \frac{\partial q(V_{p} ,t)}{\partial V_{P} (\tau )}=-\frac{q_{w} \,e^{-\frac{\tau^{2}}{4t}}}{V_{P} (t)} $$

(56)

Taking the integral of Eq. 57 yields

$$ q(V_{p} ,t)=-\frac{q_{w} \,}{V_{P} (t)}\int {e^{-\frac{\tau^{2}}{4t}}} \partial V_{P} (\tau ) $$

(57)

Note that V_p(t) is taken outside the integral since q is calculated at a fixed time. Thus, V_p(t) is fixed. From Eq. 57, we get

$$ c_{t} \frac{\partial p}{\partial t}=\frac{\partial q(V_{p} ,t)}{\partial V_{P} (\tau )} $$

(58)

Substituting Eq. 58 into Eq. 56 yields

$$ c_{t} \frac{\partial p}{\partial t}=-\frac{q_{w} \,e^{-\frac{\tau^{2}}{4t}}}{V_{P} (t)} $$

(59)

If we assume a constant rate instead of a pressure drop, Eq. 59 becomes

$$ c_{t} \int {\frac{\partial p}{\partial t}} =-q_{w} \int {\frac{1}{V_{P} (t)}\,e^{-\frac{\tau^{2}}{4t}}} $$

(60)

Solving for the pressure drop and then rearranging, we get

$$ {\Delta} p=\frac{q_{w} }{c_{t} }\int {\frac{\partial t}{V_{P} (t)}\,e^{-\frac{\tau^{2}}{4t}}} $$

(61)

For bottomhole flowing pressure, Eq. 61 can be written as

$$ {\Delta} p_{wf} =\frac{q_{w} }{c_{t} }\int {\frac{\partial t}{V_{P} (t)}\,e^{-\frac{{\tau_{w}^{2}}}{4t}}} $$

(62)

Equation 62 represents the base of our bottomhole flowing pressure calculation, utilizing the drainage radius and volume data obtained from the FMM. This process, beginning with the FMM, can be used to estimate the cumulative oil production.

Appendix 2. Two-dimensional and Gullfaks model

Table 11 The FMM cumulative oil and ranking in well configuration 2 for 16 realizations using solution gas drive

Table 12 The FMM cumulative oil and ranking in well configurations 3 for 16 realizations using solution gas drive

Table 13 The FMM cumulative oil and ranking in well configuration 4 for 16 realizations using solution gas drive

Table 14 The FMM cumulative oil in 10 configurations for 16 realizations

Table 15 The FMM cumulative oil in 10 configurations for 16 realizations