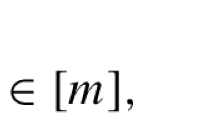A matrix nonconvex relaxation approach to unconstrained binary polynomial programs

Abstract

This paper is concerned with a class of unconstrained binary polynomial programs (UBPPs), which covers the classical binary quadratic program and has a host of applications in many science and engineering fields. We start with the global exact penalty of its DC constrained SDP reformulation, and propose a continuous relaxation approach by seeking a finite number of approximate stationary points for the factorized form of the global exact penalty with increasing penalty parameters. A globally convergent majorization-minimization method with extrapolation is developed to capture such stationary points. Under a mild condition, we show that the rank-one projection of the output for the relaxation approach is an approximate feasible solution of the UBPP and quantify the lower bound of its minus objective value from the optimal value. Numerical comparisons with the SDP relaxation method armed with a special random rounding technique and the DC relaxation approaches armed with the solvers for linear and quadratic SDPs confirm the efficiency of the proposed relaxation approach, which can solve the instance of 20,000 variables in 15 min and yield a lower bound for the optimal value and the known best value with a relative error at most 1.824 and 2.870%, respectively.

Appendices

Appendix A: The proof of Proposition 3

Proof

For the sake of simplicity, in the following arguments, we omit the index l involved in the iterates, the function $\varTheta _{\rho _{l}}$ and the set $\varDelta _{\!\rho _{l}}$.

• (i) From the definition of $V^{k+1}$ and the feasibility of $V^k$ to subproblem (12), we have

  $$\begin{aligned}&\langle \nabla \!{\widetilde{f}}(U^k)\!+\!\rho \varGamma ^{k},V^{k+1}\rangle \!+\!\rho \Vert V^{k+1}\Vert _F^2\!+\!(L_k/2)\Vert V^{k+1}\!-\!U^k\Vert _F^2\nonumber \\&\le \langle \nabla \!{\widetilde{f}}(U^k)\!+\!\rho \varGamma ^{k},V^{k}\rangle \!+\!\rho \Vert V^{k}\Vert _F^2\!+\!(L_k/2)\Vert V^{k}\!-\!U^k\Vert _F^2. \end{aligned}$$

  (26)

  Recall that $\varGamma ^k\in \partial {\widetilde{\psi }}(V^k)\subseteq -\partial (-{\widetilde{\psi }})(V^k)$. From the convexity of $-{\widetilde{\psi }}$ and [42, Theorem 23.5], ${\widetilde{\psi }}(V^{k})-(-{\widetilde{\psi }})^*(-\varGamma ^{k})=\langle \varGamma ^k,V^k\rangle$. By combining the expression of $\varTheta _{\rho }$ with (26) and $V^{k+1}\in {\mathcal {S}}$,

  $$\begin{aligned} \varTheta _{\rho }(V^{k+1},\varGamma ^{k},V^k)&\le {\widetilde{f}}(V^{k+1})+\langle \nabla \!{\widetilde{f}}(U^k),V^{k}-V^{k+1}\rangle +\rho \Vert V^k\Vert _F^2\!+\!\rho {\widetilde{\psi }}(V^k)\nonumber \\&\quad +\frac{\gamma {\underline{L}}}{2}\Vert V^{k+1}\!-\!V^k\Vert _F^2 +\frac{L_k}{2}\Vert V^{k}\!-\!U^k\Vert _F^2-\frac{L_k}{2}\Vert V^{k+1}\!-\!U^k\Vert _F^2,\nonumber \\&\le {\widetilde{f}}(V^k)+\rho \Vert V^k\Vert _F^2\!+\!\rho {\widetilde{\psi }}(V^k) +\frac{\gamma {\underline{L}}}{2}\Vert V^{k+1}\!-\!V^k\Vert _F^2\nonumber \\&\quad +\frac{L_k+L_{\!{\widetilde{f}}}}{2}\Vert V^{k}\!-\!U^k\Vert _F^2 -\frac{L_k\!-\!L_{\!{\widetilde{f}}}}{2}\Vert V^{k+1}\!-\!U^k\Vert _F^2 \end{aligned}$$

  (27)

  where the second inequality is using (11a) with $V=V^{k+1},Z=U^k$ and (11b) with $V=V^{k},Z=U^k$. Notice that ${\widetilde{\psi }}(V^k)-\langle V^k,\varGamma ^{k-1}\rangle \le (-{\widetilde{\psi }})^*(-\varGamma ^{k-1})$. Together with the definition of $\varTheta _{\rho }$ and $U^k=V^k+\beta _k(V^k\!-\!V^{k-1})$, it follows that

  $$\begin{aligned} \varTheta _{\rho }(V^{k+1},\varGamma ^{k},V^k)&\le \varTheta _{\rho }(V^{k},\varGamma ^{k-1},V^{k-1}) +\frac{\gamma {\underline{L}}}{2}\Vert V^{k+1}\!-\!V^k\Vert _F^2+\frac{L_k\!+\!L_{\!{\widetilde{f}}}}{2}\Vert V^{k}\!-\!U^k\Vert _F^2\nonumber \\&\quad -\frac{L_k\!-\!L_{\!{\widetilde{f}}}}{2}\Vert V^{k+1}\!-\!U^k\Vert _F^2 -\frac{\gamma {\underline{L}}}{2}\Vert V^{k}\!-\!V^{k-1}\Vert _F^2\\&\le \varTheta _{\rho }(V^{k},\varGamma ^{k-1},V^{k-1}) -\frac{L_k\!-\!\gamma {\underline{L}}\!-\!L_{\!{\widetilde{f}}}}{2}\Vert V^{k+1}\!-\!V^k\Vert _F^2\\&\quad -\frac{\gamma {\underline{L}}\!-2L_{\!{\widetilde{f}}}\beta _k^2}{2}\Vert V^k\!-\!V^{k-1}\Vert _F^2 +(L_k\!-\!L_{\!{\widetilde{f}}})\beta _k\langle V^{k+1}\!-\!V^k,V^{k}\!-\!V^{k-1}\rangle . \end{aligned}$$

  Since $|2(L_k\!-\!L_{\!{\widetilde{f}}})\beta _k\langle V^{k+1}\!-\!V^k,V^k\!-\!V^{k-1}\rangle | \le \mu (L_k\!-\!L_{\!{\widetilde{f}}})^2\Vert V^{k+1}\!-\!V^k\Vert _F^2+\frac{\beta _k^2}{\mu }\Vert V^k\!-\!V^{k-1}\Vert _F^2$ for any $\mu >0$, the following inequality holds for any $\mu >0$:

  $$\begin{aligned} \varTheta _{\rho }(V^{k+1},\varGamma ^{k},V^k)&\le \varTheta _{\rho }(V^{k},\varGamma ^{k-1},V^{k-1}) -\Big [\frac{\gamma {\underline{L}}-2L_{\!{\widetilde{f}}}\beta _k^2}{2}-\frac{\beta _k^2}{2\mu }\Big ]\Vert V^k\!-\!V^{k-1}\Vert _F^2\\&\quad -\Big [\frac{L_k\!-\!\gamma {\underline{L}}\!-\!L_{\!{\widetilde{f}}}}{2} -\frac{(L_k\!-\!L_{\!{\widetilde{f}}})^2\mu }{2}\Big ]\Vert V^{k+1}\!-\!V^k\Vert _F^2. \end{aligned}$$

  By taking $\mu =\frac{L_k-\gamma {\underline{L}}\!-\!L_{\!{\widetilde{f}}}}{(L_k-L_{\!{\widetilde{f}}})^2}$, the desired result follows from the last inequality.

• (ii)–(iii) By part (i), the sequence $\{\varTheta _{\rho }(V^{k},\varGamma ^{k-1},V^{k-1})\}$ is nonincreasing. Note that $\varTheta _{\rho }$ is proper lsc and level-bounded by the expression of $\varTheta _{\rho }$ and [43, Proposition 11.21]. Hence, $\varTheta _{\rho }$ is bounded below by [43, Theorem 1.9]. This means that the sequence $\{(V^k,\varGamma ^k)\}$ is bounded, and the limit $\varpi ^*{:}{=}{\displaystyle \lim\nolimits_{k\rightarrow \infty }}\varTheta _{\rho }(V^k,\varGamma ^{k},V^{k-1})$ exists. Hence, part (ii) follows. We next argue that part (iii) holds. From $\nu _k=\frac{(\gamma {\underline{L}}-2L_{\!{\widetilde{f}}}{\overline{\beta }}^2)(L_0-L_{\!{\widetilde{f}}} -\gamma {\underline{L}})-(L_0-L_{\!{\widetilde{f}}})^2{\overline{\beta }}^2}{L_0-L_{\!{\widetilde{f}}}-\gamma {\underline{L}}}>0$ and part (i), $\lim _{k\rightarrow \infty }\Vert V^k\!-\!V^{k-1}\Vert _F=0$. To show that $\varTheta _{\rho }\equiv \varpi ^*$ on the set $\varDelta _{\rho }$, we pick any $({\widehat{V}},{\widehat{\varGamma }},{\widehat{U}})\in \varDelta _{\rho }$. By part (ii), there exists ${\mathcal {K}}\subseteq {\mathbb {N}}$ such that $\lim _{{\mathcal {K}}\ni k\rightarrow \infty }(V^{k},\varGamma ^{k-1},V^{k-1})=({\widehat{V}},{\widehat{\varGamma }},{\widehat{U}})$. From the expression of $\varTheta _{\rho }(V^{k},\varGamma ^{k-1},V^{k-1})$,

  $$\begin{aligned} \varpi ^*&=\lim _{{\mathcal {K}}\ni k\rightarrow \infty }\big [{\widetilde{f}}(V^{k})+\rho \langle \varGamma ^{k-1},V^{k}\rangle +\rho \Vert V^{k}\Vert _F^2 +\rho (-{\widetilde{\psi }})^*(-\varGamma ^{k-1})\big ]\\&={\widetilde{f}}({\widehat{V}})+\rho \langle {\widehat{\varGamma }},{\widehat{V}}\rangle +\rho \Vert {\widehat{V}}\Vert _F^2 +\rho (-{\widetilde{\psi }})^*(-{\widehat{\varGamma }})=\varTheta _{\rho }({\widehat{V}},{\widehat{\varGamma }},{\widehat{V}}) =\varTheta _{\rho }({\widehat{V}},{\widehat{\varGamma }},{\widehat{U}}), \end{aligned}$$

  where the second equality is using the continuity of $(-{\widetilde{\psi }})^*$ by noting that $(-{\widetilde{\psi }})^*(U)=\frac{1}{4}\Vert U\Vert _{*}^2$ is implied by [43, Proposition 11.21], the third one is using ${\widehat{V}}\in {\mathcal {S}}$ implied by $\{V^{k}\}_{k\in {\mathcal {K}}}\subseteq {\mathcal {S}}$, and the last one is using ${\widehat{V}}={\widehat{U}}$ implied by $\lim _{{\mathcal {K}}\ni k\rightarrow \infty }\Vert V^{k}\!-\!V^{k-1}\Vert _F=0$.

• (iv) By invoking [43, Exercise 8.8], for any $(V,\varGamma ,U)\!\in \!{\mathcal {S}}\times {\mathbb {R}}^{m\times p}\times {\mathbb {R}}^{m\times p}$, it holds that

  $$\begin{aligned} \partial \varTheta _{\rho }(V,\varGamma ,U) =\left[ \begin{matrix} \nabla \!{\widetilde{f}}(V)\!+\!2\rho V+\rho \varGamma +\gamma {\underline{L}}(V\!-\!U)+{\mathcal {N}}_{{\mathcal {S}}}(V)\\ \rho V-\rho \partial (-{\widetilde{\psi }})^*(-\varGamma )\\ \gamma {\underline{L}}(U\!-\!V) \end{matrix}\right] . \end{aligned}$$

  (28)

  From the definition of $V^{k}$, we have $0\in \nabla \!{\widetilde{f}}(U^{k-1})\!+\!\rho \varGamma ^{k-1}+2\rho V^k+L_{k-1}(V^{k}\!-\!U^{k-1}) +{\mathcal {N}}_{{\mathcal {S}}}(V^{k}).$ Since $\varGamma ^{k-1}\in \partial {\widetilde{\psi }}(V^{k-1})\subseteq -\partial (-{\widetilde{\psi }})(V^{k-1})$, from [42, Theorem 23.5] it follows that $V^{k-1}\!\in \partial (-{\widetilde{\psi }})^*(-\varGamma ^{k-1})$. By combining with the last equality, we immediately obtain that

  $$\begin{aligned} \left[ \begin{matrix} \nabla \!{\widetilde{f}}(V^{k})-\!\nabla \!{\widetilde{f}}(U^{k-1}) -\!L_{k-1}(V^{k}\!-\!U^{k-1})+\gamma {\underline{L}}(V^k\!-\!V^{k-1})\\ \rho (V^k\!-\!V^{k-1})\\ \gamma {\underline{L}}(V^{k-1}\!-\!V^k) \end{matrix}\right] \!\in \partial \varTheta _{\rho }(V^k,\varGamma ^{k-1},V^{k-1}). \end{aligned}$$

This along with $U^{k-1}=V^{k-1}+\beta _{k-1}(V^{k-1}\!-\!V^{k-2})$ implies the desired result. $\square$

Appendix B: Theoretical analysis of Algorithm 2

In this part, we provide the theoretical analysis of Algorithm 2. First of all, we establish the convergence of Algorithm B. Algorithm B is similar to the proximal DC algorithm proposed in [26], but the conclusion of [26, Theorem 3.1] can not be directly applied to it since the convexity of f is not required here. To achieve its convergence, we define the potential function

$$\begin{aligned}{} & {} \varXi _{\!\rho _{l}}(X,W,Z)\!{:}{=}f(X)+\!\rho _{l}\langle I+W,X\rangle +\delta _{\varOmega }(X)\\{} & {} \quad +\!\rho _{l}\delta _{{\mathbb {B}}}(-W)+\frac{L_{\!f}}{2}\Vert X\!-\!Z\Vert _F^2 \end{aligned}$$

where ${\mathbb {B}}{:}{=}\{Z\in {\mathbb {S}}^p\ |\ \Vert Z\Vert _*\le 1\}$ is the nuclear norm unit ball, and need the following proposition.

Proposition 5

Fix an $l\in {\mathbb {N}}$. Let $\{(X^{l,k},W^{l,k})\}$ be given by Algorithm B from $X^{l,0}=X^{l}$. Then,

• (i) for each k, $\varXi _{\!\rho _{l}}(X^{l,k+1},W^{l,k},X^{l,k}) \!\le \!\varXi _{\!\rho _{l}}(X^{l,k},W^{l,k-1},X^{l,k-1}) \!-\frac{L_{\!f}-(L_{l,k}+L_{\!f})\beta _{l,k}^2}{2} \Vert X^{l,k}\!-\!X^{l,k-1}\Vert _F^2;$

• (ii) the sequence $\{(X^{l,k},W^{l,k})\}$ is bounded, and the cluster point set of $\{(X^{l,k},W^{l,k-1},X^{l,k-1})\}$, denoted by $\varUpsilon _{\!\rho _{l}}$, is nonempty and compact;

• (iii) the limit $\omega ^*\!{:}{=}\lim _{k\rightarrow \infty }\varXi _{\!\rho _{l}}(X^{l,k},W^{l,k-1},X^{l,k-1})$ exists whenever ${\overline{\beta }}<\!\sqrt{\frac{L_f}{L_{l,0}+L_f}}$, and moreover, $\varXi _{\!\rho _{l}}(X',W',Z')=\omega ^*$ for every $(X',W',Z')\in \varUpsilon _{\!\rho _{l}}$;

• (iv) for each $k\in {\mathbb {N}}$, with $\eta _{l}=\sqrt{9L_{\!f}^2\!+\!4L_{l,0}^2\!+\!\rho _{l}^2}$ it holds that

  $$\begin{aligned} \textrm{dist}(0,\partial \varXi _{\!\rho _{l}}(X^{l,k},W^{l,k-1},X^{l,k-1})) \!\le \!\eta _{l}\big [\Vert X^{l,k}\!-\!X^{l,k-1}\Vert _F +\Vert X^{l,k-1}\!-\!X^{l,k-2}\Vert _F\big ]. \end{aligned}$$

Proof

The proof is similar to that of Proposition 3, and we include it for completeness. From the Lipschitz continuity of $\nabla \!f$ on ${\mathbb {B}}_{\varOmega }$, a compact set containing $(1\!+\!\tau )\varOmega -\tau \varOmega$ for all $\tau \in [0,1]$, for every $X\!\in {\mathbb {B}}_{\varOmega }$,

$$\begin{aligned} f(X)\le f(Y)+\langle \nabla \!f(Y),X\!-\!Y\rangle +(L_{\!f}/2)\Vert X\!-\!Y\Vert _F^2; \end{aligned}$$

(29a)

$$\begin{aligned} -f(X)\le -f(Y)-\langle \nabla \!f(Y),X\!-\!Y\rangle +(L_{\!f}/2)\Vert X\!-\!Y\Vert _F^2, \end{aligned}$$

(29b)

where $L_{\!f}$ is the Lipschitz constant of $\nabla \!f$ in ${\mathbb {B}}_{\varOmega }$. For the sake of simplicity, in the following arguments, we omit the index l involved in the iterates, the function $\varXi _{\!\rho _{l}}$ and the set $\varUpsilon _{\!\rho _{l}}$.

(i) By the definition of $X^{k+1}$, the strong convexity of the objective function of (23), and the feasibility of $X^{k}$ to subproblem (23), it follows that

$$\begin{aligned}&\langle \nabla \!f(Y^k)\!+\!\rho (I\!+\!W^{k}),X^{k+1}\rangle +({L_k}/{2})\Vert X^{k+1}\!-\!Y^{k}\Vert _F^2\nonumber \\&\le \langle \nabla \!f(Y^k)\!+\!\rho (I\!+\!W^{k}),X^{k}\rangle +({L_k}/{2})\Vert X^{k}\!-\!Y^{k}\Vert _F^2 -({L_k}/{2})\Vert X^{k+1}\!-\!X^k\Vert _F^2, \end{aligned}$$

which, after a suitable rearrangement, can be equivalently written as

$$\begin{aligned} \rho \langle I\!+\!W^{k},X^{k+1}\rangle&\le \langle \nabla \!f(Y^k),X^k\!-\!X^{k+1}\rangle +\rho \langle I\!+\!W^{k},X^{k}\rangle +0.5L_k\Vert X^{k}\!-\!Y^{k}\Vert _F^2\nonumber \\&\quad -0.5L_k\Vert X^{k+1}\!-\!X^k\Vert _F^2-0.5L_k\Vert X^{k+1}\!-\!Y^{k}\Vert _F^2. \end{aligned}$$

(30)

Since $W^{k}\in \partial \psi (X^{k})\subseteq -\partial (-\psi )(X^{k})$ and the spectral function is the support of ${\mathbb {B}}$, the unit ball in ${\mathbb {S}}^p$, we have $-W^{k}\in {\mathbb {B}}$ and $-\langle W^k,X^k\rangle =\Vert X^k\Vert \ge -\langle W^{k-1},X^k\rangle$ by [42, Corollary 23.5.3]. Thus, for each k, $\delta _{{\mathbb {B}}}(W^k)=0$ and $\langle I\!+\!W^{k},X^k\rangle \le \langle I\!+\!W^{k-1},X^k\rangle$. Along with the definition of $\varXi _{\rho }$ and (30),

$$\begin{aligned} \varXi _{\rho }(X^{k+1},W^{k},X^{k})&\le f(X^{k+1})+\langle \nabla \!f(Y^k),X^k\!-\!X^{k+1}\rangle +\rho \langle I\!+\!W^{k-1},X^k\rangle \nonumber \\&\quad +\frac{L_k}{2}\Vert X^{k}\!-\!Y^{k}\Vert _F^2-\frac{L_k}{2}\Vert X^{k+1}\!-\!Y^{k}\Vert _F^2 -\frac{L_k\!-\!L_{\!f}}{2}\Vert X^{k+1}\!-\!X^{k}\Vert _F^2,\nonumber \\&\le f(X^k)+\rho \langle I\!+\!W^{k-1},X^k\rangle +\frac{L_k\!+L_{\!f}}{2}\Vert X^{k}\!-\!Y^{k}\Vert _F^2\\&\quad -\frac{L_{k}\!-\!L_{\!f}}{2}\Vert X^{k+1}\!-\!Y^{k}\Vert _F^2 -\frac{L_k-L_{\!f}}{2}\Vert X^{k+1}\!-\!X^{k}\Vert _F^2,\nonumber \end{aligned}$$

(31)

where the second inequality is obtained by using (29) with $X=X^{k+1},Y=Y^k$, and (29b) with $X=X^{k},Y=Y^k$. Substituting $Y^k=X^k+\beta _k(X^k\!-\!X^{k-1})$ into (31) and using $L_k\ge L_f$ yields

$$\begin{aligned} \varXi _{\rho }(X^{k+1},W^{k},X^{k})&\le \varXi _{\rho }(X^{k},W^{k-1},X^{k-1}) -\frac{L_{\!f}\!-\!(L_k+L_{\!f})\beta _k^2}{2}\Vert X^k\!-\!X^{k-1}\Vert _F^2\\&\quad -\frac{L_{k}\!-\!L_{\!f}}{2}\Vert X^{k+1}\!-\!Y^{k}\Vert _F^2 -\frac{L_k-L_{\!f}}{2}\Vert X^{k+1}\!-\!X^{k}\Vert _F^2\\&\le \varXi _{\rho }(X^{k},W^{k-1},X^{k-1}) -\frac{L_{\!f}\!-\!(L_k+L_{\!f})\beta _k^2}{2}\Vert X^k\!-\!X^{k-1}\Vert _F^2. \end{aligned}$$

(ii)-(iii) Part (ii) is immediate by noting that $\{X^k\}\subseteq \varOmega$ and $\{W^k\}\subseteq {\mathbb {B}}$. It suffices to prove part (iii). By part (i), the sequence $\{\varXi _{\rho }(X^{k},W^{k-1},X^{k-1})\}$ is nonincreasing. Note that $\varXi _{\rho }$ is proper lsc and level-bounded. By [43, Theorem 1.9], it is bounded below. Hence, the limit $\omega ^*$ is well defined. By part (i) and $L_{\!f}\!-\!(L_k+L_{\!f})\beta _k^2\ge L_{\!f}\!-\!(L_0+L_{\!f}){\overline{\beta }}^2>0$, we have $\lim _{k\rightarrow \infty }\Vert X^k\!-\!X^{k-1}\Vert _F=0$. Next we show that $\varXi _{\rho }\equiv \omega ^*$ on the set $\varUpsilon _{\!\rho }$. Pick any $({\widehat{X}},{\widehat{W}},{\widehat{Z}})\in \varUpsilon _{\!\rho }$. By part (ii), there exists an index set ${\mathcal {K}}\subseteq {\mathbb {N}}$ such that ${\displaystyle \lim _{{\mathcal {K}}\ni k\rightarrow \infty }}(X^{k},W^{k-1},X^{k-1})=({\widehat{X}},{\widehat{W}},{\widehat{Z}}).$ From the expression of $\varXi _{\rho }$,

$$\begin{aligned} \omega ^*&=\lim _{{\mathcal {K}}\ni k\rightarrow \infty }\varXi _{\rho }(X^{k},W^{k-1},X^{k-1}) =\lim _{{\mathcal {K}}\ni k\rightarrow \infty }\big [f(X^{k})+\rho \langle (I\!+\!W^{k-1}),X^{k}\rangle \big ]\\&= f({\widehat{X}})+\rho \langle I+{\widehat{W}},{\widehat{X}}\rangle =\varXi _{\rho }({\widehat{X}},{\widehat{W}},{\widehat{X}}) =\varXi _{\rho }({\widehat{X}},{\widehat{W}},{\widehat{Z}}), \end{aligned}$$

where the second equality is since $\Vert X^k\!-\!X^{k-1}\Vert _F\rightarrow 0$ and $\{(X^k,W^k)\}\subseteq \varOmega \times {\mathbb {B}}$, and the last one is due to ${\widehat{X}}={\widehat{Z}}$, implied by $\lim _{{\mathcal {K}}\ni k\rightarrow \infty }(X^{k},X^{k-1})=({\widehat{X}},{\widehat{Z}})$.

(iv) By the optimality condition of (23), $0\in \!\nabla \!f(Y^{k-1})+\rho (I+\!W^{k-1})+L_{k-1}(X^k-Y^{k-1}) +{\mathcal {N}}_{\varOmega }(X^k)$. Recall that $W^{k-1}\in \partial \psi (X^{k-1})\subseteq -\partial (-\psi )(X^{k-1})$ and the conjugate of the spectral function is $\delta _{{\mathbb {B}}}$. By [42, Theorem 23.5], we have $X^{k-1}\in \partial \delta _{{\mathbb {B}}}(-W^{k-1}) ={\mathcal {N}}_{{\mathbb {B}}}(-W^{k-1})$. Together with the expression of $\varXi _{\rho }$, it is not hard to obtain that

$$\begin{aligned} \!\left[ \begin{matrix} \nabla \!f(X^{k})\!-\!\nabla \!f(Y^{k-1})\!+\!L_{\!f}(X^k\!-\!X^{k-1})\!-\!L_{k-1}(X^{k}\!-\!Y^{k-1})\\ \rho (X^k\!-\!X^{k-1})\\ L_{\!f}(X^{k-1}\!-\!X^k) \end{matrix}\right] \!\in \partial \varXi _{\rho }(X^k,W^{k-1},X^{k-1}), \end{aligned}$$

which implies that the desired inequality holds. The proof is then completed. $\square$

Remark 6

(a) When f is convex, the coefficient $L_{\!f}$ appearing in (31) can be removed, and the restriction on ${\overline{\beta }}$ in part (iii) can be improved as ${\overline{\beta }}<\!\sqrt{{L_{\!f}}/{L_{l,0}}}$. This coincides with the requirement of [26, Proposition 3.1] for the convex f.

(b) Let $({\widehat{X}},{\widehat{W}})$ be a cluster point of $\{(X^{l,k},W^{l,k})\}$. By the outer semicontinuity of ${\mathcal {N}}_{\varOmega }$ and $\partial \psi$, ${\widehat{W}}\in \partial \psi ({\widehat{X}})$ and $0\in \nabla \!f({\widehat{X}})\!+\rho _{l}(I+{\widehat{W}}) +{\mathcal {N}}_{\varOmega }({\widehat{X}})$, which by the expression of $\partial \varXi _{\!\rho _{l}}$ and Definition 2 means that $\varPi _1(\varUpsilon _{\!\rho _{l}})\subseteq \varPi _1(\textrm{crit}\,\varXi _{\!\rho _{l}})\subseteq {\widehat{\varOmega }}_{\!\rho _{l}}$. Here $\varPi _1(\varUpsilon _{\!\rho _{l}})=\{Z\in {\mathbb {S}}^p\,|\,\exists W\ \mathrm{s.t.}\ (Z,W,Z)\in \varUpsilon _{\!\rho _{l}}\}$.

By [2, Sect. 4.3], the indicator functions $\delta _{\varOmega }$ and $\delta _{{\mathbb {B}}}$ are semialgebraic, which implies that $\varXi _{\!\rho _{l}}$ is a KL function (see [2] for the detail). By using Proposition 5 and the same arguments as those for [26, Theorem 3.1] (see also [2, Theorem 3.1]), we obtain the following conclusion.

Theorem 3

Let $\{(X^{l,k},W^{l,k})\}$ be generated by Algorithm B with $X^{l,0}=X^{l}$ and ${\overline{\beta }}<\!\sqrt{\frac{L_{\!f}}{L_{l,0}+L_{\!f}}}$ for solving (4) associated to $\rho _l$. Then, the sequence $\{X^{l,k}\}$ is convergent, and its limit is a critical point of (4) associated to $\rho _l$. If this limit is rank-one, it is also a local minimizer of (3).

Next we focus on the stopping criterion of Algorithm 2 that aims to seek an approximate feasible point of (3). When this criterion occurs at some $l<l_\textrm{max}$, we say that Algorithm 2 exits normally. The following proposition states that under a certain condition it can exit normally.

Proposition 6

Fix an $l\in {\mathbb {N}}$. Let $\{X^{l,k}\}$ be the sequence generated by Algorithm B from $X^{l_0}=X^{l}\in \varOmega$ satisfying $\langle I,X^l\rangle -\!\Vert X^l\Vert \le c_0$ for some $c_0\in (0,1)$. Let $\varepsilon \in \!(0,c_0]$ be a given tolerance and write ${\widehat{\rho }}{:}{=}\max \big \{\frac{2\varpi }{(1-\sqrt{1-0.5\varepsilon /p})\sqrt{1-c_0}},\frac{2\varpi }{\varepsilon }\big \}$ for $\varpi \!=6.5(L_{\!f}\!+\!L_{l,0})p^2\!+\!2p\Vert \nabla \!f(I)\Vert _F$. Then,

• (i) when $\rho _{l}\ge {\widehat{\rho }}$, for each $k\in {\mathbb {N}}$ with ${\varepsilon }/{2}\le \langle I,X^{l,k}\rangle -\Vert X^{l,k}\Vert \le c_0$,

  $$\begin{aligned} \Vert X^{l,k+1}\Vert \ge \Vert X^{l,k}\Vert +0.5(1-\!\sqrt{1-0.5p^{-1}\varepsilon })\sqrt{1-c_0}. \end{aligned}$$

  (32)

• (ii) There exists $1\le {\overline{k}}\le \big \lceil \frac{2(c_0-\varepsilon )}{(1-\sqrt{1-0.5p^{-1}\varepsilon })\sqrt{1-c_0}}\big \rceil +1$ such that $\langle I,X^{l,k}\rangle -\Vert X^{l,k}\Vert \le \varepsilon$ for all $k\ge {\overline{k}}$.

Proof

(i) Fix any $k\in {\mathbb {N}}$. From the definition of $X^{l,k+1}$, for any $X\in \varOmega$ it holds that

$$\begin{aligned} \rho _l\langle W^{l,k},X^{l,k+1}\!-\!X\rangle&\le \langle \nabla \!f(Y^{l,k}),X\!-\!X^{l,k+1}\rangle +\frac{L_{l,k}}{2}\Vert X\!-\!Y^{l,k}\Vert _F^2\!-\!\frac{L_{l,k}}{2}\Vert X^{l,k+1}\!-\!Y^{l,k}\Vert _F^2\nonumber \\&\le \langle \nabla \!f(Y^{l,k}),X\!-\!X^{l,k+1}\rangle +\frac{L_{l,k}}{2}\big [\Vert X\Vert _F^2+2\Vert X^{l,k+1}\!-X\Vert _F\Vert Y^{l,k}\Vert _F\big ]\nonumber \\&\le \langle \nabla \!f(Y^{l,k})\!-\!\nabla \!f(I)\! +\!\nabla \!f(I),X\!-\!X^{l,k+1}\rangle +6.5L_{l,0}p^2\nonumber \\&\le (L_{\!f}\Vert Y^{l,k}\!-\!I\Vert _F\!+\!\Vert \nabla \!f(I)\Vert _F)\Vert X\!-\!X^{l,k+1}\Vert _F\!+\!6.5L_{l,0}p^2\nonumber \\&\le 2p(3L_{\!f}p+\Vert \nabla f(I)\Vert _F)\!+\!6.5L_{l,0}p^2\le \varpi \end{aligned}$$

(33)

where the third inequality is by $L_{l,k}\le L_{l,0}$ for all $k\in {\mathbb {N}}$ and $\Vert X\Vert _F\le p$ for $X\in \varOmega$. Then,

$$\begin{aligned} -\langle W^{l,k},X\rangle \le \frac{\varpi }{\rho _l}-\langle W^{l,k},X^{l,k+1}\rangle \le \frac{\varpi }{\rho _l}+\Vert W^{l,k}\Vert _*\Vert X^{l,k+1}\Vert =\frac{\varpi }{\rho _l}+\Vert X^{l,k+1}\Vert . \end{aligned}$$

(34)

Let $X^{l,k}$ have the eigenvalue decomposition $U\textrm{Diag}(\lambda (X^{l,k}))U^{\top }$ with $U\!=[u_1 \cdots u_p]\in {\mathbb {O}}^p$. Since $\langle I,X^{l,k}\rangle -\Vert X^{l,k}\Vert \le c_0<1$ and $\textrm{diag}(X^{l,k})=e$, for every $j\in [p]$ it holds that

$$\begin{aligned} \lambda _1(X^{l,k})u_{j1}^2=1-{\textstyle \sum _{i=2}^p}\lambda _i(X^{l,k})u_{ji}^2 \ge 1-{\textstyle \sum _{i=2}^p}\lambda _i(X^{l,k})\ge 1-c_0>0 \end{aligned}$$

(35)

where $u_{ji}$ is the jth component of $u_i$. Take ${\widehat{X}}\!=\!\lambda _1(X^{l,k}){\widehat{u}}_1{\widehat{u}}_1^{\top }$ with ${\widehat{u}}_{j1}\!=\!\frac{u_{j1}}{\sqrt{\Vert X^{l,k}\Vert u_{j1}^2}}$ for each $j\in [p]$. Then, ${\widehat{X}}\in \varOmega$. Now using (34) with $X={\widehat{X}}$ and recalling that $W^{l,k}=-u_1u_1^{\top }$, we obtain

$$\begin{aligned}&\rho _l^{-1}\varpi +\Vert X^{l,k+1}\Vert \ge \langle -W^{l,k},{\widehat{X}}\rangle =\Vert X^{l,k}\Vert (u_1^{\top }{\widehat{u}}_1)^2 =\Big (\sqrt{u_{11}^2}+\cdots +\sqrt{u_{p1}^2}\Big )^2\nonumber \\&\quad =\Vert X^{l,k}\Vert +\!\Big [\sqrt{u_{11}^2}+\cdots +\sqrt{u_{p1}^2}-\!\sqrt{\Vert X^{l,k}\Vert }\Big ] \Big [\sqrt{u_{11}^2}+\cdots +\sqrt{u_{p1}^2}+\!\sqrt{\Vert X^{l,k}\Vert }\Big ]\nonumber \\&\quad \ge \Vert X^{l,k}\Vert +\Big [\sqrt{u_{11}^2}+\cdots +\sqrt{u_{p1}^2}-\!\sqrt{\Vert X^k\Vert }\Big ]\sqrt{\Vert X^{l,k}\Vert }\nonumber \\&\quad =\Vert X^{l,k}\Vert +\!\Big [\sqrt{u_{11}^2}+\cdots +\sqrt{u_{p1}^2}-\sqrt{\Vert X^{l,k}\Vert }(u_{11}^2+\cdots +u_{p1}^2)\Big ]\sqrt{\Vert X^{l,k}\Vert }, \end{aligned}$$

(36)

where the second inequality is using $\sqrt{u_{11}^2}+\cdots +\sqrt{u_{p1}^2}\ge \!\sqrt{\Vert X^{l,k}\Vert }$ implied by (35), and the last equality is by $\sum _{j=1}^pu_{j1}^2=1$. Since $\Vert u_1\Vert =1$, there exists ${\widehat{j}}\in [p]$ such that $u_{{\widehat{j}}1}^2\le \frac{1}{p}$. Note that $1-\sqrt{\Vert X^{l,k}\Vert u_{j1}^2}\ge 0$ for all $j\in [p]$. From (36), it then follows that

$$\begin{aligned} \rho _l^{-1}\varpi +\Vert X^{l,k+1}\Vert&\ge \Vert X^{l,k}\Vert +\Big [\sqrt{u_{{\widehat{j}}1}^2}-\! \sqrt{\Vert X^{l,k}\Vert }u_{{\widehat{j}}1}^2\Big ]\sqrt{\Vert X^{l,k}\Vert }\\&=\Vert X^{l,k}\Vert +\big (1-\!\sqrt{\Vert X^{l,k}\Vert u_{{\widehat{j}}1}^2}\big )\sqrt{\Vert X^{l,k}\Vert u_{{\widehat{j}}1}^2}\\&\ge \Vert X^{l,k}\Vert +\big (1-\!\sqrt{\Vert X^{l,k}\Vert /p}\big )\sqrt{\Vert X^{l,k}\Vert u_{{\widehat{j}}1}^2}\\&\ge \Vert X^{l,k}\Vert +(1\!-\!\sqrt{1-0.5p^{-1}\varepsilon })\sqrt{1-c_0} \end{aligned}$$

where the second inequality is due to $u_{{\widehat{j}}1}^2\le \frac{1}{p}$, and the last one is using $p-\Vert X^{l,k}\Vert \ge \frac{\varepsilon }{2}$ and (35). Together with $\rho _l\ge \frac{2\varpi }{(1-\sqrt{1-0.5p^{-1}\varepsilon })\sqrt{1-c_0}}$, we get the desired result.

(ii) Since the proof is similar to that of Proposition 4 (ii), we here omit it. $\square$

Now we can not provide a mild condition as in Lemma 2 to ensure that some $X^l\in \varOmega$ with $\langle I,X^l\rangle \!-\!\Vert X^l\Vert \le \!c_0$ occurs, and then Algorithm 2 exists normally. We leave it for a future topic.

To close this part, we show that the rank-one projection of a normal output of B, i.e. $X^{l}$ for some $l<l_\textrm{max}$, is an approximately feasible solution of (1), and provide a lower estimation for the difference between its minus objective value and the optimal value of (1).

Theorem 4

Let $X^{l_{\!f}}$ be a normal output of Algorithm 2, for which subproblem (21) is solved by Algorithm B with $X^{l,0}=X^{l}$ and $\beta _{l,k}\equiv 0$. Let $x^{l_{\!f}}=\Vert X^{l_{\!f}}\Vert ^{1/2}P_1$ with $P\in \!{\mathbb {O}}(X^{l_{\!f}})$. Then, for each $l^*\in \{0,1,\ldots ,l_{\!f}\!-\!1\}$, it holds that

$$\begin{aligned} \!f(x^{l_{\!f}}(x^{l_{\!f}})^{\top })\!-\!f(X^{l^*})&\le \rho _{l_{\!f}}\Vert X^{l_{\!f}}\Vert -\frac{\rho _{l^*}p}{r^*}\\&\quad +\!\sum _{j=l^*}^{l_{\!f}-1}(\rho _{j}\!-\!\rho _{j+1})\Vert X^{j+1}\Vert ^2 \!+\!\alpha _{\!f}\epsilon \ \textrm{and}\ \Vert x^{l_{\!f}}\circ x^{l_{\!f}}\!-e\Vert \le \epsilon \end{aligned}$$

where $r^*\!=\textrm{rank}(X^{l^*})$. Consequently, when $f(X^{l^*})\le -\upsilon ^*$, where $\upsilon ^*$ is the optimal value of (1),

$$\begin{aligned} -f(x^{l_{\!f}}(x^{l_{\!f}})^{\top })-\upsilon ^* \ge -\rho _{l_{\!f}}\Vert X^{l_{\!f}}\Vert +\rho _{l^*}p/r^*-{\textstyle \sum _{j=l^*}^{l_{\!f}-1}}(\rho _{j}-\rho _{j+1})\Vert X^{j+1}\Vert -\alpha _{\!f}\epsilon . \end{aligned}$$

Proof

Fix any $l\in \{0,1,\ldots ,l_{\!f}\}$. For each $k\in {\mathbb {N}}$, from $\beta _{l,k}\equiv 0$ and (30), it follows that

$$\begin{aligned} \langle \nabla f(X^{l,k})+\rho _l(I+W^{l,k}),X^{l,k+1}\!-\!X^{l,k}\rangle +L_{l,k}\Vert X^{l,k+1}\!-\!X^{l,k}\Vert _F^2\le 0. \end{aligned}$$

Note that $f(X^{l,k+1})\le f(X^{l,k})+\langle \nabla \!f(X^{l,k}),X^{l,k+1}\!-\!X^{l,k}\rangle +\frac{L_f}{2}\Vert X^{l,k+1}\!-\!X^{l,k}\Vert _F^2$ by using (29) with $X=X^{l,k+1},Y=X^{l,k}$. Together with the last inequality, it follows that

$$\begin{aligned} f(X^{l,k+1})-f(X^{l,k})+\rho _l\langle (I+W^{l,k}),X^{l,k+1}\!-\!X^{l,k}\rangle \le \frac{L_{\!f}-2L_{l,k}}{2}\Vert X^{l,k+1}\!-\!X^{l,k}\Vert _F^2. \end{aligned}$$

Since $W^{l,k}\in \partial \psi (X^{l,k})$, by the concavity of $\psi$, $-\Vert X^{l,k+1}\Vert +\Vert X^{l,k}\Vert \le \langle W^{l,k},X^{l,k+1}\!-\!X^{l,k}\rangle .$ Together with $\langle I,X^{l,k+1}\rangle =\langle I,X^{l,k}\rangle =p$ by $X^{l,k+1},X^{l,k}\in \varOmega$, and $L_{l,k}\ge L_{\!f}$, we obtain $f(X^{l,k+1})\!-\!\rho _l\Vert X^{l,k+1}\Vert \le f(X^{l,k})-\rho _l\Vert X^{l,k}\Vert .$ From this recursion formula, it follows that

$$\begin{aligned} f(X^{l,k+1})+\rho _l\Vert X^{l,k+1}\Vert \le \cdots \le f(X^{l,0})-\rho _l\Vert X^{l,0}\Vert =f(X^{l})-\rho _{l}\Vert X^{l}\Vert . \end{aligned}$$

Since $X^{l+1}$ must come from the iterate sequence $\{X^{l,k}\}_{k\in {\mathbb {N}}}$, for each $l\in \{0,1,\ldots ,l_{\!f}\}$,

$$\begin{aligned} f(X^{l+1})-\rho _l\Vert X^{l+1}\Vert \le f(X^{l})-\rho _{l}\Vert X^{l}\Vert . \end{aligned}$$

(37)

Note that $\varOmega \ni X^{l_{\!f}}=\sum _{i=1}^p\lambda _i(X^{l_{\!f}})P_iP_i^{\top }$ where $P_i$ denotes the ith column of P. By the Lipschitz continuity of f relative to $\varOmega$ with modulus $\alpha _{\!f}$, it follows that

$$\begin{aligned} f(X^{l_{\!f}})&=f\big ({\textstyle \sum _{i=1}^p}\lambda _i(X^{l_{\!f}})P_iP_i^{\top }\big ) =f\big (\lambda _1(X^{l_{\!f}})P_1P_1^{\top }+{\textstyle \sum _{i=2}^p}\lambda _i(X^{l_{\!f}})P_iP_i^{\top }\big ) \nonumber \\&\ge f(x^{l_{\!f}}(x^{l_{\!f}})^{\top })- \alpha _{\!f}\Vert {\textstyle \sum _{i=2}^p}\lambda _i(X^{l_{\!f}})P_iP_i^{\top }\Vert _F \ge f(x^{l_{\!f}}(x^{l_{\!f}})^{\top })-\alpha _{\!f}\epsilon . \end{aligned}$$

(38)

In addition, adding $(\rho _{l}-\rho _{l+1})\Vert X^{l+1}\Vert$ to the both sides of (37) yields that

$$\begin{aligned} f(X^{l+1})-\rho _{l+1}\Vert X^{l+1}\Vert \le f(X^{l})-\rho _{l}\Vert X^{l}\Vert +(\rho _{l}\!-\!\rho _{l+1})\Vert X^{l+1}\Vert . \end{aligned}$$

From this recursion formula, $f(X^{l_{\!f}})-\rho _{l_{\!f}}\Vert X^{l_{\!f}}\Vert \le f(X^{l^*})-\rho _{l^*}\Vert X^{l^*}\Vert +{\textstyle \sum _{j=l^*}^{l_{\!f}-1}}(\rho _{j}-\rho _{j+1})\Vert X^{j+1}\Vert .$ Combining this inequality with (38) and noting that $\Vert X^{l^*}\Vert \ge p/r^*$ yields the first part. Recall that $\textrm{diag}(X^{l_{\!f}})=e$. Then, $\Vert x^{l_{\!f}}\circ x^{l_{\!f}}-e\Vert =\Vert \sum _{i=2}^p\lambda _i(X^{l_{\!f}})P_i\circ P_i\Vert =\langle I,X^{l_{f}}\rangle -\Vert X^{l_{\!f}}\Vert \le \epsilon$. $\square$