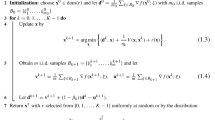Abstract
We consider a distributed non-convex optimization problem of minimizing the sum of all local cost functions over a network of agents. This problem often appears in large-scale distributed machine learning, known as non-convex empirical risk minimization. In this paper, we propose two accelerated algorithms, named DSGT-HB and DSGT-NAG, which combine the distributed stochastic gradient tracking (DSGT) method with momentum accelerated techniques. Under appropriate assumptions, we prove that both algorithms sublinearly converge to a neighborhood of a first-order stationary point of the distributed non-convex optimization. Moreover, we derive the conditions under which DSGT-HB and DSGT-NAG achieve a network-independent linear speedup. Numerical experiments for a distributed non-convex logistic regression problem on real data sets and a deep neural network on the MNIST database show the superiorities of DSGT-HB and DSGT-NAG compared with DSGT.





Similar content being viewed by others
Data availability
The datasets tested in this study are available on the LIBSVM website, https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/. The MNIST database used in this study is available on this site: http://yann.lecun.com/exdb/mnist/.
Notes
Each epoch evaluates m component gradients at each agent.
References
Tychogiorgos, G., Gkelias, A., Leung, K.K.: A non-convex distributed optimization framework and its application to wireless ad-hoc networks. IEEE Trans. Wireless Commun. 12(9), 4286–4296 (2013)
Olshevsky, A.: Efficient information aggregation strategies for distributed control and signal processing. Phd thesis, Massachusetts Inst. Tech. (2010)
Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 3(1), 11–22 (2011)
Chang, T., Hong, M., Wai, H., Zhang, X., Lu, S.: Distributed learning in the nonconvex world: From batch data to streaming and beyond. IEEE Signal Process. Mag. 37(3), 26–38 (2020)
Bottou, L., Curtis, F.E., Nocedal, J.: Optimization methods for large-scale machine learning. SIAM Rev. 60(2), 223–311 (2018)
Assran, M., Loizou, N., Ballas, N., Rabbat, M.: Stochastic gradient push for distributed deep learning. In: Proc. 36th Int. Conf. Mach. Learn. pp. 344–353 (2019)
Robbins, H., Monro, S.: A stochastic approximation method. Ann. Math. statist. 1, 400–407 (1951)
Yan, Y., Yang,T., Li, Z., Lin, Q., Yang, Y.: A unified analysis of stochastic momentum methods for deep learning. In: Proc. Int. Joint Conf. Artif. Intell. pp. 2955–2961 (2018)
Sutskever, T., Martens, J., Dahl, G., Hinton, G.: On the importance of initialization and momentum in deep learning. In: Int. Conf. Mach. Learn. pp. 1139–1147 (2013)
Liu, Y., Gao, Y., Yin, W.: An improved analysis of stochastic gradient descent with momentum. In: Proc. Adv. Neural Inf. Process. Syst. pp. 6–12 (2020)
Gitman, I., Lang, H., Zhang, P., Xiao, L.: Understanding the role of momentum in stochastic gradient methods. In: Proc. Adv. Neural Inf. Process. Syst. pp. 9633–9643 (2019)
Ghadimi, S., Lan, G.: Accelerated gradient methods for nonconvex nonlinear and stochastic programming. Math. Program. 156, 59–99 (2016)
Nedić, A., Ozdaglar, A.: Distributed subgradient methods for multi-agent optimization. IEEE Trans. Autom. Control 54(1), 48–61 (2009)
Yuan, K., Ling, Q., Yin, W.: On the convergence of decentralized gradient descent. SIAM J. Optim. 26(3), 1835–1854 (2016)
Ghadimi, E., Shames, I., Johansson, M.: Multi-step gradient methods for networked optimization. IEEE Trans. Signal Process. 61(21), 5417–5429 (2013)
Jakovetić, D., Xavier, J., Moura, J.M.F.: Fast distributed gradient methods. IEEE Trans. Autom. Control 59(5), 1131–1146 (2014)
Nedić, A., Olshevsky, A., Shi, W.: Achieving geometric convergence for distributed optimization over time-varying graphs. SIAM J. Optim. 27(4), 2597–2633 (2017)
Xu, J., Zhu, S., Soh, Y.C., Xie, L.: Augmented distributed gradient methods for multi-agent optimization under uncoordinated constant stepsizes. In: Proc. 54th IEEE Conf. Decis. Control (CDC) pp. 2055–2060 (2015)
Gao, J., Liu, X.W., Dai, Y.H., Huang, Y.K., Yang, P.: Achieving geometric convergence for distributed optimization with Barzilai-Borwein step sizes. Sci. China Inf. Sci. 65(4), 149203 (2022)
Jakovetić, D., Krejić, N., Krklec Jerinkić, N.: Exact spectral-like gradient method for distributed optimization. Comput. Optim. Appl. 74, 703–728 (2019)
Xin, R., Khan, U.A.: Distributed heavy-ball: A generalization and acceleration of first-order methods with gradient tracking. IEEE Trans. Autom. Control 65(6), 2627–2633 (2020)
Qu, G., Li, N.: Accelerated distributed Nesterov gradient descent. IEEE Trans. Autom. Control 65, 2566–2581 (2020)
Li, H., Cheng, H., Wang, Z., Wu, G.C.: Distributed Nesterov gradient and heavy-ball double accelerated asynchronous optimization. IEEE Trans. Neural Netw. Learn. Syst. 32(12), 5723–5737 (2021)
Shen, Y., Yang, S.: A heavy-ball distributed optimization algorithm over digraphs with row-stochastic matrices. In: 2020 39th Chinese Control Conf. pp. 4977–4982 (2020)
Gao, J., Liu, X.W., Dai, Y.H., Huang, Y.K., Yang, P.: A family of distributed momentum methods over directed graphs with linear convergence. IEEE Trans. Autom. Control (2022). https://doi.org/10.1109/TAC.2022.3160684
Lü, Q., Liao, X., Li, H., Huang, T.: A Nesterov-like gradient tracking algorithm for distributed optimization over directed networks. IEEE Trans. Syst. Man Cybern. Syst. 51(10), 6258–6270 (2021)
Jakovetić, D., Moura, J.M., Xavier, J.: Linear convergence rate of a class of distributed augmented lagrangian algorithms. IEEE Trans. Autom. Control 60(4), 922–936 (2015)
Mansoori, F., Wei, E.: A general framework of exact primal-dual first-order algorithms for distributed optimization. In: 2019 IEEE Conf. Decis. Control pp. 6386–6391 (2019)
Zeng, J., Yin, W.: On nonconvex decentralized gradient descent. IEEE Trans. Signal Process. 66(11), 2834–2848 (2018)
Lorenzo, P.D., Scutari, G.: Next: In-network nonconvex optimization. IEEE Trans. Signal Inf. Process. Netw. Process. 2(2), 120–136 (2016)
Daneshmand, A., Scutari, G., Kungurtsev, V.: Second-order guarantees of distributed gradient algorithms. Comput. Math. Model. 30(4), 3029–3068 (2020)
Chen, J., Sayed, A.H.: Diffusion adaptation strategies for distributed optimization and learning over networks. IEEE Trans. Signal Process. 60(8), 4289–4305 (2012)
Yuan, K., Alghunaim, S.A., Ying, B., Sayed, A.H.: On the influence of bias-correction on distributed stochastic optimization. IEEE Trans. Signal Process. 68, 4352–4367 (2020)
Pu, S., Nedić, A.: Distributed stochastic gradient tracking methods. Math. Program. 187(1), 409–457 (2021)
Johnson, R., Zhang, T.: Accelerating stochastic gradient descent using predictive variance reduction. In: Proc. Adv. Neural Inf. Process Syst. pp. 315–323 (2013)
Nguyen, L.M., Liu, J., Scheinberg, K., Taká, M.: SARAH: A novel method for machine learning problems using stochastic recursive gradient. In: Proc. Int. Conf. Mach. Learn. pp. 2613–2621 (2017)
Li, H., Zheng, L., Wang, Z., Yan, Y., Feng, L., Guo, J.: S-DIGing: A stochastic gradient tracking algorithm for distributed optimization. IEEE Trans. Emerg. Top. Comput. Intell. 6(1), 53–65 (2022)
Li, B., Cen, S., Chen, Y., Chi, Y.: Communication-efficient distributed optimization in networks with gradient tracking and variance reduction. J. Mach. Learn. Res. 21, 1–51 (2020)
Xin, R., Khan, U.A., Kar, S.: Variance-reduced decentralized stochastic optimization with accelerated convergence. IEEE Trans. Signal Process. 68, 6255–6271 (2020)
Sun, B., Hu, J., Xia, D., Li, H.: A distributed stochastic optimization algorithm with gradient-tracking and distributed heavy-ball acceleration. Front. Inform. Technol. Electron. Eng. 22(11), 1463–1476 (2021)
Hu, J., Xia, D., Cheng, H., Feng, L., Ji, L., Guo, J., Li, H.: A decentralized Nesterov gradient method for stochastic optimization over unbalanced directed networks. Asian J. Control 24(2), 576–593 (2022)
Erofeeva, V., Granichin, O., Sergeenko, A.: Distributed stochastic optimization with heavy-ball momentum term for parameter estimation. In: Proc. 2021 5th Scientific School Dynamics of Complex Networks and their Applications (DCNA) pp. 69–72 (2021)
Lian, X., Zhang, C., Zhang, H., Hsieh, C., Zhang, W., Liu, J.: Can decentralized algorithms outperform centralized algorithms? A case study for decentralized parallel stochastic gradient descent. In: Proc. Adv. Neural Inf. Process. Syst. pp. 5330–5340 (2017)
Vlaski, S., Sayed, A.H.: Distributed learning in non-convex environments-part I: Agreement at a linear rate. IEEE Trans. Signal Process. 69, 1242–1256 (2021)
Vlaski, S., Sayed, A.H.: Distributed learning in non-convex environments-part II: Polynomial escape from saddle-points. IEEE Trans. Signal Process. 69, 1257–1270 (2021)
Tang, H., Lian, X., Yan, M., Zhang, C., Liu, J.: D\(^2\): Decentralized training over decentralized data. In: Proc. 35th Int. Conf. Mach. Learn. pp. 4848–4856 (2018)
Lu, S., Zhang, X., Sun, H., Hong, M.: Gnsd: a gradient-tracking based nonconvex stochastic algorithm for decentralized optimization. In: Proc. 2019 IEEE Data Sci. Workshop pp. 315–321 (2019)
Xin, R., Khan, U.A., Kar, S.: An improved convergence analysis for decentralized online stochastic non-convex optimization. IEEE Trans. Signal Process. 69, 1842–1858 (2021)
Zhang, J., You, K.: Decentralized stochastic gradient tracking for non-convex empirical risk minimization. ArXiv preprint arXiv:1909.02712 (2019)
Xin, R., Khan, U.A., Kar, S.: Fast decentralized non-convex finite-sum optimization with recursive variance reduction. SIAM J. Optim. 32(1), 1–28 (2022)
Yu, H., Jin, R., Yang, S.: On the linear speedup analysis of communication efficient momentum sgd for distributed non-convex optimization. In: Proc. Int. Conf. Mach. Learn. pp. 7184–7193 (2019)
Ghadimi, S., Lan, G.: Stochastic first- and zeroth-order methods for nonconvex stochastic programming. SIAM J. Optim. 23(4), 2341–2368 (2012)
Polyak, B.T.: Introduction to optimization. Optimization Software Inc, New York (1987)
Ghadimi, E., Feyzmahdavian, H.R., Johansson, M.: Global convergence of the heavy-ball method for convex optimization. In: Proc. 2015 Eur. Control Conf. pp. 310–315 (2015)
Nesterov, Y.: Introductory lectures on convex optimization: A basic course. Springer Science & Business Media, UK (2013)
Zhu, M., Martinez, S.: Discrete-time dynamic average consensus. Automatica 46(2), 322–329 (2010)
Sun, H., Lu, S., Hong, H.: Improving the sample and communication complexity for decentralized nonconvex optimization: Joint gradient estimation and tracking. In: Proc. Int. Conf. Mach. Learn. pp. 9217–9228 (2020)
Erdos, P., Renyi, A.: On random graphs i. Publ. Math. Debrecen 6, 290–297 (1959)
Funding
This work was supported by the National Natural Science Foundation of China (Grant Numbers 12071108, 11671116, 12021001, 11991021, 11991020, 11971372, 11701137); and the Strategic Priority Research Program of CAS (Grant number XDA27000000).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declared that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A Proof of Lemma 8
Proof
Using \(W_\infty W=W_\infty\) and (4c), we obtain
where the inequality follows from Lemma 2(c) and \(\Vert W-W_\infty \Vert =\delta\). Notice that
Taking the conditional expectation on (A1) and using (A2) lead to
Consider the second term on the right-hand side of (A3). Note that
where the last inequality follows from Assumption 1 and \(\mathbb {E}[\langle \nabla \mathbf {f}_{k},\nabla \mathbf {f}_{k}-\mathbf {d}_{k}\rangle \mid \mathcal {F}_k]=0\). We note that
where the first inequality uses Lemma 1(c) with \(\eta =1\) and the last inequality uses \(\Vert W-I_{np}\Vert \le 2\) and (13). Next, we consider the last term on the right-hand side of (A4). From (4), it follows that
Denote
By Assumption 3,
In light of Assumption 1 and \(\Vert W^2\Vert =1\),
Substituting (A5) and (A10) into (A4) yields
Consider the third term on the right-hand side of (A3). Using \(W_\infty (W-W_\infty )=0\) and (4c), we have
where the second and third equalities use \(\mathbb {E}[\mathbf {d}_k\mid \mathcal {F}_k]=\nabla \mathbf {f}_k\). Since, for \(\forall i\ne j\in \mathcal {V}\), it holds that
we get
where the inequality uses that \(\text {diag}(W^TW^2)\) is nonnegative. Using Assumption 3 and combining (A13) with (A12) obtain
Consider the fourth term on the right-hand side of (A3). By the Cauchy-schwarz inequality, we have
where the last inequality applies \(\Vert W-W_\infty \Vert =\delta\), Lemma 2(c) and Assumption 1. Next, we bound \(\Vert \varvec{\theta }_{k+1}-\varvec{\theta }_{k}\Vert\). Note that
where the first inequality uses \(\Vert W-I_{np}\Vert \le 2\) and \(\Vert W\Vert =1\). Substituting (A16) into (A15) yields
where \(\eta _i>0, i=1,2,3\) and the last inequality uses Lemma 1(a) with \(p=1\). Taking the conditional expectation on (A17) and using (13) lead to
Applying (A11), (A14) and (A18) to (A3) and then taking the total expectation, we further obtain
We set \(\eta _1=\frac{1-\delta ^2}{8\delta ^2}\), \(\eta _2=\frac{1-\delta ^2}{32\delta ^2}\) and \(\eta _3=\frac{1-\delta ^2}{16\delta ^2}\). If \(0<\alpha \le \frac{1-\delta ^2}{16(1-\beta )L\delta }\), then we get
If \(0<\alpha \le \min \left\{ \frac{1-\delta ^2}{8\delta },1\right\} \frac{1}{2(1-\beta )L}\), then the desired result follows from applying (A20) and the values of \(\eta _1\), \(\eta _2\) and \(\eta _3\) to (A19). \(\square\)
Appendix B Proof of Lemma 17
Proof
First, using the same argument as that in the proof of Lemma 8, we have
Consider the second term on the right-hand side of (B21). Following the same steps as (A4), there holds
Then, let us consider the second term on the right-hand side of (B22).
where the first inequality applies Lemma 1(c) with \(\eta =1\) and the last inequality uses \(\Vert W-I_{np}\Vert \le 2\) and (13). Next, we consider the last term on the right-hand side of (B22). From (5), it follows that
Denote
By Assumption 3,
In light of Assumption 1 and \(\Vert W^2\Vert =1\),
Using (B24) and (B25), we have
Combining (B23), (B26) with (B22) gets
Consider the third term on the right-hand side of (B21). It has the same bound as the corresponding term of (A3), that is,
Consider the fourth term on the right-hand side of (B21). Following the same steps as (A15), we have
Moreover,
where the first inequality uses \(\Vert W-I_{np}\Vert \le 2\) and \(\Vert W\Vert =1\). Substituting (B30) into (B29) yields
where \(\eta _i>0, i=1,2,3\) and the last inequality uses Lemma 1(a) with \(p=1\). Taking the conditional expectation on (B31) and using (13) lead to
Applying (B27), (B28) and (B32) to (B21) and then taking the total expectation, we further obtain
We set \(\eta _1=\frac{1-\delta ^2}{8\delta ^2}\), \(\eta _2=\frac{1-\delta ^2}{32\delta ^2}\) and \(\eta _3=\frac{1-\delta ^2}{16\delta ^2}\). It can then be verified that if \(0<\alpha \le \frac{1-\delta ^2}{16(1-\beta ^2)L\delta }\),
If \(0<\alpha \le \min \{\frac{1-\delta ^2}{8\delta },1\}\frac{1}{2(1-\beta ^2)L}\), then the desired result follows from applying (B34) and the values of \(\eta _1\), \(\eta _2\) and \(\eta _3\) to (B33). \(\square\)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Gao, J., Liu, XW., Dai, YH. et al. Distributed stochastic gradient tracking methods with momentum acceleration for non-convex optimization. Comput Optim Appl 84, 531–572 (2023). https://doi.org/10.1007/s10589-022-00432-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-022-00432-5