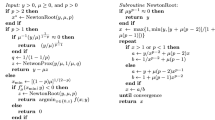1 Introduction

In this paper, we focus on the following problem:

$$\begin{aligned} \begin{aligned}&\min \, \varphi (x) \\&\Vert x \Vert _1 \le \tau , \end{aligned} \end{aligned}$$
(1)

where \(\varphi :\mathbb {R}^n \rightarrow \mathbb {R}\) is a function whose gradient is Lipschitz continuous with constant \(L>0\), \(\Vert x \Vert _1\) denotes the \(\ell _1\)-norm of the vector x and \(\tau\) is a suitably chosen positive parameter.

Problem (1) includes, as a special case, the so called LASSO problem, obtained when

$$\begin{aligned} \varphi (x) = \Vert Ax-b \Vert ^2, \end{aligned}$$

with A and b being a \(m \times n\) matrix and a m-dimensional vector, respectively. Here and in the following, \(\Vert \cdot \Vert\) denotes the Euclidean norm. Loosely speaking, in LASSO problems the \(\ell _1\)-norm constraint is able to induce sparsity in the final solution, and then these problems are widely used in statistics to build regression models with a small number of non-zero coefficients [17, 32].

Standard optimization algorithms (like, e.g., interior-point methods), besides being very expensive when the number of variables increases, do no properly exploit the main features and structure of the considered problem. This is the reason why, in the last decade, a number of first-order methods have been considered in the literature to deal with problem (1). Those methods can be divided into two main classes: projection-based approaches, like, e.g., gradient-projection methods [15, 31] and limited-memory projected quasi-Newton methods [30], which efficiently handle the problem by making use of tailored projection strategies [8, 16], and projection-free methods, like, e.g., Frank–Wolfe variants [5, 6, 25, 26], that embed a cheap linear minimization oracle.

As highlighted before, the main goal when using the \(\ell _1\) ball is to get very sparse solutions (i.e., solutions with many zero components). In this context, it hence makes sense to devise strategies that allow to quickly identify the set of zero components in the optimal solution. This would indeed guarantee a significant speed-up of the optimization process. A number of active-set strategies for structured feasible sets is available in the literature (see, e.g., [3, 4, 7, 9, 10, 13, 18, 19, 22,23,24, 28] and references therein), but none of those directly handles the \(\ell _1\) ball.

In this paper, inspired by the work carried out in [10], we propose a tailored active-set strategy for problem (1) and embed it into a first-order projection-based algorithm. At each iteration, the method first sets to zero the variables that are guessed to be zero at the final solution. This is done by means of the tailored active-set estimate, which aims at identifying the manifold where the solutions of problem (1) lie, while guaranteeing, thanks to a descent property, a reduction of the objective function at each iteration. Then, the remaining variables, i.e., those variables estimated to be non-zero at the final solution, are suitably modified by means of a non-monotone gradient-projection step.

The paper is organized as follows. In Sect. 2, we describe the active-set strategy and analyze the descent property connected to it. We then devise, in Sect. 3, our first-order optimization algorithm and carry out a global convergence analysis. We further report a numerical comparison with some well-known first order methods using two different classes of \(\ell _1\)-constrained problems (that is, LASSO and constrained sparse logistic regression) in Sect. 4. Finally, we draw some conclusions in Sect. 5.

2 The active-set estimate

Since the feasible set of problem (1) is convex and can be written as convex combination of the vectors \(\pm \tau e_i\), \(i=1,\ldots ,n\), we can characterize the stationary points as follows.

Definition 1

A feasible point \(x^*\) of problem (1) is stationary if and only if

$$\begin{aligned} \begin{aligned}&\nabla \varphi (x^*)^T(\tau e_i - x^*) \ge 0, \quad i = 1,\ldots , n, \\&\nabla \varphi (x^*)^T(-\tau e_i - x^*) \ge 0, \quad i = 1,\ldots , n. \end{aligned} \end{aligned}$$
(2)

In the next proposition, we state some “complementarity-type” conditions for stationary points of problem (1).

Proposition 1

Let \(x^*\) be a stationary point of problem (1). Then

  1. (i)

    \(x_i^*>0 \, \Rightarrow \, \nabla \varphi (x^*)^T (\tau e_i - x^*)=0\),

  2. (ii)

    \(x_i^*<0 \, \Rightarrow \, \nabla \varphi (x^*)^T (-\tau e_i - x^*)=0\).

Proof

If \(|x_i^*| = \tau\), then \(x^* = \tau \, {{\,\mathrm{sgn}\,}}(x^*_i) \, e_i\) and the result trivially holds. To prove point (i), now let \(0< x_i^* <\tau\). Taking into account (2), by contradiction we assume that

$$\begin{aligned} \nabla \varphi (x^*)^T (\tau e_i - x^*)>0. \end{aligned}$$
(3)

Let \(d^+\in \mathbb {R}^n\) be defined as follows:

$$\begin{aligned} d^+=\frac{x_i^*}{\tau -x_i^*}(x^*-\tau e_i). \end{aligned}$$

We have

$$\begin{aligned} \begin{aligned} \Vert x^*+d^+\Vert _1&=\biggr (1+ \frac{x_i^*}{\tau -x_i^*}\biggl )\sum _{j\ne i} |x^*_j|+\biggr |x_i^*+ \frac{x_i^*}{\tau -x_i^*}(x_i^*-\tau )\biggl | \\&\le \biggr (1+ \frac{x_i^*}{\tau -x_i^*}\biggl )(\tau -|x_i^*|)=\tau , \end{aligned} \end{aligned}$$
(4)

so that \(d^+\) is a feasible direction in \(x^*\). Therefore, (3) and (4) imply that \(d^+\) is a feasible descent direction for \(\varphi (\cdot )\) in \(x^*\). This contradicts the fact that \(x^*\) is a stationary point of problem (1) and point (i) is proved. To prove point (ii), we can use the same arguments as above, considering \(-\tau< x_i^* < 0\) and, assuming by contradiction that \(\nabla \varphi (x^*)^T (-\tau e_i - x^*)>0\), we obtain that

$$\begin{aligned} d^-=\frac{|x_i^*|}{\tau +x_i^*}(x^*+\tau e_i) \end{aligned}$$

is such that \(\Vert x^*+d^-\Vert _1 \le \tau\), that is, \(d^-\) is a feasible and descent direction for \(\varphi (\cdot )\) in \(x^*\), leading to a contradiction. \(\square\)

With little abuse of standard terminology, given a stationary point \(x^*\) we say that a variable \(x^*_i\) is active if \(x^*_i=0\), whereas a variable \(x^*_i\) is said to be non-active if \(x^*_i \ne 0\). We can thus define the active set \({\bar{A}}_{\ell _1}(x^*)\) and the non-active set \({\bar{N}}_{\ell _1}(x^*)\) as follows:

$$\begin{aligned} {\bar{A}}_{\ell _1}(x^*) = \{i :x^*_i=0\}, \quad {\bar{N}}_{\ell _1}(x^*) = \{1,\ldots ,n\} \setminus {\bar{A}}_{\ell _1}(x^*). \end{aligned}$$

Now, we show how we estimate these sets starting from any feasible point x of problem (1). In order to obtain such an estimate we first need to suitably reformulate our problem (1) by introducing a dummy variable z. Let \({\bar{\varphi }}(x,z) :\mathbb {R}^{n+1} \rightarrow \mathbb {R}\) be the function defined as \({\bar{\varphi }}(x,z) = \varphi (x)\) for all (x, z). Problem (1) can then be rewritten as

$$\begin{aligned} \begin{aligned}&\min \, {\bar{\varphi }}(x,z) \\&\Vert x\Vert _1 +z\le \tau ,\\&z \ge 0. \end{aligned} \end{aligned}$$
(5)

Every feasible point of problem (5) can be expressed as convex combination of \(\{\pm \tau e_1,\ldots , \pm \tau e_n, \tau e_{n+1}\} \subset \mathbb {R}^{n+1}\). Therefore, we can define the following matrix, where I denotes the \(n \times n\) identity matrix:

$$\begin{aligned} {\bar{M}} = \tau \left[ \begin{array}{c | c | c} I &{} -I &{} \begin{matrix}0\\ \vdots \\ 0\end{matrix} \\ \hline \begin{matrix}0 &{}\ldots &{} 0\end{matrix}&\begin{matrix}0&\ldots&0\end{matrix}&1 \end{array} \right] \in \mathbb {R}^{(n+1) \times (2n+1)}, \end{aligned}$$

and we obtain the following reformulation of (1) as a minimization problem over the unit simplex:

$$\begin{aligned} \begin{aligned}&\min \, f(y) = {\bar{\varphi }}({\bar{M}} y) \\&e^T y = 1, \\&y \ge 0. \end{aligned} \end{aligned}$$
(6)

Note that, given any feasible point x of problem (1), we can compute a feasible point y of problem (6) such that

$$\begin{aligned} \begin{aligned}&y_i = \frac{1}{\tau } \max \{0,x_i\}, \quad i = 1,\dots ,n, \\&y_{n+i} = \frac{1}{\tau } \max \{0,-x_i\}, \quad i = 1,\dots ,n, \\&y_{2n+1} = \frac{\tau -\Vert x\Vert _1}{\tau }. \end{aligned} \end{aligned}$$
(7)

The rationale behind our approach is sketched in the three following points:

  1. (i)

    For any feasible point x of problem (1), by (7) we can compute a feasible point y of problem (6) such that

    $$\begin{aligned} y_i = 0 \, \Leftrightarrow \, x_i \le 0 \quad \text {and} \quad y_{n+i} = 0 \, \Leftrightarrow \, x_i \ge 0, \qquad i = 1,\ldots ,n. \end{aligned}$$
    (8)
  2. (ii)

    According to (8), for every feasible point x of problem (1) we have that

    $$\begin{aligned} x_i = 0 \, \Leftrightarrow \, y_i = y_{n+i} = 0, \quad i = 1,\ldots ,n. \end{aligned}$$
    (9)

    Thus, it is natural to estimate a variable \(x_i\) as active at \(x^*\) if both \(y_i\) and \(y_{n+i}\) are estimated to be zero at the point corresponding to \(x^*\) in the y space. To estimate the zero variables among \(y_1,\ldots ,y_{2n+1}\) we use the active-set estimate described in [10], specifically devised for minimization problems over the unit simplex.

  3. (iii)

    Then, we are able to go back in the original x space to obtain an active-set estimate of problem (1) without explicitly considering the variables \(y_1,\ldots ,y_{2n+1}\) of the reformulated problem.

Remark 1

The introduction of the dummy variable z is needed in order to get a reformulation of problem (1) as a minimization problem over the unit simplex satisfying (8). Since every feasible point x of problem (1) can be expressed as a convex combination of the vertices of the polyhedron \(\{x\in \mathbb {R}^n:\; \Vert x\Vert _1 \le {\tau }\}\), a straightforward reformulation of problem (1) would then be the following:

$$\begin{aligned} \min \{\varphi (My) :e^T y = 1, \, y \ge 0\}, \end{aligned}$$
(10)

with \(M = \tau \,\begin{bmatrix}&I&\vline&{-I}&\end{bmatrix}\). However, this reformulation does not work for our purposes, as there exist feasible points x of problem (1) for which no y feasible for problem (10) satisfying (8) can be found. In particular, if x is in the interior of the \(\ell _1\)-ball (e.g., the origin), we cannot find any y feasible for problem (10) such that (8) holds.

Considering problem (6) and using the active-set estimate proposed in [10] for minimization problems over the unit simplex, given any feasible point y of problem (6) we define:

$$\begin{aligned} A(y)= & {} \{i :y_i \le \epsilon \nabla f(y)^T(e_i - y)\}, \end{aligned}$$
(11)
$$\begin{aligned} N(y)= & {} \{i :y_i > \epsilon \nabla f(y)^T(e_i - y)\}, \end{aligned}$$
(12)

where \(\epsilon\) is a positive parameter. A(y) contains the indices of the variables that are estimated to be zero at a certain stationary point and N(y) contains the indices of the variables that are estimated to be positive at the same stationary point (see [10] for details of how these formulas are obtained). As mentioned above, taking into account (9), we estimate a variable \(x_i\) as active for problem (1) if both \(y_i\) and \(y_{n+1}\) are estimated to be zero. Namely,

$$\begin{aligned} A_{\ell _1}(x)= & {} \bigl \{i \in \{1,\ldots ,n\} :i \in A(y) \, \text { and } \, (n+i) \in A(y) \bigr \}, \end{aligned}$$
(13a)
$$\begin{aligned} N_{\ell _1}(x)= & {} \bigl \{i \in \{1,\ldots ,n\} :i \in N(y) \, \text { or } \, (n+i) \in N(y) \bigr \}. \end{aligned}$$
(13b)

Now we show how \(A_{\ell _1}(x)\) and \(N_{\ell _1}(x)\) can be expressed without explicitly considering the variables y and the objective function f(y) of the reformulated problem. This allows us to work in the original x space, avoiding to double the number of variables in practice.

To obtain the desired relations, first observe that

$$\begin{aligned} \nabla f(y) = {\bar{M}}^T \nabla {\bar{\varphi }} (x) = \tau \begin{bmatrix} \nabla \varphi (x) \\ -\nabla \varphi (x) \\ 0 \end{bmatrix}^T, \end{aligned}$$
(14)

and

$$\begin{aligned} \nabla f(y)^T y = \nabla {\bar{\varphi }}(x)^T {\bar{M}} y = \begin{bmatrix} \nabla \varphi (x)^T&0 \end{bmatrix} {\bar{M}} y = \nabla \varphi (x)^T x. \end{aligned}$$

Let us distinguish two cases:

  1. (i)

    \(x_i \ge 0\). Recalling (11)–(12), we have that \(i \in A(y)\) if and only if

    $$\begin{aligned} \begin{aligned} 0 \le \frac{1}{\tau }x_i =y_i&\le \epsilon \nabla f(y)^T(e_i - y) = \epsilon (\nabla _i f(y) - \nabla f(y)^T y) \\&= \epsilon (\tau \nabla _i \varphi (x) - \nabla \varphi (x)^Tx) = \epsilon \nabla \varphi (x)^T (\tau e_i - x) \end{aligned} \end{aligned}$$
    (15)

    and \((n+i) \in A(y)\) if and only if

    $$\begin{aligned} \begin{aligned} -\frac{1}{\tau } x_i \le 0 = y_{n+i}&\le \epsilon \nabla f(y)^T(e_{n+i} - y) = \epsilon (\nabla _{n+i} f(y) - \nabla f(y)^T y)\\&= \epsilon (-\tau \nabla _i \varphi (x) - \nabla \varphi (x)^Tx) = -\epsilon \nabla \varphi (x)^T (\tau e_i + x). \end{aligned} \end{aligned}$$
    (16)
  2. (ii)

    \(x_i < 0\). Similarly to the previous case, we have that \(i \in A(y)\) if and only if

    $$\begin{aligned} \begin{aligned} \frac{1}{\tau } x_i < 0 = y_i&\le \epsilon \nabla f(y)^T(e_i - y) = \epsilon (\nabla _i f(y) - \nabla f(y)^T y) \\&= \epsilon (\tau \nabla _i \varphi (x) - \nabla \varphi (x)^Tx) = \epsilon \nabla \varphi (x)^T (\tau e_i - x) \end{aligned} \end{aligned}$$
    (17)

    and \((n+i) \in A(y)\) if and only if

    $$\begin{aligned} \begin{aligned} 0 < -\frac{1}{\tau }x_i = y_{n+i}&\le \epsilon \nabla f(y)^T(e_{n+i} - y) = \epsilon (\nabla _{n+i} f(y) - \nabla f(y)^T y)\\&= \epsilon (-\tau \nabla _i \varphi (x) - \nabla \varphi (x)^Tx) = -\epsilon \nabla \varphi (x)^T (\tau e_i + x). \end{aligned} \end{aligned}$$
    (18)

From (15), (16), (17) and (18), we thus obtain

$$\begin{aligned} A_{\ell _1}(x)&= \{i :\epsilon \, \tau \nabla \varphi (x)^T (\tau e_i + x) \le 0 \le x_i \le \epsilon \, \tau \nabla \varphi (x)^T (\tau e_i - x)\ \hbox {or} \nonumber \\&\epsilon \, \tau \nabla \varphi (x)^T (\tau e_i + x) \le x_i \le 0 \le \epsilon \, \tau \nabla \varphi (x)^T (\tau e_i - x)\}, \end{aligned}$$
(19)
$$\begin{aligned} N_{\ell _1}(x)&= \{1,\ldots ,n\} \setminus A_{\ell _1}(x). \end{aligned}$$
(20)

Let us highlight again that \(A_{\ell _1}(x)\) and \(N_{\ell _1}(x)\) do not depend on the variables y and on the objective function f(y) of the reformulated problem, so no variable transformation is needed in practice to estimate the active set of problem (1). In the following, we prove that under specific assumptions, \({\bar{A}}_{\ell _1}(x^*)\) is detected by our active-set estimate, when evaluated in points sufficiently close to a stationary point \(x^*\).

Proposition 2

If \(x^*\) is a stationary point of problem (1), then there exists an open ball \({\mathcal {B}}(x^*,\rho )\) with center \(x^*\) and radius \(\rho > 0\) such that, for all \(x \in {\mathcal {B}} (x^*,\rho )\), we have

$$\begin{aligned}&A_{\ell _1}(x) \subseteq {\bar{A}}_{\ell _1} (x^*), \end{aligned}$$
(21)
$$\begin{aligned}&\quad {\bar{N}}_{\ell _1}(x^*) \subseteq N_{\ell _1} (x). \end{aligned}$$
(22)

Furthermore, if the following “strict-complementarity-type” assumption holds:

$$\begin{aligned} x_i^*=0 \, \Rightarrow \nabla \varphi (x^*)^T (\tau e_i - x^*)>0 \, \wedge \, \nabla \varphi (x^*)^T (\tau e_i + x^*)<0, \end{aligned}$$
(23)

then, for all \(x \in {\mathcal {B}} (x^*,\rho )\), we have

$$\begin{aligned} A_{\ell _1}(x)= & {} {\bar{A}}_{\ell _1} (x^*), \end{aligned}$$
(24)
$$\begin{aligned} {\bar{N}}_{\ell _1}(x^*)= & {} N_{\ell _1} (x). \end{aligned}$$
(25)

Proof

Let \(i\in N_{\ell _1} (x^*)\), then \(|x_i^*|>0\). Proposition 1 implies that either

$$\begin{aligned} \nabla \varphi (x^*)^T (\tau e_i - x^*)=0 \quad \text {if} \quad x_i^*>0, \end{aligned}$$

or

$$\begin{aligned} \nabla \varphi (x^*)^T (-\tau e_i - x^*)=0 \quad \text {if} \quad x_i^*<0. \end{aligned}$$

Then, the continuity of \(\nabla \varphi\) and the definition of \(N_{\ell _1} (x)\) imply that there exists an open ball \({\mathcal {B}}(x^*,\rho )\) with center \(x^*\) and radius \(\rho > 0\) such that, for all \(x\in {\mathcal {B}}(x^*,\rho )\), we have that \(i \in N_{\ell _1} (x)\). This proves (22) and, consequently, also (21). If (23) holds, the definition of \(N_{\ell _1} (x)\) and the continuity of \(\nabla \varphi\) ensures that \({\bar{A}}_{\ell _1} (x^*) \subseteq A_{\ell _1}(x)\) for all \(x\in {\mathcal {B}}(x^*,\rho )\), implying that (24) and (25) hold. \(\square\)

2.1 Descent property

So far, we have obtained the active and non-active set estimates (19)–(20) passing through a variable transformation which allowed us to adapt the active and non-active set estimates proposed in [10] to our problem (1).

In [10], the active and non-active set estimates, designed for minimization problems over the unit simplex, guarantee a decrease in the objective function when setting (some of) the estimated active variables to zero and moving a suitable estimated non-active variable (in order to maintain feasibility).

In the following, we show that the same property holds for problem (1) using the active and non-active set estimates (19)–(20). To this aim, in the next proposition we first introduce the index set \(J_{\ell _1}(x)\) and relate it with \(N_{\ell _1}(x)\).

Proposition 3

Let \(x \in \mathbb {R}^n\) be a feasible non-stationary point of problem (1) and define

$$\begin{aligned} J_{\ell _1}(x) = \Bigl \{j :j \in {{\,\mathrm{Argmax}\,}}_{i=1,\ldots ,n}\, \bigl \{|\nabla _i \varphi (x)|\bigr \} \Bigr \}. \end{aligned}$$

Then, \(J_{\ell _1}(x) \subseteq N_{\ell _1}(x)\).

Proof

Let y be the point given by (7) and consider the reformulated problem (6). Let A(y) and N(y) be the index sets given in (11)–(12), that is, the active and non-active set estimates for problem (6), respectively.

From the expression of \(\nabla f(y)\) given in (14), and exploiting the hypothesis that x is non-stationary (implying that \(\nabla \varphi (x) \ne 0)\), it follows that

$$\begin{aligned} \min _{i=1,\ldots ,2n+1} \{\nabla _i f(y)\} < 0. \end{aligned}$$
(26)

Since \(\nabla _{2n+1} f(y) = 0\) (again from (14)), it follows that

$$\begin{aligned} (2n+1) \notin {{\,\mathrm{Argmin}\,}}_{i=1,\ldots ,2n+1} \{\nabla _i f(y)\}. \end{aligned}$$

From Proposition 1 in [10], there exists \(\nu \in \{1,\ldots ,2n\}\) such that

$$\begin{aligned}&\nu \in \displaystyle {{\,\mathrm{Argmin}\,}}_{i=1,\ldots ,2n} \{\nabla _i f(y)\}, \end{aligned}$$
(27)
$$\begin{aligned}&\quad \nu \in N(y). \end{aligned}$$
(28)

In particular, we can rewrite (27) as

$$\begin{aligned} \nabla _{\nu } f(y) = \tau \min _{i=1,\ldots ,n} \{\nabla _1 \varphi (x), \ldots , \nabla _n \varphi (x), -\nabla _1 \varphi (x), \ldots , -\nabla _n \varphi (x)\}. \end{aligned}$$

Taking into account (26), we obtain

$$\begin{aligned} -|\nabla _{\nu } f(y)| \le -\tau |\nabla _i \varphi (x) |, \quad \forall i = 1, \ldots ,n. \end{aligned}$$
(29)

Now, let \(j \in \{1,\ldots ,n\}\) be the following index:

$$\begin{aligned} j = {\left\{ \begin{array}{ll} \nu , \quad &{} \text { if } \nu \in \{1,\ldots ,n\}, \\ \nu -n, \quad &{} \text { if } \nu \in \{n+1,\ldots ,2n\}. \end{array}\right. } \end{aligned}$$
(30)

Using again (14), we get \(|\nabla _{\nu } f(y) | = |\nabla _j f(y) | = \tau |{\nabla _j \varphi (x)} |\). This, combined with (29), implies that

$$\begin{aligned} j \in {{\,\mathrm{Argmax}\,}}_{i=1,\ldots ,n}\, \bigl \{|\nabla _i \varphi (x) |\bigr \}. \end{aligned}$$

Finally, using (28) and (30), it follows that at least one index between j and \((n+j)\) belongs to N(y). Therefore, from (13b) we have that \(j \in N_{\ell _1}(x)\) and the assertion is proved. \(\square\)

Now, we need an assumption on the parameter \(\epsilon\) appearing in (19)–(20). It will allow us to prove the subsequent proposition, stating that \(\varphi (x)\) decreases if we set the variables in \(A_{\ell _1}(x)\) to zero and suitably move a variable in \(J_{\ell _1}(x)\).

Assumption 1

Assume that the parameter \(\epsilon\) appearing in the estimates (19)–(20) satisfies the following conditions:

$$\begin{aligned} 0 < \epsilon \le \frac{1}{\tau ^2 n L (2C+1)}, \end{aligned}$$

where \(C>0\) is a given constant.

Proposition 4

Let Assumption 1hold. Given a feasible non-stationary point x of problem (1), let \(j \in J_{\ell _1}(x)\) and \(I = \{1,\ldots ,n\} \setminus \{j\}\). Let \({\hat{A}}_{\ell _1}(x)\) be a set of indices such that \({\hat{A}}_{\ell _1}(x) \subseteq A_{\ell _1}(x)\). Let \({\tilde{x}}\) be the feasible point defined as follows:

$$\begin{aligned} {\tilde{x}}_{{\hat{A}}_{\ell _1}(x)} = 0; \quad {\tilde{x}}_{I\setminus {\hat{A}}_{\ell _1}(x)} = x_{I\setminus {\hat{A}}_{\ell _1}(x)}; \quad {\tilde{x}}_j = x_j -{{\,\mathrm{sgn}\,}}(\nabla _j \varphi (x))\displaystyle {\sum _{h \in {\hat{A}}_{\ell _1}(x)} |x_h |}. \end{aligned}$$

Then,

$$\begin{aligned} \varphi ({\tilde{x}})-\varphi (x)\le - CL \Vert {\tilde{x}}-x \Vert ^2, \end{aligned}$$

where \(C > 0\) is the constant appearing in Assumption 1.

Proof

Define

$$\begin{aligned} {\hat{A}}^+ = {\hat{A}}_{\ell _1}(x) \cap \{i :x_i \ne 0\}. \end{aligned}$$
(31)

Since \(\nabla \varphi\) is Lipschitz continuous with constant L, from known results (see, e.g., [29]) we can write

$$\begin{aligned} \begin{aligned} \varphi ({\tilde{x}})&\le \varphi (x) + \nabla \varphi (x)^T ({\tilde{x}}-x) + \frac{L}{2} \Vert {\tilde{x}}-x \Vert ^2 \\&= \varphi (x) + \nabla \varphi (x)^T ({\tilde{x}}-x) + \frac{L(2C+1)}{2} \Vert {\tilde{x}}-x \Vert ^2 - CL\Vert {\tilde{x}}-x \Vert ^2 \end{aligned} \end{aligned}$$

and then, in order to prove the proposition, what we have to show is that

$$\begin{aligned} \nabla \varphi (x)^T ({\tilde{x}}-x) + \frac{L(2C+1)}{2} \Vert {\tilde{x}}-x \Vert ^2 \le 0. \end{aligned}$$
(32)

From the definition of \({\tilde{x}}\), we have that

$$\begin{aligned} \begin{aligned} \Vert {\tilde{x}}-x \Vert ^2&= \sum _{i\in {\hat{A}}^+} x_i^2 + \Bigg (\sum \limits _{i\in {\hat{A}}^+} {|x_i|} \Bigg )^2 \le \sum _{i\in {\hat{A}}^+} x_i^2 + |{\hat{A}}^+ |\sum _{i\in {\hat{A}}^+} x_i^2 \\&= (|{\hat{A}}^+ |+1) \sum _{i\in {\hat{A}}^+} x_i^2. \end{aligned} \end{aligned}$$
(33)

Furthermore,

$$\begin{aligned} \begin{aligned} \nabla \varphi (x)^T ({\tilde{x}}-x)&= -\sum _{i \in {\hat{A}}^+} \nabla _i \varphi (x) x_i - |\nabla _j \varphi (x) | \sum _{i \in {\hat{A}}^+} |x_i| \\&= \sum _{i \in {\hat{A}}^+} |x_i| (-\nabla _i \varphi (x) \, {{\,\mathrm{sgn}\,}}(x_i) - |\nabla _j \varphi (x) |). \end{aligned} \end{aligned}$$
(34)

Since \(j \in J_{\ell _1}(x)\), from the definition of \(J_{\ell _1}(x)\) it follows that \(-|\nabla _i \varphi (x) | \ge -|\nabla _j \varphi (x) |\) for all \(i \in \{1,\ldots ,n\}\). Therefore, we can write

$$\begin{aligned} \begin{aligned} \nabla \varphi (x)^T x&= \sum _{i=1}^n \nabla _i \varphi (x) {{\,\mathrm{sgn}\,}}(x_i)\, |x_i| \ge \sum _{i=1}^n -|\nabla _j \varphi (x) | \,|x_i| \\&= -|\nabla _j \varphi (x) | \,\Vert x\Vert _1 \ge -|\nabla _j \varphi (x) |\, \tau . \end{aligned} \end{aligned}$$
(35)

Using (19) and (35), for all \(i\in {\hat{A}}^+\) we have that

$$\begin{aligned} x_i&\le \epsilon \tau (\nabla _i \varphi (x) \tau - \nabla \varphi (x)^T x) \le \epsilon \tau ^2 (\nabla _i \varphi (x) + |\nabla _j \varphi (x) |), \\ -x_i&\le -\epsilon \tau (\nabla _i \varphi (x) \tau + \nabla \varphi (x)^T x) \le \epsilon \tau ^2 (-\nabla _i \varphi (x) + |\nabla _j \varphi (x) |), \end{aligned}$$

and then,

$$\begin{aligned} |x_i | = {{\,\mathrm{sgn}\,}}(x_i) \, x_i \le \epsilon \tau ^2 (\nabla _i \varphi (x) \, {{\,\mathrm{sgn}\,}}(x_i) + |\nabla _j \varphi (x) |), \quad \forall i\in {\hat{A}}^+. \end{aligned}$$

Combining this inequality with (33), we obtain

$$\begin{aligned} \Vert {\tilde{x}}-x \Vert ^2 \le \epsilon \tau ^2 (|{\hat{A}}^+ |+1) \sum _{i \in {\hat{A}}^+} |x_i| (\nabla _i \varphi (x) \, {{\,\mathrm{sgn}\,}}(x_i) + |\nabla _j \varphi (x) |) \end{aligned}$$
(36)

From (34) and (36), it follows that the left-hand side term of (32) is less than or equal to

$$\begin{aligned} \biggl (\epsilon \tau ^2 \frac{L(2C+1)}{2} (|{\hat{A}}^+ |+1) - 1\biggr ) \sum _{i \in {\hat{A}}^+} |x_i| (\nabla _i \varphi (x) \, {{\,\mathrm{sgn}\,}}(x_i) + |\nabla _j \varphi (x) |) \end{aligned}$$

The desired result is hence obtained, since inequality (32) follows from the assumption we made on \(\epsilon\), using the fact that \(|{\hat{A}}^+ | \le n - 1\) (as a consequence of Proposition 3) and \(\sum _{i \in {\hat{A}}^+} |x_i| (\nabla _i \varphi (x) \, {{\,\mathrm{sgn}\,}}(x_i) + |\nabla _j \varphi (x) |) \ge 0\) (as a consequence of (36)). \(\square\)

We would like to highlight that the parameter \(\epsilon\) depends on n by Assumption 1. However, from the proof of the above proposition, it is clear that n could be replaced by \(|{\hat{A}}^+|+1\), with \({\hat{A}}^+\) defined as in (31). Note that \(|{\hat{A}}^+|\) might be much smaller than n.

3 The algorithm

Based on the active and non-active set estimates described above, we design a suitable active-set algorithm for solving problem (1), exploiting the property of our estimates and using an appropriate projected-gradient direction. At the beginning of each iteration k, we have a feasible point \(x^k\) and we compute \(A_{\ell _1}(x^k)\) and \(N_{\ell _1}(x^k)\), which, for ease of notation, we will refer to as \(A_{\ell _1}^k\) and \(N_{\ell _1}^k\), respectively. Then, we perform two main steps:

  • First, we produce the point \({\tilde{x}}^k\) as explained in Proposition 4, obtaining a decrease in the objective function (if \(x^k \ne {\tilde{x}}^k\));

  • Afterward, we move all the variables in \(N^k_{\ell _1}\) by computing a projected-gradient direction \(d^k\) over the given non-active manifold and using a non-monotone Armijo line search. In particular, the reference value \({\bar{\varphi }}\) for the line search is defined as the maximum among the last \(n_m\) function evaluations, with \(n_m\) being a positive parameter.

In Algorithm 1, we report the scheme of the proposed algorithm, named Active-Set algorithm for minimization over the \(\ell _1\)-ball (AS- \(\ell _1\)).

figure a
figure b

The search direction \(d^k\) at \({\tilde{x}}^k\) (see line 7 of Algorithm 1) is made of two subvectors: \(d^k_{A_{\ell _1}^k}\) and \(d^k_{N_{\ell _1}^k}\). Since we do not want to move the variables in \(A_{\ell _1}^k\), we simply set \(d^k_{A_{\ell _1}^k}=0\). For \(d^k_{N_{\ell _1}^k}\), we compute a projected gradient direction in a properly defined manifold. In particular, let \({\mathcal {B}}_{N_{\ell _1}^k}\) be the set defined as

$$\begin{aligned} {\mathcal {B}}_{N_{\ell _1}^k} = \{x\in \mathbb {R}^n :\Vert x\Vert _1 \le \tau , \, x_i = 0, \, \forall i\notin N_{\ell _1}^k\} \end{aligned}$$
(37)

and let \(P(\cdot )_{{\mathcal {B}}_{N_{\ell _1}^k}}\) denote the projection onto the \({\mathcal {B}}_{N_{\ell _1}^k}\). We also define

$$\begin{aligned} {\hat{x}}^k = P\bigl (\tilde{x}^k-m^k\nabla \varphi ({\tilde{x}}^k)\bigr )_{{\mathcal {B}}_{N_{\ell _1}^k}}, \end{aligned}$$
(38)

where \(0< {\underline{m}} \le m^k \le {\overline{m}} < \infty\) and with \({\underline{m}}\), \({\overline{m}}\) being two constants. Then, \(d^k_{N_{\ell _1}^k}\) is defined as

$$\begin{aligned} d^k_{N_{\ell _1}^k} = {\hat{x}}^k-{\tilde{x}}^k. \end{aligned}$$
(39)

In the practical implementation of AS- \(\ell _1\), we compute the coefficient \(m^k\) so that the resulting search direction is a spectral (or Barzilai–Borwein) gradient direction. This choice will be described in Sect. 4.

3.1 Global convergence analysis

In order to prove global convergence of AS- \(\ell _1\) to stationary points, we need some intermediate results. We first point out a property of our search directions, using standard results on projected directions.

Lemma 1

Let Assumption 1hold and let \(\{x^k\}\) be the sequence of points produced by AS- \(\ell _1\). At every iteration k, we have that

$$\begin{aligned} \nabla \varphi ({\tilde{x}}^k)^Td^k \le { - \frac{1}{{\overline{m}}}} \Vert d^k\Vert ^2 \end{aligned}$$
(40)

and \(\{d^k\}\) is a bounded sequence.

Proof

Using the properties of the projection, at very iteration k we have

$$\begin{aligned} ({\tilde{x}}^k - m^k\nabla \varphi ({\tilde{x}}^k)-{\hat{x}}^k)^T(x -{\hat{x}}^k) \le 0, \quad \forall x\in {\mathcal {B}}_{N_{\ell _1}^k}, \end{aligned}$$

with \(B_{N_{\ell _1}^k}\) and \({\hat{x}}^k\) being defined as in (37) and (38), respectively. Choosing \(x={\tilde{x}}^k\) in the above inequality and recalling the definition of \(d^k\) given in (39), we get

$$\begin{aligned} \nabla \varphi ({\tilde{x}}^k)^Td^k \le - \frac{1}{m^k} \Vert d^k\Vert ^2. \end{aligned}$$

Since \(m^k \le {\overline{m}}\), for all k we obtain (40).

Furthermore, from the property of the projection we have that

$$\begin{aligned} \Vert d^k\Vert = \Vert P({\tilde{x}}^k - m^k\nabla \varphi ({\tilde{x}}^k)) - {\tilde{x}}^k\Vert \le m^k \Vert \nabla \varphi ({\tilde{x}}^k)\Vert . \end{aligned}$$

Since \(m^k \le {\overline{m}}\) and \(\{\nabla \varphi ({\tilde{x}}^k)\}\) is bounded, it follows that \(\{d^k\}\) is bounded. \(\square\)

We now prove that the sequence \(\{{\bar{\varphi }}^k\}\) converges.

Lemma 2

Let Assumption 1hold and let \(\{x^k\}\) be the sequence of points produced by AS- \(\ell _1\). Then, the sequence \(\{ {\bar{\varphi }}^k\}\) is non-increasing and converges to a value \({\bar{\varphi }}\).

Proof

First note that the definition of \({\bar{\varphi }}^k\) ensures \(\bar{\varphi }^k\le \varphi ({\tilde{x}}^0)\) and hence \(\varphi ({\tilde{x}}^k)\le \varphi ({\tilde{x}}^0)\) for all k. Moreover, we have that

$$\begin{aligned} {\bar{\varphi }}^{k+1} = \max \limits _{0\le i\le \min \{n_m,k+1\}} \varphi ({\tilde{x}}^{k + 1 -i}) \le \max \{ {\bar{\varphi }}^k , \varphi ({\tilde{x}}^{k+1})\}. \end{aligned}$$

Since \(\varphi ({\tilde{x}}^{k+1}) \le {\bar{\varphi }}^k\) by the definition of the line search, we derive \({\bar{\varphi }}^{k+1} \le {\bar{\varphi }}^k\), which proves that the sequence \(\{ {\bar{\varphi }}^k\}\) is non-increasing. This sequence is bounded from below by the minimum of \(\varphi\) over the unit simplex and hence converges. \(\square\)

The next intermediate result shows that the distance between \(\{x^k\}\) and \(\{{\tilde{x}}^k\}\) converges to zero and that the sequences \(\{\varphi (x^k)\}\) and \(\{\varphi ({\tilde{x}}^k)\}\) converge to the same point, using similar arguments as in [20].

Proposition 5

Let Assumption 1hold and let \(\{x^k\}\) be the sequence of points produced by AS- \(\ell _1\). Then,

$$\begin{aligned}&\lim _{k \rightarrow \infty } \Vert {\tilde{x}}^k-x^k\Vert = 0, \end{aligned}$$
(41)
$$\begin{aligned}&\quad \lim _{k\rightarrow \infty } \varphi ({\tilde{x}}^k) = \lim _{k\rightarrow \infty } \varphi ( x^k) ={\bar{\varphi }}. \end{aligned}$$
(42)

Proof

For each \(k\in \mathbb {N}\), choose \(l(k)\in \{k - \min (k,n_m),\dots ,k\}\) such that \({\bar{\varphi }}^k = \varphi ({\tilde{x}}^{l(k)})\). From Proposition 4 we can write

$$\begin{aligned} \varphi ({\tilde{x}}^{l(k)})\le \varphi (x^{l(k)}) - CL \Vert {\tilde{x}}^{l(k)}-x^{l(k)} \Vert ^2. \end{aligned}$$
(43)

Furthermore, from the instructions of the line search and the fact that the sequence \(\{\varphi ({\tilde{x}}^{l(k)})\}\) is non-increasing, for all \(k \ge 1\)we have

$$\begin{aligned}\varphi (x^{l(k)}) \le \varphi ({\tilde{x}}^{l(k -1)}) + \gamma \alpha ^{l(k) -1} \nabla \varphi ({\tilde{x}}^{l(k) -1})^T d^{l(k) -1},\end{aligned}$$

and then,

$$\begin{aligned} \varphi ({\tilde{x}}^{l(k)}) \le \varphi ({\tilde{x}}^{l(k -1)}) + \gamma \alpha ^{l(k) -1} \nabla \varphi ({\tilde{x}}^{l(k) -1})^T d^{l(k) -1} - CL \Vert {\tilde{x}}^{l(k)}-x^{l(k)} \Vert ^2. \end{aligned}$$
(44)

Since \(\{\varphi ({\tilde{x}}^{l(k)})\}\) converges to \({\bar{\varphi }}\), we have that (43) and (44) imply

$$\begin{aligned}&\lim _{k\rightarrow \infty } \Vert {\tilde{x}}^{l(k)} - x^{l(k)}\Vert = 0, \nonumber \\&\quad \lim _{k\rightarrow \infty } \alpha ^{l(k)-1} \nabla \varphi ({\tilde{x}}^{l(k) -1})^T d^{l(k) -1} =0 . \end{aligned}$$
(45)

Furthermore, from Lemma 1 we have

$$\begin{aligned} \nabla \varphi ({\tilde{x}}^{l(k) -1})^T d^{l(k) -1} \le {- \frac{1}{{\overline{m}}}} \Vert d^{l(k) -1}\Vert ^2, \end{aligned}$$

and then the following limit holds:

$$\begin{aligned} \lim _{k\rightarrow \infty } \alpha ^{l(k) -1} \Vert d^{l(k) -1}\Vert = 0. \end{aligned}$$
(46)

Considering that \(x^{l(k)} = {\tilde{x}}^{l(k)-1} + \alpha ^{l(k) -1} d^{l(k) -1}\), (46) implies

$$\begin{aligned} \lim _{k\rightarrow \infty } \Vert {\tilde{x}}^{l(k)-1} - x^{l(k)}\Vert = 0. \end{aligned}$$

Furthermore, from the triangle inequality, we can write

$$\begin{aligned} \Vert {\tilde{x}}^{l(k)-1} - {\tilde{x}}^{l(k)}\Vert \le \Vert {\tilde{x}}^{l(k)-1} - x^{l(k)}\Vert +\Vert x^{l(k)} - {\tilde{x}}^{l(k)}.\Vert \end{aligned}$$

Then,

$$\begin{aligned} \lim _{k\rightarrow \infty } \Vert {\tilde{x}}^{l(k)-1} - {\tilde{x}}^{l(k)}\Vert = 0 \end{aligned}$$
(47)

and in particular, from the uniform continuity of \(\varphi\) over \(\{x\in \mathbb {R}^n : \Vert x\Vert _1 \le \tau \}\), we have

$$\begin{aligned} \lim _{k\rightarrow \infty }\varphi ({\tilde{x}}^{l(k)-1}) = \lim _{k\rightarrow \infty }\varphi ({\tilde{x}}^{l(k)}) = {\bar{\varphi }}. \end{aligned}$$
(48)

Let

$$\begin{aligned} {\hat{l}}(k) = l(k+n_m+2). \end{aligned}$$

We show by induction that, for any given \(j\ge 1\),

$$\begin{aligned}&\lim _{k\rightarrow \infty } \Vert x^{{\hat{l}}(k) -{(j-1)}} -{\tilde{x}}^{{\hat{l}}(k) -{(j-1)}}\Vert = 0, \end{aligned}$$
(49)
$$\begin{aligned}&\lim _{k\rightarrow \infty } \Vert {\tilde{x}}^{{\hat{l}}(k) -{(j-1)}} -{\tilde{x}}^{{\hat{l}}(k) -{j}}\Vert = 0, \end{aligned}$$
(50)
$$\begin{aligned}&\lim _{k\rightarrow \infty } \varphi ({\tilde{x}}^{{\hat{l}}(k)-j}) = \lim _{k\rightarrow \infty } \varphi ({\tilde{x}}^{l(k)}). \end{aligned}$$
(51)

If \(j=1\), since \(\{{\hat{l}}(k)\}\subset \{l(k)\}\) we have that (49), (50) and (51) follow from (45), (47) and (48), respectively.

Assume now that (49), (50) and (51) hold for a given j. Then, reasoning as in the beginning of the proof, from the instructions of the line search and considering that \(\{\varphi ({\tilde{x}}^{l(k)})\}\) is non-increasing, we can write

$$\begin{aligned} \varphi ({\tilde{x}}^{{\hat{l}}(k)-j}) \le \varphi (x^{{\hat{l}}(k)-j}) - CL \Vert {\tilde{x}}^{{\hat{l}}(k)-j}-x^{{\hat{l}}(k)-j} \Vert ^2 \end{aligned}$$

and

$$\begin{aligned} \varphi (x^{{\hat{l}}(k) -j})\le \varphi ({\tilde{x}}^{{\hat{l}}(k-(j+1))}) + \gamma \alpha ^{{\hat{l}}(k) -(j+1)} \nabla \varphi ({\tilde{x}}^{{\hat{l}}(k) -(j+1)})^\top d^{{\hat{l}}(k) -(j+1)}. \end{aligned}$$

Therefore we get

$$\begin{aligned} \begin{aligned} \varphi ({\tilde{x}}^{{\hat{l}}(k)-j}) \le&\varphi ({\tilde{x}}^{{\hat{l}}(k -(j+1))}) + \gamma \alpha ^{{\hat{l}}(k) -(j+1)} \nabla \varphi ({\tilde{x}}^{{\hat{l}}(k)-(j+1)})^T d^{{\hat{l}}(k)-(j+1)} + \\&- CL \Vert {\tilde{x}}^{l(k)-j}-x^{l(k)-j} \Vert ^2, \end{aligned} \end{aligned}$$

so that

$$\begin{aligned}&\lim _{k\rightarrow \infty } \alpha ^{{\hat{l}}(k)-(j+1)} \nabla \varphi ({\tilde{x}}^{{\hat{l}}(k)-(j+1)})^T d^{{\hat{l}}(k)-(j+1)}=0, \end{aligned}$$
(52)
$$\begin{aligned}&\lim _{k\rightarrow \infty } \Vert {\tilde{x}}^{l(k)-j}-x^{l(k)-j} \Vert =0 . \end{aligned}$$
(53)

The limit in (53) implies (49) for \(j+1\). The properties of the direction stated in Lemma 1, combined with (52), ensure that

$$\begin{aligned} \lim _{k\rightarrow \infty } \alpha ^{{\hat{l}}(k) -(j+1)} \Vert d^{{\hat{l}}(k) -(j+1)}\Vert = 0. \end{aligned}$$
(54)

Furthermore, since \(x^{{\hat{l}}(k)-j} = {\tilde{x}}^{{\hat{l}}(k)-(j+1)} + \alpha ^{{\hat{l}}(k) -(j+1)} d^{{\hat{l}}(k) -(j+1)}\), we have that (54) implies

$$\begin{aligned} \lim _{k\rightarrow \infty } \Vert {\tilde{x}}^{{\hat{l}}(k)-(j+1)} - x^{{\hat{l}}(k)-j}\Vert = 0. \end{aligned}$$

Using the triangle inequality, we can write

$$\begin{aligned} \Vert {\tilde{x}}^{{\hat{l}}(k)-(j+1)} - {\tilde{x}}^{{\hat{l}}(k)-j}\Vert \le \Vert {\tilde{x}}^{{\hat{l}}(k)-(j+1)} - x^{{\hat{l}}(k)-j}\Vert +\Vert x^{{\hat{l}}(k)-j} - {\tilde{x}}^{{\hat{l}}(k)-j}\Vert . \end{aligned}$$

Then,

$$\begin{aligned} \lim _{k\rightarrow \infty } \Vert {\tilde{x}}^{{\hat{l}}(k)-(j+1)} - {\tilde{x}}^{{\hat{l}}(k)-j}\Vert = 0 \end{aligned}$$

and in particular, from the uniform continuity of \(\varphi\) over \(\{x\in \mathbb {R}^n : \Vert x\Vert _1 \le \tau \}\), we can write

$$\begin{aligned} \lim _{k\rightarrow \infty }\varphi ({\tilde{x}}^{{\hat{l}}(k)-(j+1)}) = \lim _{k\rightarrow \infty }\varphi ({\tilde{x}}^{{\hat{l}}(k)-j}) = {\bar{\varphi }}. \end{aligned}$$

Thus we conclude that (50) and (51) hold for any given \(j\ge 1\).

Recalling that

$$\begin{aligned}&{\hat{l}}(k)-(k+1) = l(k+n_m+2)-(k+1)\le n_m+1, \\&\Vert {\tilde{x}}^{k+1} - {\tilde{x}}^{{\hat{l}}(k)}\Vert \le \sum _{{j = k+1}}^{{\hat{l}}(k)-1} \Vert {\tilde{x}}^{j+1} - {\tilde{x}}^{j}\Vert , \end{aligned}$$

we have that (50) implies

$$\begin{aligned} \lim _{k\rightarrow \infty } \Vert {\tilde{x}}^{k+1} - {\tilde{x}}^{{\hat{l}}(k)}\Vert = 0. \end{aligned}$$
(55)

Furthermore, since

$$\begin{aligned} \Vert x^{k+1} - {\tilde{x}}^{{\hat{l}}(k)}\Vert \le \Vert x^{k+1} - {\tilde{x}}^{k+1}\Vert +\Vert {\tilde{x}}^{k+1} - {\tilde{x}}^{{\hat{l}}(k)}\Vert , \end{aligned}$$

from (55) and (49) we have

$$\begin{aligned} \lim _{k\rightarrow \infty } \Vert x^{k+1} - {\tilde{x}}^{{\hat{l}}(k)}\Vert = 0. \end{aligned}$$
(56)

Since \(\{\varphi ({\tilde{x}}^{{\hat{l}}(k)})\}\) has a limit, from the uniform continuity of \(\varphi\) over \(\{x\in \mathbb {R}^n : \Vert x\Vert _1 \le \tau \}\), (56) and (55) it follows that

$$\begin{aligned} \lim _{k\rightarrow \infty } \varphi (x^{k+1}) =\lim _{k\rightarrow \infty } \varphi (x^k) = \lim _{k\rightarrow \infty } \varphi ({\tilde{x}}^{{\hat{l}}(k)}) = {\bar{\varphi }} \end{aligned}$$

and

$$\begin{aligned} \lim _{k\rightarrow \infty } \varphi ({\tilde{x}}^{k+1}) = \lim _{k\rightarrow \infty } \varphi ({\tilde{x}}^k) = \lim _{k\rightarrow \infty } \varphi ({\tilde{x}}^{{\hat{l}}(k)}) = {\bar{\varphi }}, \end{aligned}$$

proving (42). From the instructions of the algorithm and Proposition 4, we can write

$$\begin{aligned} \varphi ({\tilde{x}}^k)\le \varphi (x^k) - CL \Vert {\tilde{x}}^k-x^k \Vert ^2, \end{aligned}$$

and then from (42) we have that (41) holds. \(\square\)

The following proposition states that the directional derivative \(\nabla \varphi ({\tilde{x}}^k)^Td^k\) tends to zero.

Proposition 6

Let Assumption 1hold and let \(\{x^k\}\) be the sequence of points produced by AS- \(\ell _1\). Then,

$$\begin{aligned} \lim _{k\rightarrow \infty } \nabla \varphi ({\tilde{x}}^k)^Td^k = 0. \end{aligned}$$
(57)

Proof

To prove (57), assume by contradiction that it does not hold. Lemma 1 implies that the sequence \(\{\nabla \varphi ({\tilde{x}}^k)^Td^k\}\) is bounded, so that there must exist an infinite set \(K\subseteq {\mathbb {N}}\) such that

$$\begin{aligned}&\nabla \varphi ({\tilde{x}}^k)^Td^k < 0, \quad \forall k \in K, \end{aligned}$$
(58)
$$\begin{aligned}&\quad \lim _{k \rightarrow \infty , \, k \in K} \nabla \varphi ({\tilde{x}}^k)^Td^k = -\eta < 0, \end{aligned}$$
(59)

for some real number \(\eta >0\). Taking into account (41) and the fact that the feasible set is compact, without loss of generality we can assume that both \(\{x^k\}_K\) and \(\{{\tilde{x}}^k\}_K\) converge to a feasible point \(x^*\) (passing into a further subsequence if necessary). Namely,

$$\begin{aligned} \lim _{k\rightarrow \infty , \, k\in K} x^k = \lim _{k\rightarrow \infty , \, k\in K} {\tilde{x}}^k = x^*. \end{aligned}$$
(60)

Moreover, since the number of possible different choices of \(A^k\) and \(N^k\) is finite, without loss of generality we can also assume that

$$\begin{aligned} A^k = {\hat{A}}, \quad N^k = {\hat{N}}, \quad \forall k \in K, \end{aligned}$$

and, using the fact that \(\{d^k\}\) is a bounded sequence, that

$$\begin{aligned} \lim _{k\rightarrow \infty , \, k\in K} d^k = {\bar{d}} \end{aligned}$$
(61)

(passing again into a further subsequence if necessary). From (59), (60), (61) and the continuity of \(\nabla \varphi\), we can write

$$\begin{aligned} \nabla \varphi (x^*)^T {\bar{d}} = -\eta < 0. \end{aligned}$$
(62)

Taking into account (58), from the instructions of AS- \(\ell _1\) we have that, at every iteration \(k \in K\), a non-monotone Armijo line search is carried out (see line 2 in Algorithm 2) and a value \(\alpha ^k \in (0,1]\) is computed such that

$$\begin{aligned} \varphi (x^{k+1}) \le \varphi ({\tilde{x}}^{l(k)}) + \gamma \, \alpha ^k \, \nabla \varphi ({\tilde{x}}^k)^T d^k, \end{aligned}$$

or equivalently,

$$\begin{aligned} \varphi ({\tilde{x}}^{l(k)}) - \varphi (x^{k+1}) \ge \gamma \, \alpha ^k \, |\nabla \varphi ({\tilde{x}}^k)^T d^k |. \end{aligned}$$

From

(42), the left-hand side of the above inequality converges to zero for \(k \rightarrow \infty\), hence

$$\begin{aligned} \lim _{k \rightarrow \infty , \, k \in K} \alpha ^k\, |\nabla \varphi ({\tilde{x}}^k)^T d^k | = 0. \end{aligned}$$

Using (59), we obtain that \(\displaystyle {\lim _{k \rightarrow \infty , \, k \in K} \alpha ^k = 0}\). It follows that there exists \({\bar{k}} \in K\) such that

$$\begin{aligned} \alpha ^k < 1, \quad \forall k \ge {\bar{k}}, \, k \in K. \end{aligned}$$

From the instructions of the line search procedure, this means that \(\forall k \ge {\bar{k}}, \, k \in K\)

$$\begin{aligned} \varphi \Bigl ( {\tilde{x}}^k + \frac{\alpha ^k}{\delta } d^k \Bigr ) > \varphi ({\tilde{x}}^{l(k)}) + \gamma \, \frac{\alpha ^k}{\delta }\, \nabla \varphi ({\tilde{x}}^k)^T d^k \ge \varphi ({\tilde{x}}^k) + \gamma \, \frac{\alpha ^k}{\delta }\, \nabla \varphi ({\tilde{x}}^k)^T d^k. \end{aligned}$$
(63)

Using the mean value theorem, \(\xi ^k\in (0,1)\) exists such that

$$\begin{aligned} \varphi \Bigl ( {\tilde{x}}^k+ \frac{\alpha ^k}{\delta } d^k \Bigr ) = \varphi ({\tilde{x}}^{l(k)}) + \frac{\alpha ^k}{\delta }\nabla \varphi \Bigl ( {\tilde{x}}^k + \xi ^k\frac{\alpha ^k}{\delta } d^k \Bigr )^T d^k, \quad \forall k \ge {\bar{k}}, \, k \in K. \end{aligned}$$
(64)

In view of (63) and (64), we can write

$$\begin{aligned} \nabla \varphi \Bigl ( {\tilde{x}}^k + \xi ^k \frac{\alpha ^k}{\delta } d^k \Bigr )^T d^k > \gamma \, \nabla \varphi ({\tilde{x}}^k)^T d^k, \quad \forall k \ge {\bar{k}}, \, k \in K. \end{aligned}$$
(65)

From (60), and exploiting the fact that \(\{\xi ^k\}_K\), \(\{\alpha ^k\}_K\) and \(\{d^k\}_K\) are bounded sequences, we get

$$\begin{aligned} \lim _{k \rightarrow \infty , \, k \in K} {\tilde{x}}^k + \xi ^k \frac{\alpha ^k}{\delta } d^k = \lim _{k \rightarrow \infty , \, k \in K} {\tilde{x}}^k = x^*. \end{aligned}$$

Therefore, taking the limits in (65) we obtain that \(\nabla \varphi (x^*)^T {\bar{d}} \ge \gamma \, \nabla \varphi (x^*)^T {\bar{d}}\), or equivalently, \((1-\gamma ) \nabla \varphi (x^*)^T {\bar{d}} \ge 0\). Since \(\gamma \in (0,1)\), we get a contradiction with (62). \(\square\)

We are finally able to state the main convergence result.

Theorem 1

Let Assumption 1hold and let \(\{x^k\}\) be the sequence of points produced by AS- \(\ell _1\). Then, every limit point \(x^*\) of \(\{x^k\}\) is a stationary point of problem (1).

Proof

From Definition 1, we can characterize stationarity using condition (2). In particular, we can define the following continuous functions \(\Psi _i(x)\) to measure the stationarity violation at a feasible point x:

$$\begin{aligned} \Psi _i(x) = \max \{0, -\nabla \varphi (x)^T(\tau \,e_i - x) , -\nabla \varphi (x)^T(-\tau \,e_i - x) \}, \quad i = 1,\ldots ,n, \end{aligned}$$

so that a feasible point x is stationary if and only if \(\Psi _i(x) = 0\), \(i = 1,\ldots ,n\).

Now, let \(x^*\) be a limit point of \(\{x^k\}\) and let \(\{x^k\}_K\), \(K \subseteq {\mathbb {N}}\), be a subsequence converging to \(x^*\). Namely,

$$\begin{aligned} \lim _{k\rightarrow \infty , \, k\in K} x^k = x^*. \end{aligned}$$
(66)

Note that \(x^*\) exists, as \(\{x^k\}\) remains in the compact set \(\{x\in \mathbb {R}^n | \Vert x \Vert _1 \le \tau \}\). Since the number of possible different choices of \(A^k\) and \(N^k\) is finite, without loss of generality we can assume that

$$\begin{aligned} A^k = {\hat{A}}, \quad N^k = {\hat{N}}, \quad \forall k \in K \end{aligned}$$

(passing into a further subsequence if necessary).

By contradiction, assume that \(x^*\) is non-stationary, that is, an index \(\nu \in \{1,\ldots ,n\}\) exists such that

$$\begin{aligned} \Psi _\nu (x^*) > 0. \end{aligned}$$
(67)

First, suppose that \(\nu \in {\hat{A}}\). Then, from the expressions (19), we can write

$$\begin{aligned} 0 \le x^k_\nu \le \epsilon \tau \nabla \varphi (x^k)^T(\tau e_\nu - x^k) \qquad \text {or} \qquad 0 \ge x^k_\nu \ge \epsilon \tau \nabla \varphi (x^k)^T(\tau e_\nu + x^k), \end{aligned}$$

so that \(\Psi _\nu (x^k) = 0\), for all \(k \in {\bar{K}}\). Therefore, from (66), the continuity of \(\nabla \varphi\) and the continuity of the functions \(\Psi _i\), we get \(\Psi _\nu (x^*) = 0\), contradicting (67).

Then, \(\nu\) necessarily belongs to \({\hat{N}}\). Namely, \(x^*\) is non-stationary over \({\mathcal {B}}_{N_{\ell _1}^k}\), with \({\mathcal {B}}_{N_{\ell _1}^k}\) defined as in (37). This means that

$$\begin{aligned} x^* \ne P\bigl (x^* - {\underline{m}} \nabla \varphi (x^*)\bigr )_{{\mathcal {B}}_{N_{\ell _1}^k}}. \end{aligned}$$
(68)

Using Proposition 6 and Lemma 1, we have that \(\lim _{k\rightarrow \infty , \, k\in K} \Vert d^k\Vert = 0\), that is, recalling the definition of \(d^k\) given in (38)–(39),

$$\begin{aligned} \lim _{k\rightarrow \infty , \, k\in K} \Biggl \Vert {\tilde{x}}^k - P\bigl (\tilde{x}^k- m^k\nabla \varphi ({\tilde{x}}^k)\bigr )_{{\mathcal {B}}_{N_{\ell _1}^k}} \Biggr \Vert = 0. \end{aligned}$$

From the properties of the projection we have that

$$\begin{aligned}\Biggl \Vert {\tilde{x}}^k - P\bigl (\tilde{x}^k- m^k\nabla \varphi ({\tilde{x}}^k)\bigr )_{{\mathcal {B}}_{N_{\ell _1}^k}} \Biggr \Vert \ge \Biggl \Vert {\tilde{x}}^k - P\bigl (\tilde{x}^k- {\underline{m}}\nabla \varphi ({\tilde{x}}^k)\bigr )_{{\mathcal {B}}_{N_{\ell _1}^k}}, \Biggr \Vert \end{aligned}$$

so that the following holds

$$\begin{aligned} \lim _{k\rightarrow \infty , \, k\in K} \Biggl \Vert {\tilde{x}}^k - P\bigl (\tilde{x}^k- {\underline{m}}\nabla \varphi ({\tilde{x}}^k)\bigr )_{{\mathcal {B}}_{N_{\ell _1}^k}} \Biggr \Vert = 0. \end{aligned}$$

Using (66), the continuity of the projection and taking into account (41) in Proposition 6, we obtain

$$\begin{aligned} \Biggl \Vert x^* - P\bigl (x^* -{\underline{m}} \nabla \varphi (x^*)\bigr )_{{\mathcal {B}}_{N_{\ell _1}^k}} \Biggr \Vert = 0. \end{aligned}$$

This contradicts (68), leading to the desired result. \(\square\)

4 Numerical results

In this section, we show the practical performances of AS- \(\ell _1\) on two classes of problems frequently arising in data science and machine learning that can be formulated as problem (1):

  • LASSO problems [32], where

    $$\begin{aligned} \varphi (x) = \Vert Ax-b\Vert ^2, \end{aligned}$$
    (69)

    for given matrix \(A\in \mathbb {R}^{m\times n}\) and vector \(b\in \mathbb {R}^m\);

  • \(\ell _1\)-constrained logistic regression problems, where

    $$\begin{aligned} \varphi (x) = \sum _{i=1}^l \log (1 + \exp (-y_i x^T a_i)), \end{aligned}$$
    (70)

    with given vectors \(a_i\) and scalars \(y_i \in \{1,-1\}\), \(i=1,\ldots ,l\).

In our implementation of AS- \(\ell _1\), we used a non-monotone line search with memory length \(n_m = 10\) (see Algorithm 2) and a spectral (or Barzilai–Borwein) gradient direction for the variables in \(N_{\ell _1}^k\). In particular, the coefficient \(m^k\) appearing in (38) was set to 1 for \(k=0\) and, for \(k \ge 1\), we employed the following formula, adapting the strategy used in [2, 4, 11]:

$$\begin{aligned} m^k = {\left\{ \begin{array}{ll} \max \{{\underline{m}}, \, m^k_a\}, \quad &{} \text {if } 0< m^k_a < {\overline{m}}, \\ \max \bigl \{{\underline{m}}, \, \min \{{\overline{m}}, \, m^k_b\}\bigr \}, \quad &{} \text {if } m^k_a \ge {\overline{m}}, \\ \max \Biggl \{{\underline{m}}, \, \min \biggl \{1, \, \dfrac{\Vert \nabla _{N_{\ell _1}^k} \varphi ({\tilde{x}}^k) \Vert }{\Vert {\tilde{x}}^k_{N_{\ell _1}^k} \Vert }\biggr \}\Biggr \}, \quad &{} \text {if } m^k_a \le 0, \end{array}\right. } \end{aligned}$$

where \({\underline{m}} = 10^{-10}\), \({\overline{m}} = 10^{10}\), \(m^k_a = \dfrac{(s^{k-1})^T y^{k-1}}{\Vert s^{k-1} \Vert ^2}\), \(m^k_b = \dfrac{\Vert y^{k-1} \Vert ^2}{(s^{k-1})^T y^{k-1}}\), \(s^{k-1} = {\tilde{x}}^k_{N_{\ell _1}^k}-{\tilde{x}}^{k-1}_{N_{\ell _1}^k}\) and \(y^{k-1} = \nabla _{N_{\ell _1}^k} \varphi ({\tilde{x}}^k) - \nabla _{N_{\ell _1}^k} \varphi ({\tilde{x}}^{k-1})\).

The \(\epsilon\) parameter appearing in the active-set estimate (19) should satisfy Assumption 1 to guarantee the descent property established in Proposition 4 and the convergence of the algorithm. Since the Lipschitz constant L is in general unknown, we approximate \(\epsilon\) following the same strategy as in [9, 10, 12], where similar estimates are used. Starting from \(\epsilon = 10^{-6}\), we update its value along the iterations, reducing it whenever the expected decrease in the objective, stated in Proposition 4, is not obtained.

In our experiments, we implemented AS- \(\ell _1\) in Matlab and compared AS- \(\ell _1\) with the two following first-order methods, implemented in Matlab as well:

Finally, we report a comparison between AS- \(\ell _1\) and AS-PG, an active-set algorithm devised in [10], showing the benefit of explicitly handling the \(\ell _1\)-ball.

For every considered problem, we set the starting point equal to the origin and we first run AS- \(\ell _1\), stopping when

$$\begin{aligned} \Vert x^k - P\bigl (x^k-\nabla \varphi (x^k)\bigr )_{\ell _1}\Vert \le 10^{-6}, \end{aligned}$$

where \(P(\cdot )_{\ell _1}\) denotes the projection onto the \(\ell _1\)-ball. Then, the other methods were run with the same starting point and were stopped at the first iteration k such that

$$\begin{aligned} \varphi (x^k) \le f^* + 10^{-6}(1+|f^*|), \end{aligned}$$

with \(f^*\) being the objective value found by AS- \(\ell _1\). A time limit of 3600 s was also included in all the considered methods.

In NM-SPG, we used the default parameters (except for those concerning the stopping condition). Moreover, in AS- \(\ell _1\) and NM-SPG we employed the same projection algorithm [8], downloaded from Laurent Condat’s webpage https://lcondat.github.io/software.html.

In all codes, we made use of the Matlab sparse operator to compute \(\varphi (x)\) and \(\nabla \varphi (x)\), in order to exploit the problem structure and save computational time. The experiments were run on an Intel Xeon(R) CPU E5-1650 v2 @ 3.50GHz with 12 cores and 64 Gb RAM.

The AS- \(\ell _1\) software is available at https://github.com/acristofari/as-l1.

4.1 Comparison on LASSO instances

We considered 10 artificial instances of LASSO problems, where the objective function \(\varphi (x)\) takes the form of (69). Each instance was created by first generating a matrix \(A \in \mathbb {R}^{m \times n}\) with elements randomly drawn from a uniform distribution on the interval (0, 1), using \(n=2^{15}\) and \(m = n/2\). Then, a vector \(x^*\) was generated with all zeros, except for \(\text {round}(0.05m)\) components, which were randomly set to 1 or \(-1\). Finally, we set \(b = Ax^* + 0.001 v\), where v is a vector with elements randomly drawn from the standard normal distribution, and the \(\ell _1\)-sphere radius \(\tau\) was set to \(0.99\Vert x^*\Vert _1\).

The detailed comparison on the LASSO instances is reported in Table 1. For each instance and each algorithm, we report the final objective function value found, the CPU time needed to satisfy the stopping criterion and the percentage of zeros in the final solution, with a tolerance of \(10^{-5}\). In case an algorithm reached the time limit on an instance, we consider as final solution and final objective value those related to the last iteration performed. NM-SPG reached the time limit on all instances, being very far from \(f^*\) on 6 instances out of 10, with a difference of even two order of magnitude. AFW gets the same solutions as those obtained by AS- \(\ell _1\), being however an order of magnitude slower than AS- \(\ell _1\).

The same picture is given by Fig. 1, where we report the average optimization error \(f(x^k)-f_{\text {best}}\) over the 10 instances, with \(f_{\text {best}}\) being the minimum objective value found by the algorithms. We can notice that AS- \(\ell _1\) clearly outperforms the other two methods.

Fig. 1
figure 1

Average optimization error over LASSO instances (y axis) vs CPU time in seconds (x axis). The y axis is in logarithmic scale

Full size image
Table 1 Comparison on 10 LASSO instances. For each method, the first column (Obj) indicates the final objective value, the second column (CPU time) indicates the required time in seconds, where a star means that the time limit of 3600 s was reached, and the third column (%zeros) indicates the percentage of zeros in the final solution, with a tolerance of \(10^{-5}\). For each problem, the fastest algorithm is highlighted in bold
Full size table

4.2 Comparison on logistic regression instances

For the comparison among AS- \(\ell _1\), NM-SPG and AFW on \(\ell _1\)-constrained logistic regression problems, where the objective function \(\varphi (x)\) takes the form of (70), we considered 11 datasets for binary classification from the literature, with a number of samples l between 100 and 25,000, and a number of attributes n between 500 and 100,000. We report the complete list of datasets in Table 2.

Table 2 Datasets used in the comparison on \(\ell _1\)-constrained logistic regression problems, where l is the number of instances and n is the number of attributes
Full size table

For each dataset, we considered different values of the \(\ell _1\)-sphere radius \(\tau\), that is, 0.01n, 0.03n and 0.05n. The final results are shown in Table 3. As before, for each instance and each algorithm, we report the final objective function value found, the CPU time needed to satisfy the stopping criterion and the percentage of zeros in the final solution, with a tolerance of \(10^{-5}\). In case an algorithm reached the time limit on an instance, we consider as final solution and final objective value those related to the last iteration performed. Excluding the instance obtained from the Rev1_train.binary dataset with \(\tau = 0.05n\), the three solvers get very similar solutions on all instances, with a difference of 0.02 at most in the final objective values. When considering \(\tau = 0.01n\), AS- \(\ell _1\) is the fastest solver on 4 instances out of 11. Note that on the instance from the Farm-ads-vect dataset, AS- \(\ell _1\) is able to get the solution in a third of the CPU time needed by the other two solvers. On the other instances, the CPU time needed by AS- \(\ell _1\) is always comparable with the one needed by the fastest solver. Looking at the results for larger values of \(\tau\), we can notice that the instances get more difficult and in general less sparse. For \(\tau = 0.03n\) and \(\tau = 0.05n\), AS- \(\ell _1\) is the fastest solver on all the instances but two, those obtained from the Arcene and the Dorothea datasets, which are however addressed within 2 s. On other instances, such as those built from the Real-sim and the Rev1_train.binary datasets, AS- \(\ell _1\) is one or even two orders of magnitude faster with respect to NM-SPG and AFW.

Table 3 Comparison on \(\ell _1\)-constrained logistic regression problems with different values of the sphere radius \(\tau\)
Full size table

In Fig. 2 we report the average optimization error \(f(x^k)-f_{\text {best}}\) over the 11 instances, for each value of \(\tau\), with \(f_{\text {best}}\) being the minimum objective value found by the algorithms. We can notice that AFW is outperformed by the other two algorithms, which have similar performance when considering the average optimization error above \(10^{-2}\). When considering the average optimization error below \(10^{-2}\), we see that AS- \(\ell _1\) outperforms NM-SPG too.

Fig. 2
figure 2

Average optimization error over \(\ell _1\)-constrained logistic regression instances (y axis) vs CPU time in seconds (x axis). The y axis is in logarithmic scale

Full size image

4.3 Comparison with AS-PG

We now compare AS- \(\ell _1\) with AS-PG, an active set algorithm that uses a projected gradient direction, presented in [10]. As for AFW, AS-PG was run by reformulating (1) as an optimization problem over the unit simplex. In Figs. 3 and 4, we report the comparison over LASSO and logistic regression instances, respectively. The considered LASSO instances are obtained as before with \(n=2^{12}\) and \(m = n/2\). As we can easily see by taking a look at the plots, the proposed approach guarantees better performances.

Fig. 3
figure 3

Average optimization error over LASSO instances (y axis) vs CPU time in seconds (x axis). The y axis is in logarithmic scale

Full size image
Fig. 4
figure 4

Average optimization error over \(\ell _1\)-constrained logistic regression instances (y axis) vs CPU time in seconds (x axis). The y axis is in logarithmic scale

Full size image

5 Conclusions

In this paper, we focused on minimization problems over the \(\ell _1\)-ball and described a tailored active-set algorithm. We developed a strategy to guess, along the iterations of the algorithm, which variables should be zero at a solution. A reduction in terms of objective function value is guaranteed by simply fixing to zero those variables estimated to be active. The active-set estimate is used in combination with a projected spectral gradient direction and a non-monotone Armijo line search. We analyzed in depth the global convergence of the proposed algorithm. The numerical results show the efficiency of the method on LASSO and sparse logistic regression instances, in comparison with two widely-used first-order methods.