Newton-type methods near critical solutions of piecewise smooth nonlinear equations

Abstract

It is well-recognized that in the presence of singular (and in particular nonisolated) solutions of unconstrained or constrained smooth nonlinear equations, the existence of critical solutions has a crucial impact on the behavior of various Newton-type methods. On the one hand, it has been demonstrated that such solutions turn out to be attractors for sequences generated by these methods, for wide domains of starting points, and with a linear convergence rate estimate. On the other hand, the pattern of convergence to such solutions is quite special, and allows for a sharp characterization which serves, in particular, as a basis for some known acceleration techniques, and for the proof of an asymptotic acceptance of the unit stepsize. The latter is an essential property for the success of these techniques when combined with a linesearch strategy for globalization of convergence. This paper aims at extensions of these results to piecewise smooth equations, with applications to corresponding reformulations of nonlinear complementarity problems.

1 Introduction

In the recent publications [10, 11, 17], it has been demonstrated that for smooth nonlinear equations with singular (and possibly nonisolated) solutions, the local behavior of various Newton-type methods is strongly affected by the existence of critical solutions, as defined in [18].

Specifically, [17] extends the results in [14] from the basic Newton method to perturbed versions, establishing their local convergence to a solution satisfying a certain 2-regularity property, from wide domains of starting points. This framework covers a large range of Newton-type methods, including those supplied with stabilization mechanisms, and developed especially for tackling the case of nonisolated solutions, like the Levenberg–Marquardt method [22, 23] (see also [24, Chapter 10.2], and [2, 26, 27] for advanced local convergence theories), the LP-Newton method [5], and stabilized sequential quadratic programming for optimization [7, 16, 19, 25] (see also [20, Chapter 7]). Under the mentioned 2-regularity property, the convergence rate of the methods in the framework is linear with a common ratio of 1/2, and cannot be any faster, whereas the 2-regularity requirement can only hold at those singular solutions that are critical.

The results of [17] were further extended in [10] to the case of constrained equations, with applications to complementarity problems through their piecewise decompositions.

The special convergence pattern of the basic Newton method established in [14] serves as a basis of some techniques for acceleration of its convergence, such as extrapolation and overrelaxation [13, 15]. However, when combined with a linesearch strategy for globalization of convergence, these techniques are only useful when the basic method asymptotically accepts the unit stepsize. The latter property, which is not at all automatic near singular solutions, has been established in [10].

In this paper, we aim at obtaining the results of [10, 11, 17] for a much more general setting of (unconstrained and constrained) piecewise smooth equations, which further allows to treat complementarity problems directly rather than through their piecewise decompositions. We emphasize that we do not propose any new algorithms here, and therefore, do not provide numerical comparisons; we rather analyze theoretical properties of known (classes of) algorithms under nonstandard circumstances. The results in this work strongly rely on those in [10, 11, 17], and are obtained by combining techniques from these references with specificities of piecewise smooth structures. However, these combinations involve some rather subtle ingredients, like choosing a direction with appropriate collection of active smooth selections associated to it in Theorems 1 and 2, the role of condition (32) for globalization issues, separation of constraints into two parts in Theorem 3, etc. All these ingredients are crucial to cover a much wider territory then in [10, 11, 17], which is demonstrated by rather nontrivial direct (i.e., not requiring any decompositions) applications to complementarity problems in Sect. 4.

The rest of the paper is structured as follows. In Sect. 2, we consider unconstrained piecewise smooth equations. Section 2.1 contains the problem setting and the related objects and terminology, including the basic piecewise Newton method. We also discuss the requirement of 2-regularity, needed for the subsequent development, and its relations to the concept of a critical solution. In Sect. 2.2, we provide an upper estimate of the set of active smooth selections at nearby points, playing the key role for the entire paper, and discuss the related assumptions. Section 2.3 provides the result on local convergence for a large class of algorithms that can be modeled as a perturbed piecewise Newton method. Section 2.4 deals with asymptotic acceptance of the unit stepsize. Section 3 is concerned with extensions of the obtained results to the case of constrained piecewise smooth equations. Finally, in Sect. 4, we consider the applicability of the developed theory to nonlinear complementarity problems reformulated using the min complementarity function.

Some words about our notation which is fairly standard. By $\langle \cdot ,\, \cdot \rangle$ and $\Vert \cdot \Vert$ we denote the Euclidean inner product and the corresponding norm, respectively, unless specified otherwise. For a given index set J, we write $u_J$ for the subvector of a vector u, with components $u_j$, $j\in J$. Similarly, $M_J$ stands for a submatrix of a matrix M, with rows $M_j$, $j\in J$. By ${\mathcal {I}}$, we denote an identity matrix of a size always clear from the context. Furthermore, $\ker M$ and ${\mathop {\mathrm{im}}}M$ stand for the null space and the range space of a matrix (linear operator) M, respectively. Finally, $R_U(u)$ stands for the radial cone to a set U at $u\in U$, i.e., the set of directions $v\in {\mathbb {R}}^p$ such that $u+tv\in U$ for all $t>0$ small enough.

2 Piecewise Newton-type methods

2.1 Problem setting and preliminaries

We consider the equation

$$\begin{aligned} \varPhi (u) = 0, \end{aligned}$$

(1)

where $\varPhi :{\mathbb {R}}^p\rightarrow {\mathbb {R}}^p$ is a piecewise smooth mapping. By the latter we mean that $\varPhi$ is continuous, and there exist smooth selection mappings $\varPhi ^1,\, \ldots ,\, \varPhi ^q:{\mathbb {R}}^p\rightarrow {\mathbb {R}}^p$ with

$$\begin{aligned} \varPhi (u)\in \{ \varPhi ^1(u),\, \ldots ,\, \varPhi ^q(u)\} \quad \forall \, u\in {\mathbb {R}}^p. \end{aligned}$$

A mapping is called smooth, if it is continuously differentiable.

For a given $u\in {\mathbb {R}}^p$, let

$$\begin{aligned} {\mathcal {A}}(u) := \{ j\in \{ 1,\, \ldots ,\, q\} \mid \varPhi (u) = \varPhi ^j(u)\} \end{aligned}$$

(2)

stand for the set of indices of all selection mappings active at u. By the continuity requirements, the set-valued mapping ${\mathcal {A}}(\cdot )$ is evidently outer semicontinuous, i.e., ${\mathcal {A}}(u)\subset {\mathcal {A}}({\bar{u}})$ holds for any ${\bar{u}}\in {\mathbb {R}}^p$ and all $u\in {\mathbb {R}}^p$ close enough to ${\bar{u}}$. From [6, Lemma 4.6.1] we have that $\varPhi$ is directionally differentiable at ${\bar{u}}$ in any direction $v\in {\mathbb {R}}^p$, with the directional derivative $\varPhi '({\bar{u}};\, v)$, and

$$\begin{aligned} \varPhi ({\bar{u}}+v) = \varPhi ({\bar{u}})+\varPhi '({\bar{u}};\, v)+o(\Vert v\Vert ) \end{aligned}$$

(3)

as $v\rightarrow 0$. Moreover, $\varPhi '({\bar{u}};\, \cdot )$ is everywhere continuous, and

$$\begin{aligned} \varPhi '({\bar{u}};\, v)\in \{ (\varPhi ^j)'({\bar{u}})v\mid j\in {\mathcal {A}}({\bar{u}})\} \quad \forall \, v\in {\mathbb {R}}^p. \end{aligned}$$

(4)

Let $G:{\mathbb {R}}^p\rightarrow {\mathbb {R}}^{p\times p}$ be any mapping possessing the following property:

$$\begin{aligned} G(u)\in \{ (\varPhi ^j)'(u)\mid j\in {\mathcal {A}}(u)\} \quad \forall \, u\in {\mathbb {R}}^p. \end{aligned}$$

(5)

Near a current iterate $u^k\in {\mathbb {R}}^p$, piecewise Newton-type methods rely on the following approximation of Eq. (1):

$$\begin{aligned} \varPhi (u^k)+G(u^k)(u-u^k) = 0. \end{aligned}$$

(6)

Observe that there exists $j_k\in {\mathcal {A}}(u^k)$ such that (6) can be written as

$$\begin{aligned} \varPhi ^{j_k}(u^k)+(\varPhi ^{j_k})'(u^k)(u-u^k) = 0, \end{aligned}$$

(7)

which is the classical Newton method iteration system for the smooth equation

$$\begin{aligned} \varPhi ^{j_k}(u) = 0. \end{aligned}$$

(8)

According to the outer semicontinuity property of ${\mathcal {A}}(\cdot )$, for any $u^k$ close enough to some fixed solution ${\bar{u}}$ of (1), it holds that $j_k\in {\mathcal {A}}(u^k)$ implies $j_k\in {\mathcal {A}}({\bar{u}})$. If ${\mathcal {A}}({\bar{u}})$ is a singleton $\{ {{\widehat{\jmath }}} \}$, then the piecewise Newton method reduces to the classical one for the smooth Eq. (8) with $j_k = {{\widehat{\jmath }}}$. In this case, various local results obtained for smooth (constrained) equations can be easily extended to the piecewise smooth setting.

The case when ${\mathcal {A}}({\bar{u}})$ may be not a singleton is much more interesting and involved, as $j_k$ can vary with k, no matter how close the iterates are to ${\bar{u}}$. This case will be addressed below, with the main emphasis on the situation when the solution ${\bar{u}}$ in question is singular in a well-defined sense implying that $(\varPhi ^{j})'({\bar{u}})$ is singular for some $j\in {\mathcal {A}}({\bar{u}})$. Observe that the latter is automatic when ${\bar{u}}$ is a nonisolated solution of (1). As explained above, our focus will be on the results on local attraction to some special solutions of this kind for various piecewise Newton-type methods, as well as on acceptance of the unit stepsize.

In order to explain which singular solutions of Eq. (1) we are interested in, let us recall the concept of 2-regularity, in one of its equivalent forms, convenient for our purposes. Assuming that a selection mapping $\varPhi ^{j}:{\mathbb {R}}^p\rightarrow {\mathbb {R}}^p$ is twice differentiable at ${\bar{u}}\in {\mathbb {R}}^p$, $\varPhi ^{j}$ is said to be 2-regular at ${\bar{u}}$ in a direction ${\bar{v}}\in {\mathbb {R}}^p$ if there exists no $v\in \ker (\varPhi ^{j})'({\bar{u}})$, $v\not = 0$, such that

$$\begin{aligned} (\varPhi ^{j})''({\bar{u}})[{\bar{v}},\, v]\in \mathop {{\mathrm{im}}}(\varPhi ^{j})'({\bar{u}}). \end{aligned}$$

Observe that this property is stable subject to small perturbations of ${\bar{v}}$, the fact that will be used in the discussion preceding Theorem 1. The key assumption in that theorem and other main results presented below is the existence of ${\bar{v}}\in \ker (\varPhi ^{j})'({\bar{u}})$, ${\bar{v}}\ne 0,$ such that $\varPhi ^{j}$ is 2-regular at ${\bar{u}}$ in the direction ${\bar{v}}$. According to [17, Proposition 1], if this assumption holds for $j\in {\mathcal {A}}({\bar{u}})$, then ${\bar{u}}$ is necessarily a critical solution of the equation

$$\begin{aligned} \varPhi ^j(u) = 0, \end{aligned}$$

(9)

in a sense of [18, Definition 1]. That is why we are talking about the behavior of Newton-type methods near critical solutions.

2.2 Key construction

For any ${\bar{u}}\in {\mathbb {R}}^p$ and $v\in {\mathbb {R}}^p$, define the index set

$$\begin{aligned} {\mathcal {A}}({\bar{u}},\, v) := \{ j\in {\mathcal {A}}({\bar{u}})\mid v\in \ker (\varPhi ^j)'({\bar{u}})\} . \end{aligned}$$

(10)

Further assuming that $\Vert v\Vert = 1$, for any $\varepsilon >0$ and $\delta >0$, define the set

$$\begin{aligned} K_{\varepsilon ,\, \delta }({\bar{u}},\, v):= \left\{ u\in {\mathbb {R}}^p\left| \, 0 < \Vert u-{\bar{u}}\Vert \le \varepsilon ,\; \left\| \frac{u-{\bar{u}}}{\Vert u-{\bar{u}}\Vert } -v\right\| \le \delta \right. \right\} . \end{aligned}$$

(11)

Proposition 1

Let $\varPhi :{\mathbb {R}}^p\rightarrow {\mathbb {R}}^p$ be piecewise smooth, with smooth selection mappings $\varPhi ^1,\, \ldots ,\, \varPhi ^q:{\mathbb {R}}^p\rightarrow {\mathbb {R}}^p$. For a given solution ${\bar{u}}$ of (1), let ${\bar{v}}\in {\mathbb {R}}^p$ be such that $\Vert {\bar{v}}\Vert = 1$ and

$$\begin{aligned} \varPhi '({\bar{u}};\, {\bar{v}}) = 0. \end{aligned}$$

(12)

Then there exist $\varepsilon >0$ and $\delta >0$ such that

$$\begin{aligned} {\mathcal {A}}(u) \subset {\mathcal {A}}({\bar{u}},\, {\bar{v}})\quad \forall \, u\in K_{\varepsilon ,\, \delta }({\bar{u}},\, {\bar{v}}). \end{aligned}$$

(13)

Proof

We argue by contradiction: suppose that there exist sequences $\{ \varepsilon _k\} \rightarrow 0+$, $\{ \delta _k\} \rightarrow 0+$, and $\{ u^k\} \subset {\mathbb {R}}^p$ such that, for all k, it holds that $u^k\in K_{\varepsilon _k,\, \delta _k}({\bar{u}},\, {\bar{v}})$, and there exists $j^k\in {\mathcal {A}}(u^k) \setminus {\mathcal {A}}({\bar{u}},\, {\bar{v}})$. Passing to subsequences, if necessary, we may suppose that $j^k = j$ is the same for all k. Outer semicontinuity of ${\mathcal {A}}(\cdot )$ at ${\bar{u}}$ yields that $j\in {\mathcal {A}}({\bar{u}})$. Thus, since $j\not \in {\mathcal {A}}({\bar{u}},\, {\bar{v}})$, (10) implies that ${\bar{v}}\not \in \ker (\varPhi ^j)'({\bar{u}})$. Hence, there exists $\gamma > 0$ such that

$$\begin{aligned} \Vert \varPhi (u^k)\Vert = \Vert \varPhi ^j(u^k)\Vert = \Vert (\varPhi ^j)'({\bar{u}})(u^k-{\bar{u}})\Vert +o(\Vert u^k-{\bar{u}}\Vert ) \ge \gamma \Vert u^k-{\bar{u}}\Vert \end{aligned}$$

(14)

for all k large enough. On the other hand, from (11) we have that

$$\begin{aligned} \left\| \frac{u^k-{\bar{u}}}{\Vert u^k-{\bar{u}}\Vert } - {\bar{v}}\right\| \le \delta _k\rightarrow 0 \end{aligned}$$

as $k\rightarrow \infty$, and therefore, according to (3), (12), and continuity of $\varPhi '({\bar{u}};\, \cdot )$,

$$\begin{aligned} \varPhi (u^k) = \Vert u^k-{\bar{u}}\Vert \varPhi '\left( {\bar{u}};\, \frac{u^k-{\bar{u}}}{\Vert u^k-{\bar{u}}\Vert }\right) +o(\Vert u^k-{\bar{u}}\Vert ) = o(\Vert u^k-{\bar{u}}\Vert ), \end{aligned}$$

contradicting (14). $\square$

The following corollary of Proposition 1 is evident.

Corollary 1

Under the assumptions of Proposition 1, let ${\mathcal {A}}({\bar{u}},\, {\bar{v}})$ consist of a single index $\widehat{\jmath }$.

Then there exist $\varepsilon >0$ and $\delta >0$ such that

$$\begin{aligned} {\mathcal {A}}(u) = \{ {{\widehat{\jmath }}} \} \quad \forall \, u\in K_{\varepsilon ,\, \delta }({\bar{u}},\, {\bar{v}}). \end{aligned}$$

(15)

The next example shows that, in general, assumption (12) cannot be dropped in Corollary 1, and hence, in Proposition 1.

Example 1

Let $p = 1$, $\varPhi (u) = \min \{ u,\, u^2\}$. Then $\varPhi$ is piecewise smooth, with smooth selection functions $\varPhi ^1(u) = u$ and $\varPhi ^2(u) = u^2$, both active at the solution ${\bar{u}}= 0$ of (1). For ${\bar{v}} = -1$, we have that ${\mathcal {A}}({\bar{u}},\, {\bar{v}}) = \{ {{\widehat{\jmath }}}\}$ with ${{\widehat{\jmath }}} = 2$, as $(\varPhi ^2)'(0) = 0$ and $(\varPhi ^1)'(0){\bar{v}} = -1$. At the same time, for all $u < 0$, we have $|\varPhi (u)| = -u$, and hence, $\varPhi '(0;\, {\bar{v}}) = -1$, so that (12) does not hold, and (15) (and hence, (13)) do not hold as well, since ${\mathcal {A}}(t\bar{v}) = \{ 1\}$ for all $t>0$.

Remark 1

Assumption (12) in Proposition 1 is implied by the following condition related to some further restrictions on the kind of piecewise smoothness, which will play an important role for constrained equations (cf. (32)), and especially for constrained reformulations of complementary problems in Sect. 4 below:

$$\begin{aligned} \exists \, j\in {\mathcal {A}}({\bar{u}},\, {\bar{v}})\quad \text{ such } \text{ that } \quad \Vert \varPhi (u)\Vert \le \Vert \varPhi ^j(u)\Vert \quad \forall \, u\in K_{\varepsilon ,\, \delta }({\bar{u}},\, {\bar{v}}), \end{aligned}$$

(16)

with some $\varepsilon > 0$ and $\delta > 0$. Indeed, by the same reasoning as in the proof of Proposition 1, from (3), (10), and (16), we obtain that

$$\begin{aligned} \Vert \varPhi '({\bar{u}};\, {\bar{v}})\Vert= & {} \Vert u-{\bar{u}}\Vert \varPhi '\left( {\bar{u}};\, \frac{u-{\bar{u}}}{\Vert u-{\bar{u}}\Vert }\right) +o(\Vert u-{\bar{u}}\Vert )\\= & {} \Vert \varPhi (u)\Vert +o(\Vert u-{\bar{u}}\Vert )\\\le & {} \Vert \varPhi ^j(u)\Vert +o(\Vert u-{\bar{u}}\Vert )\\= & {} \Vert u-{\bar{u}}\Vert \left\| (\varPhi ^j)'({\bar{u}})\frac{u-{\bar{u}}}{\Vert u-{\bar{u}}\Vert }\right\| +o(\Vert u-{\bar{u}}\Vert )\\= & {} o(\Vert u-{\bar{u}}\Vert ) \end{aligned}$$

for $u\in K_{\varepsilon ,\, \delta }({\bar{u}},\, {\bar{v}})$ as $\varepsilon \rightarrow 0+$, $\delta \rightarrow 0+$, yielding (12).

The converse implication is valid assuming that ${\mathcal {A}}({\bar{u}},\, {\bar{v}})$ consists of a single index ${{\widehat{\jmath }}}$. In this case, the inequality in (16) with $j={{\widehat{\jmath }}}$ holds as equality for $\varepsilon > 0$ and $\delta > 0$ small enough. This is an immediate consequence of Corollary 1. The next example demonstrates that when ${\mathcal {A}}({\bar{u}},\, {\bar{v}})$ is not a singleton, condition (12) may hold when (16) does not.

Fig. 1

Piecewise Newton method for Example 2

Example 2

Let $p = 1$, $\varPhi (u) = \min \{ -u^2,\, -u^2+\varphi (u)\}$, where $\varphi :{\mathbb {R}}\rightarrow {\mathbb {R}}$ is given by

$$\begin{aligned} \varphi (u) := \left\{ \begin{array}{ll} u^5\sin (1/u),&{}{\text{ if }} u\not = 0,\\ 0,&{}{\text{ if }} u = 0. \end{array} \right. \end{aligned}$$

Then $\varPhi$ is piecewise smooth, with smooth selection functions $\varPhi ^1(u) = -u^2$ and $\varPhi ^2(u) = -u^2+\varphi (u)$, both active at the solution ${\bar{u}}= 0$ of (1), and

$$\begin{aligned} \varPhi (u) = \left\{ \begin{array}{ll} \varPhi ^1(u),&{}{\text{ if }} \varphi (u)\ge 0,\\ \varPhi ^2(u),&{}{\text{ if }} \varphi (u) < 0. \end{array} \right. \end{aligned}$$

For any ${\bar{v}}\ne 0$, we have that ${\mathcal {A}}({\bar{u}},\, {\bar{v}}) = \{ 1,\, 2\}$, as $(\varPhi ^1)'(0) = (\varPhi ^2)'(0) = 0$, implying further that $\varPhi (u) = O(u^2)$, thus (12) is satisfied. At the same time, take any sequence $\{ u^k\} \rightarrow 0+$ such that for all k it holds that $\sin (1/u^k) > 0$. Then $\varPhi (u^k) = \varPhi ^1(u^k) = -(u^k)^2$, and hence,

$$\begin{aligned} |\varPhi ^2(u^k)| = |-(u^k)^2+\varphi (u^k)| < |\varPhi (u^k)|, \end{aligned}$$

where we have taken into account that $\varphi (u) = O(|u|^5) = o(u^2)$. On the other hand, by a similar reasoning, if $\sin (1/u^k) < 0$, then $\varPhi (u^k) = \varPhi ^2(u^k) = -(u^k)^2+\varphi (u^k)$, and hence,

$$\begin{aligned} |\varPhi ^1(u^k)| = (u^k)^2 < |\varPhi (u^k)|. \end{aligned}$$

Therefore, (16) does not hold.

Figure 1 shows the graphs of the smooth selections $\varPhi ^1$ (dashed line) and $\varPhi ^2$ (solid line), and a typical run of the method given by (6): white circles show the iterates corresponding to $\varPhi ^1$, while black circles – to $\varPhi ^2$.

Proposition 1 gives a key for extending the results in [11, 17] to the piecewise smooth case.

2.3 Attraction to critical solutions

We first present a result on local attraction of the perturbed piecewise Newton method to a solution which is critical with respect to some smooth selection mappings active at this solution. The essence of this result is as follows: Proposition 1 allows to show that the perturbed piecewise Newton method fits the algorithmic framework of [17, Theorem 1] when this framework is applied to the smooth equations corresponding to an appropriate collection of active smooth selections.

For given ${\bar{u}}\in {\mathbb {R}}^p$ and ${\bar{v}}\in {\mathbb {R}}^p$, assuming that ${\mathcal {N}} = \ker (\varPhi ^j)'({\bar{u}})$ is the same for all $j\in {\mathcal {A}}({\bar{u}},\, {\bar{v}})$, we will use the uniquely defined decomposition of every $u\in {\mathbb {R}}^p$ into the sum $u=u_1+u_2$, with $u_1\in {\mathcal {N}}^\bot$ and $u_2\in {\mathcal {N}}$. Let $\Pi$ be the orthogonal projector onto ${\mathcal {N}}$ in ${\mathbb {R}}^p$.

The assumption that the null spaces of $(\varPhi ^j)'({\bar{u}})$ coincide for all $j\in {\mathcal {A}}({\bar{u}},\, {\bar{v}})$ may seem restrictive, while in fact it is not, in the following sense. Suppose that for a given ${\bar{v}}$, there exist $j_1,\, j_2\in {\mathcal {A}}({\bar{u}},\, {\bar{v}})$ such that $\ker (\varPhi ^{j_1})'({\bar{u}})\not = \ker (\varPhi ^{j_2})'({\bar{u}})$. Therefore, there must exist ${\widehat{v}}\in {\mathbb {R}}^p$ such that it belongs, say, to the first of these null spaces but not to the second. Then, for any real t close enough to 0, it holds that ${\bar{v}}+t{\widehat{v}}\in \ker (\varPhi ^{j_1})'({\bar{u}})$, ${\bar{v}}+t\widehat{v}\not \in \ker (\varPhi ^{j_2})'({\bar{u}})$, while the evident outer semicontinuity of ${\mathcal {A}}({\bar{u}},\, \cdot )$ implies that ${\mathcal {A}}({\bar{u}},\, {\bar{v}}+t{\widehat{v}})\subset {\mathcal {A}}({\bar{u}},\, {\bar{v}})$. By (4), we then have that, in particular, ${\mathcal {A}}({\bar{u}},\, {\bar{v}}+t{\widehat{v}})$ cannot contain both indices $j_1$ and $j_2$ simultaneously. Continuing this procedure with ${\bar{v}}$ replaced by ${\bar{v}}+t{\widehat{v}}$, we end up with ${\bar{v}}$ such that either ${\mathcal {A}}({\bar{u}},\, {\bar{v}})$ is a singleton, or the null spaces of $(\varPhi ^j)'({\bar{u}})$ coincide for all $j\in {\mathcal {A}}({\bar{u}},\, {\bar{v}})$. Moreover, this ${\bar{v}}$ can be taken arbitrarily close to the original one, and therefore, the 2-regularity properties in the original direction will be preserved for this ${\bar{v}}$.

Theorem 1

Let $\varPhi :{\mathbb {R}}^p\rightarrow {\mathbb {R}}^p$ be piecewise smooth, with smooth selection mappings $\varPhi ^1,\, \ldots ,\, \varPhi ^q:{\mathbb {R}}^p\rightarrow {\mathbb {R}}^p$. For a given solution ${\bar{u}}$ of (1), let ${\bar{v}}\in {\mathbb {R}}^p$ with $\Vert {\bar{v}}\Vert = 1$ be satisfying the following requirements:

• 1. For every $j\in {\mathcal {A}}({\bar{u}},\, {\bar{v}})$, the selection mapping $\varPhi ^j$ is twice differentiable near ${\bar{u}}$, with its second derivative being Lipschitz-continuous with respect to ${\bar{u}}$, that is,

  $$\begin{aligned} (\varPhi ^j)''(u)-(\varPhi ^j)''({\bar{u}})=O(\Vert u-{\bar{u}}\Vert ) \end{aligned}$$

  (17)

  as $u\rightarrow {\bar{u}}$, $\ker (\varPhi ^j)'({\bar{u}}) = {\mathcal {N}}$, where the linear subspace ${\mathcal {N}}$ does not depend on j, and $\varPhi ^j$ is 2-regular at ${\bar{u}}$ in direction ${\bar{v}}$.

• 2. Condition (12) holds.

Then, for any $G:{\mathbb {R}}^p\rightarrow {\mathbb {R}}^{p\times p}$ satisfying (5), any $\varOmega :{\mathbb {R}}^p\rightarrow {\mathbb {R}}^{p\times p}$ and $\omega :{\mathbb {R}}^p\rightarrow {\mathbb {R}}^p$ satisfying

$$\begin{aligned} \varOmega (u) = O(\Vert u-{\bar{u}}\Vert ),\quad \omega (u) = O(\Vert u-{\bar{u}}\Vert ^2), \end{aligned}$$

(18)

$$\begin{aligned} \Pi \varOmega (u) = O(\Vert u_1-{\bar{u}}_1\Vert )+O(\Vert u-{\bar{u}}\Vert ^2), \end{aligned}$$

(19)

$$\begin{aligned} \Pi \omega (u) = O(\Vert u-{\bar{u}}\Vert \Vert u_1-{\bar{u}}_1\Vert )+O(\Vert u-{\bar{u}}\Vert ^3) \end{aligned}$$

(20)

as $u\rightarrow {\bar{u}}$, and any ${{\widehat{\varepsilon }}} >0$ and ${{\widehat{\delta }}} >0$, there exist $\varepsilon > 0$ and $\delta > 0$ such that for every starting point $u^0\in K_{\varepsilon ,\, \delta }({\bar{u}},\, {\bar{v}})$, there exists the unique sequence $\{ u^k\} \subset {\mathbb {R}}^p$ such that for each k, the iterate $u^{k+1}$ solves

$$\begin{aligned} \varPhi (u^k)+(G(u^k)+\varOmega (u^k))(u-u^k) = \omega (u^k), \end{aligned}$$

(21)

and for this sequence, and for each k, it holds that $u_2^k\not ={\bar{u}}_2$, $u^k\in K_{{{\widehat{\varepsilon }}} ,\, {{\widehat{\delta }}} }({\bar{u}},\, {\bar{v}})$, $\{ u^k\}$ converges to ${\bar{u}}$, $\{ \Vert u^k-{\bar{u}}\Vert \}$ converges to zero monotonically,

$$\begin{aligned} \frac{\Vert u_1^{k+1}-{\bar{u}}_1\Vert }{\Vert u_2^{k+1}-{\bar{u}}_2\Vert } = O(\Vert u^k-{\bar{u}}\Vert ) \end{aligned}$$

(22)

as $k\rightarrow \infty$, and

$$\begin{aligned} \lim _{k\rightarrow \infty } \frac{\Vert u_2^{k+1}-{\bar{u}}_2\Vert }{\Vert u_2^k-{\bar{u}}_2\Vert } = \frac{1}{2} . \end{aligned}$$

(23)

Proof

According to Proposition 1, if ${{\widehat{\varepsilon }}} >0$ and ${{\widehat{\delta }}} >0$ are small enough, then for all $u^k\in K_{{{\widehat{\varepsilon }}} ,\, {{\widehat{\delta }}} }({\bar{u}},\, {\bar{v}})$, Eq. (21) coincides with

$$\begin{aligned} \varPhi ^j(u^k)+ ((\varPhi ^j)'(u^k)+\varOmega (u^k))(u-u^k) = \omega (u^k) \end{aligned}$$

(24)

for some $j\in {\mathcal {A}}({\bar{u}},\, {\bar{v}})$, defining a perturbed Newton method step for the smooth Eq. (9). The proof in [17, Theorem 1] does not depend on the index j of this equation. Rather, it relies on the existence of the perturbed Newton method step $v^k$ for this equation at $u^k\in K_{\widehat{\varepsilon },\, {{\widehat{\delta }}} }({\bar{u}},\, {\bar{v}})$ with sufficiently small ${{\widehat{\varepsilon }}} >0$ and ${{\widehat{\delta }}} >0$, and on the description of $v^k$ in the form of the estimates on $v_1^k$ and $v_2^k$, i.e., the properties established in [17, Lemma 1]. Note that $u = u^k+v^k$ solves Eq. (24). It remains to observe that, under the stated assumptions, this lemma is applicable to Eq. (9) and the corresponding iteration Eq. (24) for every $j\in {\mathcal {A}}({\bar{u}},\, {\bar{v}})$, and since this index set is finite, the needed estimates on $v_1^k$ and $v_2^k$ can be considered the same for all $j\in {\mathcal {A}}({\bar{u}},\, {\bar{v}})$. Then the assertion in [17, Theorem 1] gives the desired conclusions. $\square$

Remark 2

According to [17, Lemma 1], the iterates in Theorem 1 also satisfy

$$\begin{aligned} u^{k+1}-u^k = O(\Vert u^k-{\bar{u}}\Vert ) \end{aligned}$$

(25)

as $u^k\rightarrow {\bar{u}}$, an estimate that will be needed below.

Similarly to Proposition 1, assumption (12) cannot be dropped in Theorem 1, even when $\varOmega (\cdot )\equiv 0$ and $\omega (\cdot )\equiv 0$ so that (21) transforms into (6).

Example 1

(continued) In that example, $\varPhi ^2$ is 2-regular at 0 in the direction ${\bar{v}} = -1$ (as $(\varPhi ^2)''(0)[{\bar{v}}] = -2$). Therefore, all assumptions of Theorem 1 are satisfied with this ${\bar{v}}$, except for (12).

For any $u^0 < 0$, no matter how close to 0, we have that $\varPhi (u^0) = u^0$, ${\mathcal {A}}(u^0) = \{ 1\}$, and according to (5), $G(u^0) = 1$. Then the next iterate generated by solving (6) is $u^1 = 0$, disagreeing with the assertion of Theorem 1.

Example 2

(continued) This example demonstrates the situation when Theorem 1 is applicable with ${\mathcal {A}}({\bar{u}},\, {\bar{v}})$ not being a singleton. Indeed, one can easily see that, say, for ${\bar{v}} = 1$, requirement 1 of Theorem 1 is satisfied (with ${\mathcal {N}} ={ \mathbb {R}}$), while (12) in requirement 2 has already been demonstrated above.

Numerical experiments show that switching between different smooth selections is typical for iterates generated by solving (6).

As explained in [17], the perturbation terms $\varOmega$ and $\omega$ serve to cover various specific Newton-type methods within the general framework (21). We next mention several such methods available for the piecewise smooth setting. To begin with, as already mentioned above, taking $\varOmega (\cdot )\equiv 0$ and $\omega (\cdot )\equiv 0$ yields the basic piecewise Newton method (6).

Subproblem (6) can be replaced by the following unconstrained convex optimization problem:

$$\begin{aligned} \begin{array}{llll} \text{ min }&\displaystyle \frac{1}{2} \Vert \varPhi (u^k)+G(u^k)(u-u^k)\Vert ^2, \end{array} \end{aligned}$$

(26)

which is always solvable (unlike (6)), though the solution set can be a non-singleton affine manifold. The family of algorithms employing this subproblem (e.g., with specific rules for choosing a solution of (26) when it is not unique, like picking up the solution minimizing $\Vert u-u^k\Vert$) can be referred to as the piecewise Gauss–Newton method.

A stabilized version of both the piecewise Newton method and the piecewise Gauss–Newton method is the piecewise Levenberg–Marquardt method [4, 8]. It generates the next iterate as the solution of the subproblem

$$\begin{aligned} \begin{array}{ll} \text{ min }&\displaystyle \frac{1}{2} \Vert \varPhi (u^k)+G(u^k)(u-u^k) \Vert ^2 +\frac{1}{2} \rho (u^k)\Vert u-u^k\Vert ^2, \end{array} \end{aligned}$$

(27)

where $\rho :{\mathbb {R}}^p\rightarrow {\mathbb {R}}_+$ defines the regularization parameter. If $\rho (u^k)>0$, the objective function of this subproblem is strongly convex quadratic, and in particular, the subproblem has a unique solution. A typical choice is $\rho (u) := \Vert \varPhi (u)\Vert ^\tau$ with some $\tau > 0$. For our purposes here, we require that $\tau \ge 2$. Since $\Vert \cdot \Vert$ denotes the Euclidean norm, solving (27) is the same as solving the linear equation

$$\begin{aligned} G(u^k)^\top \varPhi (u^k)+(G(u^k)^\top G(u^k)+\rho (u^k){\mathcal {I}})(u-u^k) = 0. \end{aligned}$$

(28)

A different stabilizing construction is the piecewise LP-Newton method [5]. In our setting, its subproblem has the form

$$\begin{aligned} \begin{array}{ll} \text{ min } &{} \gamma \\ \text{ s.t. } &{} \Vert \varPhi (u^k)+G(u^k)(u-u^k)\Vert \le \gamma \Vert \varPhi (u^k)\Vert ^2, \\ &{}\Vert u-u^k\Vert \le \gamma \Vert \varPhi (u^k)\Vert , \end{array} \end{aligned}$$

(29)

with variables $(u,\, \gamma )\in {\mathbb {R}}^p\times { \mathbb {R}}$. If $\Vert \cdot \Vert$ denotes the $l_\infty$-norm, then this is a linear program (hence the name of the method). It can be easily seen that (29) is always solvable, unless $u^k$ is a solution of (1), but a solution of (29) need not be unique, and it is assumed that an arbitrary solution can be picked up.

By considerations similar to those in [17], it follows that under the assumptions of Theorem 1, all these methods can be interpreted through the perturbed piecewise Newton method framework (21). Specifically, if $u^k\in K_{\widehat{\varepsilon },\, {{\widehat{\delta }}} }({\bar{u}},\, {\bar{v}})$ with sufficiently small ${{\widehat{\varepsilon }}} >0$ and ${{\widehat{\delta }}} >0$, then $u^{k+1}$ produced by these methods satisfies (21) with appropriate choices of $\varOmega$ and $\omega$ (sometimes not defined explicitly). This implies that the conclusions of Theorem 1 are valid for all these methods.

2.4 Acceptance of the unit stepsize

Our next result is concerned with acceptance of the unit stepsize by the piecewise Newton method supplied with a natural linesearch procedure, near a solution which is critical with respect to some active smooth selection mappings. Again, the key tool is Proposition 1 allowing to show that this method fits [11, Proposition 3] applied to proper active smooth selections. To that end, we state the following model algorithm.

Algorithm 1

Choose $u^0\in {\mathbb {R}}^p$, $\sigma \in (0,\, 1)$, $\theta \in (0,\, 1)$, and set $k=0$.

• 1. If $\varPhi (u^k)=0$, stop.

• 2. Compute ${\widetilde{u}}^{k+1}$ as a solution of (6), and set $v^k = {\widetilde{u}}^{k+1}-u^k$.

• 3. Set $\alpha =1$. If the inequality

  $$\begin{aligned} \Vert \varPhi (u^k+\alpha v^k)\Vert \le (1-\sigma \alpha )\Vert \varPhi (u^k)\Vert \end{aligned}$$

  (30)

  is satisfied, set $\alpha _k=\alpha$. Otherwise, replace $\alpha$ by $\theta \alpha$, check the inequality (30) again, etc., until (30) becomes valid.

• 4. Set $u^{k+1}=u^k+\alpha _k v^k$.

• 5. Increase k by 1 and go to Step 1.

Theorem 2

Under the assumptions of Theorem 1, for any $G:{\mathbb {R}}^p\rightarrow {\mathbb {R}}^{p\times p}$ satisfying (5), any ${{\widehat{\varepsilon }}} >0$, ${{\widehat{\delta }}} >0$, and any $\sigma \in (0,\, 3/4)$ and $\theta \in (0,\, 1)$, there exist $\varepsilon > 0$ and $\delta > 0$ such that for every starting point $u^0\in K_{\varepsilon ,\, \delta }({\bar{u}},\, {\bar{v}})$, Algorithm 1uniquely defines the sequence $\{ u^k\}$, $u^k\in K_{{{\widehat{\varepsilon }}},\, {{\widehat{\delta }}} }({\bar{u}},\, {\bar{v}})$ for all k, and (30) holds with $\alpha = 1$ for all k large enough.

Proof

The reasoning is essentially the same as for Theorem 1, but with [17, Lemma 1] replaced by [11, Lemma 1], and with [17, Theorem 1] replaced by [11, Proposition 3]. One should also note that since ${\mathcal {A}}({\bar{u}},\, {\bar{v}})$ is finite, all the constants arising along the way of proving [11, Proposition 3] can be chosen the same for all $j\in {\mathcal {A}}({\bar{u}},\, {\bar{v}})$. $\square$

Apart from playing a key role in establishing that Algorithm 1 can be expected to inherit the linear convergence rate of the piecewise Newton method, Theorem 2 is essential in this context for justification of known techniques for acceleration of convergence, such as extrapolation and overrelaxation; see [13, 15] and [11, 12].

3 Constrained case

3.1 Problem setting

We now consider the constrained version of Eq. (1), namely,

$$\begin{aligned} \varPhi (u) = 0,\quad u\in U, \end{aligned}$$

(31)

where $U\subset {\mathbb {R}}^p$ is a closed convex set. Such constraints can be exogenous by nature (e.g., when solutions of the unconstrained equation make physical sense only if they satisfy these constraints, like nonnegativity restrictions on the components of u representing quantities), or be intrinsic ingredients of the problem setting (e.g., in some reformulations of complementarity conditions). On the other hand, artificially imposing relevant constraints can be essential for justification of strong local convergence properties of Newton-type methods [5, 8], as well as for globalization of their convergence.

Even though Theorem 2 is valid and characterizes an important local feature of Algorithm 1, the linesearch procedure in this algorithm does not make much sense, in general, as the direction $v^k$ of the piecewise Newton method does not need to be a direction of descent for $\Vert \varPhi (\cdot )\Vert$ at $u^k$. However, suppose that there exists $U\subset {\mathbb {R}}^p$ with the following property:

$$\begin{aligned} \Vert \varPhi (u)\Vert \le \Vert \varPhi ^j(u)\Vert \quad \forall \, j\in \{ 1,\, \ldots ,\, q\} ,\; \forall \, u\in U \end{aligned}$$

(32)

(cf. (16)). This important kind of piecewise smoothness has already been considered in [9, (4.8)]. Since there exists $j_k\in {\mathcal {A}}(u^k)$ such that $u^k+v^k$ solves (7), and assuming that $\Vert \varPhi ^{j_k}(u^k)\Vert = \Vert \varPhi (u^k)\Vert \not = 0$, we obtain in a standard way that $v^k$ is a direction of descent for $\Vert \varPhi ^{j_k}(\cdot )\Vert$ at $u^k$, where this function is smooth with its gradient at $u^k$ equal to $((\varPhi ^{j_k})'(u^k))^\top \varPhi ^{j_k}(u^k)/\Vert \varPhi ^{j_k}(u^k)\Vert$. Assuming now that $u^k\in U$, and $v^k$ is a feasible direction for U at $u^k$ (which is of course not automatic, and has to be ensured by appropriate modifications of Algorithm 1; see below), from (32) we have that

$$\begin{aligned} \Vert \varPhi (u^k+\alpha v^k)\Vert \le \Vert \varPhi ^{j_k}(u^k+\alpha v^k)\Vert <\Vert \varPhi ^{j_k}(u^k)\Vert = \Vert \varPhi (u^k)\Vert \end{aligned}$$

for all $\alpha > 0$ small enough.

Employing Proposition 1, one can readily extend Theorems 1 and 2 to the constrained case, along the lines of [10]. Specifically, under the additional assumption ${\bar{v}}\in \mathop {\mathrm{int}}R_U({\bar{u}})$, one can claim that in these theorems $\varepsilon > 0$ and $\delta > 0$ can be taken small enough so that the sequence $\{ u^k\}$ in question entirely belongs to U.

However, as will be demonstrated in Sect. 4, such results cannot be applied directly to, say, constrained reformulations of complementarity problems, because the requirement ${\bar{v}}\in \mathop {\mathrm{int}}R_U({\bar{u}})$ appears too restrictive for the choices of U relevant in that context, in the absence of strict complementarity. To that end, in the next Sect. 3.2, we will assume that the interiority assumption on ${\bar{v}}$ holds only for a part of constrains, while the other constraints are observed by the iteration of the piecewise Newton method itself. Afterwards, we will show how this framework, being combined with the unconstrained Theorem 1, allows to cover various implementable Newton-type methods intended for solving the constrained problem (31). In Sect. 4, all the developed machinery will be applied to complementarity problems.

3.2 Main result for the constrained case

Combining Theorem 1 with [10, Lemma 3.1], we obtain the following constrained counterpart of that theorem, but concerned with the basic piecewise Newton method only. Later in this section, we demonstrate how this result, combined with Theorem 1 for the unconstrained case, allows to cover various Newton-type methods for solving the constrained Eq. (31).

Theorem 3

Let $\varPhi :{\mathbb {R}}^p\rightarrow {\mathbb {R}}^p$ be piecewise smooth, with smooth selection mappings $\varPhi ^1,\, \ldots ,\, \varPhi ^q:{\mathbb {R}}^p\rightarrow{ \mathbb {R}}^p$. For a given solution ${\bar{u}}$ of (31), let ${\bar{v}}\in {\mathbb {R}}^p$ with $\Vert {\bar{v}}\Vert = 1$, a convex set $P = P({\bar{v}})\subset { \mathbb {R}}^p$, and a set $Q = Q({\bar{v}})\subset {\mathbb {R}}^p$, with $U = P\cap Q$, be satisfying the following requirements:

• 1. For every $j\in {\mathcal {A}}({\bar{u}},\, {\bar{v}})$, the selection mapping $\varPhi ^j$ is twice differentiable near ${\bar{u}}$, (17) holds as $u\in U$ tends to ${\bar{u}}$, $\ker (\varPhi ^j)'({\bar{u}}) = {\mathcal {N}}$, where the linear subspace ${\mathcal {N}}$ does not depend on j, and $\varPhi$ is 2-regular at ${\bar{u}}$ in a direction ${\bar{v}}$.

• 2. Condition (12) holds.

• 3. It holds that ${\bar{v}}\in \mathop {\mathrm{int}}P$.

• 4. There exist ${\widetilde{\varepsilon }} > 0$ and ${\widetilde{\delta }} > 0$ such that for every $j\in {\mathcal {A}}({\bar{u}},\, {\bar{v}})$, and for any $u^k\in K_{{\widetilde{\varepsilon }}\, {\widetilde{\delta }} }({\bar{u}},\, {\bar{v}})\cap U$, any solution of the equation

  $$\begin{aligned} \varPhi ^j(u^k)+(\varPhi ^j)'(u^k)(u-u^k) = 0 \end{aligned}$$

  belongs to Q.

Then, for any $G:{\mathbb {R}}^p\rightarrow {\mathbb {R}}^{p\times p}$ be satisfying (5), and any ${{\widehat{\varepsilon }}} >0$ and ${{\widehat{\delta }}} >0$, there exist $\varepsilon > 0$ and $\delta > 0$ such that for every starting point $u^0\in K_{\varepsilon ,\, \delta }({\bar{u}},\, {\bar{v}})\cap U$, there exists the unique sequence $\{ u^k\} \subset {\mathbb {R}}^p$ such that for each k, the iterate $u^{k+1}$ solves (6), and for this sequence, and for each k, it holds that $u_2^k\not ={\bar{u}}_2$, $u^k\in K_{{{\widehat{\varepsilon }}} ,\, {{\widehat{\delta }}} }({\bar{u}},\, {\bar{v}})\cap U$, $\{ u^k\}$ converges to ${\bar{u}}$, $\{ \Vert u^k-{\bar{u}}\Vert \}$ converges to zero monotonically, and estimates (22) and (23) hold.

Similarly to Remark 1, one can see that requirement 2 in Theorem 3 is automatically satisfied if

$$\begin{aligned} \exists \, {{\widehat{\jmath }}} \in {\mathcal {A}}({\bar{u}},\, {\bar{v}})\quad \text{ such } \text{ that } \quad \Vert \varPhi (u)\Vert \le \Vert \varPhi ^{{{\widehat{\jmath }}} }(u)\Vert \quad \forall \, u\in K_{\varepsilon ,\, \delta }({\bar{u}},\, \bar{v})\cap U, \end{aligned}$$

(33)

with some $\varepsilon > 0$ and $\delta > 0$. Observe that (33) holds if (32) is valid.

Under the assumptions of Theorem 3, one can also apply Theorem 2 in order to establish asymptotic acceptance of the unit stepsize; there is no need to state this result separately in the constrained case.

We now consider some implementable Newton-type methods for problem (31).

Given a current iterate $u^k\in U$, the next iterate $u^{k+1}$ of the constrained piecewise Gauss–Newton method is defined by solving the subproblem

$$\begin{aligned} \begin{array}{llll} \text{ min }&\displaystyle \frac{1}{2} \Vert \varPhi (u^k)+G(u^k)(u-u^k)\Vert ^2&\text{ s.t. }&u\in U. \end{array} \end{aligned}$$

(34)

The objective function of this subproblem is convex quadratic, and if U is polyhedral, (34) always has a solution due to the Frank–Wolfe theorem [3, Theorem 2.8.1], but a solution of this subproblem needs not be unique, in general. However, under the assumptions of Theorem 3, we evidently obtain that, when initialized appropriately, the piecewise Gauss–Newton method uniquely defines the iterative sequence coinciding with the sequence of the unconstrained piecewise Newton method, and hence, inherits all the properties of the latter, specified in Theorem 1.

An alternative possibility is to solve the unconstrained piecewise Newton iteration system (6) for $u_N^k$, or the unconstrained piecewise Gauss–Newton subproblem (26) for $u_{GN}^k$, and then define $u^{k+1}$ as the projection of $u_N^k$ or $u_{GN}^k$ onto U. This yields the projected piecewise Newton method and the projected piecewise Gauss–Newton method, respectively. Recall that neither existence nor uniqueness of solutions of (6) can be guaranteed without further assumptions, while (26) is always solvable, but its solution set can be a non-singleton affine manifold. Yet again, under the assumptions of Theorem 3, we readily get the same conclusions as for the constrained piecewise Gauss–Newton method: all the three methods behave identically to the unconstrained piecewise Newton method, when initialized appropriately.

The stabilized version of the constrained piecewise Gauss–Newton method is the constrained piecewise Levenberg–Marquardt method [21] with the following constrained counterpart of subproblem (27):

$$\begin{aligned} \begin{array}{llll} \text{ min }&\displaystyle \frac{1}{2} \Vert \varPhi (u^k)+G(u^k)(u-u^k) \Vert ^2 +\frac{1}{2} \rho (u^k)\Vert u-u^k\Vert ^2&\text{ s.t. }&u\in U. \end{array} \end{aligned}$$

(35)

Assuming that $\rho (u^k) > 0$ (which holds automatically for typical choices of $\rho (\cdot )$ discussed above, provided the current iterate $u^k\in U$ is not a solution of (31)), this subproblem has the unique solution $u^{k+1}$. According to Theorem 3, if ${{\widehat{\varepsilon }}} >0$ and $\widehat{\delta }>0$ are small enough, then the inclusion $u^k\in K_{\widehat{\varepsilon },\, {{\widehat{\delta }}} }({\bar{u}},\, {\bar{v}})$ implies the existence of the unique $u_N^k$ solving (6), and this $u_N^k$ belongs to U. In particular, it is feasible in (35), and therefore,

$$\begin{aligned} \Vert \varPhi (u^k)+G(u^k)(u^{k+1}-u^k)\Vert ^2+\rho (u^k)\Vert u^{k+1}-u^k\Vert ^2 \le \rho (u^k)\Vert u_N^k-u^k\Vert ^2, \end{aligned}$$

implying that

$$\begin{aligned} \Vert \varPhi (u^k)+G(u^k)(u^{k+1}-u^k)\Vert \le \sqrt{\rho (u^k)} \Vert u_N^k-u^k\Vert . \end{aligned}$$

Moreover, according to estimate (25) in Remark 2 applied with $\varOmega \equiv 0$ and $\omega \equiv 0$, we have that $u_N^k-u^k = O(\Vert u^k-{\bar{u}}\Vert )$ as $u^k\rightarrow {\bar{u}}$. Therefore, if $\rho (\cdot )=\Vert \varPhi (\cdot )\Vert ^\tau$ with $\tau \ge 2$, then $u^{k+1}$ solves (21) with $\varOmega \equiv 0$ and some $\omega (\cdot )$ satisfying $\omega (u) = O(\Vert u-{\bar{u}}\Vert \Vert \varPhi (u)\Vert )$ as $u\rightarrow {\bar{u}}$. As demonstrated in [17], these perturbation mappings $\varOmega$ and $\omega$ satisfy (18)–(20). This allows to apply Theorem 1, with the corresponding conclusions for the constrained piecewise Levenberg–Marquardt method.

The constrained piecewise LP-Newton method is a natural extension of (29) to the constrained setting, and in fact, the method was originally introduced in [5] precisely for the constrained setting, with the subproblem

$$\begin{aligned} \begin{array}{ll} \text{ min } &{} \gamma \\ \text{ s.t. } &{} \Vert \varPhi (u^k)+G(u^k)(u-u^k)\Vert \le \gamma \Vert \varPhi (u^k)\Vert ^2, \\ &{}\Vert u-u^k\Vert \le \gamma \Vert \varPhi (u^k)\Vert ,\\ &{}u\in U, \end{array} \end{aligned}$$

(36)

with variables $(u,\, \gamma )\in {\mathbb {R}}^p\times {\mathbb {R}}$. For $u_N^k$ defined as above, we then have that $(u_N^k,\, \Vert u_N^k-u^k\Vert /\Vert \varPhi (u^k)\Vert )$ is feasible in (36), and hence, the optimal value $\gamma (u^k)$ of this problem satisfies $\gamma (u^k)\le \Vert u_N^k-u^k\Vert /\Vert \varPhi (u^k)\Vert$. Similarly to (29), subproblem (36) is always solvable, and for any solution $u^{k+1}$ it holds that

$$\begin{aligned} \Vert \varPhi (u^k)+G(u^k)(u^{k+1}-u^k)\Vert \le \gamma (u^k)\Vert \varPhi (u^k)\Vert ^2\le \Vert u_N^k-u^k\Vert \Vert \varPhi (u^k)\Vert . \end{aligned}$$

This leads to the same conclusions for the constrained piecewise LP-Newton method as those derived above for the constrained piecewise Levenberg–Marquardt method.

4 Applications to complementarity problems

Consider now the nonlinear complementarity problem (NCP)

$$\begin{aligned} x\ge 0,\quad F(x)\ge 0,\quad \langle x,\, F(x)\rangle =0, \end{aligned}$$

(37)

with a smooth mapping $F:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$.

4.1 Unconstrained reformulation

Setting $u := x$ (and $p := n$), problem (37) is equivalent to Eq. (1) with the mapping $\varPhi :{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ defined by

$$\begin{aligned} \varPhi (u):=\min \{ u,\, F(u)\} , \end{aligned}$$

(38)

where the min-operation is applied componentwise.

Let $q := 2^n$, and fix any one-to-one mapping $j\mapsto I(j)$ from $\{ 1,\, \ldots ,\, q\}$ to the set of all different subsets of $\{ 1,\, \ldots ,\, n\}$ (including $\emptyset$ and the entire $\{ 1,\, \ldots ,\, n\}$). Then the mapping $\varPhi$ defined in (38) is piecewise smooth, and the corresponding smooth selection mappings $\varPhi ^j:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ have the components

$$\begin{aligned} \varPhi ^j_i(u) := \left\{ \begin{array}{ll} u_i,&{} \text{ if } i\in I(j),\\ F_i(u) &{} \text{ otherwise }, \end{array} \right. \quad i = 1,\, \ldots ,\, n,\; j = 1,\, \ldots ,\, q. \end{aligned}$$

(39)

Therefore, for a given $u\in {\mathbb {R}}^n$, the set of indices of active selection mappings defined according to (2) takes the form

$$\begin{aligned} {\mathcal {A}}(u) = \{ j\in \{ 1,\, \ldots ,\, q\} \mid I(j) = J\cup I_<(u),\; J\subset I_=(u)\} , \end{aligned}$$

(40)

where

$$\begin{aligned} \begin{array}{ccl} I_>(u)&{}:=&{}\{ i\in \{ 1,\, \ldots ,\, n\} \mid u_i > F_i(u)\} ,\\ I_=(u)&{}:=&{}\{ i\in \{ 1,\, \ldots ,\, n\} \mid u_i = F_i(u)\} ,\\ I_<(u)&{}:=&{}\{ i\in \{ 1,\, \ldots ,\, n\} \mid u_i < F_i(u)\} \end{array} \end{aligned}$$

is a natural partitioning of the index set $\{1,\, \ldots ,\, n\}$. Hence, the requirement (5) on the choice of a mapping $G:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^{n\times n}$ can be written for the rows $G_i(u)$ of G(u) as follows:

$$\begin{aligned} {\text{ for }} {\text{ some }} J\subset I_=(u),\quad G_i(u) = \left\{ \begin{array}{ll} e^i, &{} \text{ if } i\in J\cup I_<(u),\\ F_i'(u) &{} {\text{ otherwise }}, \end{array} \right. \quad i = 1,\, \ldots ,\, n, \end{aligned}$$

(41)

where $e^i = (0,\, \ldots ,\, 0,\, 1,\, 0,\, \ldots ,\, 0)$, with 1 at the i-th place, $i = 1,\, \ldots ,\, n$.

With these objects defined, in order to solve NCP (37), one can apply the methods discussed in Sect. 2.3 to Eq. (1) with $\varPhi$ defined in (38).

We proceed with deriving conditions allowing to apply Theorem 1 in this context. Observe that if ${\bar{x}}$ is a solution of (37), then

$$\begin{aligned} \begin{array}{ccccl} I_>&{}:=&{}I_>({\bar{x}})&{}=&{}\{ i\in \{ 1,\, \ldots ,\, n\} \mid {\bar{x}}_i > F_i({\bar{x}}) = 0\} ,\\ I_=&{}:=&{}I_=({\bar{x}})&{}=&{}\{ i\in \{ 1,\, \ldots ,\, n\} \mid {\bar{x}}_i = 0 = F_i({\bar{x}})\} ,\\ I_<&{}:=&{}I_<({\bar{x}})&{}=&{}\{ i\in \{ 1,\, \ldots ,\, n\} \mid 0 = {\bar{x}}_i < F_i({\bar{x}})\} . \end{array} \end{aligned}$$

For brevity, we will use the notation $\setminus J := I_=\setminus J$.

The following is [20, Proposition 3.21]; we state it here for convenience of references below.

Lemma 1

Let ${\bar{x}}$ be a solution of (37) with $F:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ being differentiable at ${\bar{x}}$, and consider any ${\bar{\xi }} \in {\mathbb {R}}^n$, ${\bar{\xi }} \not = 0$.

Then condition (12) is satisfied for $\varPhi$ defined in (38), ${\bar{u}}:= {\bar{x}}$, ${\bar{v}} := {\bar{\xi }} /\Vert {\bar{\xi }} \Vert$, if and only if ${\bar{\xi }}$ is a solution of the linear complementarity system

$$\begin{aligned} \xi _{I_<} = 0,\quad F_{I_>}'({\bar{x}})\xi = 0,\quad \xi _{I_=} \ge 0,\quad F_{I_=}'({\bar{x}})\xi \ge 0,\quad \langle \xi _{I_=},\, F_{I_=}'({\bar{x}})\xi \rangle = 0. \end{aligned}$$

(42)

Proposition 2

Let ${\bar{x}}$ be a solution of (37) with $F:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ being twice differentiable near ${\bar{x}}$, with its second derivative being Lipschitz-continuous with respect to ${\bar{x}}$. Assume that for some collection of index sets $J_r\subset I_=$, $r = 1,\, \ldots ,\, s$, and for some ${\bar{\xi }} \in {\mathbb {R}}^n$, ${\bar{\xi }} \not = 0$, the following properties are satisfied:

• 1. It holds that

  $$\begin{aligned} {\bar{\xi }} _J\not = 0\quad \text{ or }\quad \frac{\partial F_{\setminus J\cup I_>}}{\partial x_{\setminus J\cup I_>}} ({\bar{x}}) {\bar{\xi }} _{\setminus J\cup I_>} \not = 0\quad \forall \, J\subset I_=:\; J\not = J_r\; \forall \, r = 1,\, \ldots ,\, s. \end{aligned}$$

  (43)

• 2. For every $r \in \{ 1,\, \ldots ,\, s\}$,

  $$\begin{aligned} \left\{ \xi \in {\mathbb {R}}^n\left| \, \xi _{J_r\cup I_<} = 0,\; \frac{\partial F_{\setminus J_r\cup I_>}}{\partial x_{\setminus J_r\cup I_>}} ({\bar{x}}) \xi _{\setminus J_r\cup I_>} = 0 \right. \right\} = {\mathcal {N}}, \end{aligned}$$

  (44)

  where the linear subspace ${\mathcal {N}}$ does not depend on r.

• 3. For every $r \in \{ 1,\, \ldots ,\, s\}$, there exists no $\xi \in {\mathbb {R}}^n$ with $\xi _{\setminus J_r\cup I_>}\not = 0$, satisfying

  $$\begin{aligned} \xi \in {\mathcal {N}},\quad \frac{\partial ^2F_{\setminus J_r\cup I_>}}{\partial x_{\setminus J_r\cup I_>}^2} ({\bar{x}}) \left[ {\bar{\xi }} _{\setminus J_r\cup I_>},\, \xi _{\setminus J_r\cup I_>}\right] \in \mathop {\mathrm{im}}\frac{\partial F_{\setminus J_r\cup I_>}}{\partial x_{\setminus J_r\cup I_>}} ({\bar{x}}). \end{aligned}$$

  (45)

• 4. It holds that

  $$\begin{aligned} {\bar{\xi }} \in {\mathcal {N}} \end{aligned}$$

  (46)

  and

  $$\begin{aligned} {\bar{\xi }} _{\setminus J_\cup } \ge 0,\quad \frac{\partial F_{J_\cap }}{\partial x_{\setminus J_\cup \cup I_>}} ({\bar{x}}) {\bar{\xi }} _{\setminus J_\cup \cup I_>} \ge 0, \end{aligned}$$

  (47)

  where

  $$\begin{aligned} J_\cup := \bigcup _{r = 1}^s J_r,\quad J_\cap := \bigcap _{r = 1}^s J_r. \end{aligned}$$

  (48)

Then the assumptions of Theorem 1are satisfied for $\varPhi$ defined in (38), ${\bar{u}}:= {\bar{x}}$, ${\bar{v}} := {\bar{\xi }} /\Vert {\bar{\xi }} \Vert$, and with ${\mathcal {A}}({\bar{u}},\, {\bar{v}}) = \{ j\in \{ 1,\, \ldots ,\, 2^n\} \mid \exists \, r\in \{ 1,\, \ldots ,\, s\}: I(j) = J_r\cup I_<\}.$

It is easy to see that using the definitions in (48), the set ${\mathcal {N}}$ in (44) can be written as

$$\begin{aligned} {\mathcal {N}} = \left\{ \xi \in {\mathbb {R}}^n\left| \, \xi _{J_\cup \cup I_<} = 0,\; \frac{\partial F_{\setminus J_\cap \cup I_>}}{\partial x_{\setminus J_\cup \cup I_>}} ({\bar{x}}) \xi _{\setminus J_\cup \cup I_>} = 0 \right. \right\} . \end{aligned}$$

(49)

Indeed, $\xi _{J_r\cup I_<} = 0$ holds for all $r = 1,\, \ldots ,\, s$ if and only if $\xi _{J_\cup \cup I_<} = 0$, and taking into account these equalities,

$$\begin{aligned} \frac{\partial F_{\setminus J_\cap \cup I_>}}{\partial x_{\setminus J_\cup \cup I_>}} ({\bar{x}}) \xi _{\setminus J_\cup \cup I_>} = F_{\setminus J_\cap \cup I_>}'({\bar{x}})\xi = \frac{\partial F_{\setminus J_\cap \cup I_>}}{\partial x_{\setminus J_r\cup I_>}} ({\bar{x}}) \xi _{\setminus J_r\cup I_>} \end{aligned}$$

for all $r = 1,\, \ldots ,\, s$. It remains to observe that, according to (48),

$$\begin{aligned} \setminus J_\cap = \setminus \bigcap _{r = 1}^s J_r = \bigcup _{r = 1}^s \setminus J_r. \end{aligned}$$

Proof

According to (39) and (40), for any $J\subset I_=$ and the associated $j\in {\mathcal {A}}({\bar{x}})$ with $I(j) = J\cup I_<$, we have that (after the appropriate re-ordering of rows and columns)

$$\begin{aligned} (\varPhi ^j)'({\bar{x}}) = \left( \begin{array}{cc} {\mathcal {I}}_{J\cup I_<}&{}0\\ \displaystyle \frac{\partial F_{\setminus J\cup I_>}}{\partial x_{J\cup I_<}} ({\bar{x}})&{} \displaystyle \frac{\partial F_{\setminus J\cup I_>}}{\partial x_{\setminus J\cup I_>}} ({\bar{x}}) \end{array} \right) . \end{aligned}$$

(50)

Then

$$\begin{aligned} \ker (\varPhi ^j)'({\bar{x}}) = \left\{ \xi \in {\mathbb {R}}^n\left| \, \xi _{J\cup I_<} = 0,\; \frac{\partial F_{\setminus J\cup I_>}}{\partial x_{\setminus J\cup I_>}} ({\bar{u}}) \xi _{\setminus J\cup I_>} = 0 \right. \right\} . \end{aligned}$$

(51)

In particular, (44) and (46) imply that $\ker (\varPhi ^j)'({\bar{x}}) = {\mathcal {N}}$ and ${\bar{\xi }} \in \ker (\varPhi ^j)'({\bar{x}})$ for all $j\in {\mathcal {A}}$, where

$$\begin{aligned} {\mathcal {A}} := \{ j\in \{ 1,\, \ldots ,\, 2^n\} \mid \exists \, r\in \{ 1,\, \ldots ,\, s\}: I(j) = J_r\cup I_<\} \subset {\mathcal {A}} ({\bar{x}}). \end{aligned}$$

(52)

Furthermore, (44), (46), and (51), imply that the condition

$$\begin{aligned} {\bar{\xi }} \not \in \ker (\varPhi ^j)'({\bar{x}})\quad \forall \, j\in {\mathcal {A}}({\bar{x}})\setminus {\mathcal {A}} \end{aligned}$$

can be written as (43). Summarizing these considerations, we conclude that ${\mathcal {A}}({\bar{u}},\, {\bar{v}})$ defined according to (10) coincides with ${\mathcal {A}}$ in (52), and $\ker (\varPhi ^j)'({\bar{u}}) = {\mathcal {N}}$ for all $j\in {\mathcal {A}}({\bar{u}},\, {\bar{v}})$.

We next deal with the 2-regularity condition completing requirement 1 of Theorem 1. Take any $j\in {\mathcal {A}}({\bar{u}},\, {\bar{v}})$ and the associated $r\in \{ 1,\, \ldots ,\, s\}$ with $I(j) = J_r\cup I_<$. Observe that according to (50),

$$\begin{aligned} \mathop {\mathrm{im}}(\varPhi ^j)'({\bar{x}}) = \left\{ y\in {\mathbb {R}}^n\left| \, y_{\setminus J_r\cup I_>} -\frac{\partial F_{\setminus J_r\cup I_>}}{\partial x_{J_r\cup I_<}} ({\bar{x}}) y_{J_r\cup I_<}\in \mathop {\mathrm{im}}\frac{\partial F_{\setminus J_r\cup I_>}}{\partial x_{\setminus J_r\cup I_>}} ({\bar{x}}) \right. \right\} , \end{aligned}$$

(53)

and according to (39), (44), and (46),

$$\begin{aligned} (\varPhi ^j)''({\bar{x}})[{\bar{\xi }} ] = \left( \begin{array}{cc} 0&{}0\\ \displaystyle \frac{\partial ^2F_{\setminus J_r\cup I_>}}{\partial x_{J_r\cup I_<} \partial x_{\setminus J_r\cup I_>}} ({\bar{x}}) \left[ {\bar{\xi }} _{\setminus J_r\cup I_>}\right] &{} \displaystyle \frac{\partial ^2F_{\setminus J_r\cup I_>}}{\partial x_{\setminus J_r\cup I_>}^2} ({\bar{x}}) \left[ {\bar{\xi }} _{\setminus J_r\cup I_>}\right] \end{array} \right) . \end{aligned}$$

Then, for any $\xi \in \ker (\varPhi ^j)'({\bar{x}})$, from (51) we have

$$\begin{aligned} (\varPhi ^j)''({\bar{x}})[{\bar{\xi }} ,\, \xi ] = \left( \begin{array}{c} 0\\ \displaystyle \frac{\partial ^2F_{\setminus J_r\cup I_>}}{\partial x_{\setminus J_r\cup I_>}^2} ({\bar{x}}) \left[ {\bar{\xi }} _{\setminus J_r\cup I_>},\, \xi _{\setminus J_r\cup I_>}\right] \end{array} \right) . \end{aligned}$$

Combining this with (53), we conclude that violation of (45) for any $\xi \in {\mathbb {R}}^n$ with $\xi _{\setminus J_r\cup I_>}\not = 0$ precisely means that $\varPhi ^j$ is 2-regular at ${\bar{u}}$ in the direction ${\bar{v}}$.

It remains to observe that relations (46)–(47) and (49) imply that ${\bar{\xi }}$ is a solution of the complementarity system (42). Therefore, according to Lemma 1, (12) is also satisfied. $\square$

Fig. 2

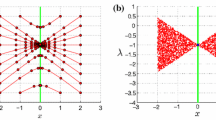
Piecewise Newton method for Example 3

Example 3

Let $n=2$, $F(x)=(x_1^2+\varphi _1(x),\, x_2+\varphi _2(x))$, where $\varphi :{\mathbb {R}}^2\rightarrow {\mathbb {R}}^2$ is a sufficiently smooth function with $\varphi (0) = 0$, $\varphi '(0) = 0$. Then NCP (37) has a solution ${\bar{x}}= 0$, with $I_> = I_< = \emptyset$.

Take $s = 2$, and consider the index sets $J_1 = \{ 2\}$, $J_2 = \emptyset$. Then, for both $r = 1$ and $r = 2$, the set in the left-hand side of (44) has the form ${\mathcal {N}} = {\mathbb {R}}\times \{ 0\}$, also agreeing with (49). Therefore, ${\bar{\xi }} = (\pm 1,\, 0)$ satisfies (46). Furthermore, any set $J\subset \{ 1,\, 2\}$ distinct from $J_1$ and $J_2$ must contain the index 1, and hence, the first inequality in (43) is satisfied.

For both $r = 1$ and $r = 2$, (45) takes the form

$$\begin{aligned} \xi _2 = 0,\quad \left( 2+\frac{\partial ^2\varphi _1}{\partial x_1^2} (0)\right) \xi _1 = 0, \end{aligned}$$

which may only hold with $\xi = 0$ if we assume that $\frac{\partial ^2\varphi _1}{\partial x_1^2} (0)\not = -2$.

Finally, the index sets in (48) take the form $J_\cup = \{ 2\}$, $J_\cap = \emptyset$, and condition (47) transforms into ${\bar{\xi }} _1\ge 0$, and hence, all the assumptions of Proposition 2 are satisfied with ${\bar{\xi }} = (1,\, 0)$ [but not with $(-1,\, 0)$].

Figure 2 demonstrates some iterative sequences generated by the piecewise Newton method, for $\varphi (x) = (x_1x_2,\, x_1^2-x_2^2)$, and with (41) used with $J = I_=(u)$. In Fig. 2a–f, sequences are initialized within any of six domains such that only one of smooth selections active at ${\bar{x}}= 0$ remains active on the interior of a given domain, and thick black lines show the boundaries of these domains. Figure 2a demonstrates the convergence pattern specified in Theorem 1, from the convergence domain associated with ${\bar{v}} = (1,\, 0)$, with iterative sequences converging linearly, with the common contingent direction ${\bar{v}}$ at ${\bar{x}}$. In Fig. 2c–e, the convergence patterns are quite different, with superlinear convergence rate in Fig. 2c and e, and with one-step termination at Fig. 2d. Finally, in Fig. 2b and f, the first step changes the active selection, and then inherits the convergence pattern of a new one.

The statement of Proposition 2 can be somehow simplified by assuming that $s=1$, i.e., the corresponding ${\mathcal {A}}({\bar{u}},\, {\bar{v}})$ is a singleton.

Corollary 2

Let ${\bar{x}}$ be a solution of (37) with $F:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ being twice differentiable near ${\bar{x}}$, with its second derivative being Lipschitz-continuous with respect to ${\bar{x}}$. Assume that for some ${\widehat{J}}\subset I_=$, and for some ${\bar{\xi }} \in {\mathbb {R}}^n$, ${\bar{\xi }} \not = 0$, it holds that

$$\begin{aligned} {\bar{\xi }} _{{\widehat{J}}\cup I_<} = 0,\quad \frac{\partial F_{\setminus {\widehat{J}}\cup I_>}}{\partial x_{\setminus {\widehat{J}}\cup I_>}} ({\bar{x}}){\bar{\xi }} _{\setminus {\widehat{J}}\cup I_>} = 0, \end{aligned}$$

(54)

$$\begin{aligned} {\bar{\xi }} _{\setminus {\widehat{J}}}> 0,\quad \frac{\partial F_{{\widehat{J}}}}{\partial x_{\setminus {\widehat{J}}\cup I_>}} ({\bar{x}}) {\bar{\xi }} _{\setminus {\widehat{J}}\cup I_>} > 0, \end{aligned}$$

(55)

and there exists no $\xi \in {\mathbb {R}}^n$, with $\xi _{\setminus \widehat{J}\cup I_>}\not = 0$, satisfying

$$\begin{aligned} \xi _{{\widehat{J}}\cup I_<} = 0,\quad \frac{\partial F_{\setminus {\widehat{J}}\cup I_>}}{\partial x_{\setminus {\widehat{J}}\cup I_>}} ({\bar{x}}) \xi _{\setminus {\widehat{J}}\cup I_>} = 0, \end{aligned}$$

(56)

$$\begin{aligned} \frac{\partial ^2F_{\setminus {\widehat{J}}\cup I_>}}{\partial x_{\setminus {\widehat{J}}\cup I_>}^2} ({\bar{x}}) \left[ {\bar{\xi }} _{\setminus {\widehat{J}}\cup I_>},\, \xi _{\setminus {\widehat{J}}\cup I_>}\right] \in \mathop {\mathrm{im}}\frac{\partial F_{\setminus {\widehat{J}}\cup I_>}}{\partial x_{\setminus {\widehat{J}}\cup I_>}} ({\bar{x}}). \end{aligned}$$

(57)

Then the assumptions of Theorem 1are satisfied for $\varPhi$ defined in (38), ${\bar{u}}:= {\bar{x}}$, ${\bar{v}} := {\bar{\xi }} /\Vert {\bar{\xi }} \Vert$, and with ${\mathcal {A}}({\bar{u}},\, {\bar{v}}) = \{ {{\widehat{\jmath }}} \}$, where ${{\widehat{\jmath }}}$ is defined by the equality $I({{\widehat{\jmath }}} ) = {\widehat{J}}\cup I_<$.

Proof

Evidently, in the setting of this corollary, the index sets $J_\cup$ and $J_\cap$ defined in (48) coincide with ${\widehat{J}}$; (54) corresponds to (44), (46); (55) implies (47); (56)–(57) correspond to (45). Therefore, it remains to show that the condition

$$\begin{aligned} {\bar{\xi }} _J\not = 0\quad \text{ or }\quad \frac{\partial F_{\setminus J\cup I_>}}{\partial x_{\setminus J\cup I_>}} ({\bar{x}}) {\bar{\xi }} _{\setminus J\cup I_>} \not = 0\quad \forall \, J\subset I_=:\; J\not = {\widehat{J}}, \end{aligned}$$

(58)

corresponding to (43), is automatically satisfied under the assumptions of this corollary.

Indeed, consider any $J\subset I_=$. If $i\in J\setminus \widehat{J}$, then the first inequality in (55) implies ${\bar{\xi }} _i > 0$, and hence, ${\bar{\xi }} _J\not = 0$, and (58) holds. Suppose now that $\bar{\xi }_J = 0$, and let $i\in {\widehat{J}}\setminus J$. Then by the first equality in (54), and by the second inequality in (55), it holds that

$$\begin{aligned} \left\langle \frac{\partial F_i}{\partial x_{\setminus J\cup I_>}} ({\bar{x}}),\, {\bar{\xi }} _{\setminus J\cup I_>}\right\rangle = \langle F_i'({\bar{x}}),\, {\bar{\xi }} \rangle = \left\langle \frac{\partial F_i}{\partial x_{\setminus {\widehat{J}}\cup I_>}} ({\bar{x}}),\, {\bar{\xi }} _{\setminus {\widehat{J}}\cup I_>} \right\rangle > 0, \end{aligned}$$

(59)

and (58) holds again. $\square$

As demonstrated in the proof above, under (54), condition (55) is sufficient for (58). However, one cannot just replace (55) in Corollary 2 by a weaker assumption (58), as one will have to additionally assume that

$$\begin{aligned} {\bar{\xi }} _{\setminus {\widehat{J}}} \ge 0,\quad \frac{\partial F_{{\widehat{J}}}}{\partial x_{\setminus {\widehat{J}}\cup I_>}} ({\bar{x}}) {\bar{\xi }} _{\setminus {\widehat{J}}\cup I_>} \ge 0, \end{aligned}$$

(60)

in order to ensure (47) in Proposition 2. Moreover, under (54) and (60), it can be verified that the converse implication is valid as well, i.e., (55) and (58) are actually equivalent, and therefore, any improvement in the statement of Corollary 2 cannot be achieved this way.

Example 1

(continued) Observe that the mapping $\varPhi$ in this example agrees with (38) for the NCP (37) with $F(x) = x^2$. We have $I_> = I_< = \emptyset$, and one must take ${\widehat{J}} = \emptyset$ (corresponding to ${{\widehat{\jmath }}} = 2$) in order to satisfy (54) with some ${\bar{\xi }} \not = 0$. Then (58) holds trivially with any ${\bar{\xi }} \not = 0$, but (60), and hence (55), are violated for $\bar{\xi }< 0$. Observe further that all the other assumptions of Proposition 2 are satisfied, but as demonstrated above, its assertion is not valid with such ${\bar{\xi }}$.

Proposition 2 combined with Theorems 1 and 2 ensure that all the properties of the algorithms discussed in Sects. 2.3 and 2.4 remain valid when these algorithms are applied with $\varPhi$ defined by (38), with any $G:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^{n\times n}$ satisfying (41), and for appropriate choices of ${\bar{v}}$.

Example 1

(continued) This example also demonstrates that in the context of Corollary 2, the claim above is not valid with assumption (55) replaced by (58).

Fig. 3

Piecewise Newton method for Example 4

Fig. 4

Piecewise Levenberg–Marquardt method for Example 4

Fig. 5

Piecewise LP-Newton method for Example 4

Example 4

([1, Example 3.3]) Let $n=2$, $F(x)=((x_1-1)x_2,\, (x_1-1)^2)$. Then the solution set of NCP (37) has the form $(\{ 1\} \times {\mathbb {R}}_+)\cup ({\mathbb {R}}_+\times \{ 0\} )$, and the two solutions violating strict complementarity are $(0,\, 0)$ and $(1,\, 0)$.

Consider ${\bar{x}}= (1,\, 0)$. Then $I_> = \{ 1\}$, $I_= = \{ 2\}$, $I_< = \emptyset$, $F'({\bar{x}}) = 0$, and we now consider the two possible choices of ${\widehat{J}}\subset I_=$:

• For ${\widehat{J}} = \{ 2\}$, we have that (54) holds with any ${\bar{\xi }} \in {\mathbb {R}}^2$ satisfying ${\bar{\xi }} _2 = 0$, but the second inequality in (55) cannot hold for any ${\bar{\xi }}$. Therefore, Proposition 2 is not applicable with this choice of ${\widehat{J}}$.

• For ${\widehat{J}} = \emptyset$, we have that (54) holds trivially with any ${\bar{\xi }} \in {\mathbb {R}}^2$, (55) reduces to the requirement ${\bar{\xi }} _2>0$, and

  $$\begin{aligned} F''({\bar{x}})[{\bar{\xi }} ] = \left( \begin{array}{cc} {\bar{\xi }} _2&{}{\bar{\xi }} _1\\ 2{\bar{\xi }} _1&{}0 \end{array} \right) , \end{aligned}$$

  implying that (56)–(57) cannot hold with any nonzero $\xi \in {\mathbb {R}}^2$ provided ${\bar{\xi }} _1\not =0$. Therefore, Corollary 2 is applicable with this choice of ${\widehat{J}}$, and with any ${\bar{\xi }} \in {\mathbb {R}}^2$ satisfying ${\bar{\xi }} _1\not =0$, ${\bar{\xi }} _2>0$.

In Figs. 3, 4 and 5, the horizontal and vertical lines form the solution set. These figures show some iterative sequences generated by the piecewise Newton method, the piecewise Levenberg–Marquardt method, and the piecewise LP-Newton method, and the domains from which convergence to ${\bar{x}}$ was detected. We also show the curves where the activity of different smooth selections of $\varPhi$ changes. The observed behavior agrees with considerations above.

Consider now any $u^k\in {\mathbb {R}}^2$ close to ${\bar{x}}$, and such that $u_1^k \not = 1$, $u_2^k > (u_1^k-1)^2$. Then ${\mathcal {A}}(u^k) = \{ {{\widehat{\jmath }}} \}$ with ${{\widehat{\jmath }}}$ corresponding to ${\widehat{J}} = \emptyset$, and hence,

$$\begin{aligned} \varPhi (u^k) = F(u^k) = \left( \begin{array}{c} (u_1^k-1)u_2^k\\ (u_1^k-1)^2 \end{array} \right) ,\quad G(u^k) = F'(u^k) = \left( \begin{array}{cc} u_2^k&{}u_1^k-1\\ 2(u_1^k-1)&{}0 \end{array} \right) . \end{aligned}$$

The unique solution of (6) has the form ${\widetilde{u}}^{k+1} = ((u_1^k+1)/2,\, u_2^k/2)$, implying that ${\widetilde{u}}_1^{k+1} -1 = (u_1^k-1)/2$. By direct computations,

$$\begin{aligned} \Vert \varPhi ({\widetilde{u}}^{k+1})\Vert = \frac{1}{4} \Vert \varPhi (u^k)\Vert , \end{aligned}$$

implying that (30) holds with $\alpha = 1$ for $v^k = {\widetilde{u}}^{k+1}-u^k$ provided $\sigma \le 3/4$. Therefore, for such $\sigma$, Step 3 of Algorithm 1 accepts the unit stepsize, and hence, Step 4 produces $u_1^{k+1} = \widetilde{u}_1^{k+1}$. In particular, one can readily check that the requirements $u_1^{k+1} \not = 1$ and $u_2^{k+1} > (u_1^{k+1}-1)^2$ remain valid, as for the previous iterate $u^k$. This implies that considerations above apply to all subsequent iterations, and hence, Algorithm 1 initialized at $u^0\in {\mathbb {R}}^2$ close enough to ${\bar{x}}$, and such that $u_1^0 \not = 1$, $u_2^0 > (u_1^0-1)^2$, generates the sequence $\{ u^k\}$ by full piecewise Newton method steps, and all such sequences converge linearly to ${\bar{x}}$. This behavior is illustrated by Figure 3a.

4.2 Constrained reformulation

In order to introduce a reasonable constrained reformulation of NCP (37), we first need to reformulate this problem using slack variable $y\in {\mathbb {R}}^n$:

$$\begin{aligned} F(x)-y = 0,\quad x\ge 0,\quad y\ge 0,\quad \langle x,\, y\rangle =0. \end{aligned}$$

(61)

Observe that ${\bar{x}}$ is a solution of NCP (37) if and only if $({\bar{x}},\, F({\bar{x}}))$ is a solution of (61).

Setting $u := (x,\, y)$ (and $p := 2n$), we will consider a constrained reformulation (31) of NCP (37), with $\varPhi :{\mathbb {R}}^n\times {\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\times {\mathbb {R}}^n$ defined by

$$\begin{aligned} \varPhi (u) := \left( \begin{array}{c} F(x)-y\\ \Psi (u) \end{array} \right) , \end{aligned}$$

(62)

and with $U := {\mathbb {R}}^n_+\times {\mathbb {R}}^n_+$, where $\Psi :{\mathbb {R}}^n\times {\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ is defined by

$$\begin{aligned} \Psi (u) := \min \{ x,\, y\}. \end{aligned}$$

(63)

The mapping $\varPhi$ defined by (62)–(63) is piecewise smooth, and the corresponding smooth selection mappings $\varPhi ^j:{\mathbb {R}}^n\times {\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\times {\mathbb {R}}^n$ are given by

$$\begin{aligned} \varPhi ^j(u) := \left( \begin{array}{c} F(x)-y\\ \Psi ^j(u) \end{array} \right) ,\quad j = 1,\, \ldots ,\, q, \end{aligned}$$

(64)

where the mappings $\Psi ^j:{\mathbb {R}}^n\times {\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ have the components

$$\begin{aligned} \Psi ^j_i(u) := \left\{ \begin{array}{ll} x_i &{} \text{ if } i\in I(j),\\ y_i &{} \text{ otherwise }, \end{array} \right. \quad i = 1,\, \ldots ,\, n,\; j = 1,\, \ldots ,\, q. \end{aligned}$$

(65)

It can be easily verified that for the objects defined above, condition (32) is satisfied. At the same time, Example 1 demonstrates that condition (32) with $U ={ \mathbb {R}}^n\times {\mathbb {R}}^n$ (i.e., in the unconstrained case) is violated for $\varPhi$ defined in (38) or (62). This demonstrates one of the roles of constraints in this reformulation, which are redundant for the reformulation itself.

For a given $u\in {\mathbb {R}}^n\times {\mathbb {R}}^n$, the set of indices of active selection mappings defined according to (2) has the same form (40) as above, but with

$$\begin{aligned} \begin{array}{ccl} I_>(u)&{}:=&{}\{ i\in \{ 1,\, \ldots ,\, n\} \mid x_i > y_i\} ,\\ I_=(u)&{}:=&{}\{ i\in \{ 1,\, \ldots ,\, n\} \mid x_i = y_i\} ,\\ I_<(u)&{}:=&{}\{ i\in \{ 1,\, \ldots ,\, n\} \mid x_i < y_i\} . \end{array} \end{aligned}$$

Therefore, in order to satisfy (5), the mapping $G:{\mathbb {R}}^n\times {\mathbb {R}}^n\rightarrow {\mathbb {R}}^{2n\times 2n}$ must be of the form

$$\begin{aligned} G(u) = \left( \begin{array}{cc} F'(x)&{}-{\mathcal {I}}\\ \Gamma ^1(u)&{}\Gamma ^2(u) \end{array} \right) , \end{aligned}$$

(66)

where the rows of $\Gamma ^1:{\mathbb {R}}^n\times {\mathbb {R}}^n\rightarrow {\mathbb {R}}^{n\times n}$ and $\Gamma ^2:{\mathbb {R}}^n\times {\mathbb {R}}^n\rightarrow {\mathbb {R}}^{n\times n}$ satisfy

$$\begin{aligned} \begin{array}{c} \Gamma _i^1(u) = \left\{ \begin{array}{ll} e^i &{} \text{ if } i\in J\cup I_<(u),\\ 0 &{} \text{ otherwise }, \end{array} \right. \quad \Gamma _i^2(u) = \left\{ \begin{array}{ll} 0 &{} \text{ if } i\in J\cup I_<(u),\\ e^i &{} \text{ otherwise }, \end{array} \right. \; i = 1,\, \ldots ,\, n, \\ \text{ for } \text{ some } J\subset I_=(u). \end{array} \end{aligned}$$

(67)

Observe that for a given solution ${\bar{x}}$ of NCP (37), and for ${\bar{u}}= ({\bar{x}},\, F({\bar{x}}))$, the index sets $I_> = I_>({\bar{x}})$, $I_= = I_=({\bar{x}})$, and $I_< = I_<({\bar{x}})$, defined in Sect. 4.1, coincide with $I_>({\bar{u}})$, $I_=({\bar{u}})$, and $I_<({\bar{u}})$, respectively.

Proposition 3

Under the assumptions of Corollary 2, the assumptions of Theorem 3are satisfied for $\varPhi$ defined in (62)–(63) and $U:=P\cap Q={\mathbb {R}}^n_+\times {\mathbb {R}}^n_+$ with

$$\begin{aligned} P := \{ (x,\, y)\in {\mathbb {R}}^n\times {\mathbb {R}}^n\mid x_{\setminus {\widehat{J}}} \ge 0,\; y_{{\widehat{J}}} \ge 0\} ,\quad \end{aligned}$$

(68)

$$\begin{aligned} Q := \{ (x,\, y)\in {\mathbb {R}}^n\times {\mathbb {R}}^n\mid x_{{\widehat{J}}\cup I_<\cup I_>} \ge 0,\; y_{\setminus {\widehat{J}}\cup I_<\cup I_>} \ge 0\} , \end{aligned}$$

(69)

for ${\bar{u}}:= ({\bar{x}},\, F({\bar{x}}))$, ${\bar{v}} := ({\bar{\xi }} ,\, {\bar{\eta }} )/\Vert ({\bar{\xi }} ,\, {\bar{\eta }} )\Vert$ with ${\bar{\eta }} \in {\mathbb {R}}^n$ defined by

$$\begin{aligned} \displaystyle {\bar{\eta }} _{{\widehat{J}}\cup I_<} := \frac{\partial F_{\widehat{J}\cup I_<}}{\partial x_{\setminus {\widehat{J}}\cup I_>}} ({\bar{x}}) \bar{\xi }_{\setminus {\widehat{J}}\cup I_>} ,\quad {\bar{\eta }} _ {\setminus {\widehat{J}}\cup I_>} := 0, \end{aligned}$$

(70)

and for ${{\widehat{\jmath }}} \in {\mathcal {A}}({\bar{u}})$ with $I(\widehat{\jmath }) = {\widehat{J}}\cup I_<$.

Proof

According to (40), and (64)–(65), for any $J\subset I_=$ and the associated $j\in {\mathcal {A}}({\bar{u}})$ with $I(j) = J\cup I_<$, we have that (after the appropriate re-ordering of rows and columns)

$$\begin{aligned} (\varPhi ^j)'({\bar{u}}) = \left( \begin{array}{cc} F'({\bar{x}}) &{} -{\mathcal {I}}\\ {\mathcal {I}}_{J\cup I_<}&{}0\\ 0&{}{\mathcal {I}}_{\setminus J\cup I_>} \end{array} \right) , \end{aligned}$$

(71)

and in particular

$$\begin{aligned} (\varPhi ^{{{\widehat{\jmath }}} })'({\bar{u}}) = \left( \begin{array}{cc} F'({\bar{x}}) &{} -{\mathcal {I}}\\ {\mathcal {I}}_{{\widehat{J}}\cup I_<}&{}0\\ 0 &{} {\mathcal {I}}_{\setminus {\widehat{J}}\cup I_>} \end{array} \right) . \end{aligned}$$

(72)

The latter equality implies that

$$\begin{aligned} \ker (\varPhi ^{{{\widehat{\jmath }}} })'({\bar{u}}) = \left\{ (\xi , \eta ) \in {\mathbb {R}}^n\times {\mathbb {R}}^n\left| \begin{array}{l} \displaystyle \xi _{{\widehat{J}}\cup I_<} = 0,\, \frac{\partial F_{\setminus {\widehat{J}}\cup I_>}}{\partial x_{\setminus {\widehat{J}}\cup I_>}} ({\bar{x}}) \xi _{\setminus {\widehat{J}}\cup I_>} = 0,\\ \displaystyle \eta _{{\widehat{J}}\cup I_<} = \frac{\partial F_{{\widehat{J}}\cup I_<}}{\partial x_{\setminus {\widehat{J}}\cup I_>}} ({\bar{x}}) \xi _{\setminus {\widehat{J}}\cup I_>} ,\, \eta _ {\setminus {\widehat{J}}\cup I_>} = 0 \end{array} \right. \right\} . \end{aligned}$$

(73)

In particular, relations in (54) imply that ${\bar{v}} = ({\bar{\xi }} ,\, {\bar{\eta }} )\in \ker (\varPhi ^{\widehat{\jmath }})'({\bar{u}})$, with ${\bar{\eta }}$ defined in (70).

Furthermore, we show that (55) implies

$$\begin{aligned} {\bar{v}} \not \in \ker (\varPhi ^j)'({\bar{u}})\quad \forall \, j\in {\mathcal {A}}({\bar{u}})\setminus \{ {{\widehat{\jmath }}} \} . \end{aligned}$$

(74)

Indeed, according to (71) we have that (74) can be written as follows:

$$\begin{aligned} \begin{array}{c} \displaystyle {\bar{\xi }} _J \not = 0\; \text{ or }\; \frac{\partial F_{\setminus J\cup I_>}}{\partial x_{\setminus J\cup I_>}} ({\bar{x}}) {\bar{\xi }} _{\setminus J\cup I_>} \not = 0\; \text{ or }\; {\bar{\eta }} _{J\cup I_<} \not = \frac{\partial F_{J\cup I_<}}{\partial x_{\setminus J\cup I_>}} ({\bar{x}}) {\bar{\xi }} _{\setminus J\cup I_>}\; \text{ or }\; {\bar{\eta }} _ {\setminus J} \not = 0\\ \forall \, J\subset I_=,\; J\not = {\widehat{J}}. \end{array} \end{aligned}$$

(75)

Consider any $J\subset I_=$, and suppose that the first condition in (75) is violated, i.e., ${\bar{\xi }} _J = 0$. Then, employing the first equality in (54), we obtain the chain of equalities in (59) for all $i = 1,\, \ldots ,\, n$. Employing this chain and (54), (70), it can be directly verified that (75) is in fact equivalent to (58). Then the corresponding argument in the proof of Corollary 2 yields that (55) implies (75), and hence, (74).

We next establish 2-regularity of $\varPhi ^{{{\widehat{\jmath }}} }$ at ${\bar{u}}$ in the direction ${\bar{v}}$. According to (72), we have

$$\begin{aligned} \mathop {\mathrm{im}}(\varPhi ^{{{\widehat{\jmath }}} })'({\bar{u}}) = \{ (y,\, z)\in {\mathbb {R}}^n\times {\mathbb {R}}^n\mid (y,\, z) {\text{ satisfies} }\,\,(77)\} \end{aligned}$$

(76)

with

$$\begin{aligned} (y+z)_{\setminus {\widehat{J}}\cup I_>} \displaystyle -\frac{\partial F_{\setminus {\widehat{J}}\cup I_>}}{\partial x_{{\widehat{J}}\cup I_<}} ({\bar{x}}) z_{{\widehat{J}}\cup I_<}\in \mathop {\mathrm{im}}\frac{\partial F_{\setminus {\widehat{J}}\cup I_>}}{\partial x_{\setminus {\widehat{J}}\cup I_>}} ({\bar{x}}), \end{aligned}$$

(77)

and according to (54) and (64),

$$\begin{aligned} (\varPhi ^{{{\widehat{\jmath }}} })''({\bar{u}})[{\bar{v}}] = \left( \begin{array}{c@{\quad }c@{\quad }c} \displaystyle \frac{\partial ^2F}{\partial x_{{\widehat{J}}\cup I_<} \partial x_{\setminus {\widehat{J}}\cup I_>}} ({\bar{x}}) \left[ {\bar{\xi }} _{\setminus {\widehat{J}}\cup I_>}\right] &{} \displaystyle \frac{\partial ^2F}{\partial x_{\setminus {\widehat{J}}\cup I_>}^2} ({\bar{x}}) \left[ {\bar{\xi }} _{\setminus {\widehat{J}}\cup I_>}\right] &{}0\\ 0&{}0&{}0 \end{array} \right) . \end{aligned}$$

follows. Then, for any $v = (\xi ,\, \eta )\in \ker (\varPhi ^{\widehat{\jmath }})'({\bar{u}})$, from (73) we have

$$\begin{aligned} (\varPhi ^{{{\widehat{\jmath }}} })''({\bar{u}})[{\bar{v}} ,\, v] = \left( \begin{array}{c} \displaystyle \frac{\partial ^2F}{\partial x_{\setminus {\widehat{J}}\cup I_>}^2} ({\bar{u}}) \left[ {\bar{\xi }} _{\setminus {\widehat{J}}\cup I_>},\, \xi _{\setminus {\widehat{J}}\cup I_>}\right] \\ 0 \end{array} \right) . \end{aligned}$$

Combining this with (76), we conclude that violation of (56)–(57) for any $\xi \in {\mathbb {R}}^n$ with $\xi _{\setminus {\widehat{J}}\cup I_>}\not = 0$ precisely gives the needed 2-regularity property.

Considerations above demonstrate that requirement 1 in Theorem 3 holds.

Recall now that (32) implying (33) is automatically satisfied in this setting, thus also yielding requirement 2 in Theorem 3.

Requirement 3 in Theorem 3 readily follows from (55), (68), and the first equality in (70).

Finally, from (71)–(72) we readily have that for any $u^k\in {\mathbb {R}}^n\times { \mathbb {R}}^n$, any solution $u^{k+1} = (x^{k+1},\, y^{k+1})$ of the Eq. (6) satisfies

$$\begin{aligned} x^{k+1}_{{\widehat{J}}\cup I_<} = 0,\quad y^{k+1}_{\setminus \widehat{J}\cup I_>} = 0. \end{aligned}$$

(78)

Moreover, since ${\bar{x}}_{I_>} > 0$ and ${\bar{y}}_{I_<} > 0$, from Theorem 1 it follows that $x^{k+1}_{I_>} > 0$, $y^{k+1}_{I_<} > 0$ assuming that $u^k\in K_{{\widetilde{\varepsilon }} ,\, {\widetilde{\delta }} }({\bar{u}},\, {\bar{v}})$ with sufficiently small ${\widetilde{\varepsilon }} > 0$ and ${\widetilde{\delta }} > 0$. Combining these inequalities with (78), we conclude that $u^{k+1}$ belongs to Q defined in (69). This yields requirement 4 in Theorem 3. $\square$

Proposition 3 combined with Theorem 3 and the results for the unconstrained case allows to ensure that all the properties of the algorithms discussed in Sect. 3.2 remain valid when these algorithms are applied with $\varPhi$ defined in (62)–(63) and $U := {\mathbb {R}}^n_+\times {\mathbb {R}}^n_+$, with any $G:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^{n\times n}$ satisfying (66)–(67), and for appropriate choices of ${\bar{v}}$.

In conclusion of this section, we emphasize that the material presented in it can be readily extended from NCPs to more general complementarity systems, which, in particular, would allow to cover Example 2. We do not provide this extension here, in order to avoid extra technicalities.