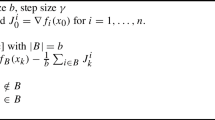Fastest rates for stochastic mirror descent methods

Abstract

Relative smoothness—a notion introduced in Birnbaum et al. (Proceedings of the 12th ACM conference on electronic commerce, ACM, pp 127–136, 2011) and recently rediscovered in Bauschke et al. (Math Oper Res 330–348, 2016) and Lu et al. (Relatively-smooth convex optimization by first-order methods, and applications, arXiv:1610.05708, 2016)—generalizes the standard notion of smoothness typically used in the analysis of gradient type methods. In this work we are taking ideas from well studied field of stochastic convex optimization and using them in order to obtain faster algorithms for minimizing relatively smooth functions. We propose and analyze two new algorithms: Relative Randomized Coordinate Descent (relRCD) and Relative Stochastic Gradient Descent (relSGD), both generalizing famous algorithms in the standard smooth setting. The methods we propose can be in fact seen as particular instances of stochastic mirror descent algorithms, which has been usually analyzed under stronger assumptions: Lipschitzness of the objective and strong convexity of the reference function. As a consequence, one of the proposed methods, relRCD corresponds to the first stochastic variant of mirror descent algorithm with linear convergence rate.

Appendices

Appendix 1: Relative randomized coordinate descent with short stepsizes

As promised, we provide a simplified version of relRCD along with a simplified analysis. We give two slightly different ways to analyze the convergence. However, neither of them provides a speedup comparing to Algorithm 1 . We mention this for educational purposes, to illustrate our techniques. This issue was be addressed in Section 3, providing us a potential speedup comparing to Algorithm 1.

Throughout this section, we assume that f is L-smooth and $\mu$-strongly convex relative to some separable function h.

1.1 Algorithm

We introduce here Algorithm 2 —Relative Randomized Coordinate descent with short stepsizes. From now, let us denote $\mathbf{1}^i$ to be i-th column of $n\times n$ identity matrix. The update is given by (7) with

$$\begin{aligned} Q_t=\left\{ x \;\Big |\; x=x_t+\sum _{i\in M_t}\mathrm {span}\left( \mathbf{1}^i\right) \right\} . \end{aligned}$$

Subset of coordinates $M_t$ is chosen randomly such that $\mathbf{P}(i\in M_t)=\mathbf{P}(j\in M_t)$ for all $i,j\le n$ and $|M_t|=\tau$.

1.2 Key lemma

It will be useful to introduce

$$\begin{aligned} x_{(t+1,*)}\quad \overset{\text {def}}{=} \quad {{\,\mathrm{argmin}\,}}_{x\in Q}\{\langle \nabla f(x_t),x \rangle +LD_{h}(x,x_t)\} \end{aligned}$$

as we will use this notation in the analysis.

The following lemma describes behavior of Algorithm 2 in each iteration, providing us on the expected upper bound on the value in the next iterate using the previous iterate.

Lemma 7.1

(Iteration decrease for Algorithm 2) Suppose that f is L-smooth and $\mu$-strongly convex relative to separable function h. Then, running Algorithm 2 we obtain for all $x\in Q$:

$$\begin{aligned} \mathbf{E}\left[ f(x_{t+1})\right] \quad \le \quad \frac{n-\tau }{n}\mathbf{E}\left[ f(x_{t})\right] + \frac{\tau }{n} f(x)+\left( L-\frac{\tau }{n}\mu \right) \mathbf{E}\left[ D_{h}(x,x_t)\right] -L\mathbf{E}\left[ D_{h}(x,x_{t+1})\right] . \end{aligned}$$

Proof

$$\begin{aligned} \mathbf{E}\left[ f(x_{t+1})|x_t\right]&{\mathop {\le }\limits ^{(5)}} f(x_{t})+ \mathbf{E}\left[ \Big ( \langle \nabla f(x_t), x_{t+1}-x_t \rangle +LD_{h}(x_{t+1},x_t)\Big )\;|\;x_t\right] \\& = f(x_{t})+ \mathbf{E}\left[ \sum _{i\not \in M_t}\Big (\left( \nabla f(x_t)\right) ^{(i)}( x_{t+1}-x_t)^{(i)} +LD_{h^{(i)}}\left( x_{t+1}^{(i)},x_t^{(i)}\right) \Big )\;|\;x_t\right] \\&\quad + \mathbf{E}\left[ \sum _{i\in M_t}\Big (\left( \nabla f(x_t)\right) ^{(i)}(x_{t+1}-x_t)^{(i)} +LD_{h^{(i)}}\left( x_{t+1}^{(i)},x_t^{(i)}\right) \Big )\;|\;x_t\right] \\&{\mathop {=}\limits ^{(*)}} f(x_{t}) + \mathbf{E}\left[ \sum _{i\in M_t}\Big (\left( \nabla f(x_t)\right) ^{(i)}(x_{t+1}-x_t)^{(i)} +LD_{h^{(i)}}\left( x_{t+1}^{(i)},x_t^{(i)}\right) \Big )\;|\;x_t\right] \\ &= f(x_{t}) + \frac{\tau }{n}\left\langle \nabla f(x_t), x_{(t+1,*)}-x_t\right\rangle +\frac{\tau }{n}LD_{h}\left( x_{(t+1,*)},x_t\right) \\&{\mathop {\le }\limits ^{(9)}} f(x_{t}) + \frac{\tau }{n} \langle \nabla f(x_t) ,x-x_t \rangle +\frac{\tau }{n} LD_{h}(x,x_t) -\frac{\tau }{n} L D_h(x,x_{(t+1,*)}) \\&{\mathop {\le }\limits ^{(8)}} \frac{n-\tau }{n} f(x_{t})+ \frac{\tau }{n} f(x) + \frac{\tau }{n} (L-\mu )D_{h}(x,x_t)-\frac{\tau }{n} L D_h(x,x_{(t+1,*)}). \end{aligned}$$

(27)

The equality $(*)$ above holds due to the fact that $x_{t+1}^{(i)}=x_{t}^{(i)}$ for $i\not \in M_t$. Note that

$$\begin{aligned} \mathbf{E}\left[ D_{h}(x,x_{t+1})\;|\;x_t\right] \quad = \quad \frac{n-\tau }{n}D_h(x,x_t)+ \frac{\tau }{n} D_h(x,x_{(t+1,*)}). \end{aligned}$$

Plugging it into (27), we get

$$\begin{aligned} \mathbf{E}\left[ f(x_{t+1})|x_t\right]&{\mathop {\le }\limits ^{(27)}}\frac{n-\tau }{n} f(x_{t})+ \frac{\tau }{n} f(x)+\frac{\tau }{n}(L-\mu )D_{h}(x,x_t)-L\mathbf{E}\left[ D_{h}(x,x_{t+1})|x_t\right] \\&\quad +\frac{n-\tau }{n}LD_h(x,x_t))\\&= \frac{n-\tau }{n} f(x_{t})+ \frac{\tau }{n} f(x)+\left( L-\frac{\tau }{n}\mu \right) D_{h}(x,x_t)-L\mathbf{E}\left[ D_{h}(x,x_{t+1})|x_t\right] . \end{aligned}$$

Taking the expectation over the algorithm and using the tower property we obtain the desired result. $\square$

The lemma above provides us with the expected decrease in the objective every iteration. It holds for all $x\in Q$, particularly for $x=x_t$ we obtain that the sequence $\{f(x_t)\}$ is nonincreasing in expectation.

1.3 Strongly convex case: $\mu >0$

The following theorem uses recursively Lemma 7.1 with $x=x_*$, obtaining a convergence rate of Algorithm 2 .

Theorem 7.2

(Convergence rate for Algorithm 2) Suppose that f is L-smooth and $\mu$-strongly convex relative to separable function h for $\mu >0$. Running Algorithm 2 for k iterations we obtain:

$$\begin{aligned} \sum _{t=1}^{k}c_t \big (\mathbf{E}\left[ f(x_t)\right] -f(x_*)\big ) \le \frac{(L-\frac{\tau }{n}\mu )D_{h}(x_*,x_0) +\frac{n-\tau }{n}(f(x_0)-f(x_*))}{1-\frac{L}{\mu }+\frac{L}{\mu }\Big ( \frac{L}{L-\frac{\tau }{n}\mu } \Big )^{k-1}}, \end{aligned}$$

where $c= (c_1,\ldots ,c_k)\in \mathbb {R}^k_+$ is a positive vector with entries summing up to 1.

Proof

The proof follows by applying Lemma 8.1 on Lemma 7.1 with $x=x_*$ for $f_t=\mathbf{E}\left[ f(x_t)\right] ,\,D_t=\mathbf{E}\left[ D_h(x_*,x_t)\right] ,\,f_*= f(x_*),\, \delta =\tfrac{\tau }{n},\,\ \varphi =L,\, \psi =\mu$. $\square$

Note that the term driving the convergence rate in Theorem 7.2 is $\left( L/(L-\tfrac{\tau }{n}\mu )\right) ^{1-k} = \left( 1-\tfrac{\tau }{n}\tfrac{\mu }{L}\right) ^{k-1},$ where k is the number if iterations. In the special case when $\tau =n$, using simple algebra one can verify that Theorem 7.2 matches the results from Theorem 2.5.

1.4 Non-strongly convex case: $\mu =0$

The following theorem provides us with the convergence rate of Algorithm 2  when f is convex but not necessarily relative strongly convex (i.e., $\mu =0$).

Theorem 7.3

(Convergence rate for Algorithm 2) Suppose that f is convex and L-smooth relative to separable function h. Running Algorithm 2 for k iterations we obtain:

$$\begin{aligned} \sum _{t=1}^{k}c_t(\mathbf{E}\left[ f(x_t)\right] -f(x_*)) \quad \le \quad \frac{LD_{h}(x,x_0)+\frac{n-\tau }{n}\left( f(x_0) -f(x_*)\right) }{1+\frac{\tau (k-1)}{n}}, \end{aligned}$$

where $c=(c_1,\ldots ,c_k)\in \mathbb {R}^k$ is a positive vector proportional to $\big (\frac{\tau }{n},\,\frac{\tau }{n},\,\ldots ,\,\frac{\tau }{n},\,1 \big )$.

Proof

For simplicity, denote $r_t=\mathbf{E}\left[ f(x_t)\right] -f(x_*)$. We can follow the proof of Theorem 7.2 using Lemma 8.1 to get the equation (35), which can be rewritten for $\mu =0$ as follows:

$$\begin{aligned} LD_{h}(x,x_0) \quad \ge \quad r_{k}+ \frac{\tau }{n}\sum _{t=1}^{k-1} r_t -\frac{n-\tau }{n}r_0. \end{aligned}$$

The inequality above can be easily rearranged as

$$\begin{aligned} \frac{LD_{h}(x,x_0)+\frac{n-\tau }{n}r_0}{1+(k-1)\frac{\tau }{n}} \quad \ge \quad \frac{1}{1+(k-1)\frac{\tau }{n}}\left( r_{k}+ \frac{\tau }{n}\sum _{t=1}^{k-1} r_t \right) . \end{aligned}$$

$\square$

As previously, Theorem 7.3 captures known results of Relative Gradient Descent for $\tau =n$ (Theorem 2.5).

1.5 Improvements using a symmetry measure

For completeness, we provide a different analysis of Algorithm 2  using a different power function which is a combination of $f(x_{t})-f(x_*)$ and $D_h(x_{*},x_t)$.⁵ We will obtain a slight improvement in terms of the convergence rate thanks to exploiting a possiblesymmetry in Bregman distance, as proposed in [3]:

Definition 7.4

(Symmetry measure) Given a reference function h, the symmetry measure of $D_h$ is defined by

$$\begin{aligned} \alpha (h) \quad \overset{\text {def}}{=} \quad \inf _{x,y} \left\{ \frac{D_h(x,y)}{D_h(y,x)} \;\Big | \; x\ne y \right\} . \end{aligned}$$

(28)

Note that we clearly have $0\le \alpha (h)\le 1$. A symmetry measure $\alpha _h$ was also used in [3]. In our case, considering the symmetric measure for $D_h$ would improve the result from the next theorem. However our results does not rely on it and hold even if there is no symmetry present, i.e. $\alpha (h)=0$.

Theorem 7.5

(Convergence rate for Algorithm 2) Suppose that f is L-smooth and $\mu$-strongly convex relative to separable function h. Denote $Z_t^{L}\overset{\text {def}}{=}LD_h(x_{*},x_t)+f(x_{t})-f(x_*)$. Running Algorithm 2 for k iterations we obtain:

$$\begin{aligned} \mathbf{E}\left[ f(x_{k})-f(x_*)\right] \quad \le \quad \frac{Z_0^{L}}{1+\frac{\tau }{n}k} \end{aligned}$$

when $\mu =0$ and

$$\begin{aligned} \mathbf{E}\left[ Z^{L}_{k}\right] \quad \le \quad \left( 1- \frac{\tau }{n} \frac{\mu }{L} - \frac{\tau }{n}\Big (1-\frac{\mu }{L} \Big )\frac{\mu \alpha (h)}{\mu \alpha (h)+L}\right) ^k Z_0^{L} \end{aligned}$$

when $\mu > 0$.

Proof

From Lemma 7.1 we have

$$\begin{aligned} \mathbf{E}\left[ Z_{t+1}^{L}\right] \quad \le \quad \mathbf{E}\left[ Z_t^{L}\right] - \frac{\tau }{n}\mathbf{E}\left[ Z_{t}^{\mu }\right] . \end{aligned}$$

(29)

If $\mu =0$, we can easily telescope the above and get the following inequality

$$\begin{aligned} \mathbf{E}\left[ f(x_{k})-f(x_*)\right] \quad \le \quad Z_0^{L} - \frac{\tau }{n}k\mathbf{E}\left[ f(x_{k})-f(x_*)\right] , \end{aligned}$$

which leads to

$$\begin{aligned} \mathbf{E}\left[ f(x_{k})-f(x_*)\right] \quad \le \quad \frac{Z_0^{L}}{1+\frac{\tau }{n}k}. \end{aligned}$$

Let us look at the case when $\mu \ne 0$. Firstly note that from relative strong convexity of f combining with definition of the symmetric measure $\alpha (h)$ we have

$$\begin{aligned} f(x_t)-f(x_*) \quad \ge \quad \mu D_h(x_t,x_*) \quad \ge \quad \mu \alpha (h) D_h(x_*,x_t) . \end{aligned}$$

(30)

Therefore, (29) can be rewritten as

$$\begin{aligned} \mathbf{E}\left[ Z_{t+1}^{L}\right]&{\mathop {\le }\limits ^{(29)}}\mathbf{E}\left[ Z_t^{L}\right] - \frac{\tau }{n}\mathbf{E}\left[ Z_{t}^{\mu }\right] \\&= \mathbf{E}\left[ Z_t^{L}\right] - \frac{\tau }{n}\frac{\mu }{L} \mathbf{E}\left[ Z_{t}^{L}\right] -\frac{\tau }{n}\Big ( 1-\frac{\mu }{L} \Big ) (f(x_t)-f(x_*))\\ &= \mathbf{E}\left[ Z_t^{L}\right] - \frac{\tau }{n}\frac{\mu }{L}\mathbf{E}\left[ Z_{t}^{L}\right] -\frac{\tau }{n}\Big ( 1-\frac{\mu }{L} \Big ) \frac{\mu \alpha (h)}{\mu \alpha (h)+L}(f(x_t)-f(x_*))\\&\quad -\frac{\tau }{n}\Big ( 1-\frac{\mu }{L} \Big ) \frac{L}{\mu \alpha (h)+L}(f(x_t)-f(x_*))\\&{\mathop {\le }\limits ^{(30)}}\mathbf{E}\left[ Z_t^{L}\right] - \frac{\tau }{n}\frac{\mu }{L}\mathbf{E}\left[ Z_{t}^{L}\right] -\frac{\tau }{n}\Big ( 1-\frac{\mu }{L} \Big ) \frac{\mu \alpha (h)}{\mu \alpha (h)+L}(f(x_t)-f(x_*)) \\&\quad - \frac{\tau }{n}\Big ( 1-\frac{\mu }{L} \Big ) \frac{L}{\mu \alpha (h)+L}\mu \alpha (h)D_h(x_*,x_t)\\& = \mathbf{E}\left[ Z_t^{L}\right] - \frac{\tau }{n}\frac{\mu }{L}\mathbf{E}\left[ Z_{t}^{L}\right] -\frac{\tau }{n}\Big ( 1-\frac{\mu }{L} \Big ) \frac{\mu \alpha (h)}{\mu \alpha (h)+L}\mathbf{E}\left[ Z_t^{L}\right] \\& = \left( 1- \frac{\tau }{n} \frac{\mu }{L} - \frac{\tau }{n}\Big ( 1-\frac{\mu }{L} \Big )\frac{\mu \alpha (h)}{\mu \alpha (h)+L}\right) \mathbf{E}\left[ Z_t^{L}\right] . \end{aligned}$$

Using recursively the inequality above, we get

$$\begin{aligned} \mathbf{E}\left[ Z^{L}_{k}\right] \quad \le \quad \left( 1- \frac{\tau }{n} \frac{\mu }{L} - \frac{\tau }{n}\Big ( 1-\frac{\mu }{L} \Big )\frac{\mu \alpha (h)}{\mu \alpha (h)+L}\right) ^k Z_0^{L}. \end{aligned}$$

$\square$

Note that as soon as $\alpha (h)=0$, rate from the theorem above is up to the constant same as rate from Theorem 7.2 since $\left( L/ (L-\frac{\tau }{n}\mu )\right) ^{-1} = 1-\frac{\tau }{n}\frac{\mu }{L}.$ However both theorems are measuring a convergence rate for a different quantity. On the other hand, in the best case if $\alpha (h)=1$ we have

$$\begin{aligned} 1-\frac{\tau }{n} \frac{\mu }{L} - \frac{\tau }{n}\Big ( 1-\frac{\mu }{L} \Big )\frac{\mu }{\mu +L} \quad = \quad 1-\frac{\tau }{n} \frac{\mu }{L} -\frac{\tau }{n} \frac{\mu }{L} \left( 1-\frac{2\mu }{L+\mu } \right) \quad \ge \quad 1-2\frac{\tau }{n}\frac{\mu }{L}, \end{aligned}$$

thus the convergence rate we obtained might be up to 2 times faster comparing to rate from Theorem 7.2. Thus the convergence rate is also up to 2 times faster comparing to Theorem 2.5 for the case $\tau =n$ if $\alpha (h)<0$. On the other hand, Theorem 7.5 provides us with convergence rate of $\mathbf{E}\left[ D_h(x_*,x_k)\right]$, as the following inequality trivially holds:

$$\begin{aligned} \mathbf{E}\left[ D_h(x_*,x_k)\right] \quad \le \quad \frac{\mathbf{E}\left[ Z^{L}_{k}\right] }{L}. \end{aligned}$$

Suppose that we have a fixed budget on the total work of the algorithm, i.e. we can make only $k/\tau$ iterations. It is a simple exercise to notice that the bound on the suboptimality for Theorems 7.2, 7.3 and 7.5 after $k/\tau$ iterations is not getting better when minibatch size $\tau$ is decreasing. We address next section in order to solve this issue.

Appendix 2: Key technical lemmas

For completeness, we firstly give proof of Three point property.

1.1 Proof of the three point property

Note that $\phi (x)+D_h(x,z)$ is differentiable and convex in x. Using the definition of $z_+$ we have

$$\begin{aligned} \langle \nabla \phi (z_+)+\nabla h(z_+)-\nabla h(z),x-z_+ \rangle \quad \ge 0 \quad ,\ \forall x\in Q . \end{aligned}$$

Using definition of $D_h(\cdot ,\cdot )$ we can see that

$$\begin{aligned} \langle \nabla h(z_+)-\nabla h(z),x-z_+ \rangle \quad = \quad D_h(x,z)-D_h(z_+,z)-D_h(x,z_+). \end{aligned}$$

Putting the above together, we see that

$$\begin{aligned} 0& \le \langle \nabla \phi (z_+)+\nabla h(z_+)-\nabla h(z),x-z_+ \rangle \\& = D_h(x,z)-D_h(z_+,z)-D_h(x,z_+) +\langle \nabla \phi (z_+),x-z_+ \rangle \\& \le D_h(x,z)-D_h(z_+,z)-D_h(x,z_+) + \phi (x)-\phi (z_+). \end{aligned}$$

The last inequality is due to convexity of $\phi$.

1.2 Key lemma for analysis

The following lemma allows us to get a convergence rate for Algorithms

Lemma 8.1

Suppose that for positive sequences $\{f_t\}, \{D_t\}$ we have

$$\begin{aligned} f_{t+1}\quad \le \quad (1-\delta )f_t+ \delta f_*+\left( \varphi -\delta \psi \right) D_t-\varphi D_{t+1}, \end{aligned}$$

(31)

where $\delta ,\,\varphi ,\,\psi \in \mathbb {R}$ satisfy $1\ge \delta >0$ and $\varphi \ge \psi >0$. Then, the following inequality holds

$$\begin{aligned} \sum _{t=1}^{k}c_t \big (f_t-f_*\big ) \le \frac{(\varphi -\delta \psi )D_0 +(1-\delta )(f_0-f_*)}{1-\frac{\varphi }{\psi }+\frac{\varphi }{\psi }\Big ( \frac{\varphi }{\varphi -\delta \psi } \Big )^{k-1}}, \end{aligned}$$

where $c_t\overset{\text {def}}{=}C_t/\sum _{t=1}^kC_t$ for

$$\begin{aligned} C_t \quad \overset{\text {def}}{=} \quad {\left\{ \begin{array}{ll}\left( \frac{\varphi }{\varphi -\delta \psi } \right) ^{t-1} \frac{\varphi -\psi }{\delta ^{-1}\varphi -\psi }, & 1\le t\le k-1 \\ \left( \frac{\varphi }{\varphi -\delta \psi } \right) ^{k-1}, & t=k. \end{array}\right. } \end{aligned}$$

Proof

Let us multiple the inequality (31) by $\big (\frac{\varphi }{\varphi -\delta \psi }\big )^t$ for iterates $t=0,1,\ldots ,k-1$ and sum them:

$$\begin{aligned} \sum _{t=0}^{k-1} \left( \frac{\varphi }{\varphi -\delta \psi } \right) ^t f_{t+1} &\le \sum _{t=0}^{k-1} \left( \frac{\varphi }{\varphi -\delta \psi } \right) ^t \Big ( (1-\delta ){n}f_t+ \delta f_*\Big )\\&\quad +\sum _{t=0}^{k-1} \left( \frac{\varphi }{\varphi -\delta \psi } \right) ^t \left( \left( \varphi -\delta \psi \right) D_{t}-\varphi D_{t+1} \right) . \end{aligned}$$

Rearranging the terms, we get

$$\begin{aligned}&\sum _{t=0}^{k-1} \Big ( \frac{\varphi }{\varphi -\delta \psi } \Big )^t\Big ( f_{t+1}- (1-\delta )f_t- \delta f_* \Big ) \end{aligned}$$

(32)

$$\begin{aligned}&\quad \le \left( \varphi -\delta \psi \right) D_0-\Big ( \frac{\varphi }{\varphi -\delta \psi } \Big )^{k-1}\varphi D_k \\&\quad \le \left( \varphi -\delta \psi \right) D_0. \end{aligned}$$

(33)

For simplicity, throughout this proof denote $r_t=f_{t}-f_*$. Let us continue with the bound above:

$$\begin{aligned} \left( \varphi -\delta \psi \right) D_0&{\mathop {\ge }\limits ^{(33)}} \left( \frac{\varphi }{\varphi -\delta \psi } \right) ^{k-1} f_k+ \sum _{t=1}^{k-1} \left( \frac{\varphi }{\varphi -\delta \psi } \right) ^{t-1} \left( f_{t}- (1-\delta )\frac{\varphi }{\varphi -\delta \psi }f_t\right) \\&\quad -(1-\delta )f_0 -\delta \sum _{t=0}^{k-1} \left( \frac{\varphi }{\varphi -\delta \psi } \right) ^t f_* \\&{\mathop {=}\limits}\left( \frac{\varphi }{\varphi -\delta \psi } \right) ^{k-1} f_k+ \sum _{t=1}^{k-1} \left( \frac{\varphi }{\varphi -\delta \psi } \right) ^{t-1} \frac{\varphi -\psi }{\delta ^{-1}\varphi -\psi }f_t \\&\quad -(1-\delta )f_0 -\delta \sum _{t=0}^{k-1} \left( \frac{\varphi }{\varphi -\delta \psi } \right) ^t f_* \end{aligned}$$

(34)

$$\begin{aligned}&{\mathop {=}\limits ^{(*)}}&\left( \frac{\varphi }{\varphi -\delta \psi } \right) ^{k-1} r_{k}+ \sum _{t=1}^{k-1} \left( \frac{\varphi }{\varphi -\delta \psi } \right) ^{t-1} \frac{\varphi -\psi }{\delta ^{-1}\varphi -\psi }r_t -(1-\delta )r_0. \end{aligned}$$

(35)

Equality $(*)$ is obtained by the fact that the sum of terms corresponding to $f(\cdot )$ is 0 (this can be easily seen as it is equal to (32)).

Recall that we have

$$\begin{aligned} C_t \quad = \quad {\left\{ \begin{array}{ll}\left( \frac{\varphi }{\varphi -\delta \psi } \right) ^{t-1} \frac{\varphi -\psi }{\delta ^{-1}\varphi -\psi }, & 1\le t\le k-1 \\ \left( \frac{\varphi }{\varphi -\delta \psi } \right) ^{k-1}, & t=k. \end{array}\right. } \end{aligned}$$

and $c_t\overset{\text {def}}{=}C_t/\sum _{t=1}^kC_t$. Since the sum of terms corresponding to $f_t$ for some t or $f_*$ in (34) is 0 (because it is equal to (32)), we have

$$\begin{aligned} \sum _{t=1}^k C_t& = \left( \frac{\varphi }{\varphi -\delta \psi } \right) ^{k-1} + \sum _{t=1}^{k-1} \left( \frac{\varphi }{\varphi -\delta \psi } \right) ^{t-1} \frac{\varphi -\psi }{\frac{n}{\tau }\varphi -\psi } \\ &= (1-\delta ) +\delta \sum _{t=0}^{k-1} \Big (\frac{\varphi }{\varphi -\delta \psi } \Big )^t \\& = (1-\delta ) + \delta \frac{\Big ( \frac{\varphi }{\varphi -\delta \psi } \Big )^{k}-1}{\frac{\varphi }{\varphi -\delta \psi }-1} \\ &= (1-\delta ) + \frac{\Big ( \frac{\varphi }{\varphi -\delta \psi } \Big )^{k}-1}{\frac{\psi }{\varphi -\delta \psi }} \\& = (1-\delta ) + \left( \varphi -\delta \psi \right) \frac{\Big ( \frac{\varphi }{\varphi -\delta \psi } \Big )^{k}-1}{\psi } \\& = 1-\frac{\varphi }{\psi }+\frac{\varphi }{\psi }\left( \frac{\varphi }{\varphi -\delta \psi } \right) ^{k-1}. \end{aligned}$$

(36)

Thus, we can rewrite (35) as follows

$$\begin{aligned} \sum _{t=1}^{k}c_tr_t&{\mathop {\le }\limits ^{(35)}}&\bigg (\left( \varphi -\delta \psi \right) D_0 +(1-\delta )r_0\bigg )\frac{1}{\sum _{t=1}^kC_t}\\&{\mathop {=}\limits ^{(36)}}&\bigg (\left( \varphi -\delta \psi \right) D_0 +(1-\delta )r_0\bigg ) \frac{1}{1-\frac{\varphi }{\psi }+\frac{\varphi }{\psi }\Big ( \frac{\varphi }{\varphi -\delta \psi } \Big )^{k-1}}. \end{aligned}$$

$\square$

Appendix 3: Proofs for Section 4

1.1 Proof of Corollary 4.6

Denote $l_t=(L_t)^{-1}$ for simplicity. It is easy to see that

$$\begin{aligned} c_t=L\,l_t,\quad C_k=1+L\sum _{t=1}^{k-1}l_t,\quad \sum _{t=0}^{k-1} c_tl_t=L+L\left( \sum _{t=1}^{k-1} l_t^2\right) . \end{aligned}$$

Denote

$$\begin{aligned} A=(L-\mu )D_h(x_*,x_0)+\sigma ^2L. \end{aligned}$$

Minimizing RHS of (25) to obtain the best rate is equivalent to minimize

$$\begin{aligned} \frac{A+\sigma ^2L\left( \sum _{t=1}^{k-1} l_t^2\right) }{1+L\sum _{t=1}^{k-1}l_t}. \end{aligned}$$

Notice that the expression above is minimized for constant $l_t$, as if $l_t\ne l_s$, setting $l_t=l_s=\frac{l_t+l_s}{2}$ leads to strictly smaller value of the expression. Therefore, it suffices to minimize

$$\begin{aligned} \frac{A+\sigma ^2L(k-1) l^2}{1+L(k-1) l} \end{aligned}$$

in l. First order optimality condition yields

$$\begin{aligned} 2\sigma ^2 L(k-1)l (1+L(k-1)l)=(A+\sigma ^2 L(k-1)l^2)L(k-1), \end{aligned}$$

which is equivalent to

$$\begin{aligned} \sigma ^2L(k-1) l^2 +2\sigma ^2l-A=0. \end{aligned}$$

The quadratic equation above have a single solution

$$\begin{aligned} l=\frac{-\sigma ^2+\sqrt{\sigma ^4+\sigma ^2AL(k-1)}}{\sigma ^2L(k-1) } , \end{aligned}$$

which finishes the proof.

1.2 Proof of Lemma 4.7

For simplicity, denote $l_t=(L_t^{-1})$. Thus, $\{l_t\}$ is nonincreasing sequence. Note that the rate from the Theorem 4.5 is O(1/k) if and only if both

$$\begin{aligned} \frac{1}{C_k} \quad \text {and} \quad \sum _{t=0}^{k-1} \frac{c_tl_t}{C_k} \end{aligned}$$

are O(1/k).

Let us now consider that $\{c_t\}$ is nonincreasing for $t\ge T$. Suppose that

$$\begin{aligned} 1>\liminf \frac{c_{t}}{c_{t-1}}\overset{\text {def}}{=}r_c. \end{aligned}$$

Then for all k there is $K\ge k$ such that

$$\begin{aligned} 1>\frac{1+r_c}{2}>\frac{c_{K}}{c_{K-1}}. \end{aligned}$$

Thus there is infinitely many t such that

$$\begin{aligned} 1>\frac{1+r_c}{2}>\frac{c_{t}}{c_{t-1}}. \end{aligned}$$

Since $\{c_t\}$ is nonincreasing for $t\ge T$, we have that $\{c_t\}\rightarrow 0$ which is a contradiction with the assumption that $\tfrac{1}{C_t}=O(1/t)$. Thus we have

$$\begin{aligned} 1=\liminf \frac{c_{t}}{c_{t-1}}=\lim \frac{c_{t}}{c_{t-1}}, \end{aligned}$$

which implies that

$$\begin{aligned} \lim L_t-L_{t-1}=\mu . \end{aligned}$$

The above means that $L_t=\Theta (t)$. We have just proven the lemma for asymptotically nonincreasing $\{c_t\}$.

Now, suppose that $\{c_t\}$ is increasing sequence for $t\ge T$. Then we have for all $t\ge T$

$$\begin{aligned} \tfrac{L_{t-1}}{L_t-\mu }>1. \end{aligned}$$

Thus $L_t<L_{t-1}+\mu$, which implies that $L_t=O(t)$ and $l_t=\Omega (1/t)$.

On the other hand, looking at $\sum _{t=0}^{k-1} \tfrac{c_tl_t}{C_k}$ as the weighted sum of $l_t$, since $l_{k-1}$ is the smallest from $\{l_t \}$ we immediately have

$$\begin{aligned} O(1/k)= \sum _{t=0}^{k-1} \frac{c_tl_t}{C_k} \ge l_{k-1}\ge l_k, \end{aligned}$$

which means that $l_t=O(1/t)$. Thus, $l_t=\Theta (1/t)$ and $L_t=\Theta (t)$.

1.3 Proof of Lemma 4.8

First, we introduce two technical lemmas.

Lemma 9.1

Let us fix $\alpha >0$. There exist a convex continuous function $\gamma _\alpha (x)$ on $\mathbb {R}_+$ such that for all $x>0$ we have

$$\begin{aligned} \gamma _{\alpha }(x+\alpha )=\log (x)+\gamma _{\alpha }(x). \end{aligned}$$

(37)

Proof

We will construct function $\gamma _{\alpha }$ in the following way - Let us set $\gamma _{\alpha }(x)=0$ for $x\in [1,1+\alpha )$. For $x\ge 1+\alpha$ let us set recursively $\gamma _{\alpha }(x+\alpha )=\log (x)+\gamma _{\alpha }(x)$ and for $x<1$ let us set $\gamma _{\alpha }(x)=-\log (x)$. Clearly, equality (37) holds.

We will firstly prove that $\gamma _{\alpha }$ is continuous on $\mathbb {R}_+$ and differentiable on $R_+\backslash \{1\}$. Let us start with intervals $[1+k\alpha ,1+(k+1)\alpha )$ for all k.

Clearly, $\gamma _{\alpha }$ it is continuous and differentiable on $[1,1+\alpha )$. Suppose now inductively that $\gamma _{\alpha }$ is continuous and differentiable on $[1+k\alpha ,1+(k+1)\alpha )$ for some $k\ge 0$. Then, for $x\in [1+(k+1)\alpha ,1+(k+2)\alpha )$ we have

$$\begin{aligned} \gamma _{\alpha }(x)=\log (x-\alpha )+\gamma _{\alpha }(x-\alpha ). \end{aligned}$$

Since both $\log (x-\alpha )$ and $\gamma _{\alpha }(x-\alpha )$ are continuous and differentaible functions on $[1+(k+1)\alpha ,1+(k+2)\alpha )$, $\gamma _{\alpha }(x)$ is also continuous and differentaible on $[1+(k+1)\alpha ,1+(k+2)\alpha )$.

Clearly, $\gamma _{\alpha }$ it is continuous and differentiable on (0, 1).

It remains to show continuity and differentiability in the points $\{1+k\alpha \}$ for $k\ge 1$ and continuity in $\{1\}$. It is a simple exercise to see the continuity and differentiability in $\{1+\alpha \}$. For $1+k\alpha$ where $k\ge 2$ we can show it inductively—as $\gamma _{\alpha }(x-\alpha )$ and $\log (x-\alpha )$ are continuous and differentiable on $(1+(k-\tfrac{1}{2})\alpha ,1+(k+\tfrac{1}{2})\alpha )$, then $\gamma _{\alpha }(x)$ is continuous and differentiable on $(1+(k-\tfrac{1}{2})\alpha ,1+(k+\tfrac{1}{2})\alpha )$ as well and thus it is continuous and differentiable in point $\{1+k\alpha \}$. On top of that, $\gamma _\alpha$ is clearly continuous in $\{1\}$.

We have just proven that $\gamma _\alpha$ is continuous on $\mathbb {R}_+$ and differentiable on $\mathbb {R}_+\backslash \{1\}$.

Now we can proceed with the proof of convexity. We will show that the (sub)derivative of $\gamma _{\alpha }$ is nonegative for all $x>0$. Clearly, $\gamma _{\alpha }'(x)\ge 0$ for $x\in (0,1)$ and subdifferential in $\{1\}$ is nonegative as well. Let us write $x=1+\{x\}_\alpha +k\alpha$, where $0\le \{x\}_\alpha <\alpha$ and $k\ge -1$. Then we have

$$\begin{aligned} \gamma _{\alpha }'(x)& = \lim _{\epsilon \rightarrow 0} \frac{ \gamma _{\alpha }(x+\epsilon )-\gamma _{\alpha }(x)}{\epsilon }\\&= \lim _{\epsilon \rightarrow 0} \frac{\sum _{i=0}^{k-1}\left( \log \left( 1+\{x\}_\alpha +i\alpha +\epsilon \right) - \log \left( 1+\{x\}_\alpha +i\alpha \right) \right) }{\epsilon }\\&\quad +\frac{\gamma _{\alpha }(1+\{x\}_\alpha +\epsilon )-\gamma _{\alpha }(1+\{x\}_\alpha )}{\epsilon } \\&{\mathop {=}\limits ^{(*)}}&\lim _{\epsilon \rightarrow 0} \frac{\sum _{i=0}^{k-1}\left( \log \left( 1+\{x\}_\alpha +i\alpha +\epsilon \right) - \log \left( 1+\{x\}_\alpha +i\alpha \right) \right) }{\epsilon }\\&{\mathop {\ge }\limits ^{(**)}}&0. \end{aligned}$$

Equality $(*)$ holds since for small enough $\epsilon$ we have $1+\{x\}_\alpha +\epsilon <2\alpha$ and inequality $(**)$ holds due to the fact that logarithm is an increasing function. $\square$

Denote

$$\begin{aligned} \Gamma _{\alpha }(x)\overset{\text {def}}{=}\exp (\gamma _{\alpha }(x)) \end{aligned}$$

(38)

for $\gamma _{\alpha }$ given from Lemma 9.1. Thus, $\Gamma _{\alpha }$ is log-convex function satisfying

$$\begin{aligned} \Gamma _{\alpha }(x+\alpha )=x\Gamma _{\alpha }(x). \end{aligned}$$

(39)

Note that when $\alpha =1$, function $\gamma$ can be chosen as log Gamma function and thus $\Gamma _1$ can be chosen to be standard Gamma function.

The following lemma is crucial for our analysis, allowing us to bound the ratio of functions $\Gamma _{\alpha }(\cdot )$ with nearby arguments.

Lemma 9.2

Consider a function $\Gamma _{\alpha }$ defined above. Then, we have for all $0\le s\le \alpha$ and $x>0$:

$$\begin{aligned} x^{1-\frac{s}{\alpha }} \le \frac{\Gamma _{\alpha }(x+\alpha )}{\Gamma _{\alpha }(x+s)} \le (x+\alpha )^{1-\frac{s}{\alpha }}. \end{aligned}$$

(40)

Proof

Using convexity of $\gamma _{\alpha }$ we have

$$\begin{aligned} \Gamma _{\alpha }(x+s) \le \Gamma _{\alpha }(x)^{1-\frac{s}{\alpha }} \Gamma _{\alpha }(x+\alpha )^{\frac{s}{\alpha }} {\mathop {=}\limits ^{(39)}} x^{\frac{s}{\alpha }-1}\Gamma _{\alpha }(x+\alpha ). \end{aligned}$$

Rearranging the above we obtain

$$\begin{aligned} x^{1-\frac{s}{\alpha }} \le \frac{\Gamma _{\alpha }(x+\alpha )}{\Gamma _{\alpha }(x+s)} . \end{aligned}$$

On the other hand, using convexity of $\gamma _{\alpha }$ again we obtain

$$\begin{aligned} \Gamma _{\alpha }(x+\alpha ) \le \Gamma _{\alpha }(x+s)^{\frac{s}{\alpha }} \Gamma _{\alpha }(x+s+\alpha )^{1-\frac{s}{\alpha }} {\mathop {=}\limits ^{39}} (x+s)^{1-\frac{s}{\alpha }}\Gamma _{\alpha }(x+s). \end{aligned}$$

By rearranging the above, we get

$$\begin{aligned} \frac{\Gamma _{\alpha }(x+\alpha )}{\Gamma _{\alpha }(x+s)} \le (x+s)^{1-\frac{s}{\alpha }} \le (x+\alpha )^{1-\frac{s}{\alpha }} . \end{aligned}$$

$\square$

We can now proceed with the proof of Lemma 4.8 itself.

Proof

Note that

$$\begin{aligned} c_t&= \prod _{i=0}^{t-1}\frac{L_i}{L_{i+1}-\mu } \\&{\mathop {=}\limits ^{(39)}}\frac{\frac{\Gamma _{\alpha }(L+t\alpha )}{\Gamma _{\alpha }(L)}}{\frac{\Gamma _{\alpha }(L+(t+1)\alpha -\mu )}{\Gamma _{\alpha }(L-\mu +\alpha )}} \\& = \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \frac{\Gamma _{\alpha }(L+t\alpha )}{\Gamma _{\alpha }(L-\mu +(t+1)\alpha )}. \end{aligned}$$

(41)

Let us firstly consider the case when $\alpha >\mu$. Choosing $x= L-\mu +t\alpha$ and $s=\mu$ in (40) we get

$$\begin{aligned} (L-\mu +t\alpha )^{1-\frac{\mu }{\alpha }} \le \frac{\Gamma _{\alpha }(L-\mu +(t+1)\alpha )}{\Gamma _{\alpha }(L+t\alpha )} \le (L-\mu +(t+1)\alpha )^{1-\frac{\mu }{\alpha }}. \end{aligned}$$

The inequality above allows us to get the following bound on $c_t$

$$\begin{aligned} \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} (L-\mu +t\alpha )^{\frac{\mu }{\alpha }-1} \ge c_t \ge \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} (L-\mu +(t+1)\alpha )^{\frac{\mu }{\alpha }-1}. \end{aligned}$$

(42)

Clearly, $\{c_t\}$ is decreasing and thus using the bound above we obtain

$$\begin{aligned} C_k& = \sum _{t=0}^{k-1}c_t \quad {\mathop {\ge }\limits ^{(42)}} \quad \sum _{t=0}^{k-1} \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} (L-\mu +(t+1)\alpha )^{\frac{\mu }{\alpha } -1}\\& = \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \sum _{t=0}^{k-1} (L-\mu +(t+1)\alpha )^{\frac{\mu }{\alpha } -1}\\&{\mathop {\ge }\limits ^{(*)}}&\frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \int _{0}^{k} (L-\mu +(t+1)\alpha )^{\frac{\mu }{\alpha } -1} dt\\&= \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \int _{0}^{(k)\alpha } (L-\mu +\alpha +t)^{\frac{\mu }{\alpha } -1} \frac{1}{\alpha } dt\\& = \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \frac{1}{\alpha } \Big [\frac{(L-\mu +\alpha +t)^{\frac{\mu }{\alpha }}}{\frac{\mu }{\alpha }} \Big ]_{t=0}^{k\alpha }\\& = \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \frac{(L-\mu +(k+1)\alpha )^{\frac{\mu }{\alpha }}- (L-\mu +\alpha )^{\frac{\mu }{\alpha }}}{\mu }\\&{\mathop {\ge }\limits ^{(40)}}&(L-\mu )^{1-\frac{\mu }{\alpha }} \frac{(L-\mu +(k+1)\alpha )^{\frac{\mu }{\alpha }}- (L-\mu +\alpha )^{\frac{\mu }{\alpha }}}{\mu }. \end{aligned}$$

Inequality $(*)$ holds since $(L-\mu +(t+1)\alpha )^{\mu /\alpha -1}$ is decreasing in t. On the other hand, we have

$$\begin{aligned} \sum _{t=1}^{k-1}\frac{c_t}{L_t}&{\mathop {\le }\limits ^{(42)}}\sum _{t=1}^{k-1} \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} (L-\mu +t\alpha )^{\frac{\mu }{\alpha } -1} \frac{1}{L+t\alpha }\\&= \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \sum _{t=1}^{k-1} \frac{1}{L+t\alpha } (L-\mu +t\alpha )^{\frac{\mu }{\alpha } -1}\\&{\mathop {\le }\limits ^{(*)}}\frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)}\sum _{t=1}^{k-1} (L-\mu +t\alpha )^{\frac{\mu }{\alpha } -2}\\&{\mathop {\le }\limits ^{(**)}}\frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)}\int _0^k (L-\mu +t\alpha )^{\frac{\mu }{\alpha } -2} dt\\&= \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \int _0^{k\alpha } (L-\mu +t)^{\frac{\mu }{\alpha } -2} \frac{1}{\alpha } dt \\&= \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \frac{1}{\alpha } \left[ \frac{(L-\mu +t)^{\frac{\mu }{\alpha }-1}}{\frac{\mu }{\alpha }-1} \right] _0^{k\alpha } \\&= \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \frac{(L-\mu )^{\frac{\mu }{\alpha }-1}-(L-\mu +k\alpha )^{\frac{\mu }{\alpha }-1}}{\alpha -\mu } \\&{\mathop {\le }\limits ^{(40)}}(L-\mu +\alpha )^{1-\frac{\mu }{\alpha }} \frac{(L-\mu )^{\frac{\mu }{\alpha }-1}-(L-\mu +k\alpha )^{\frac{\mu }{\alpha }-1}}{\alpha -\mu }. \end{aligned}$$

Inequality $(*)$ holds due to the fact that $(L+t\alpha )^{-1}\le (L-\mu +t\alpha )^{-1}$ and inequality $(**)$ holds since $(L-\mu +t\alpha )^{\mu /\alpha -2}$ is decreasing in t. Thus we have

$$\begin{aligned} \sum _{t=0}^{k-1}\frac{c_t}{L_t} \le \frac{1}{L} + (L-\mu +\alpha )^{1-\frac{\mu }{\alpha }} \frac{(L-\mu )^{\frac{\mu }{\alpha }-1}-(L-\mu +k\alpha )^{\frac{\mu }{\alpha }-1}}{\alpha -\mu }. \end{aligned}$$

and we have just proven the first part of the lemma.

Let us now look at the case when $\alpha \le \mu$. It will be useful to denote $\lfloor \mu \rfloor _\alpha$ as the largest integer such that $\mu - \lfloor \mu \rfloor _\alpha \alpha$ is positive. Denote also

$$\begin{aligned} \{\mu \}_\alpha \overset{\text {def}}{=}\mu - \lfloor \mu \rfloor _\alpha \alpha . \end{aligned}$$

Using (39) we obtain

$$\begin{aligned} \frac{\Gamma _{\alpha }(L+t\alpha )}{\Gamma _{\alpha }(L-\mu +(t+1)\alpha )}&= \frac{\Gamma _{\alpha }(L+t\alpha )(L+t\alpha +\alpha -\mu ) (L+t\alpha +2\alpha -\mu )\dots (L+t\alpha +(\lfloor \mu \rfloor _\alpha -1)\alpha -\mu )}{\Gamma _{\alpha }(L+t\alpha +\lfloor \mu \rfloor _\alpha \alpha -\mu )}\\&= \frac{\Gamma _{\alpha }(L+t\alpha )(L+t\alpha + \alpha -\mu )(L+t\alpha +2\alpha -\mu )\dots (L-\{\mu \}_\alpha +(t -1)\alpha )}{\Gamma _{\alpha }(L-\{\mu \}_\alpha +t\alpha )}. \end{aligned}$$

Upper and lower bounding the equality above we get

$$\begin{aligned} \frac{\Gamma _{\alpha }(L+t\alpha )}{\Gamma _{\alpha }(L-\mu +(t+1)\alpha )} &\ge \frac{\Gamma _{\alpha }(L+t\alpha )}{\Gamma _{\alpha }(L-\{\mu \}_\alpha +t\alpha )} (L-\mu +(t+1)\alpha )^{\lfloor \mu \rfloor _\alpha -1}, \end{aligned}$$

(43)

$$\begin{aligned} \frac{\Gamma _{\alpha }(L+t\alpha )}{\Gamma _{\alpha }(L-\mu +(t+1)\alpha )}&\le \frac{\Gamma _{\alpha }(L+t\alpha )}{\Gamma _{\alpha }(L-\{\mu \}_\alpha +t\alpha )} (L-\{\mu \}_\alpha +(t -1)\alpha )^{\lfloor \mu \rfloor _{\alpha } -1}. \end{aligned}$$

(44)

Using (40) we have

$$\begin{aligned} (L+(t-1)\alpha )^{\frac{\{\mu \}_\alpha }{\alpha }} \le \frac{\Gamma _{\alpha }(L+t\alpha )}{\Gamma _{\alpha }(L-\{\mu \}_\alpha +t\alpha )} \le (L+t\alpha )^{\frac{\{\mu \}_\alpha }{\alpha }}. \end{aligned}$$

(45)

Now we are ready to get upper and lower bound on $c_t$:

$$\begin{aligned} c_t&{\mathop {=}\limits ^{(41)}}\frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \frac{\Gamma _{\alpha }(L+t\alpha )}{\Gamma _{\alpha }(L-\mu +(t+1)\alpha )} \\&{\mathop {\ge }\limits ^{(43)}}&\frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \frac{\Gamma _{\alpha }(L+t\alpha )}{\Gamma _{\alpha }(L-\{\mu \}_\alpha +t\alpha )} (L-\mu +(t+1)\alpha )^{\lfloor \mu \rfloor _\alpha -1} \\&{\mathop {\ge }\limits ^{(45)}}\frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} (L+(t-1)\alpha )^{\frac{\{\mu \}_\alpha }{\alpha }} (L-\mu +(t+1)\alpha )^{\lfloor \mu \rfloor _\alpha -1}. \end{aligned}$$

(46)

$$\begin{aligned} c_t&{\mathop {=}\limits ^{(41)}}\frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \frac{\Gamma _{\alpha }(L+t\alpha )}{\Gamma _{\alpha }(L-\mu +(t+1)\alpha )} \\&{\mathop {\le }\limits ^{(44)}}\frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \frac{\Gamma _{\alpha }(L+t\alpha )}{\Gamma _{\alpha }(L-\{\mu \}_\alpha +t\alpha )} (L-\{\mu \}_\alpha +(t -1)\alpha )^{\lfloor \mu \rfloor _{\alpha } -1} \\&{\mathop {\le }\limits ^{(45)}}\frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} (L+t\alpha )^{\frac{\{\mu \}_{\alpha }}{\alpha }} (L-\{\mu \}_\alpha +(t -1)\alpha )^{\lfloor \mu \rfloor _{\alpha } -1} \end{aligned}$$

(47)

Recall that we have $m_\mu =\max (\alpha ,\mu -\alpha )$. Then, we can get the following bound on $C_k:$

$$\begin{aligned} C_k-c_0& = \sum _{t=1}^{k-1}c_t \\&{\mathop {\ge }\limits ^{(46)}}&\sum _{t=1}^{k-1} \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} (L+(t-1)\alpha )^{\frac{\{\mu \}_\alpha }{\alpha }} (L-\mu +(t+1)\alpha )^{\lfloor \mu \rfloor _\alpha -1} \\&{\mathop {\ge }\limits ^{(26)}}&\sum _{t=1}^{k-1} \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} (L-m_{\mu }+t\alpha )^{\frac{\{\mu \}_\alpha }{\alpha }} (L-m_{\mu }+t\alpha )^{\lfloor \mu \rfloor _\alpha -1} \\& = \sum _{t=1}^{k-1} \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} (L-m_{\mu }+t\alpha )^{\frac{\mu }{\alpha }-1} \\ &= \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \sum _{t=1}^{k-1} (L-m_{\mu }+t\alpha )^{\frac{\mu }{\alpha }-1} \\&{\mathop {\ge }\limits ^{(*)}}&\frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \int _{0}^{k-1} (L-m_{\mu }+t\alpha )^{\frac{\mu }{\alpha }-1}dt \\& = \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \int _{0}^{(k-1)\alpha } (L-m_{\mu }+t)^{\frac{\mu }{\alpha }-1}\frac{1}{\alpha } dt \\&= \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)}\frac{1}{\alpha } \Big [\frac{(L-m_\mu +t)^{\frac{\mu }{\alpha }}}{\frac{\mu }{\alpha }} \Big ]_{t=0}^{(k-1)\alpha } \\&= \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \frac{(L-m_{\mu }+(k-1)\alpha )^{\frac{\mu }{\alpha }}-(L-m_{\mu })^{\frac{\mu }{\alpha }}}{\mu }. \end{aligned}$$

(48)

Inequality $(*)$ holds since $(L-m_\mu +t\alpha )^{\mu /\alpha -1}$ is increasing function. Note that in the case when $\alpha =\mu$, all bounds above hold with equality and we have

$$\begin{aligned} C_k= k. \end{aligned}$$

To finish the proof of the second and third part of the Lemma, it remains to upper bound $\sum _{t=0}^{k-1} c_tL_t^{-1}$. Firstly, note that

$$\begin{aligned} \frac{c_t}{L_t}&{\mathop {\le }\limits ^{(47)}}\frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} (L+t\alpha )^{\frac{\{\mu \}_{\alpha }}{\alpha }} (L-\{\mu \}_\alpha +(t -1)\alpha )^{\lfloor \mu \rfloor _{\alpha } -1} (L+t\alpha )^{-1} \\&{\mathop {\le }\limits ^{(*)}}\frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} (L+t\alpha )^{\frac{\mu }{\alpha }-1}(L+t\alpha )^{-1} \\&= \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} (L+t\alpha )^{\frac{\mu }{\alpha }-2}. \end{aligned}$$

(49)

Inequality $(*)$ holds due to the fact that $L-\{\mu \}_\alpha +(t -1)\alpha \le L+t\alpha$. We can continue bounding as follows

$$\begin{aligned} \sum _{t=1}^{k-1}\frac{c_t}{L_t}&{\mathop {\le }\limits ^{(49)}}\sum _{t=1}^{k-1}\frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)}(L+t\alpha )^{\frac{\mu }{\alpha }-2} \\ &= \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \sum _{t=1}^{k-1} (L+t\alpha )^{\frac{\mu }{\alpha }-2} \\&{\mathop {\le }\limits ^{(*)}} \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \int _{0}^{k} (L+t\alpha )^{\frac{\mu }{\alpha }-2}dt \\& = \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \int _{0}^{k\alpha } (L+t)^{\frac{\mu }{\alpha }-2} \frac{1}{\alpha }dt \\&{\mathop {=}\limits ^{(**)}} {\left\{ \begin{array}{ll} \frac{\log (L+k\mu )-\log (L)}{\mu } &\text {if } \alpha =\mu , \\ \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} \frac{(L+k\alpha )^{\frac{\mu }{\alpha }-1}-L^{\frac{\mu }{\alpha }-1}}{\mu -\alpha } &\text {if } \alpha <\mu . \end{array}\right. } \end{aligned}$$

(50)

Inequality $(*)$ holds due to the fact that for $\mu \ge 2\alpha$ we have

$$\begin{aligned} \sum _{t=1}^{k-1} (L+t\alpha )^{\frac{\mu }{\alpha }-2} \le \int _{1}^{k} (L+t\alpha )^{\frac{\mu }{\alpha }-2} dt \end{aligned}$$

and for $\mu < 2\alpha$ we have

$$\begin{aligned} \sum _{t=1}^{k-1} (L+t\alpha )^{\frac{\mu }{\alpha }-2} \le \int _{0}^{k-1} (L+t\alpha )^{\frac{\mu }{\alpha }-2} dt. \end{aligned}$$

Equality $(**)$ holds since

$$\begin{aligned} \int _{0}^{k\mu } (L+t)^{-1} \frac{1}{\mu }dt = \frac{1}{\mu } \left[ \log (L+t) \right] _{t=0}^{k\mu } = \frac{\log (L+k\mu )-\log (L)}{\mu } \end{aligned}$$

and

$$\begin{aligned} \int _{0}^{k\alpha } (L+t)^{\frac{\mu }{\alpha }-2} \frac{1}{\alpha } dt = \frac{1}{\alpha } \left[ \frac{(L+t)^{\frac{\mu }{\alpha }-1}}{\frac{\mu }{\alpha }-1} \right] _{t=0}^{k\alpha } = \frac{(L+k\alpha )^{\frac{\mu }{\alpha }-1}-L^{\frac{\mu }{\alpha }-1}}{\mu -\alpha } \end{aligned}$$

for $\alpha <\mu$.

To finish the proof, let us now consider the special case when $\alpha =\tfrac{\mu }{2}$ (in other words $L_t=L+t\tfrac{\mu }{2}$). Note that we have

$$\begin{aligned} \frac{\Gamma _{\alpha }(L-\mu +\alpha )}{\Gamma _{\alpha }(L)} = \frac{\Gamma _{\alpha }(L-\alpha )}{\Gamma _{\alpha }(L)} = \frac{1}{L-\alpha } = \frac{1}{L-\frac{\mu }{2}} . \end{aligned}$$

Thus, according to (48) and (50) we have

$$\begin{aligned} C_k&{\mathop {\ge }\limits ^{(48)}}1+ \frac{1}{L-\frac{\mu }{2}} \frac{(L-m_{\mu }+(k-1)\frac{\mu }{2})^2-(L-m_{\mu })^2}{\mu } \\& = 1+ \frac{(L+(k-2)\frac{\mu }{2})^2-(L-\frac{\mu }{2})^2}{(L-\frac{\mu }{2})\mu } \\&= \frac{(L+(k-2)\frac{\mu }{2})^2-(L-\frac{\mu }{2})^2 +(L-\frac{\mu }{2})\mu }{(L-\frac{\mu }{2})\mu } \end{aligned}$$

(51)

$$\begin{aligned}&\sum _{t=0}^{k-1} \frac{c_t}{L_t} \quad {\mathop {\le }\limits ^{(50)}} \quad \frac{1}{L}+ \frac{1}{L-\frac{\mu }{2}} \frac{(L+k\frac{\mu }{2})^{1}-L^{1}}{\frac{\mu }{2}} = \frac{1}{L}+ \frac{k}{L-\frac{\mu }{2}}. \end{aligned}$$

(52)

Combining (51), (52) with Theorem 4.5 we obtain

$$\begin{aligned} \sum _{t=1}^k \frac{c_{t-1}}{C_k} \mathbf{E}\left[ f(x_t)-f(x_*)\right]&\le \frac{(L-\mu )D_h(x_*,x_0)}{\frac{(L+(k-2)\frac{\mu }{2})^2- (L-\frac{\mu }{2})^2+(L-\frac{\mu }{2})\mu }{(L-\frac{\mu }{2})\mu }}\\&\quad +\sigma ^2 \frac{\frac{1}{L}+ \frac{k}{L-\frac{\mu }{2}}}{\frac{(L+(k-2)\frac{\mu }{2})^2- (L-\frac{\mu }{2})^2+(L-\frac{\mu }{2})\mu }{(L-\frac{\mu }{2})\mu }}\\&= \frac{(L-\mu )(L-\frac{\mu }{2})\mu D_h(x_*,x_0)+\sigma ^2\mu (1-\frac{\mu }{2L }+k) }{(L+(k-2)\frac{\mu }{2})^2-(L-\frac{\mu }{2})^2+(L-\frac{\mu }{2})\mu } \end{aligned}$$

which concludes the proof. $\square$

Appendix 4: Notation glossary

See Table 1.

Table 1 Summary of frequently used notation