Simulating a breakup event and propagating the orbits of space debris

Abstract

Explosions or collisions of satellites around the Earth generate space debris, whose uncontrolled dynamics might raise serious threats for operational satellites. Mitigation actions can be realized on the basis of our knowledge of the characteristics of the fragments produced during the breakup event and their subsequent propagation. In this context, important information can be obtained by implementing a breakup simulator, which provides, for example, the number of fragments, their area-to-mass ratio or the relative velocity distribution as a function of the characteristic length of the fragments. Motivated by the need to analyze the dynamics of the fragments, we reconstruct a simulator based on the NASA/JSC breakup model EVOLVE 4.0 that we review for self-consistency. This model, created at the beginning of the XXI century, is based on laboratory and on-orbit tests. Given that materials and methods for building satellites are constantly progressing, we leave some key parameters variable and produce results for different choices of the parameters. We will also present an application to the Iridium–Cosmos collision and we discuss the distribution function after a breakup event. The breakup model is strongly related to the propagation of the fragments; in this work, we discuss how to choose the models and the numerical integrators, we propose examples of how fragments can disperse in time, and we study the behavior of multiple simultaneous fragmentations. Finally, we compute some indicators for detecting streams of fragments. Breakup and propagation are performed using our own simulator SIMPRO, built from EVOLVE 4.0; the executable program will be freely available on GitHub.

1 Introduction and plan of the work

The high number of satellites put in orbit around the Earth since the launch of Sputnik 1 in 1957 has generated a huge amount of space debris. These fragments have different sizes, from micrometer to centimeter-size particles. Due to their high velocity impact, even small-size fragments can prove disastrous to operational satellites. Understanding the dynamics of such objects after a breakup event is of paramount importance. However, this goal can only be achieved by analyzing examples with different orbital parameters, namely the altitude, eccentricity, inclination and the angular elements that define the orbit of the ancestor body (or bodies) that generated the fragmentation event.

The need of having at disposal data associated to breakup events leads to the construction of simulators, with the aim to provide information about the fragments generated by an explosion or a collision. In this work, we revisit the breakup model EVOLVE 4.0 built by NASA Johnson Space Center (JSC) (see Johnson et al. (2001), Klinkrad (2006), AAVV (1998)). On this basis, we built a simulator called SIMPRO, which determines specific quantities characterizing the fragments after a breakup event, e.g., the number of debris, their size distribution, the area-to-mass ratio, the relative velocity distribution of the fragments with respect to the parent body. With respect to EVOLVE 4.0, SIMPRO allows one to modify the key parameters and to choose them within some intervals. In this work, we highlight that changing the values of some parameters leads to non-negligible effects in the final results.

The collection of these data might represent an essential tool to investigate the dynamics of space debris and to devise mitigation actions (for recent works on the dynamics of space debris, see, e.g., Alessi et al. (2018), Celletti and Galeş (2018), Celletti et al. (2020), Celletti et al. (2021), Celletti et al. (2022), Gkolias and Colombo (2019), Schettino et al. (2019), Skoulidou et al. (2018) and references therein). To reach this goal, it is essential to make a propagation of the orbits after the breakup. The simulator SIMPRO includes also a propagator of the orbits of the fragments, and in this work, we discuss the models that define the equations of motion for objects around the Earth, we compare Cartesian and Hamiltonian formalism and we discuss integration algorithms.

We remark that the NASA/JSC breakup model described in Johnson et al. (2001) was originally built upon data available for objects at low altitude. However, we assume that it is possible to extend its validity (at least from the theoretical point of view) by considering objects at different altitudes. This leads us to start with a description of the dynamical features of the circumterrestrial space (Sect. 1.1), before making a short review of the available breakup simulators (Sect. 1.2) and before concluding with a description of the plan of this work (Sect. 1.3).

1.1 The circumterrestrial space

When studying the dynamical behavior of satellites around the Earth, it is usually convenient to split the circumterrestrial space into three main regions as follows:

- LEO, which stands for Low-Earth-Orbits, with altitudes up to 2 000 km of altitude,

- MEO, which stands for Medium–Earth–Orbits, ranging between 2 000 and 30 000 km,

- GEO, which stands for Geostationary–Earth–Orbits, for altitudes greater than 30 000 km.

The dominant perturbation effects in each region vary according to the altitude, as it is shown in Fig. 1. In particular, in LEO one needs to consider the gravitational influence of the Earth (compare with Burnett and Schaub (2022)), an accurate expansion of the geopotential and the atmospheric drag. In MEO and GEO, the atmospheric drag is not acting, but the effects of Moon and Sun become important (see, e.g., Daquin et al. (2022)). Besides, it is also crucial to consider the solar radiation pressure, whose contribution increases as the area-to-mass ratio is larger. The influence of the other planets is typically much smaller than the other effects.

Fig. 1

The accelerations’ order of magnitude for different perturbations as a function of the altitude in LEO, MEO, GEO: air drag, geopotential terms, Jupiter, Sun and Moon attractions, solar radiation pressure for different values of the area-to-mass ratio. Tesseral resonances are marked as vertical dashed lines

Figure 1 provides also information concerning the location of the so-called tesseral resonances, which occur when there is a commensurability between the rates of variation of the satellite or fragment and the sidereal time, accounting for the rotation of the Earth; for completeness, we mention that the exact definition of tesseral resonance involves also the rates of variation of the argument of perigee and the longitude of the ascending node of the satellite or fragment (see Celletti et al. (2020) for full details).

1.2 Breakup simulators

The study of breakup models for space debris started several decades ago on the basis of on-ground experiments of collisions, explosions and hypervelocity impacts (see, e.g., Kessler and Su (1985), Reynolds (1990)). The output of a breakup model is to give information about the fragments produced by the catastrophic event, in particular their number, size distribution, area-to-mass ratio as well as the relative velocity distribution. These parameters are not constant for all fragments; hence, it is necessary to compute distributions as a function of some parameters, most notably the mass of the parent body (or bodies, in case of collisions) and the characteristic length (namely, the average of the three dimensions of the fragments). We shortly describe some of the most well-known simulators of breakup events, stressing that the list is not exhaustive.

A world-wide reference within breakup simulators is represented by the NASA/JSC model EVOLVE 4.0, presented in Johnson et al. (2001) (see also AAVV (1998)). It represents a result from combined ground tests, on-orbit size and mass estimates, orbital tracking and radar observations. It also relies on analyses of breakup events performed by NASA/JSC in LEO. The characteristic length is chosen as independent parameter, since it can be connected to hypervelocity tests and on-orbit measurements. For each characteristic length, one can compute the number of fragments, the area-to-mass distribution as well as the velocity distribution. The model distinguishes between a characteristic length less than 8 cm and bigger than 11 cm, while a bridge function should be used in between.

A more recent tool developed by NASA/JSC is the “LEO-to-GEO ENvironment Debris model”, called LEGEND (see Liou et al. (2004), Vallado and Oltrogge (2017)); it is valid up to 50 000 km of altitude. It provides an evolutionary model for the analysis of the long-term behavior of the fragments, yielding their altitude, longitude and latitude as a function of time. The fragmentation model of LEGEND differs from Evolve 4.0 in two main aspects, namely the scaling factor of explosion and the assignment of A/m ratio for each fragment.

We also mention the “Debris Analysis and Monitoring Architecture to the Geosynchronous Environment”, called DAMAGE, which has been developed at the University of Southampton (Lewis et al. (2001)). It is a debris model valid in MEO and GEO with particular attention to the long-term stability and risk assessment of objects in HEO, namely in Highly Eccentric Orbits. It uses a different fragmentation model based on low velocity impact (Yasaka (2000)).

The “Meteoroid and Space Debris Terrestrial Environment Reference model”, called MASTER, has been developed by ESA as a reference software for the description of the Earth’s debris environment (Klinkrad et al. (2000)). The fragmentation model is based on NASA EVOLVE 4.0 with the extension of fragments’ size distribution to micron orders.

The “ORbital Debris Environment Model”, called ORDEM, has been developed by NASA (see Krisko et al. (2015)) and it provides short-term evolution of the debris impact flux, making use of returned samples, observations, modeling (see also Sdunnus et al. (2004) for a comparison among widely distributed debris flux models).

Finally, the “Fragmentation Event Model and Assessment Tool”, called FREMAT (Andrisan et al. (2017)), is a project for ESA, composed by three tools called FREG, IFEST, SOFT. The first one FREG (“FRagmentation Event Generator”) simulates breakup events. The second tool IFEST (“Impact of Fragmentation Events on Spatial density Tool”) provides the evolution of the fragments and it computes the spatial density. The last tool SOFT (“Simulation of on-Orbit Fragmentation Tool”) provides the type of fragmentation, determines the location and time of the catastrophic event, and identifies the parent body.

We mention that other works are available to simulate breakup events, for which we refer to the dedicated literature (see, e.g., Letizia et al. (2016), Petit et al. (2018), Rossi et al. (2009) and references therein).

1.3 Structure of the paper

A breakup model is typically the outcome of theoretical and empirical studies. Along the years, new materials and construction methods are used to build satellites. Hence, the necessity to update, or even reformulate, the experimental ground-based tests (see Allen (2020) and references therein) and to compile large orbital data for explosion and collision debris. This might affect the choice of the different parameters that define the quantities entering the breakup model (see Sect. 2). For this reason, we allow the main parameters to vary around the values that are given in Johnson et al. (2001) and we provide some examples to assess the dependence of the method on the choice of such parameters (see Sect. 3). We also present an application to the collision between Iridium 33 and Cosmos 2251, which suggests using the simulator to set the key parameters of the model to fit breakup events for which the data are known. The simulator is also used to make a comparison between the theoretical and numerical distribution function of the orbital elements after a breakup event (Sect. 4).

Once the fragments are generated, either from an explosion or a collision, one needs to propagate each fragment to understand the dynamical evolution and, possibly, to evaluate the risk they raise for operational satellites. To propagate the orbits, we use Cartesian (for short time intervals) and Hamiltonian (for long periods of time) equations of motion (see Sect. 5).

The validity of the Cartesian and Hamiltonian frameworks, as well as the weight of the different forces (geopotential, Sun, Moon, etc.) as the orbital elements and the characteristic parameters are varied, are investigated by propagating the orbits of the fragments obtained by implementing the breakup model (see Sect. 6). This study leads to evaluate specific behaviors of the debris, like the dispersion of the cloud of fragments over time or rather the effect of multiple breakup events, taking place in nearby locations of the orbital elements. Following classical works on meteor streams (Southworth and Hawkings (1963), see also Wu et al. (2023), Zappalá et al. (1990)), we also discuss the computation of indicators for nearby streams of fragments as well as streams generated by the propagation of the orbits (Sect. 7). Conclusions and perspectives are discussed in Sect. 8.

Making available the executable simulator program SIMPRO that generates the output of a breakup event, based on EVOLVE 4.0, and combining it with the propagation of the fragments’ orbits, we hope to stimulate further interest on this topic, which certainly needs more investigations, either theoretical or experimental. The program is available upon request to the authors and it can be freely used, provided that reference to the current paper is quoted¹.

2 Fragmentation and simulator workflow

Breakup events are typically classified as due to explosions or rather to collisions. Following Johnson et al. (2001), explosions are characterized by the fraction of mass forming the debris cloud, while collisions by the fraction of mass destroyed in the breakup event (see Sect. 2.1). The probability of hazard by debris’ clouds has been extensively discussed in Chobotov et al. (1988). The workflow of a simulator of breakup events is illustrated in Sect. 2.2.

2.1 Explosions and Collisions

Explosions involve only a parent body, whose satellite type (Molniya, Titan Transtage, Soviet Eorsat, etc.) affects the output of the breakup event. Collisions are typically considered between a parent body and a projectile (with the aim to propagate the fragments). We can also consider the collision between two satellites, see Sect. 3.4, by running the simulation twice interchanging one body called the parent body and the second body called the projectile. Such an approach is a good approximation, provided that the total kinetic energy of the projectile divided by the mass of the parent body exceeds 40 J/g (see Johnson et al. (2001)).

Within explosions, one distinguishes between low- and high-intensity explosions:

• i) Low-intensity: for minor breakups, such as battery explosions, only a fraction of the total mass of the object is treated as the debris cloud;

• ii) High-intensity: $10\%$ of the mass in the debris cloud is used in the high-intensity distribution function, $90\%$ of the mass in the debris cloud is used in the low-intensity distribution function.

Within collisions, one distinguishes between non-catastrophic and catastrophic collisions; the ratio between the mass of the projectile and the parent body is crucial, since it determines how much mass is going into the ejecta, how much mass is left and whether the remaining structure breaks up.

• i) Non-catastrophic: a collision in which ejecta is created, but the remaining structure is kept intact; there is insufficient energy in the collision to cause the entire target to breakup;

• ii) Catastrophic: a collision in which ejecta is created and the remaining mass is destroyed; some of the fragments’ mass (ejecta) goes into the ejecta distribution function and some of the fragments’ mass (the remainder of the target) goes into the low-intensity distribution function. The impactor mass is always included in the ejecta distribution function.

2.2 Workflow of the breakup simulator

In both explosions or collisions, the inputs are the minimum size of the resulting fragments $L_{c}^{min}$ (see Sect. 3 for details), the orbital elements of the parent body, namely the semimajor axis a, the eccentricity e, the inclination i, the mean anomaly M, the argument of perigee $\omega$ and the longitude of the ascending node $\Omega$. In case of a collision, one needs also to specify the masses of the parent body and the projectile, the collision velocity and the type of parent body (e.g., upper stage or spacecraft).

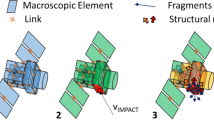
Following Johnson et al. (2001), an algorithm for computing the size, the area-to-mass ratio A/m and the orbital elements of each generated fragment is implemented along the workflow shown in Fig. 2. More precisely, the number of fragments larger than $L_{c}^{min}$ is computed; then, for each generated fragment, a size, as well as an area-to-mass ratio value A/m and an ejection velocity value $\Delta v$ are assigned by using the area-to-mass distribution and the velocity distribution functions of the NASA/JSC breakup model EVOLVE 4.0. Assuming an isotropic distribution of the ejection velocity, the components $(\Delta v_x, \Delta v_y, \Delta v_z)$ of the ejection velocity vector, referred to the quasi-inertial system of axes Oxyz, centered in the Earth with the x axis pointing to the vernal equinox and the z axis coinciding with the Earth’s rotation axis, are determined as

$$\begin{aligned} \Delta v_x=\Delta v \, \sqrt{1-C^2} \, \cos \varphi \,, \qquad \Delta v_y=\Delta v \, \sqrt{1-C^2}\,, \qquad \Delta v_z=\Delta v \, C\,, \end{aligned}$$

where $\varphi$ is a randomly generated angle between $[0^o,360^o)$ and C is a random number between $-1$ and 1. Knowing the orbital elements of the parent body, then its orbital state vector, namely the position and velocity vectors at the epoch of fragmentation, are computed and used to determine the orbital state vector of each fragment. Clearly, each fragment is assumed to occupy the same position (the position of the parent body) at the initial time, while the velocity of a given fragment is obtained by incrementing the velocity of the parent body with $(\Delta v_x, \Delta v_y, \Delta v_z)$. Finally, the sign of total energy of the two-body problem (Earth-fragment) is checked and, in case of elliptic trajectories, the orbital elements of the fragment are computed. The procedure is shortly described in the workflow in Fig. 2 and detailed in Sect. 3.

Fig. 2

Workflow of a breakup event (explosion or collision)

3 Breakup model

During the process of simulating a breakup event, one needs to make a number of choices which affect important quantities, characterizing the output. These choices are mainly based on experimental tests on different materials and breakup conditions. In Sects. 3.1, 3.2, 3.3, we review the work presented in Johnson et al. (2001), allowing the variation of some parameters, so that one can evaluate the effect of each specific choice and adapt the values to more recent studies on material and fragmentations. Indeed, we highlight that changing the values of some parameters leads to non-negligible effects. In addition, we describe how the formulas characterizing the breakup model are implemented, including the assignment procedure of the size $L_c$, the area-to-mass ratio A/m and ejection velocity $\Delta v$ values to each generated fragment. An application to the Iridium 33 and Cosmos 2251 collision is presented in Sect. 3.4.

3.1 Number of fragments in an explosion or collision

An important quantity associated to the fragments is the characteristic length $L_c$, defined as the average of the three orthogonal projection dimensions X, Y, Z of the fragment ( Krisko and Hall (2004)):

$$\begin{aligned} L_c={1\over 3} (X+Y+Z)\ . \end{aligned}$$

Given a characteristic length, let say $L_c^{min}$, the cumulative number of fragments in an explosion or collision $N_{frag}$ of diameter $L_c$, with $L_c\ge L_c^{min}$, can be determined through the following formulae:

$$\begin{aligned} N_{frag}(L_c\ge L_c^{min})= & 6\ S\ (\hat{L}_c^{min})^{-\kappa _{exp}}\qquad \qquad \ \ \mathrm{for\ explosions},\nonumber \\ N_{frag}(L_c\ge L_c^{min})= & 0.1\ \hat{M}^{0.75}\ (\hat{L}_c^{min})^{-\kappa _{col}}\qquad \ \ \mathrm{for\ collisions}, \end{aligned}$$

(1)

where in Johnson et al. (2001) it was set²$\kappa _{exp}=1.6$, $\kappa _{col}=1.71$ and S is a scaling parameter within the interval $0.1\le S\le 2$ (see Table 1). Following Johnson et al. (2001), the quantity S takes different values, according to the nature of the parent body, see Table 1. In our implementation, we let S vary in an interval with fixed extremes. The formulae in (1) have been obtained in Johnson et al. (2001) by considering natural variations of structure and energy, through different hypervelocity impact experiments.

Table 1 The quantity S for different parent bodies

The hat in equations (1) denotes normalized quantities, namely

$$\begin{aligned} \hat{L}_c^{min} = L_c^{min}/[m] \end{aligned}$$

(2)

and

$$\begin{aligned} \hat{M}= & (m_t+m_p)/[kg]\qquad \qquad \ \textrm{for}\ \tilde{E}_p\ge \tilde{E}_p^*\nonumber \\ \hat{M}= & {{m_p v_i}\over {1000}}/[kg\ m s^{-1}]\qquad \ \ \ \ \ \textrm{for}\ \tilde{E}_p< \tilde{E}_p^* \end{aligned}$$

(3)

with $\tilde{E}_p={1\over 2}{m_p\over m_t} v_i^2$, $\tilde{E}_p^*=40/[kJ\ kg^{-1}]$, $m_t$ is the mass of a collision target object (spacecraft or upper stage), $m_p$ is the mass of an impact projectile, $v_i$ is the impact velocity, $\tilde{E}_p$ is the specific energy of the projectile, and $\tilde{E}_p^*$ is the specific energy threshold of a catastrophic collision (case of complete disintegration). For clarity, we specify that the notation in (2) means that $L_c^{min}$ is expressed in meters; similarly for the other quantities in (3), namely the masses $m_t$ and $m_p$ are given in kilograms and the impact velocity $v_i$ in meters per second.

In simulations, one needs to assign to each generated fragment a characteristic length $L_c$. In this sense, we use formulae (1) as follows. We compute the cumulative number of fragments $N_{frag}(x)$, for $x=L_c^{1}$, $x=L_{c}^{2}$, ... $x=L_{c}^{n}$, until $N_{frag}(L_{c}^{n})=0$ within the computer limit, where $L_c^{1}<L_{c}^{2}\, ...\, <L_{c}^{n}$. Clearly, the difference $N^i\equiv N_{frag}(L_{c}^{i})-N_{frag}(L_{c}^{i+1})$ represents the number of fragments of size $L_c$, with $L_c^{i} \le L_c<L_c^{i+1}$. For n sufficiently large and $\max _{i=1}^{n-1} (L_c^{i+1}-L_c^i)$ sufficiently small, to all $N_i$ fragments, with $i=1,2, \, ... \, n$, one can assign the same value of the characteristic length, for example $L_c^i$. For reasons that will become clear in Sect. 3.2, in simulations we take $L_c^1$, $L_c^2$, ... $L_c^n$ to be equidistant, with $L_c^{i+1}-L_c^i=1$ [cm], namely $L_c^{i}=L_c^{min}+i-1$ [cm], with $i=1,2, \, ... \, n$, where, for simplicity, the minimum size of the generated fragments $L_c^{min}$ (see Sect. 2.2), expressed in centimeters, is considered as a positive integer, and all fragments whose size is between two consecutive integer numbers, let say $L_c^{min}+i-1$ and $L_c^{min}+i$, are assumed to have the same size, i.e., $L_c^{min}+i-1$.

As we mentioned before, we allow the powers of the characteristic length in (1) to vary and see how the results change by taking values for $\kappa _{exp}$, $\kappa _{col}$ different than those obtained through laboratory experiments. It is clear from (1) that the number of fragments increases as $\kappa _{exp}$ or $\kappa _{col}$ gets larger; consequently, we warn that the computational time to accomplish further propagation increases with the parameters. Figure 3 gives the results for an explosion by taking $\kappa _{exp}=1.6$ as in Johnson et al. (2001), and by varying it as $\kappa _{exp}=2.5$ and $\kappa _{exp}=3$; the number of fragments is, respectively, 17, 41 and 347. We remark that, Fig. 3 shows that as the number of fragments increases, the histogram approaches an F test (Fischer) distribution.

Fig. 3

Explosion of a Molniya-type satellite, with the minimum size of characteristic length $L_c^{min}$ set to 12 cm; histogram of the size distribution, taking $\kappa _{exp}=1.6$ as in Johnson et al. (2001) generating 17 fragments (left), $\kappa _{exp}=2.5$ generating 41 fragments (middle), $\kappa _{exp}=3$ generating 347 fragments (right)

3.2 Area-to-mass ratio distribution

The A/m assignments for the generated fragments are performed by means of a bimodal probability density function (or distribution function):

$$\begin{aligned} D(\chi ,\theta )=\xi (\theta )\ N(\chi ;\mu _1,\sigma _1)+(1-\xi (\theta ))\ N(\chi ;\mu _2,\sigma _2) \end{aligned}$$

(4)

with the normal distribution functions given by

$$\begin{aligned} N(\chi ;\mu _i,\sigma _i)={1\over {\sqrt{2\pi }\ \sigma _i}}\ e^{-{{(\chi -\mu _i)^2}\over {2\sigma _i^2}}}\ , \qquad i=1,2 \end{aligned}$$

(5)

with the A/m-related parameter defined as $\chi =\log _{10}{A\over m}/[m^2kg^{-1}]$, the size parameter defined as $\theta =\log _{10}L_c/[m]$, $\mu _i$ are the means, $\sigma _i$ are the standard deviations of two overlaid and normalized Gaussian distributions, while $\xi (\theta )\in [0,1]$ are the weighting functions.

We remark that the NASA model discriminates between spacecraft, upper stages and sizes with calibrated quantities $\xi (\theta )$, $\mu _{1,2}(\theta )$, $\sigma _{1,2}(\theta )$. Details are given in Appendix B, in which the formulae are derived from the study of thousands of fragments, cataloged by the US Space Surveillance Network and through laboratory experiments (see Johnson et al. (2001) for full details). In Appendix B, we also provide the derivation of the cross-sectional area and mass.

We show in Fig. 4 the probability distribution functions, both for upper stage and spacecraft fragments, as well as for objects with $L_c<8$ cm. The plots compare the distribution functions for fragments with consecutive (integer) values of $L_c$, namely small sizes $L_c=1$ cm vs. $L_c=2$ cm, medium dimensions $L_c=6$ cm vs. $L_c=7$ cm, $L_c=12$ cm vs. $L_c=13$ cm and large diameters $L_c=36$ cm vs. $L_c=37$ cm.

Fig. 4

Probability distribution functions with the values of the constants appearing in Johnson et al. (2001) for upper stage fragments (top-left), spacecraft fragments (top-right) and small fragments (bottom), with $L_c = 12$ cm, $L_c = 13$ cm, $L_c =36$ cm, $L_c = 37$ cm in the top plots, and $L_c = 1$ cm, $L_c = 2$ cm, $L_c = 6$ cm, $L_c = 7$ cm in the bottom panel

These comparisons show that the assignment size procedure, described in Sect. 3.1, according to which the size $L_c$ of each fragment can be considered as a positive integer number, is justified. Indeed, for the fragments whose size is a real value between i cm and $i+1$ cm, where $i\in {\mathbb {N}}^*$, the assignment of the A/m values will provide similar results, either the area-to-mass distribution function for $L_c=i$ cm or the one for $L_c=i+1$ cm is used.

Knowing the area-to-mass density functions, one can assign an A/m value to each fragment resulting from a breakup event, apart from the already allocated characteristic length $L_c$. For this purpose, we can proceed numerically, by implementing an acceptance–rejection algorithm, or rather, by using the cumulative distribution function, which in this case has the form

$$\begin{aligned} F(\chi ,\theta )=\xi (\theta )\Phi _1(\chi ; \mu _1, \sigma _1)+(1-\xi (\theta ))\Phi _2(\chi ; \mu _2, \sigma _2)\ , \end{aligned}$$

(6)

where $\Phi _i(\chi ; \mu _i, \sigma _i)$, $i=1,2$, is the cumulative distribution function of the normal distribution, namely

$$\begin{aligned} \Phi _i(\chi ; \mu _i, \sigma _i)=\int _{-\infty }^\chi N_i(\chi ; \mu _i, \sigma _i)d\chi ={1\over 2}\ erf\Big ({{\chi -\mu _i}\over {\sqrt{2}\sigma _i}}\Big )+ {1\over 2}\ ,\qquad i=1,2. \end{aligned}$$

(7)

In equation (7), erf(x) is the error function.

Recalling the fact that for each generated fragment, resulting from a breakup event, we assigned an integer characteristic length (if it is expressed in cm), let us denote by $m_i$ the number of fragments of size $L_c^i=L_c^{min}+i-1$, with $i=1, 2,\, ... \, n$. Then, for the $m_i$ fragments of the same size $L_c^i$, we consider the set of equidistant probabilities $\{1/(m_i+1), 2/(m_i+1), \, ...\, m_i/(m_i+1) \}$ and solve the $m_i$ distinct equations

$$\begin{aligned} F(\chi ,\theta )=\frac{j}{m_i+1}+\frac{\zeta }{m_i+1}\,, \qquad j=1,2,\, ... \, m_i \end{aligned}$$

(8)

to find distinct $m_i$ values of $\chi$. These solutions, determined numerically for bimodal distributions and analytically for single-mode distributions, are assigned to the $m_i$ fragments of the same size. The second term of the right hand side of (8) depends on a randomly generated number $\zeta$, which we consider in the interval $[-0.1, 0.1]$ and it is introduced only for obtaining slightly different results for the breakups simulated in the same conditions.

To verify this area-to-mass assignment algorithm, we compare in Fig. 5 the probability density functions (red lines), numerically obtained by fitting the results from simulating two collision events, an upper stage object (left panel), and, respectively, a spacecraft (right panel), both of mass 1000 kg, impacted by 5 kg projectiles at the speed of 5 km/s, with the theoretical probability density functions which are provided in Appendix B on the basis of Johnson et al. (2001) (black lines). We show the results obtained for four sizes: $L_c=1$ cm, $L_c=5$ cm, $L_c=12$ cm and $L_c=24$ cm. As expected, the results are identical for small sizes and some differences can be noticed at larger sizes, given the fact that the number of fragments decreases with the increase in their size.

Fig. 5

Verification of the area-to-mass assignment algorithm. Red lines: the probability density functions obtained by fitting the results from two collision events, an upper stage object (left panel), and a spacecraft (right panel), both of mass equal to 1000 kg, impacted by 5 kg projectiles at the speed of 5 km/s. Black lines: the probability density functions (defined in Appendix B) for an upper stage object (left panel) and a spacecraft (right panel)

Finally, in Fig. 6 we report the area-to-mass distribution function matched to data for 568 upper stage debris (left) and, respectively, spacecraft debris (right) in the size regime of 12 cm to 35 cm. The results are very similar to the ones reported in Fig. 6 of Johnson et al. (2001).

Fig. 6

A/m distribution function matched to data for 568 upper stage debris (left) and spacecraft debris (right) in the size regime of 12 cm to 35 cm

3.3 Velocity distribution

The probability density function of the fragments’ velocities follows a normal distribution:

$$\begin{aligned} p(\nu )={1\over {{\sqrt{2\pi }\ \sigma _\nu }}}\ e^{-{{(\nu -\mu _\nu )^2}\over {2\sigma _\nu ^2}}} \end{aligned}$$

(9)

with $\nu =\log _{10}(\Delta v/[m\, s^{-1}])$, $\chi =\log _{10}(A/m/[m^2\, kg^{-1}])$, $\mu ^{exp}=a^{exp}\chi +b^{exp}$ is the mean for explosions, $\mu ^{col}=a^{col}\chi +b^{col}$ is the mean for collisions, and $\sigma =\sigma ^{exp}$ or $\sigma =\sigma ^{col}$ is the standard deviation, respectively, for explosions and collisions.

The values adopted in Johnson et al. (2001) are $a^{exp}=0.2$, $b^{exp}=1.85$, $a^{col}=0.9$, $b^{col}=2.9$, $\sigma ^{exp}=0.4$, $\sigma ^{col}=0.4$.

For explosions, the distribution function of the velocity distribution is

$$\begin{aligned} D_{\Delta v}^{exp}(\chi ,\nu )=N(\mu ^{exp}(\chi ),\sigma (\chi ),\nu )\ , \end{aligned}$$

and for collisions the distribution is

$$\begin{aligned} D_{\Delta v}^{col}(\chi ,\nu )=N(\mu ^{col}(\chi ),\sigma (\chi ),\nu )\ . \end{aligned}$$

To assign a $\Delta v$ value to each fragment, we proceed similarly as in the case of the A/m assignment. Here, there is an advantage in computations since, due to its single-mode normal distribution, the equation

$$\begin{aligned} {1\over 2}\ erf({{\nu -\mu _\nu }\over {\sqrt{2}\sigma _\nu }})+{1\over 2}=P_\nu \ , \end{aligned}$$

where the probability $P_\nu$ is given, can be solved analytically. Indeed, from this relation we have:

$$\begin{aligned} erf({{\nu -\mu _\nu }\over {\sqrt{2}\sigma _\nu }}) =2P_\nu -1\ , \end{aligned}$$

namely

$$\begin{aligned} {{\nu -\mu _\nu }\over {\sqrt{2}\sigma _\nu }}=erf^{-1}(2P_\nu -1) \end{aligned}$$

or

$$\begin{aligned} \nu =\mu _\nu +\sigma _\nu \ \sqrt{2}erf^{-1}(2P_\nu -1) ; \end{aligned}$$

(10)

since $\Delta v=10^\nu$, we obtain

$$\begin{aligned} \Delta v=10^{\mu _\nu +\sigma _\nu \ \sqrt{2}erf^{-1}(2P_\nu -1)}\ [m\, s^{-1}]\ . \end{aligned}$$

(11)

Figure 7 shows the distribution of the ejected velocities for debris resulted from an upper stage (left panel) and, respectively, a spacecraft (right panel). The results match those existing in the literature, see, for instance, Fig. 7 in Johnson et al. (2001).

Fig. 7

Distribution of calculated ejection velocities for 2977 debris from an upper stage (left) and spacecraft (right) in the size regime of 5 cm to 100 cm

The effect of changing the parameters is well represented in Fig. 8, where we consider an explosion of a Titan Transtage object with minimum value for $L_c^{min}$ equal to 12 cm for given values of the semimajor axis a, eccentricity e, inclination i, mean anomaly M, argument of perigee $\omega$, longitude of the ascending node $\Omega$.

Fig. 8

Explosion of a Titan Transtage object with $L_c^{min}\ge 12$ cm, $a=20\,000$ km, $e=0.1$, $i=15^o$, $M=80^o$, $\omega =70^o$, $\Omega =60^o$. Histograms of the distribution of $\Delta v$ for $a^{exp}=0.2$, $b^{exp}=1.85$, $\sigma ^{exp}=0.4$ (left) and $a^{exp}=0.5$, $b^{exp}=3$, $\sigma ^{exp}=0.8$ (right)

The explosion generates 356 fragments. The histogram of the distribution of $\Delta v$ is provided in Fig. 8, either for the values provided in Johnson et al. (2001) and for different values of $a^{exp}$, $b^{exp}$, $\sigma ^{exp}$.

Finally, we report in Fig. 9 the results obtained implementing the procedure described in Sect. 2.2. Figure 9 provides the orbital elements a, e, i after the collision of a spacecraft which generates 1192 fragments; we compute the elements with the values of the constants in (20) of Appendix B equal to those given in Table 7 and with those obtained taking a different set of constants. The results show that the values of the constants play a relevant role with respect to all elements a, e, i.

Fig. 9

Collision of a spacecraft of $10^3$ kg with a projectile of 3 kg with collision velocity equal to $2.5\cdot 10^3$ m/s; the orbital elements of the parent body are $a=20000$ km, $e=0.1$, $i=15^o$, $M=80^o$, $\omega =70^o$, $\Omega =60^o$, minimum size of $L_c$ equal to 1 cm; orbital elements with $\mu ^{SOC}_{\lambda _c^l} = -1.75$, $\sigma ^{SOC}_{\lambda _c^l} = -3.5$ (Table 7) (top) and $\mu ^{SOC}_{\lambda _c^l} = -0.5$, $\sigma ^{SOC}_{\lambda _c^l} = -0.5$ (bottom)

3.4 Application: the Iridium 33 and Cosmos 2251 collision

This section compares the number of fragments provided by formula (1) to that detected by the optical and radar sensors of the US Space Surveillance Network for the case of Iridium 33 and Cosmos 2251 collision.

The collision between the operational US communications satellite Iridium 33 and the defunct Russian communications satellite Cosmos 2251 took place on 2009 February 10 at 16:56 UTC at an altitude of 789 km, latitude of 72.51 (deg N) and longitude 97.88 (deg E). The dry masses of the two satellites were estimated as 556 kg (Iridium 33) and 900 kg (Cosmos 2251), respectively (see Kelso (2009)), while the relative velocity of the impact was evaluated as $11.57\, km/s$ (see Tan et al. (2013)).

The configuration of the Iridium–Cosmos collision, the evolution of catalogued fragments, the impact on the space environment and the collision risk with operational satellites have been analyzed in various papers (see Kelso (2009); Tan et al. (2013); Pardini and Anselmo (2017) and references therein).

The event produced two distinct debris clouds, whose largest fragments were detected and tracked by the optical and radar sensors. In fact, by 2009 June 25, the Space Surveillance Network catalogued a number of 349 fragments from Iridium 33 and a number of 809 fragments from Cosmos 2251. The collected data on the fragments include radar cross-sectional measurements, from which it is possible to estimate the size of the objects (see Orbital Debris Quarterly News (2009)). Following Orbital Debris Quarterly News (2009), we reproduce in Fig. 10 the cumulative size distributions of the Iridium 33 fragments (blue curve) and Cosmos 2251 fragments (red curve), but we also include the total number of catalogued fragments (green curve) and the number of collision fragments predicted by equation (1) (black dashed line). Taking into account the uncertainties of the breakup event and possible missing data, Fig. 10 shows a fairly good agreement between the Iridium 33 and Cosmos 2251 collision and the NASA/JSC breakup model, as it results from a comparison between the green curve and the black dashed line; the agreement improves for fragments larger than 10 cm. In fact, given the limits of the optical and radar detectors, the number of small fragments could only be estimated, and the model provided by equation (1) is one of the best candidates.

Fig. 10

Cumulative size distributions of the Iridium 33–Cosmos 2251 collision: number of catalogued fragments (by 2009 June 25) from the Iridium satellite (blue), from the Cosmos satellite (red), from both satellites (green), total number of collision fragments predicted by the NASA/JSC breakup model (black)

Since the number of collision fragments depends on many parameters, such as the mass, shape and internal structure of each body, the relative velocity, the collision angle, etc., the number of fragments provided by equation (1) should be considered only as an approximation of the physical situation. For instance, in the case of the Fengyun-1C event, equation (1) underestimates the number of catalogued fragments by a factor of three (see Liou and Johnston (2009)). When the predicted number of fragments is underestimated (or overestimated), in particular for sizes larger than 10 cm, the key parameters left variable in SIMPRO can be tuned in order to fit the model to the real data. Indeed, fitting the parameters for fragments larger than 10 cm, one can estimate the number of small-size fragments (e.g., smaller than 10 cm). In conclusion, a possible usage of SIMPRO is to set the key parameters of the model to fit the data of known breakup events.

4 Distribution function after a breakup event

In order to find the theoretical distribution of the orbital elements after a breakup event, let us assume to have an ensemble of N particles labeled by $i=1,2,\ldots ,N$, all sharing the same initial position $\underline{r} = (x_0,y_0,z_0)$, but with different velocities $v_{x,i}=v_{x0}+\Delta v_{x,i}$, $v_{y,i}=v_{y0}+\Delta v_{y,i}$, $v_{z,i}=v_{x0}+\Delta v_{y,i}$, where $\underline{v}_0\equiv (v_{x0},v_{y0},v_{z0})$ is the velocity of the parent object from which the distribution of particles was originated after a breakup event. The Keplerian elements of the parent object of mass $M_P$ are derived via the equations:

$$\begin{aligned} a=-{{{\mathcal {G}}}M\over 2E},\qquad e=\sqrt{1+{2EL^2\over ({{\mathcal {G}}}M)^2}},\qquad \cos (i) = {L_z/L} \end{aligned}$$

(12)

where E, L, $L_z$ are, respectively, the energy, the size of the angular momentum, the vertical component of the angular momentum; such quantities are defined by

$$\begin{aligned} E= & {1\over 2}\left( v_{x0}^2+v_{y0}^2+v_{z0}^2\right) -{GM\over \sqrt{x_0^2+y_0^2+z_0^2}}\ , \\ L= & \sqrt{(y_0v_{z0}-z_0v_{y0})^2+(z_0v_{x0}-x_0v_{z0})^2+(x_0v_{y0}-y_0v_{x0})^2}\ , \\ L_z= & x_0v_{y0}-y_0v_{x0}\ . \end{aligned}$$

The small variations $\Delta {\underline{v}}=(\Delta v_x,\Delta v_y,\Delta v_z)$ in the velocities at a fixed position are connected linearly with the variations of the elements of the particles generated after the breakup. Assuming we are far from the singular values $e=\sin i=0$, we can derive the relations between the small variations of the velocities and the elements as follows:

$$\begin{aligned} \Delta a= & \left( {{{\mathcal {G}}}M\over 2E^2}\right) \underline{v}_0\cdot \underline{dv}\nonumber \\ \Delta (e^2)= & \left( {4L^2\over ({{\mathcal {G}}}M)^2}\right) \underline{v}_0\cdot \underline{dv} +\left( {2E\over ({{\mathcal {G}}}M)^2}\right) \underline{L}\cdot (\underline{r}_0\times \underline{dv})\nonumber \\ \Delta (\sin ^2 i)= & \left( {{2L_{0z}^2}\over L^4}\right) \underline{L}\cdot (\underline{r}_0\times \underline{dv}) -\left( {2L_{0z}\over L^2}\right) (x_0\Delta v_{y0}-y_0\Delta v_{x0})\ . \end{aligned}$$

(13)

The equations (13) can be written in matrix form as

$$\begin{aligned} \left( \begin{array}{c} \Delta a\\ \Delta (e^2)\\ \Delta (\sin ^2i) \end{array} \right) ={{\mathcal {M}}}\ \left( \begin{array}{c} \Delta v_x\\ \Delta v_y\\ \Delta v_z \end{array} \right) \ , \end{aligned}$$

(14)

where the elements of the matrix ${{\mathcal {M}}}$ are given in terms of the constants of motion and initial velocity of the parent object. Since we are far from the singular values $e=\sin i = 0$, the matrix ${{\mathcal {M}}}$ is invertible, yielding

$$\begin{aligned} \left( \begin{array}{c} \Delta v_x\\ \Delta v_y\\ \Delta v_z \end{array} \right) ={{\mathcal {C}}}\ \left( \begin{array}{c} \Delta a\\ \Delta (e^2)\\ \Delta (\sin ^2i) \end{array} \right) \ , \end{aligned}$$

(15)

where ${{\mathcal {C}}}={{\mathcal {M}}}^{-1}$ is a constant matrix with real elements.

In the case of an isotropic breakup event, the distribution of the velocities $(\Delta v_x,\Delta v_y,\Delta v_z)$ depends only on the quadratic form $\Delta v_x^2+\Delta v_y^2+\Delta v_z^2$; since from (15) we have

$$\begin{aligned} \Delta v_x^2+\Delta v_y^2+\Delta v_z^2 =\left( \Delta a,\Delta (e^2),\Delta (\sin ^2i)\right) \cdot {{\mathcal {C}}}^T\cdot {{\mathcal {C}}}\cdot \left( \begin{array}{c} \Delta a\\ \Delta (e^2)\\ \Delta (\sin ^2i) \end{array} \right) \ , \end{aligned}$$

(16)

one obtains the distribution of the variations $(\Delta a,\Delta (e^2),\Delta (\sin ^2i))$ through the quadratic form (16). We remark that the matrix ${{\mathcal {C}}}^T{{\mathcal {C}}}$ is symmetric with nonzero diagonal elements. Thus, the eigenvalues are real and the eigenvectors are orthogonal; the eigenvectors, however, do not coincide with the directions $\Delta a$, $\Delta e$, $\Delta (\sin ^2i)$.

Equation (16) shows that the distribution in the variables $\left( \Delta a,\Delta (e^2),\Delta (\sin ^2i)\right)$ is ellipsoidal for any generic set of initial conditions. Moreover, a simple linear algebra analysis allows to find the principal axes of the ellipsoid by computing the eigenvalues and the associated eigenvectors of the $3\times 3$ symmetric matrix ${{\mathcal {C}}}^T{{\mathcal {C}}}$.

As an example, Fig. 11 compares the numerically simulated distribution of the fragments, in the $(\Delta a$, $\Delta e$, $\Delta (\sin ^2i))$ space, resulting from an explosion of a regular body (see Table 1) with the elements $a=10600$ km, $e=0.1$, $i=10^o$, $M=70^o$, $\omega =60^o$, $\Omega =80^o$, to the theoretical distribution described above. The plot shows that all particles lay inside the maximal ellipsoid, namely the one for which the distribution is equal to the maximum computed $||\Delta \underline{v}||$, and that the principal directions of the generated cloud coincide with the principal axes of the ellipsoid (black lines).

Fig. 11

Comparison between the numerically simulated distribution of fragments, in the $(\Delta a$, $\Delta e$, $\Delta (\sin ^2i))$ space, resulting from an explosion, and the theoretical distribution. The orbital elements of the parent body are $a=10600$ km, $e=0.1$, $i=10^o$, $M=70^o$, $\omega =60^o$, $\Omega =80^o$. The black segments denote the principal axes of the theoretical ellipsoid

5 Orbit propagator

The motion of an object moving around the Earth is affected by several forces that might be taken into account depending on the region where the object is moving. The position of the object at any time (past and future) can be approximated by solving a system of differential equations starting from some initial conditions given at a certain time. In this work, we used two different frameworks to provide the equations of motion that describe the model:

• (1) Cartesian framework: used for the integration of the orbital elements for short periods of time; it computes the evolution of each osculating element of the object; it is very accurate, but computationally time-consuming;

• (2) Hamiltonian framework: used for the integration of the orbital elements for long periods of time; it computes the evolution of the mean elements of the object; it is very fast, but less accurate.

In both frameworks, we take into account the following forces that act on the object, namely the attraction of the spherical Earth, the zonal spherical harmonics $J_2, J_3$ and the sectorial and tesseral harmonics $J_{22}$, $J_{31}$, $J_{32}$, $J_{33}$, the attraction of the Moon, the attraction of the Sun, the effect of solar radiation pressure and the effect of the air drag.

5.1 Set of elements

We will use different sets of elements depending on the framework. In particular, the Cartesian equations of motion will be described by a state vector (Cartesian position and velocity), while the Hamiltonian equations of motion will be described in terms of the Delaunay variables. All coordinates are referring to the geocentric quasi-inertial reference system. The elements of the Moon are referred to the ecliptic plane, while the elements of the debris and Sun are referred to the plane of the celestial equator. The following notations are adopted for each set of variables:

• (1) Cartesian coordinates: $\underline{r} = (x, y, z)$ position of the object, $\dot{\underline{r}} = (\dot{x}, \dot{y}, \dot{z})$ velocity of the object, $\underline{r}_S, \underline{r}_M$ positions of Sun and Moon (with respect to the fixed, quasi-inertial reference frame, $\theta$ sidereal time;

• (2) Orbital elements: a, e, i, M, $\omega$, $\Omega$—these elements will refer to the object. The elements with the indexes S and M denote the orbital elements of Sun and Moon, respectively;

• (3) Delaunay variables: $L=\sqrt{\mu _E a}, G=L\sqrt{1-e^2}, H=G\cos i, \ell = M, g = \omega , h = \Omega$.

As regards numerical integrations, the simulator provides a model of the complete equations of motion in Cartesian variables as well as a Hamiltonian model which is averaged with respect to all the fast angles of the problem.

5.2 The propagation of the orbits

We start by providing some examples of the propagation of orbits to study the variation over time of the orbital elements as a function of the altitude; we also want to show how the results are affected by taking different models (Sect. 5.2.1) as well as by varying the area-to-mass ratio (Sect. 5.2.2).

Apart from the integration of the Hamilton’s equations and Cartesian equations, we used also the simplified general perturbation theory (SGP4) as described in Vallado et al. (2006) to compare the results of our own integrators.

The initial conditions should be given in the same reference system as the equations of motions used for the integration. Since the application is intended to be used in experiments with real space objects, the input data is described by NORAD Two Line Elements [7]. While the Hamiltonian and Cartesian dynamics are described in the J2000 (mean-equator-mean-equinox) reference frame, the SGP4 is described in TEME (true-equator-mean-equinox).

In order to obtain the correct initial conditions, starting from TLE, we need to perform several transformations. If we denote by ${\mathcal {T}}_{TLE}$ the orbital elements extracted from TLE, which is a set of mean elements in the sense of Brouwer theory ( Brouwer (1959)), we convert into the osculating elements ${\mathcal {T}}_{OSC}$ in the J2000 frame by using the reverse procedure described in Hoots and Roehrich (1980). The osculating elements are then averaged of short-period angles to obtain the mean elements ${\mathcal {T}}_{MEAN}$. In this case, we will use the SGP4 propagator with ${\mathcal {T}}_{TLE}$, the Cartesian integrator with the state vector (position and velocity) obtained from ${\mathcal {T}}_{OSC}$ and the Hamiltonian integrator with ${\mathcal {T}}_{MEAN}$.

5.2.1 Propagation and different models

The propagation with different models is used to understand the effect of a specific perturbation in different regions. As an example, we consider an object, say Object 1, with the initial orbital elements $a=35000$ km, $e=0.1$, $i=30^o$, $M=40^o$, $\omega =120^o$, $\Omega =60^o$ and $A/m = 0.01$ and another object, say Object 2, with the initial orbital elements $a=12000$ km, $e=0.05$, $i=70^o$, $M=10^o$, $\omega =50^o$, $\Omega =30^o$ and $A/m = 0.5$. Let us consider as well two different situations:

• (i) for Object 1, we use the Hamiltonian model, starting with the $J_2$ and $J_3$ effects and adding successively the perturbations due to the Moon, Sun and SRP; we propagate the object for 100 years;

• (ii) for Object 2, we use the Cartesian model, starting with the $J_2$ and $J_3$ effects and adding successively the perturbations due to the Moon, Sun and SRP; we propagate the object for 1 year.

For these two experiments, we show only the time variation of the eccentricity and inclination, since we are outside any resonant region. For initial conditions very close to a resonance, we need a further investigation to decide which are the most significant terms in the Hamiltonian that must be included, so to get a good agreement between the Cartesian and Hamiltonian propagations. The results given in Fig. 12, which refers to the first experiment, show several features: the model without Moon and Sun is definitely not enough accurate for the description of the dynamics of the selected object; adding the attraction of the third body perturbers, the dynamics changes completely; the SRP has a minor additional effect, since the A/m value is quite small in this example.

Fig. 12

Results for Object 1 with orbital data equal to $a=35000$ km, $e=0.1$, $i=30^o$, $M=40^o$, $\omega =120^o$, $\Omega =60^o$ with $A/m = 0.01$. Evolution of eccentricity (top) and inclination (bottom) for a Hamiltonian model with $J_2$ and $J_3$ (left), adding Moon and Sun (middle), adding SRP (right)

On the other hand, Fig. 13 shows the evolution of Object 2 in a Cartesian model (including the same contributions as the Hamiltonian). Although the Cartesian model includes also the short-period variations, we also see here how each force affects the motion, with a visible effect of the SRP, since the A/m ratio of this example is relatively large.

Fig. 13

Results for Object 2 with orbital data equal to $a=12000$ km, $e=0.05$, $i=70^o$, $M=10^o$, $\omega =50^o$, $\Omega =30^o$ with $A/m = 0.5$. Evolution of eccentricity (top) and inclination (bottom) for a Cartesian model with $J_2$ and $J_3$ (left), adding Moon and Sun (middle), adding SRP (right)

5.2.2 Comparison of different equations of motions

To assess whether the Hamiltonian model is accurate enough, we can compare the results with the Cartesian and SGP4 models. In this way, we highlight the differences between the integration of Object 1 and Object 2 in all frameworks by comparing Hamiltonian and Cartesian integrations in Fig. 14 and Cartesian and SGP4 in Fig. 15.

In Fig. 14, we show the numerical propagation of Object 1 (top) and Object 2 (bottom) of semimajor axis (left), eccentricity (middle), inclination (right) using Hamilton’s equation (red) and Cartesian equations (blue).

Fig. 14

Results for orbit integrator of (top) Object 1 ($a=35000$ km, $e=0.1$, $i=30^o$, $M=40^o$, $\omega =120^o$, $\Omega =60^o$, $A/m = 0.01$) and (bottom) Object 2 ($a=12000$ km, $e=0.05$, $i=70^o$, $M=10^o$, $\omega =50^o$, $\Omega =30^o$, $A/m = 0.5$). In red we plot the solution of Hamilton’s equations and in blue the solution of Cartesian equations for semimajor axis (left), eccentricity (middle) and inclination (right)

As it is expected, the mean elements obtained by integrating the orbit in the Hamiltonian framework are an average of the short-period oscillations that are visible in the Cartesian integration.

In Fig. 15, we consider Object 2 and we show the numerical propagation of eccentricity, inclination, argument of perigee, longitude of the ascending node (from left to right) using Cartesian equations (blue) and the results obtained through SGP4 (green) after we made the transformation of the elements (see Sect. 5.2). Figure 15 shows that the solutions are very similar, at least for short periods of integration.

Fig. 15

Results for orbit integrator of Object 2 ($a=12000$ km, $e=0.05$, $i=70^o$, $M=10^o$, $\omega =50^o$, $\Omega =30^o$, $A/m = 0.5$). In green we plot the solution of SGP4 and in blue the solution of Cartesian equations for eccentricity, inclination argument of perigee, longitude of the ascending node (from left to right)

6 Fragmentation and propagation

In this Section, we present applications of the combined tools for simulating a breakup event (see Sect. 2 and 3) and for propagating the resulting fragments (see Sect. 5). We provide an example of how the fragments can get dispersed from the breakup position (Sect. 6.1); we consider also the case of multiple events taking place in nearby positions (Sect. 6.2).

6.1 Dispersion of the fragments

We provide an example of how the fragments get dispersed in space over time from the initial orbit. We consider an explosion of a Titan Transtage type with minimum size of the characteristic length $L_c$ equal to 12 cm. We assume that the orbital data are $a=10\,000$ km, $e=0.01$, $i=45^o$, $M=80^o$, $\omega =70^o$, $\Omega =60^o$.

Figure 16 shows that the fragments after one year are moderately dispersed, while they follow a path with large excursions after 20 years. We remark that such dispersion occurs in the MEO region, where the air drag does not provoke any decay effect. An example of dispersion in the LEO region was given by the collision of the two satellites Cosmos 2251 and Iridium 33 in 2009, which generated at least 1700 fragments, among which about 1000 bigger than 10 cm, which got dispersed along two circles around the Earth after only 50 minutes from the breakup.

Fig. 16

Explosion of a Titan Transtage object with $L_c\ge 12$ cm, $a=10\,000$ km, $e=0.01$, $i=45^o$, $M=80^o$, $\omega =70^o$, $\Omega =60^o$. The blue dots represent the Earth; the black dots are the fragments at breakup (top-left), after one day (top-middle), after 4 days (top-right); after one year (bottom-left), after 3 years (bottom-middle), after 20 years (bottom-right)

6.2 Multiple fragmentations

We finally simulate the breakup event of three nearby objects. We consider a first explosion of a satellite of Molniya-type physical parameters (hereafter referred to as a “Molniya-type satellite”), but with orbital elements $a=38\,600$ km, $e=0.05$, $i=20^o$, $M=80^o$, $\omega =70^o$, $\Omega =60^o$ and the other two objects with a semimajor axis at 500 km from the first object, a distance in the eccentricity equal to 0.001 with respect to the first object and a distance of $2^o$ from the inclination of the first object. In total 51 fragments are generated and the evolution is shown in Fig. 17 at the instant of the breakup and after 150 years. Also in this case, the orbital elements undergo large variations and the fragments from the three groups are mixed after 150 years.

Fig. 17

Explosion of three nearby objects with the first one with $a=38\,600$ km, $e=0.05$, $i=20^o$, $M=80^o$, $\omega =70^o$, $\Omega =60^o$ and the other two objects with a at 500 km from the first body, distance in e equal to 0.001 and in i of $2^o$ from the elements of the first object. At breakup (upper row) and after 150 years (lower row)

7 Streams of fragments

Meteor streams of asteroids have been investigated, e.g., in Southworth and Hawkings (1963), in which a quantitative criterion for stream membership has been given in terms of the measure of the difference between the orbital elements. Here, we adapt the indicator proposed in Southworth and Hawkings (1963) as indicated below by normalizing the semimajor axes, so to have only adimensional quantities. More specifically, we consider two breakup events and we label the generated fragments as those of group A and group B. We denote by $N_A$ and $N_B$, respectively, the number of fragments in stream A and B, either at the initial time or at any evolved time. We compute the averages of the semimajor axes within each stream, say ${\bar{a}}_A$, ${\bar{a}}_B$, and we define the quantity ${\bar{a}}=({\bar{a}}_A+{\bar{a}}_B)/2$. We assume that the streams are composed by the elements $P_1^{(A)}$, ..., $P_{N_A}^{(A)}$ and $P_1^{(B)}$, ..., $P_{N_B}^{(B)}$, each one with the respective orbital elements $(a,e,i,M,\omega ,\Omega )$. Then, we compute the following index:

$$\begin{aligned} {{\mathcal {I}}}(A,B)= & {1\over {[\min {(N_A,N_B)}]^2}}\ \sum _{k=1}^{\min {(N_A,N_B)}} \sum _{j=1}^{\min {(N_A,N_B)}} \Big ({{a_k^{(B)}(1-e_k^{(B)})-a_j^{(A)}(1-e_j^{(A)})}\over {{\bar{a}}}}\Big )^2\\+ & (e_k^{(B)}-e_j^{(A)})^2+\Big (2\sin {{i_k^{(B)}-i_j^{(A)}}\over 2}\Big )^2 +\sin i_k^{(B)}\sin i_j^{(A)}\ \Big (2\sin {{\Omega _k^{(B)}-\Omega _j^{(A)}}\over 2}\Big )^2\\+ & \Big ({{e_k^{(B)}+e_j^{(A)}}\over 2}\ 2\sin {{(\omega _k^{(B)}+\Omega _k^{(B)})-(\omega _j^{(A)}+\Omega _j^{(A)})}\over 2}\Big )^2\ . \end{aligned}$$

We mention that the indicator defined gives relevant results when $N_A/N_B \approx 1$. In this case, we took the minimum of these two values as the upper bounds of the sum to prevent the bias of any stream. Next, we evaluate the stream coefficient ${{\mathcal {I}}}(A,B)$ taking as stream A an explosion of a Molniya-type satellite with minimum size fragment of 2 cm; the elements of stream A are the following: $a_A=30\,000$ km, $e_A=0.1$, $i_A=5^o$, $M_A=0^o$, $\omega _A=0^o$, $\Omega _A=0^o$. The elements of the sample cases providing stream B, always of Molniya-type, are provided in Table 2; in all sample cases, the semimajor axis is lower than that of stream A. The stream coefficient ${{\mathcal {I}}}(A,B)$ given in Table 2 shows that its value increases as the streams become far away in semimajor axis. We notice that the correlation coefficient associated to the two streams would rather give a value always close to one.

Table 2 provides also the stream coefficient introduced in Zappalá et al. (1990) (see also Wu et al. (2023)), that we slightly modify as follows:

$$\begin{aligned} {{\mathcal {I}}}_Z(A,B)= & {1\over {[\min {(N_A,N_B)}]^2}}\ \sum _{k=1}^{\min {(N_A,N_B)}} \sum _{j=1}^{\min {(N_A,N_B)}} \Big (p_1({{a_k^{(B)}-a_j^{(A)}}\over {{\bar{a}}}})^2\\+ & p_2(e_k^{(B)}-e_j^{(A)})^2+p_3(\sin i_k^{(B)}-\sin i_j^{(A)})^2\Big )^{1\over 2}\ . \end{aligned}$$

The values $p_j$, $j=1,2,3$, given in Zappalá et al. (1990) are $p_1=5/4$, $p_2=2$, $p_3=2$ and they generate the indicator ${{\mathcal {I}}}_Z^{(1)}(A,B)$ in Table 2; taking the alternative definition given in Zappalá et al. (1990) with $p_1=1/2$, $p_2=3/4$, $p_3=4$, the corresponding indicator is denoted as ${{\mathcal {I}}}_Z^{(2)}(A,B)$; finally, we also consider the choice $p_1=1$, $p_2=1$, $p_3=1$ providing the indicator ${{\mathcal {I}}}_Z^{(3)}(A,B)$. In all cases, the value of the stream coefficient gets larger with the distance in semimajor axis of the two groups.

Table 2 Stream coefficients between two different explosions of a Molniya-type satellite; the elements of group A are $a_A=30\,000$ km, $e_A=0.1$, $i_A=5^o$, $M_A=0^o$, $\omega _A=0^o$, $\Omega _A=0^o$. The elements of group B are listed below

As a further example, we consider again an explosion of a Molniya satellite, characterized by the following orbital elements: $a_A=20\,000$ km, $e_A=0.2$, $i_A=6^o$, $M_A=45^o$, $\omega _A=87^o$, $\Omega _A=55^o$ with minimum fragments’ size of 2 cm; then, we consider nearby explosions and we compute the stream coefficient ${{\mathcal {I}}}(A,B)$ for different sample cases, whose elements are listed in Table 3. In all sample cases, the semimajor axes are higher than that of stream A. The results are summarized in Table 3; the behavior of ${{\mathcal {I}}}(A,B)$ is similar to that of Table 2.

Table 3 Stream coefficients between two different explosions of a Molniya-type satellite. The elements of group A are $a_A=20\,000$ km, $e_A=0.2$, $i_A=6^o$, $M_A=45^o$, $\omega _A=87^o$, $\Omega _A=55^o$. The elements of group B are listed below

As a last example, we provide a comparison of a stream, say group A, characterized by an explosion of a Molniya-type satellite with elements $a_A=20\,100$ km, $e_A=0.12$, $i_A=2^o$, $M_A=22^o$, $\omega _A=40^o$, $\Omega _A=11^o$ and the stream B obtained by evolving group A at different times, see Table 4. The low values obtained for the stream coefficients, although slightly increasing with time, are a good indication that the fragments of the evolved streams belong to the original stream.

Table 4 Stream coefficients between an explosion of a Molniya-type satellite with elements $a_A=20\,100$ km, $e_A=0.12$, $i_A=2^o$, $M_A=22^o$, $\omega _A=40^o$, $\Omega _A=11^o$ and the evolution of the generated fragments at different times

8 Conclusions and perspectives

In the present paper, we discuss the methods, algorithms and some results from the application of a new simulator SIMPRO, aiming to provide, at the same time: i) the production of synthetic initial conditions for debris clouds under a collision or breakup event, using the standard NASA’s EVOLVE 4.0 model (with the advantage of some freedom in tuning several parameters), and ii) to provide different methods of propagation of the debris cloud (in full Cartesian or Hamiltonian, averaged over the fast angle, approaches to the equations of motion) in all main orbital regimes. Our main conclusions from this study are the following.

(1) We implement the statistical distributions of NASA’s EVOLVE model for all main physical parameters of the debris distribution, leading to a prediction on the distribution of the initial velocities of the fragments in both collision and breakup events.

(2) The simulator is able to handle the distributions of item 1) above for all major types of incidents which may occur in space, leading to a wide spectrum of applications as regards the study of the propagation in time of the clouds generated under different scenarios of breakup events. We test theoretical distributions against the numerical histograms and find a satisfying agreement.

(3) We give a theoretical formulation of the distribution function of the orbital elements for given initial velocity distribution, based on a linear theory built around the covariance matrix connecting elements with initial velocities. We find that the ellipsoidal isodensity surfaces of this distribution are sufficient to represent the numerically simulated distribution in cases of small initial velocity dispersions of the fragments. However, for larger initial velocity dispersions, nonlinear corrections are required, which mostly affect the form of the distribution in the (a, e) plane, leading to the characteristic V-shaped form, similar to the one observed in the case of asteroids belonging to one family.

(4) We give comparisons between a fully Cartesian and a Hamiltonian (averaged over short-period terms) propagation of the fragments’ orbits, showing the essential equivalence between these two approaches.

(5) We discuss some examples showing the potential use of the simulator in a wide spectrum of applications, including the computation of debris streams indicators.

Perspectives for future development include:

(a) incorporation of more accurate statistical models beyond NASA’s EVOLVE 4.0,

(b) inclusion of more harmonics (besides $J_2$, $J_{22}$, $J_{3}$, $J_{31}$, $J_{32}$ and $J_{33}$) in the geopotential, or more accurate models of the third bodies (Moon and Sun) trajectories,

(c) inclusion of more functionalities, as for example, estimates on collision probabilities or the evolution of element distributions based on continuous flux models.

Since these are subjects of current investigation by many groups in astrodynamics, we let the list of possible perspectives open to future research.

Appendices

Appendix A: SIMPRO breakup algorithm

The simulator program has been written in JAVA and it is composed by a set of classes implemented for each aspect described in the present paper. Along the other important functionality, the core of the program is described by the following classes:

• BreakupAbstract: generates the fragments by computing the number of fragments larger than $L_c$ and computing $\chi$.

• BreakupCollision: for a collision, compute the number of fragments $N_{frag}$ of diameter $d\ge L_c$ according to the formula to (1). Compute also $\nu$ as in (10).

• BreakupExplosion: for an explosion, compute the number of fragments $N_{frag}$ of diameter $d\ge L_c$ according to (1). Compute also $\nu$ as in (10).

Algorithm 1

Generate the fragments after a breakup event

• BreakupFragment: For a fragment with given “id$\_$number” and size $L_c$, compute:

  • the area-to-mass ratio as $A/m=10^\chi$ or $\chi =\log _{10}(A/m)$

  • average cross-sectional area according to (21)

  • components of the velocity $(v_x,v_y,v_z)$, $\Delta v$, $\nu =\log _{10}(\Delta v)$

  • the orbital elements, given the position of the parent body and the components of the velocity vector.

Algorithm 1 provides some details on how to generate fragments after a collision or an explosion.

Appendix B: Distribution functions, cross-sectional area and mass

In this Section, we recall the formulae given in Johnson et al. (2001) for the area-to-mass ration distribution, distinguishing different types of fragments in terms of the characteristic length (see Sects. B.1, B.2, B.3). The cross-sectional area and mass are given in Sect. B.4.

1.1 B.1. Distribution function for upper stage fragments of size $L_c$, with $L_c>11$ cm

The distribution function for upper stage fragments with $L_c>11$ cm is given by

$$\begin{aligned} D_{A/m}^{RB}(\lambda _c,\chi )= & \alpha ^{RB}(\lambda _c)\ N(\chi ,\mu _1^{RB}(\lambda _c),\sigma _1^{RB}(\lambda _c))\nonumber \\ & +(1-\alpha ^{RB}(\lambda _c))\ N(\chi ,\mu _2^{RB}(\lambda _c),\sigma _2^{RB}(\lambda _c))\ , \end{aligned}$$

(17)

where $\lambda _c=\log _{10}(L_c)$, $\chi =\log _{10}(A/m)$, while

$$\begin{aligned} \alpha ^{RB}(\lambda _c)= & \left\{ \begin{array}{ll} \alpha ^{RB}_l, & {\lambda _c \le \lambda _c^l} \\ \alpha ^{RB}_a+\alpha ^{RB}_b(\lambda _c + \alpha ^{RB}_c), & {\lambda _c^l<\lambda _c<\lambda _c^u} \\ \alpha ^{RB}_r, & {\lambda _c\ge \lambda _c^u} \\ \end{array} \right. \\ \end{aligned}$$

$$\begin{aligned} \mu _1^{RB}(\lambda _c)= & \left\{ \begin{array}{ll} \mu ^{RB}_{1l}, & {\lambda _c \le \lambda _c^l} \\ \mu ^{RB}_{1a}+\mu ^{RB}_{1b}(\lambda _c + \mu ^{RB}_{1c}), & {\lambda _c^l<\lambda _c<\lambda _c^u} \\ \mu ^{RB}_{1r}, & {\lambda _c\ge \lambda _c^u} \\ \end{array} \right. \\ \sigma _1^{RB}(\lambda _c)= & \sigma _1^{RB}\\ \mu _2^{RB}(\lambda _c)= & \mu _2^{RB}\\ \sigma _2^{RB}(\lambda _c)= & \left\{ \begin{array}{ll} \sigma ^{RB}_{2l}, & {\lambda _c \le \lambda _c^l} \\ \sigma ^{RB}_{2a}+\sigma ^{RB}_{2b}(\lambda _c + \sigma ^{RB}_{2c}), & {\lambda _c^l<\lambda _c<\lambda _c^u} \\ \sigma ^{RB}_{2r}, & {\lambda _c\ge \lambda _c^u} \\ \end{array} \right. \\ \end{aligned}$$

The values of the constants appearing in Johnson et al. (2001) are given in Table 5.

Table 5 Default values of the constants appearing in Johnson et al. (2001) for upper stage fragments of size $L_c>11$ cm

1.2 B.2. Distribution function for spacecraft fragments of size $L_c$, with $L_c>11$ cm

The distribution function for spacecraft fragments with $L_c>11$ cm is given by

$$\begin{aligned} D_{A/m}^{SC}(\lambda _c,\chi )= & \alpha ^{SC}(\lambda _c)\ N(\chi ,\mu _1^{SC}(\lambda _c),\sigma _1^{SC}(\lambda _c))\nonumber \\&\quad +&(1-\alpha ^{SC}(\lambda _c))\ N(\chi ,\mu _2^{SC}(\lambda _c),\sigma _2^{SC}(\lambda _c))\ , \end{aligned}$$

(18)

where

$$\begin{aligned} \alpha ^{SC}(\lambda _c)= & \left\{ \begin{array}{ll} \alpha ^{SC}_l, & {\lambda _c \le \lambda _c^l} \\ \alpha ^{SC}_a+\alpha ^{SC}_b(\lambda _c + \alpha ^{SC}_c), & {\lambda _c^l<\lambda _c<\lambda _c^u} \\ \alpha ^{SC}_r, & {\lambda _c\ge \lambda _c^u} \\ \end{array} \right. \\ \mu _1^{SC}(\lambda _c)= & \left\{ \begin{array}{ll} \mu ^{SC}_{1l}, & {\lambda _c \le \lambda _c^l} \\ \mu ^{SC}_{1a}+\mu ^{SC}_{1b}(\lambda _c + \mu ^{SC}_{1c}), & {\lambda _c^l<\lambda _c<\lambda _c^u} \\ \mu ^{SC}_{1r}, & {\lambda _c\ge \lambda _c^u} \\ \end{array} \right. \\ \sigma _1^{SC}(\lambda _c)= & \left\{ \begin{array}{ll} \sigma ^{SC}_{1l}, & {\lambda _c \le \lambda _c^l} \\ \sigma ^{SC}_{1a}+\sigma ^{SC}_{1b}(\lambda _c + \sigma ^{SC}_{1c}), & {\lambda _c^l<\lambda _c<\lambda _c^u} \\ \sigma ^{SC}_{1r}, & {\lambda _c\ge \lambda _c^u} \\ \end{array} \right. \\ \end{aligned}$$

$$\begin{aligned} \mu _2^{SC}(\lambda _c)= & \left\{ \begin{array}{ll} \mu ^{SC}_{2l}, & {\lambda _c \le \lambda _c^l} \\ \mu ^{SC}_{2a}+\mu ^{SC}_{2b}(\lambda _c + \mu ^{SC}_{2c}), & {\lambda _c^l<\lambda _c<\lambda _c^u} \\ \mu ^{SC}_{2r}, & {\lambda _c\ge \lambda _c^u} \\ \end{array} \right. \\ \sigma _2^{SC}(\lambda _c)= & \left\{ \begin{array}{ll} \sigma ^{SC}_{2l}, & {\lambda _c \le \lambda _c^l} \\ \sigma ^{SC}_{2a}+\sigma ^{SC}_{2b}(\lambda _c + \sigma ^{SC}_{2c}), & {\lambda _c^l<\lambda _c<\lambda _c^u} \\ \sigma ^{SC}_{2r}, & {\lambda _c\ge \lambda _c^u} \\ \end{array} \right. \\ \end{aligned}$$

The values of the constants appearing in Johnson et al. (2001) are given in Table 6.

Table 6 Default values of the constants appearing in Johnson et al. (2001) for spacecraft fragments of size $L_c>11$ cm

Remark 1

The values of the side branches are computed as:

$$\begin{aligned} x_l= & x_a + x_b(\lambda ^l + x_c), \\ x_r= & x_a + x_b(\lambda ^u + x_c). \end{aligned}$$

Remark 2

The parameters for the $\alpha$ functions should be chosen such that the co-domain of $\alpha$ is a subset of [0, 1]. The parameters for the $\sigma$ functions should be chosen such that the function takes only positive values.

1.3 B.3. Distribution function for objects of size $L_c$, with $L_c<8$ cm

The distribution function for objects with $L_c<8$ cm is given by

$$\begin{aligned} D_{A/m}^{SOC}(\lambda _c,\chi )=N(\chi ,\mu ^{SOC}(\lambda _c),\sigma ^{SOC}(\lambda _c))\ , \end{aligned}$$

(19)

where

$$\begin{aligned} \mu _1^{SOC}(\lambda _c)= & \left\{ \begin{array}{ll} \mu ^{SOC}_{l}, & {\lambda _c \le \lambda _c^l} \\ \mu ^{SOC}_{a}+\mu ^{SOC}_{b}(\lambda _c + \mu ^{SOC}_{c}), & {\lambda _c^l<\lambda _c<\lambda _c^u} \\ \mu ^{SOC}_{r}, & {\lambda _c\ge \lambda _c^u} \\ \end{array} \right. \nonumber \\ \sigma _1^{SC}(\lambda _c)= & \left\{ \begin{array}{ll} \sigma ^{SOC}_{l}, & {\lambda _c \le \lambda _c^l} \\ \sigma ^{SOC}_{a}+\sigma ^{SOC}_{b}(\lambda _c + \sigma ^{SOC}_{c}), & {\lambda _c^l<\lambda _c<\lambda _c^u} \\ \end{array} \right. \end{aligned}$$

(20)

The values of the constants appearing in Johnson et al. (2001) are given in Table 7.

Table 7 Default values of the constants appearing in Johnson et al. (2001) for objects of size $L_c<8$ cm

Remark 3

A function is used to bridge the gap between 8 and 11 cm. This gap can be filled by comparing a generated random number $\zeta (L_c)\in [0,1]$ with a value $\bar{\zeta }(L_c)$ given by

$$\begin{aligned} \bar{\zeta }(L_c)=4.3\ \log _{10} L_c/[m]+4.9\ . \end{aligned}$$

If $\zeta >\bar{\zeta }$, then the appropriate bimodal distribution for large fragments is applied, otherwise the single-mode distribution for smaller objects is used.

1.4 Cross-sectional area and mass

The average cross-sectional area A is an explicit function of $L_c$ and it can be expressed as

$$\begin{aligned} A/[m^2]= & 0.540424(L_c/[m])^2\qquad \qquad \ \, \textrm{for}\ L_c<0.00167\ m\nonumber \\ A/[m^2]= & 0.556945(L_c/[m])^{2.0047077} \qquad \textrm{for}\ L_c\ge 0.00167\ m\ . \end{aligned}$$

(21)

Then, the mass of the fragments is determined by the expression

$$\begin{aligned} m={A\over {A/m}} \end{aligned}$$

(22)

with A as in (21) and the area-to-mass ratio A/m statistically sampled through the probability density function given in (4).