Periodic orbits in a galactic potential

Abstract

We make a numerical study of the periodic orbits of period-1 and their bifurcations in a galactic type potential $V=\frac{1}{2}[\alpha (x^2+y^2)+x^2y^2]$, which tends to the Yang–Mills potential $V=\frac{1}{2}x^2y^2$, when $\alpha$ tends to zero. We consider their stability diagrams, the corresponding Poincaré surfaces of section and the forms of the orbits.

1 Introduction

A general model of a galaxy has a plane of symmetry and the potential on this plane has the form $V=\frac{1}{2}(\omega _1^2 x^2+ \omega _2^2 y^2)$ + higher-order terms near the center.

A particular model that we studied in Contopoulos et al. (1994) is

$$\begin{aligned} V= \frac{1}{2}(x^2+y^2)+ \epsilon x^2y^2 \end{aligned}$$

(1)

In this model, we found the main simple periodic orbits, and we studied the asymptotic curves of the unstable orbits.

An equivalent form of this potential is the following

$$\begin{aligned} V= \frac{1}{2}[\alpha ( x^2+y^2)+ x^2y^2] \end{aligned}$$

(2)

and a particular case of this model is the Yang–Mills potential (with $\alpha$=0)

$$\begin{aligned} V=\frac{1}{2}=x^2y^2 \end{aligned}$$

(3)

This particular potential is of interest in high energy physics (Axenides et al. 2017; de Wit et al. 1988, 1989).

It was thought that this potential is completely chaotic, i.e., it does not have any stable periodic orbits (Carnegie and Percival 1984; Savvidy 1983, 1984; Sohos et al. 1989). However, Dahlqvist and Russberg in Dahlqvist and Russberg (1990) (DR hereafter) found a family of stable periodic orbits in the potential (3); therefore, this potential has both order and chaos. This stable periodic orbit is of multiplicity 9, i.e., it has 9 intersections with the $x-axis$ (with $\dot{y}>0$).

In a recent paper (Contopoulos and Harsoula 2023), we studied the periodic orbits near the Yang–Mills potential (Eq. 2), for small values of $\alpha$ close to zero. We found that the stable family found by DR bifurcates from a "basic" family of the same period when $\alpha \approx 10^{-4}$. The basic family is stable for two small intervals of $\alpha$ and generates some further period-9 (or 18, etc.) families. However, this basic family is terminated at $\alpha = \alpha _{max} \approx 16.8 \times 10^{-4}$ by joining (at a tangent bifurcation) another period-9 family that is unstable for all values of $\alpha \le \alpha _{max}$.

Therefore, the period-9 families of orbits connected with the DR stable family are not connected with families that appear for large values of $\alpha$ (of order O(1)) that are of interest for galactic dynamics.

On the other hand, (Sohos et al. 1989) studied some period-1 families of orbits in the potential (2) and found that all of them have period-doubling bifurcations of periods 2,4,...as $\alpha$ decreases and lead to infinities of unstable periodic orbits well before $\alpha$ approaches zero.

However, Sohos et al. in Sohos et al. (1989) did not study all the simple periodic orbits. Thus, in the present paper we tried to find all the periodic orbits of period-1 for large values of $\alpha$ and their bifurcations as $\alpha$ decreases.

A question remained up to now is whether any of these bifurcations is of period-9 and whether it is related to the stable period-9 orbits of the Yang–Mills potential. The answer to the first question is positive. We did find a period-9 family that has the same topology as the DR family. However, this orbit is not connected to the periodic orbit found by DR.

In the present paper, we consider in detail the periodic orbits of period-1, in Sect. 2. We study the stability and the forms of these orbits and of their bifurcations as well as the corresponding Poincaré surfaces of sections. In Sect. 3, we study the periodic orbits of period-2, and in Sect. 4 we draw our conclusions.

2 Periodic orbits of period 1

2.1 Stability and bifurcations

The energy of the potential (2) is identified with the Hamiltonian:

$$\begin{aligned} H=\frac{1}{2}(\dot{x}^2+\dot{y}^2)+ \frac{1}{2} x^2y^2 + \frac{\alpha }{2} ( x^2+y^2) = E \end{aligned}$$

(4)

We fix the value of the energy $E=\frac{1}{2}$ in Eq. (4), and we study the periodic orbits of period 1. The basic periodic orbits of period 1, for $\alpha > 0$, are the axes $x=0$ and $y=0$, and the diagonals $y= \pm x$. When $\alpha \le 0$, the orbits along the axes escape to infinity while the diagonals continue to exist.

We consider now the orbit along the $x-axis$ ($y=0$ and $\dot{y}>0$) which we call “central" period-1 orbit and study its stability for various values of $\alpha$ ($\alpha >0$) (black curves in Fig. 1a, b). For large values of $\alpha$ ($\alpha > 0.6$), this orbit is always stable.

The stability of the periodic orbits is found by calculating the Hénon index HI ( Hénon 1965). This is related to the eigenvalues $\lambda$ of the periodic orbit.¹

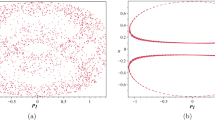
The Hénon index (HI) of the "central" period-1 periodic orbit ($x=0 ~ or~ y=0$) tends to $+1$ as $\alpha \rightarrow \infty$ (Fig. 1a). At $\alpha \approx 0.6$, the stability curve of this orbit becomes tangent to the axis $HI=-1$ where it bifurcates, for smaller values of $\alpha$, four period-2 families, two stable and two unstable (see Sect. 3). As $\alpha$ decreases and reaches the value $\alpha \approx 0.41$, the stability curve crosses the axis $HI=+1$. At this point, two stable period-1 families bifurcate that have the same HI curve (Fig. 1b green curve). The bifurcating orbits can be also seen on the Poincaré surfaces of section (Figs. 3, 4, 6, 14).

Fig. 1

The Hénon index as a function of $\alpha$ of various families of period-1 orbits (a) for $0.3<\alpha <1.5$ and (b) for $0.1<\alpha <0.6$. Black curve corresponds to the central periodic orbit ($x= \dot{x}=0$ or $y= \dot{y}=0$). Blue curves correspond to the period-1 diagonal families $y= \pm x$ and their bifurcations. These families are generated together with the central (black) period-1 orbit at $\alpha = \infty$. Green curves correspond to the period-1 bifurcations from the central (black) periodic orbit each time this becomes unstable from stable as $\alpha$ decreases, and their period-1 bifurcations. Red curves correspond to period-1 unstable bifurcations from the central periodic orbit each time this becomes stable (from unstable), while the red curve that exists for $\alpha >1$ is generated at infinity together with the central period-1 orbit

The central period-1 family (black) becomes again stable at $\alpha \approx 0.33$ and two unstable period-1 families bifurcate (Fig. 1b, red). In fact, the central family has an infinity of successive intervals of stability and instability, as $\alpha$ decreases (Fig. 1b). The range of the intervals between stability and instability decreases as $\alpha$ decreases and approaches zero as $\alpha$ approaches zero. The stability curve $HI=f(\alpha )$ of the central periodic orbit becomes tangent to but never smaller than the value $HI=-1$, for infinitely many times. At all the tangent points ($HI=-1$), four period-2 families of orbits bifurcate, two stable and two unstable (see Sect. 3).

The period-1 family of orbits (green), which bifurcates at $\alpha \approx 0.41$ from the central one for the first time, has a stability curve with a characteristic evolution (Fig. 2a). Namely, as $\alpha$ decreases, its stability curve becomes tangent to the $HI=-1$ axis (and generates there two period-2 families of orbits one stable and one unstable) and then it becomes unstable with $HI>+1$ at $\alpha \approx 0.27$. This is called “first-class" period-1 family of orbits. At the point where this family crosses the $HI=+1$ axis, two stable period-1 orbits bifurcate, with a stability curve that reaches a minimum (below the $HI=-1$ axis) and then for smaller values of $\alpha$ it grows again going beyond the $HI=+1$ axis where the orbits become and remain unstable. These are called “second-class" period-1 families of orbits. At the point where the “second-class" period-1 families cross the $HI= +1$ axis, four stable period-1 orbits bifurcate having all the same stability curve. The stability curve of these orbits crosses the $HI=-1$ axis and goes to $HI\rightarrow -\infty$. This is called "third-class" period-1 family of orbits. All the third-class orbits become unstable and they do not have further bifurcations. We see this same pattern of first-, second- and third-class families repeating itself for different intervals of $\alpha$ in Fig. 2b. In fact, this pattern is repeated an infinite number of times, as $\alpha$ decreases.

Two more stable period-1 orbits ($y= \pm x$) exist for large $\alpha$ (blue in Fig. 1). Their stability curves are the same, and $HI \rightarrow +1$ as $\alpha \rightarrow \infty$. On the other hand, as $\alpha$ decreases the stability curve of this family crosses the $HI=+1$ axis and the orbits become unstable (Fig. 1b). At this point ($\alpha \approx 0.32$), they generate by bifurcation two new period-1 orbits, that have the same HI curve, which are stable and after a tangency with the $HI=-1$ axis they become unstable crossing the $HI=+1$ axis. At this point, new stable period-1 orbits bifurcate, which become unstable for smaller $\alpha$ and never become stable again. Thus, the period-1 blue curves form a pattern that is not repeated for smaller values of $\alpha$ and it is different from the repeating patterns found by the green period-1 curves.

Fig. 2

The Hénon index as a function of $\alpha$ of families of period-1 orbits (green) bifurcating from the central periodic orbit (black) and their further period-1 bifurcations. a Orbits from the first transition of the black family from stability to instability at $\alpha \approx 0.4$ as $\alpha$ decreases, b orbits from the second transition from stability to instability at $\alpha \approx 0.24$

2.2 Surfaces of section

We now study the Poincaré surfaces of section ($x,\dot{x}$) with $y=0$ and $\dot{y}>0$ of the Hamiltonian (4).

Fig. 3

a The phase space $(x,\dot{x})$ for $y=0$ and $\dot{y}>0$ for $\alpha =1$. We see the stable central period-1 orbit $(x=\dot{x}=0)$ (black), two stable symmetric diagonal ($x=\pm y$) period-1 orbits (blue) with $(x=0~,\dot{x}\ne 0)$ and the islands of stability around them and two unstable period-1 orbits (red) with ($x\ne 0,~\dot{x}=0$). The boundary circle represents the orbit ($y=\dot{y}=0$) b The central periodic orbit ($x=\dot{x}=0$) (black) together with an ordered orbit (magenta) corresponding to an invariant curve around the central periodic orbit in a

In Fig. 3a, we show the surface of section for the case $\alpha =1$. At the center ($x=\dot{x}=0$), there is the central period-1 orbit, which is stable (black). On the $\dot{x}=0$ axis, there are two symmetric unstable period-1 orbits (red). Around these orbits there is chaos but very limited in space. On the $x=0$ axis, there are two more stable symmetric period-1 orbits (blue). These orbits are diagonal ($x= \pm y$) in the configuration space (x, y). Using equation (4), we find that at $x=y=0$ these orbits have velocities $\dot{x}= \pm \dot{y}=\pm \frac{1}{\sqrt{2}}$.

The boundary of Fig. 3a represents the periodic orbit $y=\dot{y}=0$ and is a circle given by the relation $x^2+\dot{x}^2=2E=1$. This orbit is stable.

In Fig. 3b, we plot the central periodic orbit ($x=\dot{x}=0$) in black and an ordered orbit (magenta) corresponding to an invariant curve around the central periodic orbit (shown with the same color in Fig. 3a). This orbit is like a Lissajous curve.

In Fig. 4, the same surface of section is plotted for $\alpha =0.4$. In this case, the boundary curve $y=\dot{y}=0$ is given by the relation $0.4 x^2+\dot{x}^2=2E=1$ and it is an ellipse elongated along the $x-axis$ with $max (\dot{x})$=1 and $max(x)=\frac{1}{\sqrt{\alpha }}$=1.58 (for $\alpha >1$, the ellipse is elongated along the $\dot{x}=0$ axis).

Fig. 4

The phase space $(x,\dot{x})$ for $\alpha =0.4$. The central period-1 orbit $(x=\dot{x}=0)$ is unstable (black). There are two stable symmetric period-1 orbits (green) with $(x=0~,\dot{x}\ne 0)$ (above and below the central period-1 orbit) and the diagonal ($x=\pm y$) period 1 orbits (blue). There are also two unstable period-1 orbits (red) with $x\ne 0,~\dot{x}=0$ and two stable period-2 orbits (dark green) close to the boundary of the CZV, one with $x=0$ and another with $\dot{x}=0$

In this case, the central periodic orbit ($x=\dot{x}=0$) is unstable. Two stable period-1 orbits (green) are located above and below the central orbit having $x=0$. They are surrounded by small islands of stability. These two stable periodic orbits have the form of a figure-eight, as in Fig. 7a, described in two opposite directions. The whole set of these periodic orbits is surrounded by nearly elliptical invariant curves close to the boundary.

The two unstable periodic orbits on the $\dot{x}=0$ axis (red) are at larger distances from the center than in Fig. 3, and they correspond to the red stability curve of Fig. 1a. These orbits generate a lot of chaos, through homoclinic intersections of their stable and unstable asymptotic curves, that covers most of the surface of section of Fig. 4. The diagonal period-1 orbits ($x=\pm y$) appear again in the centers of the blue islands of stability with $x=0$ (as in Fig. 3). They have also two sets of secondary period-2 islands around them.

The boundary of Fig. 4 represents here again the periodic orbit $y=\dot{y}=0$ which is unstable. Close to this boundary there are two stable period-2 orbits (dark green). One has $\dot{x}=0$ and is surrounded by islands of stability. This orbit is the same figure eight orbit, as in Fig. 7a, but rotated by $90^o$ so that it has now two intersections upwards. The same rotated orbit can be described in the opposite direction and gives a stable period-2 periodic orbit (with two points on the surface of section) near the boundary CVZ with $x=0$ (dark green) above and below the center.

Fig. 5

The characteristics ($x=f(\alpha )$) of the period-1 orbits. The central period-1 orbit has always $x=0$ (black). The green period-1 orbits have intervals with $x=0$ and intervals with $x \ne 0$ and the red period-1 orbits are always unstable and have always $x \ne 0$

Fig. 6

The phase space ($x,\dot{x}$) for a $\alpha =0.24$, where two symmetric period-1 (green) orbits (with $x=0,~\dot{x}\ne 0$) have bifurcated from the central period-1 orbit ($x=\dot{x}=0$), b $\alpha =0.2$, where the central period-1 orbit has become stable, the period-1 (green) orbits of Fig. 6a have become unstable and two new pairs of stable period-1 orbits (dark green) have bifurcated from them (with $x \ne 0,~\dot{x}\ne 0$) and c $\alpha =0.168$, where the central period-1 orbit has become unstable, four pairs of period-1 (green) orbits have bifurcated from the four period-1 (dark green) orbits of Fig. 6b and two stable period-1 orbits are above and below the central period-1 orbit (green)

In Fig. 5, we plot the characteristics ($x=f(\alpha )$) of the period-1 orbits, i.e., the x value of the periodic orbit on the Poincaré surface of section for different values of $\alpha$. The central period-1 orbit has $x=0$ for every value of $\alpha$. The green period-1 orbits have intervals with $x=0$ (first-class orbits) and intervals with $x \ne 0$ (second- and third-class orbits) for smaller values of $\alpha$. Finally, the red period-1 orbits, which are unstable, have always $x \ne 0$.

As the value of $\alpha$ decreases below $\alpha \approx 0.285$, the $1^{st}$ class (green) period-1 family becomes for the first time unstable with $HI>+1$ (Fig. 2a), and two new stable period-1 families bifurcate from it (second class) with $x \ne 0$ and $\dot{x}=0$. These new stable period-1 orbits become unstable for smaller $\alpha$ and generate four new stable period-1 orbits (third class) and four unstable period-1 bifurcating families for smaller values of $\alpha$ (Fig. 5). This doubling of period-1 orbits does not continue further beyond the eight third-class orbits, because the HI curve of the third class does not cross again the $HI=\pm 1$ axes (see Fig. 2). Further bifurcations are of period-2 and higher.

The same pattern of bifurcations for the green period-1 orbits is repeated infinitely many times, as $\alpha$ decreases, after every transition of the central family from stability to instability (Fig. 5).

In Fig. 6a–c, we give an example of these bifurcations on the Poincaré surface of section after the transition from stability to instability of the central $(x=\dot{x}=0)$ period-1 family. Namely, the central period-1 family is unstable at $\alpha =0.24$ and generates two stable period-1 orbits (green) with $x=0$ (one with $\dot{x}<0$ and another one with $\dot{x}>0$) (Fig. 6a). Then at $\alpha = 0.20$ the central period-1 orbit has become stable again and the green period-1 orbits have become unstable (dark green at $x=0$, one with $\dot{x}>0$ and another one with $\dot{x}<0$) and have generated four stable orbits (green) (Fig. 6b). Finally, at $\alpha = 0.168$ these last orbits become unstable (black dots) and generate eight stable period-1 orbits (dark green), four with $x>0$ and four with $x<0$ (Fig. 6c). For this value of $\alpha$ the central orbit has become again unstable and it has generated two more stable period-1 orbits with $x=0$, above and below (Fig. 6c).

2.3 Forms of the stable periodic orbits of period 1

In Fig. 1a, we see that for $\alpha >0.41$ there are only four stable periodic orbits of period 1, namely the axes $x=0$ and $y=0$ (black curve) and the diagonal orbits $x=\pm y$ (blue curves). For $\alpha \le 0.41$, bifurcations of the central ($x=\dot{x}=0$) period-1 orbits appear for the first time (green curves of Fig. 1b). The forms of these stable period-1 orbits are given in Fig. 7.

The first bifurcating orbit is generated when the central period-1 orbit crosses the $HI=+1$ axis for the first time at $\alpha \approx 0.41$ and becomes unstable as $\alpha$ decreases. This orbit has a figure-eight form with two equal lobes (Fig. 7a). The next stable period-1 bifurcations are generated when the central period-1 orbit becomes again unstable, from stable (at $\alpha \approx 0.23$) (Fig. 7b). These orbits have an "S"-shape and an inverse "S"-shape. The orbit of the next bifurcation (for $\alpha =0.16$) of the central period-1 orbit (from stability to instability) is given in Fig. 7c, which is a figure-eight with two extra loops one above and one below. In general, all the bifurcating orbits (for $\alpha <0.41$) have shapes like Fig. 7a, b but with two extra loops or oscillations (alternately) at each new bifurcation as $\alpha$ decreases. These orbits (bifurcating directly from the central period-1 family when this becomes unstable from stable), as $\alpha$ decreases are called “first-class orbits".

Fig. 7

The forms of the symmetric stable periodic orbits of period-1 for various values of $\alpha$ of the first-class orbits, bifurcating at successive transitions from stability to instability from the central period-1 orbit ($x=\dot{x}=0$) as $\alpha$ decreases

Fig. 8

The forms of the second-class stable period-1 orbits, bifurcating from the first-class orbits, that have two unequal lobes (a) or unequal arcs in the case of oscillations (b)

Fig. 9

The forms of the third-class stable asymmetric period-1 orbits, bifurcating from the second-class orbits with unequal arcs (a) or unequal lobes (b)

If we rotate the orbits of Fig. 7a–c by 90$^o$, we find orbits of periods 2, 3 and 4, respectively (number of intersections with the x-axis, with $\dot{x}>0$).

Besides the first-class period-1 orbits, there are other period-1 orbits bifurcating from the first-class orbits when the latter ones become unstable from stable, as $\alpha$ decreases, and they are called "second-class" period-1 orbits (see Fig. 2). These orbits consist of two unequal lobes (or unequal arcs in the case of oscillations, Fig. 8a, b). The orbits of Fig. 8 have also symmetric orbits with respect to the axis $y=0$.

Finally, there is a third class of asymmetric period-1 orbits (Fig. 9a, b) bifurcating from the second-class period-1 orbits each time the latter family crosses the $HI= +1$ axis as $\alpha$ decreases in the stability diagram (see Fig. 2). Note that in Fig. 7, 8, 9 the scales of the x-axis are much smaller than the scales of the y-axis.

Fig. 10

The forms of the diagonal period-1 orbits for several values of $\alpha$

Another type of period-1 orbits are the diagonal orbits $x= \pm y$ (Fig. 10). These orbits have been created at $\alpha =\infty$, having $HI= +1$ (blue curve of Fig. 1a) together with the central period-1 stable periodic orbit (black curve of Fig. 1a) and the unstable period-1 periodic orbit (red curve of Fig. 1a). The diagonal orbits are always stable for $\alpha >0.32$ and are straight lines (Fig. 10a). They become unstable, for the first time, as $\alpha$ decreases, at $\alpha \approx 0.32$ (Fig. 1b). There, a new bifurcation of four stable period-1 orbits begins. The shape of two of them is shown in Fig. 10b, and there are two more symmetric ones with respect to the $x=0$ axis. These new orbits become unstable at $\alpha \approx 0.19$ and four new stable period-1 orbits bifurcate. Two of them are shown in Fig. 10c and there are two more symmetric with respect to the $x=0$ axis.

2.4 Forms of the unstable periodic orbits of period 1

Apart from the period-1 orbits described above, there exist period-1 orbits that are unstable for every value of $\alpha$ (red curves in Fig. 1). In Fig. 11, some unstable periodic orbits of this kind are plotted. Some of them appear in symmetric couples (Fig. 11b, d). The family of period-1 unstable family that is generated at $\alpha = \infty$ (together with the central period-1 family) is close to a circle (Fig. 11a) for large $\alpha$. In fact, the radius of this orbit decreases as $\alpha$ increases and tends to a point for $\alpha \rightarrow \infty$. When $\alpha$ decreases the size of the orbit increases and approaches the form of a square with smooth angles (Fig. 11a). The unstable period-1 orbits of Figs. 11b–d bifurcate from the central period-1 orbit every time the latter is making a transition from instability to stability (see Fig. 1).

Fig. 11

Some unstable period-1 orbits. a This family is a small circle (approaching a point at $\alpha \rightarrow \infty$) and becomes larger and more rectangular as $\alpha$ decreases. b–d Orbits bifurcating from the stable central period-1 family, each time it crosses the $HI=+1$ axis becoming stable from unstable as $\alpha$ decreases

At the first transition of the central period-1 orbit, from instability to stability, as $\alpha$ decreases (for $\alpha \approx 0.33$) the shape of the unstable period-1 orbits is shown in Fig. 11b. There are two symmetric periodic orbits with the shape of "$\subset$" and an inverse "$\supset$" and the size of the orbits increases as $\alpha$ decreases. These orbits have reflection points at the equipotential curves (curves of zero velocity, CZV hereafter) and return along the same curves.

At the second transition of the central period-1 orbit from instability to stability (for $\alpha \approx 0.21$) the unstable orbits have the form of an oval with two extra loops, one above and the other below the main oval (Fig. 11c). This orbit can be described in two ways, clockwise and anti-clockwise. Thus, in fact there are two similar orbits with the same stability parameters. Further unstable period-1 orbits form more loops above and below (or make more oscillations like in Fig. 11d) for decreasing $\alpha$. The number of extra loops (or oscillations) increases indefinitely as $\alpha$ approaches zero. An example of an unstable orbit with many loops is given in Fig. 12 for $\alpha =0.00127$.

Fig. 12

An unstable period-1 orbit bifurcating from the stable central period-1 family for $\alpha =0.00127$ making many loops along the y-axis. Note the large difference of scales in x and y axes

Besides these unstable period-1 orbits described above, there are further unstable period-1 orbits bifurcating from the stable period-1 orbits of the first, second and third class (green curves in Fig. 2) as well as from the stable period-1 diagonal families (blue curves in Fig. 1). The forms of these unstable orbits are the same (topologically) as the forms of the stable orbits from which they are generated (Figs. 7, 8, 9, 10).

3 Periodic orbits of period 2

We have the following types of period-2 orbits: (a) Type a: A pair of stable and unstable periodic orbits (Fig. 13a, gray), bifurcating from the central period-1 orbit (Fig. 13a, black) each time the HI curve of this orbit becomes tangent to the $HI=-1$ axis. (b) Type b: A pair of stable and unstable periodic orbits (Fig. 13b, magenta) bifurcating from the first-class period-1 orbits (Fig. 13b, green) each time the HI curves of the latter orbits are tangent to the $HI=-1$ axis. When the bifurcating (magenta) HI curve crosses the $HI=+1$ axis and becomes unstable, one more period-2 orbit (magenta) bifurcates, which is initially stable as $\alpha$ decreases. (c) Type c: One stable or unstable periodic orbit bifurcating from the second- and third-class period-1 orbits (Fig. 13b, green) each time the HI curves of these orbits cross the $HI=-1$ axis (Fig. 13b, magenta) and (d) Type d: Stable and unstable periodic orbits (Fig. 13c, light blue) bifurcating from the period-1 orbits with equation $y=\pm x$ (Fig. 13c, blue) each time the HI curves of these orbits cross or are tangent to the $HI=-1$ axis.

The “type a” period-2 orbits that bifurcate from the central period-1 family (Fig. 13a, gray), form patterns, in the stability diagram ($HI=f(\alpha )$), similar to the ones of the period-1 orbits of bifurcations (compare Fig. 2 (green) and 13a (gray)). Therefore, there are “first class", “second class" and “third class" of "type a "period-2 orbits.

On the other hand, the "type b" period-2 families that bifurcate from the first-class period-1 families (Fig. 13b, magenta) have a different evolution. They are generated (stable and unstable) when the green curve has $HI=-1$. As $\alpha$ decreases, the stable ones become unstable ($HI<-1$) for a certain interval of $\alpha$ and for smaller $\alpha$ they become stable again until they cross the $HI=+1$ axis where they become unstable. At this point, new period-2 stable periodic orbits are generated, which become unstable for smaller values of $\alpha$ and remain unstable as $\alpha$ decreases.

Finally, the "type c" period-2 orbits that bifurcate from the period-1 family of the second and the third class when their stability curve crosses the $HI=-1$ axis have also different pattern (Fig. 13b, magenta). At the first crossing of the second-class period-1 orbits (at $\alpha \approx 0.27$), a period-2 family is bifurcated at $HI=+1$. This orbit is initially stable but becomes and remains unstable for smaller $\alpha$. At the second crossing of the $HI=-1$ axis of the second-class period-1 family an unstable period-2 family is bifurcated having $HI > +1$. Finally at the first intersection of the third-class period-1 orbit another period-2 family is bifurcated (initially stable and then unstable for all smaller values of $\alpha$).

The ’type d" period-2 orbits also follow a different pattern of the HI curves than the previous ones (Fig. 13c, light blue).

Fig. 13

The HI as a function of the parameter $\alpha$ for the period-2 orbits a bifurcating from the central period-1 orbit (black) forming a repeating pattern (gray) b bifurcating from the first-, second- and third-class period-1 orbits (magenta) and c bifurcating from the diagonal period-1 orbits (cyan)

In Fig. 14a, we plot the Poincaré surface of section ($x,\dot{x}$, with $y=0$ and $\dot{y}>0$), for $\alpha =0.585$. The period-2 family of orbits appears here for the first time (as $\alpha$ decreases) as a bifurcation from the central period-1 family. This value of $\alpha$ is just below the point where the stability curve of the central period-1 orbit is tangent to the axis $HI=-1$ for the first time (Fig. 1a). The central period-1 orbit is stable. There are two stable periodic orbits of period-2, with points above and below, and one more with points on the right and on the left of the central period-1 orbit (gray points in Fig. 14b). These two stable period-2 orbits have the same stability curve (Fig. 13a). There are also two unstable period-2 orbits marked with gray and black dots between the stable ones (Fig. 14b).

Further away from the central period-1 orbit there are two unstable period-1 orbits on the $\dot{x}=0$ axis (red dots on Fig. 14a). The boundary represents the orbit $y=\dot{y}=0$, which is stable. In Fig. 14a, there are also plotted the stable period-1 diagonal orbits (blue dots) (see Fig. 10a).

Fig. 14

a The Poincaré surface of section $(x,\dot{x})$ for $\alpha =0.585$, where the period-2 family of orbits have bifurcated for the first time from the central period-1 orbit. b A zoom in of the central region. Two pairs of stable and two pairs of unstable period-2 orbits have been bifurcated from the central period-1 orbit

Fig. 15

The “type a” stable period-2 orbits of first class (see text), symmetric with respect to the axes, bifurcating from the central period-1 orbit for two different values of the parameter $\alpha$ a for $\alpha$=0.56 and b for $\alpha$=0.2827

Fig. 16

a Two “type a” stable period-2 orbits of second class (see text), asymmetric with respect to the $x=0$ axis for $\alpha$=0.403 and b two "type a" stable period-2 orbits of the third class (see text) asymmetric with respect to the $x=0$ axis, for $\alpha$=0.368. These orbits are symmetric with respect to the $y=0$ axis

Fig. 17

Two “type a” asymmetric (with respect to the $y=0$ axis) unstable period-2 orbits of the first class (see text), for two different values of $\alpha$

The forms of the different types of period-2 orbits are given in Figs. 15, 16 and 17.

The orbits of Fig. 15 are stable period-2 orbits of "type a", first class (see Fig. 13) bifurcated directly from the main period-1 periodic orbit (1st class orbits) after a tangency with the $HI=-1$ axis. They are symmetric with respect to the axes and plotted for two different values of $\alpha$.

The orbits of Fig. 16 are stable period-2 orbits of "type a", second class (see Fig. 13). The orbits of Fig. 16a have bifurcated from the first-class period-2 orbits when the latter crossed the $HI=+1$ axis. The orbits of Fig. 16b are third-class orbits , that have bifurcated from the second-class period-2 orbits.

The orbits of Fig. 17a, b are unstable and are generated from the first and the second tangency of the HI curve of the period-1 stable family (black family of Fig. 13a).

If we rotate these orbits by $90^o$, we find orbits of periods 3 and 5. These orbits reach the curve of zero velocity at two points and are reflected along the same path. The period-3 orbits form one loop opposite to the side of the reflections, while the period-5 orbits from two loops.

Fig. 18

The two different period-9 orbits for $\alpha =0$ (black) and $\alpha =0.1293$ (blue). The families of these period-9 orbits do not communicate with other through bifurcations

In the same way, at the third and the fourth tangency of the period-1 family with the $HI=-1$ axis (as $\alpha$ decreases, Fig. 13a) bifurcations of orbits are generated of period-7 and period-9 (by rotation of $90^o$). These orbits form 3 and 4 loops, respectively, on the opposite side of the two reflection points.

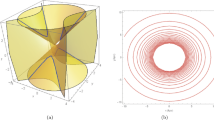
In particular, the period-9 orbit, which is a period-2 periodic orbit for $\alpha =0.1293$, rotated by $90^o$ (Fig. 18, orbit b, blue) is topologically similar to the period-9 orbit (Fig. 18, orbit a, black) of our paper (Contopoulos and Harsoula 2023), for $\alpha$=0, (from which bifurcate the stable period-9 orbits, found by DR in Dahlqvist and Russberg (1990) in the YM potential). However, the form of the period-9 orbit b of Fig. 18 has different sizes of its loops, in comparison with the loops of the period-9 orbit a of Fig. 18. The two period-9 orbits of Fig. 18 do not communicate with each other. In fact, the family of orbits (from which bifurcates the stable YM family for $\alpha \le 10^{-4}$) (orbit a of Fig. 18) disappears, at a tangent bifurcation, at $\alpha \approx 16.8 \times 10^{-4}$ (Fig. 19a), while the blue period-9 orbit (orbit b Fig. 18) belongs to a different family that exists for large values of $\alpha$. Moreover, the stability curves of the orbits a and b of Fig. 18 are very different. For $\alpha =0$ the period-9 orbit a of Fig. 18 has $HI \approx 4.5$ (Fig. 19a), while the period-9 orbit b of Fig. 18 has extremely large values of HI (Fig. 19b) close to $\alpha =0$. Therefore, the period-9 orbit found in this paper (blue in Fig. 18) has no connection with the stable period-9 orbit found by DR in the Yang–Mills potential (black in Fig. 18).

Fig. 19

The HI curves of the two different period-9 family of orbits a black period-9 orbit of Fig. 18 and b blue period-9 orbit of Fig. 18

4 Conclusions

We have found the form and the stability diagrams ($HI=f(\alpha )$) of the families of orbits of period-1 and period-2 of an extended Yang–Mills potential of the form $V=\frac{1}{2}[\alpha (x^2+y^2)+x^2y^2]$, which is appropriate for galactic dynamics.

The stability diagrams of the period-1 periodic orbits follow a certain recurrent pattern. Namely there are first-, second- and third-class bifurcations of period-1 orbits from the central ($x=\dot{x}=0$) period-1 orbit. The third class of period-1 orbits have HI with absolute values that increase constantly as $\alpha$ decreases, and as a consequence, there is no bifurcation to a fourth-class period-1 orbits.

At the transitions of the central period-1 orbit from stability to instability, there are bifurcations of stable period-1 orbits (of the first class), while at the transitions from instability to stability there are bifurcations of unstable period-1 families that remain constantly unstable as $\alpha$ decreases.

We have also studied the typical Poincaré surfaces of section ($x, \dot{x}$ for $y=0$ and $\dot{y}>0$) for various values of $\alpha$.

We quote below some general remarks: Sohos et al. in Sohos et al. (1989) considered successive bifurcations beyond the period-2 orbits, as $\alpha$ decreases, of periods 4,8, etc., and found that all these orbits become unstable well before the Yang–Mills case ($\alpha =0$) is reached. This type of cascade of bifurcations is a general feature of the dynamical systems (see Contopoulos (2002)) and leads to an infinity of unstable periodic orbits. However, in Sohos et al. (1989) they did not consider all the period-1 bifurcations that we describe in the present paper. Namely there are further period-1 and period-2 orbits and all of them form cascades of bifurcations with infinities of unstable periodic orbits.

We know from the general theory of bifurcations (Contopoulos 2002) that the intervals between the successive period doublings (periods 1,2,4, etc.) decrease by a factor of about 8.72. Therefore, if the interval between the generation of a period 1 and the following period 2 orbit is $\Delta \alpha$ the total interval of period doublings is:

$$\begin{aligned} \Delta _T= \Delta \alpha + \frac{\Delta \alpha }{8.72}+ \frac{\Delta \alpha }{8.72^2}+...= \frac{\Delta \alpha }{1-\frac{1}{8.72}} \approx 1.13 \Delta \alpha \end{aligned}$$

(6)

We give an example below: in the case of the first-class period-1 family that bifurcates from the central family (at $\alpha \approx 0.42$), the generation of the first period-2 family happens for $\alpha \approx 0.34$ (Fig. 13b). Therefore, the first interval between two successive bifurcations is $\Delta \alpha$=0.08. As a consequence, the infinite cascade of bifurcations, for this case, terminates after an interval $\Delta _T=1.13.\Delta \alpha \approx 0.0904$. Thus, at $\alpha = \alpha _T=0.42-0.0904 \approx 0.33$ starts an infinity of unstable bifurcating families, for smaller values of $\alpha$. Similar results are found for any other set of period-doubling bifurcations.

As a consequence, all these infinities of unstable orbits reach the Yang–Mills case ($\alpha =0$). Thus, they cannot be connected to the stable YM orbits found in Dahlqvist and Russberg (1990).

In fact, as we have seen in Contopoulos and Harsoula (2023) the stable period-9 family of orbits of the YM potential, as $\alpha$ increases, is terminated at a tangent bifurcation with another unstable period-9 orbit at a very small positive value of $\alpha \approx 16.8 \times 10^{-4}$. Therefore, this family has no connection with the families that bifurcated from the central period-1 orbits. Similarly, the periodic orbits of periods 11,7,5,3, that we studied in our previous paper (Contopoulos and Harsoula 2023) are not connected with the bifurcations of the period-1 families of orbits that we study in this paper.

Our study of periodic orbits will be extended in the future in more realistic galactic potentials including, for example, a black hole and a dark matter halo.