Detection of separatrices and chaotic seas based on orbit amplitudes

Abstract

The maximum eccentricity method (MEM, (Dvorak et al. in Astron Astrophys 426(2):L37–L40, 2004)) is a standard tool for the analysis of planetary systems and their stability. The method amounts to estimating the maximal stretch of orbits over sampled domains of initial conditions. The present paper leverages on the MEM to introduce a sharp detector of separatrices and chaotic seas. After introducing the MEM analogue for nearly-integrable action-angle Hamiltonians, i.e., diameters, we use low-dimensional dynamical systems with multi-resonant modes and junctions, supporting chaotic motions, to recognise the drivers of the diameter metric. Once this is appreciated, we present a second-derivative-based index measuring the regularity of this application. This quantity turns to be a sensitive and robust indicator to detect separatrices, resonant webs and chaotic seas. We discuss practical applications of this framework in the context of N-body simulations for the planetary case affected by mean-motion resonances, and demonstrate the ability of the index to distinguish minute structures of the phase space, otherwise undetected with the original MEM.

Appendices

Appendix A: Application to a discrete case

The framework presented applies also for nearly-integrable discrete systems. For illustrative purpose, following Guillery and Meiss (2017), let us consider the 4-dimensional mapping on ${\mathbb {T}}^{2} \times {\mathbb {R}}^{2}$ reading

$$\begin{aligned} \left\{ \begin{aligned} x_{1}'&=x_{1}+y_{1}, \\ x_{2}'&=x_{2}+y_{2}, \\ y_{1}'&=y_{1}-\frac{1}{2\pi }\big ( a\sin (2\pi x_{1})+c \sin (2\pi (x_{1}+x_{2})) \big ), \\ y_{2}'&=y_{2}-\frac{1}{2\pi }\big ( b\sin (2\pi x_{2})+c \sin (2\pi (x_{1}+x_{2})) \big ), \end{aligned} \right. \end{aligned}$$

(17)

where a, b, c are real parameters. When $c=0$, the mapping is a product of two uncoupled standard-maps. In the following, we consider $a=0.1$, $b=0.1$ and $c=0.07$, and we generate $500 \times 500$ initial conditions distributed in the $(y_{1},y_{2})$ action plane $[-0.25,0.65]^{2}$ (fixing $x_{1}=x_{2}=0$) iterated up to the final time $T=10^{3}$. The numerical setting follows closely Guillery and Meiss (2017), who dealt with fast Lyapunov indicators (FLIs, Froeschlé et al. 1997. In Fig. 8, we show alternatively the results of the D and $\left\Vert \varDelta D\right\Vert$ analysis to provide a global representation of the phase space. Although the diameter reveal the low-order resonant strips, it does not provide clear insights about the geography of lower order resonances, and the distribution of chaotic motions near the resonant crossings. This “flatness” in the map is reinflated by the $\left\Vert \varDelta D\right\Vert$ index, which reinvigorates minute details of the geography of low-order resonant structures.

B Analytical properties of the diameter for the pendulum model

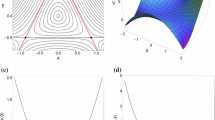
The non-differentiability of the diameter near the stable equilibrium and its discontinuity when crossing transversally the separatrix of the pendulum (as observed numerically in Fig. 1) are proven analytically.

Proposition 1

(Diameter in elliptic region.) Let ${\mathcal {H}}(p,q)=\frac{p^{2}}{2}+\frac{q^{2}}{2}$ be the Hamiltonian of the linear oscillator, $(p,q) \in D \subset {\mathbb {R}}^{2}$. Then we have

$$\begin{aligned} D(p_{0},q_{0}) = 2\sqrt{p_{0}^{2}+q_{0}^{2}} . \end{aligned}$$

(18)

Proof

The system is 1-DoF  and integrable. Following Pédenon-Orlanducci et al (2022), we parameterise orbits with their energy levels, thus accounting for an infinitely large time-window. The flow generates circles around the origin with radii

$$\begin{aligned} r(p_{0},q_{0})=\sqrt{p_{0}^{2}+q_{0}^{2}}. \end{aligned}$$

(19)

The diameter thus reads

$$\begin{aligned} D(p_{0},q_{0})=2r(p_{0},q_{0}). \end{aligned}$$

(20)

Along the line of initial condition $q_{0}=0$, one get

$$\begin{aligned} D(p_{0},0)=2\sqrt{p_{0}^{2}}=2\vert p_{0}\vert , \end{aligned}$$

(21)

and in particular D is not differentiable at $p_{0}=0$. $\square$

Proposition 2

(Discontinuity when crossing the separatrix) Let ${\mathcal {H}}(p,q)=\frac{p^{2}}{2}-\cos q$ be the Hamiltonian of the pendulum, $(p,q) \in D \times [-\pi ,\pi ]$, $D \subset {\mathbb {R}}$. The diameter is discontinuous on the energy level labelling the separatrix.

Proof

The librational domain corresponds to the range of energy $E \in [-1,1)$, the circulational domain to $E >1$, and the separatrix has energy $E=1$. Let $E_{0}$ denote the initial energy associated to $(p_{0},q_{0})$. The diameter reads

$$\begin{aligned} D(p_{0},q_{0})= \left\{ \begin{aligned}&2 \sqrt{2(E_{0}+1)}, \, E_{0} \in [-1,1), \\&\sqrt{2(E_{0}+1)} - \sqrt{2(E_{0}-1)}, \, E_{0} > 1, \end{aligned} \right. \end{aligned}$$

(22)

from which follows the discontinuity announced at $E_{0}=1$. $\square$